
Numerical Solution of Sasando String Motion Model
Ari Kusumastuti
1
, Muhammad Khudzaifah
1
, Heni Widayani
1
, and Aminatus Zuhriah
2
1
Department of Mathematics, UIN Maulana Malik Ibrahim Malang
2
Bachelor Degree of Mathematics, UIN Maulana Malik Ibrahim Malang
Jalan Gajayana No.10, Malang, East Java 65144
Keywords: Numerical solution, CTCS, String Motion, Sasando
Abstract: This study describes the problem of string motion on the Sasando musical instrument. This research focuses
on the numerical solution of Sasando string motion model which is a partial differential equation. The
method used to find out the numeric solution is CTCS (Central Time Central Space) method. The explicit
formula of discretization and Von Neuman stability analysis are considered here. The results show the
solution of is stable, which means the movement of the string toward the equilibrium value .
1 INTRODUCTION
Applied mathematics is needed in every part of life
especially to help solve problems related to
mathematical models. Mathematical modeling is a
field of mathematics that seeks to represent and
explain real problems into mathematical equations.
For example, the vibration phenomenon that occurs
along the strings of Sasando can be analyzed by
using mathematical model. The mathematical model
for this problem has been done by Kusumastuti, et
al(Kusumastuti & Brylliant, 2017).
Sasando is one of the traditional musical
instruments originated from Rote Island of Ndao
Regency of East Nusa Tenggara. The distinctive and
beautiful sound makes many people, not only local
people but also the foreign community interested to
examine how this instrument is able to create
beautiful sounds. The problem of string motion on
the Sasando musical instrument is a difficult
problem to analyze directly. Therefore, an effort is
needed to understand the problem, one of which is to
establish a proper measure that can represent the
problem in its real state. In mathematics, this is
known as the mathematical model. The
mathematical model for motion problems in the
Sasando musical instrument is seen as an abstraction
of the strings problem on the complex Sasando
musical instrument presented in the form of a
mathematical language. By modeling the strings on
the Sasando musical instrument, it can be seen the
vibration pattern of the string on the Sasando
instrument in the mathematical equation. Thus, the
understanding of the strings on the Sasando musical
instrument becomes more systematic and easier to
analyze further.
Purwanto, have done research on the analysis
and synthesis of sound signals generated from the
instrument of semi-acoustic guitar. In the study the
strings of the guitar were picked and then the sound
produced was recorded using the SOUND FORGE
program. The recording sound data is then analyzed
by FFT to obtain the sound signal spectrum, and the
components of the composer of the sound signal,
such as fundamental frequency, harmonic
frequency, amplitude, and amplitude ratio. Then the
sound signal construction based on the components
that have been obtained. And the results show that
by adding the damping factor to the sound signal
model make a similar sound with the original sound
from guitar. (Purwanto, et al., 2006)
This study is a follow-up study of previous
research by Kusumastuti, et al who has analyzed the
construction of a strap motion model on a sasando
instrument. In this work, numerical analysis is done
using finite difference method, i.e. Central Time
Central Space (CTCS). Triatmodjo states that finite
difference method is usually used to find the
numerical solution of partial differential equations.
Finite difference schemes approximate the solution
by discretization the partial differential equation.
Kusumastuti, A., Khudzaifah, M., Widayani, H. and Zuhriah, A.
Numerical Solution of Sasando String Motion Model.
DOI: 10.5220/0008525005370541
In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 537-541
ISBN: 978-989-758-407-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
537

CTCS scheme is a numerical approach using a
central difference to the time and center difference
to space. (Triatmodjo, 2002)
From the above background explanation, the
authors have an idea to study the numerical solution
of Sasando string motion model using CTCS
Method.
2 SASANDO STRING MODEL
In general, the string position of Sasando musical
instrument as shown in Figure 1:
Figure1:Sasando String Position(Kusumastuti &
Brylliant, 2017)
Based onFigure1, string that make base tone do
is in the middle, i.e. string 16
th
(marked in blue).The
distance between these two hooks is 35 cm. The
location of the buffer holder is in the middle, so the
lengths on both sides of the string are the same (l).
The type of wire material used is nylon which has a
modulus of elasticityas
. The
modulus of elasticity constant of the Sasando strings
shows the degree of flexibility of the strings.
Kusumastuti, et al generated a string
mathematical model on the musical instrument
Sasando which classified as hyperbolic PDE given
by:
02
2
1
2
2
2
2
2
=
+
+−
t
u
k
x
u
l
c
c
t
u
d
(1)
The construction of a string mathematical model
on the Sasando musical instrument is formed from
the use of the laws of physics. Fingerpicking given
to the Sasando strings generate potential energy ()
and kinetic energy () along the string.
The potential energy () of the Sasando strand
represents the total of each potential energy
occurring on the Sasando strings. In the case of the
Sasando strings being picked, there are several
potential energies that occur, among which are :
1. Spring Potential Energy
as:
(2)
2. Stress potential energy
as:
(3)
3. Friction potential energy
as:
(4)
From equation (2), (3), and (4) can be generated
potential energy for Model
which is the
overall potential energy, so can be written as
(5)
When the strings of Sasando are struck an
oscillatory motion occurs on the strings, so there is
kinetic energy on the Sasando strings. Kinetic
energy on the Sasando strings is defined as follows:
(6)
The next step is to determine the Lagrange equation.
The Lagrange equation is defined as the difference
between the kinetic energy model
and
the model potential energy
, so that the
Lagrange equation is obtained as follows:
(7)
By deriving the Lagrange equation in equation
(7), we find the equation (1).
Based on equation (1) there are several parameters,
namely:
1. The length of the strings of Sasando , is the
distance Between the two ends of the Sasando
string is 16 cm.
2. The damper constant
that affects the
wavelength during the insulated string is 1.5.
3. The speed of elasticity (c) is
and the
function is expressed as follows:
with initial condition as
and
and boundary condition as
and
for
ICMIs 2018 - International Conference on Mathematics and Islam
538

(Kusumastuti & Brylliant, 2017)
3 MAIN RESULTS
3.1 Discretization
Strauss in (Strauss, 1983)states that the finite
difference method is a common method to solve
differential equation, ordinary or partial differential
equations. This method based on the Taylor series
expansion. For partial differential equation with two
independent variables, i.e. space () and time () the
stability and convergence depend on the used
scheme. For hyperbolic PDE with proper initial and
boundary condition, central scheme for space is
commonly used to approximate the second order
derivative of space. Then, forward, backward, or
central scheme could be used for time variable.
Implementation of forward scheme of time in
simulation more simple than backward scheme
which used inverse matrix calculation.
Let with
and
with As stated in(Burden & Faires,
2011), the Euler explicit scheme for
at
can be written as
(8)
We central scheme for second order derivative of
time. Central Time Central Space (CTCS) scheme
to approximate second order derivative of time and
space can be written as:
(9)
(10)
Substitution of (8), (9), and (10)approximation to
hyperbolic PDE (1) and do some tedious calculation
give the discretization scheme as
(11)
where
3.2 Stability Analysis
The scheme stability was done using Von Neumann
stability test. It said stable if, Substitution
of
to equation (3.5) give us
or equivalent with equation below
Since
, then
=
multiplied by , then we get
or
(3.6)
So, the roots of (3.6) are
Since equation (12) contains cosα, in this case we
choose the discrete point which is
and. From tedious
calculation obtained sufficient condition for
is
While sufficient condition for
is.If
, the guarantee that discretization
scheme will be stable.
3.3 Numerical Simulation
With the value of = 16 cm,
= 1.5, = 1 m/s
2
,
substituted to equation (3.5), then the numerical
scheme is
(13)
Numerical Solution of Sasando String Motion Model
539
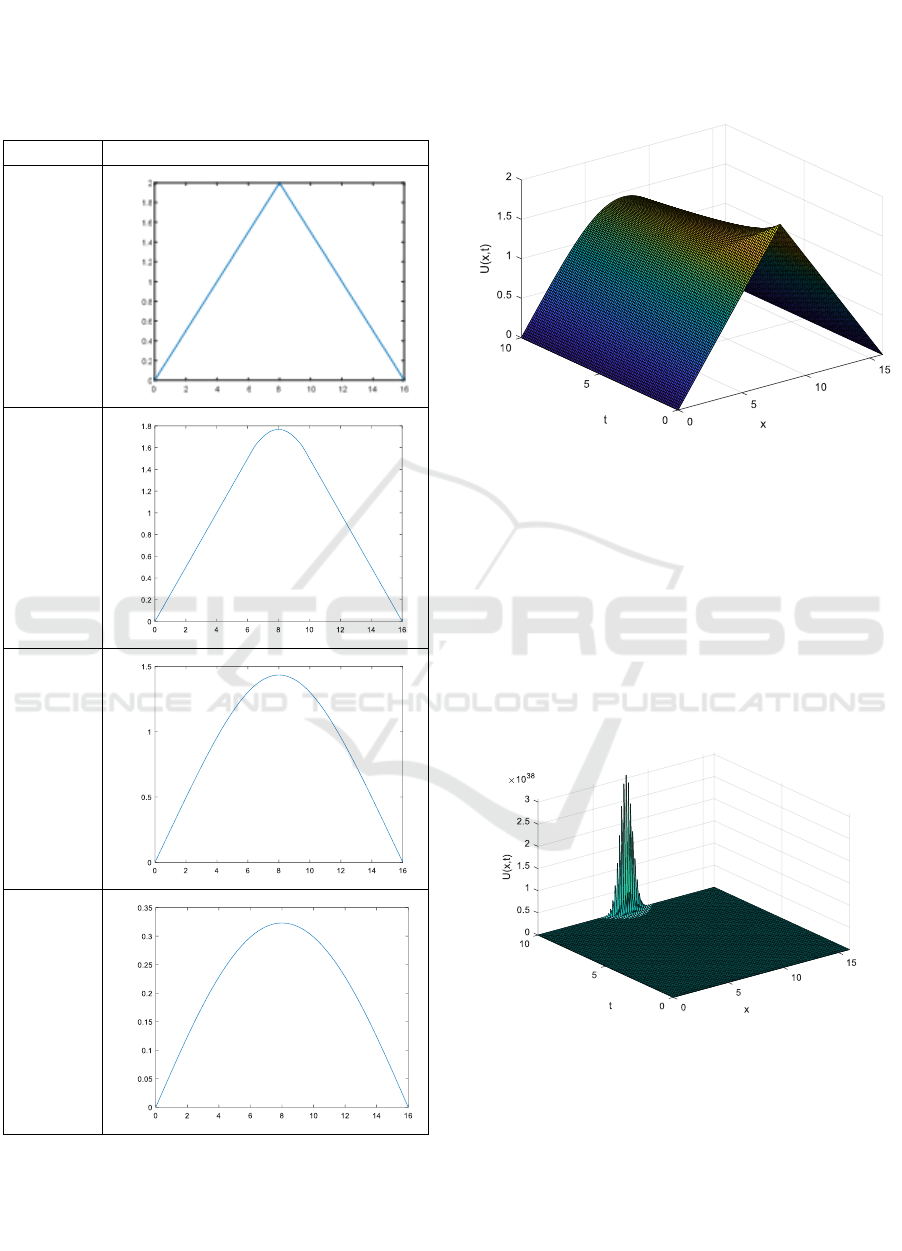
The graph simulations were performed using
MATLAB R2017b, with a numerical solution for
equation (13). Taken Δt = 0.1, resulting in graph
output as follows:
Table 1. Numerical Solutions of equation (1) with Δt = 0.1
Output
Table 1 shows the simulation results of the graph
for equation (13) with Δt = 0.1, describing the
movement of the Sasando stretch deviation which
changes to the value of t where .
From Table 1 above shows that the higher the
value, the Sasando strings toward the equilibrium
point .
The graphical output when Δt = 0.1 for equation
(13) using Matlab is as follows:
Figure2:Three-dimension solution of Sasando string
motion with
Figure 2 shows the simulation results of the
numerical solution of the wavelength model on the
Sasando musical instrument when
illustrates the movement of the deviation which
changes to the values of x and t, and from the graph
shows that the result of the graph is stable where the
movement of the string goes to the equilibrium point
(0.0).
While the graph output when Δt = 0.2 for
equation (13) using Matlab is as follows:
Figure 3: Three-dimension solution of Sasando string
motion with
Figure 3 shows the simulation results of the
numerical solution of the wavelength model on the
Sasando musical instrument when Δt = 0.2 describes
the deviation movements that are changing against
the values of x and t, and from the graph shows that
the results are unstable.
ICMIs 2018 - International Conference on Mathematics and Islam
540

From the results of Table 1, Figure 2 and Figure
3, it can be concluded that the movement of strings
on the Sasando musical instrument is stable with the
condition Δt ≤ 0.1 which means higher, Sasando's
strings move closer to the equilibrium point (0.0).
REFERENCES
Burden, R. L. & Faires, J. . D., 2011. Numerical Analysis.
Ninth Edition penyunt. Boston: Brooks/Cole.
Kusumastuti, A. & Brylliant, D. N., 2017. Analisis
Konstruksi Model Gerak Dawai pada Alat Musik
Sasando, Malang: UIN Maulana Malik Ibrahim
Malang.
Purwanto, A., S. & Saputra, E. R., 2006. Analisis dan
Sintesa Bunyi Dawai pada Gitar Semi-Akustik.
Yogyakarta, Fakultas Matematika dan Ilmu
Pengetahuan Alam UNY, pp. 240-246.
Strauss, W. A., 1983. Partial Differential Equations an
Introduction. Second Edition penyunt. New York:
John Wiley & Sons, Ltd.
Triatmodjo, B., 2002. Metode Numerik Dilengkapi dengan
Program Komputer. Yogyakarta: Beta Offset.
Numerical Solution of Sasando String Motion Model
541
