Estimated Optimum Internal Illuminance Distribution based on

Standard Deviation and Mean of Variation of Window Opening

Position in a Room

Gramandha Wega Intyanto

, Yose Rizal

, Eko Mulyanto Yuniarno

and Yoyon Kusnendar Suprapto

Department of Electrical Engineering, Institut Teknologi Sepuluh Nopember (ITS), Surabaya, 60111, Indonesia

Department of Computer Engineering, Institut Teknologi Sepuluh Nopember (ITS), Surabaya, 60111, Indonesia

Department of Architecture Engineering, Universitas Lancang Kuning, Pekanbaru, 28265, Indonesia

Keywords: Daylight, Internal Illuminance, Sky Component, Standard Deviation.

Abstract: Lighting system is one of the factors that affect the psychological comfort and user activity of a building.

Lighting in a room during the day is obtained from the sunlight, diffusion of light in the sky (cloud

overcast), and reflection of light from the surrounding environment. The light received indoors is influenced

by window openings, which should meet the size requirement under the SNI (Indonesian National Standard)

of at least 1/6 of the room area. Previous research only discussed the optimal size of window openings of a

room. This time the researchers sought the ideal window opening position of three different window

opening positions in one spatial field. Investigation of internal illuminance distribution was carried out by

calculations of sky component on the daylight factor. The internal illuminance distribution investigation

results obtained from the sky component calculations were later analyzed with standard deviation and

average. According to the analysis in this study, the greater the average and the smaller the standard

deviation, the better the distribution value of the room. From the analysis in the simulations carried out by

the researchers based on calculations, it can be concluded that the window’s position in the middle of the

wall has the optimal distribution. Further research is expected to be useful to architects in window position

decision-making in accordance with activity requirements to optimize energy saving by minimizing the use

of artificial lights at the daytime.

1 INTRODUCTION

Natural lighting is the most influential spectrum of

adaptation of human vision. Daylight consideration

in a room is based on human activity in the room.

The most important thing of natural lighting is that it

can affect the psychology of the inhabitants indoors.

It also allows for energy saving through the

reduction of the use of artificial light (Looman,

2017). The distribution of natural lighting in a room

depends on three factors: the geometry of the room,

the placement and orientation of the window as well

as other openings, and internal surface

characteristics (Code et al., 2001).

An opening can be oriented to receive direct

sunlight in certain times of day. The dimensions of a

window or openings can control the amount of light

that enters the room. Apertures can be oriented away

from direct sunlight and receive very strong lighting

from the dome of the sky (Acosta et al., 2015). The

dome of the heavens is a very constant source of

light, even in cloudy skies. In addition, cloudy sky

conditions can soften the direct sunlight and provide

balanced distribution of lighting levels in the room

(Phillips, 2004).

The amount of light can be measured using the

luminace value (flux, lighting), i.e., by assuming the

light from the outside and calculating the lighting

inside an interior space or using the amount of

relative daylight factor, i.e., by calculating the

lighting ratio at the indoor measurement point with

outdoor lighting (Rizal, Robandi and Yuniarno,

2016). The value of the daylight factor remains—the

illumination outside the room corresponds to the

indoor illumination; if it is dim outside, the indoors

will be dim too. To figure out the optimum

illumination in a room among different variants of

window opening positions, the researchers

conducted research by looking for mean and

standard deviation. The space with the largest

Intyanto, G., Rizal, Y., Yuniarno, E. and Suprapto, Y.

Estimated Optimum Internal Illuminance Distribution based on Standard Deviation and Mean of Variation of Window Opening Position in a Room.

DOI: 10.5220/0008903900002481

In Proceedings of the Built Environment, Science and Technology International Conference (BEST ICON 2018), pages 5-10

ISBN: 978-989-758-414-5

average and the smallest standard deviation was

considered the optimal one.

2 DAYLIGHT FACTOR AND

WINDOW OPENING

2.1 Daylight Factor

Figure 1: Daylight factor (Rizal, Robandi and Yuniarno,

2016).

Daylight factor is the ratio of the internal

illuminance value at the reference point in the room

and the external illuminance. These values are

obtained in the state of daylight as shown in Figure 1

(cloudy sky conditions or conditions of no sunlight

and at the same time) (Rizal, Robandi and Yuniarno,

2016). The definition of daylight factor is

represented in equation (1).

(1)

Factors that influence the daylight factor at a

point in a room are as follows:

• Sc, the illuminace that reaches the reference

point in the room directly from the sky;

• ERc, the illuminace that reaches the reference

point in the room, which is influenced by the

reflection of existing surfaces outside the room,

such as buildings and streets; and

• IRc, the illuminace that reaches the reference

point in the room, which is influenced by the

reflection of the surface in the room, such as

material, wall color, etc.

The sum of the above three factors produces Df

as represented in equation (2) (Code et al.,

2001)(Cibse, 1999).

(2)

2.2 Window Opening Composition

Window is a component that is often used in

buildings and has a great influence in regulating the

entry of light in the room. Functional design and

shapes of a window have the advantage of

maximizing incoming light in a room that affects the

activity of the occupant or user in the room. In

addition, window has the advantage of minimizing

the use of artificial lighting. Window size, position,

characteristics, and relationship with the wall surface

can define the light in the room. For this task, the

development of façade technology sets the most

important window element to ensure the quantity of

natural light in the room, followed by two elements

of window composition, namely the size and

position of the window placement (Acosta,

Campano and Molina, 2016).

Window dimensions and positions affect the

amount, distribution or penetration, as well as the

diversity of natural light. Dimensions (height and

width) of exposed walls on facades with window

positions affect the transition of natural light

(Iversen et al., 2013). High positioning of a window

will affect the natural light penetrating the room,

while the width of the window affects the evenness

of the distribution of natural light in the room (IEA,

2000).

3 ESTIMATED OPTIMAL

INTERNAL ILLUMINANCE

DISTRIBUTION

3.1 Window Opening Variants

In this paper, the estimation of internal illuminance

distribution was performed on window opening

variants of a 12 m

(4 m long and 3 m wide) room.

For the window to meet the size requirement of 1/6

of the room area, it should have the size of 2 m

(1.33 m wide and 1.5 m tall). There were 3 variants

differentiated by the position of the window

openings horizontally.

Figure 2: Three variants of window openings horizontally.

(A: against the corner of the window, B: against the

intersection of the window opening, C: against the outer

window).

BEST ICON 2018 - Built Environment, Science and Technology International Conference 2018

The window position was horizontally shifted to

the middle position (Sample A), the edge position

(Sample B), and the corner position (Sample C). The

positions of the window openings can be seen more

clearly in Figure 2. Meanwhile, the size and position

of the window landing against the room are outlined

in Table 1.

Table 1: Three variants of window opening horizontally

Sample

Window

Position

Distance of

the bottom of

the window

to the floor

Distance of the

right side of

the window to

the wall

A Middle 0.75 0.835

B Edge 0.75 0.435

C Corner 0.75 1.67

3.2 Calculation of Sky Component

Sky component is the most influential in daylight

factor as seen in equation (2). The calculation of the

sky component value in this paper was derived from

the calculation of window dimensions (rectangular-

shaped) and the distance to the floor point in the

room by utilizing the BRE table (Cie Standard

Overcast Sky) (Mangkuto, 2017). The dimensions of

the window in question include the window height,

width, and distance to the point representing the

average of the surrounding area on the floor as

shown in Figure 3.

Figure 3: Three-variable calculation

The point on the floor generated by the sky

component is called a reference point. The value at

this reference point will be used to distribute the

internal illuminance. The reference point was

obtained by determining the minimum distance limit

under the window to the floor, namely 0.75 m. If the

distance of the bottom of the window to the floor

exceeded 0.75 m, the additional distance would be

calculated. The sky component estimate was based

on the reference point against the window angle as

shown in equation (3).

(3)

3.3 Calculation of Sky Component

After obtaining the sky component value as

described in equations (3) and (4), we distributed the

internal illuminance in accordance with the

condition of the room area. The internal illuminance

distribution was performed in several stages. The

first stage was dividing the room in a grid. The grid

value was filled from the reference point of the sky

component and represented the average distance

value of the grid area. In the next stage, the internal

illuminance value was input into the daylight factor

formula in equation (5).

3.3.1 Grid Distribution

Prior to estimating the internal illuminance

distribution based on the sky component (Sc), a grid

was first made to determine the 0.2 m

grid spacing

reference point. Grid preparation in each room had

the purpose to include the internal illuminance value

at each midpoint of the grid based on the sky

component at the reference point. The internal

illuminance value was the average of the grid area

(0.2 m

) as shown in Figure 4.

Figure 4: Grid Distribution

3.3.2 Entry of the Sky Component Value on

Each Grid

The value of component sky was derived from the

window dimensions. This value is one of the most

influential in daylight factor. In addition, the value

of daylight factor is and , but the value of both was

ignored. This is because the effect of reflection in

the room, such as refraction of the color of the walls,

objects in the room, materials, among others, was

Estimated Optimum Internal Illuminance Distribution based on Standard Deviation and Mean of Variation of Window Opening Position in a

Room

not used, and neither was the influence of the

reflection outside the room, such as the reflection of

buildings and objects outside. So the only factor

affecting Df that was considered in this paper was Sc

as seen in equation (4).

(4)

3.3.3 Calculating Internal Illuminance

After the daylight factor value based on sky

component was obtained, the Ei (internal

illumination) value was found with equations (4) and

(5), that is Daylight Factor ratio. The daylight factor

value was derived from the sky component value.

The external illumination was 3000 lux. This value

was obtained under the average external illumination

condition in Indonesia in April. Then, the internal

illuminance value was obtained as seen in equation

(5).

(5)

Afterwards, the internal illuminance distribution

in the room based on the window variants was

obtained as seen in Table 2.

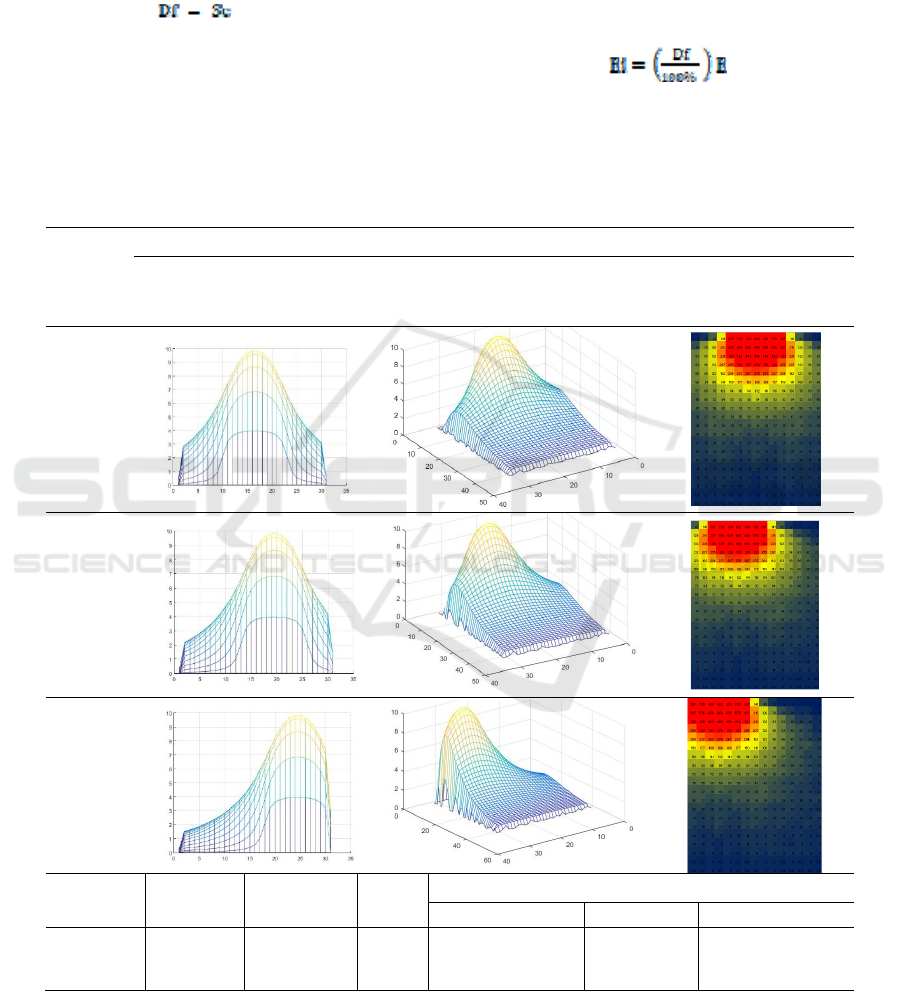
Table 2: Results of the analysis of the illumination distribution for three window opening variants

Sample

Room

Room View

The front

(Window Opening)

(Df in Room (%))

The back side

(Df in room (%))

The top position

(Ei in Room (lux))

Sample

Window

Position

Standard

Deviation

Mean

Internal illuminance Percentage Value

High (%) Average (%) Low (%)

A middle 148.1 95.58 10 27 63

B edge 148.8 93.46 9.7 24.3 66

C corner 149.5 86.2 9 20 71

BEST ICON 2018 - Built Environment, Science and Technology International Conference 2018

4 RESULTS AND ANALYSIS

4.1 Analysis of the Internal illuminance

distribution

After the internal illuminance distribution value of

the sky component was obtained, it was then

analysed to determine the optimal window variant

among the three variants of the window positions.

The analysis of the distribution used standard

deviation and mean equations. The standard

deviation of the internal illuminance in a

predetermined room was found using equation (6).

(6)

Meanwhile, the mean of the internal illuminance

in the room was found using equation (7).

(7)

4.2 Internal illuminance distribution

Results

The results of the analysis of the internal

illuminance distribution was illustrated using colors

(Table. 2), with the lowest illuminance of 0–65 lux

being represented by dark blue-yellowish blue,

medium illuminance of 66–237 lux being

represented by yellow-orange, and the highest

illuminance of 238–822 lux being represented by

orange-bright red. The analysis of the window

samples is described below.

4.2.1 Sample A

The room with a window in the middle had three

areas, namely one with the lowest illuminance of 0–

65 lux (63% dark blue area-yellowish blue), one

with medium illuminance of 66–237 lux (27%

orange), and one with the highest illuminance of

238–822 lux (10% orange-bright red), with

illumination tending to be distributed in front of the

window. From the 300 reference points in the

sample area, a mean (AEi) of 86.2 lux and a

standard deviation (SEi) of 149.5 lux were obtained.

4.2.2 Sample B

The room with a window located on the edge had

three areas, namely one with the lowest illuminance

of 0–65 lux (66% dark blue-yellowish blue), one

with medium illumination of 66–237 lux (24.3%

orange), and one with the highest illuminance of

238–822 lux (9.7% orange-bright red), with

illumination tending to be distributed in front of the

window. From the 300 reference points in the

sample area, a mean (AEi) of 93.46 lux and a

standard deviation (SEi) of 145.8 lux were obtained.

4.2.3 Sample C

The room with a window located in the corner had

three areas, namely one with the lowest illuminance

of 0–65 lux (71% dark blue-yellowish blue), one

with medium illuminance of 66–237 lux (20%

orange), and one with the highest illuminance of

238–822 lux (9% orange-bright red), with

illumination tending to be distributed in front of the

window. From the 300 reference points in the

sample area, a mean (AEi) of 86.2 lux and a

standard deviation (SEi) of 149.5 lux were.

Based on the description of Sample A, Sample B,

and Sample C, we show the results of the

explanation in the Df and illumination value on the

number of sides of the 3D reconstruction (from the

simulation we created) as in Table 2.

5 CONCLUSIONS

Based on the standard deviation and mean values,

the room with the biggest mean and the smallest

standard deviation of the three sample rooms was

the room which had the most optimal value of

internal illuminance distribution. It can be concluded

that in this study, of the three room samples studied,

the position of window openings that had the

optimal internal illuminance distribution value was

one of Sample A, with the window opening

positioned in the middle of the wall plane.

The more the window opening position is away

from the side of the wall, the smaller the value of the

internal illuminance distribution, meaning that if the

room is far apart, the opening of the window will

darken. On the contrary, if the wall is closer to the

window opening, the value of the internal

illuminance distribution will be greater, meaning

that the room will be brighter.

This research proves quantitatively that the

position of window openings can affect the value of

sky component on daylight factor and internal

illuminance. This is evidenced when the window

openings in the room are shifted, the value of

Estimated Optimum Internal Illuminance Distribution based on Standard Deviation and Mean of Variation of Window Opening Position in a

Room

daylight factor and internal illuminance at the

reference point will change.

REFERENCES

Acosta, I. et al. (2015) ‘Analysis of the accuracy of the

sky component calculation in daylighting

simulation programs’, Solar Energy, 119, pp. 54–

67. doi: 10.1016/j.solener.2015.06.022.

Acosta, I., Campano, M. A. and Molina, J. F. (2016)

‘Analysis of Energy Savings and Visual Comfort

Produced by the Proper Use of Windows’,

International Journal of Engineering and

Technology, 8(5), pp. 358–365. doi:

10.7763/IJET.2016.V8.913.

Cibse (1999) ‘Daylighting and window design.’, CIBSE,

Publicaciones IDAE, LG10_1999, pp. 8–98.

Code, N. E. et al. (2001) Tata cara perancangan sistem

pencahayaan buatan pada bangunan gedung ., Sni

03-6575-2001.

IEA (2000) ‘Daylight in Buildings’, Task 21/ ECBCS

Annex 29, 03(3), p. 262. doi:

10.1001/jama.1936.02770020010056.

Iversen, A. et al. (2013) Daylight calculations in practice.

Looman, R. (2017) Architecture and the Built

environtment. Available at:

http://www.nrel.gov/docs/fy00osti/28049.pdf.

Mangkuto, R. A. (2017) ‘Akurasi Perhitungan Faktor

Langit dalam SNI 03-2396-2001 Tentang

Pencahayaan Alami pada Bangunan Gedung The

Accuracy of Sky Component Calculation in SNI

03-2396-2001 on’, (December 2016).

Phillips, D. (2004) Daylighting. Natural Light in

Architecture., Industrial medicine & surgery. doi:

10.1016/j.enbuild.2006.03.005.

Rizal, Y., Robandi, I. and Yuniarno, E. M. (2016)

‘Daylight Factor Estimation Based on Data

Sampling Using Distance Weighting’, Energy

Procedia. The Author(s), 100(September), pp. 54–

64. doi: 10.1016/j.egypro.2016.10.153.

APPENDIX NOMENCLATURE

Daylight factor

Internal illuminance

External illuminance

Sky component

Internal reflection component

External reflection component

Window opening height

Window opening width

Distance of the window opening to the

reference point

The mean of internal illuminance

Standart deviation total internal illuminance

Reference point

Total reference point

BEST ICON 2018 - Built Environment, Science and Technology International Conference 2018