Topolet: From Atomic Hand Posture Structures to a Comprehensive

Gesture Set

Amin Dadgar and Guido Brunnett

Computer Science, Chemnitz University of Technology, Straße der Nationen 62, 09111, Chemnitz, Germany

Keywords:

Generative Poselet, Topolet, Topological-based Temporal Model, Hidden Markov Model, Gestures’ Compre-

hensive Set, Context-Free Gesture Recognition, Description-based (Data) Speciﬁcation.

Abstract:

We propose a type of time-series model for hierarchical hand posture database which can be viewed as a

Markovian temporal structure. The model employs the topology of the points’ cloud, existing in each layer

of the database, and exploits a novel type of atomic structure, we refer to as Topolet . Moreover, our temporal

structure utilizes a modiﬁed version of another atomic gesture structure, known as Poselet. That modiﬁcation

considers Poselets from the vector-based generative perspective (instead of the pixel-based discriminative

one). The results suggest a considerable improvement in the accuracy and time-complexity. Furthermore,

in contrast to other approaches, our Topolet is capable of considering random gestures, thus introduces a

comprehensive set of gestures (suitable for context-free application domain) within the shape-based approach.

We prove that the Topolet could be enhanced to different resolutions of gestures’ set which provide the system

with the potential to be adapted to different application requirements.

1 INTRODUCTION

Hand gesture recognition systems would beneﬁt from

a number of atomic structures within postures which

could capture the temporal information necessary to

relate a large set of postures to different gestures ef-

ﬁciently. These atomic structures would systemat-

ically construct interrelationships between different

postures, and thus relate different gestures more effec-

tively. Such structures could eradicate the necessity

of repetitive recording of similar postures and distinct

modeling of their temporal relation in different ges-

tures. Therefore, they exhibit potentials to resolve the

issue of high time-space complexities when a com-

prehensive/random gestures’ set is considered.

In the context of human body pose/action recog-

nition the novel idea of Grouplets was proposed by

(Yao and Fei-Fei, 2010). From that Orderlet (Yu

et al., 2015) and Gesturelet (Meshry et al., 2016)

for body pose, and Poselet (Bourdev and Malik,

2009) for hand gesture recognition were derived.

These Grouplets provide tools to formulate atomic

structures, however, they have a number of limita-

tions: First, they are action-dependent and thus, can-

not consider a random and comprehensive set of ac-

tions/gestures. Second, they lack an effective tem-

poral relationship, as the number of features are too

large. Finally, all these features are deﬁned as the

Figure 1: The data structure and the degree-of-freedom for

each (sub)layer: global translation (Tr, layer 1) with 3DoF,

global rotation (Arm, layer 2) with 3DoF, wrist rotation

(Wr, layer 3) with 2DoF, little ﬁn states (ﬂ, 3DoF), mid-

dle ﬁn states (fm, 3DoF), index ﬁn states (ﬁ, 3DoF), thumb

ﬁn states (ft, 4DoF), inter-ﬁnger states (Intr, 4DoF).

discriminative features on pixel-level data. That type

of data are highly dependent on camera view-point.

Therefore, any possible smaller structures on pixel-

level hardly follow a unique arrangement. Addition-

ally, pixel-level features may be invisible for a con-

siderable time interval. Therefore, robust sequential

relation could not be derived.

To address the last issue, we employ the pose-level

vector of hand. The hand’s pose-vector introduces

a type of data which can robustly be trackable over

time. The high degree-of-freedom (28), and thus the

presence of enormous number of states, is resolved

by employing the hierarchical database proposed by

(Dadgar and Brunnett, 2018). There, each posture is

restructured by a set of sub-vectors and layers ( Figure

1). Furthermore, for a set of postures that the database

Dadgar, A. and Brunnett, G.

Topolet: From Atomic Hand Posture Structures to a Comprehensive Gesture Set.

DOI: 10.5220/0007244701570164

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 157-164

ISBN: 978-989-758-354-4

157

Figure 2: An example of allowable transition for the Topo-

let of layer 2 (global rotation) to the neighboring Poselets in

that space. The skeletons indicate the hidden states (in 3D

pose conﬁguration space), and hand meshes indicate obser-

vation states (in 2D pixel space).

contains, each layer’s space consists of an equal num-

ber of points. We consider these points as one type of

our atomic structures (the generative Poselet).

Hidden Markov Model (HMM) (Rabiner, 1989)

has been frequently employed to acquire the tempo-

ral information of hand gesture between successive

frames and describe that gesture by a sequence of

states (Yang et al., 1994). Our novel method of ac-

quiring temporal information extends the speciﬁca-

tions of HMM to the topology of the layers in our

hierarchical database. Our divide-and-conquer ap-

proach considers each of the mentioned generative

Poselet as one hidden state of our HMM-like method.

At each point in time only a few Poselets (features)

are relevant to construct a posture as the gesture pro-

ceeds, thus the second issue would be addressed.

To overcome the ﬁrst issue, our procedure re-

duces the number of required temporal models to one-

model-for-one-layer. This approach is in the con-

trary of the conventional one-model-for-one-gesture

method. Therefore, for any gestures one requires

to have only a limited (but ﬁxed) number of HMM-

like structure. One can use our structure to construct

a comprehensive gestures’ set or enable a context-

free (gesture-independent) application domain recog-

nition. Since our temporal information is acquired

based on the topology of each layer we refer to it as

the Topolet (topology + Poselet, Section 3.1).

In our results ( Section 4) we prove the ﬂexibility

of the model in dealing with different resolutions of

the postures’ set based on shape feature. Moreover,

we demonstrate the potentials of our Topolet to per-

form the gesture recognition task in real-time.

2 RELATED WORK

Hand gesture is inherently stochastic (Yang et al.,

1994). That is, if a person repeats (or if a group of

individuals performs) a certain gesture, the measure-

ments of that gesture will be different. That implies,

there are hidden speciﬁcations which are common in

the different recordings for one certain gesture (Yang

et al., 1994). In the ﬁeld of hand gesture recognition,

(Yang et al., 1994) employed nine HMMs for recog-

nizing nine 2D gestures in drawing the digits from 1

to 9 with a mouse. These gestures were single-path

(palm point) ones and no details about ﬁnger poses

were estimated. To unfold the hidden patterns of ges-

tures, HMM needs an index of the previous state (s)

of the system together with the approximate dynam-

ics (a

i j

) of the system which would be represented in a

transitional matrix (A). Additionally, it is necessary to

store the same-class variations of the observations in

an emission matrix (B) together with the initialization

variable (π). To calculate and employ these variables

three standard problems must be solved (Rabiner,

1989): evaluation, decoding, and training. Standard

solutions to these problems, which relate them to each

other under Bayesian framework (Rabiner, 1989).

Bayesian semantics enable the HMM to cope with

uncertainties in both human performances and sens-

ing processes (Yang et al., 1994). The standard solu-

tions to these problems exhibit inefﬁciencies. In order

to more efﬁciently employ HMM for the purpose of

hand gesture recognition, the approach of collecting

the training data is an important decision.

There are two ways of collecting gestures’ data:

example-based and description-based (Yang et al.,

1994). Most gesture recognition systems employ the

example-based speciﬁcation because it shows more

ﬂexibility on small variations of one gesture (Yang

et al., 1994). However, its main drawback is the

difﬁ- culty of considering a large number of gestures

(Yang et al., 1994). The description-based speciﬁca-

tion was applied to the ﬁeld of sign language (Starner

and Pentland, 1995) and was capable of consider-

ing greater number of gestures. However, because of

lacking a meaningful relation between the syntaxes

and the hidden states, the description-based speciﬁca-

tion exhibits two main problems: First, the number of

learned HMMs has to be still large (Yang et al., 1994).

Second, slight variations of the same gestures can be

easily misclassiﬁed. In order to acquire a comprehen-

sive temporal information, description-based speciﬁ-

cation is a preferable method of data collection, how-

ever its two drawbacks must be addressed ﬁrst. To

address those issues, we extend the HMM’s speciﬁ-

cations to a topology-based scheme ( Section 3.1).

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

158

Figure 3: Next posture (P

) in a gesture sequence mod-

eled with eight parallel HMMs (Pl means Poselet). Bigger,

lower and equal indexes of next Poselets indicate forward,

backward, and no transitions, respectively.

3 METHODOLOGY

One main difﬁculty with HMM is to determine an ap-

propriate number of hidden states (Sangjun et al.,

2015). That especially is a problem when HMM is

employed to model random/comprehensive gestures’

set. That is, when a large number of gestures with var-

ied lengths is to be recognized, the number of states

also must be altered. In order to model all gestures the

underlying structure of the acquired temporal infor-

mation should be ﬂexible to considerable modiﬁca-

tions. That obliges the system to repetitively perform

that difﬁcult task of state-number estimation. We ef-

fectively address that issue by employing the genera-

tive Poselets as the states in each (sub)layer. Since the

number of Poselets in each (sub)layer is ﬁxed, there-

fore, the number of states and thus the structure of our

HMM-like Topolet also remains unchanged.

Our proposed Topolet could also effectively ad-

dress the ﬁrst problem of description-based speciﬁca-

tion (Section 2). More speciﬁcally, we utilize one-

HMM-for-one-layer training scheme based on the

topology of the points’ trajectory in each (sub)layer

(nearest neighbors of each Poselet). Therefore, us-

ing these atomic structures, Poselet and Topolet, the

number of HMM-like structures will be ﬁxed to the

number of (sub)layers (e.g. eight). Therefor, the issue

of linear growth of the complexities with the number

of considered gestures is effectively addressed.

We also propose an effective novel method to cal-

culate the emission matrix. More speciﬁcally, we

model the same-class variations of the Poselets, and

thus postures/gestures, based on the inter-topological-

spaces between the neighboring Poselets. That could

eliminate the necessity of recording several gesture

sequences which belong to an identical class and in-

crease the ﬂexibility of the system when slight vari-

ations in gestures are observed. Therefore, it ad-

dresses the second issue existing in the construction

of description-based database.

The entire temporal information is encoded in all

these layered-wise HMM-like structures in parallel

(Figures 2 and 3). That is, one posture is constructed

by orderly-connecting all Topolets at each point in

time. A gesture also is formed by considering all these

Topolets over a period of time. To acquire the Topo-

lets, however, it is necessary to appropriately modify

the solutions to the standard problems of HMM.

3.1 Topolet: Temporal Information of

Poselet’s Topoloy

Data Structure: The Poselets’ vector (

−→

Pl) for each

(sub)layer is as follow (See Figures 1 and 3):

= {p

, p

}: global translation (p, position),

= {a

}: global (Arm) rotation (a, angels),

= {w

,}: wrist rotation (angel),

= { f l

, f l

}: little ﬁnger ( f l) states,

= { f r

, f r

}: ring ﬁnger ( f r) states,

= { f m

, f m

}: mid ﬁnger ( f m) states,

= { f i

, f i

}: index ﬁnger ( f i) states

= { f t

, f t

}: thumb ﬁn ( f t) states and

= { f l

, f r

, f m

, f i

} inter ﬁnger states, where

u,m, and l denote the upper part, middle part and the

lower part of each ﬁnger, respectively.

Database Enhancement: To introduce the required

modiﬁcations to HMM structure we enhance the pre-

viously proposed database (Dadgar and Brunnett,

2018) in two directions. First, we form the global

(forearm) rotation layer (L

) using the quaternions

(instead of Euler angles). That assists us to eradi-

cate the duplicated rotations introduced by Euler axis

uniform quantization. Second, we loosely divide the

ﬁnger-state layer (L

) into ﬁve sub-layers (little ﬁnger

, ring L

, middle L

, index L

,and thumb L

Figure 1). That facilitates the system to consider one

Topolet for each ﬁnger. Furthermore, these two en-

hancements enrich the gestures vocabulary that could

be considered by our system.

Parameters of the Topolet: We determine the en-

tire temporal information of all gestures as a set of

parallel Topolets: Λ = {T l

,T l

|i = [1,5], j = [1,5]},

where T l denotes a Topolet, i is the layer index and j

is the ﬁnger index. The Topolet of layer i is deﬁned as:

T l

= {Pl

,π

}, where Pl denotes a Poselet,

s is index of the Poselet in the layer, A

marks the

transitional matrix, B

deﬁnes the emission matrix,

and π

determines the initialization variable of the

Topolet for that layer. In our implements, we assume

that the detection and localization of hand is a solved

problem. Therefore, we do not consider the layer one

Topolet: From Atomic Hand Posture Structures to a Comprehensive Gesture Set

159

a) b) c) d) e) f) g)

Figure 4: Topology of the layers for Arm-rotation (Figure a), Wrist-rotation (Figure b), Inter-Finger states (Figures f and g),

and sub-layers Little-Fingers states (Figure c) and Thumb-Finger states (Figure d and e) in Low-resolution (LD). The little,

ring, index, and middle state spaces are similar (Figure c). Therefore, only one ﬁnger is shown.

in this work.

Transitional Matrix A

: According to the above

data structure and the Figures 1 and 4, the Poselets

of the layers L

, L

, and L

are situated on lattices (n-

orthotope). More speciﬁcally, Layers two (L

), three

), and ﬁve (L

) are 3-orthotope (cube), 2-orthotope

(rectangle), and 4-orthotope, respectively. We con-

sider each point in the lattices as the hidden state of in

our HMM-like structure. Therefore, the topological-

based formation of the transitional matrix for each

layer using n-nearest-neighbors scheme is as follow-

ing: For any given Poselet (current-state) we ﬁnd the

-nearest-neighbors (n

possible next-states) in that

speciﬁc lattice. These neighbors determine the possi-

ble transitions from each Poselet at each point in time

to other Poselets. The speciﬁc topological structure

of each layer introduces a particular number of neigh-

bors for any current state in that layer. For example, in

layer L

, which has a rectangular topology, the local

number of neighbors for each state, n

, when n = 1,

is either 2, 3, or 4 (green and orange Poselets in Fig-

ures 9.b). Based on that local number of neighbors

the transitional probability to a speciﬁc state is set as

1/n

. Thus, the transitional matrices for these layers

) are constructed.

The transitional matrix of Layer 4 (L

), which

consists of ﬁve sub-layers of ﬁnger-states, is com-

puted by a different approach. In that layer, little,

ring, middle, and index ﬁngers each contains 3DoF

and thumb has 4DoF topological structure ( Figure 1),

but the Poselets do not form complete lattices ( Fig-

ure 4.c-e). Therefore, n-nearest neighbors cannot be

computed correctly. But the number of states for each

ﬁnger is limited, hence the possible transitions be-

tween these states are visually determined ( Figure 6).

These transitional matrices for ﬁngers are speciﬁed as

. In our implements, we set n = 1. However,

other values (such as n = 2, Bakis model (Rabiner,

1989)) which suit different system/application spec-

iﬁcations (e.g. camera frame-rate) are also possible.

Furthermore, our Topolet handles the self-transition.

That facilitates the system to recognize the stationary

(alongside with dynamic) gestures which remain at a

speciﬁc posture for an interval of time.

In addition to the mentioned advantages, our

topology-based computation of the transitional ma-

trix extends the conventional HMM in the following

ways: First, it enables the system to consider the left-

right forward and right-left backward transitions both

at the same time and in one uniﬁed structure. Second,

the major problem with conventional HMMs is that

one cannot use a single observation sequence to train

the parameters. That is principally due to a large num-

ber of transient states exists between two main states.

Hence, to make a reliable estimation of all parame-

ters, one has to use multiple observation sequences.

In our Topolet, the training is performed based on the

topological positions of the trajectory points. There-

fore, one could train the inter-space of two states as

transient postures, and hence eradicate the necessity

of several observation sequences for training.

Higher-Resolution Transitional Matrix: To provide

the system with a richer set of postures, and hence

smoother gestures, a collection of higher-resolution

is calculated. These matrices are calculated based

on the layers of mid-resolution database (MD) which

contains higher number of Poselets ( Figure 5) as

compared to the low-resolution database (LD). Thus

the number of states and size of the transitional matri-

ces are increased. Enhancing the resolution of the lay-

ers L

is accomplished by uniformly increas-

ing the population of Poselets of these layers’ space (

Figure 5). However, the number of Poselets for each

ﬁnger (sub)layer is manually increased. For exam-

ple, different versions for Bend-state (Bend

, Bend

Bend

, and Bend

) are visually deﬁned ( Figure 6).

The calculated higher-resolution matrices, and

thus richer set of gestures, emphasizes an other im-

portant advantage of our Topolet. That is, the increase

in the size of the transitional matrices does not lead

to higher time-complexity during the search. This is

due to the fact that the local number of next Poselets

(states) is determined by the value of n, which in our

implementation is set to one (= 1). The topological

properties of these layers (n

) do not change after we

increase the resolution of them. Therefore, no extra

time-complexity is imposed to the system.

Initialization Variable π

: The initial state proba-

bilities are calculated similar to conventional HMM:

=⇒ {0, Pl 6= 1 and 1, Pl = 1}.

Emission Matrix B

: Conventionally HMM is de-

ﬁned as follows (Rabiner, 1989) (Yang et al., 1994):

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

160

a) b) c) d) e) f) g)

Figure 5: Topology of the layers for Arm-rotation (Figure a), Wrist-rotation (Figure b), Inter-Finger states (Figures f and g),

and sub-layers Little-Fingers states (Figure c) and Thumb-Finger states (Figure d and e) in Mid-resolution (MD). The little,

ring, index, and middle state spaces are similar (Figure c). Therefore, only one ﬁnger is shown.

Figure 6: Visually determining the transitions between ﬁn-

gers’ states. This ﬁgure shows the transitional matrix of the

ﬁnger states for the mid-resolution database. The allowed

transitions are marked with : a. Up, b. Forward, c. Half-

Bend

, d. Half-Bend

, e. Bend

, f. Bend

, g. Bend

, h.

Bend

, i. Half-Close

, j. Half-Close

, k. Half-Close

, l.

Half-Close

, m. Close. Notice that, in our implementation,

the self-transition is allowed.

Figure 7: Eight different paths of one gesture in experi-

ment 2 which is consisted of a sequence of 250 complete

(all-eight-layers) postures. At each point in time one com-

plete posture can be constructed by using all eight indexes

of Poselets in each layer.

If a multi (P)-path gesture has N (= 10) postures, the

size of the transition matrix will be 10 × 10. Further-

more, if there are M (= 5) gestures of the same class

in the observation/training data (with variations), the

size of the emission matrix will be N × M (10 × 5).

One main issue with this deﬁnition is the inaccu-

rate and inefﬁcient determination of the number of

emissions. More speciﬁcally, we cannot systemati-

cally determine how many same-class variations of

a gesture should be recorded to calculate the emis-

sion matrix efﬁciently. Our Topolet, however, intro-

duces a systematic approach for computing that ma-

trix. That is, the emissions are calculated based on

the distance of the inter-space points to the neighbor-

ing points. That topological information determines

the same-class variations accurately and thus, reduces

the required number of recordings for identical class

of gestures. Furthermore, in our approach we do not

need an extra signal processing technique (on pixel-

level) to convert the continuous paths into P-symbols,

as it is reported in (Yang et al., 1994).

To determine the emission matrix we utilize

two mentioned databases (MD and LD) in K-means

framework (MacQueen, 1967). That is, the Pose-

lets within LD database are employed as the initializa-

tion centers of the K-means (the number of LD Pose-

lets determines the number of clusters). Whereas, the

Poselets in MD database are regarded as the points’

cloud which are to be clustered ( Figure 9.c). There-

fore, those Poselets, which are classiﬁed in one clus-

ter, is considered as the same-class variations for each

state. Within this efﬁcient approach, the emission

probabilities determine the closeness of each emis-

sion to the center of that cluster. Thus, each proba-

bility is calculated based on the ratio of two distances

as:

∑

, where d

marks the distance of each ele-

ment from the center of cluster. Since each K-means

cluster has different number of Poselets, we consider

the minimum number, existing in all clusters, as the

number of emissions, M

, for that layer. Therefore,

× M

emission matrix is constructed.

4 EXPERIMENT

To demonstrate the efﬁcacy of our Topolet, we con-

duct ﬁve experiments. For these experiments, the

input to the recognition system is created as follow-

ing: First, a Viterbi-like algorithm is employed to re-

turn a path of Q states, based on the (maximum-a-

posterior) probabilities of the n

-nearest neighbors for

each layer. The initial state and length of the Topolet,

Q, for each layer are the inputs to the Viterbi algo-

rithm. Furthermore, the number of returned paths is

equal to the number of considered layers of interest

in each experiment. For example, if an experiment

is aimed at evaluating the performance of complete

posture sequence, eight different paths (one for each

layer) is returned ( Figure 7). Second, the Poselet ’s

image corresponding to each of these state-indexes’

sequence is retrieved ( Figure 9.a). Similarly, if the

experiment is on multiple layers (Exp 2-5), the input

Topolet: From Atomic Hand Posture Structures to a Comprehensive Gesture Set

161

Figure 8: Process of combining eight parallel Poselets to construct a posture. The next posture is constructed from the

nearest-neighbors of these Poselets. The Poselet spaces’ colors correspond to the colors’ code of each layer in Figure 1.

will be the combination of all Poselets in the paral-

lel format to form a complete posture image ( Figure

8). Third, the OpenCV’s contour extraction method

(Bradski, 2000) is applied to the input frames to ex-

tract the contour points. In our experiments, the input

and searched images’ size is 800 × 600 pixels, and

the 3D hand model’s length and width (in 3D frontal

view) are 10 and 4 units (cm), respectively.

Estimation is performed using the maximum-a-

prior (MAP) criterion and the Chamfer distance as

the penalty function. The criterion ﬁnds the optimal

Poselet at each layer by comparing the contour points

of the nearest Poselets and of the input. If the input

is a sequence of Poselets in one layer, the solution to

each frame is one index which minimizes the penalty

function. Whereas, if the input is a sequence of com-

plete postures, the solution will be a set of (eight) in-

dexes. During the search, the previous state of each

Poselet in the sequence is known.

The ﬁrst experiment evaluates the estimation ac-

curacy and time of the Topolet for layer-two (forearm-

rotation), layer-three (wrist-rotation), and layer-ﬁve

(inter-ﬁnger rotation), separately. The goal is to

demonstrate, by employing our Topolet we can out-

perform the results (mean errors and fps) in com-

parison with layered-exhaustive search (Dadgar and

Brunnett, 2018). For this experiment, we have created

a synthetic gesture consiting of 250 Poselets, and as

the results show ( Table 1), considerable improvement

is recorded during estimation using our Topolet. The

estimation of the layers- three and ﬁve is relatively

easier than the layer-two, because we set the forearm

to bind-pose (frontal and upward-view in this case) in

those two searches ( Figure 9.a). On the other hand,

that frontal-view of the Poselets leads to a slower fps

than many other views of the forearm. That is due

to the higher number of contour points existing in the

frontal view of the hand. That greater number of con-

tour points obliges more expensive contours extrac-

tion and slower pixel-wise comparison process than

other views.

In experiments two and three we consider the

combination of all layers (L

, L

, and L

Table 1: Comparison of the Topolet and layered-exhaustive

search (Layered-EXH) methods. This experiment is per-

formed on layer-two (L

), layer-three (L

), and layer-ﬁve

). The performance improvement (duration and accu-

racy of the searches) based on our (Topolet) is evident.

Exp1 Topolet L

Mean 3D Error (cm) 0.246 0.244 0

Mean 2D Error (px) 0.7 0.7 0

Search Time (s) 0.094 0.108 0.195

Exp1 Layered-EXH L

Mean 3D Error (cm) 1.503 0.557 0

Mean 2D Error (px) 11.4 16.5 0.1

Search Time (s) 1.859 2.480 1.718

Accordingly, we consider a synthetic gesture with

250 postures for experiment-two and 2500 postures

for experiment-three. While the experiment-two is

oriented to evaluate the performance on the low-

resolution (LD) database, the experiment-three is tar-

geted to examine the efﬁciency of the Topolet on

the mid-resolution (MD) database. The goal of the

experiment-three is to demonstrate the possibilities

of decreasing the errors (compared to experiment-

two) by training our Topolet on the layers with a

more aggregated points-cloud. We can observe that

experiment-three exhibits better accuracy while the

fps remains almost the same ( Table 2). The main

source of the errors is due to the invisibility of the

ﬁngers in many inputs. Since the image sequences

are selected in a random Viterbi-like process, encoun-

tering invisible ﬁngers is inevitable. Depending on

the application, one could constraint the hand to have

reasonable rotation toward the camera by which the

Table 2: The overview of experiment-two and -three. These

two experiments are aimed to ﬁnd the optimum complete-

postures (combination of all layers). The enhancement of

the accuracy in experiment-three (which is performed on

mid-resolution (MD) database) is evident while the search

duration is not noticeably affected.

Experiments Exp 2 Exp 3

Mean 3D Error (cm) 2.221 2.019

Mean 2D Error (px) 6.5 10

Search Time (s) 0.49 0.64

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

162

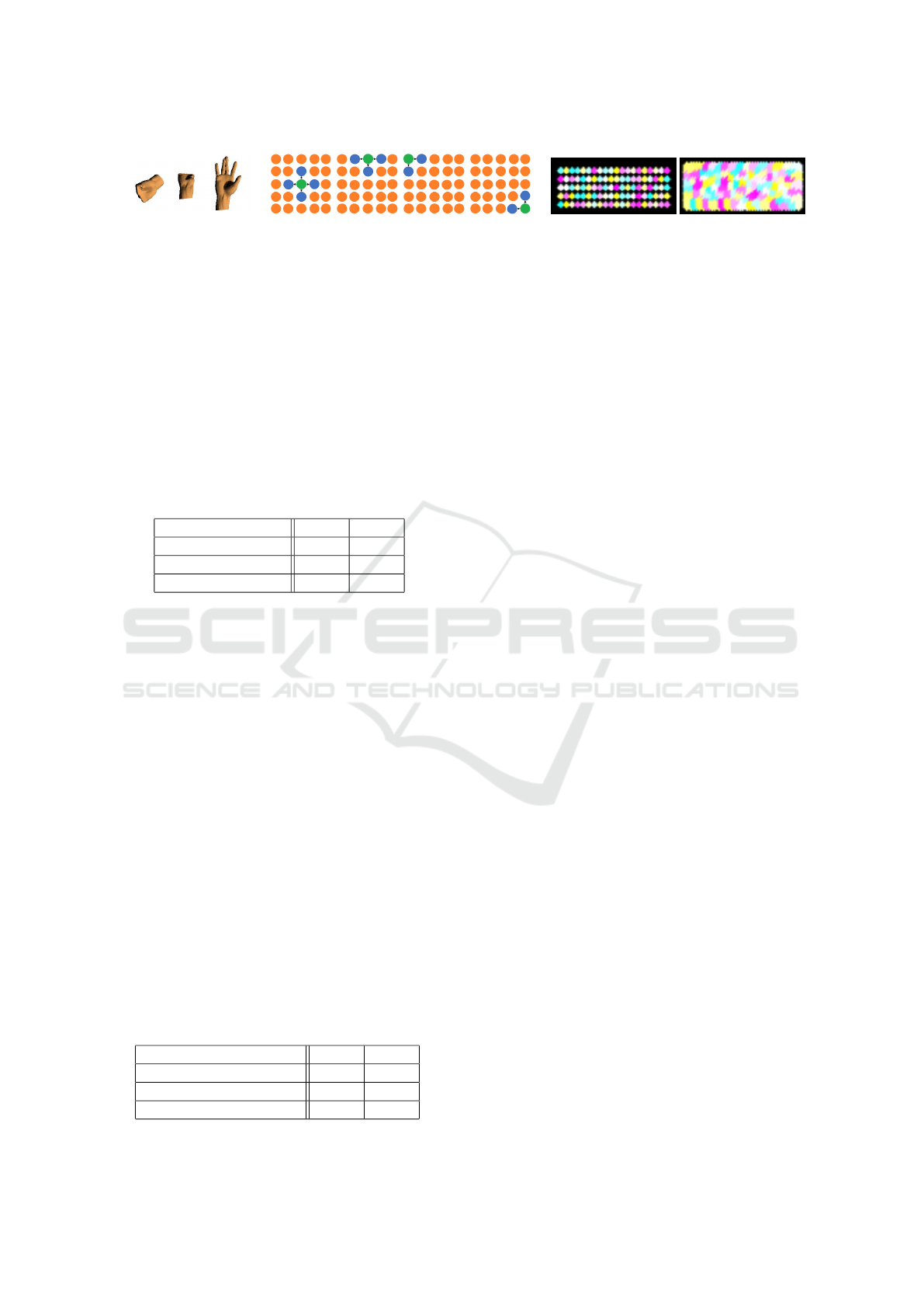
a) b) c)

Figure 9: a) Three examples of Poselets in layer-2, layer-3, and layer-5. b) n

= 4 possible n =1-nearest-neighborhoods (blue)

of the current state (green). If the current state is at the edge of the rectangle, the number of possible transition will be less

= 3 or 2). In our implementation we consider the self-transition to make the iterative gestures also possible (n

= 5, 4, or

3). Note that, n is different from n

: n determines the how far the algorithm should look for the next state in the topological

space. The value of n is constant for the entire process and we set it to one. Whereas, n

determines the actual number of

neighbors for each state. The value of n

depends on the position each state is situated in the topology. c) Kmean over the LD

and MD databases and the formation of emission matrix.

ﬁngers become (at least) partially visible. That could

increase the accuracy by a signiﬁcant factor.

Table 3: The overview of experiment-four and -ﬁve.

Experiment-four is performed on distorted contours and

experiment-ﬁve is accomplished without considering the

layer-ﬁve in the search. Enhancement of the search dura-

tion in both experiments (in comparison with experiment-

two and -three) is evident while the accuracy remained al-

most unchanged.

Experiments Exp 4 Exp 5

Mean 3D Error (cm) 2.025 2.028

Mean 2D Error (px) 10.3 10.3

Search Time (s) 0.32 0.25

The result of experiment-three shows a reason-

able accuracy, however, we have conducted two more

experiments (the experiments- four and ﬁve) to im-

prove the time-complexity of the search. Therefore,

similar to experiment-three, these experiments are de-

signed and performed on the mid-resolution database

(MD), with identical gesture sequence. However, in

experiment-four the number of contour points (in con-

tour extraction) are reduced, and in experiment-ﬁve

the layer ﬁve (inter-ﬁnger rotation) is not considered

and is set to bind-pose. The idea behind experiment-

four is to evaluate the robustness of our Topolet

when distorted contours are employed. Whereas, the

idea behind experiment-ﬁve is to examine the en-

tropy of information existing in layer-ﬁve in com-

parison to the time-complexity it imposes on the

whole process. As it is demonstrated in Table 3,

the results exhibit vivid improvements in the time-

complexities of experiments- four and ﬁve (3 fps and

4 fps, respectively) in comparison to the experiment-

Table 4: The detailed overview of experiment-four and -

ﬁve. According to the table, it is evident that contour extrac-

tion time and visualization of the Poselets using openGL is

the most expensive part of the system.

Experiments Exp 4 Exp 5

Contour Ext Time (s) 0.11 0.08

2D Distant Comp Time (s) 0.03 0.03

Visualization Time (s) 0.11 0.09

three (while the accuracy remains almost unchanged).

Additionally, the reduction of the contour points in

experiment-four has no effect on improvement of the

time-complexity after a certain value. That is, in ev-

ery other p contour point selection process, p = 4 is

the optimum value.

5 DISCUSSION & CONCLUSION

In the past decades many researchers strove to over-

come the obstacles in designing of a reliable hand ges-

ture recognition system. Those obstacles were espe-

cially more severe if the system is ought to perform

in real-time, employ single RGB camera, and recog-

nize a large set of gestures. Therefore, many systems

relaxed one or two of these requirements. We pro-

posed a type of temporal model for gestures based on

our hierarchical hand posture database to meet all the

above requirements. Our HMM-like model utilizes

the topology of the points’ cloud in each layer and ex-

ploits a novel type of atomic structure, we refer to as

Topolet. Furthermore, it beneﬁts from an enhanced

version of another atomic gesture structure, known

as Poselet . These two atomic structures allowed us

to consider random, and thus context-free application

domain, gesture set. Moreover, the system utilized

a single and RGB (instead of depth (Sharp et al.,

2015)) camera and showed a great potential to per-

form in real-time.

Our Topolet successfully addressed many tradi-

tional issues exist in conventional HMM. For exam-

ple, one difﬁculty with HMM is to determine an ap-

propriate number of hidden states even if the con-

text of application domain is known (Sangjun et al.,

2015). The database we utilized contained a ﬁx num-

ber of Poselets at each layer which was uniformly dis-

tributed within the lower (than 28) dimensional space.

Since our proposed Topolet considered these Poselets

as the transitional states, the number of states in the

temporal model was remained ﬁxed, thus the issue

was resolved. An other difﬁculty with conventional

HMM is the linear space-complexity as the number

Topolet: From Atomic Hand Posture Structures to a Comprehensive Gesture Set

163

of considered gestures increases. Our Topolet spec-

iﬁed the sequence of possible Poselets (and not pos-

tures) within a gesture. One Topolet was trained for

each layer and a concrete relation between different

Poselets of that layer is introduced. That led to con-

struction of semi-gestures (or Topolets). The Topolets

of all layers together captured the temporal informa-

tion between different postures. Therefore, the entire

temporal information of any gesture consisted of sev-

eral but limited (eight) Topolets in a parallel mode.

This limited number of Topolets remained the same

for any conﬁgurations and for any number of gestures,

and thus the issue of linear growth was resolved. Ad-

ditionally, our Topolet enhanced the structure of the

training, decoding, and evaluation algorithms. For ex-

ample, conventional HMM theoretically requires inﬁ-

nite number of examples for one gesture to reliably

train the parameters using the complex Baum-Welch

algorithm. Our method investigated the topological

relation of the Poselet points and, therefore, reliable

relations between the postures were established us-

ing one example. After all, within a vision-based

approach (RGB Camera), and in dealing with (po-

tentially) inﬁnite number of (randomly created) ges-

tures, we achieved a notable 3fps in Exp4 and 4fps

in Exp5. We used a naive contour extraction method

which was an expensive part of our process ( Table

4). By employing a real-time contour extraction al-

gorithm (deep net (Bertasius and Torresani, 2015))

we could achieve higher fps on this time consuming

process.

In addition to those proven advantages, our pro-

posed method could introduce a number of other po-

tential beneﬁts. The atomic structures could be used

to construct a comprehensive grammar between the

Poselets, Topolets, postures, and gestures. That is, if

we consider each gesture as a sentence and each pos-

ture as a word, one Poselet could be viewed as a word

syllable (with each DoF of the Poselet as a letter).

Then each of the trained Topolet speciﬁes how each of

those Poselets could evolve as the gesture proceeds in

time. Therefore, the system will be capable of form-

ing a ﬂexible description-based speciﬁcation for hand

gesture database (Wang et al., 2012). Furthermore,

in the process of gestures transition, there might be

some transient (false) gestures depending on the con-

text of the application, where the system should per-

form no speciﬁc action. With our comprehensive ges-

ture’s temporal model, one could deactivate some of

the points’ cloud in each layer and acquire the Topo-

lets on a smaller space. That feature could be used to

concretely adopt the proposed Topolet to different ap-

plication domains. The evaluation of these statements

will be the topics of future works.

ACKNOWLEDGMENT

I would like to thank the Europ

aischer Sozialfonds f

Deutschland (ESF) scholarship and the Professorship

of Graphische Datenverarbeitung und Visualisierung

at TU-Chemniz who made this research possible.

REFERENCES

Bertasius, G. and Torresani, L. (2015). DeepEdge : A

Multi-Scale Bifurcated Deep Network for Top-Down

Contour Detection. In CVPR.

Bourdev, L. and Malik, J. (2009). Poselets: Body Part De-

tectors Trained using 3D Human Pose Annotations.

IEEE Int Conf on Com Vis, pages 1365–1372.

Bradski, G. (2000). The OpenCV Library. Dr. Dobb’s Jour-

nal of Software Tools.

Dadgar, A. and Brunnett, G. (2018). Multi-Forest Classiﬁ-

cation and Layered Exhaustive Search Using a Fully

Hierarchical Hand Posture / Gesture Database. In VIS-

APP, Funchal.

MacQueen, J. B. (1967). Some Methods for Classiﬁcation

and Analysis of Multivariate Observations. Berkeley

Symp on Maths, Statis, Prob, 1(233):281–297.

Meshry, M., Hussein, M. E., and Torki, M. (2016). Linear-

Time Online Action Detection from 3D Skeletal Data

using Bags of Gesturelets. IEEE WACV.

Rabiner, L. (1989). A Tutorial on Hidden Markov Models

and Selected Applications in Speech Recognition.

Sangjun, O., Mallipeddi, R., and Lee, M. (2015). Real Time

Hand Gesture Recognition Using Random Forest and

Linear Discriminant Analysis. Proc of the Inter Conf

on Human-Agent Interaction, (October):279–282.

Sharp, T., Keskin, C., Robertson, D., Taylor, J., Shotton,

J., Kim, D., Rhemann, C., Leichter, I., Vinnikov, A.,

Wei, Y., Freedman, D., Kohli, P., Krupka, E., Fitzgib-

bon, A., and Izadi, S. (2015). Accurate, Robust, and

Flexible Real-time Hand Tracking. ACM Conf on Hu-

man Factors in Comp Sys (CHI), pages 3633—-3642.

Starner, T. E. and Pentland, A. (1995). Visual Recognition

of American Sign Language Using Hidden Markov

Models. Media, pages 189–194.

Wang, J., Liu, Z., Wu, Y., and Yuan, J. (2012). Mining Ac-

tionlet Ensemble for Action Recognition with Depth

Cameras. pages 1290–1297.

Yang, J., Xu, Y., and Chen, C. S. (1994). Gesture Inter-

face: Modeling and Learning. IEEE Proc Int Conf on

Robotics and Automation, pages 1747–52 vol.2.

Yao, B. and Fei-Fei, L. (2010). Grouplet: A Structured Im-

age Representation for Recognizing Human and Ob-

ject Interactions. IEEE Proc CVPR, pages 9–16.

Yu, G., Liu, Z., and Yuan, J. (2015). Discriminative Orderlet

Mining for Real-Time Recognition of Human-Object

Interaction. Lec Notes in Comp Sci (AI & Bioinf),

9007:50–65.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

164