A Fully Object-space Approach for Full-reference Visual Quality

Assessment of Static and Animated 3D Meshes

Zeynep Cipiloglu Yildiz

and Tolga Capin

Computer Engineering Dept., Manisa Celal Bayar University, Manisa, Turkey

Computer Engineering Dept., TED University, Ankara, Turkey

Keywords:

Visual Quality Assessment, Animation, Geometry, Contrast Sensitivity Function, Manifold Harmonics.

Abstract:

3D mesh models are exposed to several geometric operations such as simpliﬁcation and compression. Several

metrics for evaluating the perceived quality of 3D meshes have already been developed. However, most

of these metrics do not handle animation and they measure the global quality. Therefore, a full-reference

perceptual error metric is proposed to estimate the detectability of local artifacts on animated meshes. This

is a bottom-up approach in which spatial and temporal sensitivity models of the human visual system are

integrated. The proposed method directly operates in 3D model space and generates a 3D probability map that

estimates the visibility of distortions on each vertex throughout the animation sequence. We have also tested

the success of our metric on public datasets and compared the results to other metrics. These results reveal a

promising correlation between our metric and human perception.

1 INTRODUCTION

3D mesh modeling and rendering methods have ad-

vanced to the level that they are now common in 3D

games, virtual environments, and visualization appli-

cations. Conventional way of improving the visual

quality of a 3D mesh is to increase the number of

vertices and triangles. This provides a more detailed

view; nevertheless, it also leads to a performance

degradation. As a result, we need a measure for es-

timating the visual quality of 3D models, to be able

to balance the visual quality of 3D models and their

computational time.

Most of the operations on 3D meshes cause certain

distortions on the mesh surface and requires an esti-

mation of the distortion. For instance, 3D mesh com-

pression and streaming applications require a trade-

off between the visual quality and transmission speed.

Watermarking techniques introduce artifacts and one

should guarantee the invisibility of these artifacts.

Most of the existing 3D quality metrics omit the tem-

poral aspect which is challenging.

Yildiz et al. (Yildiz and Capin, 2017) propose a

perceptual visual quality metric devised for dynamic

meshes. They measure the 3D spatiotemporal re-

sponse at each vertex by modeling Human Visual Sys-

tem (HVS) processes such as contrast sensitivity and

channel decomposition. Their framework follows a

principled bottom-up approach and produces encour-

aging results. In their method, they ﬁrst construct

an intermediate representation for the dynamic mesh,

which is a 4D space-time (3D+time) volume called

spatiotemporal volume. However, 4D nature of this

representation makes the framework computationally

inefﬁcient.

In this work, we build on top of the framework

in (Yildiz and Capin, 2017) and remove the neces-

sity for the spatiotemporal volume. Thus we make

the perceptual pipeline in (Yildiz and Capin, 2017)

fully mesh-based. In this method, we beneﬁt from

the eigen-decomposition of a mesh since eigenvalues

are identiﬁed as natural vibrations of a mesh (Botsch

et al., 2010, Chapter 4) and hence, they are directly

related to the geometric quality of the mesh. We

also compare our results to the method in (Yildiz

and Capin, 2017), in terms of both accuracy and ef-

ﬁciency.

2 RELATED WORK

We can categorize the methods for mesh quality as-

sessment as perceptual and non-perceptual methods.

Non-perceptual methods such as Euclidean distance,

Hausdorff distance, root-mean squared error, etc., rely

Yildiz, Z. and Capin, T.

A Fully Object-space Approach for Full-reference Visual Quality Assessment of Static and Animated 3D Meshes.

DOI: 10.5220/0007245001690176

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 169-176

ISBN: 978-989-758-354-4

169

on purely geometric measurements without consider-

ing human visual perception; thus they are not cor-

related with the human perception. On the other

hand, perceptually-based metrics incorporate mech-

anisms of HVS. Comprehensive surveys on general

mesh quality assessment methods can be found in

(Bulbul et al., 2011) and (Lavou

e and Mantiuk, 2015);

whereas surveys on perceptual quality metrics are

presented in (Lin and Jay Kuo, 2011) and (Corsini

et al., 2013).

Image-based perceptual metrics operate in 2D

image space by using rendered images of the 3D

mesh while evaluating the visual quality. These met-

rics generally employ HVS models such as Contrast

Sensitivity Function (CSF), which maps spatial fre-

quency to visual sensitivity. Most common image

quality metric is Visible Difference Prediction (VDP)

method which produces a 2D local visible distortions

map, given reference and test images (Daly, 1992).

Similarly, Visual Equivalence Detector method out-

puts a visual equivalence map which demonstrates

the equally perceived regions of two images (Rama-

narayanan et al., 2007).

Curvature and roughness of a surface are widely

employed for describing surface quality. GL1 (Karni

and Gotsman, 2000) and GL2 (Sorkine et al., 2003)

are roughness-based metrics that use Geometric

Laplacian of the mesh vertices. Lavoue et al. (Lavou

et al., 2006) measure structural similarity between

two mesh surfaces by using curvature for extracting

structural information. This metric is improved with

a multi-scale approach in (Lavou

e, 2011). Two def-

initions of surface roughness are utilized for deriv-

ing two error metrics called 3DW PM1 and 3DWPM2

(Corsini et al., 2007). Another metric called FMPD is

also based on local roughness derived from Gaussian

curvature (Wang et al., 2012). Curvature tensor differ-

ence of two meshes is used for measuring the visible

errors between two meshes (Torkhani et al., 2014). A

novel roughness-based perceptual error metric, which

incorporates structural similarity, visual masking, and

saturation effect, is proposed by Dong et al. (Dong

et al., 2015). There are also recent studies that lever-

age machine learning methods for mesh quality as-

sessment (Yildiz et al., 2018). A metric speciﬁc to the

validation of human body models is also proposed in

(Singh and Kumar, 2017).

The literature survey shows that most of the ex-

isting visual quality metrics do not take the temporal

effects into account. Moreover, they are mostly con-

cerned with the global quality of the meshes rather

than the local visibility of distortions. These issues

were already addressed by (Yildiz and Capin, 2017).

The main objective of this study is to remove the ne-

cessity for a spatiotemporal volume in that method;

thus making the pipeline fully object-space.

3 APPROACH

In this mesh-based approach, almost the same steps

in (Yildiz and Capin, 2017) exist with several adap-

tations for 3D. The method is applied on the mesh

vertices, not on the spatiotemporal volume represen-

tation. However, this introduces a restriction for the

reference and test meshes to have the same number of

vertices, since the computations are done per vertex.

The steps of the method are displayed in Figure 1.

Frames for reference and test animations go through

the same processing pipeline and the difference be-

tween these results gives us the per vertex visible dif-

ferences prediction map. Details of each step are ex-

plained below.

3.1 Preprocessing

In this step, illumination calculation and vertex veloc-

ity estimation are performed as in the spatiotemporal

volume approach. Instead of the spatiotemporal vol-

ume calculation, Manifold Harmonics Basis (MHB)

are computed and stored to feed the Channel Decom-

position step of the proposed approach.

Illumination Calculation. Vertex shades are com-

puted using Phong reﬂection model with only diffuse

and ambient components. Most of the user experi-

ments for measuring the visual quality of 3D meshes

in the literature, use such a simple shading scheme.

Calculation of MHBs. Calculation of MHBs is a

costly operation since it requires eigen-decomposition

of the mesh Laplacian. Fortunately, once they are

computed; there is no need to recalculate them.

For a triangle mesh of n vertices, a function basis

, called MHB is calculated. The k

element of the

MHB is a piecewise linear function with values H

deﬁned at i

vertex of the surface, where k = 1...m

and i = 1...n (Vallet and L

evy, 2008). MHB is com-

puted as the eigenvectors of discrete Laplacian of

∆

whose coefﬁcients are given in Eq. 1.

∆

i j

= −

cotβ

i j

+ cotβ

i j

∗

||v

∗

(1)

where β

i j

and β

i j

are two angles opposite to edge de-

ﬁned by vertices i and j, v

∗

refers to the circumcentric

dual of simplex v, and |.| denotes the simplex volume.

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

170

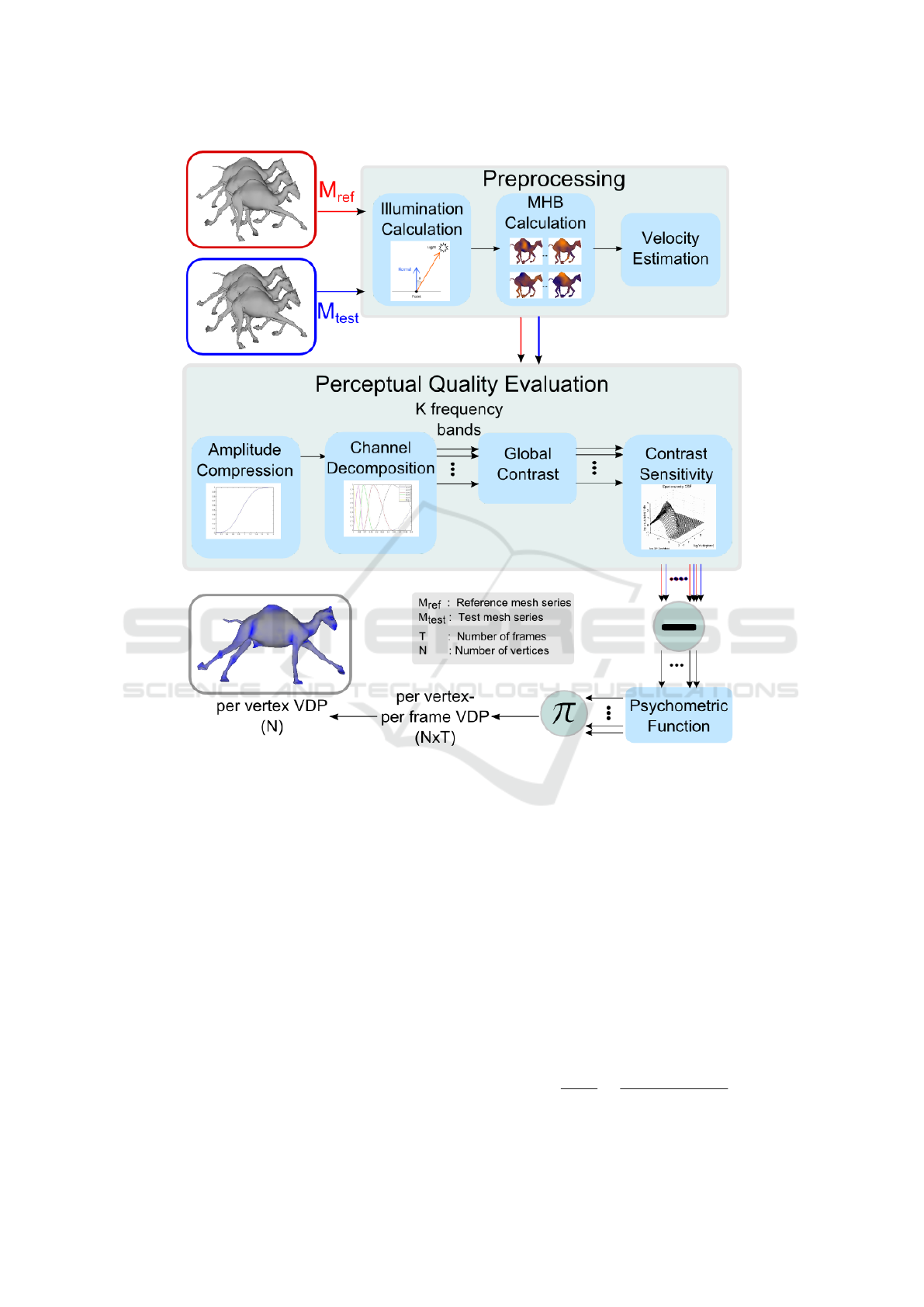
Figure 1: Method overview.

Velocity Estimation. In this step, we calculate the

velocity of each vertex at each frame and apply

smooth pursuit compensation as described in (Yildiz

and Capin, 2017). The aim of smooth pursuit com-

pensation is to handle temporal masking effect which

refers to the diminution in the visibility of distortions

as the speed of the motion increases.

3.2 Perceptual Quality Evaluation

All the steps of this method are similar to the

corresponding steps in the spatiotemporal volume

approach, except the Channel Decomposition step

which is totally different. To keep the paper

self-contained, however, all the steps are explained

shortly. Except the Channel Decomposition step, all

the steps follow the same procedures described in the

previous work, with the exception that equations are

applied per vertex instead of per voxel, since they are

not applied on the spatiotemporal volume.

Amplitude Compression. The purpose of this step

is to model the photoreceptor response to luminance

which “forms a nonlinear S-shaped curve, centered at

the current adaptation luminance and exhibits a com-

pressive behavior while moving away from the cen-

ter” (Aydin et al., 2010).

We apply the local amplitude nonlinearity model

by Daly (Daly, 1992) per vertex as in Eq. 2, where i is

the vertex index, t is the frame number, R(i,t)/R

max

is the normalized response, L(i,t) is the luminance

value of the vertex, and b = 0.63 and c

= 12.6 are

empirical constants.

R(i,t)

max

L(i,t)

L(i,t) + c

L(i,t)

(2)

A Fully Object-space Approach for Full-reference Visual Quality Assessment of Static and Animated 3D Meshes

171

Channel Decomposition. Our primary visual cor-

tex is known to be selective to certain spatial frequen-

cies and orientations (Aydin et al., 2010). Cortex

Transform (Daly, 1992) is commonly used for mod-

eling this visual selectivity mechanism of HVS.

The most important distinction of our approach

lies in the implementation of this step. In the Chan-

nel Decomposition step of the framework in (Yildiz

and Capin, 2017), Cortex Transform is used to ﬁlter

the spatiotemporal volume with DoM (Difference Of

Mesa) ﬁlters in the frequency domain. While convert-

ing the spatiotemporal volume to frequency domain,

Fourier Transform (FT) is used. However, FT requires

voxelization of the mesh surface. Manifold Harmon-

ics can be considered as the generalization of Fourier

analysis to surfaces of arbitrary topology (Vallet and

evy, 2008). Hence, we employ Manifold Harmon-

ics for applying DoM ﬁlter on the mesh and obtain 6

frequency channels as in the spatiotemporal volume

based approach.

In the processing pipeline of Manifold Harmon-

ics, ﬁrstly, Manifold Harmonics Basis is calculated

for the given triangle mesh of N vertices, which is al-

ready performed in the preprocessing step of our im-

plementation. Then the geometry is transformed into

frequency space by the help of Manifold Harmonics

Transform (MHT), which corresponds to projecting x

into MHB by solving for the coefﬁcients ˜x

given in

Eq. 3. Frequency space ﬁltering is performed by mul-

tiplying the coefﬁcients calculated in MHT step by a

frequency space ﬁlter F(w) (Eq. 4). Lastly, the mesh

is transformed back to the geometric space using in-

verse Manifold Harmonics Transform (MHT

−1

). In

its simplest form, MHT

−1

is performed using Eq. 5;

however if a ﬁltering is performed, we use Eq. 4 to

obtain ﬁltered values denoted by x

. For a more de-

tailed explanation of MHT, please refer to (Vallet and

evy, 2008) and (Botsch et al., 2010, Chapter 4).

˜x

∑

i=1

(3)

∑

k=1

F(w

) ˜x

(4)

x =

∑

k=1

˜x

(5)

One can discover the similarity between the process-

ing pipeline of Manifold Harmonics and frequency

domain ﬁltering used in (Yildiz and Capin, 2017).

MHT and MHT

−1

correspond to Fourier and Inverse

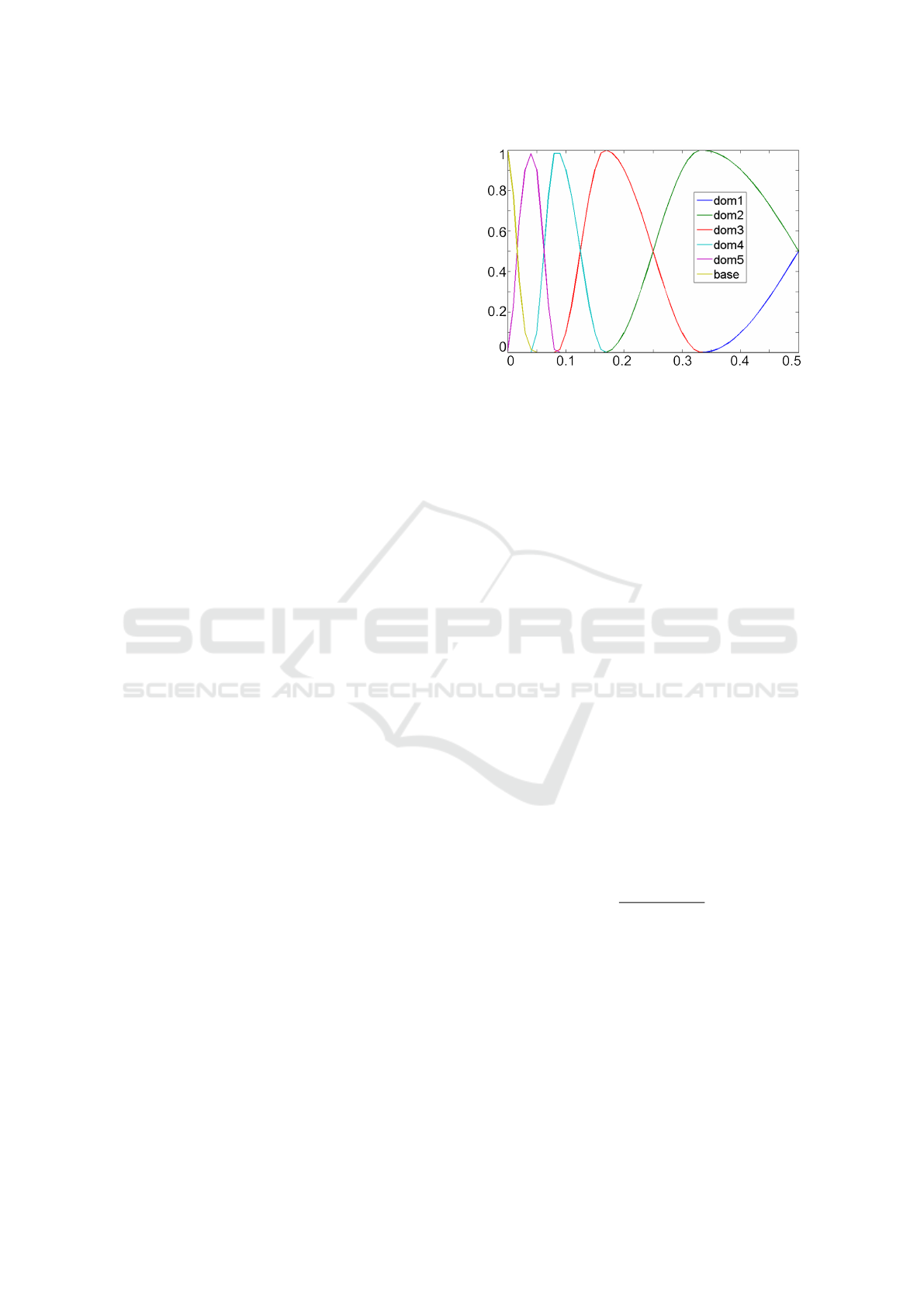
Fourier Transform, respectively. We construct DoM

ﬁlters displayed in Figure 2 to be used as the fre-

quency space ﬁlters (F(w)). The equations for calcu-

lating DoM ﬁlters can be found in (Aydin et al., 2010)

and (Yildiz and Capin, 2017).

Figure 2: Difference of Mesa (DOM) ﬁlters. (x-axis: spatial

frequency in cycles/pixel, y-axis: response).

Note that the notation in Eq 3-5 was given assum-

ing that the geometry of the mesh will be ﬁltered. It

is also possible to ﬁlter other attributes of the mesh.

For instance, for ﬁltering the color values, we need to

replace x, y, z values with r, g, b values. In our case,

we need ﬁltering the color values of the mesh with

DoM ﬁlters.

Figure 3 depicts the six frequency channels gen-

erated by applying Cortex Transform on an image,

while Figure 4 includes the outputs of the Channel

Decomposition step of our mesh-based approach for

the hand mesh. One can notice the parallelism be-

tween these results as the frequency decreases from

channel 1 to 6 and ﬁner details are captured in the

high frequency bands.

Global Contrast. Contrast values in each fre-

quency band is calculated using the global contrast

deﬁnition in Eq. 6 (Myszkowski et al., 2000); as the

sensitivity to a pattern is determined by its contrast

rather than its intensity. In the equation, C

contains

the contrast values and I

contains the luminance val-

ues in channel k, respectively.

− mean(I

)

mean(I

)

(6)

Contrast Sensitivity. The next step is to ﬁlter each

frequency channel with the Contrast Sensitivity Func-

tion (CSF). Since our model is designed for animated

meshes, we use the spatiovelocity CSF which mea-

sures the sensitivity of HVS with respect to spatial

frequency and velocity.

Each frequency band is weighted with the spa-

tiovelocity CSF in Eq. 7 (Kelly, 1979). Inputs to the

CSF are vertex velocities in each frame and the center

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

172

Figure 3: Application of Cortex Transform on an image (Image courtesy of Karol Myszkowski).

Figure 4: Output of the Channel Decomposition step for the hand mesh.

spatial frequency of each frequency band.

CSF(ρ,v) = c

(6.1 + 7.3| log(

) |

)×

v(2πc

ρ)

× exp(−

4πc

ρ(c

v + 2)

45.9

) (7)

where ρ is the spatial frequency in cycles/degree, v is

the velocity in degrees/second, and c

= 1.14, c

0.67,c

= 1.7 are empirically set coefﬁcients.

Error Pooling. Both reference and test animations

go through the above steps. K frequency bands for

each sequence are generated in this pipeline. Then the

difference between test and reference pairs for each

band is passed to a psychometric function which maps

the perceived contrast (C

) to probability of detection

using Eq. 8 (Aydin et al., 2010). Then each band is

combined using the probability summation formula

(Eq. 9) (Aydin et al., 2010).

P(C

) = 1 − exp(−| C

) (8)

P = 1 −

∏

k=1

(1 − P

) (9)

P contains the detection probabilities of each vertex

per frame. We merge the probability maps of each

frame into a single map, by averaging the values of

vertices over the frames. This gives a per vertex visi-

ble difference prediction map for the animated mesh.

4 RESULTS

In this section, the performance of the proposed ap-

proach is evaluated from accuracy and processing

time perspectives, compared to other methods.

A Fully Object-space Approach for Full-reference Visual Quality Assessment of Static and Animated 3D Meshes

173

4.1 Accuracy

In this section, we evaluate the performance of our

metric compared to the state-of-the-art metrics. Our

metric is applicable on both static and dynamic

meshes and generates a 3D local distortion map.

However, most of the publicly available datasets mea-

sure the global visual quality. Therefore, we ﬁrst mea-

sure the performance of our metric on detecting local

distortions using the dataset constructed by Yildiz and

Capin (Yildiz and Capin, 2017), which contains local

distortion maps for distorted animations with respect

to four reference animations. The dataset is composed

of four different mesh sequences with number of ver-

tices changing from 8K to 42K.

As the performance measurement, we use Spear-

man Rank Order Correlation Coefﬁcient (SROCC)

between metric results and mean opinion score

(MOS) values. Table 1 lists SROCC values for both

our metric and the metric proposed in (Yildiz and

Capin, 2017).

We also compare our global metric results to the

common metric results on LIRIS/EPFL General Pur-

pose dataset (Lavou

e et al., 2006), which is used as

benchmark in many mesh processing studies. Table

2 includes SROCC values for each model and met-

ric. Both the local and global results show that our

mesh-based approach achieves good and almost the

same correlation values with the metric in (Yildiz and

Capin, 2017).

4.2 Processing Time

We also measured the running time of our metric

compared to the previous work (Yildiz and Capin,

2017), for several meshes. Measurements are per-

formed on a 3.3 GHz PC. As depicted from Figure 5,

running time of our algorithm is almost proportional

to the number of vertices of the mesh; which is rea-

sonable because the algorithm operates per vertex.

Note that these meshes are selected to illustrate the

dependency of the running time of the algorithm on

the number of vertices. Note also these results ignore

the preprocessing times.

We know that the running time depends on the

number of voxels for the spatiotemporal volume ap-

proach (Yildiz and Capin, 2017) and it depends on

the number of vertices in our approach. Keeping this

observation in mind, we see that the spatiotemporal

volume approach runs faster for the horse and camel

animations, although the number of vertices is less

than the number of voxels in these cases. This is due

to the domination of manifold harmonics calculations

for small meshes in our approach. However, the share

Figure 5: Processing time (in seconds) of one frame for sev-

eral meshes.

of these calculations diminishes as the number of vox-

els gets much higher than the number of vertices.

4.3 Discussion

Concisely, both approaches produce comparable re-

sults from the accuracy perspective. On the other

hand, we can deduce from the computational time

measurements that our mesh-based VQA method is

more efﬁcient than the spatiotemporal volume-based

method for large meshes (i.e. # vertices > 25K).

Nevertheless, it is important to remind that mesh-

based approach conﬁnes the reference and test meshes

to have the same number of vertices. Thus, for

large meshes without connectivity changes, our mesh-

based approach is preferable because of its efﬁciency,

with the expense of Manifold Harmonics Basis calcu-

lations as a preprocessing.

It is also important to note a design issue in the

MHB calculations of our method. Calculation of the

MHBs for meshes with high number of vertices is a

problem due to its space complexity. To overcome

this problem, cotangent weight and delta matrices in

Eq. 1 are stored as sparse matrices which enables a

signiﬁcant amount of reduction in the memory space.

We have also adopted the idea in (Song et al., 2014),

where eigen-decomposition is performed on the sim-

pliﬁed version of the mesh and the results are mapped

to the original mesh using a kd-tree structure, for

mesh saliency calculations. Following this process,

for large meshes (#vertices > 25K, in our implemen-

tation), the Channel Decomposition step (Section 3.2)

is applied on the simpliﬁed versions of the meshes

and the results are expanded to the original size us-

ing a kd-tree representation. For mesh simpliﬁca-

tion, we employ the quadric edge collapse decimation

method of MeshLab’s implementation (Cignoni et al.,

2008), with boundary-preserving option is set. Al-

though the accuracy results are close to the spatiotem-

poral volume-based approach, performing MHB cal-

culations on reduced meshes may degrade the results

and further veriﬁcation is required for this choice.

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

174

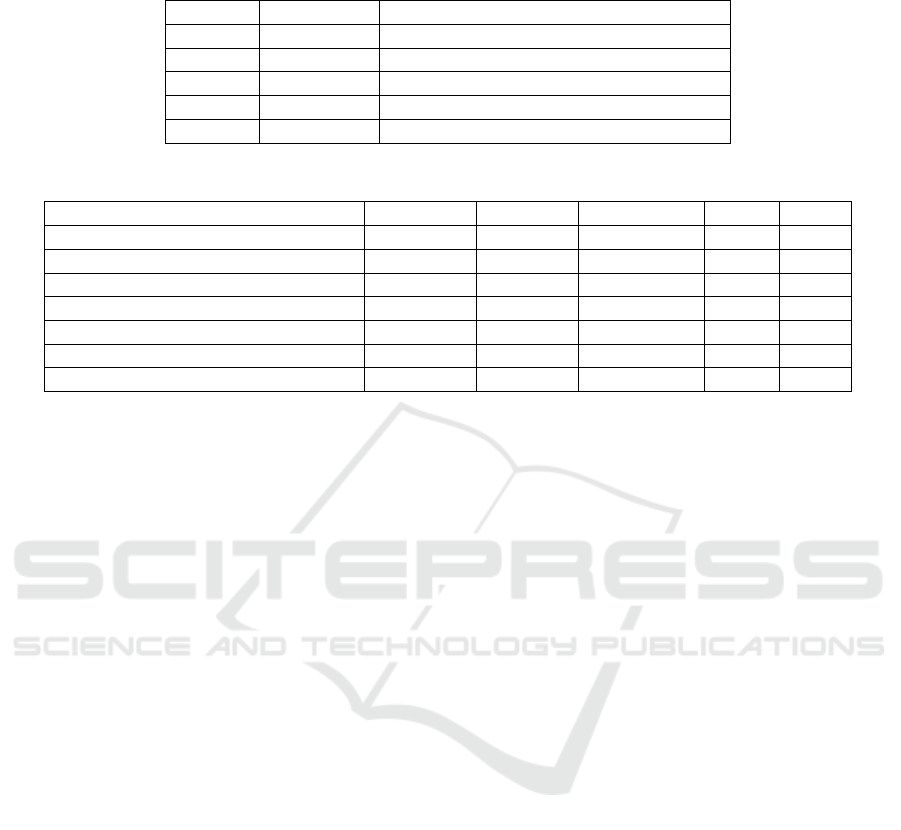
Table 1: The performance of our metric on detecting local distortions compared to the metric proposed in (Yildiz and Capin,

2017). SROCC values are given in percentages (%).

Our metric The metric in (Yildiz and Capin, 2017)

Camel 84 83

Elephant 63 65

Hand 73 71

Horse 70 70

Overall 73 72

Table 2: Spearman correlation coefﬁcients in percentages (%) for each model and metric (highest values are marked).

Armadillo Dinosaur RockerArm Venus Mean

MSDM (Lavou

e et al., 2006) 84 70 88 86 82

3DWPM2 (Corsini et al., 2007) 71 47 29 26 43

3DWPM1 (Corsini et al., 2007) 64 59 85 68 69

GL1 (Karni and Gotsman, 2000) 68 5 2 91 42

GL2 (Sorkine et al., 2003) 76 22 18 89 51

Yildiz et al. (Yildiz and Capin, 2017) 86 79 88 89 86

Our metric 86 78 88 90 86

5 CONCLUSION

The aim of this paper is to provide a general-purpose

visual quality metric for estimating the local and

global distortions in both static and animated meshes.

The method extends the costly framework in (Yildiz

and Capin, 2017) to fully operate in 3D object space.

Our approach incorporates both spatial and tempo-

ral sensitivity of the HVS. The algorithm outputs a

3D probability map of visible distortions. The most

signiﬁcant contribution of our method is that we em-

ploy manifold harmonics transformation to propose

a principled way for modeling the visual selectivity

mechanism of HVS on 3D surfaces. According to our

experimental evaluations, our metric gives promising

results compared to its counterparts.

Our method shares the advantages of the metric in

(Yildiz and Capin, 2017): It incorporates the effect of

temporal variations; which is omitted by most of the

studies in the literature. The algorithm can be used

for measuring the quality of both static and dynamic

meshes. In addition to these, our method is computa-

tionally more efﬁcient in certain cases.

The main drawback of our method is the require-

ment of ﬁxed connectivity mesh pairs. As a future

work, we intend to relax this constraint by ﬁrst apply-

ing a vertex correspondence algorithm. Moreover, a

more extensive user study, considering the effects of

several parameters, is needed.

REFERENCES

Aydin, T. O.,

Cad

ık, M., Myszkowski, K., and Seidel, H.-P.

(2010). Video quality assessment for computer graph-

ics applications. In ACM Transactions on Graphics

(TOG), volume 29, page 161. ACM.

Botsch, M., Kobbelt, L., Pauly, M., Alliez, P., and L

evy, B.

(2010). Polygon Mesh Processing. CRC press.

Bulbul, A., C¸ apin, T. K., Lavou

e, G., and Preda, M. (2011).

Assessing Visual Quality of 3-D Polygonal Models.

IEEE Signal Processing Magazine, 28(6):80–90.

Cignoni, P., Corsini, M., and Ranzuglia, G. (2008). Mesh-

lab: an open-source 3D mesh processing system.

ERCIM News, (73):45–46.

Corsini, M., Gelasca, E., Ebrahimi, T., and Barni, M.

(2007). Watermarked 3-D mesh quality assessment.

IEEE Transactions on Multimedia, 9(2):247–256.

Corsini, M., Larabi, M.-C., Lavou

e, G., Pet

ık, O., V

sa,

L., and Wang, K. (2013). Perceptual metrics for static

and dynamic triangle meshes. In Computer Graph-

ics Forum, volume 32, pages 101–125. Wiley Online

Library.

Daly, S. J. (1992). Visible differences predictor: an algo-

rithm for the assessment of image ﬁdelity. In Proceed-

ings of SPIE/IS&T Symposium on Electronic Imag-

ing: Science and Technology, pages 2–15. Interna-

tional Society for Optics and Photonics.

Dong, L., Fang, Y., Lin, W., and Seah, H. S. (2015).

Perceptual quality assessment for 3D triangle mesh

based on curvature. IEEE Transactions on Multime-

dia, 17(12):2174–2184.

Karni, Z. and Gotsman, C. (2000). Spectral compression

of mesh geometry. In Proceedings of the 27th an-

nual conference on Computer graphics and interac-

tive techniques, pages 279–286. ACM Press/Addison-

Wesley Publishing Co.

A Fully Object-space Approach for Full-reference Visual Quality Assessment of Static and Animated 3D Meshes

175

Kelly, D. (1979). Motion and vision. ii. stabilized spatio-

temporal threshold surface. Journal of the Optical So-

ciety of America, 69(10):1340–1349.

Lavou

e, G. (2011). A multiscale metric for 3D mesh vi-

sual quality assessment. In Computer Graphics Fo-

rum, volume 30, pages 1427–1437. Wiley Online Li-

brary.

Lavou

e, G., Gelasca, E. D., Dupont, F., Baskurt, A., and

Ebrahimi, T. (2006). Perceptually driven 3D distance

metrics with application to watermarking. In Optics &

Photonics, pages 63120L–63120L. International So-

ciety for Optics and Photonics.

Lavou

e, G. and Mantiuk, R. (2015). Quality assessment in

computer graphics. In Visual Signal Quality Assess-

ment, pages 243–286. Springer.

Lin, W. and Jay Kuo, C.-C. (2011). Perceptual visual qual-

ity metrics: A survey. Journal of Visual Communica-

tion and Image Representation, 22(4):297–312.

Myszkowski, K., Rokita, P., and Tawara, T. (2000).

Perception-based fast rendering and antialiasing of

walkthrough sequences. IEEE Transactions on Visu-

alization and Computer Graphics, 6(4):360–379.

Ramanarayanan, G., Ferwerda, J., Walter, B., and Bala,

K. (2007). Visual equivalence: towards a new stan-

dard for image ﬁdelity. In Proceedings of ACM

SIGGRAPH, SIGGRAPH ’07, New York, NY, USA.

ACM.

Singh, S. and Kumar, S. (2017). A pipeline and met-

ric for validation of personalized human body mod-

els. In Proceedings of the 12th International Joint

Conference on Computer Vision, Imaging and Com-

puter Graphics Theory and Applications - Volume

1: GRAPP, (VISIGRAPP 2017), pages 160–171. IN-

STICC, SciTePress.

Song, R., Liu, Y., Martin, R. R., and Rosin, P. L. (2014).

Mesh saliency via spectral processing. ACM Transac-

tions on Graphics (TOG), 33(1):6.

Sorkine, O., Cohen-Or, D., and Toledo, S. (2003). High-

pass quantization for mesh encoding. In Symposium

on Geometry Processing, pages 42–51. Citeseer.

Torkhani, F., Wang, K., and Chassery, J.-M. (2014). A

curvature-tensor-based perceptual quality metric for

3D triangular meshes. Machine Graphics and Vision,

23(1-2):59–82.

Vallet, B. and L

evy, B. (2008). Spectral geometry process-

ing with manifold harmonics. Computer Graphics Fo-

rum, 27(2):251–260.

Wang, K., Torkhani, F., and Montanvert, A. (2012). A

fast roughness-based approach to the assessment of

3D mesh visual quality. Computers & Graphics,

36(7):808–818.

Yildiz, Z. C. and Capin, T. (2017). A perceptual quality

metric for dynamic triangle meshes. EURASIP Jour-

nal on Image and Video Processing, 2017(1):12.

Yildiz, Z. C., Oztireli, A. C., and Capin, T. (2018). A ma-

chine learning framework for full-reference 3d shape

quality assessment. The Visual Computer.

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

176