Assessing Sequential Monoscopic Images for Height Estimation of
Fixed-Wing Drones
Nicklas Haagh Christensen, Frederik Falk, Oliver Gyldenberg Hjermitslev and Rikke Gade
Aalborg University, Denmark
Keywords:
UAV, Drone, Free Height Estimation, Stereo Equation, Computer Vision, Feature Detection.
Abstract:
We design a feature-based model to estimate and predict the free height of a fixed-wing drone flying at altitudes
up to 100 meters above terrain using the stereo vision principles and a one-dimensional Kalman filter. We
design this using a single RGB camera to assess the viability of sequential images for height estimation, and
to assess which issues and pitfalls are likely to affect such a system. This model is tested on both simulation
data flying above flat and varying terrain, as well as data from a real test flight. Simulation RMSE ranges from
10.7% to 21.0% of maximum flying height. Real estimates vary significantly more, resulting in an RMSE
of 27.55% of median flying height of one test flight. Best MAE was roughly 17%, indicating the error to
expect from the system. We conclude that feature-based detection appears to be too heavily influenced by
noise introduced by the drone and other uncontrollable parameters to be used in reliable height estimation.
1 INTRODUCTION
Measuring the altitude of a fixed-wing drone can be
achieved in different manners. An often used appro-
ach is by using a barometer or GPS altimeter. Free
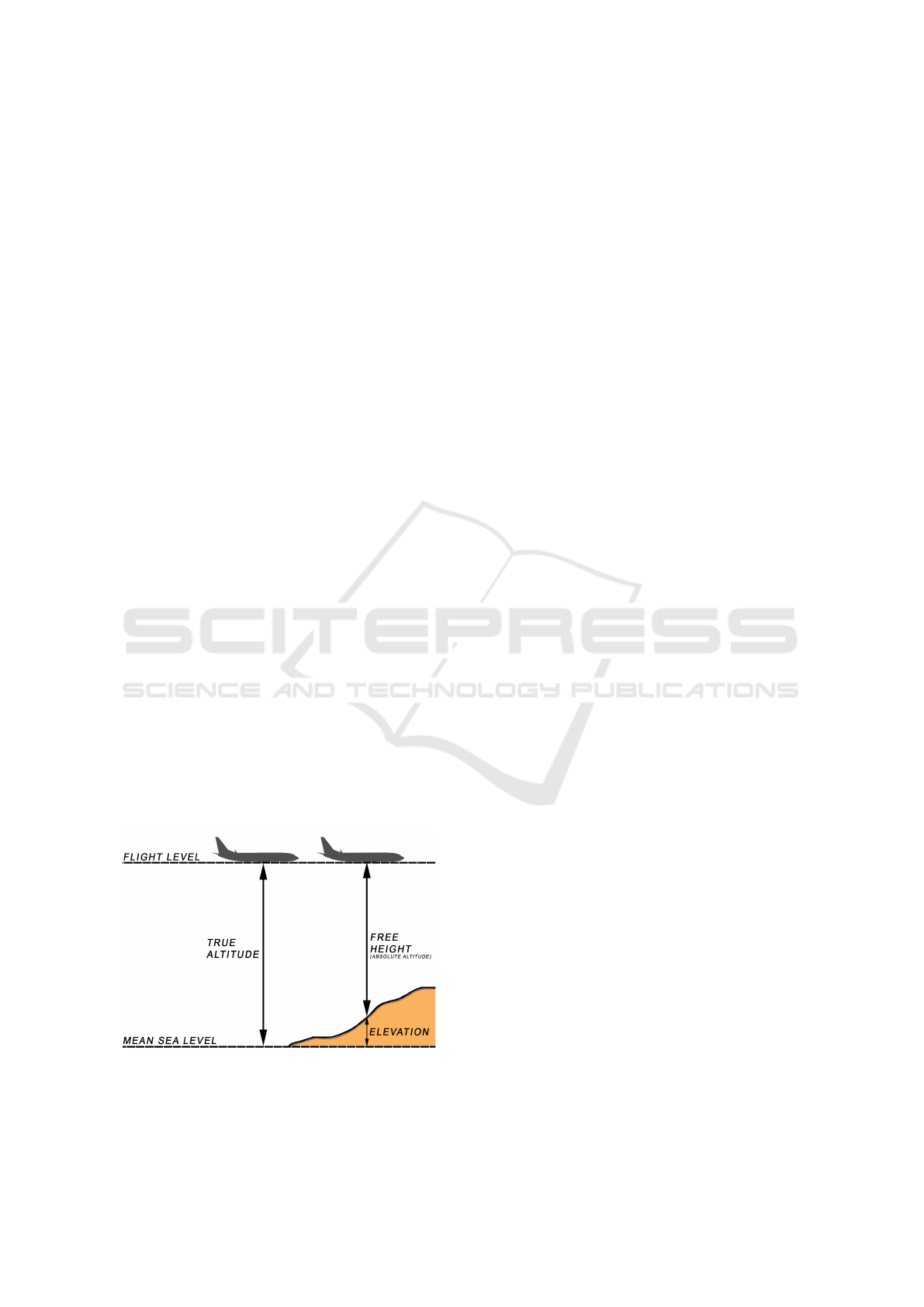
height, or absolute altitude, is the measure of distance
from the drone to the terrain below. An illustration
can be seen in Figure 1. Most drones do not account
for obstacles or increasing/decreasing terrain as their
altitude is often measured relative to the drone’s take-
off point. Therefore, there is a need to estimate the
free height of drones, independent of their take-off
point, using other methods.
Figure 1: Figure illustrating the free height of a drone.
Other free height measurements exists, such as
ultra-sonic distance measurement or laser range fin-
ders, but these are not sufficient methods when flying
at higher altitudes (> 100m) and would add additio-
nal weight to the drone as well as increasing energy
consumption as they are active sensors. As modern
drones are getting smaller and lighter, attaching addi-
tional sensors would decrease their efficiency. Since
many drones are already equipped with an RGB ca-
mera, a vision based solution is investigated to reduce
additional sensor weight. This is especially feasible
when using fixed-wing drones as they travel in a spe-
cific direction and at relatively constant speeds. Ca-
meras provide rich information while still being low
on weight and energy consumption. Implementing vi-
sion based free height estimation would allow drones
to operate safely in areas with poor GPS coverage and
become independent of variations in air pressure. Cal-
culating the distance to the terrain below the drone
would also prove beneficial in terrain with varying
ground level, and provide information necessary for
safe piloting.
2 RELATED WORK
Creating these estimates requires different approaches
in different contexts. Convolutional neural networks
have been capable of estimating depth with reasona-
ble accuracy in experimental set-ups given image data
(Eigen, 2014). This method has also shown to be able
Christensen, N., Falk, F., Hjermitslev, O. and Gade, R.
Assessing Sequential Monoscopic Images for Height Estimation of Fixed-Wing Drones.
DOI: 10.5220/0007256107510759
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 751-759
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
751

to create a height map of a given image with no prior
information (Zhou et al., 2017).
However, using a downwards facing camera on
a drone enables the advantage of stereo correspon-
dence between sequential images. Previous work
has successfully implemented photogrammetric ae-
rial depth triangulation to estimate elevation or heig-
hts using vision (Schenk, 1997), (Hadjutheodorou,
1963), (Matthies et al., 1989), (Choi and Lee, 2012).
Using the stereo principle on sequential images from
the drone seems feasible to calculate the distance to
the ground based on the motion of the drone, as has
previously been done on rotor-drones (Campos et al.,
2016). This paper explores the possibility of enabling
automatic free height estimation using optical flow
and stereo vision principles and calculate a reliability
measure for the operator on the ground. Investigating
similar work where computer vision has been used
for obstacle avoidance or mapping, the most common
methods used are optical flow or SLAM based appro-
aches (Lu et al., 2018). Feature-based methods have
rarely been used despite its potential low cost. One
example of feature-based previous work is the use of
SIFT to detect obstacles by tracking size expansion
ratios in sequential images (Al-Kaff et al., 2016).
We therefore propose to evaluate feature-based
height estimation using a single monoscopic RGB ca-
mera in order to assess potential shortcomings and
error sources of such a system. A feature-based sy-
stem would not be affected by changing illumination,
which is an unavoidable aspect in the outdoors con-
text, and is more robust in handling sudden changes in
speed or rotation. The system will be suited to drones
operating above 100 meters, and assuming a relatively
constant flight level. To this end, the existing sensors
on the drone can be used to retrieve the missing va-
riables, available from the drone’s inertial measure-
ment unit (IMU) and GPS. Based on these findings,
an evaluation should suggest potential pitfalls for fu-
ture works, and assess the viability of estimating free
height of a drone using a single RGB camera.
3 METHODS
We explore the use of the stereo equation in combi-
nation with feature detection and matching to calcu-
late the height of the drone and the reliability thereof
using sequential images from a downwards facing ca-
mera mounted to the drone. This section provides an
overview of the applied feature tracking, height esti-
mation, and reliability measure methods. The evalua-
tion approach and test methodology is also described
to clarify aspects such as drone data retrieval and ot-
her issues encountered through the process.
3.1 Feature Detection and Tracking
The system requires a method to detect robust fe-
atures that can be matched between sequential fra-
mes. Oriented FAST and Rotated BRIEF (ORB), was
chosen based on the speed of computation and rela-
tive robustness. Even though other methods such as
Scale Invariant Feature Transform (SIFT) are scale
invariant, ORB outperforms them in execution time
and with comparable accuracy allowing for real-time
tracking (Rublee et al., 2011).
ORB is a feature detector made for real-time
computations and low-power devices. It builds on
the Features from Accelerated Segment Test (FAST)
keypoint detector and a variant of the Binary Ro-
bust Independent Elementary Features (BRIEF) des-
criptor. The FAST method performs well in high
speed corner detection, by considering a circle of a
set amount pixels around a corner candidate. If the
brightness of these pixels are darker or brighter than
the candidate with a given threshold it is considered
a corner (Rosten et al., 2010). The BRIEF procedure
allows a shortcut in finding the binary strings without
having to find the descriptors. It takes a smoothened
part of an image and finds a chosen amount of loca-
tion pairs. A pixel intensity comparison are done to
these pairs.
ORB employs a Harris corner filter to discard ed-
ges. FAST keypoints are computed with an orienta-
tion component, while BRIEF descriptors are consi-
dered rotation-invariant using steering according to
the orientation of the keypoints. According to the
authors, ORB performs as good as SIFT and better
than SURF on their evaluation data while being up
to factor-2 faster. Furthermore, ORB is derived with
the purpose of running in real-time or for low-power
systems. However, an issue with ORB, compared to
other feature detectors, is that it is not scale invari-
ant. As the drone used in this test is flying at relati-
vely constant altitude between two frames, we assume
only little accuracy is missed from this. For applica-
tions where scale invariance is a necessity, computa-
tionally heavier solutions might be needed, such as
SIFT or SURF. As this is intended as an on-line solu-
tion for constant flight level, the system benefits from
the drone’s constant altitude by using less computati-
onally heavy feature detection.
With these arguments we hypothesize that ORB
is sufficient to detect and track features for reliable
disparity calculations for use in height estimation.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
752

3.2 Height Estimation
The height is calculated by using a calculation from
stereo vision and treating sequential images as stereo
vision with large baselines. Assuming two images are
taken with two cameras (left and right) with two dif-
ferent viewing positions the depth to the object can
be calculated by using the disparity between the same
object in the frames, the focal length, and the coordi-
nates of the object. For the left camera this is calcula-
ted as:
x
l
= f
X
Z
y
l
= f
Y
Z
(1)
As for the right camera:
x
r
= f
X − b
Z
y
l
= f
Y
Z
(2)
This assumes that the object has moved in the x-axis
by a baseline b. x
l
and x
r
defines the pixel coordinates
of the object, whereas X is the real life coordinate,
same as Y. These two equations can be merged into
one explaining the effect of stereo disparity:
d = x
l
− x
r
= f
X
Z
− ( f
X
Z
− f
b
Z
)
d =
f b
Z
(3)
This equation can be rearranged to define the
depth (height) in the image:
Z =
f b
d
(4)
Where Z is the depth, f is the focal length, b is
the baseline, and d is the disparity in the image. This
equation will be referred to as the Stereo Equation.
Figure 2 displays the height estimation based on
these hypothetical values and shows the effect of the
cell size in the camera. Decreasing the cell size in-
creases the accuracy of the estimated height shown by
the smaller gradient of the red curve. It is important to
note that the height estimations with small disparities
(<5) generate increased uncertainty. For instance a
one-pixel displacement given similar values as above
would estimate a height between 1.25km and 625m,
whereas the next one-pixel displacement is between
625m and 416m.
This means that increasing disparity reduces the
range of the upper and lower bounds, indicating an
increased accuracy as the range decreases with one-
third for a two pixel displacement, one-fourth for
three pixels etc.
In order to perform these calculations, it is neces-
sary to know the drone’s rotation and speed, or GPS
Figure 2: The estimated height plotted as a function of dis-
placement in pixels using the hypothetical values; 20mm
focal length and 100mm baseline. Although pixels are dis-
crete values, they have been plotted as continuous for rea-
dability.
coordinates, at the time the images are captured to re-
liably calculate the baseline between images. In this
test, GPS data is available as embedded metadata in
the video, along with a range of other information.
3.3 Measurement Filters
As noise in the measurements is a reality and in order
to provide reliable and valid results, smoothing is ne-
cessary. Three filters were considered for smoothing
the calculated height using prior heights; a weighted
average, variable weighted average dependent on the
absolute pitch of the drone, and a Kalman filter. All
three approaches were tested, and the Kalman filter
(27.6% RMSE) was deemed most suited for the si-
tuation compared to both weighted average approa-
ches. The weighted average filter was tested substan-
tially, ranging from 0.9 of the last estimate to 0.99,
resulting in a higher minimum error than the Kalman
filter (27.9% RMSE) at 0.923. The variable weigh-
ted average was modelled based on the regular weig-
hted average approach. It decreased the last estimate
weight linearly dependent on the absolute pitch of the
drone, which ranges from 0 deg to roughly 40deg,
meaning high pitch values allowed the model to adapt
quicker. This was not enough to improve on the Kal-
man filter, resulting in an RMSE of 39.0%.
The Kalman filter parameters were determined by
internal testing described in Section 3.5.2. The as-
sumption was that the measurement noise variance
(σ
m
) could be described using the stereo equation,
as single pixel deviations can be modelled using the
Equation 5.
f B
D
−
f B
D + 1
(5)
Assessing Sequential Monoscopic Images for Height Estimation of Fixed-Wing Drones
753
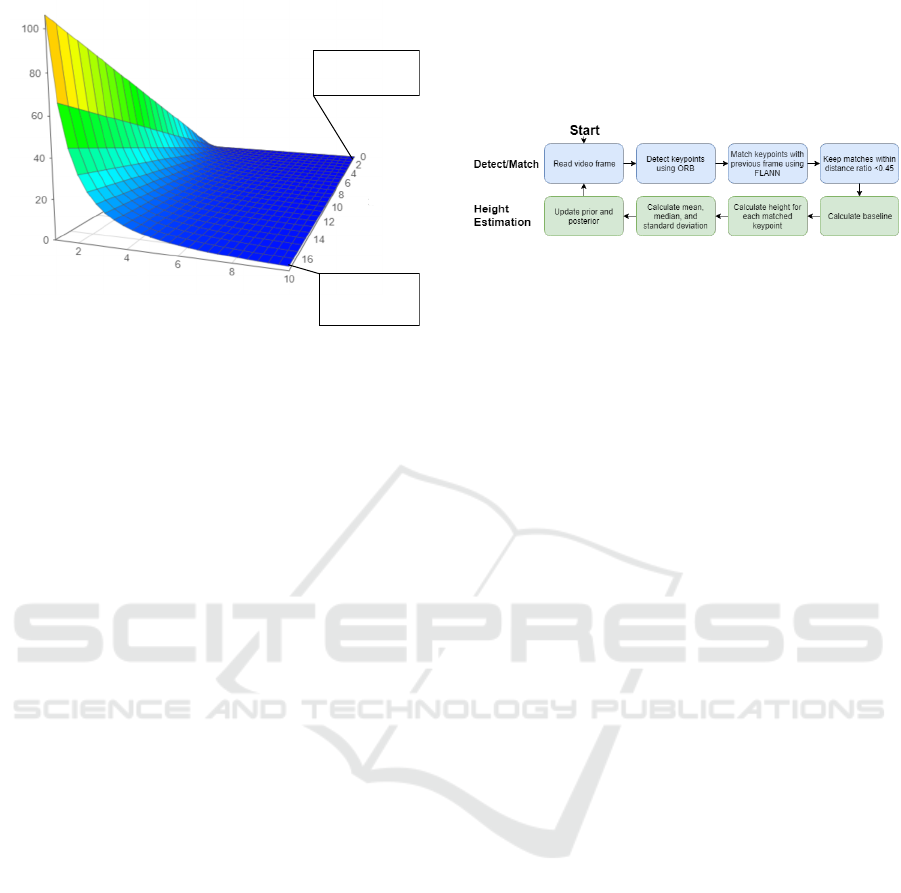
Error Range (m)
Disparity
(pixels)
Baseline (m)
Error: 1.9m
Disparity: 10p
Baseline: 17m
Error: 0.2m
Disparity: 10p
Baseline: 2m
Figure 3: Relationship between disparity and baseline on
single pixel error.
This relationship is shown in Figure 3. The er-
ror decays exponentially with disparity and increases
linearly with baseline. Not only does this show that
the measurement error can be estimated relatively pre-
cisely, it also indicates that infinitely decreasing the
baseline is a poor choice for optimizing the system,
since the disparity is dependent on the baseline but
with a much larger influence on measurement error.
This assumes that single pixel estimates are the
only measurement error we can reliably model. This
is true to the extent that more error sources are known,
but cannot be modelled for use in a Kalman filter. Ot-
her measurement errors include lens distortion, wind,
and GPS accuracy.
The model itself has a variety of errors inclu-
ding the pitch of the UAV, indifference to peripheral
keypoints, and importantly accuracy of keypoint mat-
ching. This error is denoted σ
p
for process noise vari-
ance. Some of these can be modelled mathematically,
for instance the relationship of the pitch and the dro-
nes altitude:
tan(θ)B (6)
Where the difference in altitude between frames
is dependent on the baseline of the drone and its pitch
θ. This, however, assumes that the drone has flown
linearly between frames. Though this is not always
the case, it is relevant to understand why pitch has an
effect on the result.
Keypoint detection and matching will always be
an issue in such a naive model, since very close
keypoints result in a low disparity and a large estima-
ted height, however the error itself cannot be model-
led further than experimenting. As equally large ne-
gative and positive variance do not yield equally large
errors, the error cannot even be considered normally
distributed even if it could be predicted.
3.4 Algorithm
The algorithm was programmed in Python 3.6 and
follows the structure seen in Figure 4.
Figure 4: An overview of the program used to estimate the
free height of the drone.
It starts by detecting features in a frame using
ORB and then matches it with features from the previ-
ous valid frame using FLANN. This validity is deter-
mined as the video frame closest in recording time to
the last data-frame. The match must fulfill a distance
ratio lower than 0.45 before it is considered accep-
table. This is to filter out bad matches as shown in
Lowe’s paper on Scale-Invariant Feature Transforms
(Lowe, 2004). Furthermore, matches with keypoints
further than 50 pixels apart (on the fixed axis, in our
case the x-axis) were discarded based on an internal
test comparing accuracy between 25, 50, 75, and 100
pixels.
The baseline is then calculated to be used in the
stereo equation and the height for each valid match is
calculated. The mean height for all matches is then
the estimated height for the current frame.
To avoid errors, some criteria have to be fulfilled
before the heights are used in the algorithm. If the
distance travelled is too small to be the result of flight
or the frame-to-frame roll of the drone is too large,
the frame is discarded. This also applies if there are
fewer than five matches.
3.5 Experiments
This section describes the methods used to evaluate
the concept of using feature based computer vision
to calculate the height of the drone with a downward
facing camera. The outline of the evaluation is:
• Simulation above various terrain
• Error Variance Approximation
• Experiment with data from real drone
3.5.1 Simulation
A simulation of a drone flying above virtual terrain
was created to test the concept of using feature ba-
sed stereo calculations with sequential images. This
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
754

Figure 5: A frame from the simulation with 10 meter ground
truth.
approach has the advantages of controlling all the va-
riables and testing the system in near-ideal conditi-
ons without additional measurement and model er-
ror sources mentioned in Section 3.3. The simulation
data was created and recorded in Unity3D.
In total, 10 simulations were performed. Each tes-
ted optimal parameters for both σ
p
and σ
m
, and cal-
culated the best RMSE to compare with the test with
real data.
An image of one of the frames captured for the
simulation is seen in Figure 5. Multiple simulations of
different ground truths (i.e. the actual free height) are
needed to assess the viability of the system at different
heights.
3.5.2 Kalman Filter Parameter Estimation
All parameters described in 3.3 that could be reaso-
nable modelled were tested, as were combinations of
these. Additional constants and scalars were tested as
well, and results were observed for relations to pitch,
current height, baseline, etc. Finally, tests were made
solely with constant σ
p
and σ
m
.
Tests were performed using two loops, brutefor-
cing the best combination of the two variables. Both
variables were 0-centered and increased in small in-
crements ranging from
1
1000
to
1
10
.
Results were inspected to ensure the algorithm did
not ”cheat” in order to level at best results, but reaso-
nably followed the data provided.
3.5.3 Drone Experiment
Sky-Watch is a company that specializes in drones for
mapping of terrain and survey missions. They provi-
ded footage from their fixed-wing drone for evalua-
tion purposes. These drones fly in the range of 100m
to 1 km. There was approximately 30 minutes of
video including pre-flight preparations, take-off, in-
flight, landing, and drone retrieval. The footage con-
tained two separate flights and was obtained using a
Table 1: Specifications of the camera used to record the
evaluation footage.
Model CM8359-B500SA-E
Sensor Size 3.6736 × 2.7384mm
Focal Length 2.759mm
Framerate 30 f ps
Data-rate ∼ 4/s
Resolution 1280 × 720
retired drone with an older camera. The specifications
of the camera can be seen in Table 1.
The footage was embedded with KLV metadata
which was extracted using FFmpeg. The parser was
written in Python. The resulting comma-separated va-
lues (CSV) file contained all relevant data for the test,
including the rotation of the drone, GPS-coordinates,
time stamp, heading, altitude, and azimuth. However,
the data rate was unstable, ranging from 2/s to 13/s.
An overview of the program used to estimate the
height is seen in Figure 4. Only the GPS-coordinates
and the rotation were used by the program, and the
relative altitude was used for ground truth. The ba-
seline was calculated by converting GPS coordinates
to longitude and latitude and calculating the euclidean
distance between.
The distance in latitude is in Equation 7, where
one degree latitude is 111.32 km.
lat =| lat
1
− lat
2
| ×111320000 (7)
With the difference in latitude, the total distance
travelled is calculated by finding the difference in lon-
gitude (Equation 8) and then use Pythagoras theorem
(Equation 9), assuming a straight line:
long =| long
1
− long
2
| ×40075km ×
cos(lat)
360
(8)
baseline =
p
lat
2
+ long
2
(9)
With the baseline calculated, each match’s asso-
ciated height is calculated using the stereo equation.
The resulting estimated height was compared to the
ground truth from the drone’s sensor. As the drone is
flying above flat terrain, this is deemed acceptable as
ground truth. The RMSE was calculated to compare
its reliability. Additionally, error rates such as mean
error (ME) and mean absolute error (MAE) was inves-
tigated to determine the accuracy users can expect.
Assessing Sequential Monoscopic Images for Height Estimation of Fixed-Wing Drones
755
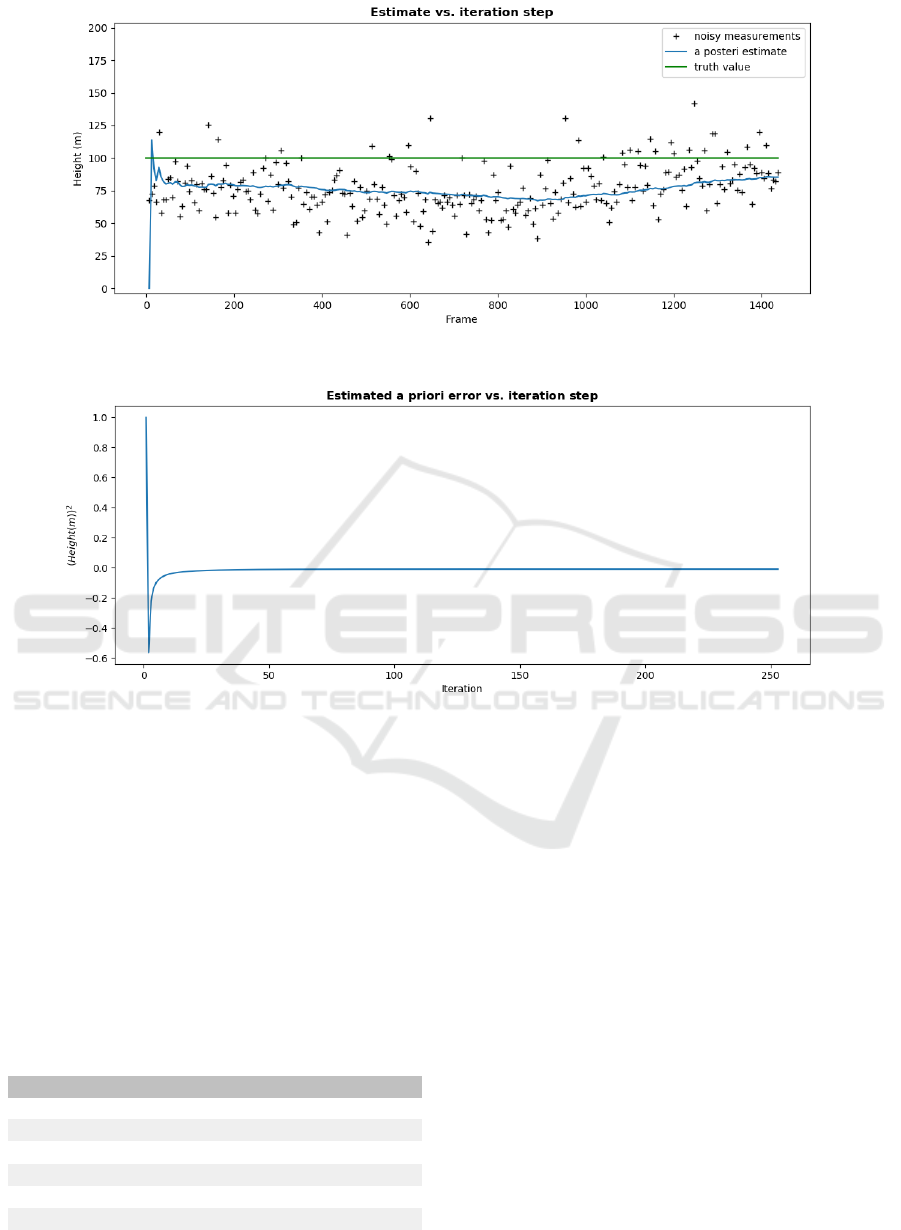
Figure 6: The estimated simulated heights at a constant 100m free height before and after filtering.
Figure 7: A priori error before updating the measurements at 100m.
4 RESULTS
4.1 Simulation with a Flat Terrain
The flat terrain tests consisted of 7 out of 10 total
simulation tests performed at heights of 10m, 20m,
30m, 40m, 50m, 75m, and 100m. An example simula-
tion is shown in Figures 6 and 7.
Table 2: Table describing the simulation RMSE, process
and measurement error, and the RMSE as a percentage of
ground truth.
Height RMSE % of truth σ
p
σ
m
10m 1.78m 17.8 0.0036 1.0
20m 3.87m 19.4 0.0081 4.0
30m 3.64m 12.1 3.6 × 10
−5
0.25
40m 4.41m 11.0 0.0001 0.36
50m 5.35m 10.7 0.0001 0.25
75m 13.23m 17.6 0.0001 0.36
100m 21.02m 21.0 0.0002 0.36
Table 2 shows the estimated best error variances
and calculated best RMSE for each height.
The results indicate that there is no relationship
between height or baseline in the measurement or pro-
cess error variance. Instead, assuming constant error
variances produced the best results overall. This way,
RMSE seems to increase from roughly 10% to 20%
of free height at 100 meters.
4.2 Simulation with Varying Terrain
The varying terrain were tested at 3 maximum free
heights, 50m, 75m, and 100m. An example simulation
is shown in Figures 8 and 9.
All results are shown in Table 3. As with the
constant flying height, there appears to be no obvious
correlation between either of the variables, but the
RMSE drops significantly with the varying height.
This seems to be caused by the dips in free height,
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
756
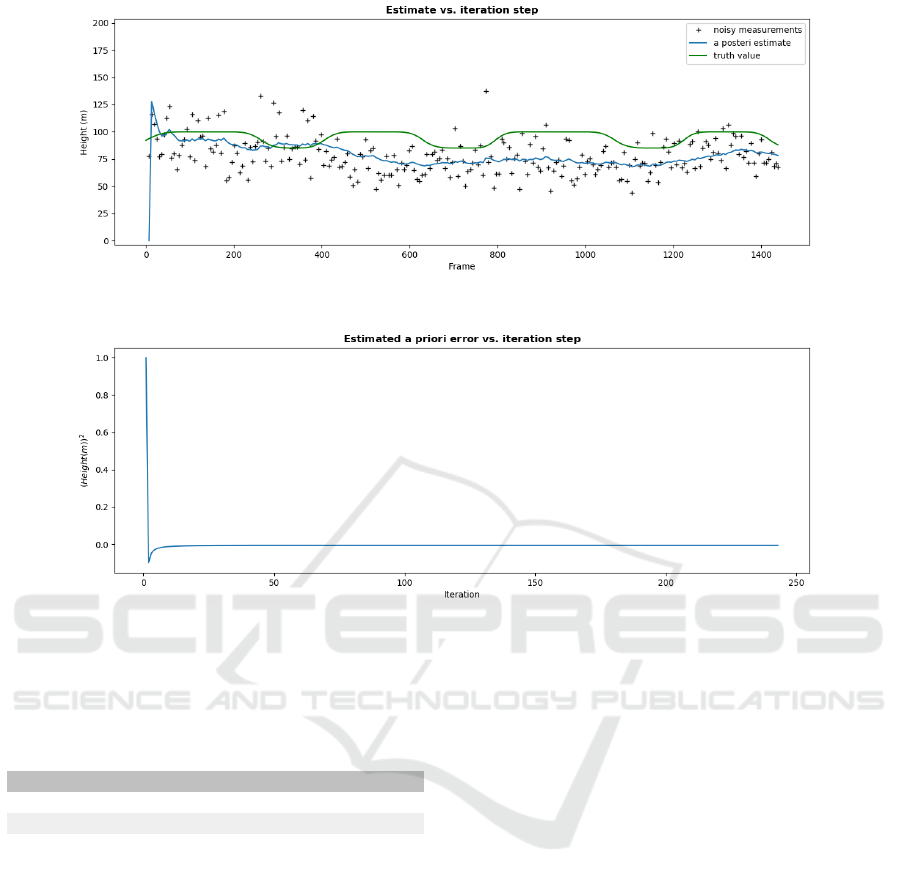
Figure 8: The estimated heights at a varying 100m free height before and after filtering.
Figure 9: A priori error before updating the measurements at 100m varying heights.
since the model appears to underestimate the
height in both tests.
Table 3: Table showing the results for the simulations with
varying terrain.
Height RMSE (m) % of truth σ
p
σ
m
50m 8.96 17.9 0.0076 25
75m 8.30 11.0 0.0035 1.69
100m 11.65 11.6 3.6 ∗ 10
−5
0.09
As mentioned previously, the estimates not increa-
sing significantly at intervals of maximum free height
is likely due to the algorithm accepting peripheral
keypoints equally with centered ones.
4.3 Testing on Drone Data
When testing the algorithm on data from the real
drone flying above a flat terrain, the results become
noisier. This can be seen in Figure 10.
As seen in the Figure, the estimate follows the
ground truth to a certain degree, however is heavily
influenced by noise. This estimate results in a total
RMSE value of 27.1, a MAE of 17, and a ME of -
3. Some of this error can be attributed to the fact
that a delay in calculated height will always be pre-
sent when using filtering methods such as Kalman.
Taking the mean of all standard deviations across all
included frames results in 58.6 meters which indicate
a lot of noise on the measurements. The negative ME
is in line with previous observations that the model
underestimates the actual height of the drone.
All previously mentioned factors such as pitch,
current height, and baseline, were tested as proba-
ble error variance sources, however none improved
on constant σ
p
and σ
m
. This is in line with simula-
tion tests, as well as the previous variable weighted
average test. Results of these one-dimensional noise
covariances are seen in Equation 10.
σ
p
= 0.000441, σ
m
= 0.9604 (10)
Looking at Figure 11 reveals that some of the er-
ror might come from inaccurate GPS coordinates or
miscalculated distance. With a top speed of 60 km
per hour, and a datarate of 4 datasets per second the
drone should not be able to gain distances between
frames larger than 4.15 meters.
Assessing Sequential Monoscopic Images for Height Estimation of Fixed-Wing Drones
757
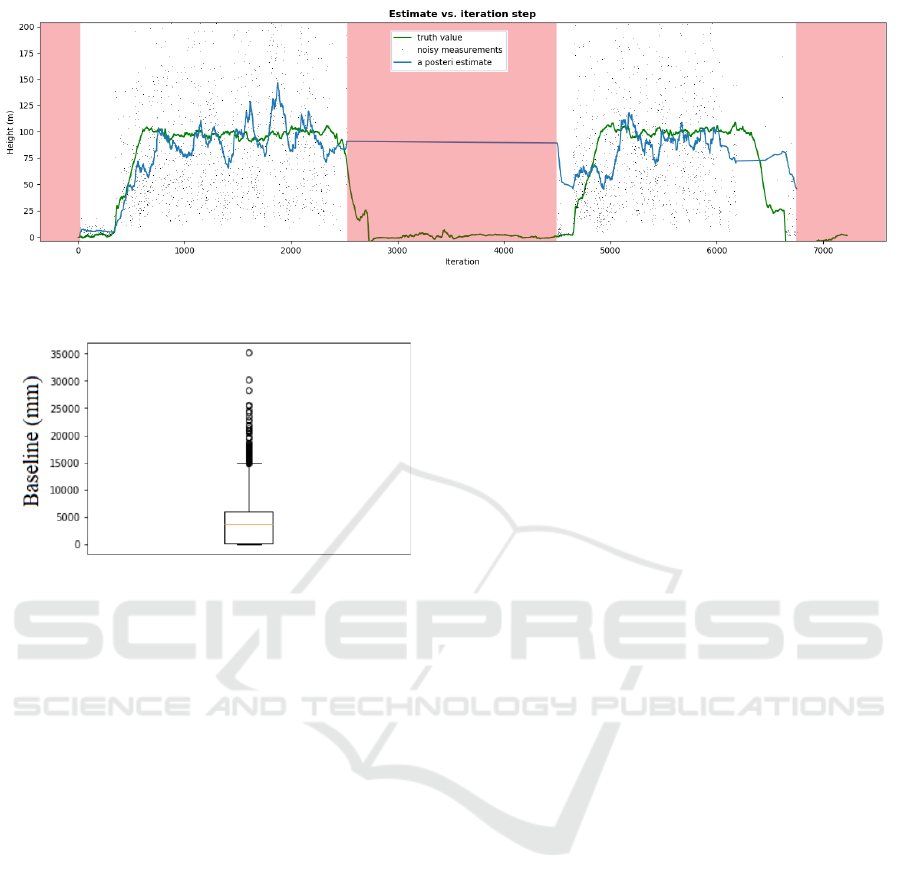
Figure 10: Ground truth, raw measurements and filtered results. Red areas represents data not included in the calculations as
the drone is not flying or no data was recorded.
Figure 11: Boxplot showing the calculated baselines for the
drone.
5 DISCUSSION AND
CONCLUSION
Comparing to simulations, data from a real drone is
much more influenced by noise and as such, measu-
ring height with a single camera does not translate
well from simulation to reality. Comparing to rela-
ted work, Campos et. al achieved MAE around 17%
(Campos et al., 2016). This is in line with our MAE
results using a relatively similar setup, however free
from abrupt stopping and starting, indicating a simi-
lar error range for current vision based free height es-
timators.
A lot of the error can be attributed to inaccurate
data such as using GPS coordinates for baselines and
roll and pitch of the drone. Another crucial part of this
approach is accurate disparity calculations, which is
affected by the chosen feature detector, camera qua-
lity, and terrain texture. In this example, ORB was
chosen for its effectiveness in real-time despite it not
being scale invariant. A scale-invariant feature detec-
tor might improve the results, but a method to run it
in real-time will be required.
Currently, systems such as these that rely on sin-
gle monoscopic cameras seem unfeasible to accura-
tely estimate a drone’s free height at any distance. The
main issue appears to be noisy data, for example poor
matches between the relatively simple ORB features,
discrepancies in data rate, and image quality (both re-
solution, color depth, and shaking). Some of these
can be solved by improving certain aspects of the har-
dware or algorithm, but camera shake and computati-
onal efficiency remain major obstacles for sequential
monoscopic real-time free height estimation.
This paper has explored some of the error sources
relating to feature-based height estimation using a sin-
gle camera and this approach does not appear feasible
for precise estimates with the current setup due to the
many error sources associated with a camera moun-
ted to a fixed wing drone. However, it does show the
beginning of a trend for vision based free height es-
timation as an alternative to barometers or GPS, and
provides some indication for what future works could
improve upon.
ACKNOWLEDGEMENTS
We would like to thank Sky-Watch for their partici-
pation in the project and for providing footage for the
evaluation of our system, as well as Rikke Gade for
all her help with the project.
REFERENCES
Al-Kaff, A., Qinggang Meng, Martin, D., de la Escalera,
A., and Armingol, J. M. (2016). Monocular vision-
based obstacle detection/avoidance for unmanned ae-
rial vehicles. pages 92–97. IEEE.
Campos, I., Nascimento, E., Freitas, G., and Chaimowicz,
L. (2016). A Height Estimation Approach for Terrain
Following Flights from Monocular Vision. Sensors,
16(12):2071.
Choi, K. and Lee, I. (2012). A Sequential Aerial Tri-
angulation Algorithm for Real-time Georeferencing
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
758

of Image Sequences Acquired by an Airborne Multi-
Sensor System. Remote Sensing, 5(12):57–82.
Eigen, D. (2014). Depth map prediction from a single image
using a multi-scale deep network. Advances in neural
information processing systems, pages 2366–2374.
Hadjutheodorou, C. (1963). Elevations from Parallax Me-
asurements. Photogrammetric Engineering, 29:840–
849.
Lowe, D. G. (2004). Distinctive Image Features from Scale-
Invariant Keypoints. International Journal of Compu-
ter Vision, 60(2):91–110.
Lu, Y., Xue, Z., Xia, G.-S., and Zhang, L. (2018). A survey
on vision-based UAV navigation. Geo-spatial Infor-
mation Science, 21(1):21–32.
Matthies, L., Kanade, T., and Szeliski, R. (1989). Kal-
man filter-based algorithms for estimating depth from
image sequences. International Journal of Computer
Vision, 3(3):209–238.
Rosten, E., Porter, R., and Drummond, T. (2010). Faster
and Better: A Machine Learning Approach to Corner
Detection. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 32(1):105–119.
Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.
(2011). ORB: An efficient alternative to SIFT or
SURF. pages 2564–2571. IEEE.
Schenk, T. (1997). Towards automatic aerial triangulation.
ISPRS Journal of Photogrammetry and Remote Sen-
sing, 52(3):110–121.
Zhou, X., Zhong, G., Qi, L., Dong, J., Pham, T. D., and
Mao, J. (2017). Surface height map estimation from
a single image using convolutional neural networks.
page 1022524.
Assessing Sequential Monoscopic Images for Height Estimation of Fixed-Wing Drones
759
