
Showing Different Images Simultaneously by using
Chromatic Temporal Response in Human Vision
Hiroki Yamada, Fumihiko Sakaue and Jun Sato
Nagoya Institute of Technology, Nagoya 466-8555, Japan
{yamada@cv., sakaue@, junsato@}nitech.ac.jp
Keywords:
Multiplex Image, Chromatic Response, Temporal Response, Human Retina.
Abstract:
In t his paper, we propose a novel method for showing different images to multiple observers simultaneously
by using the difference in their chromatic and temporal retinal response. The chromatic and temporal response
characteristics of human retina have individuality, and thus each observer observes slightly different image,
even if the same image is presented to these observers. In this paper, we formalize the chromatic and temporal
relationship between the input stimulus and the response in human vision, and propose a method for showing
arbitrary different images to individual observers simultaneously by using the difference in chromatic temporal
response characteristics. We also show a method for obtaining chromatic and temporal response of human
vision. Experimental results from a special camera which reproduces the impulse response of human retina
show that our proposed method can represent different and arbitrary images to multiple observers.
1 INTRODUCTION
In this paper, we consider multiplex image presenta-
tion, which enables us to show different images to
multiple observers simultaneously by using a single
display. If the multiplex image p resentation is reali-
zed with a TV in a living room, multiple observers
can watch d ifferent T V programs simultaneously by
using a single TV set as sh own in Fig.1. Also, if we
use the multiplex image presentation on a vehicle dis-
play, the passengers can enjoy amusement programs
on the display, while the driver uses the navigation
system on the same display.
Recently Nonoyama et al. (Nonoyama et al.,
2013) p roposed a method fo r presenting different
images to multiple observers by using the difference
in spectral sensitivity characteristics of individual hu-
man vision. They showed that it is possible to encode
multiple images into a single multi-band image, and
decode these multiple image s by using the spectral
sensitivity char a cteristics of individual h uman vision.
The method does not require any special glasses and
does not have limitation in viewpoints and hence very
efficient. However, since it encodes multiple image s
using small difference in spectral sensitivity of human
vision, the images observed by multiple observers are
not separated clearly if the color variations of multiple
images are similar to each other or the spectral sensi-
tivities of multiple observers are close to each other.
Figure 1: Multiplex image presentation. Multiple observers
can enjoy different TV programs simultaneously by using a
single display.
More recently, Ikeba et al (Ikeb a e t al., 2017) used
the difference of the temporal response characteristics
of individual human vision for solving the problem of
chromatic similarity in multiple imag es and mu ltiple
observers. Although their method works well even if
the objective images have similar color variations, ob-
served images are not separated clearly if the temp o-
ral response characteristics of mu ltiple observers are
close to e ach other.
For solving these problems, we in this paper pro-
pose a multiplex image presentation method based on
multiple response characteristics of human vision. In
particular, we combine chromatic response characte-
Yamada, H., Sakaue, F. and Sato, J.
Showing Different Images Simultaneously by using Chromatic Temporal Response in Human Vision.
DOI: 10.5220/0007256700670074
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 67-74
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
67
ristics with temporal response characteristics in hu-
man vision for separating observed images more cle-
arly. By combining multiple characteristics in human
vision, we show that different images can be obser ved
by multiple observers, even if the co lor variations of
objective images are similar to each oth er, and even if
one characteristic in human vision is identical among
multiple observers.
2 RELATED WORK
The multiplex imag e presentation enables us to show
multiple different images to individual observers (Ha-
mada et al., 2 010; Kakehi et al., 2005; Nonoyama
et al., 2013; Muramatsu et al., 2 016; Ikeba et al.,
2017). It is often used for displaying 3D im a ges to
human observers, in which left and right eyes of the
observer observe different images.
Unfortu nately, the existing multiplex image pre-
sentation methods requ ire special equipments, suc h as
stereo glasses f or separating a single multiplex image
into multiple images. The para llax barriers (Berthier,
1896; Ives, 1902) and lenticular lenses (Lippmann,
1908) are also used for separating multiplex images
accordin g to the viewpoint of observers. However, the
position of the viewpoint is fixed in these methods,
and thus observers cannot observe objective images
at arbitrary viewpoints. For moving observers, Perlin
et al. (Perlin et al., 2000) prop osed a method, which
controls light rays of the display according to the vie-
wpoint of the observer, so that the observer can see
appropriate images at any viewpoint. More rece ntly,
complex light field displays were developed a nd used
for showing dense light fields toward multiple obser-
vers simultaneously (Masia et al., 2013; Wetzstein
et al., 2011; Wetzstein et al., 2012; Hirsch et al.,
2014; Lanma n and Luebke, 2013; Huan g et al., 2015).
These meth ods are very useful when we want to dis-
play same 3D in formation to all the observers. Ho-
wever, if we want to display different images to indi-
vidual observers regardless of their viewpoints, these
existing methods fail, since all these m ethods are ba-
sed on the geometric difference of viewpoints.
Recently, Nonoyama et al.(Nonoyama et al.,
2013) proposed a new method for disp la ying multi-
plex images without using the geometric properties
of ligh t fields. In their me thod, they used not th e
characteristics of equipments, but the characteristics
of human observers for displaying different images
to individual observers. In particular, they u sed the
difference of spectral sensitivity of human vision for
displaying different images to individual observers.
Their method does not req uire special glasses nor the
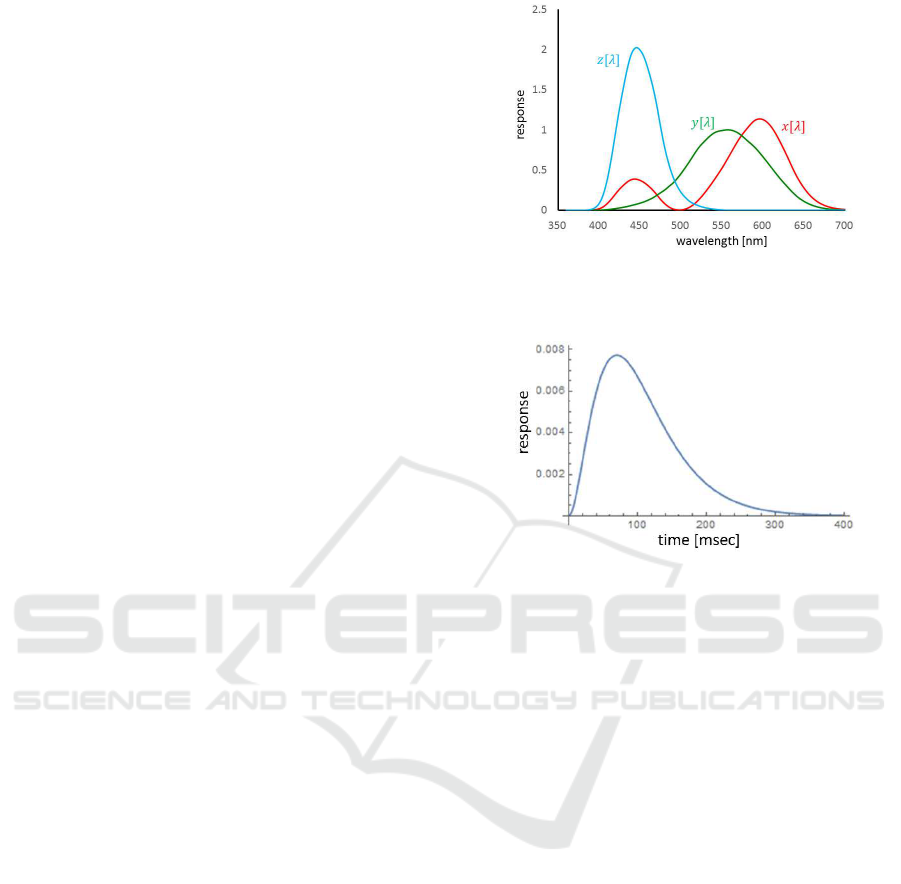
Figure 2: Color matching functions defined by CIE ( CIE,
1931), which describe the spectral sensitivity of a standard
human observer.
Figure 3: I mpulse response of human vision.
fixation of viewpoints. However, it cannot be used
when the spectral sensitivities of observers are simi-
lar to each other o r objective images of multiple ob-
servers have similar co lor variation.
In order to overcome these problems, Ikeba et
al. (Ikeba et al., 2017) proposed a method for dis-
playing multiplex images by using the temporal re-
sponse ch a racteristics of human vision. In their met-
hod, the difference in the reaction time of human re-
tina was used for pre senting different images to mul-
tiple observers.
Unfortu nately, these methods fail to present cle-
arly separate d images to individual observers. Thus,
we in this pa per combine multiple response charac-
teristics of human observers. In particular, we com-
bine chromatic response characteristics and temporal
response c haracteristics of human vision, a nd realize
better separation of observed images.
3 CHROMATIC TEMPORAL
RESPONSE OF VISION
We first consider the ch romatic and temporal response
characteristics of human vision. The chromatic re-
sponse of human vision can be c haracterized by the
spectral sensitivity of 3 different photoreceptor cells
in human retina, that is L-cone , M-cone and S-cone.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
68

(a) H
x
(λ, t)
(b) H
y
(λ, t)
(c) H
z
(λ, t)
Figure 4: Chromatic temporal response function of human
vision.
These three co ne cells are sensitive to long wave-
length light, medium wavelength light and short wa-
velength light respectively.
The c olor perc eption caused by these 3 cone cells
can be associated with physical light spectra by using
the c olor matching functions, x(λ), y(λ) and z(λ),
whose spectral d istributions are as shown in Fig. 2.
These 3 color matc hing functions can be considered
as the spectra l sensitivity of a stand ard human obser-
ver in 3 channels. Thus, we in this paper consider the
individuality in chroma tic response o f human vision
as the individuality in color matching functions, x(λ),
y(λ) and z(λ).
On the other hand, the temporal response of hu-
man vision is described by the temporal impulse re-
sponse of photoreceptor cells, that is the change in
response in time when the light impulse is incident
on a photoreceptor cell. It is known that the imp ulse
response S(t) of a typical photoreceptor cell can be
described as sh own in Fig. 3 (Cao et al., 2007).
It is known that the spectral sensitivity an d the
impulse response are different for every person (Cao
et al., 2007). Th us, we consider a chromatic temporal
response function H(λ, t), wh ich describes th e chro-
matic and temp oral response characteristics, for every
person.
Since the chromatic tempo ral response function
includes the spectral sensitivity characteristics an d
the temporal response cha racteristics, it is a two-
dimensional f unction having r e sponse in two d irecti-
ons, i.e. wavelength direction and time direction, as
shown in Fig. 4. A lso , since it is considered that the
spectral sensitivity characteristics and the tem poral
response characteristic are different for every chan-
nel, the chromatic temporal response function is de-
fined for each channel H
j
(λ, t), j ∈ {x, y, z} as shown
in Fig. 4.
We next consider the observation model based on
the chromatic temporal response function H
j
(λ, t). If
Figure 5: Multi-band projector.
we h ave an in put light E(λ, t) at time t, the observed
intensity y
t
j
of j-th channel at time t can be described
as follows:
y
t
j
=
Z
t
t−T
Z
λ
H
j
(λ, t − t
′
)E(λ, t
′
)dλdt
′
(1)
where, T is the observation period. We use the obser-
vation model in Eq.(1) f or multiplex image presenta-
tion in the following part of this paper.
4 MULTIPLEX IMAGE
PRESENTATION
4.1 Temporal Super-resolution of
Multi-band Projector
In order to realize the multiplex image presentation,
we in this paper control the spectral distribution and
temporal change of incident light by using a high-
speed multi-band projector.
Fig. 5 shows a multi-band projector composed of
multiple p rojectors and narr ow ban d-pass filters, and
it can control the spectr al distribution of p rojected
light at each point on a screen. The incide nt light
E(λ, t) of the multi-band projector can be described
by the spectral distribution E
i
(λ) of i-th band in the
multi-ban d projector and its intensity p
t
i
at time t as
follows:
E(λ, t) =
N
∑
i=1
E
i
(λ)p
t
i
(2)
where, N is the number of bands in the multi-band
projector.
By using such a multi-band projector, the obser-
vation mo del in Eq.( 1) can be rewritten as follows:
y
t
j
=
T
∑
k=1
N
∑
i=1
h
j
ki
p
t−k+1
i
(3)
where, h
j
ki
is the response of j-th channel ( j ∈ {x, y, z})
at discrete time k when the light impulse of i-th b and
Showing Different Images Simultaneously by using Chromatic Temporal Response in Human Vision
69

(a) switch timing is shifted in 3 projecto rs
(b) temporal super resolution from 3 projectors
Figure 6: Temporal super resolution of projector.
is incident o n th e photoreceptor cell at time 0, and it
is described by using the ch romatic temporal response
function H
j
(λ, t) and the spectral distribution E
i
(λ) of
i-th band of the multi-band projector as follows:
h
j
ki
=
Z
t−k+1
t−k
Z
λ
H
j
(λ, t − t
′
)E
i
(λ)dλdt
′
(4)
Furthermore, in order to control temporal re-
sponse of human vision, a very fast light projection
system is required. However, there is no high speed
projector or display with high frame rate. Therefor e ,
we consider temporal super resolution of projection
systems by using multiple projectors whose timing of
switching images is shifted to each other.
For example, if we have three projectors whose
image switch timing is shifted with one third of the
projection cycle as shown in Fig. 6 (a), then the in-
tensity of image projected from these three projectors
changes as shown in 6 (b). As a result, we can chang e
images three times faster than the original projectors,
and c an achieve temporal super resolution of image
projection. If we have K projectors for eac h band in
the multi-band projec tor, the observation model of the
high-speed multi-ba nd projector can be described as
follows:
y
t
j
=
T
∑
k=1
N
∑
i=1
K
∑
l=1
h
j
ki
p
t−k−l+2
i
(5)
In this way, a high-speed multi-band projector can be
realized.
4.2 Computing Projection Images for
Multiplex Image Presentation
We next compute projection images for showing dif-
ferent images to different observers simultaneously
using the high-speed multi-band projector.
Suppose we have M observers, and the chroma-
tic temporal response functions {H
l
x
(λ, t), H
l
y
(λ, t),
H
l
z
(λ, t)} (l = 1, ··· , M) of these M observers are
Figure 7: Temporal double-pulse method.
known. Then, the response function h
jl
ki
of l-th obser-
ver can be computed from Eq.(4). Thus, given a set
of sequential projection images p
t
i
of the high-speed
multi-ban d projector, the observation y
tl
j
(p
t
i
) in j-th
channel of the l-th observer at time t can b e c omputed
from Eq.(5).
Now, what we want to do is to show M different
objective images ˆy
tl
j
(l = 1, ·· · , M) to M observers.
Thus, we estimate a set of sequential projection ima-
ges p
t
i
of the high-speed m ulti-band projector by sol-
ving the following minimization p roblem:
{ ˆp
t
i
} = argmin
p
t
i
M
∑
l=1
T
∑
t=1
{x,y,z}
∑
j
( ˆy
tl
j
− y
tl
j
(p
t
i
))
2
(6)
However, since the p rojectors can only project
images with a fixed range of inte nsity, the projection
images p
t
i
must h old the following inequality.
0 ≤ p
t
i
≤ I
max
(7)
where, I
max
is the maximum inten sity of projecto r
light. Thus, we estimate the projection images p
t
i
by
solving Eq.(6) subject to Eq.(7). Then, the multiplex
image presentation can be realized by presenting the
image p
t
i
from th e high-spee d multi-band projector to-
ward these M observers.
5 MEASURING CHROMATIC
TEMPORAL RESPONSE OF
HUMAN VISION
We next consider a m e thod for measuring chroma-
tic temp oral respo nse function of human vision. For
measuring the chromatic respo nse characteristics, we
use the existing method proposed by Muramatsu et
al. (Muramatsu et al., 20 16), which uses the meta-
merism in human color p e rception an d estimate the
spectral sensitivity of human v isio n efficiently.
For measuring th e tempor al response cha racteris-
tics, we use the temporal double-pulse method pro-
posed in the field of exper imental p sychology (Uchi-
kawa and Yoshizawa, 1993). Since the temporal
double-pulse method is not familiar in the computer
vision field, we briefly explain the meth od.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
70
x y z
(a) summa tion index
(b) imp ulse re sponse
Figure 8: Summation index and estimated impulse response
of human vision.
In th is method, we show a white reference light
and a sequential test light in the same field of view.
The test light changes its color without changing its
brightn ess by p roviding two c olor pulses as shown in
Fig. 7, wher e dL is the amount of color in color pulse.
If dL is small, th e human vision cannot distinguish
the test light from the white reference light, but if dL
becomes large, the hu man vision ca n distinguish these
two lights. So, we measure the thre shold value of dL
changin g the test light.
In the test light, the length D of each pulse is
fixed, but the interval of two color pulses is changed
as shown in Fig. 7. The interval is called a stimulus-
onset asynchrony (SOA). If SOA is large enough, two
pulses are observed independently in the human vi-
sion, and double pulses and a single pulse dose n ot
cause any d ifference in the observation. Therefore,
the threshold value dL
d
of the double pulse is same
as the threshold value dL
s
of the single pulse. Howe-
ver, when SOA become s small, the imp ulse responses
of double pulse overlap, and the photoreceptor has
more excitation than that of the single pulse. As a
result, dL
d
becomes smaller than dL
s
. Since the ra-
tio of dL
d
and dL
s
changes according to the shape of
the impulse response function, the im pulse response
function can be estimated from the ratio obtained by
changin g SOA. The ratio is called a summation index
and is defined as follows:
SI = − log
dL
d
dL
s
(8)
If two imp ulse responses of the double pulse do not
overlap, SI is equal to − log
1
1
= 0, and if they overlap
completely, SI is e qual to − log
1
2
= 0.3.
For estimating the impulse respo nse function S(t)
efficiently, it is modeled by using two para meters, τ
(a) x cha nnel (b) y channel
(c) z chan nel
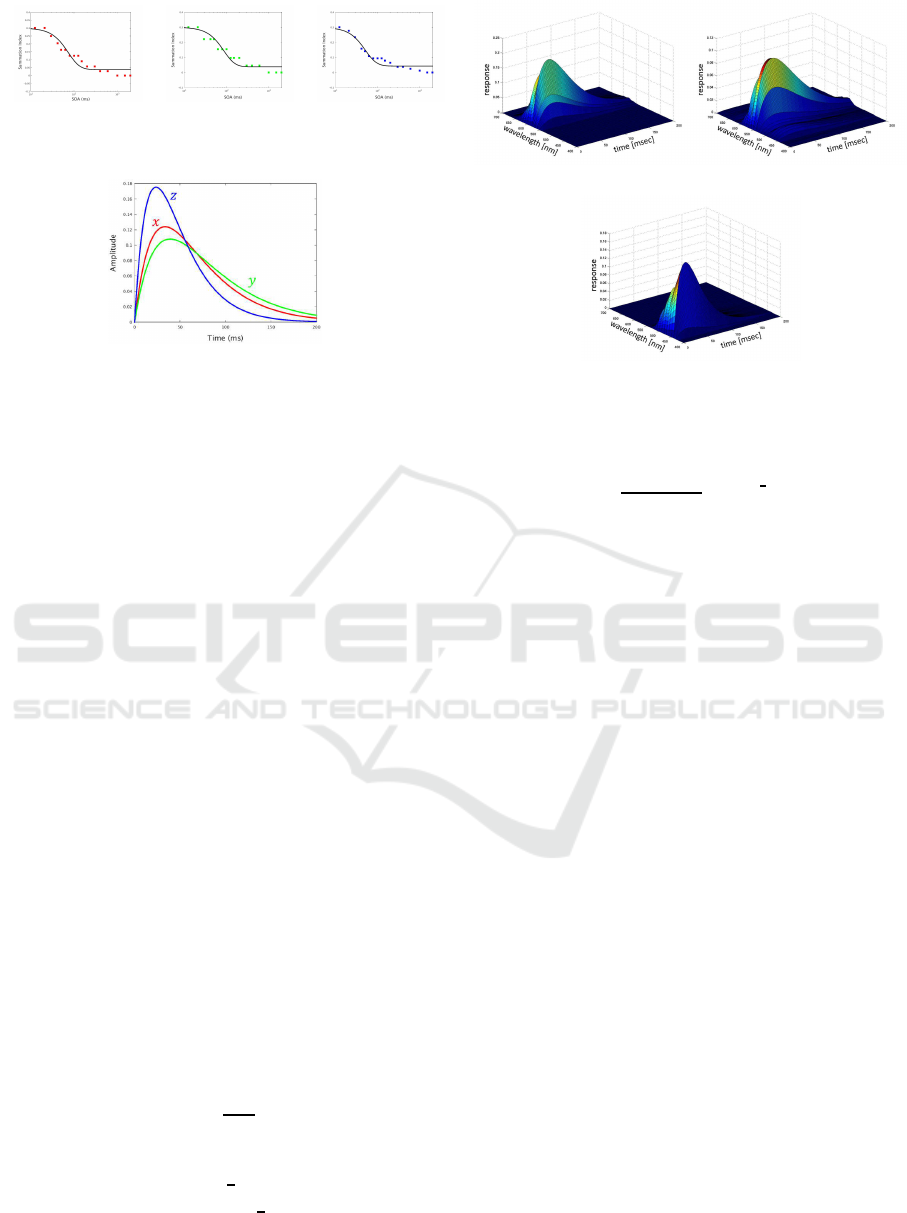
Figure 9: Estimated chromatic temporal response functions.
and n, as follows:
S(t) =
1
τ
n
(n − 1)!
t
n−1
e
−
t
τ
(9)
Thus, the estimation of S(t) is considered as the esti-
mation of τ and n.
Now, if we give some τ and n, then the impulse
response S(t) is fixed from Eq.(9) and the summation
index
ˆ
SI(τ, n) can be computed from Eq .(8). There-
fore, we estimate τ a nd n, so that the computed sum-
mation index
ˆ
SI(τ, n) becomes identical to the o bser-
ved summation index SI. Thus, we estimate τ and n
by solvin g the following minimization problem:
{
ˆ
τ, ˆn} = arg min
{τ,n}
||SI −
ˆ
SI(τ, n)||
2
(10)
In this way, we can estimate the impulse response of
an observer.
Then, by c ombining the spectral sensitivity and
the impulse response, the chromatic temporal re-
sponse function can be computed. In this research,
it is assum e d that the two characteristics are indepen-
dent, and the chromatic temporal response f unction
is described as the product of the spectral sensitivity
characteristic X (λ) ∈ {x(λ), y(λ), z(λ)} and the im-
pulse response S(t) as follows:
H(λ, t) = S(t)X (λ) (11)
The estimated chr omatic temporal response
function can be used for rea lizing the multiplex image
presentation descr ibed in section 4.
Showing Different Images Simultaneously by using Chromatic Temporal Response in Human Vision
71
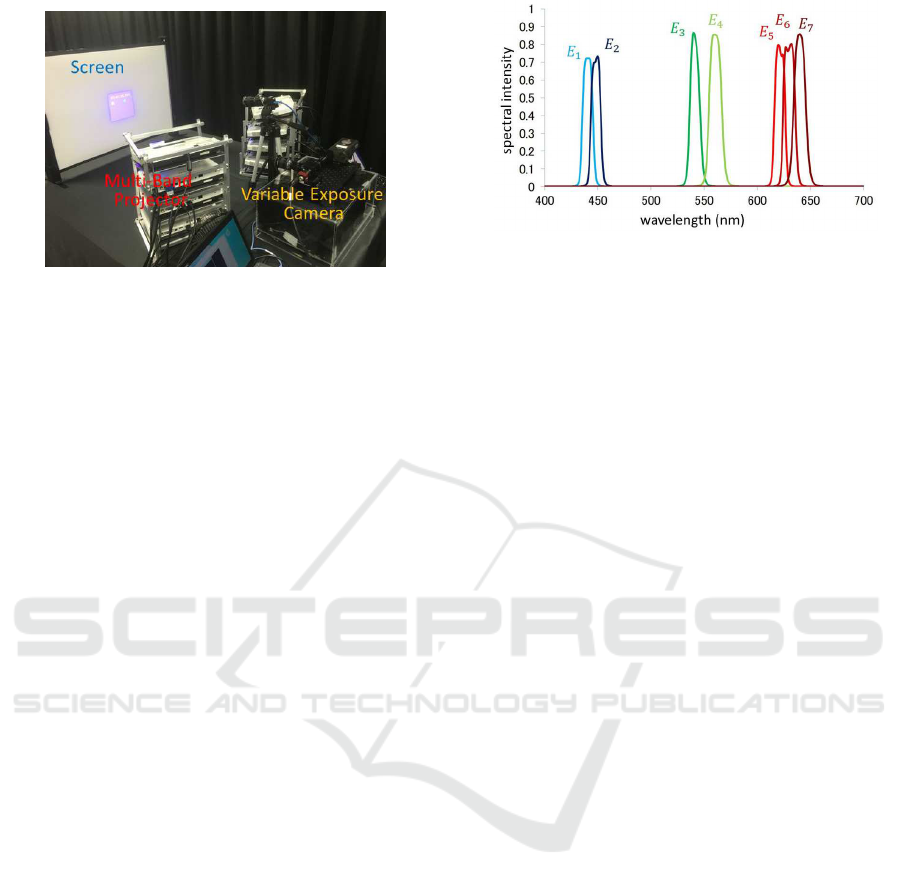
Figure 10: Experimental setup.
6 EXPERIMENTS
6.1 Estimation of Chromatic Temporal
Response Function
We first show the results of c hromatic temporal re-
sponse estimation .
For measuring the summation index from the tem-
poral do uble-pulse method, we used a hig h-speed dis-
play whose refresh rate is 240 fps. We changed the
SOA of double pulse in the test light from 0 msec to
3000 msec, and measured the magnitude of color dL
when the observer perceived the chang e in color.
Fig. 8 (a ) shows the summation index of x, y and
z channels estimated from the tempor a l double-pulse
method. The points in the graph represent the sum-
mation index obtained from actual m easurement, and
the solid lines show the summation index computed
from the parameters estimated by usin g these points.
Fig. 8 (b) shows impulse response of x, y and
z channels estimated from the summation index in
Fig. 8 (a).
By combining the spectral sensitivity estimated
from the metamerism (Muramatsu et al., 2016), the
chromatic temporal response functions wer e obtained
as shown in Fig. 9.
6.2 Multiplex Image Presentation
We next show results of the proposed multiplex image
presentation.
Since it is impossible to extract and show ima-
ges observed by real human vision, we evaluated our
multiplex image presentation by usin g a camera as an
observer. Since the temporal response function of a
standard camera cannot be controlled, we reproduced
the chromatic temporal response function of human
vision by using a variable exposure time camera pro-
posed by Uda et al. (Uda et al., 2016), which can con-
Figure 11: Spectral distribution of the multi-band (7-band)
projector used in our experiments.
trol the temporal exposure patter n freely in a single
exposure time.
Our experimental setup is as shown in Fig. 10.
The images are projected to the screen from the multi-
band projector, and they are observed by the variable
exposure time camera. The spectral distribution of the
multi-ban d projector is as shown in Fig. 11. We re-
produced two different chromatic temporal response
functions, “observer A” and “observer B”, by usin g
the variable exp osure time camera.
Fig. 12 (a) shows objective images for these two
observers, which we want to show them. As we can
see in these images, the objective images for these
two observers are completely different. Fr om these
objective image, we computed sequential projection
images of the multi-band projector. The derived ima-
ges were projected from the multi-band projector and
observed by the variable exposure time camera. For
compariso n, we also implemented and tested two ex-
isting methods. T he first one is a method proposed by
Nonoyama (Nonoyama et al., 201 3) wh ich only uses
the difference in spectral sensitivity, and the second
one is a method proposed by Ikeba (Ikeba et al., 2017)
which only uses the difference in temporal re sponse.
Fig. 12 (b) shows images obser ved by observer A
and B when we used the proposed me thod, and (c)
and (d) show observed images in Nonoyama’s met-
hod and I keb a’s method respectively. As we can see in
these images, the proposed method enables us to show
more clear and more independent images to these ob-
servers. The RMSE values also sh ow that the propo-
sed method provides us mo re accu rate observation in
multiplex image presentation.
Fig. 13 shows results f rom different ob je ctive ima-
ges. As we can see in these resu lts, our method works
under various objective images.
We next evaluate the e fficiency o f the temporal
super-resolution of projector in th e multiplex image
presentation. Fig. 14 sh ows the comparison of multi-
plex image presentation implem ented by using high-
speed projectors, temporal super-resolution of pro-
jectors and standard projectors. From these resu lts,
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
72

(c) existing method (d) existing method
(a) objec tive image (b) prop osed method (spectral) (tempor al)
observer Aobserver B
RMSE 16.17 19.93 18.78
Figure 12: The results of multiplex image presentation.
observer A observer B observer A observer B
objective imageobserved image
Figure 13: The results of multiplex image presentation (other results).
objective image high-speed projector super-resolution standard pro je ctor
observer Aobserver B
RMSE 11.06 12.37 12.48
Figure 14: Comparison of multiplex image presentation f r om high speed projectors, temporal super-resolution of projectors
and standard projectors.
Showing Different Images Simultaneously by using Chromatic Temporal Response in Human Vision
73

we find that the temporal super-resolution provides us
better quality in mu ltiplex image presentation than the
standard pro je ctors.
7 CONCLUSION
In th is paper, we proposed a novel method for sho-
wing different images to multiple observers simulta-
neously by using the difference in their chromatic and
temporal retinal response.
We first formalized the chromatic and tempo ral
relationship between the incident light and the re-
sponse in human vision. Then, w e proposed a met-
hod for showing arbitrary different images to indivi-
dual observers simultaneously by using the difference
in chr omatic temporal response function in human vi-
sion. We also showed a method for obta ining the
chromatic and temp oral response function of human
vision.
The experimental results show that the use of mul-
tiple visu a l response character istics is efficient for re-
alizing more ac curate multiple image presentation.
REFERENCES
T. Hamada, K. Nagano and T. Scritters. A multiplexed
image system for a public screen. In Proc. Virtual
Reality International Conference. 321–323, 2010.
Y. Kakehi, M. Iida, T. Naemura, Y. Shirai, M. Matsushita
and A. Ohguro. Lumisight table: An interactive view-
dependent tabletop display. Computer Graphics and
Applications, 25, 48–53, 2005.
M. Nonoyama, F. Sakaue and J. Sato. Multiplex image pro-
jection using multi-band projectors. In Proc. IEEE
Workshop on Color and Photometry in Computer Vi-
sion, 2013.
K. Muramatsu, F. Sakaue and J. Sato. Estimating spectral
sensitivity of human observer for multiplex image
projection. In Proc. International Conference on
Computer Vision Theory and Applications, 183–191,
2016.
D. Ikeba, F. Sakaue and J. Sato. Showing Different Ima-
ges to Observers by using Difference in Retinal Im-
pulse Response. In Proc. International Conference on
Image Analysis and Processing, 718–729, 2017.
CIE. Commission internationale de l’Eclairage procee-
dings. Cambridge University Press, 1931.
D. Cao, A. Zele and J. Pokorny. L inking impulse response
functions to reaction time. Vision Research, 47, 1060–
1077, 2007.
A. Berthier. Images stereoscopiques de grand format. Cos-
mos, 34:205–210, 227–233, 1896.
F. Ives. A novel stereogram. Journal of the Franklin Insti-
tute, 153:51–52, 1902.
G. Lippmann. E preuves reversibles donnant la sensation du
relief. Journal of Physics, 7(4):821–825, 1908.
K. Perlin, S. Paxia and J.S. Kollin. An Autostereoscopic
Display. In ACM SIGGRAPH, 2000.
B. Masiaa, G. Wetzsteinb, P. Didykc and D. Guti errez. A
survey on computational displays: Pushing the boun-
daries of optics, computation, and perception. Com-
puter & Graphics, 37(8), 2012–1038, 2013.
G. Wetzstein, D. Lanman, W. Heidrich, and R. Raskar. Lay-
ered 3d: tomographic image synthesis for attenuation-
based light field and high dynamic range displays. In
ACM Transactions on Graphics, 30(4), 2011.
G. Wetzstein, D. Lanman, M. Hirsch, and R. Rasker. Ten-
sor displays: Compressive light field synthesis using
multilayer displays with directional backlighting. In
ACM Transactions on Graphics, 2012.
M. Hirsch, G. Wetzstein, and R. Rasker. A compressive
light field projection system. In ACM Transactions on
Graphics, 2014.
D. Lanman and D. Luebke. Near-eye light field displays. In
ACM SIGGRAPH Asia, 2013.
F. Huang, K. Chen, and G. Wetzstein. The light field stereo-
scope immersive computer graphics via factored near-
eye light field displays with focus cues. In ACM SIG-
GRAPH, 2015.
Uchikawa, K., and Yoshizawa, T. Temporal Response to
Chromatic and Achromatic Change Inferred from
Temporal Double-Pulse Integration. Journal of the
Optical Society of America, A, 1697–1705, 1993.
S. Uda, F. Sakaue and J. Sato. Variable exposure time ima-
ging for obtaining hdr images. In Proc. International
Conference on Computer Vision Theory and Applica-
tions, 118–124, 2016.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
74
