System Identification Algorithms Applied to Glottal Model Fitting

Piotr Barycki, Irene Murtagh and Barry Kirkpatrick

TU Dublin, Blanchardstown Campus, Dublin, Ireland

Keywords: Glottal Flow, Glottal Model, Pathological Speech, System Identification.

Abstract: This study proposes a new method of fitting a glottal model to the glottal flow estimate using system

identification (SI) algorithms. Each period of the glottal estimate is split into open and closed phases and each

phase is modelled as the output of a linear filter. This approach allows the parametric model fitting task to be

cast as a system identification problem and sidesteps issues encountered with standard glottal parametrisation

algorithms. The study compares the performance of two SI methods: Steiglitz-McBride and Prony. The tests

were performed on synthetic glottal signals (n=121) and real speech (n=50 healthy, n=23 pathological). The

effectiveness of the techniques is quantified by calculating the Normalised Root Mean Squared Error

(NRMSE) between the estimated glottal fit and the glottal estimate. Tests on synthetic glottal signals show

that the average performance of the Steiglitz-McBride method (97.25%) was better than the Prony method

(70.41%). Real speech tests produced results of 64.29% and 51.57% for healthy and pathological speech

respectively. The results show that system identification techniques can produce robust parametric model

estimates of the glottal waveform and that the Steiglitz-McBride method is superior to the Prony method for

this task.

1 INTRODUCTION

The glottal waveform represents the activity of the

vocal folds and can provide vital information about

the vocal folds and their behaviour. The glottal

waveform can be estimated from the speech signal

and is utilised in many speech processing

applications, including speech coding, synthesis and

speech disorder diagnosis (Klatt, 1990). Parametric

models of the glottal waveform are often employed

and despite the success of the glottal signal in

applications, challenges remain in accurately and

robustly estimating the parameters of these models.

This is the case for healthy speech but is particularly

notable for pathological speech. This study aims to

present a new model of the glottal waveform and test

methods to estimate the parameters of this model.

This is partly motivated by the need to develop a

method that can accurately and robustly estimate the

glottal parameters of pathological speech.

Parameterisation of the glottal signal consists of

two steps: (1) glottal waveform estimation and (2)

fitting a parametric model to the estimated glottal

waveform. Glottal waveform estimation is achieved

by removing the effect of the vocal tract from the

speech waveform, often by estimating a vocal tract

filter and inverse filtering the speech signal with this

filter to remove the vocal tract component. The

resulting glottal estimate will have the parametric

model fitted by applying an appropriate optimisation

procedure. This is typically a nonlinear optimisation

problem, depending on the particular glottal model

and how the problem is cast. This is the case for the

Liljencrants-Fant (LF) model, which is currently the

most widely adopted glottal waveform model. Both

of these steps have a number of known difficulties as

reported in (Li et al, 2011, 2012) (Fu, Murphy, 2006).

It is often impossible to fully remove the vocal

tract component from the speech waveform. This can

result in distortion of the glottal waveform often

presenting as ripples in the glottal waveform (Fant,

Lin 1987). This can also cause problems with correct

estimation of glottal opening and closing instants

(GOI and GCI respectively) and in turn, inaccurate

glottal parameter estimation. In fitting the parametric

model to the estimated glottal waveform, due to the

necessity to employ nonlinear optimisation methods,

the accuracy of the final glottal parameters depends

critically on the initial estimates used to initialise the

optimisation procedure (Strik, 1993). Bad initial

estimates will result in suboptimal estimation of the

parameters (Li et al, 2012). This problem becomes

124

Barycki, P., Murtagh, I. and Kirkpatrick, B.

System Identiﬁcation Algorithms Applied to Glottal Model Fitting.

DOI: 10.5220/0007259801240131

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 124-131

ISBN: 978-989-758-353-7

particularly challenging for pathological speech,

when the glottal parameters may be outside the

typical range expected for healthy speech.

This paper proposes a new way to model the

glottal waveform, which in turn allows the

application of new algorithms to estimate the glottal

parameters. The model being proposed considers the

open and closed phase of the glottal signal

individually and models the glottal signal within each

phase as the impulse response of a linear filter. This

allows fitting of the parametric model to the glottal

estimate to be cast as a system identification problem.

In this case the input is modelled as an impulse, the

output is either the open or closed phase of the glottal

estimate and the problem is to estimate the filter that

can best approximate the output for the given input

signal. Many system identification algorithms exist

that could be used for this task (Ljung, 1999),

including algorithms that have been developed to be

robust to noise in the output signal. This is

particularly beneficial for glottal signals with high

levels of aspiration noise, which is often the case for

pathological speech.

The remainder of this paper is arranged as

follows. Section 2 presents some background on

existing glottal models before presenting the details

of the new approach being proposed in this paper.

Section 3 describes how the model and associated

algorithms are tested. Section 4 presents the results

with discussion and Section 5 presents the

conclusions.

2 MODELING THE GLOTTAL

WAVEF OR M

Many signal models of the glottal waveform have

been proposed in the literature. These include the

Rosenberg model (Rosenberg, 1971), the

KLGLOTT88 (Klatt, 1990), the R++ model

(Veldhuis,1998), the CALM model (Doval et al,

2003) and the LF model, among others. Signal

models of the glottal flow generally focus on the

differentiated glottal flow. Typically, a separate

mathematical function is used to model the open and

return phases of the differentiated glottal signal, such

that they join at the GCI and the glottal pulse is

differentiable at the GCI. An example model signal of

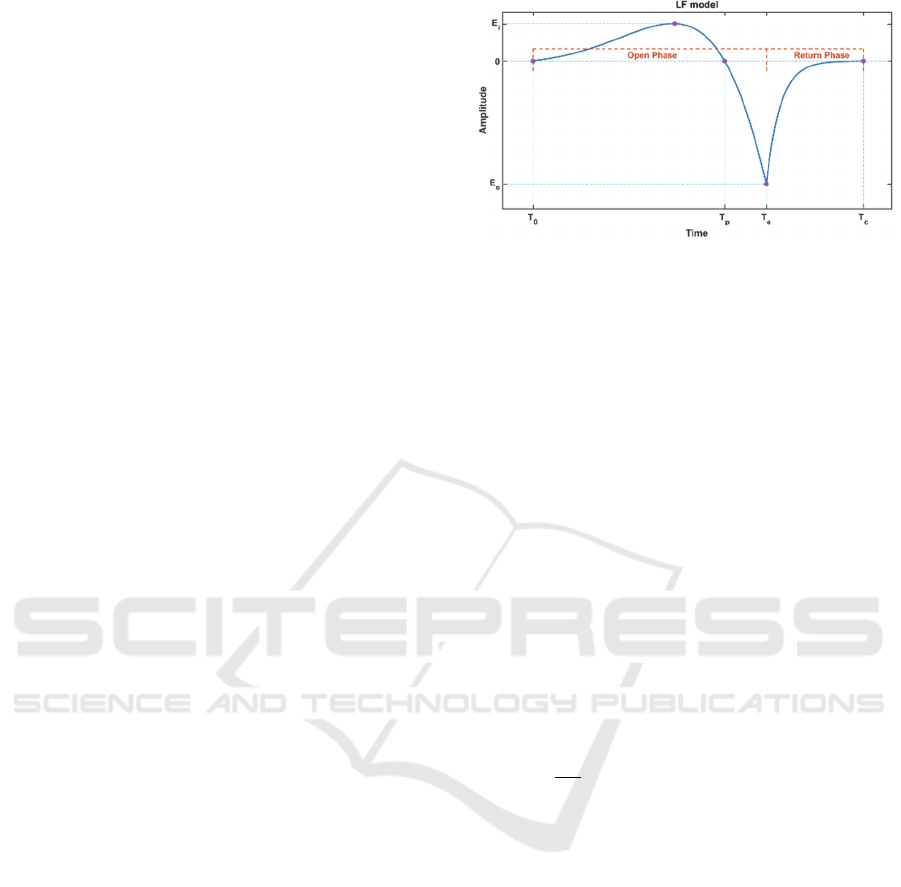
the differentiated glottal flow waveform generated

with the LF model is depicted in Figure 1.Most

models have a similar approach, in that they have a

separate

mathematical function for modelling the

Figure 1: LF model diagram of a differentiated glottal pulse.

open and return phases of the signal. The primary

difference between many of these models is the

functions employed to model each phase.

Currently the most widely adopted glottal model

is the LF model, equation 1. The model consists of

two parts, representing the open and return phases of

the glottal signal. The LF model is a five-parameter

model. The entire model can be defined using the

timing parameters T

, T

and T

, the pitch period T and

the amplitude of the glottal closure instant (GCI) E

and T

are times relative to the start of the pitch

period as depicted in Figure 1. T

is the time constant

of the exponential in the return phase. The time

parameter T

marks the instant of the glottal closure

and E

is the corresponding amplitude. Despite

having several more parameters, the LF model is

constrained by the five primary parameters and the

remaining parameters can be estimated from the

primary parameters.

























sin



, 0









































,







0, 

(1)

Fu and Murphy (2006) proposed a new glottal

source estimation method based on a joint source-

filter separation technique using the LF model. Their

proposed technique estimates the parameters based

on the Rosenberg model and then converts them to

the LF parameters. They perform tests on synthetic

speech covering six phonation types and real healthy

speech files to verify the performance of their method

on ‘real-world’ data. They report a high accuracy of

the synthetic speech results and robustness against

additive glottal noise, stating that this allows their

new method to be applied to a wide range of voice

types. Tests on real speech report performance

comparable with that of the synthetic speech and state

that their model provides rather reliable estimation in

the case of natural utterances.

Li et al. (2011) proposed a new approach for LF

model based glottal source parameter estimation by

System Identiﬁcation Algorithms Applied to Glottal Model Fitting

125

extended Kalman filtering and use synthetic speech to

conduct tests. They quantify the results by calculating

the error rates of the estimated shape controlling

parameters and report the method to be effective for

a wide range of LF parameters and overall, perform

better than the standard time-domain LF-model

fitting algorithm when tested on synthetic speech.

Work of Muthukumar et al. (2013) proposes

estimating the LF model parameters using a gradient

descent optimization algorithm. The accuracy of their

approach inherently depends on the accuracy of the

initial parameters. They iteratively fit a LF model to

the inverse filtered glottal signal and then optimise it

to minimize the RMS error. As a way of quantifying

the performance of their approach, they conducted a

listening test, comparing their model with a baseline

system described in (Yoshimura et al, 2001). The

majority of the listeners chose the proposed system as

more natural sounding and the results were deemed

statistically significant.

Previous studies on glottal fitting report

difficulties with the standard model fitting approach

and aim to overcome them in different ways. A major

problem is with estimating the vocal tract filter

without the glottal flow having an effect on the output

speech. This issue was already reported by Fant and

Lin back in (1987).

The glottal waveform estimation step can be

impacted by source-tract interaction and the

performance limitations inherent in some inverse

filtering algorithms (Quatieri, 2006). In the IAIF

method (Alku, 1991), the vocal tract filter is

estimated using an adaptive filter algorithm and

subsequently applied to estimate the glottal signal. A

more recent Quasi Closed Phase (QCP) method

described in (Airaksinen et al, 2014) eliminates the

source effect using weighted linear prediction (WLP)

and focuses on the samples located in the closed

phase. Recent work of Sahoo and Routray (2016)

implements system identification methods in a novel

glottal inverse filtering method. They report that

when compared to the most widely used IAIF and the

more recent QCP methods, their model using system

identification techniques produced results indicating

their model outperforms IAIF and QCP, however, at

the cost of computational speed.

2.1 Proposed Glottal Model

This study proposes modelling the open and return

phases of the glottal signal as the impulse response of

two linear filters. The input impulse occurs at the GCI

and the resulting filter outputs produce the open and

return phases of the glottal signal. For practical

purposes in processing the glottal signal the open

phase will be reversed in time and treated as a causal,

stable impulse response.

In the method proposed by Doval et al (2003), the

differentiated glottal flow signal is modelled as the

response of a linear filter. The model is referred to as

the causal-anticausal linear model (CALM), as the

glottal signal is modelled as having both causal and

anticausal components. The return phase corresponds

with the causal component and the open phase

corresponds with the anticausal component. The

method proposed in this study adopts a similar

approach, by modelling the glottal signal as the output

of linear filters. However, our approach treats the two

phases as outputs of two independent linear filters as

opposed to one a causal-anticausal linear filter model

considered by CALM, and models those filters using

SI methods.

The transfer functions requirements for the glottal

modelling filters are determined by matching them to

the LF model. The LF equation for the return phase is

a decaying exponential which corresponds with the

impulse response of a continuous time first order

filter. The open phase, when time reversed,

corresponds with a damped sinusoid or equivalently

the impulse response of a continuous time stable

second order filter. The corresponding transfer

functions in the Z transform domain are given in

equation 2 for the open phase transfer function,





(), and equation 3 for the return phase transfer

function, 



(). The meeting point of the open and

return phases represents the GCI, T

, with amplitude

value of E

. The input impulse for each filter is set to

an amplitude of 1. For the open phase the input

impulse is applied at the sample corresponding with

the GCI. For the closed phased the impulse is applied

at the sample adjacent to the GCI within the closed

phase.













































(2)





























(3)

This model establishes the framework for

estimating the parameters of the glottal waveform as

a system identification problem allowing us to bypass

the problems posed by the issues encountered with

standard glottal parametrisation algorithms. The input

and output signals for open and closed phases are

known and a method to estimate the system that can

produce the corresponding response is required to

estimate the glottal parameters.

BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing

126

2.2 Parameter Estimation

Numerous algorithms exist that could be used to solve

the system identification problem to estimate the

glottal parameters for the proposed models (Ljung,

1999). For this study Prony’s method (Hayes, 2009)

and the Steiglitz McBride method (Steiglitz,

McBride, 1965) where selected to estimate the

parameters of the transfer function models of the open

and return phases of the glottal signal.

Prony’s method was selected as it has a relatively

low computational complexity only requiring the

solution of a set of linear equations, to provide the

parameters of a given model. A disadvantage of

Prony’s method is that it is known to have poor

performance when presented with a noisy output

signal (Kumaresan et al, 1984).

The Steiglitz-McBride algorithm is an iterative

technique of linear system identification. It works by

minimising the mean-square error between the output

of the system and the estimated model output and

improving the estimate at each iteration. The first

iteration of the Steiglitz-McBride algorithm requires

a means to make an initial estimate of the model

parameters to initialise the algorithm. This is often

achieved by applying Prony’s method. The Steiglitz-

McBride algorithm was selected for this study as it is

known to be robust to noise in the output signal and

can provide optimal estimates in the case of white

noise in the output signal (Steiglitz, McBride, 1965

and Stoica, Soderstrom, 1981). This study employs

Prony’s method to initialise the Steiglitz-McBride

algorithm.

3 THE EXPERIMENT

The aim of this study is to test a new model of the

glottal waveform that utilises SI algorithms to

parametrise the glottal signal. Two SI algorithms are

considered, the Prony method and the Steiglitz Mc

Bride algorithm, as described in section 2.2. The

experiment is designed to (1) quantify the

performance of the SI algorithm in terms of the

accuracy of the glottal fit, (2) to determine their

robustness to noise in the glottal estimate and (3) to

identify the performance of the algorithms in real

speech and identify differences in performance of

each algorithm between healthy and pathological

speech.

Tests are performed to fit the proposed glottal

model to glottal waveform estimates using each of the

two SI algorithms considered. These tests are

performed on both synthetic glottal pulses and on

glottal estimates from real speech, including

pathological speech. To quantify the quality of the

glottal fit to a glottal pulse the Normalised Root Mean

Square Error (NRMSE) is employed. The NRMSE

will be displayed in the form of a percentage in which

an NRMSE of 100% represents a perfect fit of the

model to the glottal estimate and 0% represents a

performance level corresponding with that of a best

line fit to the glottal waveform estimate. Testing is

performed on both synthetic glottal signals and glottal

estimates from real speech.

3.1 Synthetic Glottal Waveforms

The first part of this study tests the algorithms on

synthetic glottal signals. Synthetic glottal signals

allow the comparison between the glottal fit with the

true glottal signal, unlike for real speech in which the

true glottal signal is not known and only an estimate

is available. Glottal signal estimates from real speech

are likely to have unquantifiable sources of variation

introduced by errors in the inverse filtering algorithm

used to estimate the glottal signal. This typically

introduces features into the glottal signal that are not

accounted for by the glottal model and can impact the

results. Using synthetic glottal signals bypasses these

issues and allows the test set to cover a broad range

of glottal parameters and noise levels in a controlled

manner.

The tests with synthetic glottal signals consist of

3 parts:

 Test 1 - The first part consists of testing 100

synthetic glottal pulses with no noise over a range of

voice types. This test determines the accuracy of the

proposed model and accompanying SI algorithms

across a range of voice types with no noise present.

 Test 2 - The second part of the test is similar to

test 1, but with noise added. This test determines the

accuracy of the proposed model and accompanying

SI algorithms across a range of voice types when

noise is present in the glottal signal.

 Test 3 - The third part of the test is to determine

the accuracy of the fit as the noise level is varied. The

parameters of the glottal pulse are held constant. This

test indicates the robustness of the methods to noise

in the glottal signal.

All synthetic glottal pulses were created using the

LF model equations as given in equation (1). The

parameters were varied to simulate the variations in

real human speech.

For test 1 the 100 pulses are split into 2 groups of

50 pulses, representative of male and female speech.

System Identiﬁcation Algorithms Applied to Glottal Model Fitting

127

Table 1: Artificial speech timing parameters.

The 50 pulses representing male speech contain

100 samples per pitch period, this corresponds with a

pitch of 100 Hz and sampling frequency of 10000 Hz.

The 50 pulses representing female speech contain 41

samples per pitch period, this corresponds with a

pitch of 244 Hz and sampling frequency of 10000 Hz.

Within each set of 50 pulses the glottal parameters are

selected to have 10 pulses each of the voice types;

modal, fry, breathy, falsetto and harsh. The timing

parameters used to create these voice types are given

in Table 1 (Ghosh, Narayanan, 2011). To create 10

samples of each voice type, the timing parameters

were randomly varied in the range of 5% about the

values in Table 1.

For test 2, the signal to noise ratio (SNR) of the

glottal signals was set to 40 dB. This was achieved by

adding white noise to each of the glottal pulses in the

test set for test 1. The value of 40dB was chosen as it

is the typical SNR value reported for modal speech

(Ghosh, Narayanan, 2011). For test 3, 21 glottal

pulses were generated with SNR levels varying

between 0 and 100 dB, increasing in 5 dB increments.

The glottal pulses each contained 100 samples per

pitch period and had the timing parameters of modal

speech. Only the SNR value varied between the 21

glottal pulses.

3.2 Real Speech

Tests on synthetic glottal signals provide insight on

the effectiveness of the methods, but does not present

as challenging a task as real speech. The real speech

tests show how the method performs on samples with

levels of signal complexity not represented in the

synthetic glottal signals. It also indicates how the

performance is impacted when the methods being

tested are combined with non-ideal glottal estimation

algorithms. The real speech tests consist of two parts,

the first part investigates real healthy speech and the

second part investigates real pathological speech. The

real speech files have been accessed from the Speech

Synthesis book by D.G. Childers (Childers, 1999).

The study uses healthy and pathological speech

samples from patients 20 to 80 years old consisting of

/a/ and /i/ vowel utterances. The signals were sampled

at 10 kHz and recorded using a Bruel & Kjaer

microphone. The speech database assembled for this

study is as follows:

 Healthy speech – 50 utterances of the vowel /a/,

25 male and 25 female.

 Pathological speech - 23 utterances of the vowel

/i/, 8 male and 15 female.

The files were inverse filtered to extract the glottal

flow derivatives using the IAIF method described in

(Alku, 1991). The GCI locations were determined

using the SEDREAMS algorithm reported in

(Drugman, 2012). Using the GCI locations of the

inverse filtered signals, each glottal estimate signal

was divided into sections of individual pitch periods.

The glottal model fitting algorithms were then applied

to each pitch period. The NRMSE values were

calculated between each glottal signal and its glottal

model fit and the average NRMSE value for each

speech file was recorded.

4 RESULTS AND DISCUSSION

The following section presents the test results in two

subsections, first section documents the synthetic

glottal signal results and the second presents the

results from real speech tests.

4.1 Tests Using Synthetic Glottal

Signals

The performance of the algorithms is compared by

investigating the NRMSE values between the

estimated fit and the original glottal signal. The

results for synthetic glottal signals are presented in

Table 2.

 Test 1 – For the 50 pulses simulating a 100 Hz

male speech, the NRMSE values for Steiglitz-

McBride and Prony methods are 97.99% and 97.93%

respectively. Tests on the set of 50 pulses created to

simulate a 240 Hz speech signal sampled at 10000 Hz

produced the following results: The mean NRMSE

value for the Prony algorithm was 98.24% and

98.86% for the Steiglitz-McBride method. These

result shows that the performance of the two methods

was approximately equal for these tests.

 Test 2 – The NRMSE values for the Prony and

Steiglitz-McBride algorithms tested on the 50 pulses

with added noise for male samples are 29.20% and

96.23% respectively. For female samples, the results

are 55.66 % and 96.55% for Prony and Steiglitz-

BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing

128

McBride algorithms respectively. A notable drop in

performance occurs in the results for the Prony

method when noise is introduced, consistent with

reports that the Prony algorithm does not perform

well in noisy environments (Kumaresan et al, 1984).

The Steiglitz McBride results are comparable with the

results recorded when no noise was present in the

glottal signal.

 Test 3 – The results of this test are illustrated in

Figure 2. The NRMSE values are plotted against the

corresponding SNR values. This indicates the decline

in performance as noise levels increase for each

algorithm. It can be noted from Figure 2 that between

SNR of 100 and 70 dB, both algorithms perform

similarly. As the noise level increases, the

performance of the Prony method begins to

deteriorate noticeably more than the performance of

the Steiglitz-McBride algorithm. Taking the 90%

NRMSE value as a reference point, it can be seen that

the performance of the Prony method drops below

this level at SNR at approximately 60 dB while the

Steiglitz-McBride algorithm provides a 90%+ fit to

approximately 30 dB SNR level. This indicates that

the Steiglitz-McBride method performs more

robustly than the Prony method for noisy glottal

signals.

A statistical analysis test was carried out to verify

whether the results provide any statistical

significance. The results of Steiglitz-McBride and

Prony algorithms were compared using the student t-

test. The null hypothesis states that the samples from

the two datasets have the same mean at the 5%

significance level. In all cases, the null hypothesis is

rejected indicating the difference in the means is

statistically significant.

Figure 2: Graph comparing NRMSE values with their

respective SNR values for Prony and Steiglitz-McBride

methods.

4.2 Tests Using Real Speech

The second part of the study consisted of performing

tests on real speech, including both healthy and

pathological speech. The results are presented in

Table 3. For healthy speech the mean NRMSE value

for the Prony method was 29.23% and for the

Steiglitz-McBride method was 64.29%. For the

pathological speech results, the Prony methods mean

NRMSE value was 25.66% while the mean NRMSE

Table 2: Artificial speech test results.

Table 3: Real speech test results.

value of the Steiglitz-McBride method is 51.57%.

The Steiglitz-McBride method demonstrated better

accuracy at fitting the glottal model to the estimated

glottal waveform for both healthy and pathological

speech. The results for real speech are notably lower

than those reported for synthetic glottal signals.

To verify the statistical significance of the results

for real speech, we again used the student t-test, with

the same null hypothesis and levels of significance.

For both, healthy and pathological results, the test

rejected the null hypothesis indicating the difference

in the means is statistically significant, when

comparing Steiglitz-McBride and Prony algorithms.

4.3 Sample Fits

This section presents sample fits of the glottal model

to the inverse filtered estimate for both healthy and

pathological speech using the Steiglitz-McBride

algorithm. The example glottal fit in Figure 3 is for a

healthy glottal pulse and has a match of 75.57%. The

fit in Figure 4 illustrates the Steiglitz-McBride

method applied to the glottal waveform of a

pathological speech sample and has an NRMSE of

54.17%.

System Identiﬁcation Algorithms Applied to Glottal Model Fitting

129

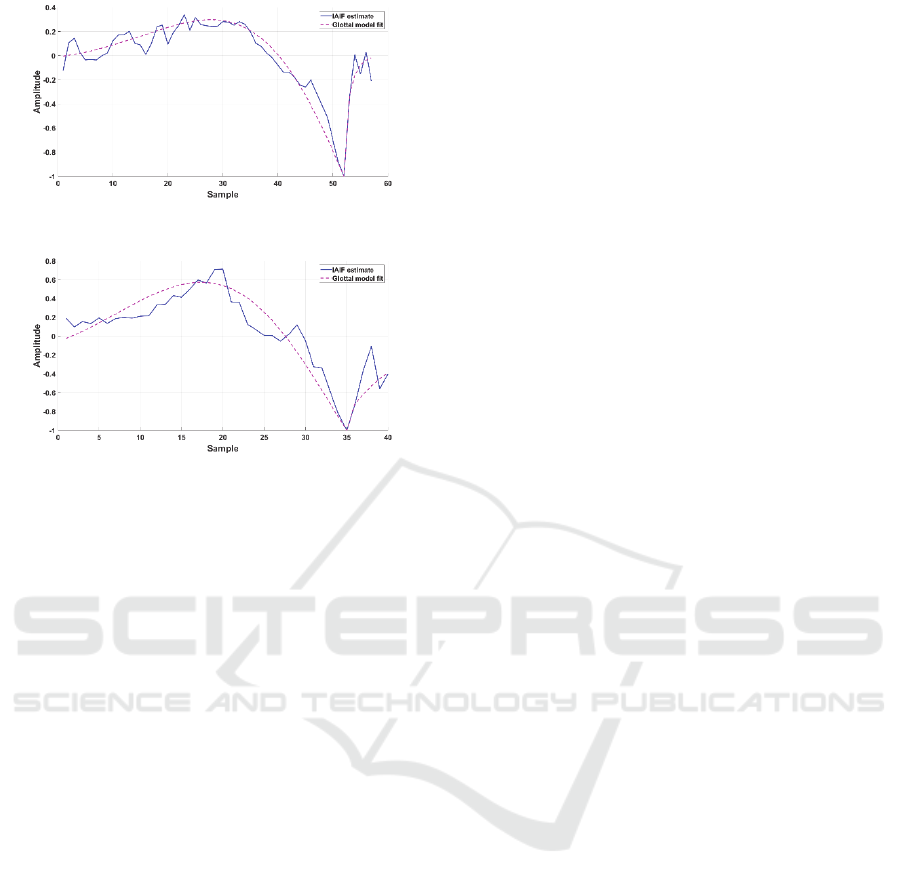
Figure 3: 75.57% NRMSE glottal fit.

Figure 4: 54.17% NRMSE glottal fit.

Many factors can influence the quality of the

glottal fit and the NRMSE value, including the

complexity of the signal, the presence of noise in the

glottal signal, the number of samples available for

parameter estimation in each pitch period and the

accuracy of the GCI locations. The presence of noise

in the glottal signal causes the NRMSE values to

decrease, even when a good fit is achieved. The fit in

Figure 3 is a representative example of this.

Pathological speech typically contains more

aspiration noise than healthy speech and may have

features not modelled by existing glottal models. The

accuracy of the glottal fitting depends on the accuracy

of the glottal estimation algorithms. If the inverse

filtering method is not accurate, it can lead to artefacts

in the glottal estimate. All these factors can affect the

performance of the model fitting algorithms and in

turn the accuracy of the fit. This is notably evident in

Figure 4, in which the glottal pulse contains features

that cannot be captured by the model, which is

reflected in the NRMSE value.

5 CONCLUSION

Accurate glottal model parametrisation for real

speech proves to be challenging problem, most

notably for pathological speech. The purpose of this

study was to investigate if this challenge can be

overcome by using a different approach.

The results of this study show that it is possible to

reliably fit and parametrise the glottal model of the

speech signal using system identification algorithms

applied through the newly proposed approach. The

method created accurate fits for artificial speech

samples and fit the glottal models with the average

accuracy of 64.29% for healthy and 51.57% for

pathological speech using the Steiglitz-McBride

method. The method demonstrates the effectiveness

of the proposed approach for a wide range of voice

qualities and different levels of noise in the glottal

signal.

The study also found that out of the two methods

used, the Steiglitz-McBride algorithm performs the

operation more robustly in both, synthetic and real

speech. The synthetic speech test results for samples

without additive noise show that both algorithms have

similar performance, however, results from samples

containing noise show superior performance of the

Steiglitz-McBride method. The Prony method was

found to perform poorly in noisy environments.

Results from real speech tests show that the Steiglitz-

McBride method outperforms the Prony method in all

cases.

This study shows promising results of the

proposed approach and indicate that it could be an

effective tool in estimating glottal models for healthy

speech and for the more challenging case of

pathological speech. Further research is required to

more comprehensively evaluate the method, on larger

real speech datasets and with a broader range of

performance metrics, to identify the strengths and

weaknesses of the method and compare it with

existing glottal model fitting methods.

ACKNOWLEDGEMENT

The authors would like to acknowledge the

Technological University Dublin for funding this

research project.

REFERENCES

Airaksinen, M. et al. (2014) Quasi Closed Phase Glottal

Inverse Filtering Analysis with Weighted Linear

Prediction. IEEE/ACM Transactions on Audio, Speech

and Language Processing (TASLP). 22 (3), pp. 596-

607.

Airas, M. (2008) TKK Aparat: An Environment for Voice

Inverse Filtering and Parameterization. Logopedics

Phoniatrics Vocology. 33 (1), pp. 49-64.

Alku, P. (1992) Glottal Wave Analysis with Pitch

Synchronous Iterative Adaptive Inverse

Filtering. Speech Communication. 11 (2-3), pp. 109-

118.

BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing

130

Boersma, P. (2006) Praat: Doing Phonetics by

Computer. Http://www.Praat.Org/.

Childers, D.G. (1999) Speech Processing. : John Wiley &

Sons, Inc.

Doval, B., d'Alessandro, C. & Henrich, N. (2003) The

Voice Source as a causal/anticausal Linear Filter. ISCA

Tutorial and Research Workshop on Voice Quality:

Functions, Analysis and Synthesis.

Drugman, T. (2012) Glottal Analysis Toolbox

(Gloat). Downloaded November.

Fant, G., Liljencrants, J. & Lin, Q. (1985) A Four-

Parameter Model of Glottal Flow. Stl-Qpsr. 4 (1985),

pp. 1-13.

Fu, Q. & Murphy, P. (2006) Robust Glottal Source

Estimation Based on Joint Source-Filter Model

Optimization. IEEE Transactions on Audio, Speech,

and Language Processing. 14 (2), pp. 492-501.

Ghosh, P.K. & Narayanan, S.S. (2011) Joint Source-Filter

Optimization for Robust Glottal Source Estimation in

the Presence of Shimmer and Jitter. Speech

Communication. 53 (1), pp. 98-109.

Hanratty, J., Deegan, C., Walsh, M. and Kirkpatrick, B.,

(2016) Analysis of Glottal Source Parameters in

Parkinsonian Speech. . 2016.

Hayes, M.H. (2009) Statistical Digital Signal Processing

and Modeling. : John Wiley & Sons.

Klatt, D.H. & Klatt, L.C. (1990) Analysis, Synthesis, and

Perception of Voice Quality Variations among Female

and Male Talkers. The Journal of the Acoustical Society

of America. 87 (2), pp. 820-857.

Kumaresan, R., Tufts, D. & Scharf, L.L. (1984) A Prony

Method for Noisy Data: Choosing the Signal

Components and Selecting the Order in Exponential

Signal Models. Proceedings of the IEEE. 72 (2), pp.

230-233.

Li, H., O'Brien, D. & Scaife, R. (2012) Comparison of

Time-and Frequency-Domain Based LF-Model Fitting

Methods for Voice Source Parametrisation.

Li, H., Scaife, R. & O’Brien, D. (2011) LF Model Based

Glottal Source Parameter Estimation by Extended

Kalman Filtering. Proceedings of the 22nd IET Irish

Signals and Systems Conference.

Li, H., Scaife, R. & O'Brien, D. (2012) Automatic LF-

Model Fitting to the Glottal Source Waveform by

Extended Kalman Filtering. Signal Processing

Conference (EUSIPCO), 2012 Proceedings of the 20th

European. : IEEE, pp. 2772.

Ljung, L. (1999) System Identification-Theory for the User

2nd Edition PTR Prentice-Hall. Upper Saddle River,

NJ.

Muthukumar, P.K., Black, A.W. & Bunnell, H.T. (2013)

Optimizations and Fitting Procedures for the

Liljencrants-Fant Model for Statistical Parametric

Speech Synthesis. Interspeech. pp. 397.

Quatieri, T.F. (2006) Discrete-Time Speech Signal

Processing: Principles and Practice. : Pearson

Education India.

Rosenberg, A.E. (1971) Effect of Glottal Pulse Shape on

the Quality of Natural Vowels. The Journal of the

Acoustical Society of America. 49 (2B), pp. 583-590.

Sahoo, S. & Routray, A. (2016) A Novel Method of Glottal

Inverse Filtering. IEEE/ACM Transactions on Audio,

Speech and Language Processing (TASLP). 24 (7), pp.

1230-1241.

Steiglitz, K. & McBride, L. (1965) A Technique for the

Identification of Linear Systems. IEEE Transactions on

Automatic Control. 10 (4), pp. 461-464.

Stoica, P. & Soderstrom, T. (1981) The Steiglitz-McBride

Identification Algorithm Revisited--Convergence

Analysis and Accuracy Aspects. IEEE Transactions on

Automatic Control. 26 (3), pp. 712-717.

Strik, H., Cranen, B. & Boves, L. (1993) Fitting a LF-

Model to Inverse Filter Signals. Third European

Conference on Speech Communication and

Technology.

Veldhuis, R. (1998) A Computationally Efficient

Alternative for the liljencrants–fant Model and its

Perceptual Evaluation. The Journal of the Acoustical

Society of America. 103 (1), pp. 566-571.

Yoshimura, T., Tokuda, K., Masuko, T., Kobayashi, T. &

Kitamura, T. (2001) Mixed Excitation for HMM-Based

Speech Synthesis. Seventh European Conference on

Speech Communication and Technology.

System Identiﬁcation Algorithms Applied to Glottal Model Fitting

131