Prediction of Malaria Vaccination Outcomes from Gene Expression Data

Ahmad Shayaan, Indu Ilanchezian and Shrisha Rao

International Institute of Information Technology Bangalore, Bengaluru, India

Keywords:

Malaria, Vaccine Trials, Gene Expression, Machine Learning, Statistical Analysis.

Abstract:

Vaccine development is a laborious and time-consuming process and can beneﬁt from statistical machine

learning techniques, which can produce general outcomes based on the patterns observed in the limited avail-

able empirical data. In this paper, we show how limited gene expression data from a small sample of subjects

can be used to predict the outcomes of malaria vaccine. In addition, we also draw inferences from the gene ex-

pression data, with over 22000 columns (or features), by visualizing the data, and reduce the data dimensions

based on this inference for efﬁcient model training. Our methods are general and reliable and can be extended

to vaccines developed against any pathogen. Given the gene expression data from a sample of subjects ad-

ministered with a novel vaccine, our methods can be used to test the outcome of that vaccine, without the

need for empirical observations on a larger population. By carefully tuning the available data and the machine

learning models, we are able to achieve greater than 98% accuracy, with sensitivity and speciﬁcity of 0.93 and

1 respectively, in predicting the outcomes of the malaria vaccine in developing immunogenicity against the

malaria pathogen.

1 INTRODUCTION

The testing phase of the vaccine development pro-

cess typically involves three stages. In the ﬁrst stage,

the vaccine is administered only to a small sample

of subjects and provides empirical observations on

the outcomes of the vaccine. The second and third

stages involve randomized, single- or double-blinded

efﬁcacy testing on larger populations, with appropri-

ate placebo controls (Sanford et al., 1993). However,

“phase 2 results can inaccurately predict safety and/or

effectiveness for medical products in a wide range of

diseases and patient populations” (US Food and Drug

Administration, 2017). These inaccuracies in predict-

ing the safety and effectiveness of vaccines can lead

to adverse outcomes.

The motivation for this work, therefore, is to al-

low data collected in the ﬁrst stage, although limited,

to be processed by statistical machine learning meth-

ods to produce general observations applicable to a

larger population. In effect, the outcomes of the vac-

cine administration is estimated statistically with only

the data available from the ﬁrst stage of testing. The

observations from the ﬁrst stage can help improve the

timing and safety requirements in the second and third

phase trials by predicting the susceptibility of subjects

to a disease after vaccination.

Gene expression data have been previously used in

combination with statistical machine learning meth-

ods for medical diagnostics and risk analysis of

diseases—for example, the risk of acute myeloid

leukemia as studied by Wilson et al. (2006). Related

literature also describes the use of gene expression

data and statistical methods in the vaccine develop-

ment pipeline. Trtica-Majnaric et al. (2010) use neu-

ral networks to predict the outcomes of an inﬂuenza

vaccine. However, they use blood sample analysis to

predict the outcomes but not gene expression data.

Gene expression data are used for vaccine respon-

siveness prediction by Bucasas et al. (2011) for the

inﬂuenza vaccine. However, their work uses a re-

gression model to predict the antibody responses fol-

lowing vaccination. This approach can be problem-

atic: “While biomarkers have many important uses

in clinical practice and product testing, most have not

been shown to reliably predict clinical outcomes” (US

Food and Drug Administration, 2017).

Our methods, on the other hand, use classiﬁca-

tion models to predict whether the malaria vaccine

RTS,S is effective in developing immune responses

in particular subjects. RTS,S is a malaria vaccine de-

veloped by GlaxoSmithKline (Malaria Vaccine Initia-

tive, 2017). These classiﬁcation models can be used

to accurately predict vaccine outcomes with given ob-

Shayaan, A., Ilanchezian, I. and Rao, S.

Prediction of Malaria Vaccination Outcomes from Gene Expression Data.

DOI: 10.5220/0007260501550162

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 155-162

ISBN: 978-989-758-353-7

155

servations of the gene expression data collected at

particular times on a limited number of subjects. We

extensively analyze the gene expression data and dis-

cover the relationships between the features (i.e., gene

expression values) and the vaccine outcomes. Based

on these relationships, we reduce the dimensionality

of the data, choose appropriate model classes, and

evaluate their performances. Speciﬁcally, we use the

Logistic Regression (LR), Support Vector Machines

(SVMs) and Multi-Layer Perceptron (MLP) models.

We show that our methods are reliable in pre-

dicting the outcomes of the administered vaccine—

whether the vaccinated person is immunized against

the disease or not—with the high accuracy of ∼ 98%,

with speciﬁcity and sensitivity being 0.93 and 1 re-

spectively. These methods can be used to efﬁciently

train statistical models for vaccine testing with a lim-

ited number of data samples. The inferences made

by these statistical models can then be used to predict

the outcomes of possible vaccine trials, thus helping

design better trials.

The rest of this document describes our methods

in detail. Section 2 describes the materials and data

used for our study. It discusses in detail the data tun-

ing method to increase the generalization capability of

the model and the procedure for the selection of rel-

evant features for vaccine outcome prediction. Sec-

tions 3 brieﬂy describes statistical machine learning

models suitable for this application and the reasons

for their suitability and the evaluation metrics used

for assessing the performance of our methods. 4 dis-

cusses the results. Section 5 presents the conclusion.

2 MATERIALS

The dataset is based on expression data from a malaria

vaccine trial collected by the Walter Reed Army Insti-

tute of Research (Vahey et al., 2010). The data were

originally collected in September 2009 and were up-

dated recently in August 2018. The gene expressions

are arranged in GeneChip HG-U133 Plus2.0 arrays.

The GeneChip Human Genome U133A Plus 2.0 Ar-

ray is a single array representing around 22,000 well-

characterized human genes that can be used to explore

human biology and disease processes (ThermoFisher,

2001). The dataset was downloaded from the Na-

tional Center for Biotechnology Information (NCBI),

series number GSE18323

Our code and dataset are available at

https://github.com/ashayaan/vaccine efﬁcacy.

See https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?

acc=GSE18323.

The dataset contains gene expression data of 39

human subjects, who were assessed at different times

during the trial. The expression data were collected

on the day of the third vaccination, twenty-four and

seventy-two hours after vaccination, and two weeks

after the vaccination. Finally, the gene expression

data 5 days post-challenge with Plasmodium falci-

parum (the malaria pathogen) were also collected.

Out of the 39 subjects, 13 subjects showed pos-

itive vaccine outcomes and 26 showed negative vac-

cine outcomes. The dataset is arranged in the form of

individual ﬁles that contain the gene expression data

for each subject, for every stage of the study. Each

ﬁle has 22,278 rows, that contains the gene expres-

sion values normalized to base 2 logarithmic scale.

2.1 Data Tuning

The limited (precisely 39) available data points are

insufﬁcient to train a generalizable machine learn-

ing model. To counter the problem of data scarcity

and to achieve generalizability, we use data aug-

mentation techniques to increase the number of data

points without signiﬁcantly changing the data distri-

bution (Van Dyk and Meng, 2001).

We augment the dataset by sampling data points

from a normal distribution and adding a minuscule

amount of noise to each of the attributes as suggested

by Van Dyk and Meng (2001). This is repeated for

data available at every time instance: the day of vac-

cination, 24 hours, 72 hours and two weeks after vac-

cination. Noise is sampled from a uniform distribu-

tion in the range 0 to 0.01. The value of the noise

terms is small enough so that the attributes still corre-

spond to the class labels. The range for the uniform

distribution is empirically selected, so that the added

noise does not drastically change the data points and

the models do not overﬁt the data.

Adding noise does not affect the quality of the data

because real-world data has unavoidable noise from

the instruments that are used to collect the data. By

adding noise explicitly to our attributes, the model can

be made more robust and generalizable. The noise

term should avoid adding bias and should be indepen-

dent of other noise terms (Zhu and Wu, 2004).

A large number of data points should not be cre-

ated by adding noise. If a large number of synthetic

data points were created, these data points would sat-

urate the model, which would overﬁt the data. While

adding the noise term to the attributes, the ratio of the

protected vs. non-protected subjects should be pre-

served. This further ensures that the behavior of the

model trained on the augmented dataset remains sim-

ilar to a model trained on the actual dataset.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

156

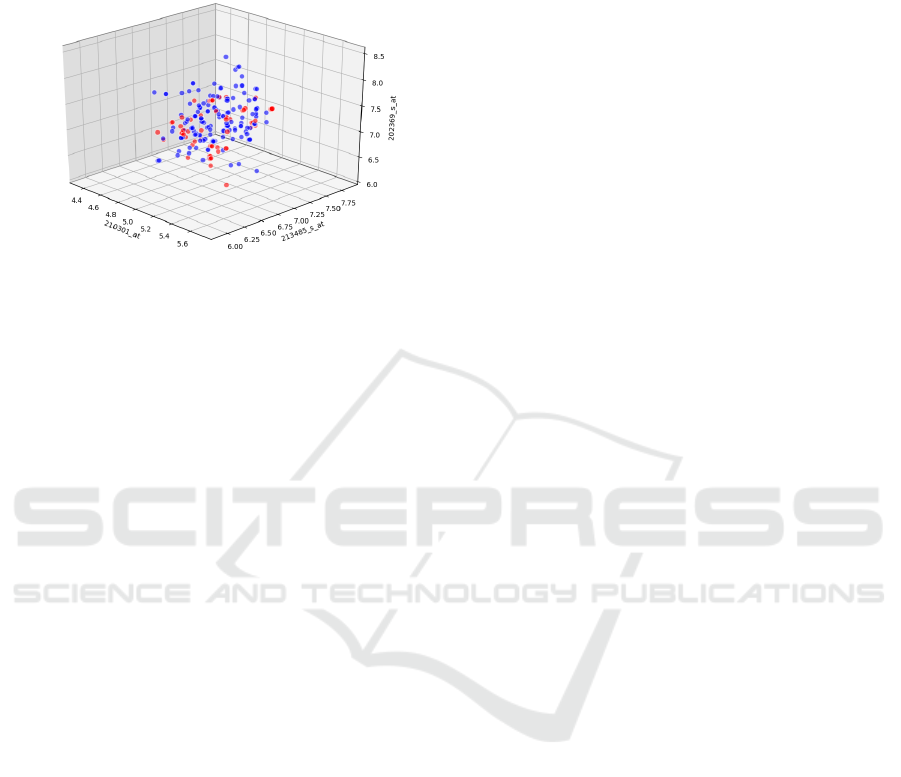
After adding the noise to the data, we plot the

data to see the class distribution. We select three

dimensions out of 22, 278 features to plot a three-

dimensional scatter plot.

Figure 1: Class Distribution.

Figure 1 shows feature clusters in a three-dimensional

subspace of the 22,278-dimensional feature space for

the two different classes—positive vaccine outcomes

and negative outcomes. Although plotted for three di-

mensions sampled uniformly, this plot is general in

nature and holds for any three features selected from

the distribution of all features. Red dots denote data

points showing positive outcomes and blue dots de-

note data points with negative outcomes. It is evident

from this ﬁgure that the feature clusters are highly

overlapping for the chosen set of three features. A

three-dimensional space is therefore not suitable for

further analysis, and statistical methods must employ

a larger number of dimensions to achieve separabil-

ity of classes. The feature space is extremely high-

dimensional and the separability in high-dimensional

space can only be analyzed using statistical methods.

We show that in a feature space of dimensions as high

as 700, the classes are linearly separable. The high

dimensionality of the data, with 22,278 attributes, in-

creases the training time and also increases the risk of

overﬁtting.

2.2 Feature Selection

Feature selection methods help with these problems

by reducing the dimensions without much loss of the

total information. They also help to better understand

the features and their relationship with the target vari-

able. Feature selection methods have also been shown

to increase the prediction accuracy of some models

(Guyon and Elisseeff, 2003).

Two schemes were used to select features from the

entire feature space: Principal Component Analysis

(PCA-features) and sampling of features based on a

normal distribution (sampled features).

PCA is used to reduce the dimensionality of a

large set of variables to obtain a smaller set that still

contains most of the information in the large set. It

works by ﬁnding the direction of maximum variances

in the dataset and then projecting the data points in

the space spanned by these directions (Jolliffe, 2011).

The feature sampling scheme works by sampling

features from a uniform distribution of the complete

set of features. For every feature, the scheme either

selects it or not, so the search space for the features is

exponential in the number of features (Dash and Liu,

1997). We use a sample of 719 features, this being

the minimum number of features required for class

separability. The number of features to be sampled

is a hyperparameter and is chosen empirically based

on training results. The model is then trained for ev-

ery set of sampled features and the accuracy score is

evaluated. The set of features that produced the best

accuracy score are then stored and used to train a new

model to make the necessary predictions.

The features are visualized in a pair plot as shown

in Figure 2. A pair plot is used to visualize both

the distributions of single variables and the relation-

ships between two variables. Pair plots can also help

identify trends in the dataset and ﬁnd the set of fea-

tures that are highly correlated with the target vari-

able. From Figure 2 it can be observed that there ex-

ists a separation between the classes. The attributes

that were used to visualize the data were selected from

the feature space using the feature sampling scheme.

3 METHODS

To predict the outcomes of the malaria vaccination,

various machine learning models were explored. The

augmented gene expression values before the stage

where the subjects were challenged with Plasmodium

falciparum (Pf), were all combined to form the train-

ing set for the model. This was done so that the mod-

els that were being trained can also learn how the out-

comes of the vaccine changes with time. The gene ex-

pression values after the challenge with Pf were used

as the test set. Thus the training set contained 229

data points and the test set contained 51 data points.

3.1 Support Vector Machines

Support Vector Machines (SVMs) have been the core

of numerous domains such as bioinformatics studies,

molecular genetics, DNA, data mining and psychiatry

(Touati et al., 2018).

In order to predict the outcome of the malaria vac-

cine, we use the SVM classiﬁcation method which

Prediction of Malaria Vaccination Outcomes from Gene Expression Data

157

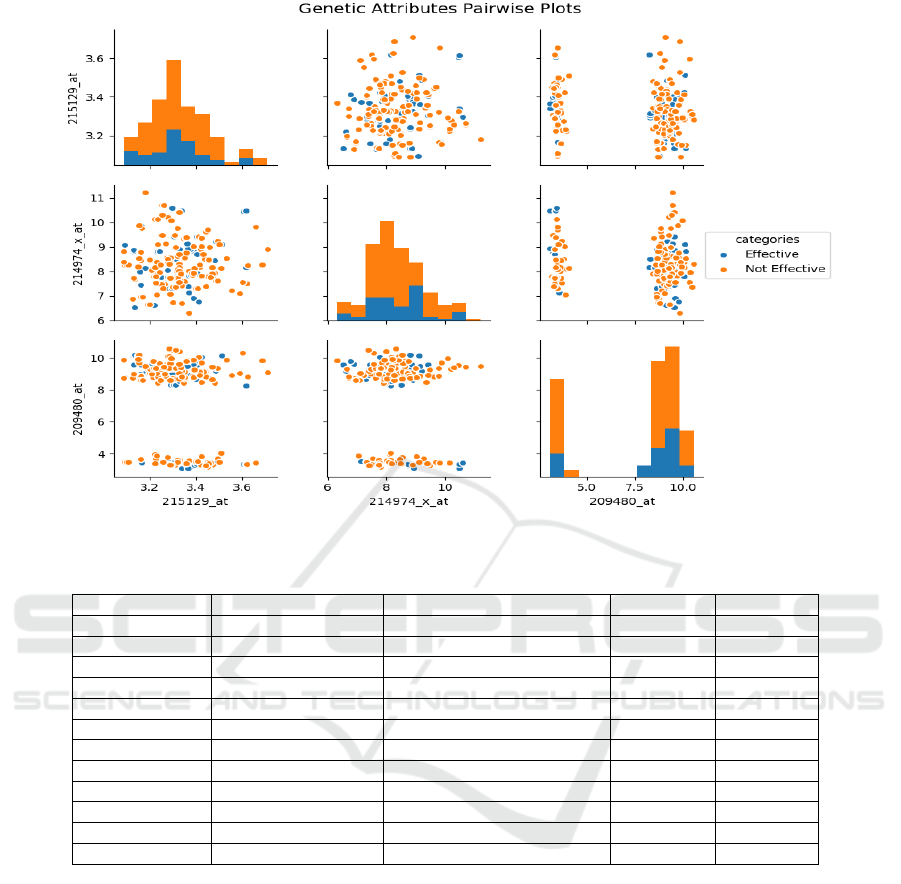
Figure 2: Pairwise plot of attributes.

Table 1: Test set evaluation scores for all the models.

Model Trained Feature Space used Mean Accuracy Score (%) Sensitivity Speciﬁcity

LR-1 All Features 94.11 0.8 1

LR-2 Sampled Features 98.03 0.93 1

LR-3 PCA-Features 43.17 0.27 0.5

RBF-SVM All Features 70.58 0 1

RBF-SVM Sampled Features 70.58 0 1

RBF-SVM PCA-Features 70.58 0 1

Linear-SVM All Features 96.07 0.87 1

Linear-SVM Sampled Features 92.15 1 0.89

Linear-SVM PCA-Features 49.01 0.58 0.27

MLP-ReLU All Features 70.58 0 1

MLP-tanh All Features 70.58 0 1

MLP-Logistic All Features 70.58 0 1

aims to ﬁnd the optimal hyperplane that separates two

different classes. We also used the kernel trick in

SVM to make the predictions—the kernel function

k(x) projects the data points to a higher dimensional

feature space where the data points may be linearly

separable. We use two variants of kernel function—

linear kernel (Linear-SVM) and RBF kernel (RBF-

SVM). The RBF kernel tries to separate the classes

using a nonlinear separator, whereas the linear kernel

tries to ﬁt a linear separator. In general, the RBF ker-

nel is more powerful than the linear kernel (Hsu et al.,

2016).

For each of these variants, we train three differ-

ent SVM models—ﬁrst using all features, the second

and third using PCA-features and sampled features as

described in Section 2.2.

The SVMs learn the best hyperplane that separates

the classes into the projected features space. At the

time of prediction, the class labels are assigned based

on which side of the hyperplane the point is present

on. For every trained model, the necessary evaluation

parameters, described later, were recorded.

3.2 Logistic Regression

The aim of the Logistic Regression (LR) model was to

capture the linear relationship between the target vari-

ables and the attributes. The LR model can only cap-

ture the linear relationship between the input vector

and the target variable because the hyperplane that it

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

158

creates to separate the classes is formed by taking lin-

ear combinations of the input vector (Trtica-Majnaric

et al., 2010).

To predict the outcomes of the vaccine, three LR

models were tested. One of the LR models was tested

on all of the features that are available in the dataset.

The second was tested only on the features that were

extracted as described in Section 2.2 by the sampling

scheme (sampled features), and the third on the PCA-

features. At the output a binary variable was used,

with 0 representing the set of subjects that had neg-

ative vaccine outcomes, and 1 representing the set of

subjects that showed positive vaccine outcomes.

3.3 Multi-Layer Perceptrons

Three Multi-Layer Perceptrons (MLPs) were trained

to predict the outcomes of the vaccine. All the

MLPs consisted of 200 hidden layers. The initial

learning rate for the gradient descent algorithm was

set as 0.001 and was adjusted after every iteration.

The maximum number of training epochs for all the

MLPS was set to 500. The MLP models were trained

on the entire feature set available in the dataset.

The MLPs differed from one another in the acti-

vation functions used to introduce non-linearity. The

activation functions that were used to train the MLPs

were ReLU activation, tanh activation, and logistic

activation. The ReLU activation function is a half-

rectiﬁed non-linearity; it is linear for positive values

and zero otherwise (Zhang and Woodland, 2015). The

tanh activation function is a re-scaled version of the

logistic activation function, i.e., the output range of

tanh from -1 to 1 is a scaled version of the output

range of the logistic activation over the range from 0

to 1 (Karlik and Olgac, 2011). Different activation

functions were used to see if the evaluation parame-

ters change with the change in the activation function.

MLPs were used because they make no prior as-

sumptions concerning the data distribution. They can

model highly non-linear functions and can be trained

to accurately generalize when presented with new

data (Gardner and Dorling, 1998). These features of

MLPs make their use a very good alternative to other

statistical approaches. It has been shown that MLPs

can be trained to approximate virtually any smooth

function (Hornik et al., 1989).

3.4 Evaluating Model Performance

To evaluate the performances of the models, the mean

accuracy score was recorded for every model. In ad-

dition to the mean accuracy score, we also calculate

the positive hit rate and the negative hit rate to better

compare the models based on their predictions. The

positive hit rate is also called model sensitivity, while

the negative hit rate is called model speciﬁcity. These

two quantities are important for investigating the abil-

ity of a model to accurately recognize positive and

negative outcomes (Trtica-Majnaric et al., 2010). The

sensitivity is computed as follows:

sensitivity =

a + d

(1)

where a is the number of true positives, and d is

the number of false negatives. The speciﬁcity is cal-

culated as follows:

speciﬁcity =

b + c

(2)

where b is the number of true negatives, and c is

the number of false positives. Any model with high

sensitivity can be used to identify the subjects with

the successful administration since a model with high

sensitivity can correctly identify the subjects show-

ing positive outcomes. A model with a high speci-

ﬁcity can be used to conﬁrm the test results since it

is more speciﬁc in recognizing the subjects that are

not affected by the vaccine. In general, a good model

should have high values for both sensitivity and speci-

ﬁcity (Simon and Boring, 1990).

The true positive and false positive rates were also

used to plot the Receiver Operating Characteristic

(ROC) curve and calculate the area under the curve

(AUC). An ROC curve is a graph showing the per-

formance of a classiﬁcation model at all classiﬁca-

tion thresholds, and the AUC measures discrimina-

tion (Hanley and McNeil, 1982). Discrimination is

the ability of a model to correctly classify those with

and without the effects of the vaccine.

4 RESULTS AND DISCUSSION

4.1 Evaluation Metrics

Table 1 shows the evaluation of the LR, SVM and

MLP models with variations: different subsets of fea-

tures for LR, SVM, and MLP, linear or non-linear

separation for SVM, and various activation functions

for MLPs. The best performing model with the high-

est mean accuracy score of 98.03% is the LR model

trained with the sampled features. This model also

has high speciﬁcity and sensitivity values, 0.93 and 1

respectively. It is also the most efﬁcient in the sense

that it uses only a subset of features (and not all fea-

tures) in the training data to make inferences on test

data. The Linear-SVM model using all features also

Prediction of Malaria Vaccination Outcomes from Gene Expression Data

159

Table 2: AUC for different models.

Model Feature set uses Area under the ROC curve

LR All Features 0.90

LR Sampled Features 0.97

Linear-SVM All Features 0.93

Linear-SVM Sampled Features 0.94

has high mean accuracy score, sensitivity and speci-

ﬁcity of 96.07%, 0.87 and 1 respectively. These val-

ues are only slightly lower than the best model, but

this level of accuracy is achieved after training on the

whole set of features, unlike the LR model which uses

only a subset of features. The MLP models with dif-

ferent activation functions were also tested on the fea-

tures given by PCA as well as on the sampled features,

but the mean accuracy was very low and thus these

models have not been reported here.

Table 3: Average sensitivity and speciﬁcity of the LR mod-

els.

Actual Outcomes

Predicted Outcomes

0 1

LR-complete

0 1.0 0.0

1 0.20 0.80

LR-sampled

0 1.0 0.0

1 0.07 0.93

Table 4: Average sensitivity and speciﬁcity of the SVM

models

Actual Outcomes

Predicted Outcomes

0 1

SVM-complete

0 1.0 0.0

1 0.13 0.87

SVM-sampled

0 0.89 0.11

1 0.0 1.0

Tables 3 shows the sensitivities, speciﬁcities, false

positives and false negatives of the LR models using

all features and sampled features respectively. Sim-

ilarly, Table 4 shows these four values for the SVM

models trained using all features and sampled fea-

tures. The false positive rates (with actual outcome

0 and predicted outcome 1) and the false negative

rates (with actual outcome 1 and predicted outcome

0) are low for all of these models. The best LR model

trained with sampled features also gives the lowest

false negative rate of 0.07.

4.2 Comparison of Linear and

Non-Linear Models

It is evident from Table 1 that linear models, such as

LR and Linear-SVM, signiﬁcantly outperform non-

linear models, such as RBF-SVM, MLP with ReLU,

tanh and logistic activations. The higher accuracies

of linear models on test data indicate that the posi-

tive and negative vaccine outcome classes are sepa-

rated by a linear decision boundary. The use of a non-

linear model, such as RBF-SVM or MLP, results in

overﬁtting of training data, which hinders the gener-

alizability of the model on the test set. Hence, we

observe lower test set accuracies with the use of non-

linear models than with linear models. Linear models

have accuracies over 95%, whereas non-linear models

only have accuracies of ∼ 70% (as shown in Table 1),

which is a signiﬁcant difference. Due to overﬁtting,

these models tend to classify all samples to the posi-

tive outcome class, hence resulting in a speciﬁcity of

1, with 0 sensitivity.

Thus, we have shown empirically that the data

points are linearly separable in the sampled feature

space consisting of over 700 features and the com-

plete feature space with over 22000 features. How-

ever, the data points are not separable in a lower-

dimensional space (for example, the 3-dimensional

feature space shown in Figure 1). In that case, the

features are undersampled.

4.3 Effect of Feature Selection

The mean prediction accuracy of the LR model in-

creases when it is trained only on the sampled fea-

tures (Table 1). This indicates that there are some fea-

tures present in the entire feature space that are not

highly correlated with the target variable, and if these

features were considered, the model may misclassify

leading to lower prediction accuracy. The LR model

trained on the sampled features has a higher sensi-

tivity score, and hence is better to ﬁnd the subjects

positively affected by the vaccine, than the LR model

trained on all of the features.

The Linear-SVM models do not demonstrate a

similar boost in the performance when trained only

on the sampled features. Table 1 shows that the mean

accuracy for the model trained only on the sampled

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

160

features is slightly lower than the model trained on

the entire feature set.

However, the Linear-SVM model trained only on

the sampled features had the highest sensitivity of all

the models evaluated. This model is the best when the

requirement is to ﬁnd the subjects positively affected

by the vaccine. The high sensitivities for both the LR

and Linear-SVM models trained on the sampled fea-

tures suggest that the feature set that was used to train

these models is better than the entire feature set, for

predicting the positive outcomes of the vaccine.

The models trained on the PCA-features do not

perform as well as the other models. The sensitiv-

ity and speciﬁcity for these models are also very low.

Thus, the features extracted with the PCA scheme,

that is the directions of maximum variances, are not

suitable for estimating the target variables.

4.4 ROC and AUC

For the linear models, the ROC curves were plotted

and the area under the curve (AUC) was also com-

puted. The AUC is classiﬁcation-threshold-invariant,

and measures the quality of the model’s predictions

irrespective of what classiﬁcation threshold is cho-

sen (Hanley and McNeil, 1982). The higher the AUC,

the better the model in distinguishing a positive ex-

ample from a negative one. Table 2 gives the area

under the ROC curve for the different models. The

LR model trained on the sampled feature set has the

highest AUC, indicating that it distinguish between

the two classes with a very high probability. The AUC

for the Linear-SVM trained on the sampled features is

higher than the AUC of the Linear-SVM trained on all

of the features, which on account of the higher sensi-

tivity of the ﬁrst model.

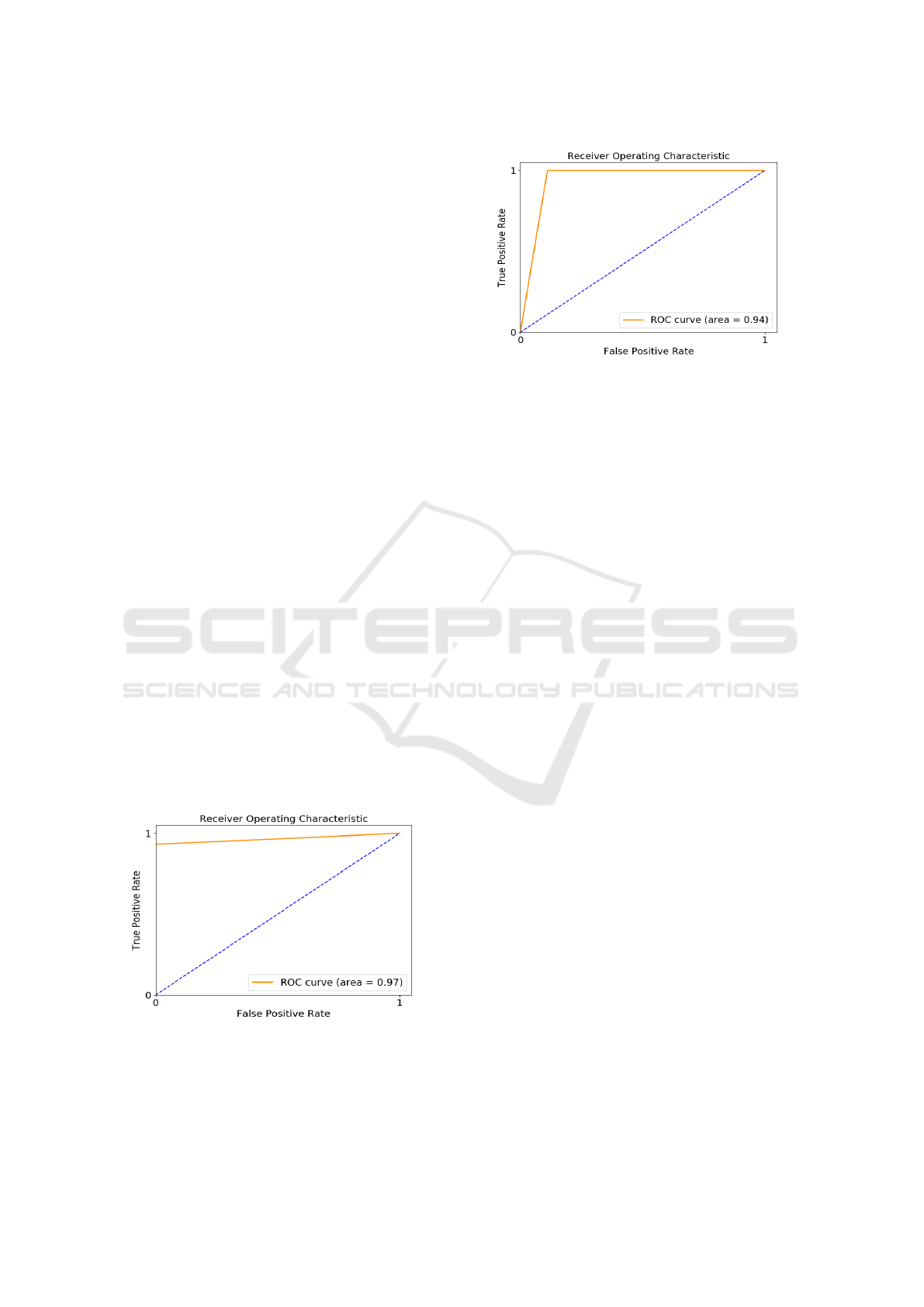
Figure 3: ROC Curve for the LR trained on sampled fea-

tures.

Figures 3 and 4 show the ROC curves for the LR

and Linear-SVM models trained on the sampled fea-

tures. The ROC curves are not smooth because of the

Figure 4: ROC Curve for the Linear-SVM trained sampled

features.

sparsity of data points. The dashed line in the ﬁg-

ures represents the threshold AUC, which is 0.5. A

model with AUC less than the threshold is no better

than randomly assigning class labels (Hanley and Mc-

Neil, 1982).

5 CONCLUSION

In this paper, we have used gene expression data to

predict the outcomes of a vaccine trial, with malaria

as the exemplar. Prior works have tried to predict the

outcomes of vaccine trials (e.g., for inﬂuenza), but

have not used gene expression data to do so. Our work

builds machine learning models to predict, with high

accuracy, the test outcomes of a malaria vaccine from

the gene expression data. The models we present are

able to predict the outcomes of the vaccine with a

mean accuracy of 98.03%. Such a high prediction

accuracy indicates that the study of gene expressions

can be successfully used to accurately predict the out-

comes of the malaria vaccine. The models also have

a high sensitivity and speciﬁcity values, i.e., the same

model can be used to correctly identify subjects that

had a positive reaction to the vaccine as well as sub-

jects who did not respond to the vaccine.

The models described in this paper can be applied

in real-world vaccine trials to screen human subjects

and predict the outcomes of the vaccine. Our models

can be used in conjunction with standard procedures

to improve safety and/or effectiveness of vaccine tri-

als. Using the models, we also ﬁnd that some of the

gene expression attributes are more useful than oth-

ers, in predicting vaccination outcomes. These gene

expression attributes which are highly correlated with

the class labels can be used to design better vaccines,

which may be effective for larger populations. Our

models can also be used to assist other primary health

care research that considers the outcomes of vaccine

trials.

Prediction of Malaria Vaccination Outcomes from Gene Expression Data

161

The methods used in this paper are not limited to

predicting the outcomes of the malaria vaccine—they

can also be used to predict the outcomes for any vac-

cine for which the gene expression data are available

in the HG-U133 Plus2.0 format. The feature selection

scheme (Section 2.2) can be used to ﬁnd the gene ex-

pression attributes that are better correlated with the

target variable for any particular vaccine for which

predictions are to be made. Along with feature se-

lection schemes, non-linear models such as MLP can

be used where appropriate, to capture complex rela-

tionships (in case of some other diseases) between the

gene expression data and the vaccine outcomes.

REFERENCES

Bucasas, K., M Franco, L., Shaw, C., Bray, M., Wells, J.,

no, D., Arden, N., Quarles, J., Couch, R., and Bel-

mont, J. (2011). Early patterns of gene expression cor-

relate with the humoral immune response to inﬂuenza

vaccination in humans. The Journal of Infectious Dis-

eases, 203:921–9.

Dash, M. and Liu, H. (1997). Feature selection for classiﬁ-

cation. Intelligent Data Analysis, 1(3):131–156.

Gardner, M. W. and Dorling, S. (1998). Artiﬁcial neural

networks (the multilayer perceptron)—a review of ap-

plications in the atmospheric sciences. Atmospheric

Environment, 32(14-15):2627–2636.

Guyon, I. and Elisseeff, A. (2003). An introduction to vari-

able and feature selection. Journal of Machine Learn-

ing Research, 3(Mar):1157–1182.

Hanley, J. A. and McNeil, B. J. (1982). The meaning and

use of the area under a receiver operating characteris-

tic (roc) curve. Radiology, 143(1):29–36.

Hornik, K., Stinchcombe, M., and White, H. (1989). Multi-

layer feedforward networks are universal approxima-

tors. Neural Networks, 2(5):359–366.

Hsu, C.-W., Chang, C., and Lin, C.-J. (2016). A practical

guide to support vector classiﬁcation. https://www.

csie.ntu.edu.tw/ cjlin/papers/guide/guide.pdf.

Jolliffe, I. (2011). Principal component analysis. In In-

ternational Encyclopedia of Statistical Science, pages

1094–1096. Springer.

Karlik, B. and Olgac, A. V. (2011). Performance analysis of

various activation functions in generalized mlp archi-

tectures of neural networks. International Journal of

Artiﬁcial Intelligence and Expert Systems, 1(4):111–

122.

Malaria Vaccine Initiative (2017). RTS, S. https://www.

malariavaccine.org/malaria-and-vaccines/ﬁrst-

generation-vaccine/rtss.

Sanford, J. P., Philipose, N. M., Mitchell, V. S., et al. (1993).

The Children’s Vaccine Initiative: Achieving the Vi-

sion. National Academies Press.

Simon, D. and Boring, J. R. (1990). The History, Physi-

cal, and Laboratory Examinations. 3rd edition. But-

terworths.

ThermoFisher (2001). Genechip

human genome U133

plus 2.0 array. https://www.thermoﬁsher.com/order/

catalog/product/900468.

Touati, R., Messaoudi, I., ElloumiOueslati, A., and Lachiri,

Z. (2018). Classiﬁcation of Helitron’s Types in the

C.elegans Genome based on Features Extracted from

Wavelet Transform and SVM Methods. In Proceed-

ings of the 11th International Joint Conference on

Biomedical Engineering Systems and Technologies -

Volume 4: BIOINFORMATICS,, pages 127–134. IN-

STICC, SciTePress.

Trtica-Majnaric, L., Zekic-Susac, M., Sarlija, N., and Vi-

tale, B. (2010). Prediction of inﬂuenza vaccination

outcome by neural networks and logistic regression.

Journal of Biomedical Informatics, 43(5):774–781.

US Food and Drug Administration (2017). 22 Case

Studies Where Phase 2 and Phase 3 Trials had Diver-

gent Results. https://www.fda.gov/downloads/

aboutfda/reportsmanual

sforms/reports/ucm535780.pdf.

Vahey, M. T., Wang, Z., Kester, K. E., Cummings, J., Hep-

pner Jr, D. G., Nau, M. E., Ofori-Anyinam, O., Co-

hen, J., Coche, T., Ballou, W. R., et al. (2010). Ex-

pression of genes associated with immunoproteasome

processing of major histocompatibility complex pep-

tides is indicative of protection with adjuvanted RTS,

S malaria vaccine. The Journal of Infectious Diseases,

201(4):580–589.

Van Dyk, D. A. and Meng, X.-L. (2001). The art of data

augmentation. Journal of Computational and Graph-

ical Statistics, 10(1):1–50.

Wilson, C. S., Davidson, G. S., Martin, S. B., Andries, E.,

Potter, J., Harvey, R., Ar, K., Xu, Y., Kopecky, K. J.,

Ankerst, D. P., et al. (2006). Gene expression proﬁl-

ing of adult acute myeloid leukemia identiﬁes novel

biologic clusters for risk classiﬁcation and outcome

prediction. Blood, 108(2):685–696.

Zhang, C. and Woodland, P. C. (2015). Parameterised

sigmoid and relu hidden activation functions for dnn

acoustic modelling. In Sixteenth Annual Conference

of the International Speech Communication Associa-

tion.

Zhu, X. and Wu, X. (2004). Class noise vs. attribute noise:

A quantitative study. Artiﬁcial Intelligence Review,

22(3):177–210.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

162