Visual Analytics of Multidimensional Projections for Constructing

Classiﬁer Decision Boundary Maps

Mateus Espadoto

1,2

, Francisco Caio M. Rodrigues

1,2

and Alexandru C. Telea

Institute of Mathematics and Statistics, University of S

ao Paulo, Brazil

Johann Bernoulli Institute, University of Groningen, The Netherlands

Keywords:

Machine Learning, Dimensionality Reduction, Image-based Visualization.

Abstract:

Visualizing decision boundaries of modern machine learning classiﬁers can notably help in classiﬁer design,

testing, and ﬁne-tuning. Dense maps are a very recent method that overcomes the key sparsity-related limita-

tion of scatterplots for this task. However, the trustworthiness of dense maps heavily depends on the underlying

dimensionality-reduction (DR) techniques they use. We design and perform a detailed study aimed at ﬁnding

the best DR techniques to use when creating trustworthy dense maps, by studying a large collection of 28 DR

algorithms, 4 classiﬁers, and 2 datasets from a real-world challenging classiﬁcation problem. Our results show

how one can pick suitable DR algorithms to create dense maps that help understanding classiﬁer behavior.

1 INTRODUCTION

Over the last few decades, advances in machine learn-

ing (ML) enabled breakthroughs in application areas

such as computer vision, natural image processing,

path planning, and business intelligence. However,

most ML methods work largely as black boxes, due to

the lack of interpretability behind the decision func-

tions they employ. The more complex such meth-

ods become, like in the case of the more recent deep

learning (DL) methods, the harder is for their users to

understand, customize, and trust them (Ribeiro et al.,

2016). As such, recent work has focused on visually

explaining how ML techniques learn and take their

decisions (F

eraud and Cl

erot, 2002; Rauber et al.,

2017b; Rauber et al., 2017a).

One interpretability challenge regards the so-

called decision boundaries of classiﬁers. Formally

put, let D be the data space input by a classiﬁer. The

classiﬁer can be seen as a function f that assigns a

class label to every point in D. Understanding how

f , deﬁned by the training process, partitions D into

same-class regions, separated by so-called decision

boundaries, can help many tasks related to classi-

ﬁer design, e.g., locate how training samples affect

the classiﬁcation of test samples close to them in D;

spot areas in D that require more training samples;

and ﬁnd if the classiﬁer technique used is too ‘stiff’

to separate complex labeled-sample distributions in

D (Hamel, 2006; Migut et al., 2015):

Visualizing complex-shaped decision boundaries

embedded in a high-dimensional space D is very chal-

lenging. All existing solutions essentially perform

some form of dimensionality reduction (DR) to map

D to R

so as to create directly visible metaphors of

the boundaries. However, such solutions have sev-

eral limitations: Visualizing color-coded scatterplots

of training and/or test sets does not actually show the

decision boundaries, leaving the user to guess where

these lie (Rauber et al., 2017b). Image-based dense

maps improve upon this by coloring each pixel of the

target (screen) image by the assigned label(s) of sam-

ples in D that project there. Limitations of such solu-

tions include handling only a speciﬁc classiﬁer (e.g.

SVM in (Hamel, 2006)) or using a small-multiple

metaphor, which does not scale for high-dimensional

spaces D (Migut et al., 2015).

A recent attempt to alleviate the above limitations

was proposed by (Rodrigues et al., 2018). The key

asset of this method is that it creates dense bound-

ary maps for any classiﬁer in a generic manner. To

do this, however, a ‘suitable’ DR method needs to

be chosen so as to project D to R

. However, it is

well known that different DR methods create widely

different projections for the same input data (Nonato

and Aupetit, 2018; van der Maaten and Postma, 2009;

Sorzano et al., 2014). Hence, the displayed dense

maps depend on the combination of the classiﬁer be-

ing studied and the DR method being used to project

data. However, (Rodrigues et al., 2018) only tan-

Espadoto, M., Rodrigues, F. and Telea, A.

Visual Analytics of Multidimensional Projections for Constructing Classiﬁer Decision Boundary Maps.

DOI: 10.5220/0007260800280038

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 28-38

ISBN: 978-989-758-354-4

gentially touch such aspects, as they study only the

use of t-SNE (van der Maaten and Hinton, 2008) and

LAMP (Joia et al., 2011) DR techniques for four clas-

siﬁers: k-Nearest Neighbors (k-NN), Support Vec-

tor Machines (SVM), Logistic Regression (LR), and

Convolutional Neural Networks (CNN).

In this paper, we aim to methodically cover the

areas left open in (Rodrigues et al., 2018) regarding

the choice of a suitable DR technique. Speciﬁcally,

we address the following questions:

• How do the depicted decision boundaries differ as

a function of the chosen DR technique?

• Which DR techniques are best for a trustworthy

depiction of decision boundaries?

• How do misclassiﬁcations affect a classiﬁer’s de-

cision boundaries?

To answer these questions, we proceed as fol-

lows. Section 2 overviews related work and the dense

map technique in (Rodrigues et al., 2018). Section 3

presents the experimental setup we used to study how

dense maps depend on DR techniques and classiﬁers,

covering a combination of 28 DR techniques and 4

classiﬁers. Section 4 presents and discusses our re-

sults. Section 6 concludes the paper.

2 BACKGROUND

2.1 Preliminaries

We ﬁrst introduce a few notations. Let x =

, . . . , x

), x

∈ R, 1 ≤ i ≤ n be a n-dimensional (nD)

real-valued observation or sample, and let S = {x

1 ≤ i ≤ N be a dataset of N such samples. Let

= (x

, . . . , x

), 1 ≤ j ≤ n be the j

feature vec-

tor of S. Thus, S can be seen as a table with N rows

(samples) and n columns (dimensions). As outlined

in Sec. 1, S is sampled from a particular universe,

or subspace, D ⊂ R

, e.g., the space of all images

of digits (LeCun and Cortes, 2018). A classiﬁer for

D is a function f : D → C which associates to every

x ∈ D a class label from a categorical domain C, e.g.,

the digits 0 to 9. The function f is constructed via a

so-called training-set S

= {x

, c

}|x

∈ D, c

∈ C and

tested via a similar, but disjoint, test set S

. Different

machine learning (ML) techniques exist to construct

f , some of the best known being Support Vector Ma-

chines (SVM), k-Nearest Neighbors (k-NN), Logistic

Regression (LR), Random Forests (RF), and Convo-

lutional Neural Networks (CNN) (Krizhevsky et al.,

2012).

Exploring how well f was learned from S

is most

typically done by considering all points x ∈ S

labeled

by their inferred classes f (x). To visualize these, one

typically constructs a scatterplot using projections

or dimensionality reduction (DR) methods (Hoffman

and Grinstein, 2002; Liu et al., 2015). A projection is

a function P : D → R

, where typically m = 2, which

aims to preserve data similarities or neighborhoods.

That is, if two points x ∈ D, y ∈ D are seen to be

similar (by any application-dependent suitable metric,

e.g. Euclidean distance, cosine distance, or neighbor-

hood rank), then their projections P(x) and P(y) will

be close in the target 2D (image) space.

2.2 Decision Boundary Maps

Visualizing the behavior of a classiﬁer via the scatter-

plot P(x)|x ∈ S

color-coded by the labels f (x)|x ∈

exploits the power of projections to group similar

samples x into clusters in the scatterplot. If such a

cluster is uniformly colored, it means that all its un-

derlying (similar) samples were assigned to the same

class by the classiﬁer f . Conversely, differently col-

ored ‘outlier’ points in a cluster typically indicate

classiﬁcation problems. While useful and simple to

construct, such scatterplots have the fundamental lim-

itation that they do not show how the classiﬁer treats

the entire universe D, but only a sparse sampling S

thereof. Simply put, we do not know what happens in

the blank space between the scatterplot points.

Recently, (Rodrigues et al., 2018) aimed to over-

come this issue by proposing so-called decision-

boundary maps. In brief, this method works as fol-

lows (see also Fig. 1a): For every pixel y of the target

(projection) space, data samples x ∈ D are created,

by gathering the Y scatterplot points P(x) that project

into y and, if this number is below a user-prescribed

value U, adding U − Y synthetically created points

−1

), where y

are random points falling in the

pixel y. Here, P

−1

: R

→ D is a so-called inverse pro-

jection technique that outputs a nD data point given

a projected (2D) point. Having now R = max(U, Y )

data samples x

, . . . , x

for each image pixel, the re-

spective pixel is colored to reﬂect their assigned la-

bels L = { f (x

), . . . , f (x

)}. For this, a HSV color is

synthesized where hue (H) reﬂects the most frequent

label in L; saturation (S) is high when most labels

in L are identical and low (gray colors) when many

different labels exist in L; and value (V) encodes the

sample point density R (pixels with many samples get

brighter).

The key advantages of this method are that it is in-

dependent on the classiﬁer technique f being studied;

it has no complex-to-set free parameters; but most

importantly, it creates dense maps where each image

pixel is colored to reﬂect how f behaves for the nD

Visual Analytics of Multidimensional Projections for Constructing Classiﬁer Decision Boundary Maps

Test data S

Augmented data

-1

Classifier f

scatterplot

pixel y

subsamples y’

nD sample x

P(x)

newly created samples P

-1

(y’)

dense map

labels f(x)

Fashion MNIST

subset S

4 x 28 = 112 dense maps

select 5 best

projections

4 x 5 = 20 dense maps

4 classifiers

28 projections

4 classifiers

5 projections

stage 1

stage 2

minimum

sample

density U

Figure 1: (a) Dense map construction algorithm; (b) Two-phase experiment set-up.

point(s) that map there via the projection P. These ef-

fectively partition the image space into several same-

color zones, indicating subspaces in D where the

classiﬁer behaves identically, i.e., reﬂect the under-

lying so-called contiguity hypothesis typical in many

ML contexts (Manning et al., 2008). Zone bound-

aries effectively indicate decision boundaries where

the classiﬁer changes the assigned class. Few com-

pact zones with simple (smooth) boundaries indicate

that the classiﬁer has little difﬁculty in taking de-

cisions over D. Multiple disjoint same-color zones

and/or zones with tortuous boundaries indicate the op-

posite. Small-size ‘islands’ of one color embedded in

large zones of different colors suggest misclassiﬁca-

tions and/or training problems.

3 EXPERIMENT SETUP

However, the trustworthiness of the dense map tech-

nique in (Rodrigues et al., 2018) heavily depends on

the direct (P) and inverse (P

−1

) projection techniques

it uses. Consider, for example, a toy two-class k-NN

classiﬁer for a 3D data space D ⊂ R

trained with a

simple S

consisting of one sample of each class. We

know in this case that the decision boundary should

be a plane halfway the two training samples. So, a

good 2D projection P should ideally render two com-

pact decision zones separated by a straight line. Con-

versely, a poor P may create several same-class zones

having complex curved boundaries; if we saw such

an image, we would wrongly judge the behavior of

the classiﬁer.

The original proposal used t-SNE (van der Maaten

and Hinton, 2008) and LAMP (Joia et al., 2011) to

implement P and iLAMP (Amorim et al., 2012) for

−1

, respectively. However, tens of other projection

techniques exist – for recent surveys, see (Nonato and

Aupetit, 2018; van der Maaten and Postma, 2009;

Sorzano et al., 2014). To study which of these tech-

niques are most suitable for constructing effective

dense maps, we designed and executed a two-stage

experiment, as follows (see also Fig. 1b).

Data: We select two different subsets of the Fash-

ion MNIST (Xiao et al., 2017), a state-of-the-art

ML benchmark with clothing and accessory images,

which supersedes complexity-wise the traditional

MNIST dataset (LeCun and Cortes, 2018). Both

MNIST and Fashion MNIST have 70K grayscale im-

ages of 28 × 28 pixels, split into a training set (60K

samples) and a test set (10K samples). The two sub-

sets are as follows:

• S

: A two-class subset (classes T-Shirt and An-

kle Boot) that we hand-picked to be linearly-

separable;

• S

: An all-class subset (T-Shirt, Trouser,

Pullover, Dress, Coat, Sandal, Shirt, Sneaker,

Bag, and Ankle Boot). This is a non-linearly-

separable dataset.

Classiﬁers: We consider the same classiﬁers as in

(Rodrigues et al., 2018): LR, RF, k-NN (implemented

in scikit-learn, using their toolkit’s default parame-

ters), and CNN (implemented in keras). For CNN,

we used two convolutional layers with 64 ﬁlters each

and 3 × 3 kernels, followed by one 4096-element

fully-connected layer, trained with the Adam opti-

mizer (Kingma and Ba, 2014). These classiﬁers cre-

ate very different decision boundaries: At one ex-

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

a) Logistic Regression

b) Random Forest

Figure 2: Dense maps for Logistic Regression (a) classiﬁer and Random Forest (b) classiﬁers on the 2-class dataset, all

projections.

Visual Analytics of Multidimensional Projections for Constructing Classiﬁer Decision Boundary Maps

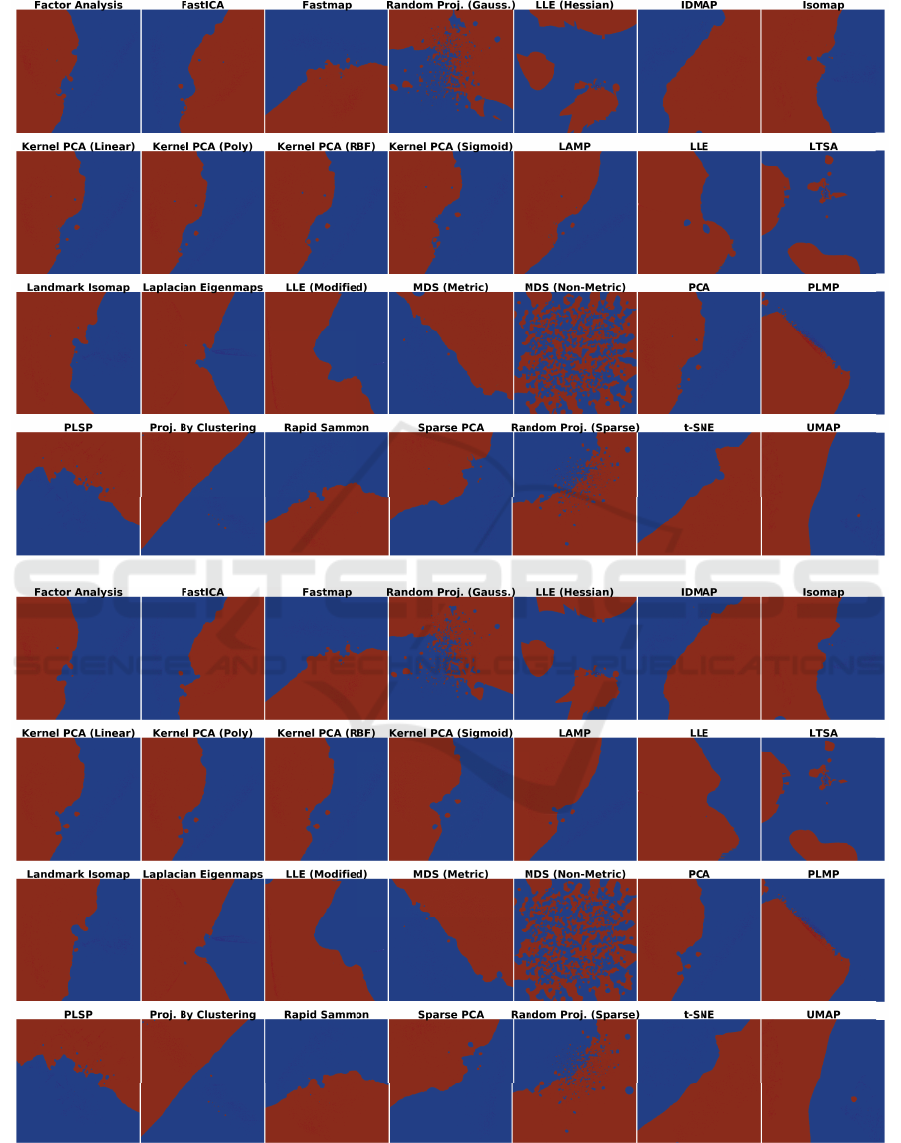
a) k Nearest Neighbors

b) Convolutional Neural Network

Figure 3: Dense maps for k-NN (a) and CNN (b) classiﬁers on the 2-class dataset, all projections.

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

treme, LR boundaries are linear (hyperplanes). k-NN

boundaries are piecewise-linear (facets of nD con-

vex polyhedra). RF creates typically more complex

boundaries than k-NN. At the other extreme, CNN

boundaries can have arbitrarily complex topologies

and geometries, due to the complex decision func-

tion f coded by the deep network structure. How-

ever, CNNs are known to perform very well for clas-

sifying images like our dataset, while at the other ex-

treme simple classiﬁers like LR are highly challenged

by such data.

Table 1: Accuracy of classiﬁers, 2-class and 10-class prob-

lems.

Classiﬁer technique 2-class 10-class

Logistic Regression (LR) 1.0000

Random Forest (RF) 1.0000 0.8332

k-Nearest Neighbors (KNN) 0.9992 0.8613

Conv. Neural Network (CNN) 1.0000 0.9080

Training: The four classiﬁers were separately trained

on the two subsets S

= 2160 samples, S

= 240

samples) and S

= 10800 samples, S

= 1200

samples). We veriﬁed that the training yielded good

accuracies in all cases and especially high ones for

the two-problem case. (Tab. 1). This is essential to

know when we next gauge the dense maps’ ability to

capture a classiﬁer behavior (see stage 1 below). Pro-

jections: We selected 28 projection techniques (P)

to create dense maps (Table 2). As selection criteria,

we considered well-known projections of high qual-

ity (following a recent survey (Nonato and Aupetit,

2018)), good computational scalability, ease of use

(P should come with well-documented parameter pre-

sets), and publicly available implementation. Table 3

lists the parameter settings (default indicates using the

standard ones the algorithms come with).

Dense Maps: We use a two-stage creation and analy-

sis of dense maps, as follows (Fig. 1b). In stage 1, for

, we create dense maps using all 28 projections for

all 4 classiﬁers, yielding a total of 112 dense maps.

All maps have a 400 × 400 pixel resolution. Since

is quite simple (two linearly separable classes),

and all classiﬁers for S

have very high accuracies

(Tab. 1), the resulting maps should display (ideally)

two compact zones separated by a smooth, ideally lin-

ear, boundary. We visually verify which of the 112

maps best comply with these criteria, and next select

the ﬁve projections (of the 28 tested ones) which re-

alize these maps. These are shown in bold in Tab. 2.

Next, in step 2 of the study, we create dense maps,

for all 4 classiﬁers again, but using the more complex

dataset. Finally, we explore these visually to gain

ﬁne-grained insights allowing us to further comment

on the dense-map suitability of the ﬁve hand-picked

projections.

Table 2: Selected Multidimensional Projections.

Factor Analysis (Jolliffe, 1986)

FastICA (Hyvarinen, 1999)

Fastmap (Faloutsos and Lin, 1995)

IDMAP (Minghim et al., 2006)

Isomap (Tenenbaum et al., 2000)

Kernel PCA (Linear) (Sch

olkopf et al., 1997)

Kernel PCA (Polynomial)

Kernel PCA (RBF)

Kernel PCA (Sigmoid)

LAMP (Joia et al., 2011)

Landmark Isomap (Chen et al., 2006)

Laplacian Eigenmaps (Belkin and Niyogi, 2002)

LLE (Roweis and Saul, 2000)

LLE (Hessian) (Donoho and Grimes, 2003)

LLE (Modiﬁed) (Zhang and Wang, 2007)

LTSA (Zhang and Zha, 2004)

MDS (Metric) (Kruskal, 1964)

MDS (Non-Metric)

PCA (Jolliffe, 1986)

PLMP (Paulovich et al., 2010)

PLSP (Paulovich et al., 2011)

Projection By Clustering (Paulovich and Minghim, 2006)

Random Projection (Gaussian) (Dasgupta, 2000)

Random Projection (Sparse) (Dasgupta, 2000)

Rapid Sammon (Pekalska et al., 1999)

Sparse PCA (Zou et al., 2006)

t-SNE (van der Maaten and Hinton, 2008)

UMAP (McInnes and Healy, 2018)

4 RESULT ANALYSIS

We next discuss the results and insights obtained in

our two-stage experiment.

4.1 Phase 1: Picking the Best

Projections

For the simple 2-class problem S

, all four classi-

ﬁers yield almost perfect accuracy (Tab. 1). Hence,

their decision boundaries are ‘where they should be’,

i.e., perfectly separating the two classes in S

. More-

over, since S

is by construction linearly separable,

this means that its dense maps, constructed for these

classiﬁers, should clearly show two compact zones

separated by a smooth, simple, boundary. We use this

as a visual criterion to rank how well projection tech-

niques can achieve this. Figures 2 and 3 show the

dense maps for all 28 tested projections for the four

tested classiﬁers, where red and blue indicate pixels

mapping samples having been assigned one of the two

labels in S

. Very interestingly, we see that even for

this very simple problem not all projections perform

the same. Our key observations are as follows:

Visual Analytics of Multidimensional Projections for Constructing Classiﬁer Decision Boundary Maps

Stability: The dense maps are surprisingly stable for

the same projection over all four classiﬁers, except

for LLA, LTSA, Random Projection (Gaussian), and

Random Projection (Sparse). Hence, we already ﬂag

these four projections as less suitable.

Smoothness: All projections have relatively smooth

boundaries, except Random Projection (Gaussian),

Random Projection (Sparse), and MDS (Non-Metric).

Since we expect smooth boundaries, these projec-

tions are less suitable. The projections which yield

boundaries closest on average to a straight line (which

is what we expect) are MDS, UMAP, Projection by

Clustering, t-SNE, and PLMP.

Compactness: Projections succeed up to widely dif-

ferent degrees in creating two compact, genus-zero,

decision zones. t-SNE, UMAP, Projection by Cluster-

ing, and IDMAP do this almost perfectly. MDS (Non-

Metric), the two Random Projections, LLE (Hessian),

and LTSA perform the worst.

Summarizing the above, we select MDS (Metric),

PLMP, Projection by Clustering, UMAP, and t-SNE

as the overall best projections to analyze further.

4.2 Phase 2: Reﬁned Insights on

Complex Data

We now examine how the ﬁve selected projections (in

phase 1) perform on the 10-class dataset S

which

is a tough classiﬁcation problem (Xiao et al., 2017).

We already see this in the lower achieved accuracies

(Tab. 1). Hence, we expect to have signiﬁcantly more

complex boundaries. Figure 4, that shows the dense

maps for our 4 classiﬁers for the 5 selected projec-

tions, conﬁrms this. Several interesting patterns are

visible, as follows.

For a given projection, the dense map patterns are

quite similar over all four tested classiﬁers. This is

correct, since the dense map is constructed based on

the scatterplot created by that projection from the test

set S

, which is ﬁxed. The variations seen along

a given column in Fig. 4 are thus precisely those

capturing the differences of decision boundaries due

to different classiﬁers. We see, for instance, that

LR tends to create slightly simpler boundaries than

the other three classiﬁers. Conversely, if we scan

Fig. 4 row-wise, we see greater variations, which can

be purely ascribed to the projection characteristics.

Techniques designed to better separate data clusters,

such as t-SNE and UMAP, show more compact deci-

sion zones with simpler boundaries than MDS, PLMP,

and Projection by Clustering. Also, the choice of

neighborhood used internally by the projection tech-

nique to estimate points in the lower dimension (2D)

does not seem to play a key inﬂuence: MDS, which

uses global neighborhoods, shows similar pattern-

variations along classiﬁers to the other four projec-

tions, all of which use local neighborhoods.

Another salient visual element of the dense maps

in Fig. 4 is the presence of many small color islands.

Let us analyze these in more detail. An island essen-

tially indicates that (at least) one sample was assigned

a label different from the labels of most samples that

are close to it in the 2D space. In turn, this means

that (a) either the projection did a bad job (the is-

land does not actually exist in the high-dimensional

space D); or (b) the island actually exist in D, i.e.,

there are very similar samples that get assigned dif-

ferent labels. Reﬁning (b), this further indicates that

(b1) the classiﬁer did a good job for a complex con-

ﬁguration in the data space D, or (b2) the classiﬁer

misclassiﬁed the point(s) in the island for some rea-

son. To understand which of these cases actually oc-

cur, we plot misclassiﬁed points atop the dense map

as half-transparent white disks. Hence, regions hav-

ing many (densely packed) misclassiﬁcations show up

as white areas. Figure 5 shows this for the LR and

CNN classiﬁers, all projections. The insets (t-SNE

dense map) exemplify how islands point to two of the

above-mentioned issues: In Fig.4a, we see two very

small color islands around the misclassiﬁed samples

A and B. These islands indicate the extent up to which

other samples, close to A or B, would also get misclas-

siﬁed. In contrast, the detail in Fig. 4b shows a (red)

island containing no white dots (misclassiﬁcations).

This island either reﬂects a real small-scale)variation

of the classiﬁer decision, or else reﬂects an artifact of

the t-SNE projection.

Separately, we see that, overall, the LR dense

maps have more white dots than the CNN ones, which

correlates with the lower LR accuracy (Tab. 1). More

interestingly, we see that the white points are non-

uniformly spread over the dense maps by different

projections. MDS and PLMP show many islands

without white dots, which indicate that these projec-

tions have trouble preserving nD similarities in 2D.

At the other extreme, t-SNE, and evenmore so UMAP,

strongly pack the white dots, which tells that misclas-

siﬁcations actually occur for quite similar data sam-

ples. These two dense maps effectively show the con-

fusion zones to the ML specialist, so one can use them

to decide which kinds of samples need to be further

added to the training set to improve accuracy.

5 DISCUSSION

We discuss next a few key aspects of our evaluation.

Best Choice: From all our experiments, t-SNE and

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

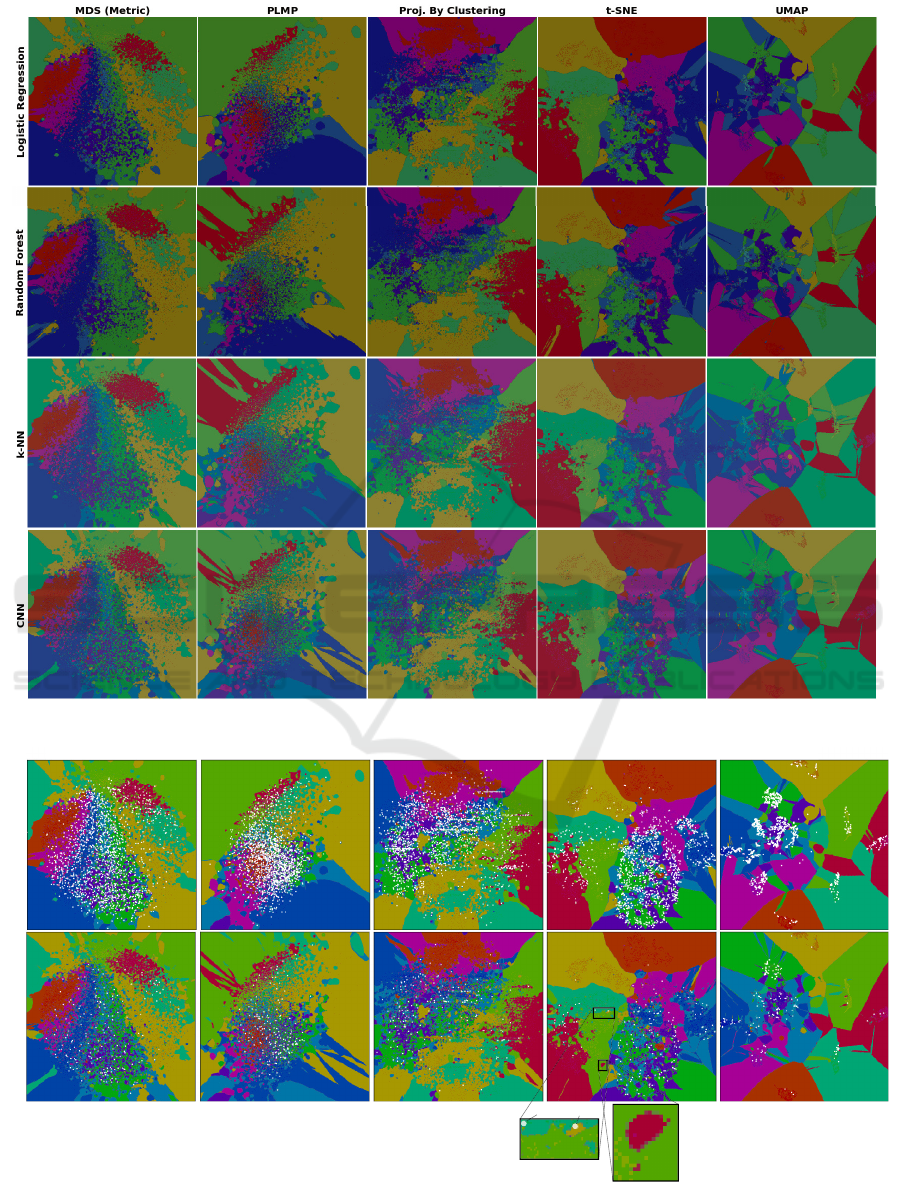
Figure 4: Dense maps for all classiﬁers, 10-class dataset, ﬁve best-performing projections.

Convolutional Neural Network

Logistic Regression

MDS(Metric) PLMP Projection by Clustering t-SNE UMAP

detail (a)

detail (b)

A B

Figure 5: Classiﬁcation errors (white dots) shown atop of the dense maps, LR and CNN classiﬁers.

Visual Analytics of Multidimensional Projections for Constructing Classiﬁer Decision Boundary Maps

UMAP appear to be the best projections for construct-

ing dense maps in terms of recognizability of decision

boundaries in the produced patterns, limited errors

(spurious islands), and concentration of confusion

zones (misclassiﬁcations). Since UMAP has similar

properties with t-SNE but is signiﬁcantly faster, we

label it as the optimal candidate for this task.

Inﬂuence Factors: As mentioned, dense maps de-

pend not only on the direct projection P but also on

its inverse P

−1

. We studied in detail the dependency

on P, but only used a single P

−1

implementation (iL-

AMP). This is due to the fact that we are not aware of

any other scalable, generic, and publicly-available in-

verse projection alternative. However, designing such

alternatives is an interesting topic in itself for future

work.

Experiment Coverage: Dense maps constructed

using projections are a novel technique in high-

dimensional visualization. Besides their use dis-

cussed here for showing classiﬁer boundaries, they

are also used to analyze projection quality (Martins

et al., 2014; Aupetit, 2007). All such maps strongly

depend on the projection technique being used. To

our knowledge, our current work that evaluates how

dense maps depend on the choice of 28 possible pro-

jection techniques, is the broadest evaluation of this

type in existence. To limit the amount of work re-

quired to analyze over hundred classiﬁer-projection

combinations, we designed a two-phase experiment

where we pre-select the best projections (using a sim-

ple classiﬁcation problem) to study next in detail.

This, of course, limits the potentially interesting in-

sights one can ﬁnd. The same is true for our choice

of using a single (though, highly-recognized complex

ML benchmark) dataset.

Replicability and Extensibility: To be useful, our

work on evaluating projection-based dense maps must

be accessible, replicable, and extensible. All involved

materials and methods (projections, datasets, dense

maps, classiﬁers, automated workﬂow scripts) are

available online (Espadoto et al., 2018). We intend to

organically extend this repository with new instances

along all above-mentioned dimensions.

6 CONCLUSIONS

In this paper we have presented a methodology for

evaluating the quality of multidimensional projec-

tions for the task of constructing 2D dense maps to

visualize decision boundaries of ML classiﬁers. To

this end, we have evaluated 28 well-known projec-

tions on a two-class, respectively ten-class, subset of

a well-known ML benchmark, using four classiﬁers

often used in practice. Our evaluation shows wide,

and to our knowledge, not yet known, differences be-

tween the behavior of the studied projections. Using

a visual analytics methodology, we next reﬁned our

analysis to a small set of ﬁve high-quality projections,

and found that t-SNE and UMAP perform best for this

task. On the practical side, our results can be used

to drive the selection of suitable projections for other

types of dense maps used in high-dimensional visu-

alization. On the methodological side, our workﬂow

can serve as a model for the exploration of a large de-

sign space in similar visual analytics contexts.

Future work can address several directions. First,

we aim to explore how dense maps depend on the in-

verse projection, and propose better alternatives to iL-

AMP. Secondly, we aim to detect, ﬂag, and possibly

eliminate projection errors, like spurious islands, so

as to make the dense map interpretation simpler and

faster. Last but not least, we will extend our pub-

licly available results (data, code, workﬂow scripts)

and hope thereby to create the starting point for a rec-

ognized benchmark for the practical analysis of the

quality of multidimensional projections.

ACKNOWLEDGEMENTS

This study was ﬁnanced in part by the Coordenac¸

de Aperfeic¸oamento de Pessoal de N

ıvel Superior -

Brasil (CAPES) - Finance Code 001.

REFERENCES

Amorim, E., Brazil, E., Daniels, J., Joia, P., Nonato, L.,

and Sousa, M. (2012). iLAMP: Exploring high-

dimensional spacing through backward multidimen-

sional projection. In Proc. IEEE VAST.

Aupetit, M. (2007). Visualizing distortions and recovering

topology in continuous projection techniques. Neuro-

computing, 10(7-9):1304–1330.

Belkin, M. and Niyogi, P. (2002). Laplacian eigenmaps and

spectral techniques for embedding and clustering. In

Advances in Neural Information Processing Systems

(NIPS), pages 585–591.

Chen, Y., Crawford, M., and Ghosh, J. (2006). Improved

nonlinear manifold learning for land cover classiﬁca-

tion via intelligent landmark selection. In Proc. IEEE

IGARSS, pages 545–548.

Dasgupta, S. (2000). Experiments with random projection.

In Proc. of the Sixteenth conference on Uncertainty in

artiﬁcial intelligence, pages 143–151. Morgan Kauf-

mann.

Donoho, D. L. and Grimes, C. (2003). Hessian eigen-

maps: Locally linear embedding techniques for high-

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

dimensional data. Proceedings of the National

Academy of Sciences, 100(10):5591–5596.

Espadoto, M., Rodrigues, F. C. M., and Telea, A. C. (2018).

Projection-based dense map evaluation. http://

snip.li/8pa.

Faloutsos, C. and Lin, K. (1995). FastMap: A fast algo-

rithm for indexing, data-mining and visualization of

traditional and multimedia datasets. ACM SIGMOD

Newsletter, 24(2):163–174.

eraud, R. and Cl

erot, F. (2002). A methodology to ex-

plain neural network classiﬁcation. Neural Networks,

15(2):237–246.

Hamel, L. (2006). Visualization of support vector machines

with unsupervised learning. In Proc. Computational

Intelligence and Bioinformatics and Computational

Biology (CIBCB). IEEE.

Hoffman, P. and Grinstein, G. (2002). A survey of visual-

izations for high-dimensional data mining. In Fayyad,

U., Grinstein, G., and Wierse, A., editors, Proc. Infor-

mation Visualization in Data Mining and Knowledge

Discovery, pages 47–82. Morgan Kaufmann.

Hyvarinen, A. (1999). Fast ICA for noisy data using gaus-

sian moments. In Proc. IEEE ISCAS, volume 5, pages

57–61.

Joia, P., Coimbra, D., Cuminato, J. A., Paulovich, F. V., and

Nonato, L. G. (2011). Local afﬁne multidimensional

projection. IEEE TVCG, 17(12):2563–2571.

Jolliffe, I. T. (1986). Principal Component Analysis and

Factor Analysis. In Principal component analysis,

pages 115–128. Springer.

Kingma, D. P. and Ba, J. (2014). Adam: A method for

stochastic optimization. arXiv:1412.6980v9 [cs.LG].

Krizhevsky, A., Sutskever, I., and Hinton, G. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. In Advances in Neural Information Pro-

cessing Systems (NIPS), pages 1097–1105.

Kruskal, J. B. (1964). Multidimensional scaling by opti-

mizing goodness of ﬁt to a nonmetric hypothesis. Psy-

chometrika, 29(1):1–27.

LeCun, Y. and Cortes, C. (2018). MNIST handwritten digits

dataset. http://yann.lecun.com/exdb/mnist.

Liu, S., Maljovec, D., Wang, B., Bremer, P.-T., and

Pascucci, V. (2015). Visualizing high-dimensional

data: Advances in the past decade. IEEE TVCG,

23(3):1249–1268.

Manning, C. D., Sch

utze, H., and Raghavan, P. (2008). In-

troduction to Information Retrieval, volume 39. Cam-

bridge University Press.

Martins, R., Coimbra, D., Minghim, R., and Telea, A.

(2014). Visual analysis of dimensionality reduction

quality for parameterized projections. Computers &

Graphics, 41:26–42.

McInnes, L. and Healy, J. (2018). UMAP: Uniform Mani-

fold Approximation and Projection for Dimension Re-

duction. arXiv:1802.03426v1 [stat.ML].

Migut, M. A., Worring, M., and Veenman, C. J. (2015).

Visualizing multi-dimensional decision boundaries

in 2D. Data Mining and Knowledge Discovery,

29(1):273–295.

Minghim, R., Paulovich, F. V., and Lopes, A. A. (2006).

Content-based text mapping using multi-dimensional

projections for exploration of document collections.

In Proc. SPIE, volume 6060. Intl. Society for Optics

and Photonics.

Nonato, L. and Aupetit, M. (2018). Multidimensional

projection for visual analytics: Linking techniques

with distortions, tasks, and layout enrichment. IEEE

TVCG. DOI:10.1109/TVCG.2018.2846735.

Paulovich, F. V., Eler, D. M., Poco, J., , Botha, C. P.,

Minghim, R., and Nonato, L. G. (2011). Piecewise

laplacian-based projection for interactive data explo-

ration and organization. Computer Graphics Forum,

30(3):1091–1100.

Paulovich, F. V. and Minghim, R. (2006). Text map ex-

plorer: a tool to create and explore document maps.

In Proc. Intl. Conference on Information Visualisation

(IV), pages 245–251. IEEE.

Paulovich, F. V., Silva, C. T., and Nonato, L. G. (2010).

Two-phase mapping for projecting massive data sets.

IEEE TVCG, 16(6):1281–1290.

Pekalska, E., de Ridder, D., Duin, R. P. W., and Kraaijveld,

M. A. (1999). A new method of generalizing Sammon

mapping with application to algorithm speed-up. In

Proc. ASCI, volume 99, pages 221–228.

Rauber, P. E., Fadel, S. G., Falcao, A. X., and Telea, A. C.

(2017a). Visualizing the hidden activity of artiﬁcial

neural networks. IEEE TVCG, 23(1):101–110.

Rauber, P. E., Falc

ao, A. X., and Telea, A. C. (2017b). Pro-

jections as visual aids for classiﬁcation system design.

Information Visualization, 17(4):282–305.

Ribeiro, M. T., Singh, S., and Guestrin, C. (2016). Why

should I trust you?: Explaining the predictions of any

classiﬁer. In Proc. ACM SIGMOD KDD, pages 1135–

1144.

Rodrigues, F. C. M., Hirata Jr, R., and Telea, A. C.

(2018). Image-based visualization of classiﬁer deci-

sion boundaries. In Proc. SIBGRAPI. in press.

Roweis, S. T. and Saul, L. L. K. (2000). Nonlinear dimen-

sionality reduction by locally linear embedding. Sci-

ence, 290(5500):2323–2326.

Sch

olkopf, B., Smola, A., and M

uller, K. (1997). Kernel

principal component analysis. In Proc. International

Conference on Artiﬁcial Neural Networks, pages 583–

588. Springer.

Sorzano, C., Vargas, J., and Pascual-Montano, A. (2014).

A survey of dimensionality reduction techniques.

arXiv:1403.2877 [stat.ML].

Tenenbaum, J. B., Silva, V. D., and Langford, J. C. (2000).

A global geometric framework for nonlinear dimen-

sionality reduction. Science, 290(5500):2319–2323.

van der Maaten, L. and Hinton, G. (2008). Visualizing data

using t-SNE. JMLR, 9(Nov):2579–2605.

van der Maaten, L. and Postma, E. (2009). Dimensionality

reduction: A comparative review. Tech. report TiCC

TR 2009-005, Tilburg University, Netherlands.

Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-

MNIST: A Novel Image Dataset for Benchmarking

Machine Learning Algorithms. arXiv:1708.07747v2

[cs.LG].

Visual Analytics of Multidimensional Projections for Constructing Classiﬁer Decision Boundary Maps

Zhang, Z. and Wang, J. (2007). MLLE: Modiﬁed lo-

cally linear embedding using multiple weights. In

Advances in Neural Information Processing Systems

(NIPS), pages 1593–1600.

Zhang, Z. and Zha, H. (2004). Principal manifolds and

nonlinear dimensionality reduction via tangent space

alignment. SIAM Journal on Scientiﬁc Computing,

26(1):313–338.

Zou, H., Hastie, T., and Tibshirani, R. (2006). Sparse prin-

cipal component analysis. Journal of Computational

and Graphical Statistics, 15(2):265–286.

APPENDIX: PROJECTION

PARAMETERS

Table 3: Parameters used for each projection.

Projection Parameters

Factor Analysis iter: 1000

FastICA fun: exp, iter: 200

Fastmap default parameters

IDMAP default parameters

Isomap neighbors: 7, iter: 100

Kernel PCA (Linear) default parameters

Kernel PCA (Polynomial) degree: 2

Kernel PCA (RBF) default parameters

Kernel PCA (Sigmoid) default parameters

LAMP iter: 100, delta: 8.0

Landmark Isomap neighbors: 8

Laplacian Eigenmaps default parameters

LLE neighbors: 7, iter: 100

LLE (Hessian) neighbors: 7, iter: 100

LLE (Modiﬁed) neighbors: 7, iter: 100

LTSA neighbors: 7, iter: 100

MDS (Metric) init: 4, iter: 300

MDS (Non-Metric) init: 4, iter: 300

PCA default parameters

PLMP default parameters

PLSP default parameters

Projection By Clustering default parameters

Random Projection (Gaussian) default parameters

Random Projection (Sparse) default parameters

Rapid Sammon default parameters

Sparse PCA iter: 1000

t-SNE perplexity: 20, iter: 3000

UMAP neighbors: 10

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications