Efﬁcient GPU Implementation of Lucas-Kanade through OpenACC

Olfa Haggui

1,2

, Claude Tadonki

, Fatma Sayadi

and Bouraoui Ouni

Centre de Recherche en Informatique (CRI), Mines ParisTech - PSL Research University,

60 boulevard Saint-Michel, 75006 Paris, France

Networked Objects Control and Communications Systems (NOCCS),

Sousse National School of Engineering, BP 264 Sousse Erriadh 4023, Tunisia

Electronics and Microelectronics Laboratory,Faculty of Sciences,

Keywords:

Optical Flow, Lucas-Kanade, Multicore, Manycore, GPU, OpenACC.

Abstract:

Optical ﬂow estimation stands as an essential component for motion detection and object tracking procedures.

It is an image processing algorithm, which is typically composed of a series of convolution masks (approxi-

mation of the derivatives) followed by 2 × 2 linear systems for the optical ﬂow vectors. Since we are dealing

with a stencil computation for each stage of the algorithm, the overhead from memory accesses is expected to

be signiﬁcant and to yield a genuine scalability bottleneck, especially with the complexity of GPU memory

conﬁguration. In this paper, we investigate a GPU deployment of an optimized CPU implementation via Ope-

nACC, a directive-based parallel programming model and framework that ease the process of porting codes

to a wide-variety of heterogeneous HPC hardware platforms and architectures. We explore each of the major

technical features and strive to get the best performance impact. Experimental results on a Quadro P5000

are provided together with the corresponding technical discussions, taking the performance of the multicore

version on a INTEL Broadwell EP as the baseline.

1 INTRODUCTION

Motion detection is an important topic in compu-

ter vision because of its central consideration in va-

rious real world applications. Related algorithms

are used in objects tracking(S.A. Mahmoudi, 2014;

V. Tarasenko, 2016), video surveillance(V. Tarasenko,

2016; Kalirajan and Sudha, 2015), basic image pro-

cessing(E. Antonakos, 2015; S. N.Tamgade, 2009),

cars technology(R. Allaoui, 2017), robotics(C. Cili-

berto, 2011), to name a few. Motion estimation con-

sists in extracting a motion vector from a sequence of

consecutive images by assuming that the intensity is

preserved during the displacement. Currently, among

the methods available in the literature, the optical ﬂow

algorithm is one of the most commonly used appro-

ach for motion evaluation, which is a basic block of

a vision process designed for a speciﬁc application.

There are different methods for optical ﬂow estima-

tion, with a pioneer work by J.J. Gibson (Gibson,

1950) in 1950.

The computing of the optical ﬂow is a subject

that has been widely studied for several decades,

with successful implementations in many interesting

applications. Besides pure optical ﬂow investigati-

ons, a combination with other techniques has been

considered too, like the work of Horn and Schunck

(K.P. Horn, 1981), that has led to multiple derived

methods and improved optical ﬂow algorithms. It in-

troduces a global constraint of smoothness over the

whole image to minimize distortions in the ﬂow. Ho-

wever, in case of small motions, this method is im-

peded by its weak robustness. The so-called Lucas-

Kanade algorithm by Lucas and Kanade (B.D. Lucas,

1981) is a local approach providing more accurate re-

sults for optical ﬂow estimation. The algorithm is less

sensitive to image noises, yields good quality results

with moderate computational cost, and is capable of

tracking even tiny motions. Considering all these fac-

tors and in comparison with other optical ﬂow algo-

rithms, Lucas-Kanade method is the most considered

one for estimating the optical ﬂow for all (or selected)

pixels, assuming that the ﬂow is constant in a local

neighborhood. The results of the algorithm is more

reliable if corner pixels (O. Haggui, 2018) are used.

Our work stands as another parallelization of

Lucas-Kanade algorithm in the context of multicore

and manycore processor. Beside our OpenACC im-

768

Haggui, O., Tadonki, C., Sayadi, F. and Ouni, B.

Efﬁcient GPU Implementation of Lucas-Kanade through OpenACC.

DOI: 10.5220/0007272107680775

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 768-775

ISBN: 978-989-758-354-4

plementation, which is not a novelty by itself, we

study the impact of OpenACC directives considera-

tions on the scalability and memory access for GPU

and CPU processors. The remainder of paper is or-

ganized as follows. Section 2 provides a basic back-

ground of the optical ﬂow method and describes the

Lucas-kanade algorithm. we start with a baseline

multicore implementation in section 3. Section 4

and 5 gives an overview of GPU architecture and

OpenACC programming paradigms respectively. In

Section 6, we describe our OpenACC parallelization

and we provide a commented report of our experi-

mental results . Section 7 concludes the paper and

outline some perspectives.

2 RELATED WORK

Beside the quality of the estimation, the execution

time is also important (A. Garcia-Dopico, 2014;

S. Baker, 2004), especially with the consideration

of the real-time constraint. Indeed, since the algo-

rithm is likely to be applied on the consecutive fra-

mes of a live video, it should as fast as possible.

Implementation of the Lucas-Kanade algorithm on

the graphics processor Unit (GPU), in the GPGPU

standpoint, is seriously considered. In (J.Marzat,

2009), Marzat, Dumortier and Ducroct propose a pa-

rallel implementation on a GPU to compute a dense

and accurate velocity ﬁeld using NVIDA Gt200 card,

which achieved 15 velocity ﬁeld estimations per se-

cond on 640x480 images. Another relevant contri-

bution is presented in (S.A. Mahmoudi, 2014), in

which the authors implemented the optical ﬂow mo-

tion tracking using Lucas-kanade combined with Har-

ris corner detector (only corner pixels are conside-

red) on a Full HD video using multiple GPUs. A

thorough implementation study is provided by Plyer,

Guy and Champagnat in (A. Plyer, 2016) denoted

by eFLOKI. It is a robust, accurate and high perfor-

mance method even on large format images. Duven-

hage, Delport and Jason(B. Duvenhage, 2010) also

investigated a GPU implementation using the Open

Graphics Library (OpenGL) and the Graphics Library

Shading Language (GLSL), with a performance simi-

lar than a comparative CUDA implementation. Other

authors have addressed the parallelization of optical

ﬂow computation on FPGA (A. Garcia-Dopico, 2014;

R. Allaoui, 2017). They conclude that both have si-

milar performance, although their FPGA implemen-

tation took much longer to develop. An implementa-

tion on the CELL processor (C66xDSP) is provided

and discussed by Zhang and Cao (F. Zhang, 2014).

Regarding the multicore parallelization of the al-

gorithm, the work by (Kruglov, 2016) for instance

describes an updated method in order to speed up

the objects movement between frames in a video se-

quence using OpenMP. Another multi-core paralleli-

zation is proposed in (N. Monz, 2012). Pal, Biemann

and Baumgartner (I. Pal, 2014) discuss how the velo-

city of vehicles can be estimated using optical ﬂow

implementation parallelized with OpenMP. Moreo-

ver, another hybrid model mitigate the bottleneck of

motion estimation algorithms with a small percentage

of source code modiﬁcation. In (N. Martin, 2015),

Nelson and Jorge proposed the ﬁrst implementation

of optical ﬂow of Lucas-kanade algorithm based on

directives of OpenACC programming paradigms on

GPU. Carlos and Guillerom (C. Garcia, 2015) evalu-

ated also the directives of OpenACC with the GPU

performance. In this context our work evaluate also a

new OpenACC implementation but which processes

and analyzes the bottlenecks of the accesses memory.

3 LUCAS-KANADE ALGORITHM

3.1 Optical Flow

The optical ﬂow is a computer vision topic, where the

main kernel is to calculate the apparent motion of fe-

atures across two consecutive frames of a given vi-

deo, thus estimating a global parametric transforma-

tion and local deformations. It is based mainly on lo-

cal spatio-temporal convolutions that are applied con-

secutively. The optical ﬂow has lots of uses, and it

is an important clue for motion estimation, tracking,

surveillance, and recognition applications. Different

methods have been proposed for optical ﬂow estima-

tion (B.D. Lucas, 1981; K.P. Horn, 1981; Gibson,

1950; Adelson and Bergen, 1985; Fleet and Jepson,

1995; Kories and Zimmerman, 1986), and they can be

grouped into block-based methods, spatio-temporal

differential methods, frequency-based methods and

correlation-based method. Each method has its ad-

vantages and its disadvantages, but the main draw-

back is the limited speed and the need of a large

memory space. Over the years, Horn and Schunck

algorithm(K.P. Horn, 1981) and Lucas-kanade algo-

rithm (B.D. Lucas, 1981) have became the most wi-

dely used techniques in computer vision. We have

focused on Lucas-kanade’s approach because is the

most adequate in terms of calculation complexity and

requires less computing resources. The main princi-

ple of the Lucas-Kanade optical ﬂow estimation is to

assume the brightness constancy to ﬁnd the velocity

vector between two successive frames (t and t+1) as

show in Figure 1, (a) and (b). The optical ﬂow vectors

Efﬁcient GPU Implementation of Lucas-Kanade through OpenACC

769

are drawn in Figure 1 (c). The accuracy of the estima-

tion of the displacement from the video sequence is

the main qualitative concern. Recalling that we have

to analyze a (live) video, a real-time processing ap-

pears very important, thus justifying all efforts to re-

ach a fast implementation.

(a) Frame t (b) Frame t+1

Figure 1: Optical Flow computation.

3.2 Description of Lucas-Kanade

Algorithm

The idea is to focus on representative pixels (cor-

ner pixels for instance), which are then checked for

motion across consecutive frames through intensity

variations, that are perceived as relative motion bet-

ween the scene and the camera. Consider a given 2D

image, a small motion is approximated by a transla-

tion. Thus, if the current frame is represented by its

intensity function I, then the intensity function H of

the next frame is such that

H(x, y) = I(x + u, y + v), (1)

where (u, v) is the displacement vector. For this pur-

pose, we have to solve for every pixel the following

so-called Lucas-Kanade equation:



∑





= −



∑



(2)

where I

, I

and I

are the derivatives of the intensity

along x, y and t direction respectively. The system re-

ally implements a least-square approach to ﬁnd the

most likely displacement (u, v), since the original

system is overdetermined. The summations within

equation (2) are over the pixels inside the sampling

window. If the condition number of the normal ma-

trix is above a given threshold, then we compute the

solution of the system (using Kramer method for in-

stance) and thus obtain the components of the optical

ﬂow vector for the corresponding pixel. An schema-

tic view of an algorithm for this computation can be

stated as follows:

1. compute the derivatives I

, I

, and I

2. compute the products I

, I

, and I

3. compute the matrix of the normal sub-matrices

and the corresponding right and sides

4. solve the linear systems for the optical ﬂow vec-

tors

The derivatives (Step 1) are computed through their

Taylor approximations using the corresponding con-

volution kernels. Then follows their point-wise pro-

ducts in step 2. Step 3 computes for each pixel the

normal matrix and the right hand side of the linear sy-

stem as described in equation (2). In the ultimate step

where we solve the previous linear systems for each

pixel, the computation of the condition numbers is im-

plicit, they are indeed evaluated and compared with a

the chosen threshold in order to decide whether we

give up or we compute the solution of the system for

the optical ﬂow vector. Figure 2 displays a schematic

view of the Lucas-Kanade computation chain.

Figure 2: Workﬂow of Lucas-Kanade algorithm.

4 BASELINE MULTICORE

IMPLEMENTATION

Our work start with a baseline sequential implementa-

tion where all operators involved in the Lucas-kanade

algorithm are separable. We are apply operators clus-

tering (O. Haggui, 2018) where the aims at merging

all the operators into a single one, in order to re-

duce the number of ﬂoating point operations(ﬂops)

and reduce the intermediate storage. Furthermore,

we are study the effect of array contraction technique

(Y. Song, 2004), it is a program transformation which

reduces the array size while preserving the correct

output to perform the data reuse and cache locality.

A special case of array contraction called array sca-

larization has been used in order to improve register

utilization. At the same time, we use a shifting stra-

tegy which is the most well-known and fundamental

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

770

tool for matrix computations to resolve the memory

alignment issues.

Table 1: Evaluation of the Multicore optimization.

# cores 1 2 4 8 10

T(s) Acc Acc Acc Acc

2000

0.08 1.96 3.78 7.15 8.89

4000

0.34 1.95 3.86 7.53 9.28

6000

0.78 1.97 3.85 7.46 9.23

8000

1.38 1.95 3.88 7.58 9.35

12000

3.27 1.97 3.87 7.56 9.33

In order to evaluate our optimization strategies, we

consider an Intel Xeon E5-2669 v4(Broadwell-EP)

CPU having a total of 44 cores divided into 4 NUMA

(Non-Uniform Memory Access) nodes. We chose to

consider just one node NUMA (11 cores) with diffe-

rent size of images. Table 1 illustrates the effect of the

optimization strategies with multicore using OpenMP

programming language . we can notice that when

increasing the image resolution, OpenMP does not

provide a great improvement because it reaching the

maximum parallelism that can be supplied. However,

our speedups are good and can be improved by consi-

dering hardware accelerators like the GPU.

5 GPU ARCHITECTURE

Graphics Processor units (GPUs) stands as one of the

most effective manycore hardware accelerator in the

HPC landscape. GPUs are increasingly considered in

the implementation of numerous scientiﬁc and com-

mercial applications. Modern GPUs consist of multi-

ple streaming multiprocessors (SMs or SMXs); each

SM consists of many scalar processors (SPs, also re-

ferred to as cores). Each GPU supports a concurrent

execution of hundreds to thousands of threads, and

each thread is executed by a scalar core as shown

in Figure 3. The elementary scheduling and execu-

tion unit is called a warp, which is composed of 32

threads. Warps of threads are grouped together into

a thread block, and blocks are grouped into a grid.

Both thread block and grid can be organized into a

one, two or three-dimensional topology (A. Brodt-

korb, 2013; T. Allen, 2016). The main advantage

of GPUs is their ability to perform signiﬁcantly more

ﬂoating point operations(FLOPs) per unit of time than

an ordinary CPU, and they well implement data pa-

rallelism. Memory system is quite different between

CPUs and GPUs. A GPU has a more complex me-

mory hierarchy and the related information are not

usually provided with necessary details by the ven-

dors. Analyzing the memory access pattern and the

Figure 3: Processing units packaging within a GPU.

Figure 4: Overview of NVIDIA memory hierarchy.

associated costs on a GPU is an extremely challenging

task, which is a very important optimization step as

memory activity in this context is likely to be the main

performance bottleneck. The memory of a GPU has

different levels. The of-chip global memory resides in

RAM of the host CPU. It is accessible by all threads

in a grid, and this is the space where data exchan-

ges occur. There are also other types of data storage

units, namely registers and shared memories, which

cannot be accessed directly by the host, but by the

thread. However, shared memory subspace is alloca-

ted per thread block and is accessible by all of its thre-

ads. Because the shared memory is on-chip, latency is

much lower than for global memory. It is frequently

used as an optimization for applications where data

are reused once inside a thread block. The L1 cache

in the NVIDIA architecture is reserved only for local

memory accesses by default. Global loads/stores are

cached within the L2 cache only. Read-only Data Ca-

che was introduced in the latest NVIDIA architecture.

Texture memory and constant memory are allocated

in the off-chip memory associated to global memory,

Efﬁcient GPU Implementation of Lucas-Kanade through OpenACC

771

but is accessed via dedicated buses. Both memories

have their own cache space and special features, and

are accessible by all threads. Figure 4 shows an over-

view of the memory hierarchy in NVIDIA GPUs.

Memory accesses are commonly known to yield

the performance bottleneck with GPUs, they have

been the major focus of code analyses for per-

formance improvements (N. K. Govindaraju, 2006;

T. Allen, 2016). The most offending overhead comes

from data transfers between the host and the device.

These transfers must pass through peripheral compo-

nents and the interconnect express bus. In addition,

with the different levels of the GPU memory system

and the large amount of data access, memory activity

is globally a critical point for performance concerns.

Accesses to global memory could get coalesced/un-

coalesced. Hence,it is possible to reduce the number

of global memory accesses as long as two conditions

are met: coalescence, where the neighboring threads

should access neighboring data and alignment, where

the addresses should be a multiple of the segment’s

size. In addition, the accesses to shared memory

could suffer from bank conﬂicts, accesses to texture

memory could come with spatial locality penalty and

accesses to constant memory could be broadcast. The

use of GPUs is more suitable with highly regular ap-

plications.

6 OVERVIEW OF OPENACC

PROGRAMMING MODEL

OpenACC(NVIDIA, 2015), (OpenACC, 2017) is an

accelerator programming standard emerged in 2011

as a model that uses high-level compiler directives

to expose parallelism in the code and generate pa-

rallel or accelerated versions for GPUs and multicore

CPUs. This paradigm relies on compilers to generate

efﬁcient code and optimize for performance. In fact,

the programmers use compiler directives to indicate

which areas of code to accelerate, without any modi-

ﬁcation into the code itself. OpenACC uses parallel

or kernels constructs to deﬁne a compute region that

will be executed in parallel on the device, where the

loop construct is used to specify the distribution of

the iterations. In fact, the main program runs on the

CPU and the parallel (child) tasks are ofﬂoaded to the

GPUs. Moreover, the purpose of having both paral-

lel and kernels constructs is that the parallel construct

provides more control to the user while the kernels

one offers more control to the compiler. OpenACC

deﬁnes three levels of parallelism: gang, worker and

vector. A schematic view of a standard OpenACC di-

agram is displayed in ﬁgure 5, Where a gang is com-

posed of one or multiple workers. All workers within

a gang can share resources such as cache memory or

processor, and a worker can computes just one vec-

tor. A vector threads performs a single operation on

multiple data (SIMD) in a single step.

Figure 5: OpenACC working diagram.

In addition to the directives to express parallelism,

the OpenACC API also contains data directives. To

avoid unnecessary data exchanges between the local

memory of the GPU and the main memory located on

the host, the programmer can give some hint infor-

mation to the OpenACC compilers through appropri-

ate data directives. Generally, the OpenACC compi-

ler is responsible for the correctness and optimization

of data movement in both memories (GPU and CPU).

OpenACC provides different types of data transfer di-

rectives, clauses and runtime. Listing 1 shows an ex-

ample of a data directive to import the input from the

host to the device using the copyin clause, and vice-

versa with copyout.

#pragma a cc d a t a

c op yi n ( I [ 0 : s i z e N t ∗ s i z e M t ] ,

I t t [ 0 : s i z e N t t ∗ s i z e M t t ] )

c o p y o u t ( F [ 0 : s i z e N t ∗ s i ze Mt ] )

{

#pragma a cc p a r a l l e l l o o p

p r i v a t e ( j , aIx , a Iy , a I t )

gang num_gangs ( )

wo r ker num_ workers ( )

v e c t o r _ l e n g t h ( )

p r e s e n t ( I [ 0 : s i z e N t ∗ s i z e Mt ] ,

I t t [ 0 : s i z e N t t ∗ s i z e M t t ] )

c r e a t e (D [ 0 : ( 2 ∗ z +1)∗ s i z e N t ] )

f o r ( i = 0 ; i <2∗ z ; i ++)

{

# pragma a cc l oo p gang , v e c t o r

f o r ( j = 0 ; j < s i z e N t − 2; j ++)

{

a I x = I [w( ( i + 1 ) , ( j +1)+1)] −

I [w( ( i + 1 ) , ( j + 1 ) ) ] ;

a I y = I [w( ( i + 1 ) + 1 , ( j + 1 ))] −

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

772

I [w( ( i + 1 ) , ( j + 1 ) ) ] ;

a I t = I t t [w( ( i + 1 ) , ( j + 1 ))] −

I [w( ( i + 1 ) , ( j + 1 ) ) ] ;

}

Listing 1: Generic code with data related directives

7 PARALLELIZATION AND

EVALUATIONS

7.1 Hardware Conﬁguration

To carry out the tests on the implementation develo-

ped in OpenACC, we have used a Quadro P5000 GPU

accelerator from NVIDIA (Pascal architecture). It in-

cludes 2560 CUDA cores with 16 GB GDDR5 me-

mory. The host is an Intel(R) Xeon(R) CPU E5-1620

v4 processors with 4 cores. We use PGI-pgcc, version

18.4.

7.2 Results of the Parallelization

In our experiments, we use different sizes of frame

and run our Lucas-Kanade implementation for the op-

tical ﬂow vectors. We start with a baseline sequen-

tial implementation in C, enhanced with an OpenCV

function to load the image frames, then we have the

derived OpenACC version to parallelize the code wit-

hout considering any data directives. The ﬁrst step

of the algorithm consists in loading the data from the

CPU to the GPU’s global memory. This step is yield a

signiﬁcant overhead. Then, we deﬁne which part will

be accelerated with the device (kernel) using the basic

directives (#pragma acc kernel and/or #pragma

acc Parallel) as describe previously in listing 1.

Table 2: Evaluation of the GPU parallelization.

Image size CPU (s) GPU (s)

2000

0.09 0.018

4000

0.34 0.057

6000

0.78 0.13

8000

1.38 0.25

12000

3.27 0.64

We can see from table 2 that the OpenACC code

on the GPU signiﬁcantly outperforms the parallel

CPU version. However, since the version at this stage

does not contain any memory optimization directive,

there is a potential room for improvement we at this

stage. To evaluate this potential, we used the NVIDIA

runtime proﬁler on our kernels to identify where me-

mory accesses look too high. We can use also Ope-

nACC ﬂag -Minfo=all,clff to print all the infor-

mation about how to optimize the code.

7.3 Data Movement Optimization

In this subsection, we analyze the behavior of the ma-

jor data movement directives and clauses in order to

reduce the overhead of data exchanges and get ride of

intermediate data accesses whenever possible.

OpenACC allows an explicit control of data al-

location together with the corresponding transacti-

ons through appropriates clauses (copyin, copyout,

present, create). OpenACC provides the cache di-

rective #pragma acc cache, which tells the compi-

ler to seek the best cache performance for the indica-

ted memory region.

Although NVIDIA provides the concept of uni-

ﬁed memory, which allows the GPU and the host

CPU to share the same global address space. This

is made technically possible using the NVLink in-

terconnect. The uniﬁed memory enables fast me-

mory accesses with large data sets. In fact, OpenACC

compiler provides the ﬂag -ta=tesla:managed for

the uniﬁed memory consideration, and the ﬂag

-ta=tesla:pinned for pinned memory. It is a me-

mory allocated using the cudaMallocHost function,

which prevents the memory from being swapped out

and thereby provides improved transfer speeds, con-

trary to the non-pinned memory obtained with a plain

malloc. In this context, the compiler relies on the

CUDA runtime to migrate data automatically through

Uniﬁed Memory, ensuring the coherence between

data references on the GPU and the corresponding

addresses on the main memory. The experimental re-

sults of our optimization investigation are summari-

zed in Table 3.

Table 3: Evaluation of our GPU optimization.

2000

4000

6000

8000

12000

(1) 0.018 0.057 0.130 0.250 0.640

(2) 0.007 0.024 0.056 0.091 0.174

(3) 0.007 0.025 0.057 0.095 0.181

(4) 0.006 0.023 0.055 0.088 0.174

(5) 0.006 0.020 0.052 0.074 0.147

(6) 0.005 0.018 0.047 0.074 0.145

• (1): Basic GPU parallelization

• (2): (1) + Data movement performance

• (3): (1) + Uniﬁed memory

• (4): (2) + cache directive

• (5): (2) + pinned

• (6): (4) + (5)

Efﬁcient GPU Implementation of Lucas-Kanade through OpenACC

773

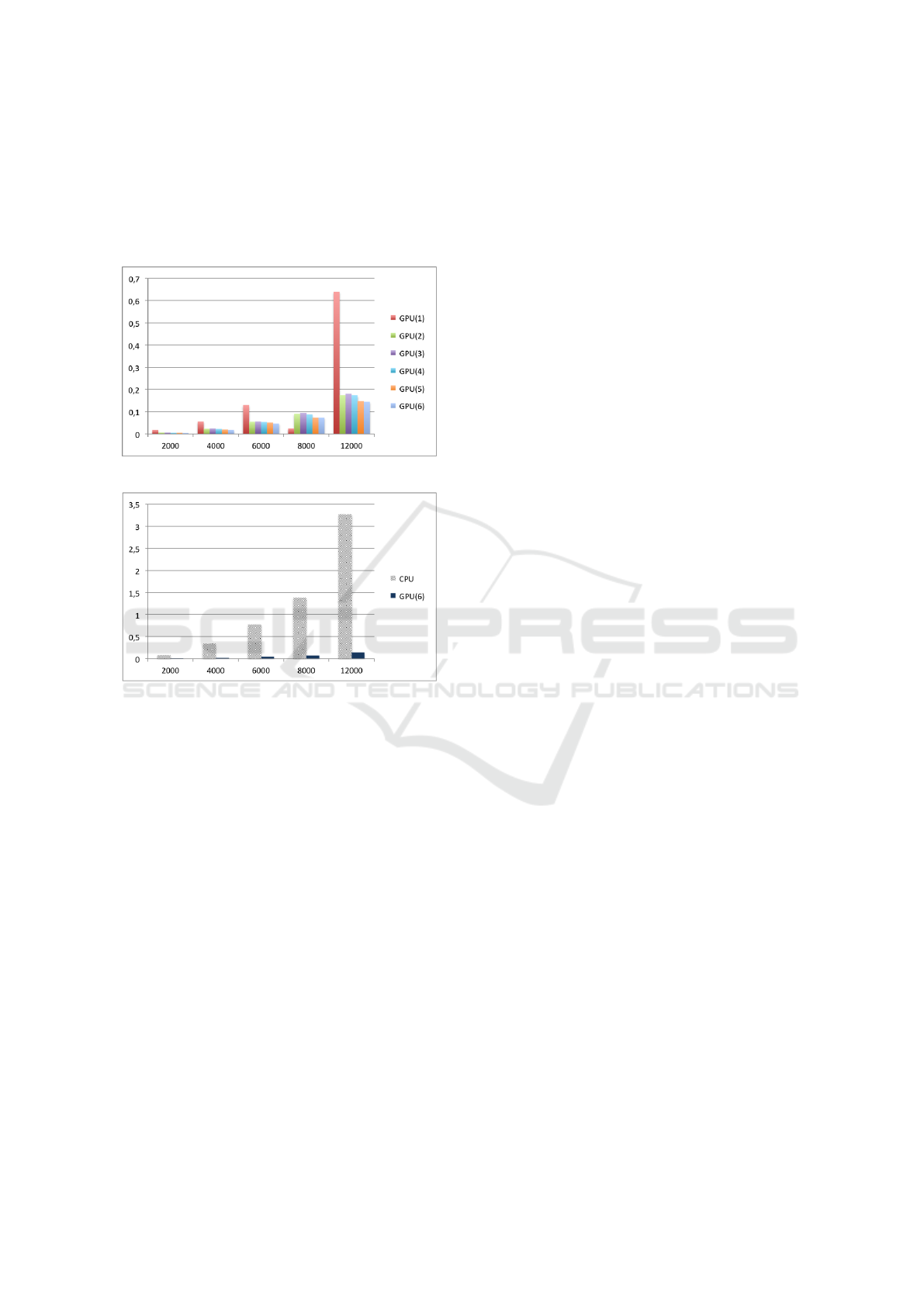
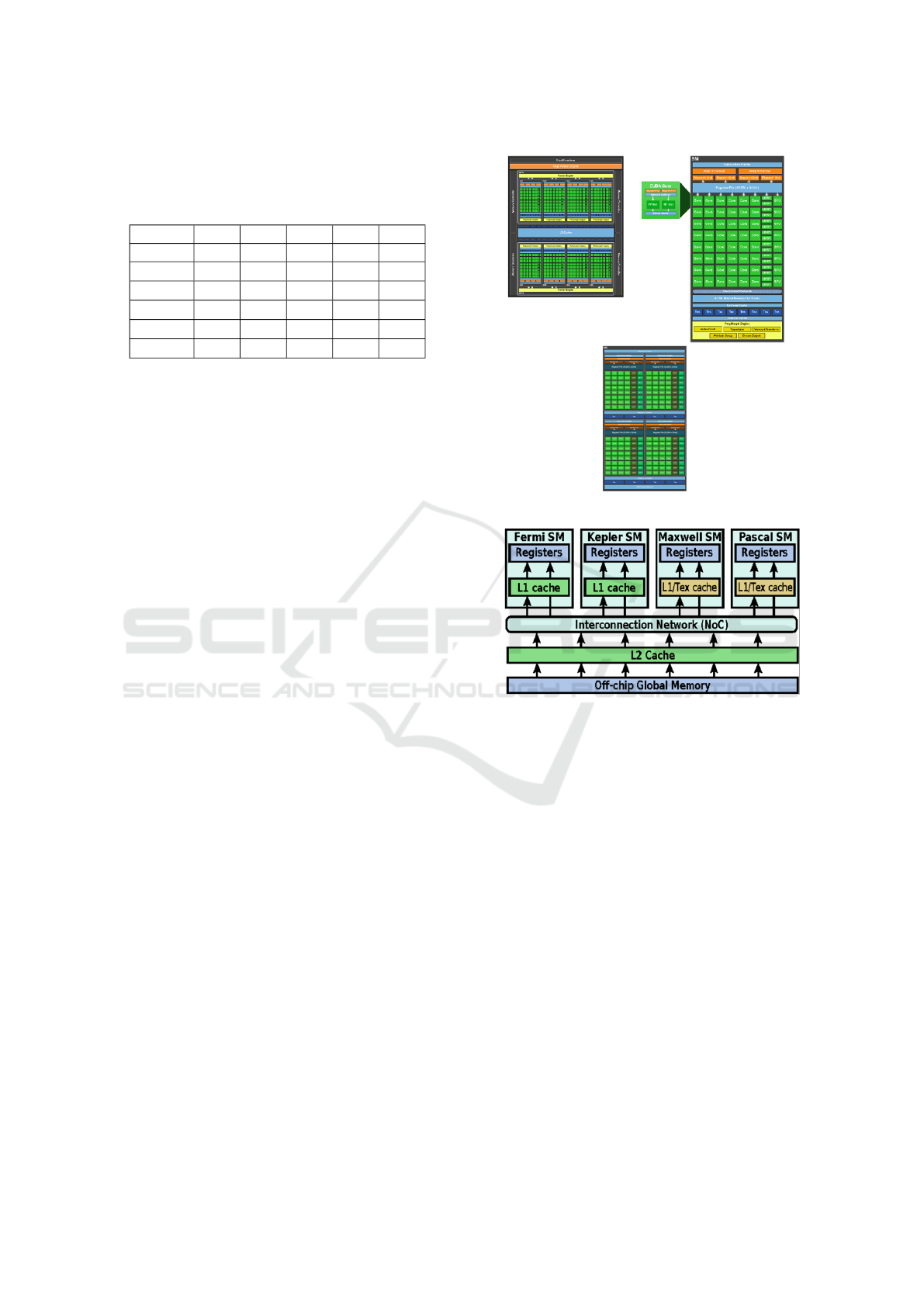
Figure 6 provides a global view of our incremen-

tal OpenACC optimization, while ﬁgure 7 displays a

comparison between the baseline CPU implementa-

tion and the fully optimized GPU one. In both cases,

the x-axis is for image sizes and the y-axis is for the

overall execution timings in seconds.

Figure 6: Incremental GPU optimization.

Figure 7: Basic CPU and fully optimized GPU.

Let summarize the steps of our work in this paper.

We consider the Lucas-Kanade algorithm for optical

ﬂows computation. We start an optimized sequential

version that we parallelize with OpenMP and we get

decent speedups. Afterwards, looking at the abso-

lute performance, we investigate what can be obtain

with a GPU using OpenACC. Using the proﬁle, we

identify the major bottleneck of the kernel: memory

transactions. We focus on efﬁcient memory organiza-

tion and movement of data, performing an incremen-

tal memory optimization to get the best performance,

which, as expected, outperforms the parallel CPU im-

plementation.

8 CONCLUSION

A fast and accurate estimation of the optical ﬂow

ﬁelds is a challenging task, both because of the stencil

nature of the computation and the memory complex-

ity of large-scale manycore accerelerator (GPU). In

this work, we investigated an OpenACC paralleliza-

tion of the Lucas-Kanade optical ﬂow algorithm with

GPUs and obtain better performance that a parallel

version on a large multicore machine. OpenACC is

a promising alternative to consider for a fast deploy-

ment on the GPU. It makes possible to migrate stan-

dard CPU code in a straightforward way without ma-

king too many modiﬁcations, and obtain a decent per-

formance compared to other complex programming

model like CUDA and OpenCL.

ACKNOWLEDGMENT

We express our sincere gratitude to the Centre de Re-

cherche en Informatique (CRI) at Mines ParisTech for

all its supports.

REFERENCES

A. Brodtkorb, T. Hagen, M. S. (2013). Graphics processing

unit(gpu) programming strategies and trends in gpu

computing. In Journal of Parallel Distributed Com-

puting.

A. Garcia-Dopico, J. L. Pedraza, M. N. A. P. S. R. J. N.

(2014). Parallelization of the optical ﬂow computa-

tion in sequences from moving cameras. In EURASIP

Journal on Image and Video Processing.

A. Plyer, G. Le Besnerais, F. C. (2016). Massively parallel

lucas kanade optical ﬂow for real-time video proces-

sing applications. In J Real-Time Image Proc.

Adelson, E. H. and Bergen, J. R. (1985). Spatio temporal

energy models for the perception of motion. In Jour-

nal Opt. Soc. Am.

B. Duvenhage, JP. Delport, J. d. V. (2010). Implementa-

tion of the lucas-kanade image registration algorithm

on a gpu for 3d computational platform stabilisation.

In Proceedings of the 7th International Conference on

Computer Graphics, Virtual Reality, Visualisation and

Interaction.

B.D. Lucas, T. K. (1981). An image registration technique

with an application to stereo vision. In In Proceedings

of Image Understanding Workshop.

C. Ciliberto, U. Pattacini, L. N. F. N. G. M. (2011). Reex-

amining lucas-kanade method for real-time indepen-

dent motion detection: Application to the icub huma-

noid robotv. In International Conference on Intelli-

gent Robots and Systems.

C. Garcia, G. Botella, F. d. S. M. P.-M. (2015). Fast-coding

robust motion estimation model in a gpu. In Real-Time

Image and Video Processing.

E. Antonakos, J. Alabort, G. T. S. Z. (2015). Feature-based

lucas–kanade and active appearance models. In IEEE

Transactions on Image Processing.

F. Zhang, Y. Gao, J. D. B. (2014). Lucas-kanade optical

ﬂow estimation on the ti c66x digital signal proces-

sor. In IEEE High Performance Extreme Computing

Conference (HPEC).

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

774

Fleet, D. J. and Jepson, A. D. (1995). Computation of com-

ponent image velocity from local phase information.

In IJCV.

Gibson, J. (1950). The perception of the visual world. In

Houghton Mifﬂin Boston.

I. Pal, R. Biemann, S. V. B. (2014). A comparison and

validation approach for trafﬁc data, acquired by ai-

rborne radar and optical sensors using parallelized

lucas-kanade algorithm. In VDE VERLAG GMBH

Berlin Offenbach.

J.Marzat, Y.Dumortier, A. (2009). Real-time dense and

accurate parallel optical ﬂow using cuda. In WSCG

Full papers proceedings, INRIA.

Kalirajan, K. and Sudha, M. (2015). Moving object de-

tection for video surveillance. In Hindawi Publishing

Corporatione Scientiﬁc World Journal.

Kories, R. and Zimmerman, G. (1986). A versatile met-

hod for the estimation of displacement vector ﬁelds

from image sequencesn. In IEEE Proc. of Workshop

on Motion-Representation and Analysis.

K.P. Horn, B. S. (1981). Determining optical ﬂow artiﬁcial

intelligence. In In Proceedings of Image Understan-

ding Workshop.

Kruglov, A. N. (2016). Tracking of fast moving objects in

real time. In Pattern Recognition and Image Analysis.

N. K. Govindaraju, S. Larsen, J. D. M. (2006). A memory

model for scientiﬁc algorithms on graphics proces-

sors. In Proceedings of the ACM/IEEE conference on

Supercomputing.

N. Martin, J. Collado, G. B. C. G. M. P. (2015). Openacc-

based gpu acceleration of an optical ﬂow algorithm.

In ACM Digital Library,SAC’15.

N. Monz, A. i. S. (2012). Parallel implementation of a ro-

bust optical ﬂow technique. In Las Palmas de Gran

Canaria.

NVIDIA (2015). Openacc programming and best practices

guide. In openacc-standard.org.

O. Haggui, C. Tadonki, L. L. F. S. B. O. (2018). Harris

corner detection on a numa manycore. In Future Ge-

neration Computer Systems.

OpenACC, A. T. (2017). The OpenACC Application Pro-

gramming Interface. OpenACC-Standard.org, 2.6 edi-

tion.

R. Allaoui, H. H. Mouane, Z. A. S. M. I. E. h. A. E. m.

(2017). Fpga-based implementation of optical ﬂow

algorithm. In 3rd International Conference on Elec-

trical and Information Technologies ICEIT.

S. Baker, I. M. (2004). Lucas kanade 20 years on:a unifying

framework. In International Journal of Computer Vi-

sion.

S. N.Tamgade, V. R. (2009). Motion vector estimation of vi-

deo image by pyramidal implementation of lucas ka-

nade optical ﬂow. In Second International Conference

on Emerging Trends in Engineering and Technology,

ICETET.

S.A. Mahmoudi, M.Kierzynka, P. M. K. K. (2014). Real-

time motion tracking using optical ﬂow on multiple

gpus. In Bulletin of The Polish Academy Of Sciences

Technical Sciences.

T. Allen, R. G. (2016). Characterizing power and perfor-

mance of gpu memory access. In E2SC2016 Salt Lake

City.

V. Tarasenko, D. P. (2016). Detection and tracking over

image pyramids using lucas and kanade algorithm. In

International Journal of Applied Engineering Rese-

arch.

Y. Song, R. Xu, C. W. Z. L. (2004). Improving data lo-

cality by array contraction. In IEEE Transactions on

Computers.

Efﬁcient GPU Implementation of Lucas-Kanade through OpenACC

775