Subpixel Catadioptric Modeling of High Resolution Corneal Reﬂections

Chengyuan Lin and Voicu Popescu

Computer Graphics and Visualization Lab, Purdue University, West Lafayette, U.S.A.

Keywords:

Corneal Reﬂections, Catadioptric Modeling, Bundle Adjustment, Epipolar Geometry, 3D Reconstruction.

Abstract:

We present a calibration procedure that achieves a sub-pixel accurate model of the catadioptric imaging system

deﬁned by two corneal spheres and a camera. First, the eyes’ limbus circles are used to estimate the positions of

the corneal spheres. Then, corresponding features in the corneal reﬂections are detected and used to optimize

the corneal spheres’ positions with a RANSAC framework customized to the corneal catadioptric model. The

framework relies on a bundle adjustment optimization that minimizes the corneal reﬂection reprojection error

of corresponding features. In our experiments, for images with a total resolution of 5, 472 × 3,648, and a

limbus resolution of 600 ×600, our calibration procedure achieves an average reprojection error smaller than

one pixel, over hundreds of correspondences. We demonstrate the calibration of the catadioptric system in

the context of sparse, feature-based, and dense, pixel-based reconstruction of several 3D scenes from corneal

reﬂections.

1 INTRODUCTION

Digital cameras now capture images with a resolution

that far exceeds conventional displays. Whereas a dis-

play cannot show simultaneously all the pixels of the

image, the underlying high resolution is useful for di-

gital zoom-in operations or for large format printing.

Another important beneﬁt of high resolution is incre-

asing the quality of 3D scene reconstructions derived

from images.

Many real world scenes contain reﬂective objects,

and high resolution images capture a wealth of scene

information in fortuitous reﬂections. Reﬂections on

convex surfaces are particularly rich in information,

as the divergent reﬂected rays sample the scene com-

prehensively, with a large ﬁeld of view. Furthermore,

reﬂections introduce additional sampling viewpoints,

which allow measuring disparity and triangulating 3D

positions from a single image.

The human eyes are convex reﬂectors, and resear-

chers have long speculated on the possibility of using

corneal reﬂections to infer 3D scene structure. One

challenge is the small baseline, i.e. a typical inter-

pupillary distance is 63 mm (Dodgson, 2004), which

translates to low depth accuracy at distances of 0.5 m

and beyond. Another challenge is the low resolution

of the corneal reﬂections. Both challenges are allevi-

ated by increases in the overall image resolution. A

third challenge is accurate calibration of the catadiop-

tric system deﬁned by the two eyes and a camera. An

accurate catadioptric model is needed to limit the se-

arch for correspondences between corneal reﬂections

to 1D epipolar curves, and for accurate triangulation

of 3D scene points.

In this paper we present a procedure for calibra-

ting the catadioptric model deﬁned by two corneal

spheres and a camera. The input is a high resolution

image of a person looking at a 3D scene. In our ex-

periments, the image resolution is 5, 472 × 3, 648 and

each corneal reﬂection has a resolution of approxima-

tely 600 × 600. First, a preliminary corneal catadiop-

tric model is inferred from the projection of the lim-

bus circles in the corneal reﬂections. Then, the model

is reﬁned iteratively using a custom RANSAC appro-

ach that relies on bundle adjustment to minimize fe-

ature reprojection error. We obtain an error between

0.16 and 0.58 pixels. We use the corneal catadioptric

model to recover dense depth through stereo matching

with the support of epipolar-like constraints (Figure

1). The truth geometry used for comparison (grey

points in Figure 1c) was obtained by scanning the toys

with an active depth sensing camera.

2 PRIOR WORK

We ﬁrst give an overview of prior efforts on acqui-

ring scenes using catadioptric imaging systems, and

then we review prior work in modeling the catadiop-

Lin, C. and Popescu, V.

Subpixel Catadioptric Modeling of High Resolution Corneal Reﬂections.

DOI: 10.5220/0007308506730683

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 673-683

ISBN: 978-989-758-354-4

673

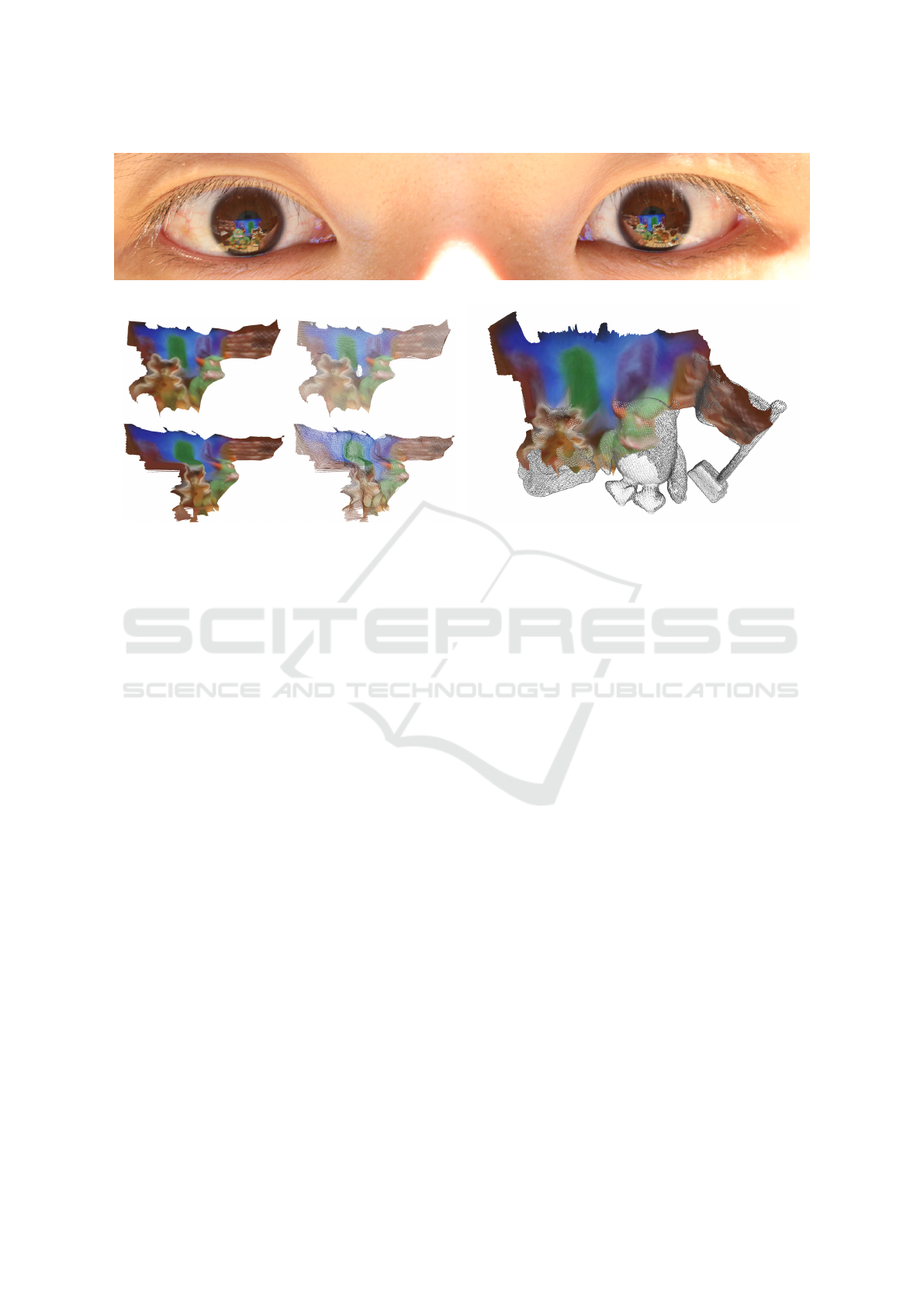
(a) Input image cropped to eye region.

(b) 3D reconstruction visualized in ﬁlled and wireframe

mode.

(grey).

Figure 1: 3D scene reconstruction with our catadioptric modeling approach.

tric imaging system deﬁned by a camera and the two

human eyes.

Researchers have long noticed the beneﬁts of de-

vising acquisition systems that combine refractive and

reﬂective elements. One such beneﬁt is an increa-

sed ﬁeld of view. Debevec used a chrome ball as a

light probe to capture the complex illumination of a

real world scene with a single shot, and to apply it to

synthetic objects integrated into the scene (Debevec,

2008). Nayar has developed omnidirectional cameras

using paraboloidal mirrors with a single viewpoint, so

their images can be resampled to conventional ima-

ges (Nayar, 1997). A second scene acquisition be-

neﬁt of catadioptric systems is the ability to integrate

multiple perspectives in the same image. The additi-

onal perspectives encode depth disparity, which ena-

bles single-shot depth from stereo (Kuthirummal and

Nayar, 2006). The additional perspectives are also

useful for devising acquisition systems that are robust

to occlusions, by guiding the scanning laser beam to-

wards hard-to-reach places (Fasano et al., 2003).

Human eyes are often captured in images, and

leveraging corneal reﬂections to infer information

about the scene is appealing and has been carefully

studied (Nitschke et al., 2013). The corneal reﬂecti-

ons are readily available, without the challenge of

augmenting the camera with reﬂective elements. Furt-

hermore, the corneal reﬂections introduce additional

viewpoints that capture parts of the scene missed from

the camera viewpoint. The additional viewpoints not

only provide a comprehensive image of the scene,

but also allow measuring disparity to extract depth.

The catadioptric system deﬁned by a camera and two

eyes requires modeling the cornea’s reﬂective surface.

Prior work models this surface as a sphere cap, which

is part of the corneal sphere, and delimited by the

sclera sphere (Nishino and Nayar, 2006). We use the

same cornea surface model. Another challenge is that,

unlike for catadioptric imaging devices where the re-

ﬂective elements have a ﬁxed, pre-calibrated position

and orientation with respect to the camera, in the case

of corneal reﬂections the eyes are free to move with

respect to the camera, and their position has to be re-

covered in every image.

One use of corneal reﬂections is to capture a pano-

ramic image of the scene, leveraging the large ﬁeld of

view sampled by the reﬂected rays (Nishino and Na-

yar, 2006). The information in the corneal reﬂection

can be used to extract gaze direction in camera-

display systems (Nitschke et al., 2011a), and also to

extract a panorama of the environment reﬂected in the

user’s eyes (Nitschke and Nakazawa, 2012). Corneal

reﬂections have also been proposed as a way of gai-

ning insight into a crime scene, demonstrating that ca-

mera resolution is now sufﬁcient for identifying hu-

mans present in such reﬂections (Jenkins and Kerr,

2013).

We discuss in detail the two prior art papers most

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

674

relevant to our work. One describes a system that does

not recover 3D scene structure from corneal reﬂecti-

ons, but rather from parabolic metal mirrors (Agra-

wal et al., 2011). Metal mirrors greatly simplify ca-

tadioptric scene reconstruction by providing a preci-

sely known reﬂective surface shape, and by genera-

ting clear and high contrast reﬂections. Furthermore,

metal mirrors are perfectly stationary which avoids

the blurriness that results from the slight user head

motion as the picture is taken. Moreover, the metal

mirrors used are about three times larger than the cor-

neal sphere, and about four times larger than the lim-

bus circle, which delimits the reﬂection in our case.

Consequently, the prior work reﬂections have a re-

solution of 2M pixels, compared to the 0.1M pixels

for our work, which aids signiﬁcantly with recon-

struction quality. The earlier system reﬁnes calibra-

tion without a preliminary RANSAC step to weed out

mismatched features. The reprojection error achieved

by the earlier system is about ﬁve times larger than

ours, most likely due to the simpler calibration reﬁ-

nement step, as discussed above. Finally, the earlier

work does not report any quantitative measure of the

3D reconstruction error. Our work validates the 3D

reconstruction quality in an absolute sense by recon-

structing objects of known size, as discussed in the

following sections.

The other paper highly relevant to our work is

the only prior art paper that actually recovers any 3D

structure from corneal reﬂections (Nishino and Na-

yar, 2004). The paper proposes the idea of ﬁnding

correspondences between a pair of corneal reﬂections

and of triangulating them into depth. We extend this

work in the following ways. First, the earlier system

calibration stops at our precalibration phase. The ear-

lier system is crudely calibrated by inferring the po-

sition of the corneal spheres from the limbus circles,

whereas our system reﬁnes this initial calibration with

our custom RANSAC + bundle adjustment approach,

which reduces the reprojection error substantially. We

achieve sub-pixel accuracy, whereas the previous pa-

per doesn’t report calibration accuracy, which we es-

timate as being orders of magnitude lower based on

the accuracy achieved by our similar precalibration

stage. Second, the earlier system requires establishing

correspondences between the two corneal reﬂections

manually, by clicking corresponding points. Our sy-

stem detects, matches, and validates correspondences

automatically. Third, the earlier system does not per-

form dense stereo reconstruction, whereas our system

does. Finally, the only scene where 3D reconstruction

is demonstrated is that of a large cube with uniformly

colored faces. Inspired by their pioneering work, with

the help of our subpixel catadioptric modeling fra-

(a) Outer view. (b) Geometric model.

Figure 2: Eye model.

mework, we demonstrate 3D scene structure recovery

from corneal reﬂections.

3 CATADIOPTRIC MODEL OF

CORNEAL REFLECTIONS

Many scenes of interest to computer vision applicati-

ons contain humans, and corneal reﬂections present

the opportunity for catadioptric stereo scene recon-

struction. Before scene reconstruction can begin, one

has to model the catadioptric system deﬁned by two

eyes and a camera.

3.1 Eye Model

Figure 2a shows an outer view of the human eye. The

most distinctive components are the color-textured

iris and the surrounding white sclera. The cornea is

the transparent outer layer of the eye that covers the

iris. The cornea has an internal pressure higher than

that of the atmosphere, which maintains the cornea’s

convex shape. The cornea surface is coated with a

thin ﬁlm of tear ﬂuid which makes it smooth, with

mirror-like reﬂective characteristics (Nitschke et al.,

2011b).

Geometrically, the eye is well approximated by

two intersecting spherical segments of different radii:

a smaller, anterior corneal segment, and a larger, pos-

terior scleral segment (Figure 2b). The intersection of

the two segments deﬁnes the limbus circle, i.e. the pe-

rimeter of the iris. In the ﬁeld of anatomy, extensive

measurements of the shape and dimensions of the cor-

nea have been conducted (Mashige, 2013). The cor-

neal segment covers about one-sixth of the eye, and

has a radius of curvature r

of 7.8 mm. The radius of

the limbus circle r

is 5.5 mm. The displacement d

between the center of the limbus circle and the center

of the corneal sphere can be obtained as

− r

≈ 5.53mm .

(1)

Subpixel Catadioptric Modeling of High Resolution Corneal Reﬂections

675

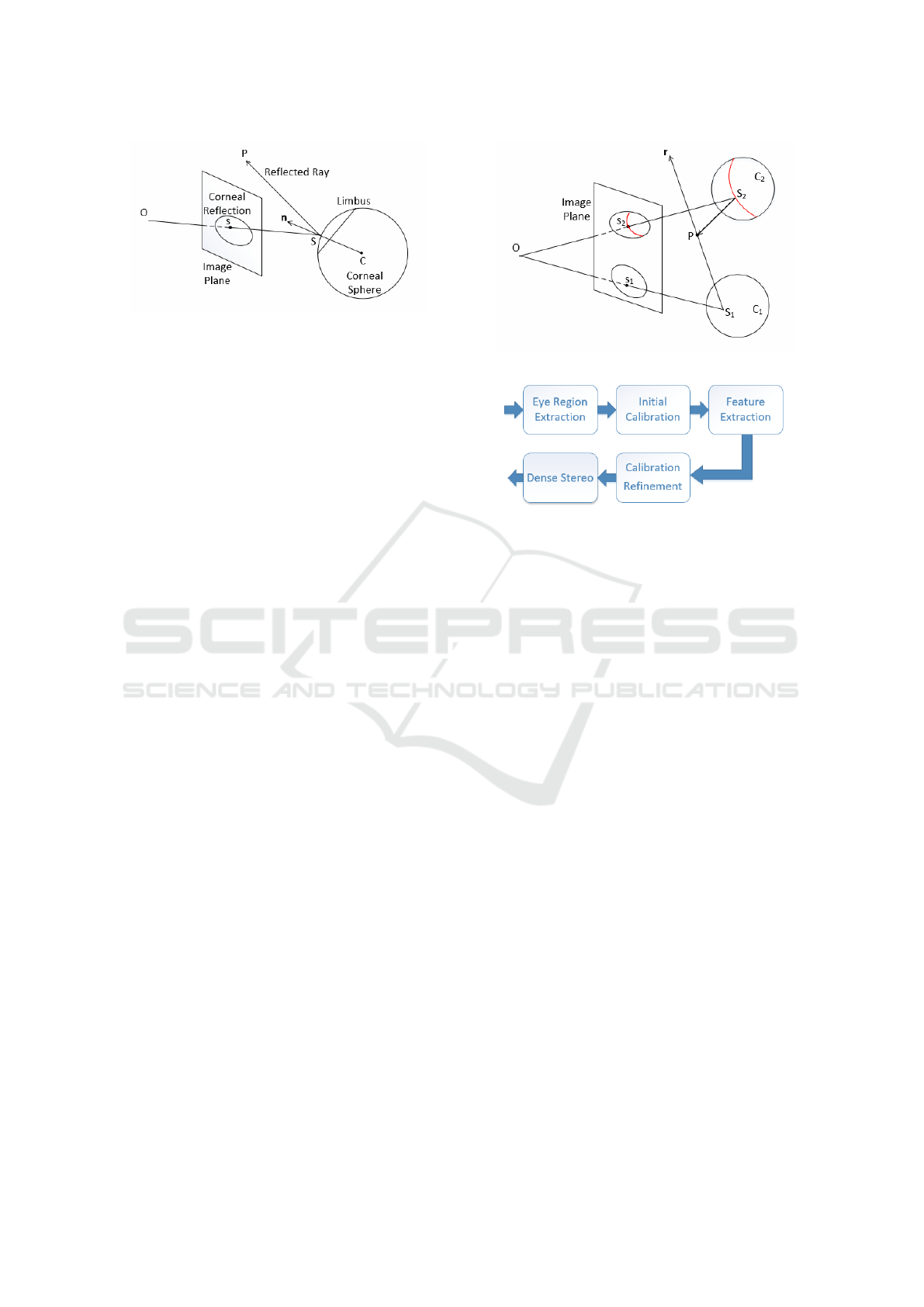
Figure 3: Corneal catadioptric imaging system.

3.2 Catadioptric Model

We model the catadioptric system deﬁned by a camera

and two eyes with the following parameters: (1) the

intrinsic parameters of the camera, (2) the limbus ci-

rcle radius r

, (3) the corneal sphere radius r

, and

(4) the 3D positions of the centers of each of the two

corneal spheres in the camera coordinate system.

We measure the camera intrinsic parameters with

a standard calibration process (Zhang, 1999). We as-

sume that both eyes have the same limbus circle ra-

dius, and we use the average value of 5.5 mm. We as-

sume both corneal spheres have the same radius, and

we use the average value of 7.8 mm. We conﬁrm the

validity of these assumptions in Section 5.3. The 3D

positions of the corneal sphere centers are found for

each image as described in the next section.

Using the catadioptric model (Figure 3), given a

pixel s in the corneal reﬂection, one can compute the

corresponding reﬂected ray SP by reﬂecting the ca-

mera ray OS off the corneal sphere. The converse,

projection operation is more challenging. Given a

scene 3D point P, we compute its corneal reﬂection

projection s = π(C, P) by ﬁrst ﬁnding its reﬂection

point S with a fourth order equation (Eberly, 2008).

Then s is computed by projecting S on the image

plane.

3.3 Epipolar Geometry

Epipolar geometry is used in stereo matching to re-

duce the dimensionality of the correspondence se-

arch space from two to one. In our case the rays re-

ﬂected by the corneal sphere are not concurrent, so

the epipole is ill-deﬁned, and traditional epipolar ge-

ometry does not apply. However, we derive epipolar-

like constraints as follows. Given a pixel s

in the

left corneal reﬂection (Figure 4), we compute its left

corneal sphere reﬂected ray r

r, we sample r

r with 3D

points, and we project each 3D point P onto the image

plane using the right corneal sphere, leveraging the

projection operation described above. The projected

points deﬁne an epipolar curve in the right corneal

Figure 4: Epipolar geometry of corneal catadioptric system.

Figure 5: System pipeline overview.

reﬂection which is known to contain the correspon-

dence s

of s

, if such a correspondence exists. Like

in traditional stereo, the search for correspondences is

conﬁned to a 1D subset of the image pixels. We note

that the epipolar curve can be described analytically

with a quartic (Agrawal et al., 2010). However, we

have opted to sample the epipolar curve by sampling

the 3D ray for a better control of the sampling rate,

as it is challenging to sample a high-order parametric

curve with steps of equal Euclidean length.

4 SYSTEM PIPELINE

Figure 5 shows the stages of our system pipeline. Ple-

ase also refer to the supplementary video for results

of each stage.

4.1 Eye Region Extraction

The ﬁrst stage crops the input image to only contain

the eyes region. We use a Haar feature-based cascade

classiﬁer specialized for eye detection, proposed by

Viola (Viola and Jones, 2001) and improved by Lien-

hart (Lienhart and Maydt, 2002). Previous approa-

ches for extracting the eye regions proceed with a pre-

liminary step of ﬁnding the faces in the input image.

In our case, a single face dominates the input image,

and it can even happen that an image does not capture

the entire face, so face detection is not necessary, and

sometimes not even possible.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

676

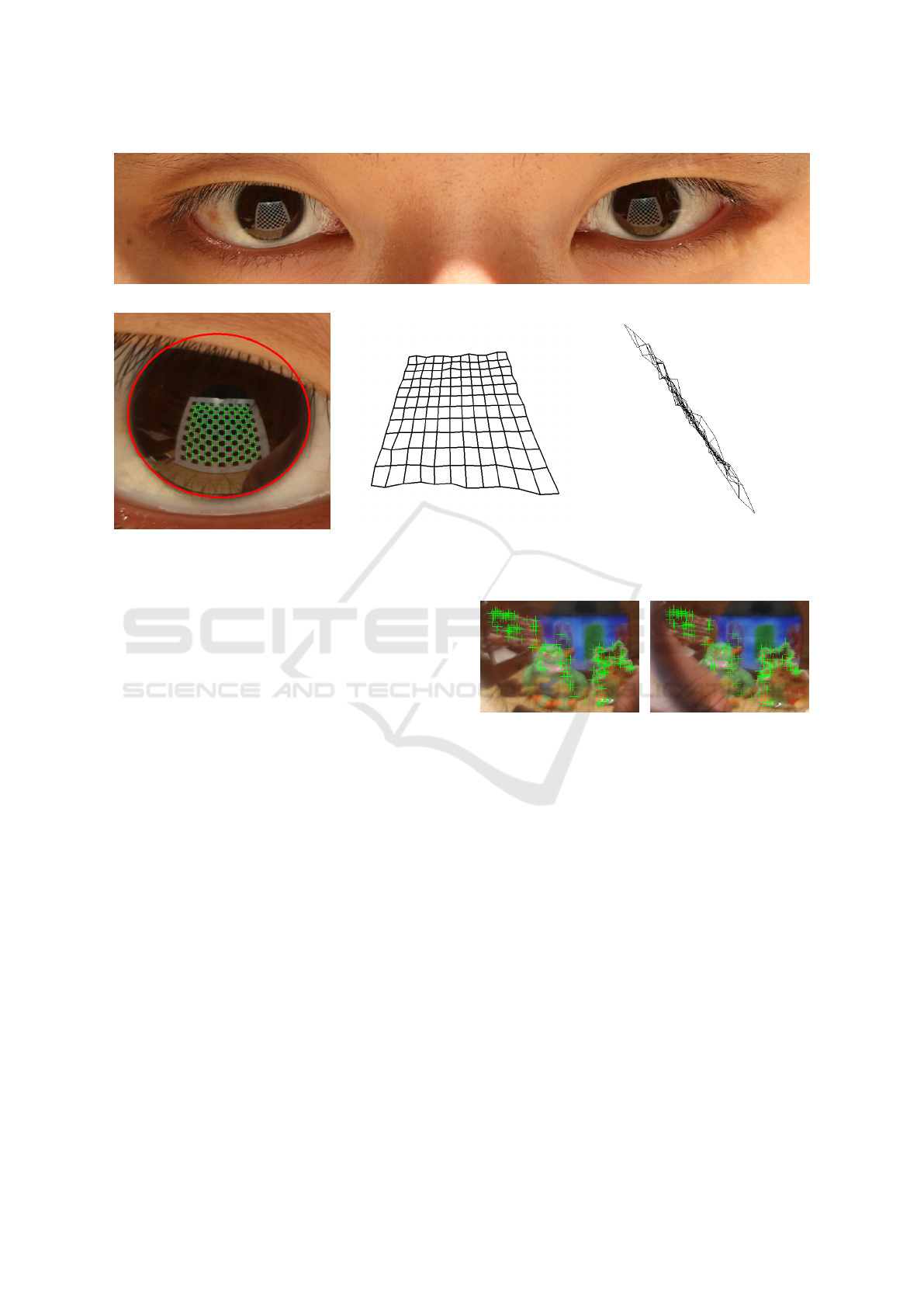
(a) Eye region of input image.

(b) Limbus and feature detection. (c) Reconstructed checkerboard. (d) Side view of checkerboard.

Figure 6: 3D reconstruction of checkerboard. The average out of plane displacement for the checker corners is 7.3 mm.

4.2 Initial Calibration

The second stage of the pipeline derives an estimate of

the position of the corneal spheres in the camera coor-

dinate system. This is achieved with a method similar

to the one described before in the context of achieving

super-resolution of corneal reﬂections (Nitschke and

Nakazawa, 2012). We summarize the procedure here

for completeness.

The limbus projection is detected in each eye re-

gion using a weak perspective assumption. Prior art

has also developed methods for recovering the limbus

under full-perspective projection assumption (Schnie-

ders et al., 2010). However, the weak-perspective as-

sumption is justiﬁed by the small limbus diameter re-

lative to the distance to the camera, and by the fact

that at this stage we are only deriving an initial es-

timate that is then reﬁned in the subsequent pipeline

stages.

The ellipse corresponding to the limbus projection

is found in a downsampled eye region image using

a Canny edge detector. Edge segments are assem-

bled from edge map pixels and the ellipse is assem-

bled from edge segments with a combinatorial se-

arch (Kassner et al., 2014). The downsampling of

the eye region not only helps accelerate ellipse de-

tection, but also serves as a low-pass ﬁlter that im-

proves robustness. In particular, the downsampling

suppresses the corneal reﬂections, which are an im-

Figure 7: Corneal reﬂection feature points for Figure 1.

portant source of noise for this stage of the pipeline.

Note that the limbus circle is never entirely visible, as

it is occluded by eyelids and eyelashes. Our edge de-

tection/combinatorial search method handles well the

variable occlusion of the limbus. Figure 6b shows a

limbus detection example. Once the ellipse is deter-

mined, using the known radius of the limbus circle,

the 3D position of the center and the orientation of

the limbus circle are computed leveraging the known

camera intrinsics. Since the radius of the corneal sp-

here is known, the corneal sphere center is computed

using the 3D position of the center and the normal of

the limbus plane (Schnieders et al., 2010).

4.3 Feature Extraction

The third stage of the pipeline extracts features in the

reﬂections within the two limbus ellipses. We de-

tect features using the FAST algorithm (Rosten and

Drummond, 2006) (Figure 7). In anticipation of fe-

Subpixel Catadioptric Modeling of High Resolution Corneal Reﬂections

677

Algorithm 1: Reﬁnement of catadiotpric model.

Input: Initial catadioptric model C

, features F

and

, # of iterations k

Output: Feature matching M, and reﬁned

catadioptric model C

1: M

= InitialMatching(F

, F

)

2: for each iteration i of k do

3: hex

= {( f

, f

), . . . , ( f

, f

)} ⊂ M

4: C

= BundleAdjustment(C

, hex

)

5: for each (l

, r

) in M

6: e

i j

= ReprojectionError((l

, r

),C

)

7: if e

i j

< ε then // inlier correspondence

8: M

+= (l

, r

), n

9: if n

> n

best

then

10: n

best

= n

, M = M

, C

best

= C

11: C = BundleAdjustment(C

best

, M)

ature matching, the features are described with the

BRIEF (Calonder et al., 2010) algorithm. Feature

scale and orientation will not vary much between the

reﬂection in the left eye and the reﬂection in the right

eye. Therefore, the additional memory and proces-

sing costs of scale and orientation invariant descrip-

tors such as SIFT (Lowe, 1999) or SURF (Bay et al.,

2006) are not justiﬁed in our context. The BRIEF des-

criptor is binary, so the hamming distance between

two descriptors can be found quickly using XOR and

counting bit operations.

4.4 Calibration Reﬁnement

The fourth stage of the pipeline reﬁnes the catadiop-

tric model with a RANSAC approach we have deve-

loped (Algorithm 1). The algorithm takes as input the

initial catadioptric model C

estimated from the lim-

bus circle projections in the second stage of the pi-

peline; the set of features F

and F

detected in the

left and right corneal reﬂections in the third stage of

the pipeline; and the number of RANSAC iterations k

over which to reﬁne the catadioptric model.

An initial matching of features M

is computed

(line 1) with an all-pairs approach that considers each

feature f

in F

and matches it to the F

feature with

the smallest distance to f

. However, in the case of

scenes with repetitive texture, a feature could have se-

veral matches with similar quality, which can lead to

matching ambiguity. We reject such features using the

ratio test (Lowe, 1999), which only keeps a feature if

its second best match is signiﬁcantly worse.

Based on this initial matching M

, each iteration

i of the RANSAC approach computes a possible reﬁ-

ned catadioptric model C

, and retains the best reﬁne-

ment (lines 2-10). The reﬁned model C

is computed

Figure 8: Detected features (green) and reprojected features

(red). The average reprojection error is 0.54 pixels.

with a bundle adjustment approach from a set of six

correspondences hex

that are drawn at random from

(line 3). The bundle adjustment uses a trust-region

optimization (Conn et al., 2000) to ﬁnd the two cor-

neal centers C

and C

(2×3 = 6 parameters), and the

3D positions P

of the six scene features (6 × 3 = 18

parameters). The optimization minimizes the sum of

correspondence reprojection errors. For correspon-

dence ( f

L j

, f

R j

) the reprojection error is:



π (C

, P

) − f



π (C

, P

) − f



, (2)

where π is the projection function of the corneal

catadioptric system (Section 3.2). An initial guess

of a feature’s 3D position P

is computed by trian-

gulation, as the midpoint of the common perpendicu-

lar segment of the two reﬂected rays at f

L j

and f

R j

The six correspondences are sufﬁcient to determine

the 6 + 18 = 24 parameters, since each of the six cor-

respondences contributes two 2D corneal projection

equations, for a total of four scalar equations:

π(C

, P

)

= f

, π(C

, P

)

= f

π(C

, P

)

= f

, π(C

, P

)

= f

(3)

Then, using the model C

, the correspondences in

are partitioned in inlier and outlier corresponden-

ces (lines 5-8). A correspondence is considered an in-

lier if its reprojection error e

i j

(Equation 2) is smaller

than a threshold ε. Inlier correspondences are coun-

ted by n

, and are collected in set M

. The model C

best

with the most inlier correspondences is found over all

k RANSAC iterations (lines 9-10). In a last step, C

best

is reﬁned over all inlier correspondences M with the

bundle adjustment procedure described above for line

4), to generate the ﬁnal catadioptric model C. The

catadioptric model reﬁnement reduces the average re-

projection error to subpixel levels (Figure 8).

In conventional structure from motion, bundle ad-

justment is used over multiple frames, which results

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

678

Figure 9: Correspondence search on epipolar curve (top),

and rotation of corresponding patches (bottom).

in a large but sparse feature correspondence matrix.

This sparsity is exploited by speciﬁc optimization

methods (e.g. Sparse Bundle Adjustment based on

Levenberg-Marquardt (Lourakis and Argyros, 2009)).

In our case, we only rely on the two images provided

by the two corneal reﬂections, so our correspondence

matrix is always full and small, hence our choice of

the trust-region optimization.

4.5 Dense Stereo

The catadioptric model reﬁnement stage produces

a sparse reconstruction of scene geometry by com-

puting the 3D positions of corresponding features.

Scene reconstruction ﬁdelity is increased in a ﬁnal

stage that attempts to compute a correspondence, and

thereby a 3D point, for each corneal reﬂection pixel.

For every pixel in the left corneal reﬂection we search

for a correspondence p

in the right corneal reﬂection

along p

s epipolar curve (Figure 9, top). The epi-

polar curve (blue) is truncated to a short arc (red) ba-

sed on a depth range estimate inferred from the sparse

reconstruction. The smaller search space accelerates

correspondence ﬁnding, and increases robustness by

removing from consideration parts of the image with

similar texture.

Given a candidate corresponding point p

on the

epipolar curve, the matching error E(p

, p

) is the

sum of squared color differences between square pat-

ches R

and R

centered at p

and p

in the left and

right reﬂections:

E(p

, p

) =

∑

⊂R

) − R

(F(p

))

. (4)

Whereas in standard stereo conﬁguration the map-

ping F from R

to R

can be approximated with the

identity, in our case there is signiﬁcant rotation be-

tween R

and R

. We use a mapping that rotates

each patch to become aligned with the epipolar curve

tangent (Figure 9, bottom).

Figure 10: Experiment setup.

5 RESULTS AND DISCUSSION

Figure 10 shows our experimental setup. All the pic-

tures were taken with a Canon E70D camera, which

has a resolution of 5,472 x 3,648, and with a 135 mm

lens. Aperture, ISO and shutter time were chosen to

best capture the corneal reﬂections. Focus bracketing

was used to obtain sharp corneal reﬂections, which

is also aided by the fact that the reﬂection in a small

convex surface is ”shallow”, forming close to the re-

ﬂective surface, and focusing close to the surface will

capture the entire reﬂection in focus, even for a small

depth of ﬁeld. We have tested our pipeline on se-

veral scenes: Checkerboard (Figure 6), Toys (Figure

1), Presents (Figure 11), and Workbench (Figure 12).

5.1 Quality

The automatically detected ellipse has an average

Hausdorff distance of 1.51 pixels to a truth ellipse ﬁt-

ted through manually chosen points (Rockafellar and

Wets, 2009).

We extract features with OpenCV’s FAST feature

detector (Rosten and Drummond, 2006). The initial

feature matching (line 1 in Algorithm 1) has a low

outlier rate, e.g. 8 out of 106 for the Toys scene. Con-

sequently, a small number of RANSAC iterations (i.e.

k = 10) are sufﬁcient to converge to an accurate cata-

dioptric model since the randomly selected sets of six

correspondences are unlikely to contain outliers. The

reﬁnement stage reduces the average reprojection er-

ror (Equation 2) substantially, as shown in Table 1.

For the Workbench scene the limbus is heavily occlu-

ded in the input image, so limbus detection is approx-

imate, which leads to a coarse initial calibration. Ho-

wever, even for this case, model reﬁnement conver-

ges, reducing the reprojection error below one pixel.

For the Checkerboard scene, the average out of

plane displacement for the 144 3D points recovered at

the 12×12 checker corners is 7.3 mm. For the dense-

stereo reconstructed points, the average out of plane

Subpixel Catadioptric Modeling of High Resolution Corneal Reﬂections

679

Table 1: Reprojection errors [pixel].

Initial Reﬁned

Checkerboard 2.44 0.16

Toys 7.93 0.54

Presents 13.88 0.57

Workbench 62.26 0.58

Figure 11: Presents scene: reﬂection, and reconstruction

aligned with truth geometry (grey points), for comparison.

displacement is also 7.3 mm. The length of the recon-

structed diagonal of the checkerboard is 0.61 m, whe-

reas the true diagonal is 0.59 m, which corresponds

to a 2.7% error. For a qualitative assessment of our

depth maps, we scanned the Toys and the Presents

scenes with a depth camera (i.e. a Structure sensor).

The truth geometry aligns with the geometry recon-

structed from corneal reﬂections (Figures 1c and 11).

For the Presents scene we ﬁtted planes to the box fa-

ces, with an average error of 15.3 mm. The normals

of parallel faces had an average angle error of 6.2

◦

5.2 Speed

We measured performance on an Intel(R) Core(TM)

i5-7600K 3.8GHz workstation. The running times of

each stage of our pipeline are given in Table 2. For

eye region extraction, we use the Haar cascade classi-

ﬁer provided in OpenCV. A minimum eye region size

is set to avoid false detections. For the limbus de-

tection in the initial calibration, we start the search at

the center of the eye region. The bulk of the limbus

detection time goes to downsampling the image. The

dense stereo stage is by far the slowest, but also the

best candidate for parallelization.

5.3 Error Analysis

Like any depth from stereo system, our depth accu-

racy depends on the baseline, on the image resolu-

tion, and on the correspondence detection error. There

isn’t much ﬂexibility for the baseline, which is ﬁxed

to the interpupillary distance. In terms of resolution,

we use one of the off-the-shelf highest resolution ca-

meras. Due to the high curvature of the corneal sp-

Figure 12: Workbench scene: reﬂection and reconstruction.

Table 2: Typical running times for our pipeline.

Pipeline stage Time [ms]

Eye region extraction 53

Initial calibration 82

Feature extraction 50

Calibration reﬁnement (Algorithm 1)

Initial feature matching (line 1) 2

RANSAC iterations (lines 2-10) 20

Final bundle adjustment (line 11) 1,053

Dense Stereo 287,327

here, correspondence detection errors result in larger

depth errors than in the case of conventional stereo,

as reﬂected rays are more divergent. The detection

error is commensurate to the feature reprojection er-

ror, which in our experiments is consistently below

one pixel. For our system, a one pixel detection er-

ror translates to an average depth error of 20 mm at

0.5m. This error is larger closer to the limbus circle,

where reﬂected rays are more divergent.

We use a catadioptric model that assumes known

and equal limbus circle radii. The limbus circle radius

is only used in the initial calibration stage, which pro-

vides an initial guess for the model reﬁnement stage.

In all our experiments this initial guess was good

enough for the model reﬁnement stage to converge,

which indicates that one can safely use the known and

equal limbus circle radii assumption. Our catadioptric

model also assumes that the corneal surfaces are sp-

herical, and that the corneal sphere radii are known

and equal. We have investigated the reconstruction

error sensitivity to deviations from these two assump-

tions analytically. The reconstruction error is compu-

ted for a 3D point P at a typical distance from the eyes

of 0.5 m. The projections p

and p

of P in the cor-

neal reﬂections are computed with our ideal catadiop-

tric model C . Then, for a given imperfect catadioptric

model C

, we compute a deviated position P

of P as

follows. First, the camera rays at p

and p

are re-

ﬂected according to C

, and then the reﬂected rays are

triangulated to obtain P

. The reconstruction error is

deﬁned as the Euclidean distance between P and P

Figure 13 shows the reconstruction error depen-

dence on cornea eccentricity and on left/right eye

asymmetry. The same 0 to 0.2 range is used for both

independent variables. Cornea eccentricity is mo-

deled by assuming the true cornea is in fact an ellip-

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

680

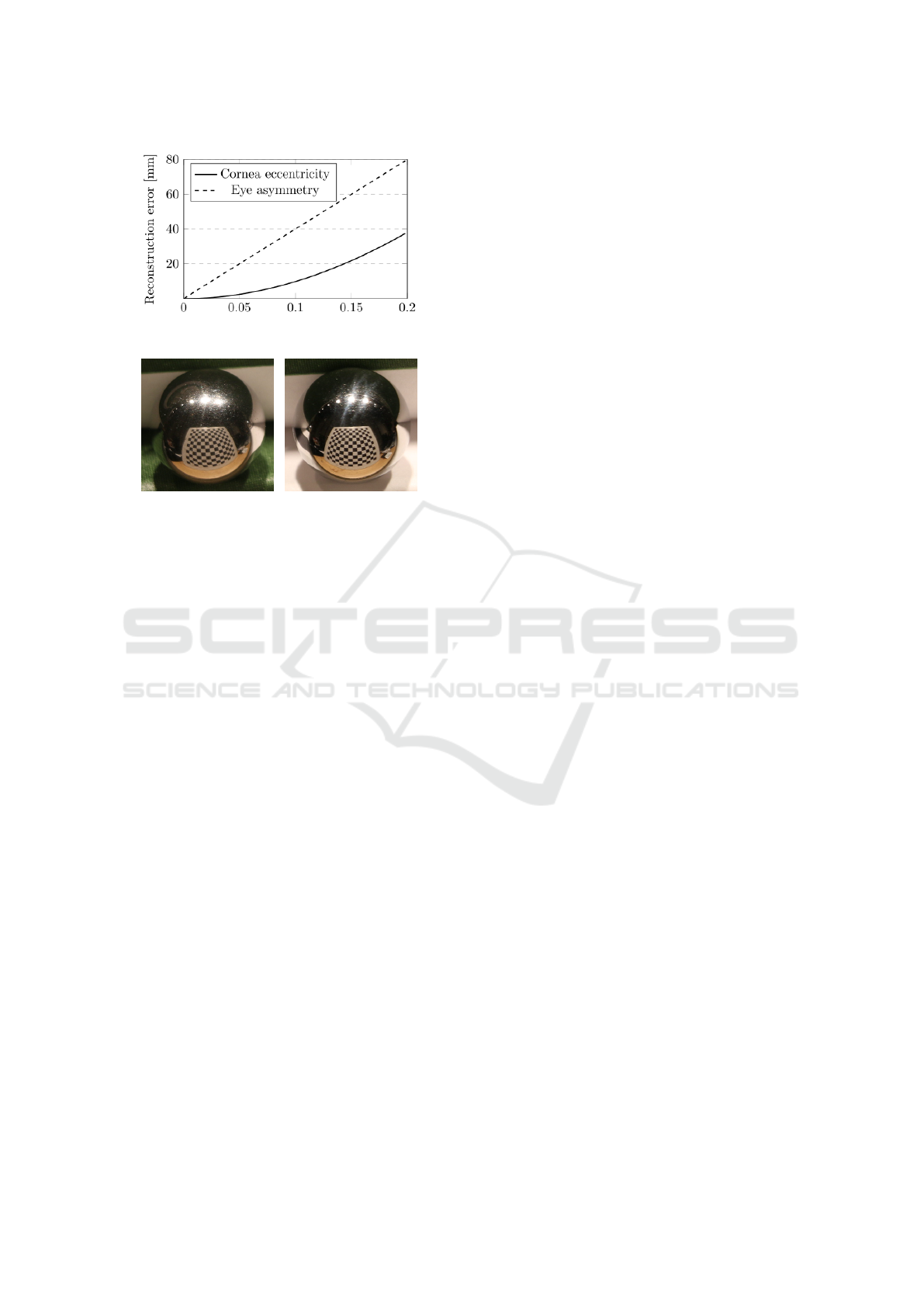
Figure 13: Reconstruction error analysis.

Figure 14: Steel ball catadioptric system, for comparison.

soid. For an eccentricity of 0.2, which corresponds

to a small/large ellipse axis ratio of 0.98, the recon-

struction error is 38 mm. The eye asymmetry is quan-

tiﬁed as the ratio of the radii of the left and right eye

corneal spheres. For an eye asymmetry of 10%, the

error is 40 mm. This analysis indicates that the recon-

struction error is quite sensitive to these two parame-

ters.

In our anatomy research review we did not ﬁnd

a human population range for these parameters. We

experimented with extending our bundle adjustment

to optimize for eye asymmetry as well, but the repro-

jection errors did not decrease signiﬁcantly. Further-

more, we have also investigated the validity of our as-

sumptions empirically, by reconstructing our scenes

from reﬂections captured from two high-grade steel

bearing balls of similar size to the human corneal sp-

heres (Figure 14). The bearing balls are truly spher-

ical and of equal size, so the bearing balls catadiop-

tric system satisﬁes all our assumptions. The recon-

structed scene accuracy was comparable to the recon-

structions from corneal reﬂections for the Checkerbo-

ard scene, which indicates indirectly that our corneal

catadioptric system assumptions are valid.

6 CONCLUSIONS AND FUTURE

WORK

We described a pipeline for extracting 3D scene struc-

ture from high resolution corneal reﬂections. The sy-

stem ﬁrst calibrates the position of the eyes with re-

spect to the camera with subpixel accuracy, and then

uses the resulting catadioptric model to triangulate

corresponding corneal reﬂection features and pixels.

One limitation of the system stems from the as-

sumption that the input image provides a perfect cor-

neal reﬂection. Future work should take into account

the iris texture, which is a considerable source of

noise for light colored eyes. Methods for separating

the local from the global illumination (Nayar et al.,

2006) could be used to this effect. Another limita-

tion of the current pipeline implementation is that the

dense stereo stage relies on a naive patch color mat-

ching algorithm, which reduces the quality of the 3D

scene reconstruction. Our paper contributes a sub-

pixel accurate calibration of the corneal catadioptric

imaging system, which can be readily used with more

sophisticated stereo matching algorithms, such as for

example those that exploit scene geometry coherence

(Ohta and Kanade, 1985), (Sun et al., 2003), (Schar-

stein and Szeliski, 2002).

Another direction of future work is to accelerate

the pipeline to interactive performance, which allows

accumulating scene 3D structure over several frames,

or even from a video stream. A ﬁrst step is to imple-

ment the dense stereo stage on a GPU. For a stationary

camera, the 3D points contributed by each frame are

already in a common coordinate system and can be

readily merged, without alignment.

Future work to extend our method beyond the lab

setting is challenging. Our work already reduces the

calibration error of the catadioptric system below one

pixel, which is an order of magnitude improvement

over prior art. But the inherent limitation that pre-

vents the reconstruction of scenes outside the lab is

the large distance from the eyes to the scene, relative

to the interpupillary distance and to the corneal re-

ﬂection pixel resolution. Indeed, even for a 0.1 pixel

reprojection error, which is the standard for the cali-

bration error of simple optical systems with one ca-

mera, corneal reﬂection reconstructions will incur er-

rors of 6.33, 25.3, and 602mm at scene distances of 1,

2, and 10m, for a 5,472 x 3,648 resolution camera pla-

ced at 0.5m from the eyes. Our corneal catadioptric

system calibration and scene reconstruction pipeline

already achieves the best results afforded by the cur-

rent resolution of commercial digital cameras, further

improvements will have to come from increasing the

resolution of the corneal reﬂections.

Although images now have sufﬁcient resolution

for direct display, giving the user the option to zoom

in on regions of interest, such as faces, and extracting

scene information from corneal and other fortuitous

reﬂections will continue to beneﬁt from further incre-

ases of image resolution. Many of these applications

Subpixel Catadioptric Modeling of High Resolution Corneal Reﬂections

681

do not require high resolution throughout the image,

and a promising direction of future work in imaging

system design is to achieve a variable resolution over

the ﬁeld of view. Although consumer-level devices,

such as phones, now have multiple cameras with vari-

ous focal lengths, achieving a high resolution at appli-

cation speciﬁed locations in the ﬁeld of view remains

intractable. A more promising approach is to rely on

a high resolution sensor with a wide angle lens and

to read and save only the pixels needed, resulting in a

versatile imaging system that helps leveraging secon-

dary rays for scene acquisition.

REFERENCES

Agrawal, A., Taguchi, Y., and Ramalingam, S. (2010).

Analytical forward projection for axial non-central di-

optric and catadioptric cameras. Computer Vision–

ECCV 2010, pages 129–143.

Agrawal, A., Taguchi, Y., and Ramalingam, S. (2011).

Beyond alhazen’s problem: Analytical projection mo-

del for non-central catadioptric cameras with quadric

mirrors. In Computer Vision and Pattern Recogni-

tion (CVPR), 2011 IEEE Conference on, pages 2993–

3000. IEEE.

Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:

Speeded up robust features. In European conference

on computer vision, pages 404–417. Springer.

Calonder, M., Lepetit, V., Strecha, C., and Fua, P. (2010).

Brief: Binary robust independent elementary featu-

res. In European conference on computer vision, pa-

ges 778–792. Springer.

Conn, A. R., Gould, N. I., and Toint, P. L. (2000). Trust

region methods. SIAM.

Debevec, P. (2008). Rendering synthetic objects into real

scenes: Bridging traditional and image-based graphics

with global illumination and high dynamic range pho-

tography. In ACM SIGGRAPH 2008 classes, page 32.

ACM.

Dodgson, N. A. (2004). Variation and extrema of human in-

terpupillary distance. In Electronic imaging 2004, pa-

ges 36–46. International Society for Optics and Pho-

tonics.

Eberly, D. (2008). Computing a point of reﬂection on a

sphere.

Fasano, A., Callieri, M., Cignoni, P., and Scopigno, R.

(2003). Exploiting mirrors for laser stripe 3d scan-

ning. In 3-D Digital Imaging and Modeling, 2003.

3DIM 2003. Proceedings. Fourth International Con-

ference on, pages 243–250. IEEE.

Jenkins, R. and Kerr, C. (2013). Identiﬁable images of by-

standers extracted from corneal reﬂections. PloS one,

8(12):e83325.

Kassner, M., Patera, W., and Bulling, A. (2014). Pupil: an

open source platform for pervasive eye tracking and

mobile gaze-based interaction. In Proceedings of the

2014 ACM international joint conference on perva-

sive and ubiquitous computing: Adjunct publication,

pages 1151–1160. ACM.

Kuthirummal, S. and Nayar, S. K. (2006). Multiview ra-

dial catadioptric imaging for scene capture. In ACM

Transactions on Graphics (TOG), volume 25, pages

916–923. ACM.

Lienhart, R. and Maydt, J. (2002). An extended set of haar-

like features for rapid object detection. In Image Pro-

cessing. 2002. Proceedings. 2002 International Con-

ference on, volume 1, pages I–I. IEEE.

Lourakis, M. A. and Argyros, A. (2009). SBA: A Software

Package for Generic Sparse Bundle Adjustment. ACM

Trans. Math. Software, 36(1):1–30.

Lowe, D. G. (1999). Object recognition from local scale-

invariant features. In Computer vision, 1999. The pro-

ceedings of the seventh IEEE international conference

on, volume 2, pages 1150–1157. Ieee.

Mashige, K. (2013). A review of corneal diameter, curva-

ture and thickness values and inﬂuencing factors. Afri-

can Vision and Eye Health, 72(4):185–194.

Nayar, S. K. (1997). Catadioptric omnidirectional camera.

In Computer Vision and Pattern Recognition, 1997.

Proceedings., 1997 IEEE Computer Society Confe-

rence on, pages 482–488. IEEE.

Nayar, S. K., Krishnan, G., Grossberg, M. D., and Raskar,

R. (2006). Fast separation of direct and global com-

ponents of a scene using high frequency illumination.

In ACM Transactions on Graphics (TOG), volume 25,

pages 935–944. ACM.

Nishino, K. and Nayar, S. K. (2004). The world in an eye

[eye image interpretation]. In Computer Vision and

Pattern Recognition, 2004. CVPR 2004. Proceedings

of the 2004 IEEE Computer Society Conference on,

volume 1, pages I–I. IEEE.

Nishino, K. and Nayar, S. K. (2006). Corneal imaging sy-

stem: Environment from eyes. International Journal

of Computer Vision, 70(1):23–40.

Nitschke, C. and Nakazawa, A. (2012). Super-resolution

from corneal images. In BMVC, pages 1–12.

Nitschke, C., Nakazawa, A., and Takemura, H. (2011a).

Display-camera calibration using eye reﬂections and

geometry constraints. Computer Vision and Image

Understanding, 115(6):835–853.

Nitschke, C., Nakazawa, A., and Takemura, H. (2011b).

Image-based eye pose and reﬂection analysis for

advanced interaction techniques and scene under-

standing. Computer Vision and Image Media

(CVIM)(Doctoral Theses Session), pages 1–16.

Nitschke, C., Nakazawa, A., and Takemura, H. (2013). Cor-

neal imaging revisited: An overview of corneal re-

ﬂection analysis and applications. IPSJ Transactions

on Computer Vision and Applications, 5:1–18.

Ohta, Y. and Kanade, T. (1985). Stereo by intra-and inter-

scanline search using dynamic programming. IEEE

Transactions on pattern analysis and machine intelli-

gence, (2):139–154.

Rockafellar, R. T. and Wets, R. J.-B. (2009). Variational

analysis, volume 317. Springer Science & Business

Media.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

682

Rosten, E. and Drummond, T. (2006). Machine learning for

high-speed corner detection. In European conference

on computer vision, pages 430–443. Springer.

Scharstein, D. and Szeliski, R. (2002). A taxonomy and

evaluation of dense two-frame stereo correspondence

algorithms. International journal of computer vision,

47(1-3):7–42.

Schnieders, D., Fu, X., and Wong, K.-Y. K. (2010). Re-

construction of display and eyes from a single image.

In Computer Vision and Pattern Recognition (CVPR),

2010 IEEE Conference on, pages 1442–1449. IEEE.

Sun, J., Zheng, N.-N., and Shum, H.-Y. (2003). Stereo mat-

ching using belief propagation. IEEE Transactions on

pattern analysis and machine intelligence, 25(7):787–

800.

Viola, P. and Jones, M. (2001). Rapid object detection using

a boosted cascade of simple features. In Computer Vi-

sion and Pattern Recognition, 2001. CVPR 2001. Pro-

ceedings of the 2001 IEEE Computer Society Confe-

rence on, volume 1, pages I–I. IEEE.

Zhang, Z. (1999). Flexible camera calibration by viewing

a plane from unknown orientations. In Computer Vi-

sion, 1999. The Proceedings of the Seventh IEEE In-

ternational Conference on, volume 1, pages 666–673.

Ieee.

Subpixel Catadioptric Modeling of High Resolution Corneal Reﬂections

683