Photorealistic Reproduction with Anisotropic Reﬂection on Mobile

Devices using Densely Sampled Images

Shoichiro Mihara, Haruhisa Kato and Masaru Sugano

KDDI Research, Inc., Saitama, Japan

Keywords:

Photorealistic Reproduction, Augmented Reality, Image-based Rendering.

Abstract:

Photorealistic reproduction of real objects with complexities of geometry and optics on mobile devices has

been a long-standing challenge in augmented reality owing to the difﬁculties of modeling and rendering the

real object faithfully. Although image-based rendering, which does not require the objects to be modeled,

has been proposed, it still fails to photorealistically reproduce the object’s complete appearance containing

complex optical properties such as anisotropic reﬂection. We propose a novel system for use on mobile

devices capable of reproducing real objects photorealistically from all angles based on new view generation

using densely sampled images. In order to realize the proposed system, we developed a method of selecting the

image closest to a given camera view from densely sampled images by quantifying the similarity of two rays,

performed rigid geometric transformation to preserve the vertical direction for stable viewing, and introduced

color correction for consistency of color between the generated view and the real world. Through experiments,

we conﬁrmed that our proposed system can reproduce real objects with complex optical properties more

photorealistically compared with conventional augmented reality.

1 INTRODUCTION

Applications designed to reproduce real objects have

become widespread throughout the market, especially

applications for mobile devices. For example, in

electronic commerce, applications for mobile devices

such as IKEA Place

are available that make it pos-

sible for the appearance of items to be observed as

if they were at hand by rendering them overlaid on a

real-world background; this is based on a technique

called augmented reality. However, the appearance

of the objects reproduced by these applications is not

photorealistic because they are not rendered based on

materials faithful to the original objects.

Modern rendering techniques can be classiﬁed

into two different categories; model-based render-

ing and image-based rendering (Levoy and Hanra-

han, 1996)(Gortler et al., 1996). As for model-

based rendering, the reﬂectance properties repre-

sented by a bidirectional reﬂectance distribution func-

tion (BRDF) is necessary to render objects photore-

alistically. However, to measure anisotropic BRDF

which arises from microstructures such as a hairline

processed metal or woven fabric, an expensive mea-

suring instrument and an enormous amount of mea-

suring time are required due to the need to observe

http://www.ikea.com/gb/en/customer-service/ikea-

apps/

light reﬂected at the object surface in all directions.

Image-based rendering that does not rely on geomet-

ric representation has been proposed to reproduce real

objects or scenes by synthesizing virtual views from

arbitrary camera positions using densely sampled im-

ages from a real or virtual environment. Although

it is a technique powerful enough to reproduce high-

quality virtual views, it still fails to photorealistically

reproduce the complete appearance containing com-

plex optical properties such as anisotropic reﬂection

because it is essentially based on interpolation of dis-

cretely sampled images which can miss capturing pro-

nounced variations in anisotropic reﬂection, which is

highly sensitive to viewing direction.

In this research, we propose a novel system for

use on mobile devices that can reproduce real ob-

jects photorealistically by generating new views from

all angles using densely sampled images. Our pro-

posed system can be utilized for various applications:

for example, examining unique cultural assets or rare

minerals for educational purposes, viewing items sold

on online shopping sites, and enjoying a realistic vir-

tual world for entertainment. The proposed system

has three main advantages. First, as with image-

based rendering, it can reproduce objects photoreal-

istically without constructing a geometric represen-

tation. Second, our proposed system can be easily

implemented and run on mobile devices with meager

Mihara, S., Kato, H. and Sugano, M.

Photorealistic Reproduction with Anisotropic Reﬂection on Mobile Devices using Densely Sampled Images.

DOI: 10.5220/0007342202170227

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 217-227

ISBN: 978-989-758-354-4

217

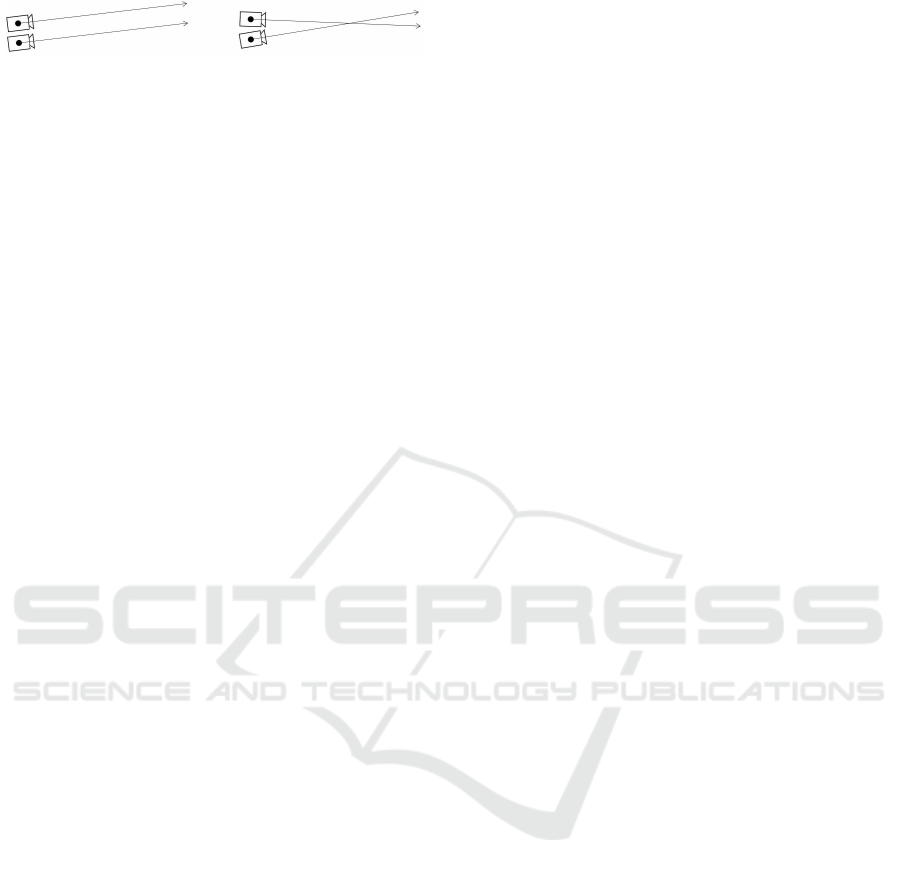
Figure 1: Problem of deﬁning the similarity of camera poses

equivalent to rays. Which one is closer to each other?

computational resources, because it depends on sim-

ple manipulation of 2D-images. Third, the direction

of generated view is not limited to object-centered di-

rection, whereas image-based rendering implicitly as-

sumes that the camera always faces objects. That is

owing to our proposed method of quantifying the sim-

ilarity of the position and orientation of the cameras

(referred to as camera poses). It is problematic to de-

ﬁne the similarity of camera poses due to differences

in unit and range, which is equivalent to deﬁning the

similarity of two rays as shown in Fig. 1. Because this

problem has not been sufﬁciently studied to date, we

address it in this research.

In order to realize the proposed system, we sug-

gest several methods described in following contribu-

tions and introduce the color correction method for

consistency of color between the generated view and

the real world. Our major technical contributions are:

1. We propose a novel system to be run on mobile

devices that has been designed to reproduce ob-

jects photorealistically from all angles. (Section 3)

2. We propose a unique method of selecting the im-

age closest to a given camera view from densely

sampled images by quantifying the similarity of

two rays. (Section 3.1)

3. We propose a well-designed rigid geometric trans-

formation preserving the vertical direction for sta-

ble viewing. This is achieved by performingtrans-

lation, rotation, and scaling sequentially. (Sec-

tion 3.2)

This paper explains the proposed methods and shows

how the proposed system improves the reality of

the displayed objects by conducting experiments in

which we compare the results of the proposed system

with conventional augmented reality.

2 RELATED WORK

The simplest way to measure the BRDF is using a

gonioreﬂectometer (Nicodemus et al., 1977). But a

vast amount of measurement time is required since

the BRDF is measured with all combinations of the

incident and reﬂection directions by moving the light

source and the sensors. Therefore, studies on how

to improve BRDF measurement efﬁciency have been

conducted (Mukaigawa et al., 2009)(Tunwattanapong

et al., 2013)(Ward et al., 2014). Although it becomes

possible to measure BRDF that is not spatially uni-

form in a 3D shape within a relativelyshort time, there

are still the limitations, for example, the inability to

measure translucent objects and objects with concave

surfaces.

An image-based rendering technique relies on

densely sampled images and can be classiﬁed into

two fundamentally different approaches. The ﬁrst ap-

proach is based on the concept of light ﬁeld (Levoy

and Hanrahan, 1996)(Gortler et al., 1996). It repre-

sents the light ray as a 4D function of position and

direction, constructed with densely sampled images.

Virtual views from arbitrary camera positions can be

synthesized by extracting slices from the light ﬁeld

and interpolating rays in an appropriate way. The

second approach is based on estimating the approx-

imate geometry in the form of depth maps (Shade

et al., 1998)(Sinha et al., 2012). Some sampled im-

ages are chosen based on the virtual camera position,

warped using the depth maps, and combined for new

view synthesis. An important advantage of these ap-

proaches is that they can synthesize photorealistic vir-

tual views with no or very little geometry informa-

tion and no explicit representation of optical prop-

erties of the objects. However, if their techniques

are applied to the reproduction of complex optical

properties which vary considerably depending on the

viewing angle, such as anisotropic reﬂection, undesir-

able artifacts of blurring and edge ghosting will oc-

cur. This is because image-based rendering is essen-

tially based on interpolation of discretely sampled im-

ages, even though some variants have been proposed

to increase realism of the rendered views (Wood

et al., 2000)(Shum et al., 2004)(Vagharshakyan et al.,

2015). Consequently, as we assume that target objects

have some complex optical properties as mentioned

above, we purposely do not depend on interpolation

techniques derived from image-based rendering. In-

stead we propose simple manipulation of 2D-images

which can produce acceptable results for our assumed

applications described in Section 5.

Photo-based augmented reality which reproduces

objects using densely sampled images has been pro-

posed by Ohta et al. (Ohta et al., 2012). This approach

is based on a kind of view-dependent texture map-

ping (Debevecet al., 1996). It has the same advantage

as image-based rendering which is able to reproduce

objects efﬁciently and photorealistically without a 3D

model. In addition, they proposed adding a method to

correct the difference in color tone between the sam-

pled images and the real environment (Ohta et al.,

2013). However, there is a problem that the repro-

duced objects appear to be unnatural as they do with

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

218

Figure 2: Conceptual diagram of the proposed system.

conventional augmented reality because only the ob-

ject image is superimposed on the background of the

real environment and global illumination effects like

shadowing and interreﬂection between the object and

the surroundings cannot be reproduced.

Meanwhile, Suzuki et al. proposed a substitutional

reality that convinces the user that he/she is perceiv-

ing a live reality instead of another reality (or past re-

ality) by showing the user a movie taken in the past

without the user noticing a reality gap (Suzuki et al.,

2012). By switching between the real-world video ob-

tained from the camera mounted on the HMD worn

by the user and the video recorded at the same place

in the past alternately without the user being aware

of it, there arises a state in which the user mistak-

enly perceives the recorded video as the real world.

The limitation of their system is that the user’s view-

point must be ﬁxed at the place where the video was

recorded. Although their research aimed at psycho-

logically verifying the concept of substitutional real-

ity, it is also applicable to augmented reality in that it

employs a phenomenon whereby past images are per-

ceived as the live reality, and our proposed system is

inspired by substitutional reality.

We propose a novel system so that the reproduced

objects are perceived as if they exist in front of the

eyes, and which performs object reproduction by sub-

stituting the image generated with densely sampled

images without estimating the explicit geometry of

the scene and BRDF of the target object.

3 PROPOSED SYSTEM

A conceptual diagram of the proposed system is

shown in Fig. 2. In an ofﬂine process, a collection

of images is sampled from all angles so that the ob-

ject to be reproduced (hereinafter referred to as the

target object) and the marker within the angle of view

are saved in the storage space along with the pose in-

formation, which is described in the next section. In

the online process, the user holds the mobile device

in front of his/her face, shoots the marker with the

camera mounted on the device, and views the image

displayed on the screen from various angles. First, the

camera pose relative to the world coordinate system is

estimated based on the marker designed as described

in Section 3.3, the similarities of the pose information

between of the camera view and of every sampled im-

age are evaluated, and the sampled image correspond-

ing to the most similar pose is selected. Then, the

selected image undergoes rigid geometric transforma-

tion so that it can be seen from the camera pose. In the

color correction process, the difference in color tone

between the sampled images and the camera view is

corrected, and the processed image is displayed on

the screen of the device. Details of each process are

described below.

3.1 Image Selection by Quantifying a

Similarity of Camera Poses

In this section, we explain how to select the sam-

pled image based on the similarity of the camera

pose. Conventional image-based rendering assumes

that possible views face the object center and sam-

pled images are selected based on only the distance

between viewpoints, ignoring the direction of view.

However, our system is designed to be used on mo-

bile devices where the viewpoints and directions can

be easily changed. Therefore, our proposed method

should be able to select a correct image from the sam-

ple collection that matches the given camera pose in-

cluding the direction of view.

Coordinate transformations between the world co-

ordinate (X,Y, Z) and the camera coordinate (x, y, z)

are denoted as

[xyz]

= R [X Y Z]

+ t , (1)

where t is the translation vector and R is the rotation

matrix (Tsai, 1987). If we evaluate the similarity of

the camera poses as the collective difference of ts and

Rs, it is necessary to perform weighting to correct the

gap between the unit and range of these parameters.

However, appropriate weight depends on the scale of

t which can change during operation. Therefore, we

propose a method to quantify the similarity of camera

poses by expressing them as a six-dimensional quan-

tity representing the camera view ray.

First, the position of the target object in the

world coordinate system is deﬁned as the target point

tar

, Z

) by the user. Then, the foot of the per-

pendicular from the target point P

tar

to the visual line

extending from the camera viewpoint P

cam

, Z

)

is deﬁned as the gaze point P

gaz

, Z

) as shown

in Fig. 3(a). When the translational vector t and rota-

tion matrix R of the camera are estimated, the coor-

Photorealistic Reproduction with Anisotropic Reﬂection on Mobile Devices using Densely Sampled Images

219

Figure 3: Conceptual diagram to explain how to deﬁne the

similarity of camera poses: (a) deﬁnition of object point and

gaze point; (b) penalty deﬁnition for evaluating similarity of

camera poses.

dinates of viewpoint P

cam

and gaze point P

gaz

can be

obtained from the following equations.

]

= −R

t , (2)





= [X

]

+ e

R [X

]

e ,

(3)

where [X

]

= [X

− X

−Y

− Z

]

and e

is a unit vector of the visual line on the camera coor-

dinate system. Finally, the camera pose can be repre-

sented by combining (X

, Z

) and (X

, Z

) into

a six-dimensional quantity, deﬁned as visual line seg-

ment E:

E ≡ (X

, Z

, X

, Z

) . (4)

The penalty of camera pose similarity is quanti-

ﬁed by the Euclidean distance between E, which rep-

resents certain camera pose, and E

′

, which represents

another pose, as shown in Fig. 3(b). In the proposed

system, sampled images and visual line segments E

′

are stored in a storage space (i is an index of stored

images), and the index i

min

(t) of the visual line seg-

ment which most closely resembles the visual line

segment of the user camera E(t) is calculated at each

time t by

min

(t) = arg min

kE(t) − E

′

. (5)

When the penalty is small, the viewpoint and the

direction of the visual line approach one another and

the overlapping of the imaging ranges of the cameras

becomes larger. The remaining gap between views

corresponding to E(t) and E

′

min

(t)

is corrected by ge-

ometric transformation described in the next section.

3.2 Generation of Displayed Image by

Geometric Transformation

Because the sampled images are captured from dis-

crete camera poses, translation and orientation of the

image (referred to as image pose) selected by equa-

tion (5) may be different from the image pose of the

camera. In order to generate the new view, rigid ge-

ometric transformation is performed on the selected

image to correct the difference of image pose. In this

section, we propose a method of sequential similar-

ity transformation that can convert the image pose in

more stable condition while maintaining the object

shape.

3.2.1 Homography Transformation

As a naive method, homography transformation can

be performed to match the marker planes in the se-

lected image and the camera image to match their im-

age pose. However, when homography transforma-

tion between the planes is performed, the shape of the

three-dimensional object is deformed. This is not ac-

ceptable for the proposed system.

3.2.2 Similarity Transformation

To generate displayed images while maintaining the

object shape, similarity transformation can be used as

a naive method. Similarity transformations between

the image coordinates (x, y) and (x

′

, y

′

) are denoted

by the following equation.











scosθ −ssinθ t

ssinθ scosθ t







′





, (6)

where θ is the rotation angle, [t

]

is the translation

vector and s is the scale transformation in the image

plane. By using coordinates of corresponding points

based on the marker within the sampled image and

the camera view, the similarity transformation matrix

is estimated by the least squares method. However,

when the camera pose changes over time, all param-

eters of the matrix may ﬂuctuate due to the estima-

tion error. Therefore, the view generated by similar-

ity transformation may make the image pose unstable,

givingthe user an unnatural impression. This problem

can be solved by sequential similarity transformation

as described below.

3.2.3 Sequential Similarity Transformation

Because the generated view of the proposed system is

viewed as if it is captured by the device’s camera, the

scale value s cannot be distinguished from the zoom

operation. To make the best use of this feature, we

propose a method of sequential similarity transforma-

tion to stabilize the image pose of the generated view

by removing the error ﬂuctuation from the rotation

angle θ and the translation vector [t

]

and allow-

ing the error only on the scale value s, which can be

temporally smoothed.

First, the world landmark vector u

wld

is deﬁned

as shown in Fig. 4 (how to deﬁne it is described at

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

220

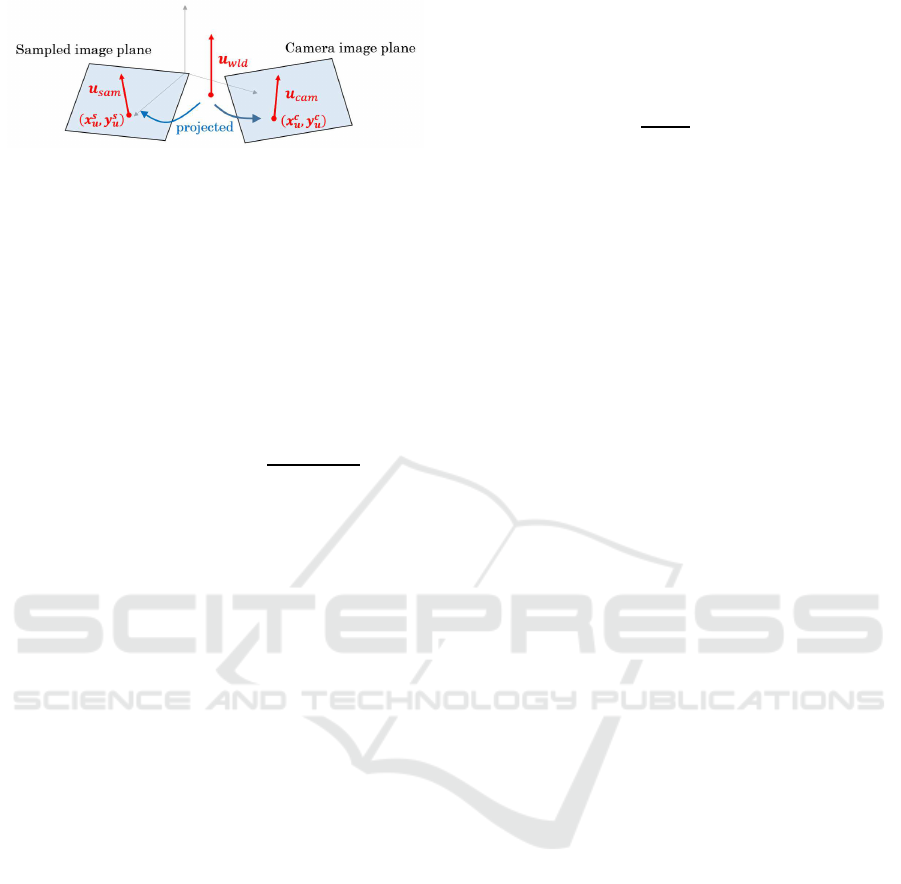
Figure 4: Conceptual diagram of world landmark vector and

projection to image planes (Note that the image planes are

actually closer).

the end of this section). Then, the vector u

wld

is pro-

jected to the camera image plane and the sampled im-

age plane, and let the projected vectors be u

cam

and

sam

respectively. The vector from the initial point

, y

) of u

sam

to the initial point (x

, y

) of u

cam

deﬁned as translation vector t

and the angle θ

be-

tween u

cam

and u

sam

are calculated:

= [x

]

− [x

]

, (7)

= sgn(u

sam

× u

cam

)arccos(

sam

· u

cam

sam

||u

cam

) , (8)

where the counterclockwise direction is positive.

Second, the sampled image is transformed se-

quentially with the translation vector t

, then rotation

is performed with the angle θ

around the initial point

, y

) of u

cam

. Rotation matrix R

is obtained by



cosθ

−sinθ

(1− cosθ

) + y

sinθ

cosθ

−x

sinθ

+ y

(1− cosθ

)



(9)

The scale value s

is estimated by the least squares

method, which matches the scale of the sampled im-

age to the camera view. Denoting the coordinates of

the corresponding point group based on the marker

within the camera image and the sampled image as

, y

) and (x

, y

) respectively, the scale value ﬁt-

ting (x

, y

) and the point group obtained by translat-

ing and rotating (x

, y

) using t

and R

is expressed

by the following equation



− x

− y



= s



























−











(10)

Let b

and A

be the matrices composed of the verti-

cal vectors of the left and right side of equation (10)

of all the corresponding points respectively, the scale

value s

is calculated by the least squares method as

= (A

)

−1

. (11)

As mentioned above, the magnitude of the error of

cannot be distinguished from the zoom operation.

Hence, when the system runs over time, it is reason-

able to smooth s

(t) with parameter M to suppress the

ﬂuctuation of the scale of the displayed image by cal-

culating

¯s

(t) =

M + 1

∑

k=t−M

(k) . (12)

Finally, the new view is generated by translating,

rotating, and scaling the selected sampled image se-

quentially with t

, R

and ¯s

. Additionally, we can

clip an appropriately sized central area from the gen-

erated view since there is an unmapped area at the

edge of it.

Next, how to deﬁne the world landmark vector

wld

is described below. Although u

wld

can be de-

ﬁned as an arbitrary vector, a vector within the imag-

ing range of the camera image and the sampled im-

age is appropriate because sequential similarity trans-

formation is based on the position and orientation of

wld

projected onto both images. Furthermore, since

the proposed system assumes the target object is sta-

tionary, the object should seem to be stationary, or

standing upright. Because humans perceive some-

thing as upright if it is consistent with the direction

of gravity (Rock, 1974), it is expected that the object

would appear to be upright if the direction of gravity

in the generated view is aligned with the direction in

the camera view that is the actual direction of gravity.

Therefore, we deﬁne u

wld

as a vector parallel to the

direction of gravity, where the initial point is camera’s

gaze point P

gaz

3.3 Correction of Color Tone

Our proposed system generates new views entirely

from densely sampled images. Consequently, if the

illumination environment is different from that when

the sampled images were captured, the color tone of

the sampled images may appear unnatural. In or-

der to make the color tone of the generated views

compatible with the actual illumination, we introduce

the color correction method proposed by Reinhard et

al. (Reinhard et al., 2001). They matched the color

tone between images not by estimating ambient light

but by adjusting the statistical values (average and

standard deviation) of each color channel after con-

verting RGB color into lαβ color space (Ruderman

et al., 1998) that has a low correlation with each chan-

nel. Although colors under actual illumination are not

completely reproduced, we can take advantage of the

simplicity and effectiveness of their method.

In order to introduce the color correction method

into the proposed system, we use a colored marker

board as shown in Fig. 5. The marker group is gener-

ated by ArUco (Garrido-Jurado et al., 2014) and each

Photorealistic Reproduction with Anisotropic Reﬂection on Mobile Devices using Densely Sampled Images

221

Figure 5: Colored marker board of the proposed system.

marker is painted arbitrarily with one of the RGB col-

ors of red(192, 0, 0), green(0, 192, 0), blue(0, 0, 192),

or yellow(128, 128, 0). Considering that the α and

β channels correspond to the complementary color

axes of yellow-blue and red-green respectively, the

marker’s colors are adjusted to ensure that the stan-

dard deviation of each channel is not too small and is

detectable by ArUco. The proposed system assumes

that the user looks at the generated view while captur-

ing the marker board of Fig. 5 and at least part of the

marker is within the angle of view of every sampled

image. Therefore, some of the same markers of the

colored marker board can be detected and identiﬁed

by ArUco in the selected image and the camera im-

age. Then, by matching the statistical values of lαβ

channels obtained from the pixel values in the color

reference area that is the internal area of the markers

identiﬁed in both the sampled image and the camera

image, it is possible to make the color tone of the gen-

erated view compatible with the actual illumination

environment.

Although we use the square ﬁducial marker in this

paper, we can also use any 2D images which have fea-

tures detectable with any well-known keypoint detec-

tor and descriptor (Rublee et al., 2011)(Alcantarilla

et al., 2013) as long as the color distribution of the im-

age is not too small such as that of a black-and-white

image. By dividing the image into several identiﬁ-

able areas corresponding to each of the markers, we

can perform color correction in the same manner as

described above.

4 EXPERIMENTS

Using computer graphics simulation and a prototype

system, we conducted several experiments to validate

the effectiveness of the proposed system. We com-

pared the shape of the object in the virtual views gen-

erated by naive transformation and sequential simi-

larity transformation using computer graphics (Sec-

tion 4.1). Color correction is veriﬁed by application to

real images having several color tones (Section 4.2).

We then demonstrate that the proposed system can re-

produce the objects with anisotropic reﬂection or mi-

crostructures (Section 4.3). We conducted a subjec-

tive experiment to validate the capability of the pro-

Figure 6: Settings of evaluation experiment of sequential

similarity transformation: (a) example of sampled images;

(b) camera settings for generating the sampled images us-

ing computer graphics; (c) example of silhouette S, S

and

silhouette error S

visualized as a binary image.

posed system to reproduce objects naturally and pho-

torealistically compared to conventional augmented

reality.

4.1 Evaluation of Sequential Similarity

Transformation

In order to verify how the shape of objects is dis-

played by sequential similarity transformation com-

pared with the other naive transformations, we con-

ducted the simulation experiment using computer

graphics. The sampled images are generated using

POV-Ray

, in which a solid primitive object, i.e., a

cuboid, cone, or sphere, is put on the colored marker

board and rendered with the camera settings as shown

in Fig. 6(a)(b). The gaze point is ﬁxed at the cen-

ter of the marker board, distance to the gaze point is

ﬁxed at d (= 6.0 in our experiment), the depression

angle φ is ﬁxed at 30

◦

(actually, we incremented φ

by 10

◦

from 20

◦

to 70

◦

, but no different trend was

found in the results so we mention only 30

◦

for the

sake of simplicity), and the azimuth angle ψ is incre-

mented by 10

◦

. Then, 360 camera images are gen-

erated by rendering only the marker board with the

same camera settings except for the azimuth angle ψ

that is incremented by 1

◦

. The ground truth images

are generated by rendering the primitive object onto

each camera image. Using the sampled images and

the camera images, the virtual views are generated by

the proposed system based on homography transfor-

mation, similarity transformation, and sequential sim-

ilarity transformation (hereinafter referred to as Hom-

trans., Sim-trans., and Proposed-trans., respectively).

To compare the generated views between each trans-

formation, the silhouette S of the object is extracted.

Then, we deﬁne the difference between S and the sil-

houette S

extracted from the ground truth image as

the silhouette error S

= S∪ S

− S ∩ S

, and n(S

) is

http://www.povray.org/

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

222

Figure 7: Comparison of the distribution of silhouette error

among Hom-trans., Sim-trans., and Proposed-trans.

Table 1: Average of n(S

) calculated from all views gen-

erated by Hom-trans., Sim-trans., and Proposed-trans. The

unit is pixel.

Cuboid Cone Sphere

Hom-trans. 2245.29 1471.35 1208.39

Sim-trans. 839.61 672.49 473.44

Proposed-trans. 521.71 317.58 290.59

calculated as an evaluation value that is the number of

pixels in S

. Fig. 6(c) shows an example of silhouette

S and S

, and silhouette error S

We generated the views by Hom-trans., Sim-

trans., and Proposed-trans. for all camera images and

calculated silhouette errors S

, and evaluated the re-

sults with the average of n(S

) as shown in Table 1.

It can be seen that n(S

) of Proposed-trans. is smaller

than the other transformations. Additionally, Fig. 7

shows the distribution of the silhouette error S

visu-

alized by summing up S

assumed as binary images

and normalized to a range of [0, 255]. We can see

that the distribution of Proposed-trans. is narrower

than the other transformations. From the above re-

sults, we conﬁrmed that by using Proposed-trans., the

displayed shape of an object was closest to the ground

truth and the position and orientation of the object

were maintained more stably compared with the other

transformations.

4.2 Evaluation of Color Correction

To verify how the color tones of the sampled im-

ages are converted by the color correction described

in Section 3.3, we conducted an experiment using real

images.

The colored marker board was printed on plain pa-

per and captured with the car model using a Logicool

web camera (C920) under a ﬂuorescent lamp, setting

the white balance (WB) for a color temperature of

4000K. The captured image is used as the sampled

image as shown in Fig. 8 (middle-left). The images

captured from the same camera position with WB ad-

Figure 8: Experimental conditions and the results of

color correction: (top-left) color reference area for color

correction; (top-right) camera images (used as target

color); (middle-left) sampled image (used as source im-

age); (middle-right) results of color correction; (bottom-

right) ground truth.

justed to a color temperature of 2000K and 6500K and

under a dark illumination environment where some

ﬂuorescent lamps were switched off (Fig. 8, bottom-

right) are used as ground truth. The images captur-

ing only the marker board by removing the car model

under each condition are used for the camera images

(Fig. 8, top-right). The color reference area is calcu-

lated as shown in the white area of Fig. 8 (top-left).

Then, color correction of the sampled image was per-

formed.

The results of color correction are shown in

Fig. 8 (middle-right). Comparing the camera images

with the results of color correction, it can be clearly

seen that their color tone corresponds closely. Fur-

thermore, when the results with the ground truths

are compared, we found that the color of the car

model is similar because the average color difference

in the CIELAB color space between the results and

the ground truths of each condition is (WB: 2000K)

11.2813, (WB: 6500K) 10.1238, and (dark illumina-

tion) 6.57909. Although we cannot claim that the

same color as the ground truth is reproduced because

there is a just noticeable difference in the CIELAB

color space of 2.3 (Sharma and Trussell, 1997), strict

color reproduction for user perception is outside the

scope of this paper since the generated view of the

proposed system is viewed through the display of a

mobile device with arbitrary color reproduction char-

acteristics.

4.3 Demonstration

In order to verify that the proposed system can dis-

play objects photorealistically even with anisotropic

reﬂection or microstructures that make them difﬁcult

to render using computer graphics, we implemented

Photorealistic Reproduction with Anisotropic Reﬂection on Mobile Devices using Densely Sampled Images

223

Figure 9: (Top) target objects; (bottom) sequences of the generated views of the proposed system for demonstration.

the prototype system on a PC and conducted a demon-

stration. Three objects as shown in Fig. 9 (top) are

used as targets: glass ball, stuffed hedgehog, and

hologram sheet. The target objects were placed on the

marker board, and we captured them manually from

all angles and stored the pictures as sampled images,

using a manual turntable to rotate objects and a tripod

to move the camera up and down. In our experimental

environment, the number of sampled images was re-

spectively 3741, 3442 and 3665 for each target object.

Fig. 9 (bottom) shows the sequences of the gener-

ated viewsof the proposed system (see supplementary

video for the entire sequences). Looking at the gener-

ated views of the glass ball and stuffed hedgehog, the

condensed light and the distorted background by the

glass ball can be seen naturally and the ﬂuffy stuffed

hedgehog is faithfully reproduced, but it is difﬁcult to

render with computer graphics. Also, looking at the

displayed images of the hologram sheet, we can see

how the color of the reﬂected light of the hologram

sheet changes depending on the viewing angle. Since

such anisotropic reﬂection requires considerable time

and cost for measurement (Ward et al., 2014), it is

difﬁcult to create a 3D model and reproduce it with

conventional augmented reality.

4.4 Subjective Experiment

We conducted a subjective experiment to verify

whether the proposed system could display real ob-

jects more photorealistically than conventional aug-

mented reality. The target object was the car model

shown in Fig. 10(b) and 3747 sampled images were

captured manually in advance from all angles. The

proposed system was implemented on an ASUS

smartphone (Zenfone AR: CPU Snapdragon 821,

RAM 8 GB). The selected sampled image is read

from the storage (UFS 2.0) frame-by-frame and the

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

224

Figure 10: Example of the displayed image used in the sub-

jective experiment: (a) Conventional augmented reality; (b)

Proposed system.

frame rate was 6-7 fps in this environmentwith an im-

age size of 1280x720. A conventional augmented re-

ality application was implemented using Vuforia and

Unity to render the model of the same car provided

by SQUIR

as shown in Fig. 10(a), employing the

shader of Pro Car Paint Shader

available at Unity

Asset Store to present a realistic car model.

In the experiment, 19 participants aged from 25

to 59 years, some of whom had expertise in image

processing, were asked to view the display of the pro-

posed system and the conventional augmented reality

from various angles in any way they wished, and were

then asked to give their impressions of the display by

answering a questionnaire. The questions are shown

in Fig. 11. Q1 to Q5 are about the naturalness of the

displayed image, and Q6 and Q7 ask about the reality

and the presence of the target object. The response to

each question is evaluated on a 5-grade Likert scale.

The results of the questionnaire evaluation are also

shown in Fig. 11. The Wilcoxon signed-rank test was

performed and revealed a signiﬁcant difference (p <

0.01) between groups for Q1, Q2, Q3 and Q7. From

these results, we can say that the proposed method

displays the color, reﬂection, shadow and shade more

naturally than conventional augmented reality. Fur-

thermore, the proposed method can present objects

more photorealistically than conventional augmented

reality. On the other hand, there is no signiﬁcant dif-

ference between groups for Q4 and Q5 despite the

fact that the proposed system displays the object using

planar images that have undergone geometric trans-

formation. This result supports the effectiveness of

sequential similarity transformation.

Finally, we can ﬁnd a weakly signiﬁcant differ-

ence (p = 0.07) for Q6. This can probably be at-

tributed to the frame rate of the proposed system be-

ing considerably lower than conventional augmented

reality. While conventional augmented reality renders

smoothly at about 30 fps, the proposed system gen-

erates a partially jumpy displayed image at 6-7 fps

due to processing load and discontinuity of the sam-

pled images. Even though no one commented that

https://squir.com/

https://www.assetstoresales.com/

they felt the jumpy displayed image was unnatural,

the frame rate and the jumpy displayed image are is-

sues that need to be improved.

5 DISCUSSION

There are three major limitations of our system. First,

the sampling density and uniformity may crucially af-

fect the quality of generated views, although we con-

ﬁrmed that our system can present satisfactory new

views from sampled images created simply using a

manual turntable to rotate the objects and a tripod to

move the camera up and down. To address this, we

can introduce a view interpolation technique derived

from image-based rendering, and generate densely

and uniformly sampled images on the virtual sphere

covering the entire 3D object, employing the method

described by Chen and Rosenberg (Chen and Rosen-

berg, 2018). However, one of the difﬁcult issues of

image-based rendering still remains, namely, unde-

sirable artifacts of blurring and edge ghosting. Fur-

thermore, the storage cost depends on the sampling

density (660MB in our subjective experiment) and it

is better to employ the data compression technique,

e.g. the method described by Ishigami et al. (Ishigami

et al., 2016), in practical use.

Second, if the visual marker is placed under

different lighting conditions, the highlights on the

displayed object and shadow/shade will be inconsis-

tent with the real-environment, which is an inherent

problem in sampling based methods including

image-based rendering, even though the differences

of brightness and color tone can be corrected by the

method described in Section 3.3. With that in mind,

we can provide two examples of application which

would not be affected by the above problem.

Reproduction of Cultural Assets in the Museum

In museums, the lighting environment is usually

ﬁxed, and our system can be applied effectively to

exhibit cultural assets which are held in the museum’s

storage facility. It is impossible to exhibit thousands

of stored assets because space is limited, but once

images of them being exhibited have been captured,

they can be viewed as though they were on exhibition

at any time.

Item Browsing in an Electronic Commerce

In this case, the lighting environment at the time of

viewing is fundamentally different from the one at the

time of capturing. However, users are primarily inter-

Photorealistic Reproduction with Anisotropic Reﬂection on Mobile Devices using Densely Sampled Images

225

Figure 11: Questionnaire and participant’s answers represented as a box plot and the result of statistical analysis of the

subjective experiment.

ested in the feel of the item material, and users can

view the appearance of the items naturally with our

system even if the lighting environment reproduced

on the screen is different from the user’s environment.

Third, if another object come in the view of the

camera, the augmented reality experience of the pro-

posed system may be inhibited because the user is

looking at the ofﬂine sampled views with only think-

ing that it is augmented reality. If the region of

the interrupting object are extracted from the camera

view by the detection and segmentation technique (He

et al., 2017), the object can be superimposed in the

generated view of the proposed system. However the

occlusion culling is still difﬁcult because it needs to

estimate the depth information from the single cam-

era view in real time.

6 CONCLUSIONS

In this research, we propose a novel system for use

on mobile devices capable of reproducing real ob-

jects photorealistically from all angles based on new

view generation using densely sampled images. In

order to realize the proposed system, we developed a

method of selecting the image closest to a given cam-

era view from densely sampled images by quantify-

ing the similarity of two rays, performed rigid geo-

metric transformation to preserve the vertical direc-

tion for stable viewing, and introduced color correc-

tion to maintain the consistency of color between the

generated view and the real world. We conducted

several experiments to verify the proposed methods

and conﬁrmed that these methods worked effectively.

Then, we demonstrated that the proposed system can

reproduce objects with anisotropic reﬂection or mi-

crostructures using a prototype system. Finally, we

conducted a subjective experiment and validated that

the proposed system can reproduce objects naturally

and photorealistically compared to conventional aug-

mented reality.

In future work, we will attempt to speed up the

process using the technique of approximate nearest

neighbors search and introduce image interpolation

techniques to make the displayed images smoother.

REFERENCES

Alcantarilla, P., Nuevo, J., and Bartoli, A. (2013). Fast ex-

plicit diffusion for accelerated features in nonlinear

scale spaces. In Proceedings of the British Machine

Vision Conference. BMVA Press.

Chen, C. and Rosenberg, E. S. (2018). Virtual content cre-

ation using dynamic omnidirectional texture synthe-

sis. In 2018 IEEE Conference on Virtual Reality and

3D User Interfaces (VR), pages 1–2. IEEE.

Debevec, P. E., Taylor, C. J., and Malik, J. (1996). Mod-

eling and rendering architecture from photographs:

A hybrid geometry-and image-based approach. In

Proceedings of the 23rd annual conference on Com-

puter graphics and interactive techniques, pages 11–

20. ACM.

Garrido-Jurado, S., Mu˜noz-Salinas, R., Madrid-Cuevas,

F. J., and Mar´ın-Jim´enez, M. J. (2014). Auto-

matic generation and detection of highly reliable ﬁdu-

cial markers under occlusion. Pattern Recognition,

47(6):2280–2292.

Gortler, S. J., Grzeszczuk, R., Szeliski, R., and Cohen, M. F.

(1996). The lumigraph. In Proceedings of the 23rd

annual conference on Computer graphics and inter-

active techniques, pages 43–54. ACM.

He, K., Gkioxari, G., Doll´ar, P., and Girshick, R. (2017).

Mask r-cnn. In Computer Vision (ICCV), 2017

IEEE International Conference on, pages 2980–2988.

IEEE.

Ishigami, F., Nagata, K., Ohta, M., and Yamashita, K.

(2016). Data compression for photo-based augmented

reality on a tablet. In Consumer Electronics, 2016

IEEE 5th Global Conference on, pages 1–2. IEEE.

Levoy, M. and Hanrahan, P. (1996). Light ﬁeld rendering. In

Proceedings of the 23rd annual conference on Com-

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

226

puter graphics and interactive techniques, pages 31–

42. ACM.

Mukaigawa, Y., Sumino, K., and Yagi, Y. (2009). Rapid

brdf measurement using an ellipsoidal mirror and a

projector. IPSJ Transactions on Computer Vision and

Applications, 1:21–32.

Nicodemus, F. E., Richmond, J. C., Hsia, J. J., Ginsberg,

I. W., and Limperis, T. (1977). Geometrical con-

siderations and nomenclature for reﬂectance, volume

160. US Department of Commerce, National Bureau

of Standards.

Ohta, M., Sato, T., Motokurumada, M., and Yamashita, K.

(2013). Real-time color correction for a photo-based

augmented reality system. In Consumer Electronics

(GCCE), 2013 IEEE 2nd Global Conference on, pages

102–103. IEEE.

Ohta, M., Yokomichi, R., Motokurumada, M., and Ya-

mashita, K. (2012). A photo-based augmented reality

system with html5/javascript. In Consumer Electron-

ics (GCCE), 2012 IEEE 1st Global Conference on,

pages 425–426. IEEE.

Reinhard, E., Adhikhmin, M., Gooch, B., and Shirley, P.

(2001). Color transfer between images. IEEE Com-

puter graphics and applications, 21(5):34–41.

Rock, I. (1974). The effect of retinal and phenomenal orien-

tation of the perception of form. Scientiﬁc American,

230(1):78–86.

Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.

(2011). Orb: An efﬁcient alternative to sift or surf.

In Computer Vision (ICCV), 2011 IEEE international

conference on, pages 2564–2571. IEEE.

Ruderman, D. L., Cronin, T. W., and Chiao, C.-C. (1998).

Statistics of cone responses to natural images: impli-

cations for visual coding. JOSA A, 15(8):2036–2045.

Shade, J., Gortler, S., He, L.-w., and Szeliski, R. (1998).

Layered depth images. In Proceedings of the 25th an-

nual conference on Computer graphics and interac-

tive techniques, pages 231–242. ACM.

Sharma, G. and Trussell, H. J. (1997). Digital color

imaging. IEEE Transactions on Image Processing,

6(7):901–932.

Shum, H.-Y., Sun, J., Yamazaki, S., Li, Y., and Tang, C.-K.

(2004). Pop-up light ﬁeld: An interactive image-based

modeling and rendering system. ACM Transactions

on Graphics (TOG), 23(2):143–162.

Sinha, S. N., Kopf, J., Goesele, M., Scharstein, D., and

Szeliski, R. (2012). Image-based rendering for scenes

with reﬂections. ACM Trans. Graph., 31(4):100–1.

Suzuki, K., Wakisaka, S., and Fujii, N. (2012). Substitu-

tional reality system: a novel experimental platform

for experiencing alternative reality. Scientiﬁc reports,

2:srep00459.

Tsai, R. (1987). A versatile camera calibration technique

for high-accuracy 3d machine vision metrology using

off-the-shelf tv cameras and lenses. IEEE Journal on

Robotics and Automation, 3(4):323–344.

Tunwattanapong, B., Fyffe, G., Graham, P., Busch, J., Yu,

X., Ghosh, A., and Debevec, P. (2013). Acquiring

reﬂectance and shape from continuous spherical har-

monic illumination. ACM Transactions on graphics

(TOG), 32(4):109.

Vagharshakyan, S., Bregovic, R., and Gotchev, A. (2015).

Image based rendering technique via sparse represen-

tation in shearlet domain. In 2015 IEEE International

Conference on Image Processing (ICIP), pages 1379–

1383. IEEE.

Ward, G., Kurt, M., and Bonneel, N. (2014). Reducing

anisotropic bsdf measurement to common practice. In

Material Appearance Modeling, pages 5–8.

Wood, D. N., Azuma, D. I., Aldinger, K., Curless, B.,

Duchamp, T., Salesin, D. H., and Stuetzle, W. (2000).

Surface light ﬁelds for 3d photography. In Pro-

ceedings of the 27th annual conference on Computer

graphics and interactive techniques, pages 287–296.

ACM Press/Addison-Wesley Publishing Co.

Photorealistic Reproduction with Anisotropic Reﬂection on Mobile Devices using Densely Sampled Images

227