
Roof Segmentation based on Deep Neural Networks
Regina Pohle-Fr¨ohlich
1
, Aaron Bohm
2
, P eer Ueberholz
2
, Ma ximilian Korb
1
and Ste ffen Goebbels
1
1
Institute for Pattern Recognition, Faculty of Electrical Engineering and Computer Science,
Niederrhein University of Applied Sciences, Reinarzstr. 49, 47805 Krefeld, Germany
2
Institute for High Performance Computing, Faculty of Electrical Engineering and Computer Science,
Niederrhein University of Applied Sciences, Reinarzstr. 49, 47805 Krefeld, Germany
Keywords:
Building Reconstruction, Deep Learning, Convolutional Neural Networks, Point Clouds.
Abstract:
The given paper investigates deep neural networks (DNNs) for segmentation of r oof regions in the context of
3D building reconstruction. Point clouds as well as derived depth and density images are used as input data.
For 3D building model generation we follow a data driven approach, because it allows the reconstruction of
roofs with more complex geometries than model driven methods. For this purpose, we need a preprocessing
step that segments roof regions of buildings according to the orientation of their slopes. In this paper, we test
three different DNNs and compare results with standard methods using thresholds either on gradients of 2D
height maps or on point normals. For the application of a U-Net, we transform point clouds to structured 2D
height maps, too. PointNet and PointNet++ directly accept unstructured point clouds as input data. Compared
to classical gradient and normal based threshold methods, our experiments with U-Net and PointNet++ lead
to better segmentation of roof structures.
1 INTRODUCTION
For a variety of simulation a nd planning applications,
3D city models are used. These models typically are
exchanged in the XML based description standard Ci-
tyGML. Each polygon represents a single wall, roof
facet or other building element according to the cho-
sen Level of Detail (LoD). Due to available data, most
CityGML models are given in LoD 2, i.e., they in-
clude roof and wall polygons but no further details
such as windows or doors. Often su ch models are ba-
sed on roof reconstruction using airborne laser scan-
ning or photogrammetric point clouds obtained from
oblique areal images. There are two main approaches
to roof reconstruction that might be used in combina-
tion on point clouds, cf. (Wang et al., 2018b): In the
first approach model driven methods fit parameterized
roof models to building sections. This lead s to simple
geometries. In some cases they differ significantly
from the real roof layout because typica lly catalo-
gues of parameterized roof models are quite small.
In addition, parameters like slope mig ht be estima-
ted wrongly due to dormers or other small building
elements. The second approach is da ta driven, where
plane segments are fitted to the point cloud and com-
bined to a watertight roof. This allows m odeling even
sophisticated r oof geometrie s that, for examp le , can
be found with churches. However, this appr oach is
sensitive to noise. Whereas ridge lin es can be de-
tected quite reliab ly by intersecting estimated planes,
step edges are difficult to reconstruct if point clouds
are sparse, as in the case of airbo rne laser scanning, or
noisy, as in the case of photogrammetric point clouds.
In our previously developed data driven modeling
workflow (see (Goebbels and Pohle-Fr¨ohlich, 2016)
and subsequent papers), we first segmented areas in
which the roof’s gradients homogeneously point into
the same direction. O nly within such areas, we then
used RANSAC to find planes. Witho ut segmentation
prior to RANSAC, one would find planes which might
be composed from many not con nected segments or
even planes that just cut larger structures. We com-
puted gradient directions on a he ight map. This is
a 2D greyscale image which is interpolated from the
z-coordinates of the point cloud. We used linear in-
terpolation on a Delaunay triangulation of the points.
Small gradients belong to flat r oofs. Gradients with
length above a threshold value point into a significant
direction. In order to gain segmentation we classi-
fied these directions. Th ere are some shortcomings
with th is method: Classification depends on compu-
ted threshold values. Moreover, to obtain the height
map we had to interpolate sparse or no isy point cloud
data. Results depend on the choice of resolution and
326
Pohle-Fröhlich, R., Bohm, A., Ueberholz, P., Korb, M. and Goebbels, S.
Roof Segmentation based on Deep Neural Networks.
DOI: 10.5220/0007343803260333
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 326-333
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the interpolation method. By interpolating, we lose
sharpness of ridge lines and step edges. In addition,
this is a 2D method. We cannot distingu ish between
points with same x- and y- coordinates that for exam-
ple occur with walls, chimneys, antennas or overhan-
ging trees.
Now the idea is to replace the segmentatio n step
by a deep neural network (DNN). In recent years,
DNNs have been applied successfully to many clas-
sification and even segmentation problems. DNNs
could be better suited to handle outliers due to anten-
nas and chimneys as well as occlusion by trees. Buil-
ding reconstruction algorithms typically use threshold
values that depend on point cloud density. DNNs
might be able to learn such th reshold values. Further-
more, due to normalization of input data, cloud den-
sity becomes less important.
However in contrast to images, point clouds are
unstructured, the amount of data is often much hig-
her, and there might be no color info rmation. Due to
the lack of structure, convolution of point clouds with
kernels is more elaborate tha n convolution of images.
Nevertheless, in rece nt years neural networks, also in-
cluding co nvolutional networks, have been developed
to directly work on point clouds.
In our paper, we evaluate 2D segmentation with
U-Net based on interpolated height m aps as well as
3D segmen ta tion directly on the point cloud with
PointNet and PointNet++. The tested networks clas-
sify 3D points to belong to six classes describing
walls, flat roofs, roofs with a main slope facing north,
roofs with gradients pointing east, south and west. Fi-
nally, we compare the results with our previous met-
hods using thresholds either on the g radient values of
the 2D height ma p or on point normals.
2 RELATED WORK
DNNs are very popular in the area of computer vision
for object classification an d semantic segmentation.
Especially, neural networks a re used for urban area
classification with airborne laser scanning data ba sed
on height maps, see (Hu and Yuan, 2016; Yang et al.,
2017). In this context Boulch et. al. (Boulch et al.,
2017) used a neural network with encoder-decoder
architecture for segmentatio n of colored, dense point
clouds. They applied SegNet and U-Net for seman-
tic labelling . In our context, 2D segmentation of roof
regions can also be done on the previously described
height maps using U-Net (Ronneberger et al., 2015),
a convolutional DNN that has su ccessfully been ap-
plied to many image segmentation tasks. The U-Net
architecture consists of extraction and extension par ts
in which multi-channel fe ature maps are organized.
In the extraction part, featur e maps are connected to
realize either convo lutions or max pooling steps to
decrease the size and increase the number of featur e
maps. The expansion part of the network is sym-
metric to the extraction part and re a lizes convolution
steps, too. Here, instead of max pooling, upconvoluti-
ons are used to increase resolution. Additionally, high
resolution feature maps of the extraction part directly
contribute to up sampling steps. However, some of the
above mentioned shortcomin gs of working with 2D
height maps remain. Therefore, it seems to be a good
idea working directly on 3D data.
Generally, CNNs require structu red data. In the
most simple case, one can achieve this by rasteriza-
tion of point clouds and transfer into voxel represen-
tation. Unfortunately, this is memory and time con-
suming and might also imply the need of interpola-
tion. On this account, in most cases the resolution of
objects has to be decreased. A popular CNN for 3D
applications is VoxNet (Maturana and Scherer, 2015).
An alternative approach to structuring point
clouds is the use o f indexing structur e s. Input d a ta of
the Kd-network are kd-trees that are computed fro m
point clouds (Klokov and Lempitsky, 2017). Apart
from point’s coordinates, other p oint-wise attributes
can be considered. In OctNet (Wang et al., 2017) the
3D points are re presented with octre es. Typically, the
hierarchy of octants is only sparsely filled. 3D CNN
operations are performed only on octants occupied by
boundaries of the 3D shapes und er investigation. Due
to using index structures, both Kd-network and Oct-
Net are not rotation independ e nt. In addition , ge ne-
ration of index structures might be time consuming.
A further disadvantage ofthese methods is that new
convolution and pooling operations are necessary.
In recent ye a rs, deep learning methods for irregu-
lar data have been researched. One promine nt repre-
sentative is PointNet (see (Qi et al., 2017a)). In its ba-
sic form only the coordinate s of the points are used for
the classification proce ss. PointNet processes every
point ide ntically and inde pendently in the first step
with a T-Net. This network is a CNN w ith convolu-
tion layers, max pooling layers and two layers with
fully connected neurons. As a result, we receive a
transformed point cloud with uniform orien tation and
size, see Figure 1. In a next step, local features are
computed for every point.
Figure 1: The T-Net transforms the left input point cloud to
the aligned right point cloud.
Roof Segmentation based on Deep Neural Networks
327

In contrast to neighborhood relations, only glo-
bal positions of points are important for reco gnition
with PointNet. Since slopes of roo fs and vertex nor-
mals typically are obtained using nearest neighboring
points, this mig ht be disadvantageous with respect to
our application. PointNet’s successor PointNet++
(Qi et al., 2017b) appears to be be tter suited for this
task. PointNet++ is a multi-scale point-based network
that considers neighborhood information by applying
PointNet on nested partitioning of th e input point set.
In (Rethage et al., 2018) a hybrid a pproach for a
fully co nvolutional point network was chosen that is
based on multi-scale feature encoding by the use of
3D convolutions in combination with direct proces-
sing of the point clouds. The network runs on unorga-
nized input clouds and uses PointNe t as a low-level
feature descriptor. Internally, the input is transfor-
med into an ordered repr esentation. This transforma-
tion is followed by 3D convolutions to learn shape-
dependent relationships of the points at multiple sca-
les. With regard to semantic point segmentation, pu-
blished results are slightly worse than fo r PointNet++.
In their work (Hua et al., 2018) , Hua et. al pro-
posed a n ew convolution operator for CNN, called
point-wise convolution. This convolution operator
can be applied at each point in a point cloud to le-
arn point-wise features. Compared to other meth ods
which used Tensorflow’s optimized convolution o pe-
rators, running time was slower. According to (Hua
et al., 2018), per class segmentation accuracy was re-
ported to b e slightly worse than for PointNet.
In (Ben-Shabat et al., 2017) a 3D modified Fisher
vector was used as hybrid representation of the p oint
cloud. The 3D Fisher vector r epresentation describes
data samples from the point cloud in varying sizes by
their deviation from a Gaussian Mixture Model. Pu-
blished results obtained on a test data set were similar
to those of PointNet.
Furthermore, 3D data is often represented as a
mesh. Then a CNN for semantic segmentation can
be applied to a graph derived from the m e sh (Wang
et al., 2018a). In this case, special pooling operati-
ons are necessary to coarsen the graph. We we re not
able to use this method because automated mesh ge-
neration failed for a significant number o f buildings.
Although so me points should become connected, dis-
tances between them were probably too large d ue to
outliers and shading effects.
Because of easy handling and good results in other
studies we did 3D segmentation with PointNet and
PointNet++. For comparison we also applied the U-
Net and classical gradient segmentation on 2D h eight
maps.
3 TRAINING DATA
DNNs require a huge amount of training d a ta . We di-
rectly obtaine d ground truth by sampling point clouds
from alrea dy existing 3D city models and received an-
notations at nearly no cost by mapping face normals
to our six classes,
Wall
,
Flat Roof
,
North
,
South
,
East
and
West
.
We worked with a 3D mo del of four square kilo-
meters of the center of the city of Krefeld tha t consists
of more than 10,000 buildings. We converted each
single CityGML building model into OBJ-format re-
presentation such that each triangle had a label (color)
referrin g to its ro of or wall polygon. Per definition,
each building’s ground plane lay in the x-y-plan e . Ad-
ditionally, we rotated the buildings re presentation in
such way that the largest edge of the building ’s ca-
dastral footprint pointed into th e direction of x-axis of
the coordinate system. We the n scaled the model to
fit within the cube [−1, 1]× [−1, 1] ×[−1, 1]. By allo-
wing three different component-wise scaling factor s,
directions of normals did change slightly. This was
tolerable because, as a preprocessing step to plane es-
timation, we still got useful segmentation into roof’s
gradient directions. If we did not scale to comple-
tely cover the interval [−1, 1] in all three dimensions
then PointNet’s preprocessing step performed geome-
tric transformatio ns that changed classification.
With the too l CloudCompare, we randomly sam-
pled 2048 or 4096 labeled surface points for efficient
processing of the da ta by PointNet. To obtain ground
truth, we computed face normals of all wall a nd roof
planes belonging to th e transformed building model,
see Figure 2. According to the normals, we classi-
fied the planes into the classes
Wall
(z-component of
normal is zero),
Flat Roof
(x- and y- components
of normals are (approximately) zero),
North
(roofs
with slope to the north, i.e. in direction of the po-
sitive y-axis),
East
(positive x-axis),
South
(nega-
tive y-axis) and
West
(negative y-axis). According
to the points’ labels, we annotated them with their
Figure 2: Distribution of face normals of roof and wall pla-
nes (left) and point normals obtained from t he point neig-
hbors (right): The normals were projected to the x-y-plane
by removing their z-coordinate. E ach dot represents the
normal vector associated with a point of the cloud. Cle-
arly, four major directions are visible, denoted as classes
North
,
East
,
South
and
West
in this paper. Normals of flat
roofs were marked in blue, white pixels represent normals
of walls.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
328

correspo nding class, see Figure 3. We ensure that
all classes contain approximately the same number of
points. PointNet++ allows for additional point-wise
Figure 3: Left: 3D model of the building, each facet is mar-
ked with a different color. Right: Ground tr uth classification
of a building’s point cloud; Facets with different slope but
same gradient direction are not distinct.
input data, and PointNet can be executed with de ri-
ved data instead of original points. To this end, we
equippe d the points with point (vertex) normals com-
puted from their nearest neig hbors. Only for network
training w e additionally considered face normals. A
point’s face normal is the normal vector of the buil-
ding’s plane that is associated with the point Also,
we generated multi-view density images by orthogo -
nally projecting all points to the x-y-, x-z− and y-z-
planes, see Figu re 4. Such density maps were already
used for o bject classification in (Minto et al., 2018).
On each plane, w e ac cumulated the num ber of points
Figure 4: Density image on the x-z-plane.
using a 256 × 256 raster. Thus, the data set contains
3D points, two (often different) cor respondin g normal
vectors and also triples of density values accor ding to
a point’s positions in the three r aster images.
For the application of U-Net on h eight maps, we
again turned each building so that the longest foot-
print edge matched the x-axis. Then, we initialized a
greyscale height map image covering the buildings’s
footpr int with height values taken fro m z-coordinates
of the point cloud. We completely filled the ima ge
using linear interpolation, see greyscale pictures in
Figure 5. This served as the net’s inpu t. To find cor-
respond ing ground truth segmentation, we used the
face norm a ls of triangles from the building model,
which were projected into the x-y-plane. If a pixel
was outside a building’s footprint then we classified it
as backgro und.
Figure 5 shows examples for height maps and as-
sociated ground truth maps. The class
Wall
is not
included in ground truth maps because walls are co-
vered by roof poin ts.
Figure 5: Height maps with ground tr uth annotation: blue
regions represent flat roofs, black areas do not belong to the
building, the other colors r epresent the classes
North
,
East
,
South
and
West
.
We used data derived from existing building mo-
dels both for training and testing . Thus, we trained
the network with 90% of sampled buildings and used
10% as test da ta . Because of computing time, we did
not apply cross-validation. But we checked that the re
is no over-fitting. Also, the ratio 90% : 10% led to
best recognition results. However, in order to evaluate
networks’ performance on real point clou ds obtained
by airborne laser scan ning, we extracted the points of
21 buildings from such a cloud. Then we removed
outliers because such points do not occur in training
data. Finally, we manually classified the points.
4 EXPERIMENTS
To measure quality of results, we use the established
intersect over union metric (IoU). For a given class
and a given building, TP (true positive) is the num -
ber of points or pixels that are correctly identified as
being members of this class: TN ( true negative) is
the number of input po ints that are co rrectly classi-
fied as not belonging to the given class. In turn, FP
(false positive) and FN (false negative) a re numbers of
wrongly classified points. Then pr ecision is defined
via
TP + TN
TP+ TN+FP + FN
and IoU :=
TP
TP + FP + FN
. The num-
ber TN does not occur in this definition because in
general most p oints do belong to other c lasses (back-
ground) and one wants to avoid a good rating for net-
works that just classify backgro und. To get a qua-
lity measure for a given class and all buildings of the
test data set, we restrict ourselves to those buildings
only, that include this class according to ground tr uth.
For e a ch of the se buildings, we separately compute
an IoU value and then determine the arithmetic mean
over all such buildings. We do not set IoU := 1 if a
class is not contained in a building’s ground truth as
it is done in PointNet. Thus, presente d IoU-values
might be smaller but more meaningful than measured
with unchanged PointNet code. Because of compu-
ting IoU values separately for each building and not
weighting with the building’s class size, we amplify
errors of small classes.
Roof Segmentation based on Deep Neural Networks
329
4.1 U-Net on Height Maps
We applied U-N e t to 25,000 patches of 2,800 greys-
cale height maps with varying parameters. Each
height map was an image with 492 × 492 pixel.
All tests were perform ed using cro ss e ntropy error
function. Nets might learn trainin g data very well but
fail with other input data. This effect is called overfit-
ting. To avoid overfitting, we generally used regula-
rization by adding a constant fraction of the absolute
sum of the net’s weights to the error fun c tion.
We selected the Adam optimizer (Kingma and
Adam, 2015) as a statistical gradient descent method.
We also tested with Adagrad (Duchi et al., 2011) and
RMSProp but, as expected, the Adam method perfor-
med best by far. It reached high IoU values around
0.8 within 1 5 epochs in some initial tests. Simple
gradient descent and Adagrad optimizer did not re-
ach values above 0.3 after 200 epochs, and RMSProp
tended towards a decrease in IoU after 100 epochs.
We worked with a learning rate of 0.0001, as
smaller rates did not yield better IoU results after the
same nu mber of epochs. To the contrast, hig her rates
resulted in significantly smaller I oU numbers.
We initialized the nets with random weights fol-
lowing a Gaussian distribution. Thus it was desirable
to get stable results independen t o f the initial values.
By repeating experiments ten times under same con-
ditions, we tested stability. Thereby, we observed two
outliers with IoU values that were about 20% lower
than the values obtained for the other eight experi-
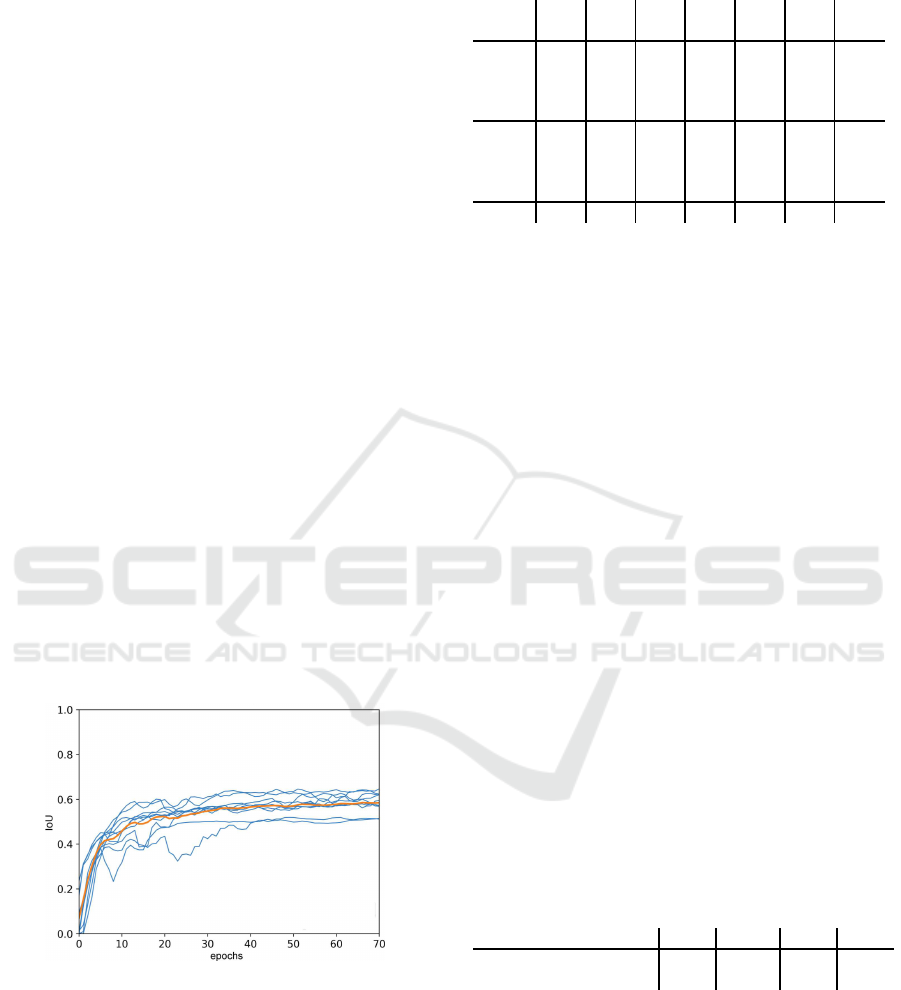
ments within the same ma gnitude, see Figur e 6.
Figure 6: IoU values for learning class
Flat Roof
with U-
Net: Blue curves belong t o independent trainings with same
net configuration, orange curve shows arithmetic mean.
Stability can be improved either by using the dro-
pout metho d (that was applied in previously me ntio-
ned stability tests) or batch normalization. But both
methods should not be used at the same time, cf. (Li
et al. , 2018). With stable networks, all further results
were obtained using a single set of initial weights.
Table 1: IoU values aft er 200 training epochs: Numbers in
the first column refer to the amount of activated neurons.
drop-
Flat North East South West
back- arith.
out
Roof
round mean
full
90% 66.8%86.1%90.2%88.0%93.9%98.6%87.3%
80%
59.7% 80.3% 88.6% 81.0% 91.6% 98.5% 83.3%
70%
59.2% 76.3% 87.2% 76.9% 89.4% 98.5% 81.3%
half
90% 61.5% 83.0% 90.0% 83.4% 92.3% 98.5% 84.8%
80%
56.3% 78.5% 88.3% 78.1% 90.5% 98.4% 81.7%
70%
52.0% 70.4% 84.6% 71,3% 86.5% 98.4% 77.2%
no 60.3% 82.2% 89.2% 81.5% 92.1% 98.4% 84.0%
By using the dropout method, a predefined n um-
ber of randomly chosen neurons are deactivated. The
desired effect is that results become more robust and
not dependent on single neurons. We analyzed two
different configurations. In the “full dropout” variant,
dropout was applied to all convolution layers. The
“half d ropout” configuration applied dropout to every
second convolution layer starting with the first. Table
1 shows that a 90% “full dropout” performed best,
i.e., 10% of neurons were randomly deactivated.
The ne tworks were trained with data grouped into
batches. For each activation la yer’s input, batch nor-
malization subtracts the batch’s me a n and divides the
result by the batch’s standa rd deviation. It also mul-
tiplies it with a trainable parameter γ and adds anot-
her trainable parameter β such th at gradient descent
can modify them in stead of having to change many
weights. As expec ted, with batch normalization, IoU
values were higher for all tested learning rates than
without use of batch normalization and dropout. With
dropout, IoU numbers were alike, but variance was
greater (cf. Figure 6) , thus stability was worse.
The architecture of U-Net allows modification of
two specific parameters: The number of top-layer fe-
ature maps a nd the size of the convolution kernel. Ta-
ble 2 shows the r esults of four trainings that only dif-
fer in the number of feature maps. Due to running
time, we decided to work with 16 feature maps. We
Table 2: Influence of the number of t op-level feature maps.
number of feature maps
32 16 8 4
running time 23h 11.8h 5.2h 2.7h
median IoU
85% 83% 62% 48%
applied 3 × 3 and 5 × 5 kernels and found that, with
using batch normalization, 5 × 5 kernel led to equally
good IoU values as 3 × 3 kernel with 90% “full dro-
pout” or with batch normalization. But due to the lar-
ger kernel size, less convolution layers were n e eded,
and running time decreased by about 30%.
We compare U-Net results with following classi-
cal segmentation approach on the 2D greyscale height
map in Table 3: On the height map, we computed gra-
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
330

Figure 7: Ground truth and prediction: Black pixel are
background, blue denotes
Flat Roof
.
dients via convo lution with 3 × 3 or 5 × 5 Sobel ker-
nel. Pixels belongin g to gradients with length below a
threshold value 0.1 were classified to be part of a flat
roof. Otherwise, a gradie nt’s direction in x-y-plane
determines the class
North
,
East
,
South
or
West
. U-
Net clearly leads to b etter segmentation results than
thresholding of gradients computed with Sobel ker-
nels. Figure 7 compares ground truth with network
results. The image pairs in the upper row show quan-
tization errors in areas with low slop e.
Table 3: IoU values achieved with U-Net in comparison to
classical segmentation.
Flat North East South West
arith.
Roof
mean
U-Net 72.8 94.6% 93.2% 94.5% 90.9% 89.2%
3 × 3 Sobel
84.4% 77.4% 65.4% 73.8% 65.8% 73.4%
5 × 5 Sobel
80.6% 81.1% 72.2% 78.1% 72.4% 76.9%
4.2 PointNet
PointNet is design ed only to handle point clouds in
which each point consists of three coordinate va-
lues. We evaluated both, with the points’ x- y- and z-
coordinates but also with replacing the three values by
the components of co rrespond ing vertex normal vec-
tors that are computed from the point’s nearest neig-
hbors. Face normals typically are not available as in-
put and were only used to define ground truth.
To select parameter values, we trained the ne twork
with the points’ coordina te s. We chose the learning
rate 0.001 that, with regard to IoU, perf ormed as well
as lower rates 0.0005 and 0.0001, wherea s higher ra-
tes 0.01 and 0.005 resulted in significantly lower IoU
values. The choice of using batch normalization im-
proved results slightly.
With in PointNet, T-Net serves as a pr eprocessing
step. This step can be followed by a similar T-Net-
Feature network. We observed slight improvements
in all tests when choosing to use both transformations.
Probably, the improvement was only small because
our input data was rotated according to the longest
footpr int edge. Hence, a suitable transformation was
in place alre a dy.
With regard to stability, by repeating a training
with random initial weights an d batch normalization
we did not observe outliers as we did for U-Net tests
based on the dropout method. However, Table 4 and
Figure 8 show that PointNet did not perform well.
The number of wall points was higher than the num-
ber of points in other classes. Therefo re, wall points
were classified better.
Figure 8: Two examples of ground truth segmentation (left)
and prediction (right) with PointNet on x, y, z coordinates.
One would expect that results should improve if
points were replaced with their corresponding point
normal vectors. The direction of a normal vector im-
mediately implies the class. Only differences between
face norm a ls (used to determine ground truth) and
point normals should lead to errors. With exception
of class
West
, PointNet applied to point nor mals in-
deed yields better but still not convincing results, see
Ta ble 4. Applyin g trained networks to manually clas-
sified real point clouds changed results for the worse.
4.3 PointNet++
In contrast to PointNet, its successor PointNet++
accepts six values per point as input. That allowed
evaluating PointNet++’ performance with two very
different inputs: We used 3D points in connection
with normal vectors as well as 3D points in combina-
tion with three projected density values, see Section
3. Since face normals can be generated only from 3D
building models and not from point clouds directly,
we tested ou r configurations with point normals. Any-
how, for training the n e tworks with mode l data we can
use either point normals or face normals detected on
planes, see Figure 9. Tab le 5 summarizes correspon-
ding results. All class sizes were chosen to be ap-
proxim ately e qual for training but not for testing with
real world data. It is not surprising that the network
performs b e tter, if training and test data matched, i.e.,
one should train with point normals. This also holds
true for testing with real world data. However, seg-
mentation results were a good deal poorer, see Table
6. Independent of chosen segmentation method, IoU
values of walls were low. That is due to the fact that
in airborne laser scanning data walls are mostly invi-
sible. Thus, only 3% of points belong to walls.
PointNet++ trained on point normals and tes-
ted on model data even perf ormed significantly better
than outcomes of classical point norm a l-based seg-
mentation using thresho ld values (Table 5). In this
situation the network apparently learne d thresholds
more easily. In case of real world point clouds, the
picture was not as clear (see Table 6). Reality an d le-
arning da ta seemed to differ too much, e.g., r eal roofs
Roof Segmentation based on Deep Neural Networks
331
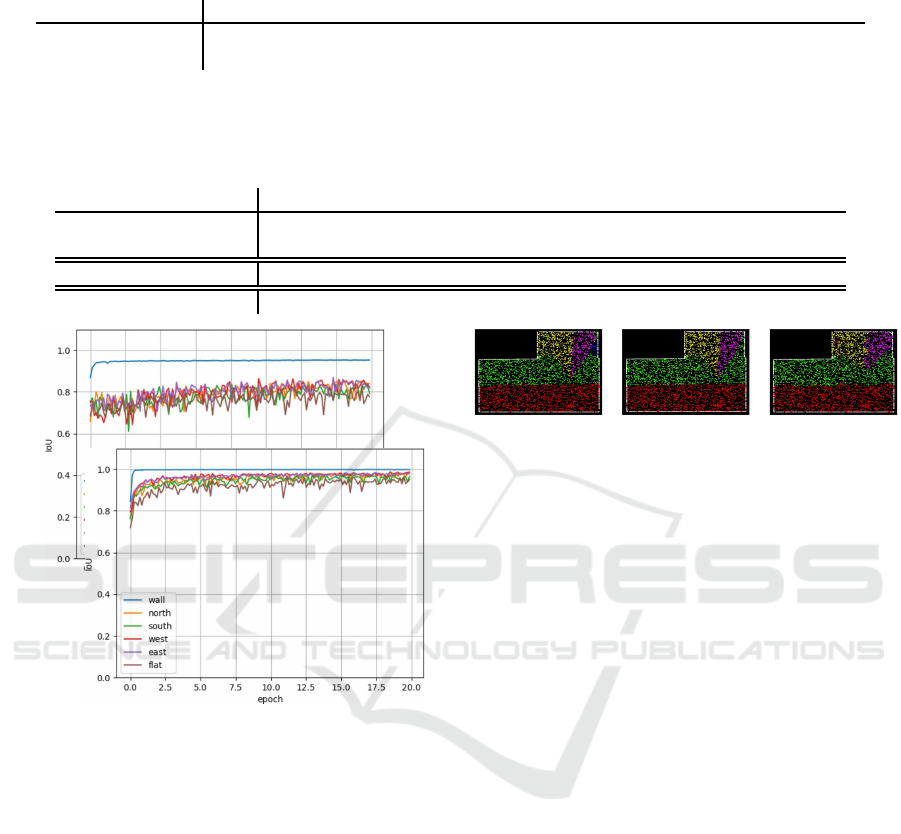
Table 4: On the one hand, PointNet was trained and tested with points and on the other hand the network was trained and
tested with point normals. For comparison, IoU values of classical segmentation are given in Table 5.
training variant
Wall North East South West Flat Roof
arithmetic mean
x, y, z coordinates 69.4% 34.8% 31.8% 27.3% 25.1% 34.9% 37.2%
point normals
92.5% 50.1% 33.7% 51.1% 18.4% 75.7% 53.6%
Table 5: PointNet++ trained over 200 epochs and t ested with points and normals of generated data as well as with density
values from three points of view: To train the network with normals, we either used point or face normals obtained from
90% of 3D models. For testing on remaining 10% of models, points were equipped with point normals. For comparison, IoU
values of segmentation on point normals (using same thresholds as for ground truth generation on face normals) are listed.
training variant
Wall North East South West Flat Roof
mean
point normals 96.3% 84.3% 83.5% 84.1% 83.5% 84.6% 86.1%
face normals
88.1% 7 0.8% 74.6% 68.3% 73.8% 69.5% 74.2%
density data 95.1% 85.4% 84.7% 85.9% 85.4% 85.9% 87.1%
classical segmentation 88.1% 69.8% 76.6% 69.9% 76.6% 68.8 % 74.9%
Figure 9: IoU values during training on points and normal
vectors with PointNet++: Upper plots belong to training
with point normals. Second plots summarize training with
face normals.
were not exactly planar.
When applying PointNet++ with point co ordina-
tes and three corresponding density values instead of
normals r esults were similar good than for training
with point norma ls. Both variants were better than
results for training with face normals, see Table 5.
Ridge lines and step edg e s were clearly visible in den-
sity images. But surprisingly, segmenta tion results al-
ong these lines appe a red noisier when using den sity
values than point normals, see Figure 10.
5 CONCLUSION
Deep learning shows potential to improve existing al-
gorithms for 3D building reconstruction. Both U-Net
Figure 10: Difference between PointNet++ segmentation
based on point normals and segmentation on density values:
ground truth (left), point normal segmentation (middle),
density value segmentation (right). To avoid error coming
from e.g. small dormers higher resolution is required. This
can be obtained by splitting up buildings into parts, cf. Fi-
gure 11.
trained on height maps and, if trained o n point nor-
mals or density images, PointNet++ are able to yield
better segmentation results than we c ould obtain with
classical gradient or normal based approaches. At le-
ast this holds true for testing with point clou ds that are
sampled from 3D city models. For application to real
world point clouds, we have to im prove our training
data. Recently, we trained with an notated real 3D data
and got similar results as on training data described in
this paper.
In ou r tests, 3D networks did not perform better
than 2D U-Net. Again, the main reason might be that
our trainin g data for roofs can be represented in 2.5D.
Most non-flat roofs possess only four main gra-
dient dir ections. Therefore, classification into flat
roofs and four direc tions generally serves well. Ho-
wever, in future work we will increase the number of
classes to improve segmentation results for sophisti-
cated roof topologies. To this end , we also have to
split up buildings into small processable parts instead
of using non-uniform scaling. This also solves the
problem that our cu rrently used networks o nly accept
quite small point clouds due to memory restrictions.
As tested with PointNet++, segmentation results o f
parts can be merged without significant loss of qua-
lity, see Figur e 11. Suitable strategies for split-up pro-
cedures have to be developed.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
332
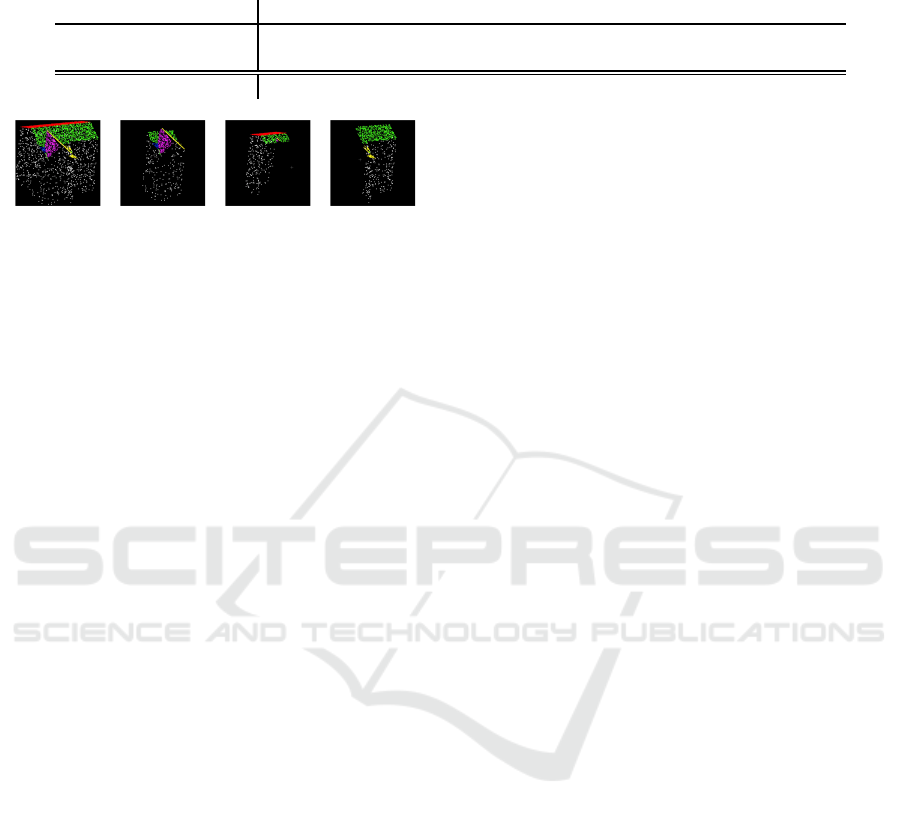
Table 6: PointNet++ tested with real world point clouds: To train the network, w e either used point or face normals obtained
from 90% of 3D models as in Table 5. For testing, we used real point clouds equipped with point normals. Results were
compared with classical threshold segmentation as in Table 5.
training variant
Wall North East South West Flat Roof
mean
point normals 65.2% 64.3% 52.0 % 70.7% 56.8% 55.7% 60.8%
face normals
53.3% 5 6.2% 57.0% 73.2% 57.1% 47.1% 57.3%
classical segmentation 52.1% 60.3% 59.5% 71.6% 59.4% 44.2% 57.9 %
Figure 11: Stable segmentation results on cloud subsets.
ACKNOWLEDGEMENT
This work was supported by a generous hardware
grant from NVIDIA.
REFERENCES
Ben-Shabat, Y., Lindenbaum, M., and Fischer, A.
(2017). 3D point cloud classification and segmenta-
tion using 3D modified fisher vector representation
for convolutional neural networks. arXiv preprint
arXiv:1711.08241.
Boulch, A., Le Saux, B., and Audebert, N. ( 2017). Un-
structured point cloud semantic labeling using deep
segmentation networks. In 3DOR.
Duchi, J., H azan, E., and Singer, Y. (2011). Adaptive
subgradient methods for online learning and stochas-
tic optimization. Journal of Machine Learning Rese-
arch, 12:12:2121–2159.
Goebbels, S. and Pohle-Fr¨ohlich, R. (2016). Roof recon-
struction from airborne laser scanning data based on
image processing methods. ISPRS Ann. Photogramm.
Remote Sens. and Spatial Inf. Sci., III-3:407–414.
Hu, X. and Yuan, Y. (2016). Deep-learning-based classifi-
cation for dtm extraction from als point cloud. Remote
sensing, 8(9):730.
Hua, B.-S., Tran, M.-K., and Yeung, S.-K. (2018). Point-
wise convolutional neural networks. In Proceedings of
the IEEE Conference on Computer Vision and Pattern
Recognition, pages 984–993.
Kingma, D. and A dam, J. B. (2015). A method for stochas-
tic optimization. In International Conference on Le-
arning Representations, pages 1–15, San Diego, CA.
Klokov, R. and Lempitsky, V. S. (2017). Escape from cells:
Deep kd-networks f or the recognition of 3D point
cloud models. 2017 IEEE International Conference
on Computer Vision (ICCV), pages 863–872.
Li, X., Chen, S., Hu, X., and Yang, J. (2018). Understan-
ding the disharmony between dropout and batch nor-
malization by variance shift. CoRR, abs/1801.05134.
Maturana, D. and Scherer, S. (2015). Voxnet: A 3D convo-
lutional neural network for real-time object recogni-
tion. In Intelligent Robots and Systems (IROS), 2015
IEEE/RSJ International Conference on, pages 922–
928. IEEE.
Minto, L., Zanuttigh, P., and Pagnutti, G. (2018). Deep
learning for 3d shape classification based on volume-
tric density and surface approximation clues. In VISI-
GRAPP (5: VISAPP), pages 317–324.
Qi, C. R., S u, H., Mo, K., and Guibas, L. J. (2017a). Point-
net: Deep learning on point sets for 3D classification
and segmentation. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 77–85.
Qi, C. R., Yi, L., Su, H., and Guibas, L. (2017b). Point-
net++: Deep hierarchical f eature learning on point
sets in a metric space. In Proceedings of the 31st
Conference on Neural Information Processing Sys-
tems (NIPS).
Rethage, D., Wald, J., Sturm, J., Navab, N., and Tombari, F.
(2018). Fully-convolutional point networks for large-
scale point clouds. arXiv preprint arXiv:1808.06840.
Ronneberger, O., Fi scher, P., and Brox, T. (2015). U-net:
Convolutional networks for biomedical image seg-
mentation. CoRR, abs/1505.04597.
Wang, P., Gan, Y., Shui, P., Yu, F., Zhang, Y., Chen, S., and
Sun, Z. (2018a). 3D shape segmentation via shape
fully convolutional networks. Computers & Graphics,
70:128–139.
Wang, P.-S., Liu, Y., Guo, Y.-X., Sun, C .-Y., and Tong, X.
(2017). O-CNN: Octree-based convolutional neural
networks for 3D shape analysis. ACM Transactions
on Graphics (TOG), 36(4):72:1–72:11.
Wang, R., Peethambaran, J., and Dong, C. (2018b). Li-
DAR point clouds to 3D urban models: A review.
IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens.,
11(2):606–627.
Yang, Z., Jiang, W., Xu, B., Zhu, Q., Jiang, S., and Huang,
W. (2017). A convolutional neural network-based 3D
semantic labeling method for als point clouds. Remote
Sensing, 9(9):936.
Roof Segmentation based on Deep Neural Networks
333
