Combining Two-level Data Structures and Line Space Precomputations

to Accelerate Indirect Illumination

K. Keul, T. Koß, F. L. Schr

oder and S. M

uller

Institute for Computational Visualistics, University of Koblenz-Landau, Germany

Keywords:

Visualization, Ray Tracing, Data Structures.

Abstract:

We present a method for combining two-level data structures and directional precomputation based on the

Line Space (LS). While previous work has shown that LS precomputation signiﬁcantly improves ray traversal

performance of typical spatial data structures, it suffers from high memory consumption and low image quality

due to internal approximations. Our method combines this technique with two-level BVHs, where the LS is

integrated within second-level object BVHs. The advantages are, among others, optimizations in terms of

approximation accuracy and required memory. In addition, we propose a method to use an accurate BVH in

combination with the fast approximation-based LS for path tracing in order to further reduce image errors of

the LS while still beneﬁtting from its gain in performance.

1 INTRODUCTION

Besides ray tracing acceleration through spatial data

structures, there have been many attempts based on

directional visibility information. Recently, the Line

Space (LS) was proposed as extension of spatial struc-

tures (Keul et al., 2016) (Billen and Dutr

e, 2016).

There, rays are clustered and classiﬁed within shafts

during initialization. A representative candidate was

used per shaft, which acted as blocker approxima-

tion during runtime (Keul et al., 2018). This accel-

erated ray traversal signiﬁcantly, however, at the cost

of approximation-based errors in the resulting image

and high memory consumption.

In the context of object instancing and rigid ob-

ject movements, two-level structures are employed,

which build a top-level structure around second-level

object structures. Their performance is in general in-

ferior compared to their single-level ﬂat counterparts

(Benthin et al., 2017). With this work, we ﬁrst pro-

pose a combination of two-level BVHs and represen-

tative candidate LS precomputations to combine the

advantages of both. Typically, second-level object

bounding volumes of two-level structures are small

and tightly-ﬁt to the contained objects. This property

makes LS approximations more accurate and reduces

image errors, as demonstrated in ﬁgure 1. In addition,

less LS nodes need to be generated and therefore less

memory is consumed, especially in scenes that rely

on object instancing.

In a second step, we propose a method for combin-

ing different data structures in path tracing systems.

While BVHs are used on earlier path segments, where

accurate results are needed, approximation-based LS

Reference (BVH)

F-LS (10) Ours: 2L-LS (4)

Figure 1: Improvements in indirect lighting calculation. We combine two-level BVHs with an approximation-based represen-

tative candidate Line Space (2L-LS). Even with a lower depth parameter (in brackets), we achieve less approximation errors

compared to a LS integrated in a single-level ﬂat BVH (F-LS). Additionally, less errors appear when used in later bounces.

228

Keul, K., Koß, T., Schröder, F. and Müller, S.

Combining Two-level Data Structures and Line Space Precomputations to Accelerate Indirect Illumination.

DOI: 10.5220/0007345902280235

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 228-235

ISBN: 978-989-758-354-4

results are used in later path segments, where accu-

racy is less relevant. By this, errors in the ﬁnal image

are nearly eliminated and the fast performance of the

LS can be used almost without any drawbacks in im-

age quality.

2 RELATED WORK

Indirect lighting calculation and ray tracing systems

are extensively studied topics, which are well pre-

sented in previous work (Ritschel et al., 2012)(Pharr

et al., 2016). Acceleration structures for ray tracing

have been researched intensively as well. Hence, we

present a brief overview of the most relevant litera-

ture in the most related topics of our work. We fo-

cus on bounding volume hierarchies (BVHs), as cur-

rent research suggests, that these result in the highest

ray tracing performance (Havran, 2000) (Zlatu

ska and

Havran, 2010) (Vinkler et al., 2016).

Bounding Volume Hierarchies. Since the ﬁrst au-

tomatic construction algorithm of BVHs was pub-

lished (Kay and Kajiya, 1986), many extensions and

optimizations for BVHs have been proposed (Aila

et al., 2012) (Aila et al., 2013). Most construction

algorithms work in a top-down manner, splitting the

scene along a promising plane in order to narrow the

domain of scene triangles that need to be tested for in-

tersection during runtime (Wald, 2007) (Wald, 2012).

Spatial splits in the BVH (called SBVH) are used

for better arrangement of the bounding volumes, but

lead to higher depths in the hierarchy (Stich et al.,

2009). More recently, SBVHs were optimized for bet-

ter SIMD parallelization (Fuetterling et al., 2016), im-

proved subdivision of the scene triangles (Ganestam

and Doggett, 2016) and better split cost prediction

through temporarily constructed BVHs (Wodniok and

Goesele, 2017). These approaches result in high qual-

ity BVH trees with good performance but higher and

mostly non-interactive construction time.

Construction algorithms based on Morton codes

result in interactive build times with the hierarchical

linear BVH (HLBVH) (Lauterbach et al., 2009) (Pan-

taleoni and Luebke, 2010) (Garanzha et al., 2011).

Recent advances extend Morton codes by also encod-

ing the object size and using adaptive axis order and

bit size to improve the handling of non-uniform scene

distribution (Vinkler et al., 2017). Morton codes were

also used to cluster scene primitives with a parallel ap-

proximate agglomerative clustering method (Gu et al.,

2013) (Meister and Bittner, 2017). Further, the Bon-

sai algorithm was proposed, where subtrees are later

gathered by a top-tree (Ganestam et al., 2015). Re-

cent methods start from fast-initialized HLBVHs that

are optimized afterwards. This can be done by conse-

quent remove-and-insert updates (Bittner et al., 2013)

(Meister and Bittner, 2018), optimization of the spa-

tial splits (Hendrich et al., 2017) or subsequent paral-

lel treelet optimization (Karras and Aila, 2013).

Two-level Data Structures. It is also possible to

use a two-level subdivision scheme with second-level

object hierarchies and a top-level structure that is built

on top of these objects. While the tree quality is typ-

ically worse in comparison to ﬂat (i.e. single-level)

structures, which is due to the irregular tree depth,

two-level approaches grant some beneﬁts. Therein,

dynamic scenes with rigid object animation are im-

plemented through transformation of the previously

built object hierarchies. Object instancing results in

less memory consumption, as the data structure used

per object can be reused. This technique was ﬁrst

proposed for k-d-trees (Wald et al., 2003), but since

also applied to other data structures like grids (Kalo-

janov et al., 2011) and BVHs in OptiX (Parker et al.,

2010) and Embree (Wald et al., 2014). However,

overlapping object hierarchies lead to multiple ob-

jects that need to be tested for intersections in or-

der to ﬁnd the nearest intersection point. For this

disadvantage, two-level BVHs were extended by us-

ing partial re-braiding (Benthin et al., 2017), which

opens and merges overlapping object BVHs during

runtime. Also, in comparison to its ﬂat counterpart,

the tree structure of two-level structures is less bal-

anced, which results in inferior SIMT parallelization

when traversing different objects. This disadvantage

is regarded in our approach, as the Line Space is able

to limit the maximum depth of object BVHs to a ﬁxed

level, leading to more balanced hierarchies.

Visibility Structures. In terms of directional data

structures, the accumulation of rays to beams is

known as beam tracing and was shown to result in

good performance, however, at the cost of high mem-

ory consumption and initialization time (Reshetov

et al., 2005) (Mortensen et al., 2007) (Laine et al.,

2009). The general approach is to generate mul-

tidimensional visibility ﬁelds around scene objects,

granting precomputed classiﬁcation schemes for the

contained rays. These methods are for instance used

in radiosity systems (Cohen and Wallace, 2012) or for

accelerated computation of indirect illumination in

ray tracing (Gaitatzes et al., 2010), sometimes based

on approximated results (Bashford-Rogers et al.,

2011).

Newer work introduces the Line Space (LS) as a

classiﬁcation scheme for rays, which groups the rays

into shafts within a regularly subdivided bounding

box, based on top of a spatial data structure (Keul

et al., 2016) (Billen and Dutr

e, 2016). Information is

Combining Two-level Data Structures and Line Space Precomputations to Accelerate Indirect Illumination

229

precomputed based on shafts and applied to all con-

tained rays during runtime. This was used as an ac-

celeration structure on top of grids and BVHs for ap-

proximate soft shadow and indirect lighting calcula-

tions (Keul et al., 2017) (Keul et al., 2018). While the

resulting images have visible artifacts due to the shaft

approximations, it was shown that some artifacts are

negligible when approximations are only used for in-

direct lighting computations (Yu et al., 2009). With

this, the LS is one magnitude faster in ray tracing

performance in comparison to typical data structures.

Besides the image quality, the main disadvantages are

the extensive memory usage and build time that arise

from the high number of precomputed shafts.

3 TWO-LEVEL LINE SPACE

An observation, used in our work, is that approxi-

mation accuracy is higher, when smaller and more

tightly-ﬁtting bounding volumes are used for the LS.

For this purpose, we adapt the LS to two-level BVHs

that grant smaller bounding volume sizes in second-

level object BVHs, leading to higher LS precision.

We ﬁrst revise the representative candidate LS tech-

nique as proposed by (Keul et al., 2018). Afterwards,

we describe the adaption to two-level BVHs, which is

one of the main contributions of this paper. Lastly, we

give a short discussion of all parameters involved.

3.1 Representative Candidate LS

Tracing cost is dividable in traversal cost of the un-

derlying tree and cost of intersection tests that are

made to ﬁnd the intersected scene primitive. The rep-

resentative candidate LS ﬁnds characteristic intersec-

tion candidates for shafts during initialization. With

this, the tree traversal is cut at a speciﬁc level, where

the representative candidate LS nodes are integrated.

Then, instead of calculating intersection tests between

rays and geometric scene primitives, the precomputed

representative shaft candidate approximates the ray

intersection within that shaft. While this improves

performance remarkably, the candidate approxima-

tion leads to visible errors.

The initialization of the representative candidate

LS is straightforward. First, the underlying spatial

data structure (i.e. the BVH) is constructed. Then

a LS node is constructed for every node in a given

depth of the underlying BVH. A LS node is a bound-

ing volume, where all sides of the bounding box sur-

face are subdivided into equally sized patches. Every

two distinctive patches are joined to result in a shaft

connecting those patches. Hence, each ray through

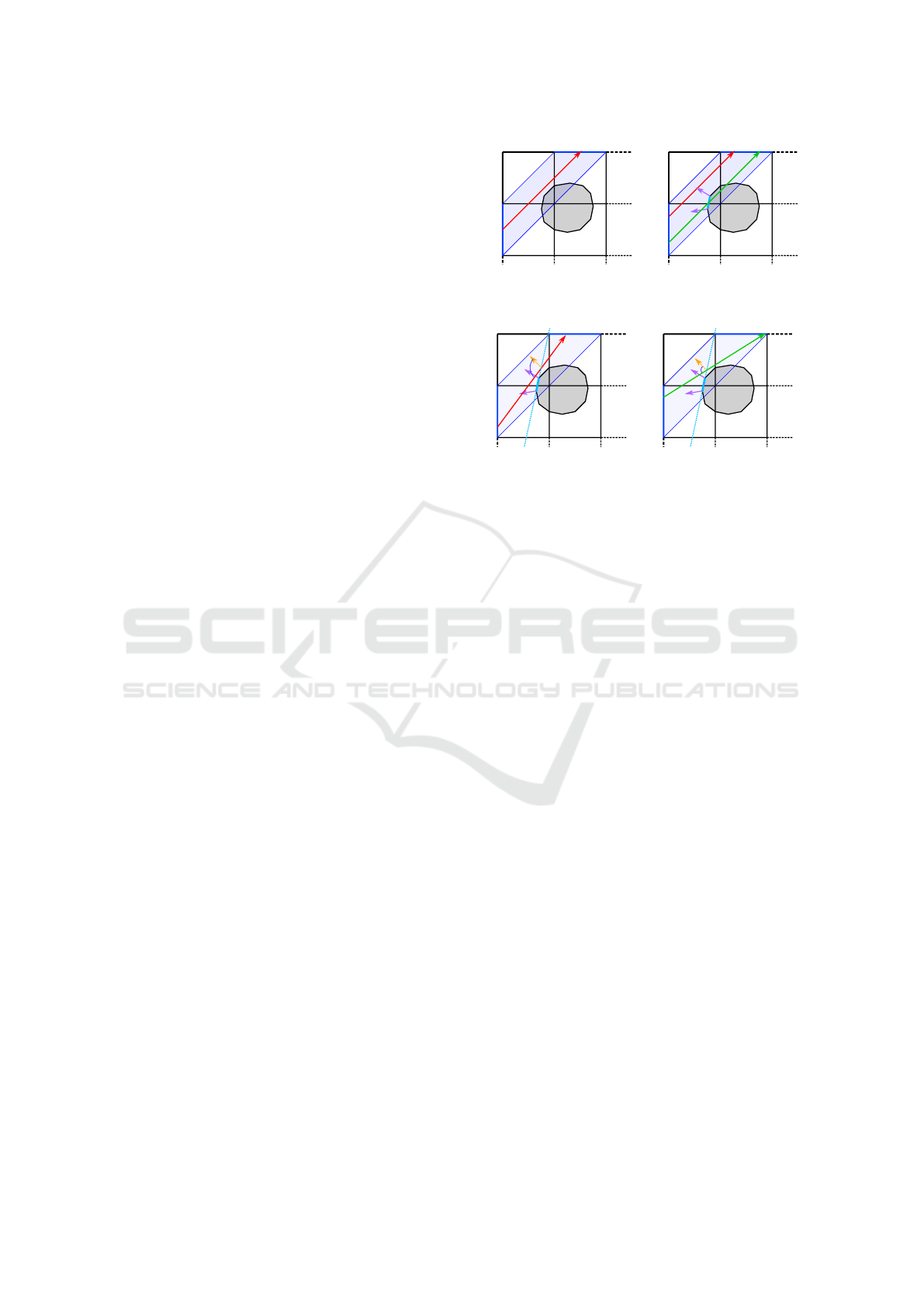
Figure 2: Initialization with representative shaft candidate

search. If the midpoint ray of the shaft between patches S

and E has no intersection (left), further rays are used (right).

Figure 3: Runtime usage of the shaft candidate c. It is used

as ”inﬁnite plane” P for all rays of the shaft. If angle α

between a ray and the extrapolated normal (yellow) is too

big, blocker approximation is refused (left). Otherwise it is

used, even with no actual object intersection (right).

the bounding volume can be assigned to a single shaft.

In the representative candidate LS every shaft has a

triangle reference, which describes the surface of the

scene primitives covered by the shaft. The triangle

(the representative candidate) is found by simple ray

traversal within the underlying data structure during

initialization. The ray used for traversal is determined

by the midpoints of the patches that represent the

shaft. If this ray has no intersection, additional rays

can be traced. If still no intersection was found, the

shaft is declared as empty. This process is shown in

ﬁgure 2. During runtime, the representative candidate

is used as a blocker approximation for all rays of the

given shaft, resulting in an ”inﬁnite plane”. However,

if the extrapolated normal of the approximation ex-

ceeds a given threshold, a potential boundary of the

contained object can be assumed, as illustrated in ﬁg-

ure 3. The approximation is then discarded and traver-

sal continues.

3.2 Two-level LS Structure

The main idea of our work is to combine the LS

with previously generated two-level BVHs, that ar-

range logical scene objects on the ﬁrst level and in-

volve scene primitives only within the second level.

The second-level object BVH nodes have a tighter ﬁt

to their content, which makes them smaller in size

and more beneﬁcial for the LS. This reduces the to-

tal number of LS nodes needed while simultaneously

improving approximation accuracy. We differentiate

four different setups of the data structure, as also vi-

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

230

Flat BVH

Two-Level BVH BVH-LS (2)

Two-Level BVH-LS (1)

Object Root Node

BVH

Top-Level BVH Geometry

Figure 4: Acceleration structures used. Flat BVHs are the most common structures. Two-level BVHs are used for rigid

object dynamics, granting minimal tree updates for object movements but worse runtime performance. The LS improves

performance, due to early approximation-based traversal termination. Our work combines the LS and two-level BVHs, to gain

fast performance and higher approximation accuracy. The numbers show the integration depth within (object-) hierarchies.

sualized in ﬁgure 4:

1. Flat BVH, as state-of-the-art ray tracing structure;

2. Two-level BVH, better suited for rigid object dy-

namics and instancing, but with higher tree com-

plexity and lower runtime performance;

3. Flat BVH with LS integration, for fast blocker ap-

proximations, but with higher memory consump-

tion and visible errors due to approximation, as in

(Keul et al., 2018);

4. Two-level BVH with LS integration, same advan-

tages as two-level BVHs and ﬂat BVH-LS, with

less approximation errors, presented in our work.

The LS adaption improves second-level object

BVHs with LS nodes, that are integrated in a speciﬁc

hierarchy depth. Similar to other two-level structures,

the two-level LS is well suited for rigid object dynam-

ics and instancing. This way, every unique logical ob-

ject contains its own BVH-LS, whereas the top-level

hierarchy stores references to those object structures

in its leafs. Therefore, the two-level LS beneﬁts sig-

niﬁcantly from object instancing, as every memory

consuming LS is only stored once per geometrical ob-

ject. Our results further demonstrate, that the perfor-

mance beneﬁt gained through LS approximations out-

performs traditional BVHs, even when used in typi-

cally slower two-level data structures. Because of the

tighter ﬁt to contained objects, the two-level LS im-

proves approximation accuracy, even when less nodes

are generated and less memory is consumed. These

theoretical considerations are summarized in table 1.

As shown in ﬁgure 4, two-level structures in gen-

eral result in more unbalanced and partly deeper tree

hierarchies compared to their ﬂat counterpart. This is

especially problematic when complex and simple ob-

jects are used simultaneously. During SIMT traver-

sal, kernels are not able to beneﬁt from thread co-

herency, which decelerates the overall traversal step.

Table 1: Expected results for the data structures. In terms of

quality, ﬂat BVHs and two-level BVHs give correct results,

while LS techniques have better runtime performance.

Memory

Performance

Quality

F-BVH 888 8899 888

2L-BVH 888 8999 888

F-LS 899 8888 899

2L-LS 889 8889 889

Our technique represents a solution to this two-level

imbalance, as the LS limits the maximum object hi-

erarchy depth to a speciﬁed level. This, along with

the approximation-based early ray termination, im-

proves SIMT thread coherency and traversal perfor-

mance, due to less overhead caused by bad thread par-

allelism. Concerning BVH initialization, any of the

existing construction or optimization algorithms can

be used. However, bad BVH quality in general re-

sults in larger bounding volumes, leading to bigger

shafts and therefore worse LS approximation accu-

racy. Consequently, a high-quality BVH builder gen-

erates a lower number of nodes, that additionally have

better scene coverage and are smaller in size, which

improves runtime performance and approximation ac-

curacy. Hence, less LS nodes are needed for better

quality and runtime performance. As the top-level

BVH has no connection to the LS, it can be created

with any build algorithm.

3.3 Parameter Discussion

As in previous work, there are two different parame-

ters for our technique: the LS integration depth and

the subdivision parameter. The integration depth is

the depth within the base structure that stores LS

nodes instead of children information. A higher depth

results in a deeper hierarchy, more LS nodes and

therefore higher memory consumption and lower run-

Combining Two-level Data Structures and Line Space Precomputations to Accelerate Indirect Illumination

231

2L-LS (0) 2L-LS (4) 2L-LS (8)

Figure 5: Indirect lighting results of different LS integration

depths (marked in brackets - 0 means root node stores LS).

Higher depths grant better approximations and less errors.

As shown, the needed integration depth is scene dependent.

time performance. However, image quality improves,

due to higher shaft precision. This is demonstrated

in ﬁgure 5. The subdivision parameter N determines

LS accuracy. Shafts are created from the surface

patches of the node’s subdivided bounding volume.

Higher subdivision leads to smaller patches and there-

fore thinner shafts and more precise approximations.

Nevertheless, signiﬁcantly more shafts are generated

and more memory is consumed. In agreement with

previous work, we favor two different parameter val-

ues for N, targeting either low memory consumption

(N = 6) or higher approximation accuracy (N = 10).

The differences in quality are presented in ﬁgure 8.

4 PATH TRACING WITH

MULTIPLE DATA

STRUCTURES

The early traversal termination with candidate ap-

proximation of the LS leads to a signiﬁcant improve-

ment in tracing performance, however, at the cost of

approximation errors. By using an adequate param-

eter set, these errors can be greatly reduced, while

in turn memory consumption increases tremendously.

Keeping this in mind, our goal is to use different pa-

rameter sets and data structures in different segments

of path tracing. With this, we can use the BVH, in sit-

uations that need correct results and the LS with dif-

ferent parameter sets depending on whether the focus

lies on accuracy or tracing performance.

During path tracing, there are several ways to de-

termine, whether a ray can be approximated or should

be calculated accurately. It is possible to use the

evaluation of the probability density function of the

current path segment or to distinguish its type, i.e.

whether a shadow, reﬂected or diffuse ray is evalu-

Direct

BVH

High Quality LS

Low Quality LS

Figure 6: 3-bounce path using different data structures de-

pending on the bounce depth. Primary and direct shadow

rays use rasterization techniques. BVH path segments have

precise results, while LS segments are traced faster.

1. Bounce 2. Bounce

3. Bounce

Figure 7: Results of different bounce depths of LS us-

age. The number marks the path depth, from which on

approximation-based LS (2L-LS (4)) is used. Later usage

of LS results in less errors as well as less performance gain.

ated. For simplicity, we make this distinction based

on the bounce depth of the current path segment in a

backward path tracing system. There, the ﬁrst bounce

(indirect illumination through one object) and its ac-

cording shadow ray are calculated correctly with a

BVH. The second bounce (indirect illumination with

two intermediate objects) is less relevant and there-

fore calculated with the faster approximation-based

LS. Further rays have decreasing relevance in illumi-

nation and are calculated with a lower-quality higher-

performance LS. This process is illustrated in ﬁgure

6 and with the resulting errors demonstrated in ﬁgure

7. Primary rays and the according shadow rays can be

rendered with rasterization-based approaches, which

are fast and generate correct results.

5 RESULTS

We tested and compared our two-level LS approach

(2L-LS) as approximation-based method for indirect

lighting calculation. Our test setup is comparable to

(Keul et al., 2018), where the single-level ﬂat BVH-

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

232

Table 2: Construction results of the single-level ﬂat BVH-LS (F-LS) and the two-level BVH-LS (2L-LS) in terms of the total

number of generated LS, memory consumption (in MB) and build time (in s). The integration depths are shown in brackets.

FIREPLACE

143k triangles

49 objects

BREAKFAST

269k triangles

45 objects

LIVING ROOM

576k triangles

78 objects

SALLE DE BAIN

1231k triangles

39 objects

BUNNY SCENE

4467k triangles

64 instances

Structure

#LS

N = 6, ≈ 38k shafts per LS

F-LS (8) 226 28.1 0.82 186 26.4 1.58 198 38.4 1.58 207 53.4 3.07 245 141.2 10.29

F-LS (10) 763 80.9 2.17 641 70.8 4.11 620 81.5 2.77 706 98.0 4.97 954 199.5 13.05

F-LS (12) 2223 206.0 5.83 2185 214.3 12.49 1936 199.1 6.33 2628 238.7 11.90 3750 407.4 23.78

2L-LS (0) 49 8.4 0.81 45 11.0 1.11 78 22.8 1.95 39 35.5 2.64 9 2.5 0.24

2L-LS (4) 526 53.4 1.62 648 68.5 2.89 940 109.2 3.60 467 76.1 3.87 24 3.8 0.29

2L-LS (8) 4195 344.9 8.27 7351 646.5 21.78 7373 631.7 15.92 6296 490.5 18.55 264 20.2 0.98

N = 10, ≈ 300k shafts per LS

F-LS (4) 16 18.0 0.52 16 21.8 1.12 16 29.6 1.36 16 46.9 2.59 16 132.9 9.83

F-LS (6) 63 57.2 1.24 54 51.4 2.70 59 70.1 2.05 59 85.1 3.31 63 170.9 11.01

F-LS (8) 226 184.8 3.78 186 147.1 7.89 198 190.6 4.31 207 194.2 6.66 245 294.4 15.39

2L-LS (0) 49 38.0 1.24 45 35.8 2.05 78 74.7 2.71 39 62.3 3.21 9 7.0 0.30

2L-LS (4) 526 366.7 6.50 648 450.0 14.10 940 708.4 12.66 467 362.1 10.45 24 16.7 0.59

2L-LS (6) 1634 1058.4 19.62 2328 1549.6 47.93 2931 1926.1 37.25 1719 1079.0 32.82 72 42.6 1.49

LS (F-LS) was proposed, which is our main com-

petitor in terms of performance. For a complete

evaluation we also compare against the pure under-

lying structures (F-BVH and 2L-BVH) which pro-

duce approximation-free results. For all BVH al-

gorithms we use state-of-the-art techniques targeting

good tree quality and fast runtime performance, as

shown in (Aila et al., 2012). We compare all meth-

ods in terms of traversal performance, memory con-

sumption and build time. Additionally, we compare

the approximation-based results per bounce to ground

truth data and show, that approximations produced by

our technique are more precise than those of F-LS.

The chosen test scenes are commonly used ar-

chitectural scenes (FIREPLACE ROOM, BREAKFAST

ROOM, LIVING ROOM and SALLE DE BAIN) and a

scene with instanced objects (BUNNY SCENE). These

scenes consist of multiple manually separated ob-

jects, which are used as second-level object BVHs,

as shown in table 3. We use a multiple-bounce path

tracing system for indirect lighting calculation with

different data structures that can be used in different

path depths, as explained in section 4. Image reso-

lution was 1024 × 1024. Primary and direct shadow

rays are not computed via ray tracing, as there are

faster rasterization-based approaches. The test sys-

tem consists of an Intel i7-6800k 3.6 GHz CPU and a

NVidia GeForce GTX 1080 GPU using GLSL Com-

pute Shaders. To guarantee a fair comparison of the

used data structures, we do not use any third party im-

plementations. Overall, the presented results conﬁrm

the theoretical considerations from section 3.2.

Table 3: Path tracing performance and per bounce error of

varying LS integration depth (in brackets) and subdivision

parameter (N) averaged over all scenes.

ALL SCENES Perf RMSE on Bounce

Structure MRays/s 1 2 3

F-BVH 70.7 – – –

2L-BVH 34.3 – – –

F-LS (8) , N = 6 377.0 .030 .011 .004

F-LS (10) , N = 6 313.0 .025 .008 .002

F-LS (12) , N = 6 268.3 .021 .006 .002

2L-LS (0) , N = 6 208.0 .023 .008 .003

2L-LS (4) , N = 6 120.2 .012 .004 .002

2L-LS (8) , N = 6 92.5 .009 .003 .002

F-LS (4) , N = 10 622.6 .044 .019 .006

F-LS (6) , N = 10 440.6 .033 .012 .004

F-LS (8) , N = 10 346.6 .018 .007 .002

2L-LS (0) , N = 10 201.8 .015 .005 .002

2L-LS (4) , N = 10 117.7 .008 .003 .001

2L-LS (6) , N = 10 102.2 .006 .002 .001

Table 2 shows construction results of our method

compared to the single-level LS. We used two differ-

ent subdivision parameters (N = 6 and N = 10) and

three different integration depths, leading to mostly

similar memory consumption for all data structures,

which makes them comparable. Obviously, mem-

ory usage and build time are dependent on the total

number of nodes containing LS information. Hence,

scenes using object instancing have signiﬁcantly less

memory consumption and by far lower build times in

two-level structures, as shown by the BUNNY SCENE.

Table 3 and ﬁgures 1 and 8 show the runtime

Combining Two-level Data Structures and Line Space Precomputations to Accelerate Indirect Illumination

233

BVH

Reference

F-LS (8)

N = 6

F-LS (10)

N = 6

2L-LS (0)

N = 6

2L-LS (4)

N = 6

F-LS (4)

N = 10

F-LS (6)

N = 10

2L-LS (0)

N = 10

2L-LS (4)

N = 10

3. Bounce 2.Bounce 1.Bounce

Figure 8: Per bounce results of F-LS and 2L-LS using different parameter sets. Obviously, higher integration depths (in

brackets) and subdivision parameters (N) lead to less errors in the resulting images. In turn, higher parameters in general

result in larger memory consumption, as illustrated by table 2. The exact performance and error values are shown in table 3.

results, i.e. tracing performance and error values

for indirect rays. Approximation-based errors pro-

duced by the LS are speciﬁed by RMSE (root-mean-

squared error) values, based on the per-pixel differ-

ences to ground truth data. The bounce depth marks

the depth from which on the shown data structure is

used - earlier bounces use the BVH for correct re-

sults. It is noticeable, that later bounces traced with

approximation-based LS structures lead to insigniﬁ-

cant errors but much faster tracing performance. Two-

level structures in general have inferior performance

in comparison to their single-level ﬂat counterparts,

as explained in section 3.2. In turn, they produce less

errors in general, even with lower depth integration

parameters. Our results also show that higher subdivi-

sion parameters need signiﬁcantly more memory and

therefore lower integration depths are used, which in

turn reduces approximation accuracy leading to worse

image results. Due to this, higher subdivision pa-

rameters are more suitable for later path segments,

in which the lower integration depth leads to better

performance, while the higher subdivision preserves

accuracy to a higher degree. Summarized results for

different data structures used in different bounces, av-

eraged over all scenes, are shown in table 4.

6 CONCLUSION

We proposed a novel combination of two-level BVHs

and recently introduced LS approximations. We ex-

plained how the combination beneﬁts from both of

their advantages, while also reducing their disadvan-

tages. The object-level LS reduces approximation er-

rors and increases tracing performance by limiting

the integration depth. Consequently, our approach re-

Table 4: Summarized path tracing results with different

data structures for different path segments averaged over all

scenes. Used LS structures are: 2L-LS 1 = 2L-LS(4) N = 6,

2L-LS 2 = 2L-LS(0) N = 10, F-LS = F-LS(8) N = 6.

Data Structure in bounce Average of all scenes (tables 2 and 3)

1 2 3 Memory (MB) MRays/s RMSE

F-BVH F-BVH F-BVH 21.0 70.7 –

F-BVH F-BVH 2L-LS 1 83.2 87.2 .002

F-BVH 2L-LS 1 2L-LS 1 83.2 103.7 .004

F-BVH 2L-LS 1 2L-LS 2 126.8 130.9 .004

F-BVH 2L-LS 2 2L-LS 2 64.6 158.1 .005

F-BVH 2L-LS 1 F-LS 140.7 189.3 .006

F-BVH F-LS F-LS 78.5 274.9 .011

sults in better runtime performance compared to tradi-

tional BVHs, with less memory consumption and ap-

proximation errors compared to single-level LS struc-

tures. Furthermore, we presented a method to con-

nect the strengths of different structures in a multiple-

bounce path tracing system, with a per bounce se-

lection that indicates, whether accurate BVH or fast

approximation-based LS results are used.

In an extensive evaluation we presented the use-

fulness of these approaches, showing different pa-

rameters and per bounce results for the ﬂat BVH-LS

and two-level BVH-LS combination and compared

the results with state-of-the-art techniques. In that,

our evaluation shows that our two-level approach is

an improvement of the ﬂat technique. Moreover, the

two-level approach makes LS approximations usable

in scenes with rigid object animations and especially

useful coupled with object instancing. Finally, the per

bounce usage reduces approximation errors at a high

level, while at the same time enables better LS usage

in combination with traditional data structures.

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

234

REFERENCES

Aila, T., Karras, T., and Laine, S. (2013). On quality metrics

of bounding volume hierarchies. In Proc. High Perfor-

mance Graphics.

Aila, T., Laine, S., and Karras, T. (2012). Understanding

the efﬁciency of ray traversal on gpus–kepler and fermi

addendum. NVIDIA Technical Report.

Bashford-Rogers, T., Debattista, K., Harvey, C., and

Chalmers, A. (2011). Approximate visibility grids for

interactive indirect illumination. In Conf. Games and

Virtual Worlds for Serious Applications.

Benthin, C., Woop, S., Wald, I., and

Afra, A. T. (2017).

Improved two-level bvhs using partial re-braiding. In

High Performance Graphics.

Billen, N. and Dutr

e (2016). Visibility acceleration using

efﬁcient ray classiﬁcation. Department of Computer

Science, KU Leuven.

Bittner, J., Hapala, M., and Havran, V. (2013). Fast

insertion-based optimization of bounding volume hier-

archies. In Computer Graphics Forum.

Cohen, M. F. and Wallace, J. R. (2012). Radiosity and real-

istic image synthesis. Elsevier.

Fuetterling, V., Lojewski, C., Pfreundt, F.-J., and Ebert,

A. (2016). Parallel spatial splits in bounding volume

hierarchies. In Eurographics Symposium on Parallel

Graphics and Visualization.

Gaitatzes, A., Andreadis, A., Papaioannou, G., and

Chrysanthou, Y. (2010). Fast approximate visibility on

the gpu using precomputed 4d visibility ﬁelds. WSCG.

Ganestam, P., Barringer, R., Doggett, M., and Akenine-

oller, T. (2015). Bonsai: rapid bounding volume hier-

archy generation using mini trees. Computer Graphics

Techniques 4.

Ganestam, P. and Doggett, M. (2016). Sah guided spatial

split partitioning for fast bvh construction. In Computer

Graphics Forum.

Garanzha, K., Pantaleoni, J., and McAllister, D. (2011).

Simpler and faster hlbvh with work queues. In Proc.

High Performance Graphics.

Gu, Y., He, Y., Fatahalian, K., and Blelloch, G. (2013). Ef-

ﬁcient bvh construction via approximate agglomerative

clustering. In Proc. High Performance Graphics.

Havran, V. (2000). Heuristic ray shooting algorithms. PhD

thesis, Czech Technical University in Prague.

Hendrich, J., Meister, D., and Bittner, J. (2017). Parallel bvh

construction using progressive hierarchical reﬁnement.

In Computer Graphics Forum.

Kalojanov, J., Billeter, M., and Slusallek, P. (2011). Two-

level grids for ray tracing on gpus. In Computer Graph-

ics Forum.

Karras, T. and Aila, T. (2013). Fast parallel construction

of high-quality bounding volume hierarchies. In Proc.

High Performance Graphics.

Kay, T. L. and Kajiya, J. T. (1986). Ray tracing complex

scenes. SIGGRAPH Comput. Graph.

Keul, K., Klee, N., and M

uller, S. (2017). Soft shadow com-

putation using precomputed line space visibility infor-

mation. Journal of WSCG.

Keul, K., Koß, T., and M

uller, S. (2018). Fast indirect light-

ing approximations using the representative candidate

line space. Journal of WSCG.

Keul, K., M

uller, S., and Lemke, P. (2016). Accelerating

spatial data structures in ray tracing through precom-

puted line space visibility. WSCG.

Laine, S., Siltanen, S., Lokki, T., and Savioja, L. (2009).

Accelerated beam tracing algorithm. Applied Acoustics.

Lauterbach, C., Garland, M., Sengupta, S., Luebke, D., and

Manocha, D. (2009). Fast bvh construction on gpus. In

Computer Graphics Forum.

Meister, D. and Bittner, J. (2017). Parallel locally-ordered

clustering for bounding volume hierarchy construction.

IEEE Trans. on Visualization and Computer Graphics.

Meister, D. and Bittner, J. (2018). Parallel reinsertion for

bounding volume hierarchy optimization. In Computer

Graphics Forum.

Mortensen, J., Khanna, P., Yu, I., and Slater, M. (2007). A

visibility ﬁeld for ray tracing. In Computer Graphics,

Imaging and Visualisation.

Pantaleoni, J. and Luebke, D. (2010). Hlbvh: hierarchical

lbvh construction for real-time ray tracing of dynamic

geometry. In Proc. High Performance Graphics.

Parker, S. G., Bigler, J., Dietrich, A., Friedrich, H., Hobe-

rock, J., Luebke, D., McAllister, D., McGuire, M., Mor-

ley, K., Robison, A., et al. (2010). Optix: a general pur-

pose ray tracing engine. ACM Transactions on Graph-

ics (TOG).

Pharr, M., Jakob, W., and Humphreys, G. (2016). Physi-

cally based rendering: From theory to implementation.

Morgan Kaufmann.

Reshetov, A., Soupikov, A., and Hurley, J. (2005). Multi-

level ray tracing algorithm. ACM Transactions on

Graphics (TOG).

Ritschel, T., Dachsbacher, C., Grosch, T., and Kautz, J.

(2012). The state of the art in interactive global illu-

mination. In Computer Graphics Forum.

Stich, M., Friedrich, H., and Dietrich, A. (2009). Spatial

splits in bounding volume hierarchies. In Proc. High

Performance Graphics.

Vinkler, M., Bittner, J., and Havran, V. (2017). Extended

morton codes for high performance bounding volume

hierarchy construction. In High Performance Graphics.

Vinkler, M., Havran, V., and Bittner, J. (2016). Perfor-

mance comparison of bounding volume hierarchies and

kd-trees for gpu ray tracing. In Computer Graphics Fo-

rum.

Wald, I. (2007). On fast construction of sah-based bound-

ing volume hierarchies. In 2007 IEEE Symposium on

Interactive Ray Tracing.

Wald, I. (2012). Fast construction of sah bvhs on the intel

many integrated core (mic) architecture. IEEE Trans-

actions on Visualization and Computer Graphics.

Wald, I., Benthin, C., and Slusallek, P. (2003). Distributed

interactive ray tracing of dynamic scenes. In Proc.

IEEE Symposium on Parallel and Large-Data Visual-

ization and Graphics.

Wald, I., Woop, S., Benthin, C., Johnson, G. S., and Ernst,

M. (2014). Embree: a kernel framework for efﬁcient

cpu ray tracing. ACM Transactions on Graphics (TOG).

Wodniok, D. and Goesele, M. (2017). Construction of

bounding volume hierarchies with sah cost approxima-

tion on temporary subtrees. Computers & Graphics.

Yu, I., Cox, A., Kim, M. H., Ritschel, T., Grosch, T., Dachs-

bacher, C., and Kautz, J. (2009). Perceptual inﬂuence

of approximate visibility in indirect illumination. ACM

Transactions on Applied Perception (TAP).

Zlatu

ska, M. and Havran, V. (2010). Ray tracing on a

gpu with cuda–comparative study of three algorithms.

WSCG.

Combining Two-level Data Structures and Line Space Precomputations to Accelerate Indirect Illumination

235