Noise Attenuation using Genetic Algorithm in CT Image

A. A. Saraiva

1 a

, M. S. de Oliveira

2 b

, J. V. M. Sousa

1 c

, N. M. Fonseca Ferreira

4 d

Antonio Valente

3,5 e

and Salviano Soares

3 f

State University of Piaui, Piripiri, Piaui, Brazil

University of S

ao Paulo, Ribeir

ao Preto, S

ao Paulo, Brazil

UTAD University, Vila Real, Portugal

Institute of Engineering of Coimbra / Polytechnic Institute of Coimbra, Portugal. Knowledge Engineering and

Decision-Support Research Center (GECAD) of the Institute of Engineering, Polytechnic Institute of Porto

INESC Technology and Science (INESC TEC), Porto, Portugal

INESC Technology and Science (INESC TEC), Porto, Portugal,

School of Science and Technology, UTAD University, Vila Real, Portugal

Keywords:

Medical Images, Genetic Algorithm, Noise Removal.

Abstract:

The techniques of image ﬁltering have undergone an explosive growth in the last years to make new advances

and challenges. This is due to the fact, among several other reasons, the increase of the volume of images

coming from several sources. Digital images have been used for a variety of purposes, from the storage

of souvenirs to accurate medical exams. However, Images may be corrupted due to several factors. The

challenge of suppression or noise attenuation has led to the search for improved techniques in order to preserve

important characteristics of the image, but, on the other hand, there is no solution available to completely solve

the problem, boosting the production of the work proposed here. In this paper proposes a method for noise

attenuation in computed tomography images using a hybrid genetic algorithm, the proposed method seeks to

optimize the results in the space of solutions composed by a series of techniques of noise ﬁltering. At the

end the proposed method is compared statistically with two other competing methods and after the resulting

ﬁltered images are shown.

1 INTRODUCTION

The techniques of image ﬁltering have undergone an

explosive growth in the last years to make new ad-

vances and challenges. This is due to the fact, among

several other reasons, the increase of the volume of

images coming from several sources. Digital images

have been used for a variety of purposes, from the

storage of souvenirs to accurate medical exams. How-

ever, Images may be corrupted due to several factors.

The challenge of suppression or noise attenuation

has led to the search for improved techniques, with the

objective of preserving important characteristics of

the image, improving visual perception in medicine,

https://orcid.org/0000-0002-3960-697X

https://orcid.org/0000-0003-2389-3334

https://orcid.org/0000-0002-5164-360X

https://orcid.org/0000-0002-2204-6339

https://orcid.org/0000-0002-5798-1298

https://orcid.org/0000-0001-5862-5706

for example, to increase the clarity of anatomical

structures present in DICOM images (

Ozmen and

Ozs¸en, 2018; Kiragu et al., 2017a; Zhang et al., 2017;

Baselice et al., 2017a), reconstruction (Barca et al.,

2017) and detection of alcohol (Kubicek et al., 2018).

However, there is no solution available to completely

solve the problem, thus motivating the search for im-

provements in existing methods, and in particular,

boosting the production of the work proposed here.

In the literature there are techniques based on meta

heuristics, as is the example of the technique de-

scribed in (Saraiva et al., 2018), where the authors

demonstrate a bioinspired hybrid method formed by a

set of ﬁlters for noise attenuation in medical images.

The ﬁltering methods by means of wavelets are

also widely used (Khmag et al., 2016; Jain and Tyagi,

2016; Broughton and Bryan, 2018), in addition to

several other methods proposed for the solution of

the noise attenuation problem (Zafari et al., 2017;

Fajardo-Delgado et al., 2016; Liu, 2015; Khmag

140

Saraiva, A., S. de Oliveira, M., Sousa, J., Ferreira, N., Valente, A. and Soares, S.

Noise Attenuation using Genetic Algorithm in CT Image.

DOI: 10.5220/0007346301400148

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 140-148

ISBN: 978-989-758-353-7

et al., 2017;

Ozmen and

Ozs¸en, 2017; Dimililer et al.,

2017; Kiragu et al., 2017b).

In the technique demonstrated in (Baselice et al.,

2017b), the authors explore a method of noise reduc-

tion in magnetic resonance imaging based on the ran-

dom markov ﬁeld (RMF), next to it is proposed the

maximum a posteriori estimator (MAP) to regularize

the 3D amplitude MRI acquisition stacks.

The peculiarity of the method is the deﬁnition of

a local Gaussian random 3D markov ﬁeld capable of

adapting to local image behavior considering a map

of hyperparameters that describe the correlation be-

tween each pixel and its neighborhood, thus allowing

adjustment of ﬁlter intensity, preserving smooth ar-

eas, edges and small details in an unsupervised man-

ner.

In addition to the previously mentioned method,

an innovative technique is demonstrated in (Badretale

et al., 2017), the technique, according to the authors,

learns directly from an end-to-end mapping of the im-

ages in a deep convolutional neural network, in this

way, when learning a series of high and low level re-

sources of a data set with images, the proposed al-

gorithm shows itself capable of creating high quality

ﬁltered images.

In this paper, a hybrid genetic algorithm is ap-

plied for gaussian noise attenuation in computerized

tomography medical image and compared with two

other methods in the literature through the use of eval-

uation metrics MSE (Talbi et al., 2015), PSNR (Fe-

dorov and Rodyhin, 2016) and SSIM (Hore and Ziou,

2010).

The GA was chosen because of its ability to

perform well in large optimization problems where

search space is unknown. In addition, the ﬁlter opti-

mization problems have been solved successfully us-

ing this technique (Momeni et al., 2017; Mahani et al.,

2017; de Paiva et al., 2016; Uzun and Akg

un, 2016).

The proposed method combines the genetic meta-

heuristic algorithm with several ﬁltering techniques

available in the literature to solve the attenuation

problem with the objective of producing high qual-

ity results through the search for possible solutions to

improve the results generated.

The hypothesis of the work , is that the proposed

model is able to present satisfactory results when

compared to other methods present in the literature

in several test cases.

Thus, in the next section, the methodology is ex-

plained. Results and discussion of results are pre-

sented in sections 3 and 4, respectively, and section

5 presents the conclusion.

2 GENETIC ALGORITHM

Genetic algorithms are the computational models

family inspired by the theory of evolution of the

species described by Charles Darwin (Goldberg,

1989). This technique is formed by algorithms in-

spired by the mechanisms of natural evolution and ge-

netic recombination, in this way it provides an adap-

tive search method that is based on the principle of

reproduction and survival of the ﬁttest.

These algorithms use a population of potential

solutions, each one codiﬁed, according to a spe-

ciﬁc problem, into a chromosome-like data structure.

These structures envolving using genetic operators

where preservation and improvement of critical infor-

mation are promoted.

According to (Santos, 2015), in Darwin’s theory

the selection principle privileges the ﬁttest individuals

with greater longevity, and therefore, they are more

likely to reproduce. Individuals with more offspring

are more likely to perpetuate their genetic informa-

tion in subsequent generations. These genetic infor-

mation store the identity of each individual and are

represented by chromosomes. Thus, these principles

are taken into account for the construction of algo-

rithms capable of ﬁnding the optimal solution for a

given problem through the evolution of populations

of solutions encoded through artiﬁcial chromosomes.

Represented as a chromosome, each potential so-

lution is subjected to an evolutionary process involv-

ing several steps, known as selection, crossover (sex-

ual recombination) and mutation.

At the end, after performing several a evolution

cycle (iterations or generations), the ﬁttest individuals

are retained and the worst are excluded.The classical

GA is exempliﬁed by algorithm 1 and described some

steps are below.

Algorithm 1: Genetic Algorithm Classic.

1: generation ← 0;

2: Generate random initial population;

3: Calculate the ﬁtness of individuals in the popula-

tion;

4: while generation < generationMax do

5: Select eligible parents;

6: Perform crossover between selected parents;

7: Apply mutation on the children generated;

8: Calculate children’s ﬁtness;

9: Replace all/some parent individuals in the

current population with children;

10: generation ← generation + 1

11: end while

• Generate Population: (Line 2) Step where n in-

Noise Attenuation using Genetic Algorithm in CT Image

141

dividuals are generated randomly, in this step each

generated individual represent a potential solution

of the problem and have their chromosomes en-

coded as binary string.

• Evaluation: (Line 3 and 8) The evaluation of the

individual is generally determined by evaluating

an objective function that represents the problem

and aims to generate a measure of ﬁtness of each

individual in the current population that guide the

search process.

• Selection: The main forms of parent selection are

the selection by ranking, tournament and roulette

(De Jong, 2012) and take into account the ﬁtness

of each individual for its execution. These meth-

ods are described in sequel.

– Roulette: In the roulette selection method, ex-

empliﬁed in Fig 1, all individuals in the popu-

lation have a probability of being selected for

reproduction. For that each individual is rep-

resented in roulette proportionally to its ﬁtness

value, then, for each individual to select, the

roulette wheel is rotated and the chosen indi-

vidual is the one whose roulette area is pointed

by the roulette needle.

Figure 1: Roulette selection method.

– Tournament: In the tournament method, a

number n of individuals is chosen in a random

fashion, and the one that gets the best ﬁtness

among them will be chosen. This process will

be repeated until the required amount of parents

is reached.

– Ranking: The ranking method behaves differ-

ently, all individuals are ranked, the worst will

be assigned to rank 1, the second worst will be

assigned to rank 2 and the better will be in the

maximum rank. The probability selection of an

individual is given by its rank over the sum of

all ranks.

• Crossover: The crossover (mutation) operator

(item below) plays a fundamental role in a GA,

through which it is possible for the population to

diversify and maintain adaptation characteristics

through generations.

Considered the predominant operator, the

crossover is responsible for the creation of new

individuals by the blending of characteristics

of the parent individuals by digitally simulating

the natural process of gene blending (Eiben

et al., 2003). Some popular crossover types are:

1-point crossover, n-point crossover, and uniform

crossover (Santos, 2015).

Exempliﬁed by the Fig 2, the 1-point crossing is

the method where a point is randomly determined

and from this point of division of the characteris-

tics of the parents, then a child is formed by the

initial part of the ﬁrst parent and by the ﬁnal part

of the second parent. The other child is formed by

the remaining material of the previous combina-

tion.

Figure 2: 1 point crossing method example.

The n-point crossover works somewhat like the

one illustrated above, but in this case instead of

just choosing a split point, n points are selected for

crossing and parenting. On the other hand in the

uniform crossover the individual child has each

element with 50% chance of belonging to the ﬁrst

or second parent.

• Mutation: The mutation operation simply ran-

domly modiﬁes a characteristic of the chromo-

some in which it is being applied, this step is im-

portant to create new values of features previously

non-existent or even that arise in low quantity

(Eiben et al., 2003). As in the crossing step, the

mutation occurs proportionally at a given proba-

bility rate. Fig 3 exempliﬁes the use of the muta-

tion.

Figure 3: Example of mutations.

In this step it is also possible to use more than one

operator, such as the Gaussian mutation operator, the

technique that draws a new value for the characteristic

from a Gaussian distribution N (µ, σ) with average µ

and standard deviation σ and the operator mutation

uniform.

BIODEVICES 2019 - 12th International Conference on Biomedical Electronics and Devices

142

3 METRIC METHODS OF

EVALUATION

The image ﬁltering search aims to reduce the number

of artifacts to represent an image, removing the noise,

as much as possible. The ideal is to get the resulting

image as close as to the original image. One of the

ways to quantify the ﬁltering is given by the proxim-

ity measurement using the Mean Square Error (MSE)

(Talbi et al., 2015) which can be deﬁned mathemati-

cally by:

MSE =

m−1

∑

x=0

n−1

∑

y=0

(I(x, y) − K(x, y))

(1)

In this equation I represents the original image and

K the ﬁnal image to be compared. The x and y are two

matrices of size MxN, respectively representing the

original x-channel and the y-channel to be compared

(after ﬁltering).

Another way to compare the quality of the im-

ages is the Peak Signal to Noise Ratio (PSNR) what is

usually a measure of image quality and can be repre-

sented by equation (2) (Fedorov and Rodyhin, 2016).

The PSNR ideal of comparison presents an optimum

value the higher its is your value.

PSNR = 10log

MAX

MSE

= 20 log

MAX

MSE

(2)

In which, MAX represents the maximum possible

value of the pixel in the image and MSE is the value

resulting from equation (1).

The main from them is that large distances be-

tween pixel intensities do not necessarily mean that

the content of the images be dramatically different.

It is important to note that a value of 0 for MSE indi-

cates perfect similarity. A value greater than 1 implies

smaller similarity and will continue to grow as the

mean difference between pixel intensities increases as

well.

In order to remedy some of the problems asso-

ciated with MSE for image comparison, one has the

Structural Similarity Index (SSIM). The SSIM is ob-

served by equation (3) (Tiwari et al., 2015).

SSIM(x, y) =

(2µ

+ c

)(σ

+ c

)

(µ

+ µ

+ c

)(σ

+ σ

+ c

)

(3)

In the equation (3) µ represents the mean, σ sym-

bolizes the standard deviation and σ

the covariance.

And c

with c

represent constants that avoid the in-

stability of values.

Unlike MSE, the SSIM value can range from -1 to

1, where 1 indicates perfect likeness.

The essence of SSIM is to model the perceived

change in the structural information of the image,

while the MSE is actually estimating the perceived

errors. There is a subtle difference between the two,

but the results can be great.

In addition, the SSIM is used to analyze small sub-

samples instead of the entire image as in MSE. The

parameters used are the mean of the pixel intensities,

the variance of the intensities, together with the co-

variance. In this way, a more robust approach is ob-

tained capable of explaining the changes in the struc-

ture of the image, instead of just the perceived change.

For the quantitative comparison of the ﬁltering

methods in this article, the objective metrics evalua-

tion methods MSE, PSNR and SSIM were used. Such

methods are known as full reference, because they

consider the original image as a reference.

4 METHODOLOGY

The proposed genetic algorithm (GAP) in this work is

based on the technique developed in (de Paiva et al.,

2016), where each individual of the population is a

two-dimensional image, however, as a contribution,

in the algorithm proposed here, the idea was recon-

structed and modiﬁed so that It is possible to perform

ﬁltering on a set of DICOM images automatically.

In choosing the size of the tournament, Paiva

found that the worst case of the tournament size 3

tends to be better than the worst of the others. How-

ever, testing the different local search rates, although

all the results were very close, the value ratio of 0.6

was the one that obtained the best results in compar-

ison to the others. Furthermore, a superiority in the

results with the beta 1.5 parameters and the popula-

tion size is demonstrated.

In this sense, based on the analysis and the results

demonstrated by the author, the proposed parameters

were used here as proposed values due to the demon-

stration of the effectiveness of each change.

The proposed method has its beginning when a se-

ries of noisy DICOM images are used as input to the

method and the other individuals of the population are

created from applied mutation operators. In algorithm

2, the pseudocode of the algorithm is shown and its

steps are described.

The beginning of the GAP consists of creating the

initial population in two steps: ﬁrst, the noise image

is used as input for three noise smoothing methods

below, thus, at the end of the ﬁrst stage, the population

has three individuals.

• 3D median ﬁlter (Jiang and Crookes, 2006)

• BM4D (Maggioni et al., 2013)

Noise Attenuation using Genetic Algorithm in CT Image

143

• Ellipsoid (Yang et al., 2008)

After the ﬁrst stage, one of the outputs of these

techniques is chosen randomly. It is then subjected

to a mutation operator also selected at random so that

quality changes are made to the previously generated

output. As mutation operators, three types were used:

• Gaussian ﬁlter: the ﬁlter that has the effect of

smoothing the image artifact through a Gaussian

function.

• Average ﬁlter: the technique that allows the

smoothing of noises in images by means of cal-

culating the average of all the ﬁlters of a given

vicinity for each pixel of the original image.

• Intensity change: is a linear operation that con-

sists of multiplying all the pixels of the image by

the same numerical factor.

At the end of this stage, the resulting image is

added to the existing population, then the mutation

process is repeated until the population reaches the

stipulated size, thus forming a hybrid population,

formed by the output of the three methods of suppres-

Algorithm 2: Genetic Algorithm Proposed (GAP).

1: function GAP(DicomPath)

2: images ←ReadAllFiles(DicomPath)

3: Population ←createPopulation(images)

4: best ←Population.best

5: while elapsedTime < maxTime do

6: cont ← 0

7: while cont < maxIter do

8: IntermPop ← Population

9: for i ← 1 to Population.size do

10: ind1, ind2 ←Parents(Population)

11: ind3 ←Crossover(ind1,ind2)

12: if (Λ ∈ [0, 1]) ≤LocalSearchRate

then

13: localSearch(ind3)

14: end if

15: IntermPop.append(ind3)

16: end for

17: Sort(IntermPop)

18: Population ←IntermPop[1..Popula-

19: -tion.size]

20: if (best =Population.best) then

21: cont ← cont + 1

22: else

23: cont ← 0

24: end if

25: end while

26: end while

27: end function

sion of the initial noise plus the images which have

gone through the process of mutation.

The GAP runs for a ﬁxed time, in which the popu-

lation continues to evolve, while there are no changes

in the best individual for a maximum number of inter-

actions, step at which the entire population is restarted

while only the best individual is preserved.

An intermediate population twice the initial pop-

ulation is created during the process of evolution

formed by the current population, plus the new in-

dividuals generated. These new individuals are cre-

ated through crossover operators, where parent selec-

tion is done through the tournament method. Soon

after the parent’s choice, a new crossover operator is

selected randomly for the generation of a new indi-

vidual (child). For this the following three types are

available for selection:

• Uniform Operator: Each pixel of the image is

chosen randomly from one of the parents with

50% chance of the value chosen to be from either

parent.

• Operator of a Line Point: Randomly choose a

line of pixels in the image, then all the pixels

above it will come from one parent and the other

pixels that are below it will come from the other

parent.

• Operator of a Column Point: Approach similar

to the ﬁrst, but the image is divided by a column

rather than a line.

Once created, the new individual can still be sub-

mitted by a local search operator, a process whose

purpose is to improve the ﬁnal quality of the solu-

tion by means of transformations in the individual, in

this step, if the condition is satisﬁed that a real value

randomly selected within the range of 0 to 1 in the al-

gorithm is less than the local search rate chosen by the

user, it will pass through one of the artifact suppres-

sion operators already mentioned in the initial step:

BM4D, 3D Median Filter or 3D Ellipsoid Filter.

With the entire intermediate population com-

pleted, individuals are sorted according to ﬁtness, so

the ﬁrst individuals are selected to form the GAP pop-

ulation for the next stage of evolution, where the al-

gorithm checks if there are no changes in the best in-

dividual of the population during deﬁned number of

evolutionary executions. If the best individual does

not change after a maximum number of iterations, that

population is restarted. A ﬂowchart of the algorithm

execution is shown in Fig 4.

BIODEVICES 2019 - 12th International Conference on Biomedical Electronics and Devices

144

Figure 4: Flowchart of the algorithm execution.

5 EXPERIMENTAL RESULTS

In this chapter, the results of the statistical analysis

will be presented through the evaluation metrics. The

established comparison is related to two other meth-

ods of ﬁltering medical images previously mentioned.

These methods are applied to a computerized to-

mography DICOM image available in the Repository

The Cancer Imaging Archive (TCIA) (Clark et al.,

2013). One of the images in the chosen DICOM is

shown in the ﬁgure 5.

Figure 5: DICOM image initial.

Table 1 refers to the amount of MSE for each im-

age after the ﬁltering, establishing values. In the col-

umn 1 shows the percentage of image degradation, in

column 2 the noise mean, and columns 3, 4 and 5 the

respective MSE values obtained for the ﬁlters of the

median 3d, ellipsoid and the GAP.

The ﬁrst analysis was made by the MSE metric,

Table 1: Evaluation of the result through MSE.

Gaussian additive noise

Noise (MSE) Median Ellipsoid GAP

1% (161.44) 46.03 118.16 28.73

2% (517.49) 107.39 159.96 52.73

3% (887.77) 184.06 218.41 77.65

4% (1193.96) 275.49 292.24 101.79

5% (1448.74) 382.22 374.82 126.63

Average 199.03 232.71 77.50

presented in all cases the ﬁlter type GAP as better, tak-

ing into account that the best results are those whose

values are the smallest. On the other hand, the MSE

has the level of conﬁdence that is contested, making

it necessary to compare with new forms.

Table 2: Evaluation of the result through PSNR.

Gaussian additive noise

Noise (PSNR) Median Ellipsoid GAP

1% (26.06) 31.53 27.42 33.56

2% (21.05) 27.84 26.10 30.88

3% (18.64) 25.45 24.69 29.25

4% (17.41) 23.73 23.54 28.10

5% (16.53) 22.33 22.36 27.00

Average 26.17 24.82 29.75

In the table 2 is shown an evaluation using a better

metric, this metric demonstrates in numerical data an

approximation of the human perception of the quality

of reconstruction, where not necessarily, but in most

cases the larger PSNR values represent a better recon-

struction of the image.

When comparing the resulting values demon-

strated below, it is clear the superiority of the data re-

sulting from the proposed method. With efﬁciency in

100% of the cases tested in this approach, it is shown

in the table that in only one case the value was similar

to the GA model. Then we notice the difference in

the values resulting from the methods being distant,

in addition, it is also remarkable that the difference

between the average of the GAP and the means of the

other methods were somewhat close.

Table 3: Evaluation of the result through SSIM.

Gaussian additive noise

Noise (SSIM) Median Ellipsoid GAP

1% (0.94) 0.96 0.95 0.96

2% (0.90) 0.94 0.93 0.95

3% (0.89) 0.92 0.92 0.94

4% (0.88) 0.91 0.91 0.93

5% (0.87) 0.91 0.90 0.93

Average 0.92 0.92 0.94

Table 3 presents the analysis results using the most

accurate evaluative metric currently used, SSIM. This

metric improves traditional methods, that show incon-

Noise Attenuation using Genetic Algorithm in CT Image

145

sistent with human visual perception.

The results presented in the tables prove that the

combined method of various artifact removal tech-

niques is very favorable in most images, in addition,

the few limitations of the GAP provide a multitude of

options to change parameters and provide improve-

ments in results.

As a visual example of the obtained results, it is

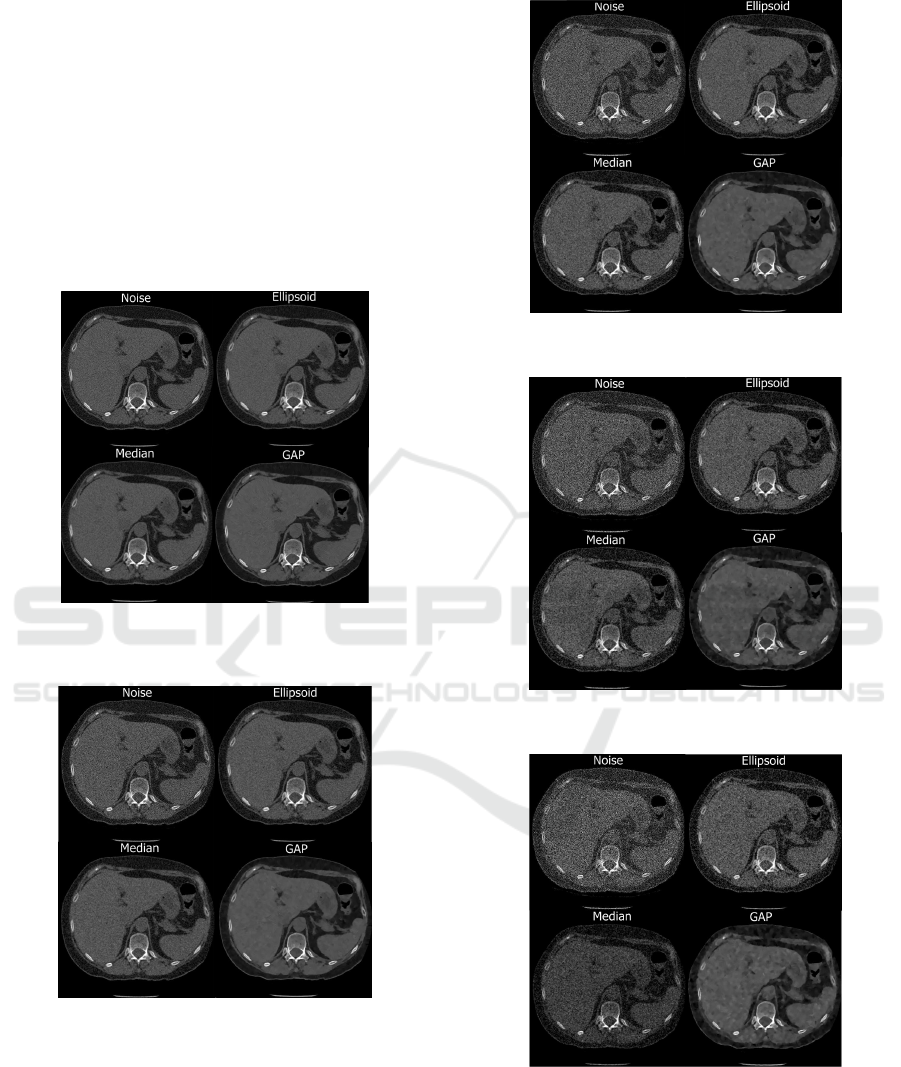
shown in ﬁgures 6, 7, 8, 9 and 10. In each ﬁgure,

four images are observed, one referring to the slice

added with noise and another three are results of the

ellipsoid, median and GAP ﬁltering.

Figure 6: Image corrupted with standard deviation = 1%

and ﬁltering results.

Figure 7: Image corrupted with standard deviation = 2%

and ﬁltering results.

In Fig 6 , the image was corrupted with gaussian

artifact and a standard deviation of 1%. In the other

ﬁgures (3-6) differ in the standard deviation of 2%,

3% , 4% and 5% respectively.

In Fig 6 it was observed that when applying the

noise with low deviation, 1%, the difference of the

GAP in relation to the others was already visually per-

ceptible. In addition, in the ﬁgures 7, 8, 9 and 10 the

Figure 8: Image corrupted with standard deviation = 3%

and ﬁltering results.

Figure 9: Image corrupted with standard deviation = 4%

and ﬁltering results.

Figure 10: Image corrupted with standard deviation = 5%

and ﬁltering results.

difference between the proposed ﬁlter and the other

two ﬁlters that serve as the basis for the quality check.

In the ﬁgures 9, 10 it was observed that when ap-

plying high noise it was visually perceptible that the

GAP was able to recover good information from the

BIODEVICES 2019 - 12th International Conference on Biomedical Electronics and Devices

146

badly corrupted images if it excelled in relation to the

other competitors.

6 DISCUSSION

With the introduction of the ﬁlter it is evident that

there is an improvement of resolution in both images,

making them more interesting for the observation of

the image.

In Table 1, it was observed that in all items the

method demonstrated the most efﬁcient ﬁltration con-

dition and presented signiﬁcant results in the percent-

age of degradation of DICOM images. However,

MSE may exhibit similarity failures.

Thus, the efﬁciency of the GAP method is demon-

strated when compared to the others exposed in tables

2 and 3, using PSNR and SSIM. Demonstrating the

ﬁnal image after ﬁltering that most closely resembles

the original image and provides an increase in quality.

7 CONCLUSION

There are several techniques for developing DICOM

image ﬁltering, this study applies a hybrid method us-

ing a genetic algorithm, in which the method obtains

optimal ﬁltering and minimizes artifacts.

The efﬁciency of the model adopted as a ﬁlter is

the result of the architecture that is distributed in a

selective and evolutionary way in two stages. The ﬁrst

stage consists of the BM4D ﬁltering, the 3d medium

ﬁlter and the ellipsoid ﬁlter.

The second stage is formed by the application of

operators of simple mutations in the previously recov-

ered image, for that was used: change of intensity,

gaussian ﬁlter and average ﬁlter.

As a comparison, the MSE, PSNR and SSIM were

used to estimate the ﬁltering efﬁciency of the re-

stored images. It was observed experimentally that

the adopted ﬁlter is efﬁcient and robust presenting

better indexes than the others in PSNR and SSIM.

With the study of the GAP can generate more ad-

vances and minimize the artifacts, resulting in a better

performance in the system. The disadvantage is the

limitations of techniques for random values, which

hamper the ideal value set in the ﬁltering.

In order to apply more efﬁcient methods of recon-

structing DICOM images, it is intended in future work

to approach methods with the application of new ﬁl-

ters to increase efﬁciency. As an example, we have

artiﬁcial intelligence in one of the stages.

ACKNOWLEDGMENT

This work is ﬁnanced by the National Funds through

the FCT - Fundac¸

ao para a Ci

encia e a Tecnologia

(Portuguese Foundation for Science and Technology)

as part of project UID/EEA/00760/2019.

REFERENCES

Badretale, S., Shaker, F., Babyn, P., and Alirezaie, J. (2017).

Fully convolutional architecture for low-dose ct image

noise reduction. In IOP Conference Series: Materials

Science and Engineering, volume 261, page 012012.

IOP Publishing.

Barca, P., Giannelli, M., Fantacci, M. E., and Caramella,

D. (2017). Evaluation of the imaging properties of

a ct scanner with the adaptive statistical iterative re-

construction algorithm. In Proceedings of the 10th In-

ternational Joint Conference on Biomedical Engineer-

ing Systems and Technologies - Volume 1: BIODE-

VICES, (BIOSTEC 2017), pages 200–206. INSTICC,

SciTePress.

Baselice, F., Ferraioli, G., and Pascazio, V. (2017a). A

3d mri denoising algorithm based on bayesian theory.

Biomedical engineering online, 16(1):25.

Baselice, F., Ferraioli, G., and Pascazio, V. (2017b). A

3d mri denoising algorithm based on bayesian theory.

Biomedical engineering online, 16(1):25.

Broughton, S. A. and Bryan, K. (2018). Discrete Fourier

analysis and wavelets: applications to signal and im-

age processing. John Wiley & Sons.

Clark, K., Vendt, B., Smith, K., Freymann, J., Kirby, J.,

Koppel, P., Moore, S., Phillips, S., Mafﬁtt, D., Pringle,

M., et al. (2013). The cancer imaging archive (tcia):

maintaining and operating a public information repos-

itory. Journal of digital imaging, 26(6):1045–1057.

De Jong, K. (2012). Evolutionary computation: a uniﬁed

approach. In Proceedings of the 14th annual confer-

ence companion on Genetic and evolutionary compu-

tation, pages 737–750. ACM.

de Paiva, J. L., Toledo, C. F., and Pedrini, H. (2016). An

approach based on hybrid genetic algorithm applied

to image denoising problem. Applied Soft Computing,

46:778–791.

Dimililer, K., UGUR, B., and Yoney, K. (2017). Tumor

detection on ct lung images using image enhancement.

In International Science and Technology Conference

(ISTEC 2016).

Eiben, A. E., Smith, J. E., et al. (2003). Introduction to

evolutionary computing, volume 53. Springer.

Fajardo-Delgado, D., S

anchez, M. G., Molinar-Solis, J. E.,

Fernandez-Zepeda, J. A., Vidal, V., and Verdi

u, G.

(2016). A hybrid genetic algorithm for color image

denoising. In Evolutionary Computation (CEC), 2016

IEEE Congress on, pages 3879–3886. IEEE.

Fedorov, O. and Rodyhin, M. (2016). A referenceless psnr

estimator of compressed jpeg images. In Radioelek-

Noise Attenuation using Genetic Algorithm in CT Image

147

tronika (RADIOELEKTRONIKA), 2016 26th Interna-

tional Conference, pages 227–230. IEEE.

Goldberg, D. (1989). Genetic algorithms in optimization,

search and machine learning. Reading: Addison-

Wesley.

Hore, A. and Ziou, D. (2010). Image quality metrics: Psnr

vs. ssim. In Pattern recognition (icpr), 2010 20th in-

ternational conference on, pages 2366–2369. IEEE.

Jain, P. and Tyagi, V. (2016). A survey of edge-preserving

image denoising methods. Information Systems Fron-

tiers, 18(1):159–170.

Jiang, M. and Crookes, D. (2006). High-performance 3d

median ﬁlter architecture for medical image despeck-

ling. Electronics Letters, 42(24):1379–1380.

Khmag, A., Ramli, A. R., Al-haddad, S., Yusoff, S., and

Kamarudin, N. (2017). Denoising of natural images

through robust wavelet thresholding and genetic pro-

gramming. The Visual Computer, 33(9):1141–1154.

Khmag, A., Ramli, A. R., bin Hashim, S. J., and Al-Haddad,

S. A. R. (2016). Additive noise reduction in natu-

ral images using second-generation wavelet transform

hidden markov models. IEEJ Transactions on Electri-

cal and Electronic Engineering, 11(3):339–347.

Kiragu, H., Mwangi, E., and Kamucha, G. (2017a). A hy-

brid mri method based on denoised compressive sam-

pling and detection of dominant coefﬁcients. In Digi-

tal Signal Processing (DSP), 2017 22nd International

Conference on, pages 1–5. IEEE.

Kiragu, H., Mwangi, E., and Kamucha, G. (2017b). A hy-

brid mri method based on denoised compressive sam-

pling and detection of dominant coefﬁcients. In Digi-

tal Signal Processing (DSP), 2017 22nd International

Conference on, pages 1–5. IEEE.

Kubicek, J., Faure-Brac, B., Penhaker, M., Scurek, R.,

Cerny, M., Augustynek, M., and Oczka, D. (2018).

Modeling of blood alcohol content using multire-

gional segmentation from ir images. In Proceedings

of the 11th International Joint Conference on Biomed-

ical Engineering Systems and Technologies - Volume

1: BIODEVICES, (BIOSTEC 2018), pages 39–47. IN-

STICC, SciTePress.

Liu, Y. (2015). Image denoising method based on thresh-

old, wavelet transform and genetic algorithm. Interna-

tional Journal of Signal Processing, Image Processing

and Pattern Recognition, 8(2):29–40.

Maggioni, M., Katkovnik, V., Egiazarian, K., and Foi, A.

(2013). Nonlocal transform-domain ﬁlter for volumet-

ric data denoising and reconstruction. IEEE transac-

tions on image processing, 22(1):119–133.

Mahani, F., Mahanipour, A., and Mokhtari, A. (2017). Op-

timization of plasmonic color ﬁlters for cmos image

sensors by genetic algorithm. In Swarm Intelligence

and Evolutionary Computation (CSIEC), 2017 2nd

Conference on, pages 12–15. IEEE.

Momeni, M., Nezhad, Z. H., and Moghaddam, M. E.

(2017). Embryonic image enhancement based on ge-

netic algorithm and generic ﬁlter. In Frontiers of Sig-

nal Processing (ICFSP), 2017 3rd International Con-

ference on, pages 141–145. IEEE.

Ozmen, G. and

Ozs¸en, S. (2017). A new denoising method

for fmri based on weighted three-dimensional wavelet

transform. Neural Computing and Applications, pages

1–14.

Ozmen, G. and

Ozs¸en, S. (2018). A new denoising

method for fmri based on weighted three-dimensional

wavelet transform. Neural Computing and Applica-

tions, 29(8):263–276.

Santos, A. I. S. A. d. (2015). Desenvolvimento de um algo-

ritmo h

ıbrido para o escalonamento de exames numa

ınica. PhD thesis.

Saraiva, A. A., Ferreira, N. F., and Valente, A. (2018).

New bioinspired ﬁlter of dicom images. In Engineer-

ing Systems and Technologies (BIOSTEC 2018), 2018

11th International Joint Conference on Biomedical.

Talbi, M., Ftima, S. B., and Cherif, A. (2015). Image

watermarking using data compression. In Computer

Networks and Information Security (WSCNIS), 2015

World Symposium on, pages 1–9. IEEE.

Tiwari, V., Bansod, P., and Kumar, A. (2015). Medi-

cal imaging in heterogeneous telemedicine network.

In Information, Communications and Signal Process-

ing (ICICS), 2015 10th International Conference on,

pages 1–5. IEEE.

Uzun, S. and Akg

un, D. (2016). An analysis of genetic

algorithm with training of image ﬁlter kernel matrix.

In Electrical, Electronics and Biomedical Engineer-

ing (ELECO), 2016 National Conference on, pages

142–146. IEEE.

Yang, F., Zuo, W., Wang, K., and Zhang, H. (2008). 3d

cardiac mri data visualization based on volume data

preprocessing and transfer function design. In Com-

puters in Cardiology, 2008, pages 717–720. IEEE.

Zafari, M., Ahmadi-Kandjani, S., and Kheradmand, R.

(2017). Noise reduction in selective computational

ghost imaging using genetic algorithm. Optics Com-

munications, 387:182–187.

Zhang, K., Zuo, W., Chen, Y., Meng, D., and Zhang, L.

(2017). Beyond a gaussian denoiser: Residual learn-

ing of deep cnn for image denoising. IEEE Transac-

tions on Image Processing, 26(7):3142–3155.

BIODEVICES 2019 - 12th International Conference on Biomedical Electronics and Devices

148