The Impact of Environmental Factors on Heart Failure

Decompensations

Garazi Artola

, Nekane Larburu

1,2

, Roberto Álvarez

1,2

, Vanessa Escolar

, Ainara Lozano

Benjamin Juez

and Jon Kerexeta

Vicomtech Research Centre, Mikeletegi Pasalekua 57, 20009, San Sebastian, Spain

Biodonostia Health Research Institute, P. Doctor Begiristain s/n, 20014 San Sebastian, Spain

Hospital Universitario de Basurto (Osakidetza Health Care System), Avda Montevideo 18, 48013, Bilbao, Spain

Keywords: Heart Failure, Hospital Admission, Open Data, Environmental Factors.

Abstract: Heart failure (HF) is defined as the incapacity of the heart to pump sufficiently to maintain blood flow to meet

the body's needs. Often, this causes sudden worsening of the signs and symptoms of heart failure

(decompensations), which may lead on hospital admissions, deteriorating patients’ quality of life and causing

an increment on the healthcare cost. Environmental exposure is an important but underappreciated risk factor

contributing to the development and severity of cardiovascular diseases, such as HF. In this paper, we describe

the development and results of a methodology to determine the effect of environmental factors on HF

decompensations by means of hospital admissions. For that, a total number of 8338 hospitalizations of 5343

different patients, and weather and air quality information from open databases have been considered. The

results demonstrate that several environmental factors, such as weather temperature, have an impact on the

HF related hospital admissions rate, and hence, on HF decompensations and patient´s quality of life. The next

steps are first to predict the number of hospital admissions based on the presented study, and second, the

inclusion of these environmental factors on predictive models to assess the risk of decompensation of an

ambulatory patient in real time.

1 INTRODUCTION

Heart failure (HF) has been defined as global

pandemic, since it affects around 26 million people

worldwide and is increasing in prevalence

(Ponikowski et al., 2014). In 2012 it was responsible

for an estimated health expenditure of around $31

billion, equivalent to more than 10% of the total

health expenditure for cardiovascular diseases in the

United States (US) (Benjamin et al., 2016). And,

according to the American Heart Association

(Heidenreich et al., 2011), these costs are estimated to

increase to $77.7 billion in 2030.

HF is characterized by the heart’s inability to pump

an adequate supply of blood to the body to meet the

body needs. Without sufficient blood flow, all major

body functions are disrupted, which lead on HF

patients’ decompensations and hospital admissions.

As several studies have already demonstrated,

environmental exposure is an important risk factor

(Angelini et al., 2017; Brook et al., 2010; Gurría,

2012; Warren et al., 2002; Woolf and Aron, 2013),

which may also contribute to the severity of HF. In

the field of HF, limited studies investigate the impact

of these factors (Burnett et al., 1997; Das et al., 2014;

Levin et al., 2018; Morris et al., 1995; Stewart et al.,

2002).

This paper presents a methodology to study the

impact of different environmental factors on HF

decompensations, and the results obtained in a real

case study.

The paper is structured as follows: Section 2 –

Related Work, introduces different studies related to

our work. Section 3 – Datasets, presents the two

types of datasets used for the study. Section 4 – Data

Analysis, describes the type of data analysis proposed

for the experiment. Section 5 – Results, provides the

results obtained in the experiment. Finally, in Section

6 – Conclusion and Future Work, the conclusions

and future studies that will follow this paper are

discussed.

Artola, G., Larburu, N., Álvarez, R., Escolar, V., Lozano, A., Juez, B. and Kerexeta, J.

The Impact of Environmental Factors on Heart Failure Decompensations.

DOI: 10.5220/0007347300510058

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 51-58

ISBN: 978-989-758-353-7

2 RELATED WORK

As mentioned before, several investigations about the

impact of environmental factors in public health are

already published. A relevant example is the

American Heart Association scientific statement on

"Air Pollution and Cardiovascular Disease" which

concluded that exposure to particulate matter (PM) air

pollution contributes to cardiovascular morbidity and

mortality (Brook et al., 2004). This study was updated

later giving new evidence of the impact of PM

exposure with cardiovascular diseases (Brook et al.,

2010). Moreover in D’Amato´s study (D’Amato et

al., 2010), urban air pollution and climate change

were demonstrated to be environmental risk factors of

respiratory diseases. A similar research indicates that

air pollution is a major preventable cause of increased

incidence and exacerbation of respiratory diseases

(Laumbach and Kipen, 2012).

Nevertheless, as said before, fewer studies in the

field of HF have been carried out, of which some most

relevant are analysed in the following lines. In 1995,

an article published in the American Journal of Public

Health investigated the association between hospital

admissions for congestive HF and air pollutants,

where ambient carbon monoxide levels were

positively associated with the admissions (Morris et

al., 1995). Two years later, another Canadian study

examined the role that ambient air pollution plays in

exacerbating cardiac disease (Burnett et al., 1997).

They found a positive association between daily

admissions fluctuations of congestive elderly HF

patients and variations in ambient concentrations of

carbon monoxide, nitrogen dioxide, sulfur dioxide,

ozone, and the coefficient of haze.

Additionally, other investigations about the effect

of meteorology in HF health status have been carried

out. In 2014, the International Journal of Cardiology

published a text where the relationships between

meteorological events and acute HF was globally

explored (Das et al., 2014). The results showed that

meteorological fluctuations appear most relevant in

the 3 days prior to the HF hospitalization with

temperature, demonstrating a relationship with HF. In

contrast, some authors demonstrated that the number

of hospitalizations for HF increases during winter

(Levin et al., 2018). Others concluded that there is a

substantial seasonal variation in HF hospitalizations

and deaths (Stewart et al., 2002).

However, to the best of our knowledge, there is still

further research to be done in order to better

determine the impact of a set of several

environmental factors on HF decompensations, being

the field where our work is focused on.

3 DATASETS

This study makes use of two different sets of data: one

related to the number of hospital admissions, and the

other one related to the environmental factors to

determine whether they have an impact on HF related

decompensations.

3.1 Hospital Admissions

The way to study HF decompensations is by means of

hospital admissions. Therefore, the first dataset

compiles the daily hospitalizations related to HF in

the public hospital OSI Bilbao-Basurto (Osakidetza),

located in the Basque Country (Spain). The hospital

has been gathering this information since 1994, but

only after 2010 this information started to be recorded

in Electronic Health Records. Due to the adaptation

to this new electronic system, the next two years the

information was not usable. Therefore, the usable

admissions dataset is from January of 2012 to August

of 2017.

The dataset consists of two attributes: (i) date of

admission for each patient, and (ii) date of discharge

of the patient. Nevertheless, only the first attribute

was used, being the date of discharge irrelevant for

this study. A total number of 8338 hospitalizations of

5343 different patients are available in this dataset,

with a mean of 4.02 admissions per day.

3.2 Environmental Data

This environmental dataset is separated in weather

information and air quality information. This

information was selected due to their demonstrated

impact on HF decompensations in previous studies

(Burnett et al., 1997; Das et al., 2014; Levin et al.,

2018; Morris et al., 1995; Stewart et al., 2002).

3.2.1 Weather

The Basque Agency of Meteorology (Euskalmet)

enables the possibility to access weather data

recorded since 2003, from the Open Data Euskadi

website (Basque Government, 2009). This

information is collected every ten minutes by each

station of Euskalmet distributed in Euskadi. The

different attributes that can be found in these datasets

are listed below (Table 1).

HEALTHINF 2019 - 12th International Conference on Health Informatics

Table 1: List of attributes of the weather dataset.

Attribute

Unit

Mean direction of wind

Mean velocity of the wind

km/h

Maximum velocity of the wind

km/h

Sigma of the velocity of the wind

km/h

Sigma of the direction of the wind

Air temperature

°C

Humidity

Precipitation

mm=l/m²

Atmospheric pressure

Level 2 (water plate)

Irradiation

w/m²

Among all the different stations distributed in the

three provinces of Euskadi, for this study the data

from the one located in Deusto (Bilbao) was selected

since it is the closest one to the patients of the study.

However, obtaining information from the nearest

station for each patient seems to be the best option.

But, as we are studying the general trend of each

variable, a constant value for each one was needed.

Henceforth, the error caused by this extrapolation is

assumed.

The preprocessing of this dataset consisted in three

steps.

First, the selection of the attributes for obtaining a

complete dataset was done, since not all the variables

were measured in all the years between 2012 and

2017 (some of them started to be measured later). In

order to obtain a complete dataset, only the attributes

measured in those years were taken into account.

Thus, the parameters of air temperature, humidity,

precipitation, and irradiation are the ones used for this

experiment.

Second, each parameter was grouped per day (data

was recorded every 10 minutes), calculating their

mean value. In addition, as the literature suggests

(Das et al., 2014), in the case of temperature, the

minimum and maximum values for each day were

also added to the dataset.

Finally, an imputation of missing values (0.33% of

the data) was done, which may be caused by technical

problems in the station. The imputation by Structural

Model & Kalman Smoothing was used for this, as it

is the one that best performs for time series with a

strong seasonality (Moritz and Bartz-Beielstein,

2017). In summary, the dataset corresponding to

weather consists of humidity (%), precipitation

(l/m

), irradiation (w/m

), mean temperature (°C),

minimum temperature (°C), and maximum

temperature (°C).

3.2.2 Air Quality

The Open Data Euskadi website also gives the

opportunity to recover information about the air

quality (Gobierno Vasco, 2017). The dataset is

formed by air quality specific parameters, which are

described in Table 2.

Table 2: List of attributes of the air quality dataset.

Attribute

Unit

Carbon Monoxide (CO)

µg/m

Nitric Oxide (NO)

µg/m

Nitrogen Dioxide (NO

)

µg/m

Nitrogen Oxides (NOX)

µg/m

Tropospheric Ozone (O

)

µg/m

Sulphur Dioxide (SO

)

µg/m

Particulate Matter 10 (PM10)

µg/m

Benzene

µg/m

Orthoxylene

µg/m

Toluene

µg/m

After selecting the parameters that were giving a

complete dataset between 2012 and 2017, the final

dataset is containing the attributes Nitric Oxide (NO),

Nitrogen Dioxide (NO

), Nitrogen Oxides (NOX),

Particulate Matter 10 (PM10), and Sulphur Dioxide

(SO

For the preprocessing part of this dataset, the

missing values that corresponded to an 11% of the

data were imputed using the same method as for the

previous dataset, the imputation by Structural Model

& Kalman Smoothing (Moritz and Bartz-Beielstein,

2017).

4 DATA ANALYSIS

Before starting the analysis and to support our

hypothesis that environmental factors may contribute

to HF patients’ health status, a pre-analysis was done.

For that, the daily mean value of the number of

hospitalizations within each month was illustrated

(Figure 1).

Figure 1 shows that in European warm period

(from June to October) there are significant less

admissions that in the cold period (from December to

March), although some studies present the opposite

results (Das et al., 2014). Hence, to confirm our

hypothesis the following study was conducted.

The Impact of Environmental Factors on Heart Failure Decompensations

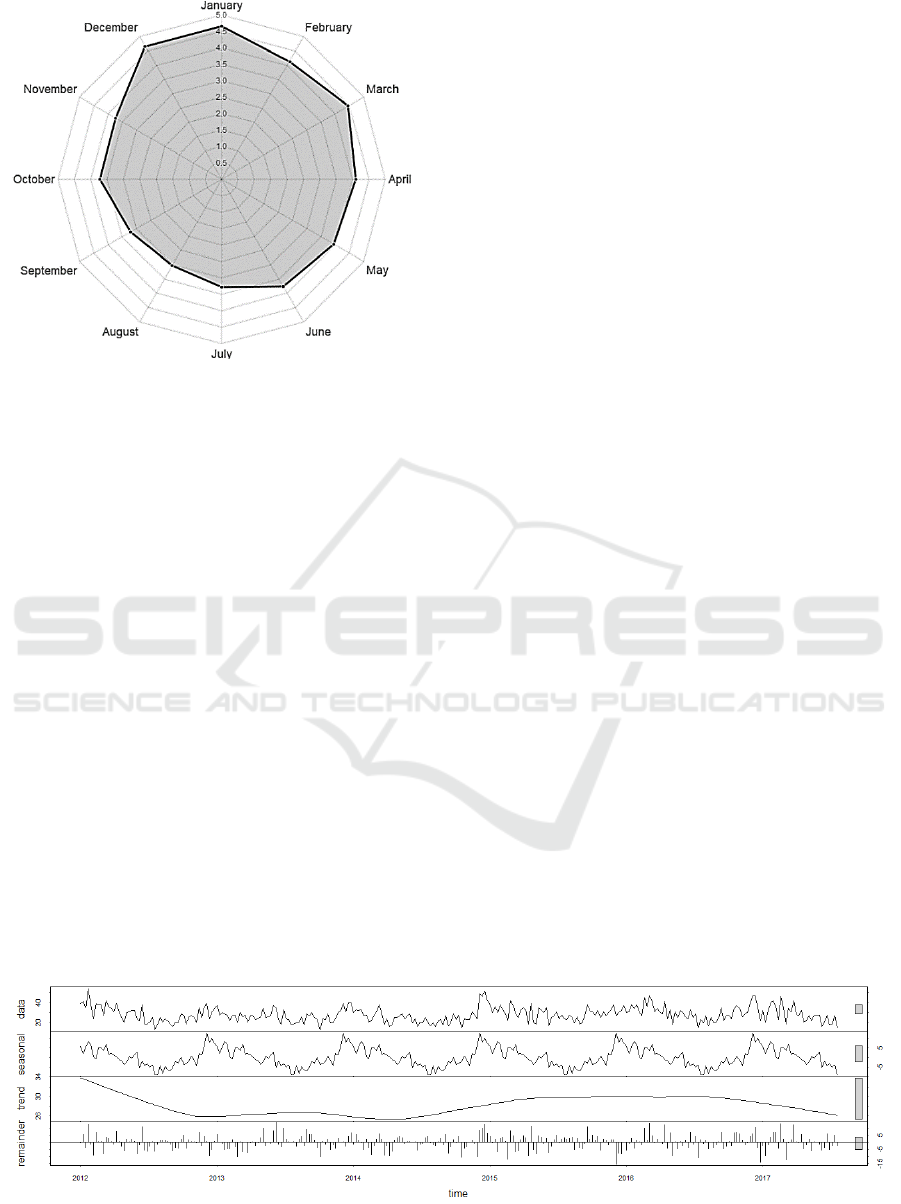
Figure 1: Average number of admissions per day in each

month.

4.1 Grouping

Note that the number of hospitalizations per day is

4.02 (Section 3.1). This is not a sufficient number to

analyse the data within each day. Therefore, each

attribute of the study was grouped by weeks: on the

one hand, admissions related data is grouped by the

total number of admissions in each week. On the

other hand, the mean, maximum, minimum and the

standard deviation of each week are used to group the

environmental attributes.

Once the data was grouped by weeks, two different

studies were done: (i) a univariate regression to

determine whether the admissions may influence

future hospitalizations’ prediction (Section 4.2), and

(ii) a multivariate regression to determine the impact

of environmental factors on admission rates (Section

4.3).

4.2 Univariate Regression

In order to study the effect of admissions in future

hospitalizations rate, firstly time series

decomposition is performed (Section 4.2.1) as

exploratory data analysis. Secondly, the best

univariate ARIMA model is tentatively identified and

finally determined (Section 4.2.2).

4.2.1 Decomposition

The hospitalization rate may vary on time depending

on several factors. In order to determine how these

variations behave, a decomposition process was

conducted. This is a mathematical procedure which

transforms a time series into three components, each

of them depicting one of the underlying categories of

patterns: seasonality, trend and random (Jebb and

Tay, 2017). Seasonality represents patterns that are

repeated in a fixed period of time (e.g. repeating

pattern over years). Trend is the underlying tendency

of the data, and random is the residuals of the original

time series after the extraction of the seasonality and

trend, which is also called noise or reminder.

In Figure 2 the decomposition of admissions on

these three components is shown. The first graph

represents the original admissions data series, and

below the seasonality of it is illustrated. Next,

admissions’ trend is presented, and the last graph

reflects the random part of the time series after the

extraction of seasonality and trend components.

Figure 2 shows a clear seasonality of admissions,

since there is a similar pattern every year. In addition,

the tendency represented in the third graph shows

changes in the number of admissions over time.

4.2.2 Univariate ARIMA

Once the decomposition was done, the

hospitalizations dataset was analysed as time series to

determine the impact of admissions on following

week’s hospitalizations. For that, the ARIMA model

was implemented.

ARIMA stands for auto-regressive integrated

moving average and it is a class of statistical models

for analysing and forecasting time series data

Figure 2: Decomposition of admission data series.

HEALTHINF 2019 - 12th International Conference on Health Informatics

(Jenkins, 2014) It is specified by three order

parameters: the auto-regressive (AR) parameter p,

which specifies the number of time lags used in the

model; the d represents the degree of differencing

(subtracting its current and previous values d times)

in the integrated component (I); and the order q of the

moving average component (MA) determines the

number of terms to include in the model.

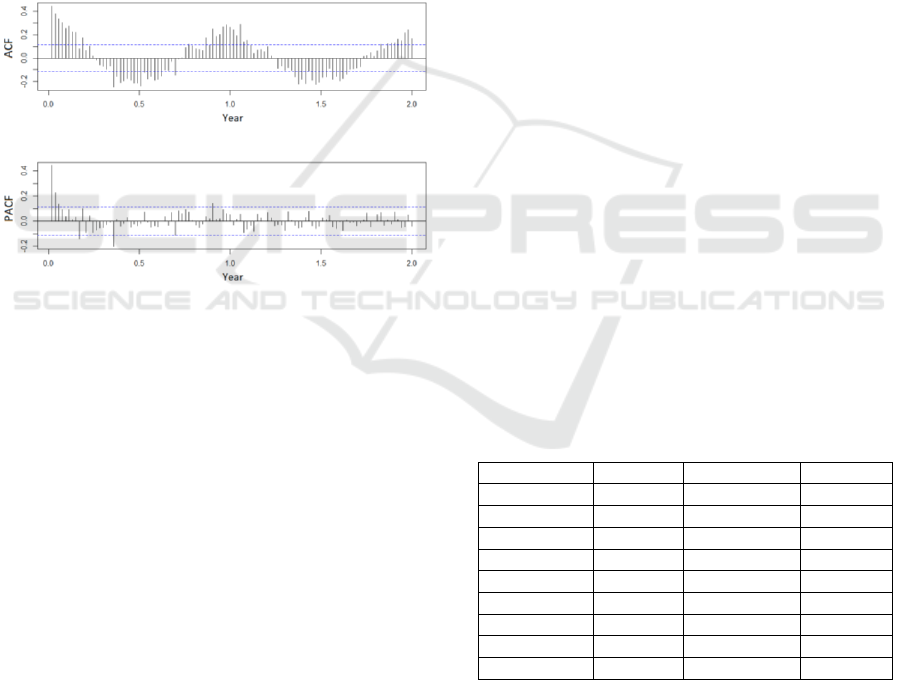
However, to determine the values of the order

parameters p, d, q the autocorrelation function (ACF)

and the partial autocorrelation function (PACF) were

computed (Jain and Mallick, 2017). Figure 3,

represents the ACF and PACF of admissions,

considering the 53 weeks of a year. It shows that there

is a correlation between the number of admissions in

a week with the adjoining precedent weeks and with

the week of the previous years.

Figure 3: Autocorrelation (ACF) and partial autocorrelation

(PACF) plots of admissions.

The smooth decreasing shape of the ACF graph

points at the AR as the best model to be applied in

ARIMA (Jebb and Tay, 2017).

However, to obtain an optimal result to estimate the

likelihood of a model to predict the future values,

different values for p, d, q were tested. For that

selection we took into account the Akaike

information criterion (AIC), from which the one that

presents the minimum AIC value was considered the

optimal (Akaike, 1974). The results showed that

ARIMA (p, d, q) = (0,1,1) got the best results

(minimum AIC).

Once these ARIMA orders were established, it was

essential to determine whether the information

extraction was performed correctly. This process

occurs in two steps: (1) visually examining an ACF

and PACF of the residuals, and (2) conducting a

Ljung-Box test. In the visual analysis of the ACF and

PACF of the residuals a significant correlation was

observed every two months. As expected, in the

widely used formal test of Ljung-Box test (Ljung and

Box, 1978), applied in our study, we saw that there

was still some remaining information extractable (p-

value = 0.028), caused by the remaining correlation

observed in the residuals every two months.

However, it has not been possible to extract further

information.

4.3 Multivariate Regression

The next step was to analyse the regression taking

also into account the environmental information. To

do that, the first step was to calculate the correlations

between all environmental factors and admission

rates. This way we could select the most significant

factors for the experiment. Following, the

multivariate ARIMA was implemented to determine

their impact all together.

4.3.1 Selection of Attributes

As mentioned before, the variables were grouped by

weeks (see Section 4.1).

The correlation was estimated using the non-

parametric test of Kendall, which measures the

strength of dependence between two numeric

variables (Rui and Vera, 2017) and it is one of the

most used test for this type of non-parametric data. In

addition, this analysis was done relating all the

attributes with the number of admissions of the

following week.

Note that, since the mean, maximum and minimum

values of the environmental factors were closely

related, only the one with the highest correlation was

taken into account per attribute. In Table 3 we

summarize the selected ones.

Table 3: Selected attributes for the experiment.

Attribute

Selected

Correlation

p-value

Humidity

Max

0.0469

0.2381

Precipitation

Mean

0.0795

0.0461

Temperature

Mean

-0.3794

1.44E-21

Irradiation

Mean

-0.2629

3.88E-11

Max

0.2107

1.82E-07

Mean

0.1876

1.95E-05

NOX

Max

0.2196

4.06E-08

PM10

Min

-0.0485

0.3243

Max

0.2692

3.17E-09

Table 3 shows that the most correlated attribute

was the temperature, showing the highest (inversed)

correlation value. This shows that the lower the

temperature, the larger is next week admission rate.

On the other hand, humidity, precipitation, and PM10

parameters do not have significant correlations in this

study, neither relevant p-values.

The Impact of Environmental Factors on Heart Failure Decompensations

Besides this analysis, environmental factors

variations, such as temperature variations, might also

affect the health status. Therefore, the impact of the

highest temperature change per week, and the

standard deviation (SD) of each attribute per week

were also studied following the same procedure

(Table 4).

Table 4 shows that the temperature change does not

affect in the next week’s admission rate. However,

some attributes’ instability (standard deviation) over

the week seems to be correlated. Hence, the standard

deviation of the attributes Irradiation, NO, NOX and

SO2 will be checked in the multivariate ARIMA

regression.

Table 4: Correlations of the attributes’ standard deviations

and the temperature change.

Attribute SD

Correlation

p-value

Humidity

0.05

0.25

Precipitation

0.06

0.11

Temperature

0.03

0.39

Irradiation

-0.20

4.13e-07

0.23

1.54e-08

0.06

0.18

NOX

0.20

3.73e-07

PM10

0.02

0.75

0.23

1.58e-07

Temp. change

0.04

0.26

4.3.2 Multivariate ARIMA

Using the model extracted from the univariate

ARIMA analysis and after the selection of the most

correlated environmental attributes, a multivariate

ARIMA model was carried out.

For that, first we employed all attributes and tested

the AIC value. If the p-value of an attribute was too

high, this value was discarded, and the AIC value was

checked again. If the value improved (AIC

decreased), we kept that value out of our model.

Otherwise we put it back. This process was done

iteratively until AIC did not decrease anymore.

5 RESULTS

In this chapter, the results obtained from univariate

and multivariate ARIMA regressions are presented.

On the one hand, univariate ARIMA shows an AIC

value of 1939.71, with p-values of <2.2e-16 for MA1

(moving average order 1 of admissions) and <6.248e-

8 for SMA1 (seasonal moving average order 1 of

admissions). It is noticeable that the result obtained is

quite precise.

Even so, adding the environmental variables

(multivariate ARIMA), it was found to be possible to

improve the predictive power of the model. At the

beginning, it was tested with all the attributes, slightly

improving the result (AIC of 1631.6). After a filtering

of attributes depending on their p-value, the optimal

model was achieved with an AIC of 1620.59. This last

model is represented in Table 5 with their respective

p-values for each variable.

Table 5: Results of the multivariate ARIMA model study.

Significant codes: 0 ‘***’, 0.001 ‘**’, 0.01 ‘*’.

Variable

Estimate

Std.

Error

p-value

ma1

-0.9230

0.0258

< 2.2e-16 ***

sma1

-0.7075

0.1192

2.929e-09 ***

Mean

Precip.

-0.2935

0.1189

0.0136 *

Mean

Temp.

-0.6056

0.1865

0.0012 **

Max. SO

0.3171

0.1176

0.007**

Std. NOX

-0.0797

0.0342

0.0197 *

Moving average order 1 of admissions

Seasonal moving average order 1 of admissions

As shown in Table 5, the attribute with most impact

on the number of admissions is the admissions itself.

This is reflected in the variables called “ma1” and

“sma1”, which are the moving average and the

seasonal moving average (season of a year)

respectively. Nevertheless, environmental factors

also have a considerable influence. For example, the

model predicts that when the mean temperature rises

C the estimated number of hospitalizations will

decrease by 0.6 (when the rest of attributes remain

constant). Moreover, the maximum value for SO

within a week also has an effect (p-value = 0.007).

Additionally, the variability of air quality parameter

(NOX) also presents an impact on admissions

predictions. Finally, the results also present that the

more it rains, the less number of hospitalizations

occur the following week.

The mean air temperature, which has high impact

on admission rate prediction (see Table 5), is

represented in a more visual way by comparing the

number of admissions per weeks with the mean

temperature, using a line graph (see Figure 4).

HEALTHINF 2019 - 12th International Conference on Health Informatics

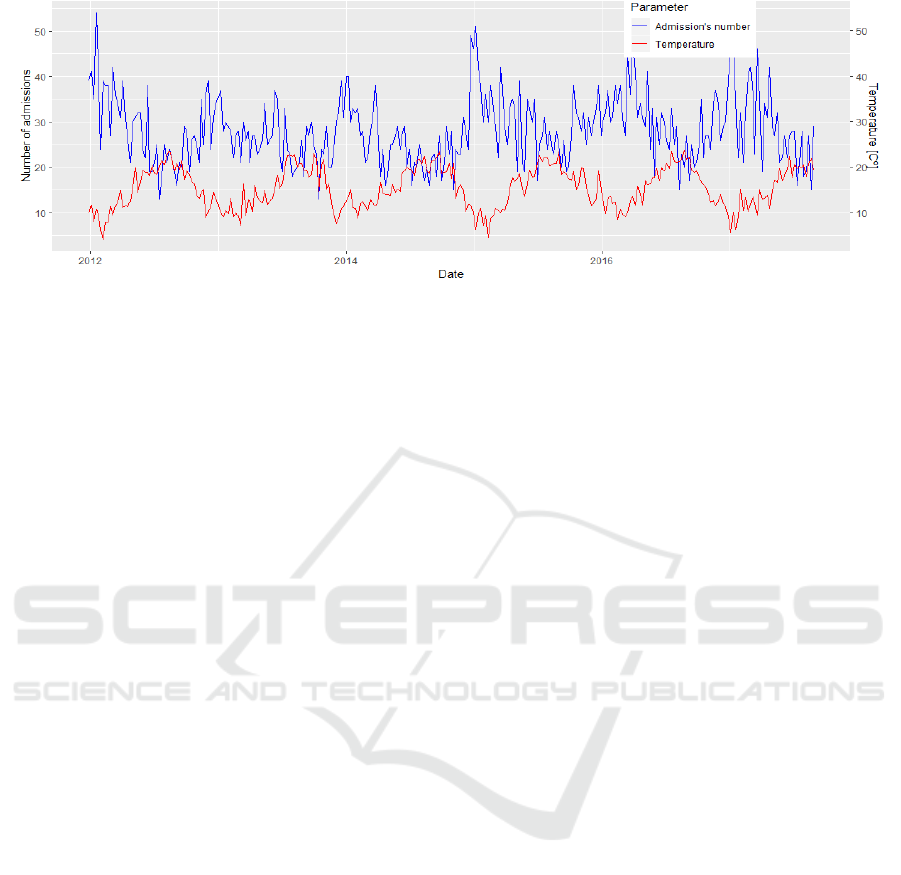
Figure 4: Comparison between the number of admissions (in blue) and the mean temperature (in red) per week over time.

6 CONCLUSIONS AND FUTURE

GUIDELINES

In this paper, the impact of different environmental

factors on Heart Failure (HF) decompensations by

means of hospital admissions is studied. For that, a

regression model for time series was built, and the

external attributes that most affect the number of

hospitalizations were tested. In this context, air

temperature was concluded to be the most significant

environmental factor, although some other attributes,

such as precipitation, along with SO

and NOX air

quality parameters, were also demonstrated to be

relevant.

In the future, these environmental factors will be

included on already built predictive models to assess

the risk of decompensation of an ambulatory patient

(Larburu et al., 2018). This model predicts the

decomposition risk within seven days, using the

previous days’ monitoring data of the patients.

Adding the environmental factors described in this

study may improve its predictiveness.

Moreover, despite the objective of the study was to

just detect environmental attributes influence in the

HF patients’ decompensations, a predictive model to

predict the admissions’ number of the following week

could be developed. This could be very useful for the

physicians to anticipate a possible bed over-

occupancy situation in hospitals. A first test of this

model has been conducted with ARIMA predicting

model. It predicts with a mean error of 4 admissions

each week (when the number of hospitalizations per

week is 28). Nevertheless, this testing error is

achieved using the same dataset for training and for

testing. Hence, unless it is not tested in a new dataset,

the results cannot be generalized. Therefore, this test

remains as future work.

ACKNOWLEDGEMENTS

This work has been funded by the Basque

Government by means of Hazitek Program, under

eCardioSurf project and by Gipuzkoako Foru

Aldundia under MANAVICO proyect.

REFERENCES

Akaike, H., 1974. A new look at the statistical model

identification. IEEE Trans. Autom. Control 19, 716–

723.

Angelini, F. et al., 2017. The Impact of Environmental

Factors in Influencing Epigenetics Related to Oxidative

States in the Cardiovascular System. Oxid. Med. Cell.

Longev.

Basque Government, B.G., 2009. Open Data Euskadi,

datos abiertos del Gobierno Vasco - Euskadi.eus. URL

http://opendata.euskadi.eus/inicio/ (accessed 9.18.18).

Benjamin, E.J. et al., 2016. Heart Disease and Stroke

Statistics-2016 Update: A Report From the American

Heart Association. Circulation 133, e38-360.

Brook, R.D. et al., 2004. Air Pollution and Cardiovascular

Disease.

Brook, R.D. et al., 2010. Particulate matter air pollution

and cardiovascular disease: An update to the scientific

statement from the American Heart Association.

Circulation 121, 2331–2378.

Burnett, R.T., Dales, R.E., Brook, J.R., Raizenne, M.E.,

Krewski, D., 1997. Association between Ambient

Carbon Monoxide Levels and Hospitalizations for

Congestive Heart Failure in the Elderly in 10 Canadian

Cities. Epidemiology 8, 162–167.

D’Amato, G., Cecchi, L., D’Amato, M., Liccardi, G., 2010.

Urban air pollution and climate change as

environmental risk factors of respiratory allergy: an

update. J. Investig. Allergol. Clin. Immunol. 20, 95–

102; quiz following 102.

The Impact of Environmental Factors on Heart Failure Decompensations

Das, D. et al., 2014. The association between

meteorological events and acute heart failure: New

insights from ASCEND-HF. Int. J. Cardiol. 177, 819–

824.

Gobierno Vasco, E.J., 2017. Calidad del aire en Euskadi

durante el 2017. URL

http://www.geo.euskadi.eus/calidad-aire-en-euskadi-

2017/s69-geodir/es/ (accessed 5.17.18).

Gurría, A., 2012. OECD Environmental Outlook to 2050 -

The Consequences of Inaction. OECD. URL

http://www.oecd.org/env/indicators-modelling-

outlooks/oecd-environmental-outlook-1999155x.htm

(accessed 9.26.18).

Heidenreich, P.A. et al., 2011. Forecasting the Future of

Cardiovascular Disease in the United States.

Circulation.

Jain, G., Mallick, B., 2017. A Study of Time Series Models

ARIMA and ETS (SSRN Scholarly Paper No. ID

2898968). Social Science Research Network,

Rochester, NY.

Jebb, A.T., Tay, L., 2017. Introduction to Time Series

Analysis for Organizational Research: Methods for

Longitudinal Analyses. Organ. Res. Methods 20, 61–

94.

Jenkins, G.M., 2014. Autoregressive–Integrated Moving

Average (ARIMA) Models, in: Wiley StatsRef:

Statistics Reference Online. American Cancer Society.

Larburu, N., Artetxe, A., Escolar, V., Lozano, A., Kerexeta,

J., 2018. Artificial Intelligence to Prevent Mobile Heart

Failure Patients Decompensation in Real Time:

Monitoring based Predictive Model. Indawi.

Laumbach, R.J., Kipen, H.M., 2012. Respiratory health

effects of air pollution: Update on biomass smoke and

traffic pollution. J. Allergy Clin. Immunol. 129, 3–11.

Levin, R.K., Katz, M., Saldiva, P.H.N., Caixeta, A.,

Franken, M., Pereira, C., Coslovsky, S.V., Pesaro, A.E.,

2018. Increased hospitalizations for decompensated

heart failure and acute myocardial infarction during

mild winters: A seven-year experience in the public

health system of the largest city in Latin America. PLOS

ONE 13, e0190733.

Ljung, G.M., Box, G.E.P., 1978. On a measure of lack of fit

in time series models. Biometrika 65, 297–303.

Moritz, S., Bartz-Beielstein, T., 2017. imputeTS: Time

Series Missing Value Imputation in R. R J. 9, 207–218.

Morris, R.D., Naumova, E.N., Munasinghe, R.L., 1995.

Ambient air pollution and hospitalization for

congestive heart failure among elderly people in seven

large US cities. Am. J. Public Health 85, 1361–1365.

Ponikowski, P. et al., 2014. Heart failure: preventing

disease and death worldwide. ESC Heart Fail. 1, 4–25.

Rui, S., Vera, C., 2017. Comparative Approaches to Using

R and Python for Statistical Data Analysis. IGI Global.

Stewart, S., McIntyre, K., Capewell, S., McMurray, J.J.V.,

2002. Heart failure in a cold climate: Seasonal

variation in heart failure-related morbidity and

mortality. J. Am. Coll. Cardiol. 39, 760–766.

Warren, R., Walker, B., Nathan, V.R., 2002. Environmental

factors influencing public health and medicine: policy

implications. J. Natl. Med. Assoc. 94, 185–193.

Woolf, S.H., Aron, L., 2013. Physical and Social

Environmental Factors. National Academies Press

(US).

HEALTHINF 2019 - 12th International Conference on Health Informatics