Artiﬁcial Neural Network Approach to Prediction of Protein-RNA

Residue-base Contacts

Morihiro Hayashida

, Jose Nacher

and Hitoshi Koyano

Department of Electrical Engineering and Computer Science, National Institute of Technology,

Matsue College, Matsue, Shimane, Japan

Department of Information Science, Faculty of Science, Toho University, Funabashi, Chiba, Japan

School of Life Science and Technology, Tokyo Institute of Technology, Meguro-ku, Tokyo, Japan

Keywords:

Fully Connected Neural Network, Protein-RNA Interaction, Residue-base Contact.

Abstract:

Protein-RNA complexes play essential roles in a cell, and are involved in the post-transcriptional regulation of

gene expression. Therefore, it is important to analyze and elucidate structures of protein-RNA complexes and

also contacts between residues and bases in their interactions. A method based on conditional random ﬁelds

(CRFs) was developed for predicting residue-base contacts using evolutionary relationships between individ-

ual positions of a residue and a base. Further, the probabilistic model was modiﬁed to improve the prediction

accuracy. Recently, many researchers focus on deep neural networks due to its classiﬁcation performance. In

this paper, we develop a neural network with ﬁve layers for predicting residue-base contacts. From computa-

tional experiments, in terms of the area under the receiver operating characteristic curve (AUC), the predictive

performance of our proposed method was comparable or better than those of the CRF-based methods.

1 INTRODUCTION

Interactions between proteins and RNAs are involved

in the post-transcriptional regulation of gene expres-

sion including alternative splicing, polyadenylation,

localization and translation (Glisovic et al., 2008).

For instance, a ribosome is formed with multiple pro-

teins and RNAs, and synthesizes proteins from mes-

senger RNAs. Disruption of protein-RNA interac-

tions may cause various diseases including cancers.

Therefore, it is needed to obtain precise knowledge of

contact positions between proteins and RNAs to un-

derstand their molecular function.

It is known that there are several RNA-binding

domains such as RNA recognition motif (RRM),

heterogeneous nuclear ribonucleoproteins (hnRNPs)

(Beyer et al., 1977), the K-homology domains (Siomi

et al., 1993), double-stranded RNA-binding domains

(dsRBD) (Feng et al., 1992), TIA-1 (Kedersha et al.,

1999) and zinc ﬁngers (Hall, 2005). The sequence

and structural properties of RNA-protein interaction

sites in 211 RNA-protein chain pairs were investi-

gated, and it was reported that 78% of hydrogen bonds

involve amino acid side chains, and the remaining

involve the protein backbone (Gupta and Gribskov,

2011). Several computational methods have been

developed for predicting RNA-binding amino acid

residues in proteins. Sun et al. proposed RNAProSite,

which utilizes the random forest (Breiman, 2001)

with electrostatic feature, triplet interface propensity,

position-speciﬁc scoring matrices (PSSM) proﬁle, ge-

ometrical characteristic and physicochemical prop-

erty (Sun et al., 2016). Sharan et al. developed an

integrated pipeline, called APRICOT, that identiﬁes

functional motifs in protein sequences using PSSMs,

hidden Markov models of RNA-binding domains, and

sequence-based features (Sharan et al., 2017). It was

reported that APRICOT achieved sensitivities higher

than or as good as RNAProSite and other high per-

forming predictors. Tang et al. proposed PredRBR

that utilizes gradient tree boosting and many kinds

of sequence and structural site features (Tang et al.,

2017).

On the other hand, concerning binding sites of

RNAs, 24.6% of hydrogen bonds involve nucleobase-

speciﬁc interactions, and the remaining involve the

RNA backbone (Gupta and Gribskov, 2011). Ali-

panahi et al. proposed DeepBind that uses many

RNA sequences with binding scores determined from

protein binding microarray experiments, and extracts

motif features by a deep learning technique, which

outperformed 26 other methods such as FeatureRE-

Hayashida, M., Nacher, J. and Koyano, H.

Artiﬁcial Neural Network Approach to Prediction of Protein-RNA Residue-base Contacts.

DOI: 10.5220/0007348101630167

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 163-167

ISBN: 978-989-758-353-7

163

DUCE (Weirauch et al., 2013) and BEEML-PBM

(Zhao et al., 2011) when the correlation between the

predicted and actual probe intensities was evaluated

(Alipanahi et al., 2015). Zeng et al. systematically

examined various models of convolutional neural net-

works to further improve DeepBind, and observed

that deploying more convolutional kernels was always

beneﬁcial, but the local-pooling and additional con-

volutional layers were useful only in the motif oc-

cupancy task when higher-order features existed, and

they did not achieve signiﬁcant improvement (Zeng

et al., 2016). These methods were developed for iden-

tifying RNA and DNA motifs bounded by transcrip-

tion factors. However, both positions in binding RNA

and protein were not identiﬁed. Methods for pre-

dicting residue-base contacts in protein-RNA interac-

tions were proposed using conditional random ﬁelds

(CRFs), which used evolutionary measurements ob-

tained from multiple sequence alignments (Hayashida

et al., 2013; Hayashida et al., 2018). For analyzing

mechanisms of protein-RNA interactions in detail, we

also deal with the problem of predicting residue-base

contacts.

Recently, artiﬁcial neural network techniques (Le-

Cun et al., 2015; Glorot et al., 2011) have been ap-

plied in many research ﬁelds due to its high classiﬁca-

tion performance. We explore neural network archi-

tectures to overcome the prediction accuracy by the

CRF-based method. For evaluating the proposed neu-

ral network, we perform computational experiments

as done in the previous study. The results show that

in terms of the area under the receiver operating char-

acteristic curve (AUC), the predictive performance of

our proposed method was comparable or better than

those of the CRF-based methods.

2 METHODS

We address the following problem. Given two se-

quences p

p = p

··· p

and r

r = r

·· ·r

of a protein

and RNA, ﬁnd whether or not p

and r

interacts for

all i and j. We brieﬂy review the CRF-based method

and an evolutionary measurement MI

(mutual infor-

mation improved) proposed by (Dunn et al., 2008) be-

tween positions of amino acids and bases, and the lat-

ter is also used by our method. After that, we explain

our neural network architecture.

2.1 Evolutionary Measurement

One method of measuring coevolutionary relationship

between positions of a residue and a base in protein

and RNA sequences is to calculate mutual informa-

tion from multiple sequence alignments. MI

was

developed to improve protein residue-residue contact

prediction by subtracting a bias from mutual informa-

tion. Suppose that we have two multiple alignments

for protein and RNA sequences, p

p = p

·· · p

and

r = r

·· ·r

, respectively, where |p

p| means the length

of p

p. If i-th residue p

and j-th base r

interact with

each other to maintain a biological system in an indi-

vidual organism, there must be some relationship be-

tween them. Then, mutual information between po-

sitions i and j is deﬁned by m

i j

∑

a∈A

∑

b∈B

Pr(p

a, r

= b) log

Pr(p

=a,r

=b)

Pr(p

=a)Pr(r

=b)

, where A and B denote

sets of amino acids and bases, respectively. MI

was

modiﬁed as m

i j

−

∑

i=1

i j

∑

j=1

i j

∑

i=1

∑

j=1

i j

for our purpose.

2.2 Conditional Random Field

(CRF)-based Method

Conditional random ﬁelds (CRFs) were proposed

by extending Markov random ﬁelds (Lafferty

et al., 2001). The CRF with a strictly positive

density in the previous study was deﬁned by

Pr(x

i j

, m

m, p

p, r

r) =

i j

exp



i j

x, m

m, p

p, r

r) +

∑

(k,l)∈N

i j

i jkl

x, m

m, p

p, r



, where x

i j

= 1

means that i-th residue and j-th base in-

teract with each other, x

i j

= −1 otherwise,

i j

x, m

m, p

p, r

r) = x

i j













i j

max

(k,l)∈N

i j

min

(k,l)∈N

i j







⊕ δ

)







i jkl

x, m

m, p

p, r

r) = x

i j



i j

− m

i j



, δ

)

de-

notes a |A| × |B| dimensional vector which only the

element corresponding to the amino acid p

and base

is one, N

i j

for i = 1, ·· · , |p

p| and j = 1, ··· , |r

r| de-

notes a set of adjacent pairs of (i, j), and was deﬁned

by (i ± 1, j), (i, j ± 1) (see Figure 1). In this method,

at the gray square in the ﬁgure was given

as one of input data for a residue-base pair (i, j),

that is, (i

, j

) ∈ {(i, j)} ∪ N

i j

∪

(k,l)∈N

i j

. The

probability model contains dependency relationships

between positions (i, j) and (i

, j

) ∈ N

i j

Parameters w

and w

in the CRF model are deter-

mined by maximizing the pseudo-likelihood function,

L(θ) =

∏

i=1

∏

j=1

Pr(x

(n)

i j

(n)

i j

, m

(n)

, p

(n)

, r

(n)

, θ)

given x

(n)

, m

(n)

for each sequence pair p

(n)

, r

(n)

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

164

3URWHLQVHTXHQFH

51$VHTXHQFH

Figure 1: Illustration of adjacent pairs of (i, j). The posi-

tions (i

, j

) at the gray squares are included in N

i j

2.3 Neural Network Architecture

We propose a neural network with ﬁve layers as

shown in Figure 2. The input layer has (2k

+ 1)

(|A|+|B|)(2k

+1) neurons having evolutionary mea-

surement values of pairs (i

, j

) for all i − k

≤ i

≤

i+k

, j −k

≤ j

≤ j+k

, and one-hot vectors corre-

sponding to subsequences from p

i−k

to p

i+k

of pro-

tein p

p and from r

j−k

to r

j+k

of RNA r

r, where k

and k

are constant integers, and a one-hot vector for

a constant number c is deﬁned as a vector that only

c-th element is one and the others are zero. For exam-

ple, when k

= 2, m

at the gray and white square

in Figure 1 is given with respect to (i, j) to the in-

put layer. In addition, amino acids can be classiﬁed,

and |A| can be equal or less than 20. The neural net-

work has three hidden layers with n

, n

, and n

neu-

rons, respectively. The output layer has two neurons

corresponding to the two classiﬁcation results. All

successive layers are fully connected and the recti-

ﬁed linear unit (ReLU) (Glorot et al., 2011) deﬁned

by f (x) = max{0, x} is applied to the output of each

neuron except the ﬁnal layer. The softmax function

is applied in the ﬁnal layer. In addition, bias variables

are added to each neuron except the input layer. Then,

the total number of parameters is ((2k

+1)

+(|A| +

|B|)(2k

+1))n

∑

i=1

i+1

}+2n

+2.

input layer hidden layers output layer

Figure 2: Illustration of the neural network with ﬁve layers.

3 RESULTS

For evaluation of the proposed method, we used the

same dataset as that in the previous study, which con-

sists of residue-base pairs included in thirteen protein-

RNA pairs in four complexes identiﬁed by ’1yl4’,

’2hgu’,’3kc4’, and ’3kcr’ in PDB (Rose et al., 2017)

as shown in Table 1.

Each line in the table shows a protein-RNA pair,

the PDB identiﬁer, the chain identiﬁer, the protein

and RNA sequences p

p, r

r in UniProt and GenBank

databases (The UniProt Consortium, 2017; Benson

et al., 2011), the length, and the number of contacts

between residues and bases in the protein and the

RNA. It was assumed that i-th residue and j-th base

interact with each other if the Euclidean distance be-

tween atoms of the residue and base is less than or

equal to 3

A because the distances of hydrogen bonds

are about 2.7 to 2.9

We used multiple sequence alignments of Pfam

and Rfam databases (Finn et al., 2016; Kalvari et al.,

2018) for the protein p

p and RNA r

r to calculate MI

We examined classiﬁcations of amino acids with 8,

10, and 15 groups according to the study (Murphy

et al., 2000), that is, |A| took 8, 10, 15, and 20, and

was calculated based on each case of A (see Ta-

ble 2).

We performed cross-validation procedures, and

took the average of AUC scores as well as the previ-

ous study, where among thirteen protein-RNA pairs in

Table 1, all residue-base pairs included in one protein-

RNA pair were used for test, and the others were used

for training. We examined the window size by varying

the values of k

and k

, and set n

= 750, n

= 680,

and n

= 250. We used the tensorﬂow-gpu library

(version 1.4.1) to minimize the cross entropy of the

output and to calculate the AUC score (Abadi et al.,

2015).

Table 3 shows the results on average AUC

scores by the CRF-based method and the proposed

fully-connected neural network method in the cases

, k

) = (1, 2), (2, 1), (2, 2). In the three cases, the

AUC scores in the case of (2, 1) were better than those

in other cases in the same classiﬁcation of amino

acids. It implies that amino acids and bases at po-

sitions (i ± 2, j ± 2) far from the position of inter-

est (i, j) were not effective to enhance the predic-

tion accuracy. On the other hand, the evolutionary

measurement MI

between positions (i ± 2, j

) and

, j ±2) for i− 2 ≤ i

≤ i +2, j −2 ≤ j

≤ j + 2 were

useful. It is expected that the neural network with

, k

) = (2, 2) would be equivalent to the neural net-

work with (2, 1) if appropriate parameters are esti-

mated as zero, and the AUC score with (2, 2) would

Artiﬁcial Neural Network Approach to Prediction of Protein-RNA Residue-base Contacts

165

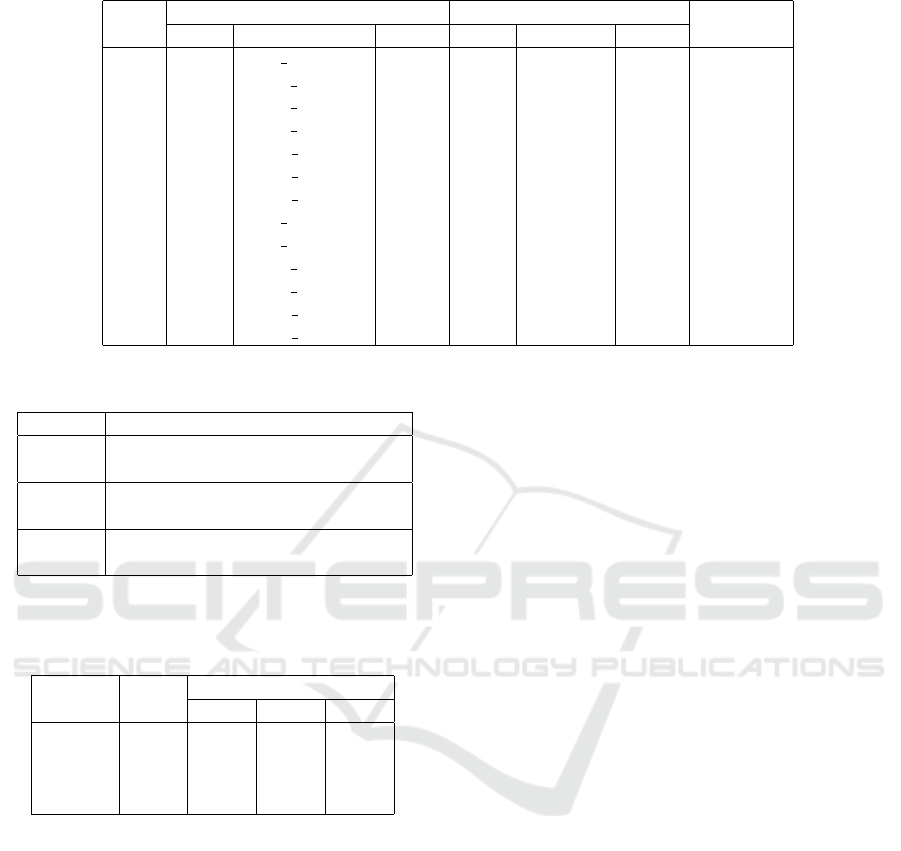
Table 1: Dataset of the residue-base pairs in protein-RNA complexes.

PDB Protein sequence RNA sequence # contacts

chain UniProt length chain GenBank length

1yl4 K RS8 THET8 135 A M26923 1889 29

1yl4 M RS10 THET8 97 A M26923 1711 20

1yl4 O RS12 THET8 122 A M26923 1972 45

1yl4 T RS17 THET8 69 A M26923 1690 29

2hgu R RL18 THETH 110 B X01554 1543 28

2hgu Z RL27 THET8 81 A X12612 1356 20

2hgu 5 RL33 THET8 48 A X12612 1445 18

3kc4 E RS5 ECOLI 67 A J01695 1701 13

3kc4 G RS7 ECOLI 147 A J01695 1941 25

3kc4 O RS15 ECO57 83 A J01695 1821 21

3kc4 Q RS17 ECOLI 69 A J01695 1690 18

3kcr W RL27 ECOLI 77 8 J01695 1356 18

3kcr 3 RL35 ECOLI 61 8 J01695 1337 12

Table 2: Grouping of amino acids (Murphy et al., 2000).

#groups groups of amino acids

8 (MLVIC) (GA) (TS) (P) (FYW)

(DENQ) (RK) (H)

10 (MLVI) (C) (G) (A) (TS) (P)

(FYW) (DENQ) (RK) (H)

15 (MLVI) (C) (G) (A) (T) (S) (P)

(FY) (W) (D) (E) (N) (Q) (RK) (H)

Table 3: Results on average AUC scores by the CRF-

based method and the proposed neural network method with

, k

) = (1, 2), (2, 1), (2, 2).

#groups CRF Proposed

(1,2) (2,1) (2,2)

8 0.692 0.671 0.674 0.668

10 0.699 0.673 0.684 0.681

15 0.699 0.670 0.711 0.682

20 0.693 0.665 0.690 0.678

be larger than or equal to that with (2, 1). However,

the AUC score with (2, 1) was larger than that with

(2, 2).

For classiﬁcation of amino acids, as reported in

the previous study, the AUC score with 15 groups

was better than others in almost all cases. In addition,

the AUC score by our method with (k

, k

) = (2, 1)

and 15 groups was better than that by the CRF-based

method.

4 CONCLUSIONS

We proposed a neural network approach to prediction

of protein-RNA residue-base contacts. In the neu-

ral network, neurons between successive layers were

fully connected, and the ReLU activation function

was applied. From the cross-validation computational

experiments to evaluate the proposed method, the re-

sults show that in terms of the area under the receiver

operating characteristic curve (AUC), the predictive

performance of our proposed method was compara-

ble or better than those of the CRF-based method.

As future work, other types of advanced neural net-

works should be examined for further improvement

of prediction accuracy, and for understanding inter-

actions between residues and bases in detail. In

our method, subsequences as long as motifs cannot

be dealt. Therefore, we would like to improve our

method to deal with longer subsequences.

ACKNOWLEDGEMENTS

This work was partially supported by Grants-in-Aid

#16K00392 and #16KT0020 from JSPS, Japan.

REFERENCES

Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z.,

Citro, C., Corrado, G. S., Davis, A., Dean, J., Devin,

M., Ghemawat, S., Goodfellow, I., Harp, A., Irving,

G., Isard, M., Jia, Y., Jozefowicz, R., Kaiser, L., Kud-

lur, M., Levenberg, J., Man

e, D., Monga, R., Moore,

S., Murray, D., Olah, C., Schuster, M., Shlens, J.,

Steiner, B., Sutskever, I., Talwar, K., Tucker, P., Van-

houcke, V., Vasudevan, V., Vi

egas, F., Vinyals, O.,

Warden, P., Wattenberg, M., Wicke, M., Yu, Y., and

Zheng, X. (2015). TensorFlow: Large-scale machine

learning on heterogeneous systems. Software avail-

able from tensorﬂow.org.

Alipanahi, B., Delong, A., Weirauch, M., and Frey, B.

(2015). Predicting the sequence speciﬁcities of DNA-

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

166

and RNA-binding proteins by deep learning. Nature

Biotechnology, 33:831–838.

Benson, D., Karsch-Mizrachi, I., Lipman, D., Ostell, J., and

Sayers, E. (2011). Genbank. Nucleic Acids Research,

39:D32–D37.

Beyer, A., Christensen, M., Walker, B., and LeStourgeon,

W. (1977). Identiﬁcation and characterization of the

packaging proteins of core 40S hnRNP particles. Cell,

11:127–138.

Breiman, L. (2001). Random forests. Machine Learning,

45:5–32.

Dunn, S., Wahl, L., and Gloor, G. (2008). Mutual in-

formation without the inﬂuence of phylogeny or en-

tropy dramatically improves residue contact predic-

tion. Bioinformatics, 24:333–340.

Feng, G.-S., Chong, K., Kumar, A., and Williams, B.

(1992). Identiﬁcation of double-stranded RNA-

binding domains in the interferon-induced double-

stranded RNA-activated p68 kinase. Proc. Natl. Acad.

Sci. USA, 89:5447–5451.

Finn, R. D., Coggill, P., Eberhardt, R. Y., Eddy, S. R.,

Mistry, J., Mitchell, A. L., Potter, S. C., Punta, M.,

Qureshi, M., Sangrador-Vegas, A., Salazar, G. A.,

Tate, J., and Bateman, A. (2016). The Pfam protein

families database: towards a more sustainable future.

Nucleic Acids Research, 44(D1):D279–D285.

Glisovic, T., Bachorik, J., Yong, J., and Dreyfuss, G. (2008).

RNA-binding proteins and post-transcriptional gene

regulation. FEBS Letters, 582:1977–1986.

Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse

rectiﬁer neural networks. In 14th International Con-

ference on Artiﬁcial Intelligence and Statistics, pages

315–323.

Gupta, A. and Gribskov, M. (2011). The role of RNA

sequence and structure in RNA-protein interactions.

Journal of Molecular Biology, 409:574–587.

Hall, T. (2005). Multiple modes of RNA recognition by

zinc ﬁnger proteins. Current Opinion in Structural

Biology, 15:367–373.

Hayashida, M., Kamada, M., Song, J., and Akutsu, T.

(2013). Prediction of protein-RNA residue-base con-

tacts using two-dimensional conditional random ﬁeld

with the lasso. BMC Systems Biology, 7(Suppl 2):S15.

Hayashida, M., Okada, N., Kamada, M., and Koyano, H.

(2018). Improving conditional random ﬁeld model

for prediction of protein-RNA residue-base contacts.

Quantitative Biology, 6:155–162.

Kalvari, I., Argasinska, J., Quinones-Olvera, N., Nawrocki,

E. P., Rivas, E., Eddy, S. R., Bateman, A., Finn, R. D.,

and Petrov, A. I. (2018). Rfam 13.0: shifting to a

genome-centric resource for non-coding RNA fami-

lies. Nucleic Acids Research, 46(D1):D335–D342.

Kedersha, N., Gupta, M., Li, W., Miller, I., and Anderson,

P. (1999). RNA-binding proteins TIA-1 and TIAR

link the phosphorylation of eIF-2α to the assembly of

mammalian stress granules. Journal of Cell Biology,

147:1431–1441.

Lafferty, J., McCallum, A., and Pereira, F. (2001). Con-

ditional random ﬁelds: Probabilistic models for seg-

menting and labeling sequence data. In Proc. Int.

Conf. on Machine Learning.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-

ing. Nature, 521:436–444.

Murphy, L., Wallqvist, A., and Levy, R. (2000). Simpli-

ﬁed amino acid alphabets for protein fold recognition

and implications for folding. Protein Engineering,

13:149–152.

Rose, P. W., Prli

c, A., Altunkaya, A., Bi, C., Bradley, A. R.,

Christie, C. H., Costanzo, L. D., Duarte, J. M., Dutta,

S., Feng, Z., Green, R. K., Goodsell, D. S., Hud-

son, B., Kalro, T., Lowe, R., Peisach, E., Randle,

C., Rose, A. S., Shao, C., Tao, Y.-P., Valasatava, Y.,

Voigt, M., Westbrook, J. D., Woo, J., Yang, H., Young,

J. Y., Zardecki, C., Berman, H. M., and Burley, S. K.

(2017). The RCSB protein data bank: integrative view

of protein, gene and 3D structural information. Nu-

cleic Acids Research, 45(D1):D271–D281.

Sharan, M., F

orstner, K., Eulalio, A., and Vogel, J. (2017).

APRICOT: an integrated computational pipeline for

the sequence-based identiﬁcation and characterization

of RNA-binding proteins. Nucleic Acids Research,

45:e96.

Siomi, H., Matunis, M., Michael, W., and Dreyfuss, G.

(1993). The pre-mRNA binding K protein contains

a novel evolutionary conserved motif. Nucleic Acids

Research, 21:1193–1198.

Sun, M., Wang, X., Zou, C., He, Z., Liu, W., and Li, H.

(2016). Accurate prediction of RNA-binding protein

residues with two discriminative structural descrip-

tors. BMC Bioinformatics, 17(1):231.

Tang, Y., Liu, D., Wang, Z., Wen, T., and Deng, L. (2017).

A boosting approach for prediction of protein-RNA

binding residues. BMC Bioinformatics, 18(13):465.

The UniProt Consortium (2017). UniProt: the univer-

sal protein knowledgebase. Nucleic Acids Research,

45:D158–D169.

Weirauch, M. T., Cote, A., Norel, R., Annala, M., Zhao,

Y., Riley, T. R., Saez-Rodriguez, J., Cokelaer, T., Ve-

denko, A., Talukder, S., Consortium, D., Bussemaker,

H. J., Morris, Q. D., Bulyk, M. L., Stolovitzky, G., and

Hughes, T. R. (2013). Evaluation of methods for mod-

eling transcription factor sequence speciﬁcity. Nature

Biotechnology, 31:126–134.

Zeng, H., Edwards, M., Liu, G., and Gifford, D.

(2016). Convolutional neural network architectures

for predicting DNA-protein binding. Bioinformatics,

32:i121–i127.

Zhao, Y., Stormo, G., Feature, N., and Eisenstein, M.

(2011). Quantitative analysis demonstrates most tran-

scription factors require only simple models of speci-

ﬁcity. Nature Biotechnology, 29:480–483.

Artiﬁcial Neural Network Approach to Prediction of Protein-RNA Residue-base Contacts

167