
Physically-based Thermal Simulation of Large Scenes for Infrared
Imaging
B. Kottler, E. Burkard, D. Bulatov and L. Harak
´
e
Department of Scene Analysis, Fraunhofer Institute of Optronics, System Technologies and Image Exploitation (IOSB),
76275 Ettlingen, Germany
Keywords:
Physics-Based, Thermal Infrared, Heat Simulation, Heat Transfer Modeling, Finite Volume Method.
Abstract:
Rendering large scenes in the thermal infrared spectrum requires the knowledge of the surface temperature
distribution. We developed a workflow starting from raw airborne sensor data yielding to a physically-based
thermal simulation, which can be used for rendering in the infrared spectrum. The workflow consists of four
steps: material classification, mesh generation, material parameter assignment, and thermal simulation. This
paper concerns the heat transfer simulation of large scenes. Our thermal model includes the heat transfer types
radiation, convection, and conduction in three dimensions within the object and with its environment, i.e. sun
and sky in particular. We show that our model can be solved by finite volume method and it shows good
agreement with experimental data of the CUBI object. We demonstrate our workflow for sensor data from
the City of Melville and produce reasonable results compared to infrared sensor data. For the large scene, the
temperature simulation finished in appropriate time of 252 sec. for five day-night cycles.
1 INTRODUCTION AND
PREVIOUS WORK
1.1 Motivation
Thermal simulation of large scenes is essential when
it comes to applications like meteorology, assessment
of atmospheric pollution, camouflage evaluation in
the military applications or detection of urban heat is-
lands and corresponding heat radiation for city plan-
ners. All these applications and especially the last one
have a strong dynamic component, since to the same
extent as augmentation of both the global earth tem-
perature rises, so does urbanization degree.
From the point of view of a city planner, whose
job is to respond to the needs of the later generations
without putting upside down the infrastructure needed
for the current one, the ability to render large three-
dimensional scenes in thermal infrared wavelength
spectrum is a very interesting aspect. In which dis-
tances along the roads should the trees be planted and
which kinds of trees should actually be used to reduce
the heat radiation to an acceptable amount? Which
heights and roof materials for the public buildings are
least susceptible to the appearance of urban heat is-
lands? Fast and reliable scene rendering in thermal
infrared allows assessing the long-term energy bal-
ance for these scenarios. The temperature of the sur-
face should be ideally modeled as a function of the
current atmospheric condition, surface geometry and
material composition, socio-economic situation, and
many others. Of course, a city planner cannot start
from scratch, but must deal with the existing realities,
or initial conditions. For a more precise simulation of
temporal development of the surface temperature and
subsequent thermal rendering, the main requirement
is to know as much as possible about the surface. Here
it is often not enough to use the existing geographical
data, because they may be obsolete or just lack some
relevant information, such as building roof materials
and roof forms.
To be able to free ourselves from too many input
requirements (accurate 3D models, numerous tem-
perature measurements), we are currently designing
an end-to-end pipeline starting at raw airborne sen-
sor data and yielding semantic and three-dimensional
environments rendered in thermal infrared. The fo-
cus of this paper will concern the simulation of the
surface temperature of large scenes. This may not
only be used directly in many applications but also
is basic for thermal rendering, i.e., determining the
heat radiance since every object having a tempera-
ture above absolute zero radiates at infrared wave-
lengths. The reason to utilize the airborne data is that
Kottler, B., Burkard, E., Bulatov, D. and Haraké, L.
Physically-based Thermal Simulation of Large Scenes for Infrared Imaging.
DOI: 10.5220/0007351400530064
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 53-64
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
53

large parts of the scene are captured and the measure-
ments of geometry and material classification are ac-
tual. From these measurements, there are plenty of
previous work achieved on accurate 3D city model-
ing and material classification (Bulatov et al., 2014;
Xiong et al., 2014). The first reason for producing
semantic scenes is that land-cover classes and mate-
rial classes are strongly correlated, e.g. within one
building, roofs consist of few materials, trees can be
represented by generic models. Otherwise assigning
materials to single roof polygons making up the scene
and figuring out the emitting properties of these ma-
terials are two tedious procedures. The second reason
is that once these models are available, further im-
portant data, such as material composition of building
walls or analysis of socio-economic developments are
easier to integrate. A particular challenge for the ge-
ometry component of the above module is the com-
plexity of the underlying scene. Besides, shadow
cast is a crucial component for surface temperature,
which cannot be employed in 2D case (Dewan and
Corner, 2014). Finally, to provide an accurate ground
truth measurement in closest-range three-dimensional
scenarios, which are appropriate for detecting urban
heat islands, among others, an efficient rendering rou-
tine can replace numerous punctual measurements of
temperatures and provide a glance into the future by
means of simulation. The complexity of the prob-
lem is the reason why there are only a few publica-
tions focused on simulation of surface temperature in
larger three-dimensional environments, as we will see
in the remainder of this section. Also, we will see that
(Xiong et al., 2016) is the most similar contribution to
our work, however, there are still several differences
and improvements it is worth being focused on.
1.2 Previous Approaches
We start our short literature review by 2D-based ap-
proaches. Essentially, convection and emission equa-
tions are retrieved from land-cover/material classi-
fication results (Bartos and Stein, 2015; Feng and
Myint, 2016; Dewan and Corner, 2014). Three-
dimensional scene elements are treated by unfold-
ing; hence, effects of shadow cast remain unconsid-
ered. However, for close-range applications around
selected monuments, the surrounding 3D terrain
(heights of the trees and buildings) must not be ne-
glected and thus the challenge is to combine the auto-
matic urban terrain reconstruction and thermal simu-
lation. A well-established software MuSES, designed
for the US army, is introduced in (Johnson et al.,
1998). In particular, it shows how the level of au-
tomatization in thermal simulation was increased with
respect to the previous system. The remaining inter-
active parts were on the one hand uploading the 3D
geometry and assigning material properties, and on
the other hand, quality control since the system was
presumable used for camouflage and deception. It be-
comes clear that an automatic creation of 3D mod-
els assigned with material properties is tempting for
a more rapid progress in the field. The authors of
(Lagouarde et al., 2010) are more interested in mea-
suring temperatures from different viewing directions
since it correlated with radiation emitted by an en-
semble of structure. In the first part of their work,
they assess directional anisotropy that is the differ-
ence between the directional and the nadir tempera-
tures. In the second part of the work, the model at a
given direction is rendered and the aggregated direc-
tional temperature at a given pixel in obtained using
the classes and the raw values for the surface temper-
ature from the first step. While the 3D models were
provided from the public sources, the authors only
made a difference between six configurations, that is
two light settings (sunlit or shaded) and the three land-
cover classes (roof, wall, and soil with materials as-
signed more or less arbitrarily). Performing the three-
dimensional aggregation of temperatures is another
critical generalization of their method. The advanced
treatment of shadows is described in (Poglio et al.,
2002). The authors adaptively subdivide the triangles
in illuminated and shaded ones, ensuring that the new
triangles are not degenerated. As for development of
the simulated scene over time, they refer to (John-
son et al., 1998). A summary of the physics of heat
transport in large scenes can be found in (Mar
´
echal
et al., 2010). In their voxel-based approach, a method
for simulating realistic winter appearance based on a
physical simulated temperature distribution for alpine
regions is presented. For us this paper gives a good
overview about components of our simulation.
Most similar to our contribution is (Xiong et al.,
2016). From raw meshes, classification of triangles
into ground, vegetation, building wall and building
roof takes place using simple 3D-based features (ele-
vation, planarity, and horizontality) and Markov Ran-
dom Fields. In the next steps, the portions of the mesh
corresponding to buildings are modeled as water-tight
multi-planar structure while the remaining elevated
portions of the mesh are ignored. For every mesh
element, heat balance equation comprising terms for
radiation, conduction, and convection is solved. The
shadows are taken into account as well in the radiation
term. This pioneering work can be questioned in two
aspects. First, the raw meshes were created from im-
ages by means of structure from motion procedures.
However, the images were not considered for assign-
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
54
ing material properties to surface triangles. The sec-
ond problem is that the vegetation was not considered
even though presence of trees is very valuable for re-
ducing the urban heat.
1.3 Contributions
Our improvements will include land-cover classifi-
cation from combined image- and point-based fea-
tures. From the image based classification result,
we triangulate the terrain using Restricted Top-Down
Quadree Triangulation (Pajarola, 2002). The triangu-
lated terrain has three important properties: memory
efficiency, accuracy, and consistence.
To this terrain mesh, we add the building mod-
els. For this contribution, we will use the terms land-
cover and material classification synonymous, assum-
ing, for example, that the building roofs and walls
are comprised by two uniform materials. Contribu-
tions achieving a more detailed subdivision of build-
ing roofs into materials using multi-spectral and high-
resolution images exist in the literature (Ilehag et al.,
2018) and thus our approach can be easily extended.
Besides, we detect high vegetation and add trees to
the mesh as well, currently modeled in the shape of
forest boxes, i.e. trees standing close to each other
are merged and single trees are disregarded. Further-
more, we are able to take shadows into account as
the simulation is performed on a surface embedded in
the 3-dimensional space and thus includes occlusion
analyses.
A physical approach was chosen to calculate the
surface temperatures with the heat equation. This is
a partial differential equation, i.e. it includes spatial
and temporal derivations. For the temporal deriva-
tions, the forward Euler integration was used. The
spatial derivations were discretized with a finite vol-
ume method. For this purpose, the simulation area
is divided into finite volumes and the flows on the
boundaries of the volumes are evaluated. We will con-
sider ten classes in total and for each of these classes,
we derive the necessary coefficients from the litera-
ture.
In this paper, we propose a framework for sim-
ulating realistic temperature distributions for large
sceneries. This is the core aspect of a complex work-
flow from sensor data to semantic urban terrain mod-
els rendered in thermal spectrum.
2 PRELIMINARIES
Since the focus of this paper concerns the temperature
simulation step of the pipeline, or the bottom block of
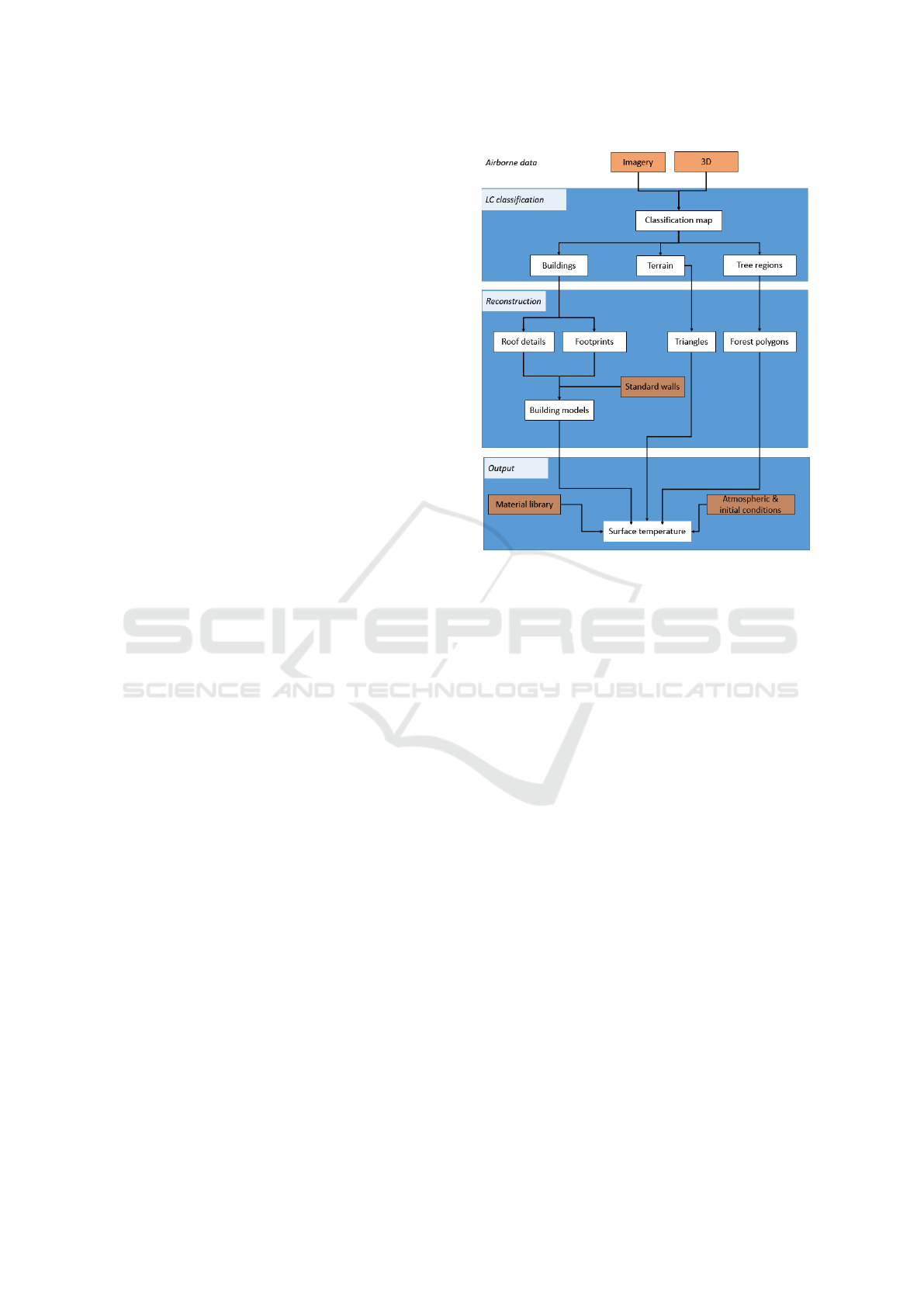
Figure 1: Pipeline – From Sensor to Surface Temperature.
Figure 1, we decided to give a short summary of the
physical background necessary for thermal simulation
and how it states the basis for infrared rendering, as
well as the preceding steps leading from raw airborne
data to a semantic 3D representation of the scene.
2.1 Infrared Rendering and Physical
Background of Thermal Flow
Starting with the Kajiya’s well-known rendering
equation, cp. (Kajiya, 1986),
L(x,
~
ω) = L
e
(x,
~
ω) + L
r
(x,
~
ω), (1)
with the total radiance L(x,
~
ω) from surface point x
in direction
~
ω which consists of the emitted radiance
L
e
and the reflected radiance from the upper hemi-
sphere of the surface L
r
, we have to take into account
the temperature dependence of the emissive radiation
term L
e
if regarding the thermal spectrum for render-
ing,
L
e
(x,
~
ω) = L
e
(x,
~
ω,T ), (2)
where T is the surface temperature at point x. In order
to evaluate this equation and render an arbitrary scene
in the infrared spectrum, one has to know the sur-
face temperature at every observed point in the scene.
However, temperature is not a property as color or
texture, but depends on the environment, time of the
day, physical material parameters, temperature his-
tory, and so on. Determining the surface temperature
Physically-based Thermal Simulation of Large Scenes for Infrared Imaging
55

of a scene at a specific point in time requires the sim-
ulation of heat transfer.
In general, heat transfer follows the first law of
thermodynamics where we will consider constant vol-
umes,
mC
v
dT
dt
= Q (3)
with the mass m, the specific heat capacity C
v
at con-
stant volume, the temperature T and the heat trans-
fer rate Q per unit area (Lienhard IV and Lienhard V,
2011). This rate is compound by the three modes of
heat transfer: radiation, conduction and convection.
For the sake of completeness, it shall be pointed out
that heat can also be chemically stored in the form
of latent heat caused by phase change, e.g. vaporiza-
tion. However, this will not be included in the thermal
model presented in this paper.
Heat conduction takes place predominantly within
solids and fluids, and the conductive heat transfer fol-
lows Fourier’s law,
mC
v
dT
dt
= K ∆T (4)
with the thermal conductivity K. Convection involves
the surrounding medium, e.g. the air in an urban
area. Free convection describes the phenomenom of
a medium being heated or cooled by a surface and
therefore starting to move. Forced convection refers
to an already moving medium, e.g. due to wind, ex-
changing heat with a surface. The convective heat
transfer depends on the difference between the sur-
face temperature T and the surrounding mediums’
temperature T
medium
,
mC
v
∂T
∂t
∝ T − T
medium
. (5)
Regarding radiative heat transfer, all matter with
a temperature greater than absolute zero emits ther-
mal radiation. For a blackbody, which is defined by
absorption end re-emission of all incoming light, the
radiation power follows the Stefan-Boltzmann law,
P = σT
4
with the Stefan-Boltzmann constant σ, and
the temperature T (Siegel and Howell, 1992). With
the so-called grey-body approach, the actual radiative
power is given by a constant fraction of a blackbodys’
radiative power, defined by the emissivity ε ∈ [0,1],
where ε = 1 equals a blackbody. In estimating the bal-
ance heat transfer in a scene with several objects, one
has to model the heat radiation of each object and tak-
ing into account the mutual visibility. This is where
the 3D geometry of the scene becomes indispensable.
With sun and sky as main participants, the challenge
is to efficiently perform shadow analysis.
Figure 2 shows an overview of the types of the
modeled thermal phenomena.
Figure 2: Overview of the considered physical phenomena
in the thermal simulation.
2.2 From Sensor Data to Semantic
Surface Representation
The semantic reconstruction and material classifica-
tion are important preprocessing steps, since the heat
simulation depends strongly on the material proper-
ties and geometry, as mentioned above.
We assume the availability of the elevation data,
sampled into DSM (Digital Surface Model). Com-
bining image and elevation data, land-cover classes
are obtained. Hereby, the building class is particu-
larly important for the subsequent 3D modeling step,
since buildings as man-made objects are heated or
cooled from the inside, or roof materials are gener-
ally different. Other important classes are: bare soil,
grass, tree, water and road. Various approaches ex-
ist for land-cover classification. We are interested
in ones which need only a few training patches and
features. Therefore, we opted for a conventional ap-
proach based on Random Forests classifier (Breiman,
2001). As image-based features, we took the chan-
nels of the multispectral image, vegetation and water
indices. As elevation-based features, we considered
relative elevation, whereby a standard interpolation
procedure was chosen to reconstruct the ground, as
well as the planarity measure (Gross and Th
¨
onnessen,
2006). Training patches were sampled interactively.
After building detection, (Bulatov et al., 2014) sug-
gest performing their delineation (for simplification
of shapes), outlining and roof detail reconstruction.
However, building models resulting from such a data-
driven approach are not water-tight, causing problems
for the simulations. Therefore and because in our
data set, the buildings are not too high, for this work,
we decided to use the freely available shapefile with
building outlines and to model every building as a
prismatic structure with elevation retrieved from sen-
sor data. Building walls are modeled as vertical trape-
zoids by projecting the endpoints of border- or step-
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
56
edges of the roof to the ground. For the tree regions,
we will concentrate on large forest regions. They are
represented as forest boxes and allow to model huge
forest areas by at most several dozens of polygons
(Decaudin and Neyret, 2004; H
¨
aufel et al., 2017). The
last data preparation step concerns meshing of the ter-
rain. Starting at the classification result, we wish to
assign a class to every triangle. Therefore, after sev-
eral morphological operations allowing to suppress
too small regions, we consider a canonical rectangu-
lar grid along the axes x and y. Tracing one diagonal
of each rectangle in the grid as well as assigning the
ground values of vertices as z coordinates results in a
coarse triangle mesh. In the initial mesh, those trian-
gle with either elevation or class discontinuities can
be subdivided along their symmetry axis into a pair of
smaller triangles. In order to avoid cracks in the fi-
nal surface (that result if a 2D mesh vertex is an inner
point of an edge, because the corresponding 3D point
is not necessarily incident with the an edge connect-
ing the 3D endpoints of this edge), adjacent triangles
must be subdivided as well and, sometimes, new ver-
tices must be inserted. This approach was referred in
(Pajarola, 2002) as restricted (top-down) quadtree tri-
angulation (RQT or RTDQT) and was implemented
in this work.
3 MODELING THERMAL
TRANSFER
In this section, we present our architecture for sim-
ulating thermal transfers for large sceneries, whose
geometry is determined by a surface model. First,
the data representation and our simulation basis re-
ferred to as surface volume are introduced. Further-
more, we give an overview of the considered physical
parameters of one surface volume element and the en-
vironmental model as well as the core equation for the
implementation. Finally, a mathematical description
of the considered physical modes of heat transfer is
given.
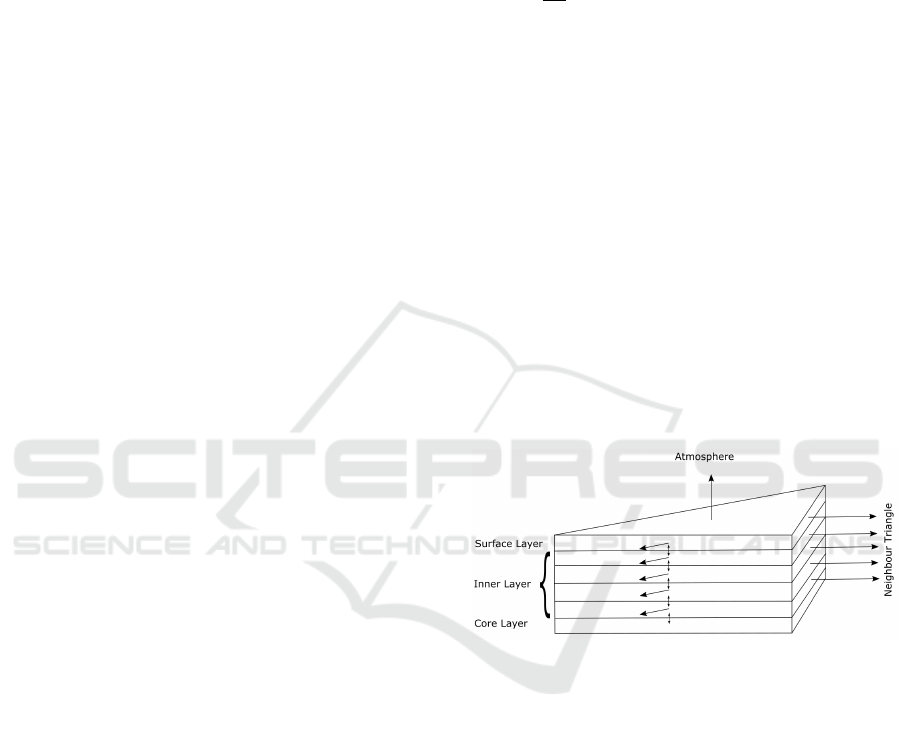
3.1 Data Representation and Model
Principle
Surface Volume Model: The basis of the simula-
tion is the heat equation, which describes the distri-
bution of heat in a given volume over time. For this,
we extend the surface model of the scene to a surface
volume by giving the surface a thickness.
There are three types of heat propagation in this
volume: the heat can be propagated by conduction
within the volume, there is a heat exchange with the
outside world and heat exchange with the inside of the
body. Mathematically, the thermal conduction in the
surface volume can be described with the heat equa-
tion and suitable boundary conditions:
C
v
ρ
∂T
∂t
= K∆T in the interior, (6)
T = T
Core
on the inner surface, (7)
∇T · n = Q on the outer surface, (8)
where n is the outer normal of the wall surface and
the thermal conductivity K of the material. In this
model, the inner side of the surface volume interacts
only with the inner body, which has an internal tem-
perature T
Core
assumed to be constant. The core tem-
perature can be used to model socio-economic condi-
tions, such as heated buildings. The outer side inter-
acts with the outer world, where the total heat flow is
denoted with Q.
For solving this partial differential equation a fi-
nite volume method in 3D is implemented. For this
purpose, the surface is discretized with a coarse trian-
gular mesh, which was given a thickness. The finite
volume method is based on balancing the thermal en-
ergy flux of the triangular prisms.
Figure 3: Principle of surface volume discretization.
Model of Geometry and Materials: The basis of
the simulation is a triangulated surface mesh repre-
senting the geometry of the scene in which the third
dimension is implicitly treated. The surface volume
model consists of N layers, that means for each trian-
gle overall 2+N temperature values have to be stored:
the surface temperature, N temperature values for ev-
ery layer, and the core temperature (see Figure 3).
Furthermore, every triangle is assumed to consist
of one specific material class, which implies a set of
parameters representing the physical properties ac-
cording to Table 1. The parameters can be divided
into material properties and environmental properties,
the latter ones depend not only on the material but on
environmental model and correspond not necessarily
to a physical equivalent.
Physically-based Thermal Simulation of Large Scenes for Infrared Imaging
57

Table 1: Overview of Parameters.
Material Properties Symbol
Albedo α
Emissivity ε
Density ρ
Specific heat C
v
Thermal conductivity K
Thickness of the layers d
s
,d
1
,...d
N
Environmental Properties
Core temperature T
Core
Free convection h
1
Forced convection h
2
Wind velocity v
wind
Air temperature T
air
Relative humidity r
h
Discretization of the Inner Model: The discretiza-
tion of the model is similar to (Bartos and Stein, 2015)
with the difference that we set the parameters using a
database and do not need to be fitted. The model of
the inner temperature for N layers leads to a system
of N +1 coupled differential equations, describing the
temperature along the profile of the surface volume.
For the first inner layer we have the equation
C
v
ρ
∂T
1
∂t
=
K
d
1
(T
s
− 2T
1
+ T
2
) + K∆T
1
, (9)
for layers with the index i = 1,...,N −1, we have
C
v
ρ
∂T
i
∂t
=
K
d
i
(T
i−1
− 2T
1
+ T
i+1
) + K∆T
i
, (10)
and for the last inner layer we have
C
v
ρ
∂T
N
∂t
=
K
d
N
(T
N−1
− 2T
N
+ T
Core
) + K∆T
N
. (11)
Model of the Environment: The model for the en-
vironment consists of a small set of functions de-
scribing the time course of the weather. The weather
parameters taken into account are the air tempera-
ture T
Air
(t) ∈ R and relative humidity r(t) ∈ [0, 100],
which can be varied between triangles. Furthermore,
the cloud cover is described by C(t) ∈ [0,1], where
0 stands for cloud-free sky and 1 for a dense cloud
cover. The atmospheric damping is summarized by
the factor I
c
(t) ∈ [0.3,0.8], which is called clearness
index. It is defined by I
c
(t) = 0.8 − 0.5C(t), cf.
(Mar
´
echal et al., 2010). The environmental param-
eters have to be precalculated from weather data or
specified by the user.
Temporal Discretization: For every triangle of the
scene the current temperature, material parameters are
stored. The time discretization is performed using a
forward Euler integration scheme. Let ∆t denote the
time step for integration of triangle i. At every time-
step n, the total flux Q
i
is computed as the sum of all
heat fluxes, hence the new temperature is computed
as
T
n+1
i
= T
n
i
+
Q
i
ρ
i
C
p
i
A
i
d
i
∆t, (12)
where d
i
denotes the thickness of the layer corre-
sponding to the triangle i. The parameter ∆t is cho-
sen after a stiffness analysis of the linear system. Nu-
merical experiments have shown that a time step of
∆t = 30s leads to stable results and records the time-
dependent weather phenomena with a good accuracy.
3.2 Physical Modeling of Thermal
Flows
In the following, we present the modeling of thermal
fluxes, describing the physical phenomena mentioned
in Section 2.1 and some details of the numerical im-
plementation.
The thermal change of a surface volume is calcu-
lated using the heat equation
C
v
ρd
s
∂T
s
∂t
= A + I +D + R + S = Q, (13)
where A describes the convective thermal exchange
with the surrounding air, I describes the inner model
of the surface, D describes the conductive thermal ex-
change with neighboring triangles, R describes the ra-
diative thermal exchange with the sky, and S describes
the thermal flow through direct sunlight. The total
flux is denoted with Q. The following deals with the
modeling of these fluxes.
3.2.1 Convective Thermal Exchange
The thermal exchange between the surface and the
surrounding air is divided into free convection and
forced convection whereas we choose a linear model.
Let h
1
denote the coefficient for free convection and
h
2
the coefficient for forced convection, v
wind
the
wind speed, and T
Air
the temperature of the air. Then
the heat flux between a surface triangle and the air
can be described by Newton’s law of cooling for free
convection and a linear model for forced convection
A = (h
1
+ h
2
· v
wind
)(T
Air
− T
s
). (14)
3.2.2 Conductive Thermal Exchange with the
Inner Model
Heat conduction dominantly depends on the materials
thermal conductivity. Assuming only homogeneous
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
58

media and considering only temperature ranges typi-
cal for urban sceneries, the thermal conductivity can
be assumed constant (Lienhard IV and Lienhard V,
2011). Regarding one-dimensional flow, the surface
temperature is coupled to the inner model with the
connection
I =
K
d
1
(T
1
− T
s
), (15)
where d
1
is the discretization parameter defining the
surface layers’ thickness.
3.2.3 Conductive Thermal Exchange Along the
Surface
In addition to conduction into the interior of the body,
there is also conduction along the surface. It is calcu-
lated with a discretization of the Laplace operator in
2D
D = K∆T
s
. (16)
The discretization of the gradient along the surface is
done with a finite volume method, where for every
face of the triangle the heat flux of the neighboring
triangle is calculated. The total flux for a triangle i
with the area A
i
is then given by
(∆T )
i
≈
1
A
i
∑
j∈N
i
L
i j
(∇T )
i j
· n
i j
. (17)
where N denotes the set of neighboring triangles of
triangle i, (∇T )
i j
the flux, n
i j
the outer normal of the
edge between triangle i and triangle j, and L
i j
the
length of that edge.
3.2.4 Radiative Thermal Exchange with the Sky
In our model, we assume that a surface triangle can be
either oriented to the sky and exchange thermal radia-
tion, or oriented to another surface triangle, which has
a similar temperature, so the thermal radiation can be
neglected.
In a preprocessing step using OpenGL renderings
of the scene with different angles, the visibility of the
surface is determined. A rendering is done in two
steps. First, the scene is rendered from the perspective
of sky and the depth information is stored for each vis-
ible object. Then the scene is rendered again, where
for each pixel the depth information is used to deter-
mine whether it is visible to the sky. If this is the case,
the pixel store the index of the corresponding triangle.
After a histogram analysis, the portion of the surface
of each triangle that is not occluded by other triangles
is determined. The visibility of the surface from the
viewpoint of the sky is then defined as the mean of all
angles and denoted by the parameter γ
Sky
∈ [0,1].
The temperature of the sky depends on the temper-
ature of the air, the dew point temperature for a cloud-
less sky and the time of day denoted by h(t) ∈ [0, 24].
The dew point temperature T
dp
is approximated by
the Magnus approximation with the air temperature
T
Air
and relative humidity r through saturation vapour
pressure (SVP) and vapour pressure (VP), c.f (Son-
ntag, 1990)
SVP(t) = 6.1078 · 10
a·T
Air
(b+T
Air
)
, (18)
VP(t) =
r
100
· SVP, (19)
T
dp
(t) = b ·
v(t)
a − v(t)
, (20)
where v(t) = log
10
V P(t)
6.1078
and
a = 7.5, b = 237.3 for T
Air
≥ 0,
a = 7.6, b = 240.7 for T
Air
< 0.
(21)
As in (Mar
´
echal et al., 2010), the temperature of the
clear sky is approximated by
T
Sky
= T
Air
(t)
0.711 + 0.0056 T
dp
(t)
+7.3 · 10
−5
T
dp
(t)
2
+ 0.013cos
2πh(t)
24
1
4
(22)
The temperature of the clouds is calculated based on
the assumption that the air temperature drops 9.84
◦
C
and dew point temperature drops 1.82
◦
C per 1000 m
of altitude. Then, the height of the clouds can be esti-
mated by
H
cloud
= (T
Air
− T
dp
)/(9.84 −1.82) · 1000. (23)
The following equation is used to estimate the clouds’
temperature:
T
cloud
= −0.00182 · H
cloud
+ T
dp
. (24)
The total temperature of the cloudy sky is approxi-
mated with the weighted mean of the cloud tempera-
ture and clear sky temperature, thus
T
total
= C · T
cloud
+ (1 −C)T
sky
, (25)
where C denotes the cloud cover index.
The total thermal flux between a given trian-
gle and the cloudy sky is calculated by the Stefan-
Boltzmann law
R = εσγ
Sky
(T
4
total
− T
4
s
), (26)
where ε denotes the emissivity of the material of the
triangle.
Physically-based Thermal Simulation of Large Scenes for Infrared Imaging
59

3.2.5 Thermal Heating by Direct Sunlight
The contribution of direct sunlight is the main source
of heat energy and therefore a critical part of the sim-
ulation.
The total amount of solar heat energy received by
a triangle depends on the total solar irradiation, which
varies during the year because of the eccentricity of
earth’s orbit, the orientation of the triangle to the sun,
atmospheric influences, and whether the triangle is
actually irradiated by the sun or shaded.
The solar irradiation outside of the atmosphere for
a surface directly faced to the sun can be approxi-
mated by
E
total
= 1367(1 + 0.033 cos(2πn/365)),
where n denotes the day of year, cf. (Mar
´
echal et al.,
2010). The fraction of the area facing the sun is cal-
culated from the sun direction s and the normal of the
surface n
s
by cos(ϕ) = s · n
s
, where ϕ denotes the an-
gle between the sun ray and surface normal. The solar
irradiance before atmospheric filtering is given by
E
Sun
= E
total
· cos(ϕ).
The atmosphere absorbs solar radiation, which is
modeled by weighting the sun irradiance with the
clearness factor I
c
. Furthermore, a fraction of the ir-
radiance is not absorbed by the surface, but reflected
back. This effect is represented by the albedo of the
surface which depends on the color and material prop-
erty of the triangle, yielding to the solar irradiance
˜
S = (1 − α)I
c
E
Sun
cos(θ), (27)
where θ is the sun’s elevation angle. If the triangle is
actually illuminated by the sun or occluded by other
triangles is stated by a factor γ
Sun
∈ {0, 1} which is
determined using an OpenGL rendering of the scene
analogous to 3.2.4. More precisely, an index image of
the scene from the viewpoint of the sun is rendered,
then γ
Sun
is set to 1 if the triangle is visible on the
rendered picture or 0 otherwise. This allows to deal
with thermal shadows in the simulation. In summary,
the solar irradiation on the surface is given by
S = (1 − α)I
c
E
Sun
cos(θ)γ
Sun
. (28)
4 RESULTS
In this section, the results for two data sets are pre-
sented. The method was implemented in MATLAB
with the parallel processing toolbox on an Intel(R) I7-
8700 3.19GHz CPU with 32GB RAM and NVIDIA
GeForce GTX 1080 GPU. The first data set represents
Figure 4: CUBI in Ettlingen with five thermistors (south,
north, east, top, west).
Figure 5: Watertight CUBI and Ground mesh with 2816
triangles.
a simple scene with known ground truth; hence it can
be used for validation. The second data set consists of
various sensor data of an urban area, so we used the
proposed four-step pipeline and compared the result
of the thermal simulation with a thermal image.
4.1 CUBI – Thermal Model Validation
CUBI is a simple geometrical object used in outdoor
experiments to collect data for testing and validation
of thermal models and infrared imaging. It has the
shape of a stair, like three compound cubes with an
edge length of 0.5m. For the validation of our ther-
mal model, we use the data of (Malaplate et al., 2007)
that include time series of different surface tempera-
ture acquired by thermistors in Ettlingen, Germany, in
May 2006. In Figure 4, the CUBI test object with the
positions of thermistors is shown.
Representing the geometry of CUBI and the
ground, a mesh with 2816 triangles was created, as
shown in Figure 5.
As material parameters for the CUBI as well as for
the ground, we use those for metal, retrieved from the
material database. For the inner model, 10 layers are
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
60
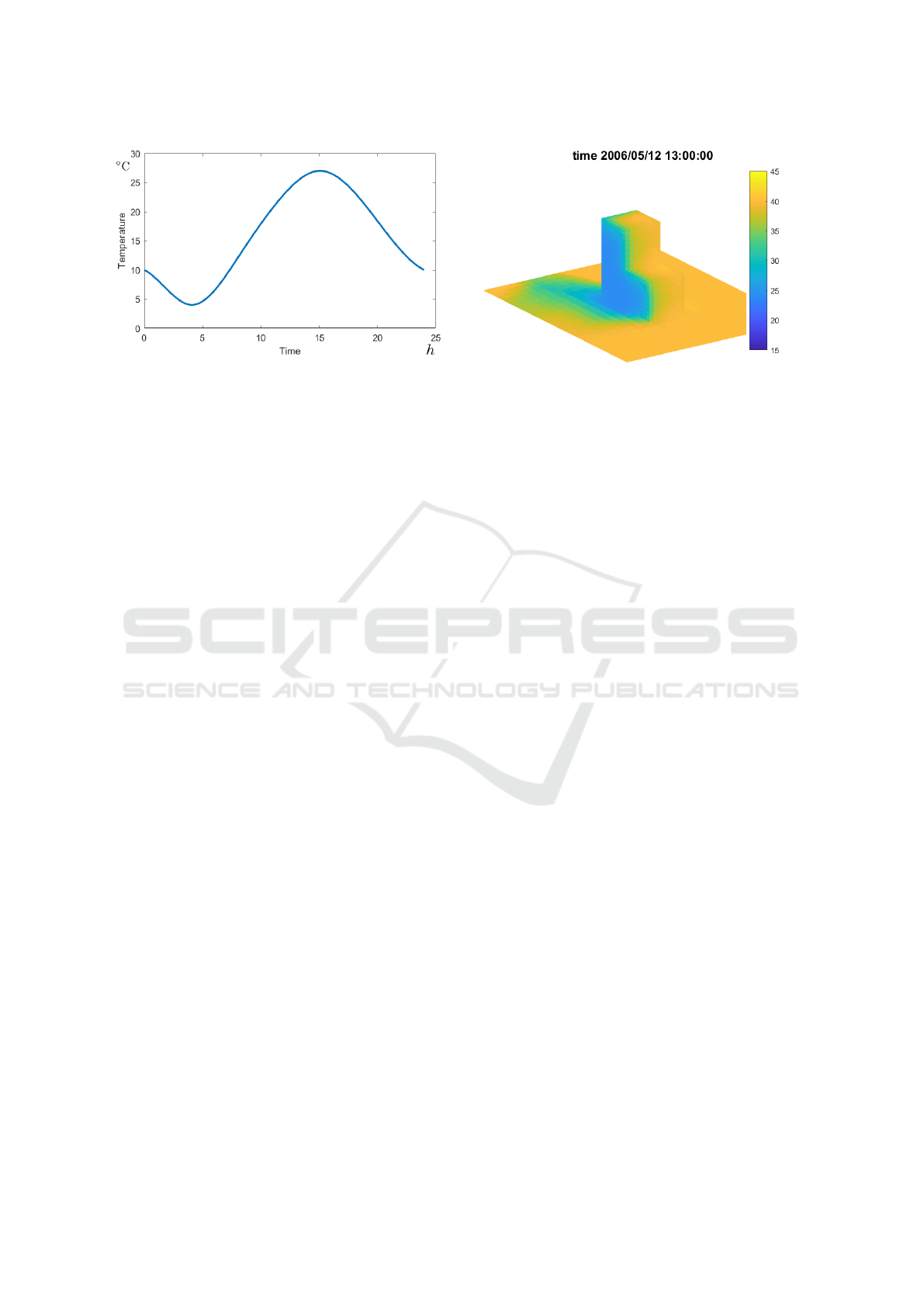
Figure 6: Simplified air temperature curve used for simula-
tion.
used with a thickness of 0.1m.
We simulate a two-days cycle from 2006-05-11 to
2006-05-12 for the location of Ettlingen 48;56; 48 N
8;24;38E with a simplified air temperature curve
shown in Figure 6. We use the same air temperature
curve for both days with a minimum temperature of
4
◦
C at 4:00 am and a maximum temperature of 27
◦
C
at 3:00 pm.
Figure 7 shows the temperature distribution of the
CUBI at 1:00 pm. The thermal shadow of the CUBI
is recognizable by the blue color on the ground on the
right part of the picture. The heat conduction is also
clearly visible as color gradient at the shadow and at
the edges of surfaces, for those one surface is in the
shade and the other is illuminated by the sun.
In Figure 8 the collected and simulated data of the
thermistors is shown. Both curves show a good qual-
itative agreement: The order of the peaks is identical.
As expected, the eastern thermistor (brown/yellow)
reaches its maximum at about 10 o’clock and then
cools down in a similar way until evening, i.e. both
curves show a small hump. Also the maximum tem-
perature is about the same at 40
◦
C. The upper and
southern termistors (red and black) reach their max-
imum at about 12 o’clock, which corresponds to the
measured data, the temperature is only slightly over-
estimated in the simulation. Finally, the western ther-
mistor reaches its maximum in the evening, which
is slightly underestimated compared to the measured
data. The northern thermistor (blue) is also underesti-
mated in the simulation. One reason for this could be
inaccuracies in the inner model. Since the CUBI is a
relatively small object, the assumption that the inter-
nal temperature is constant may be inaccurate.
In conclusion, the thermal model provides good
results for simple geometries.
Figure 7: Simulated temperature distribution of CUBI on
2006-05-12 at 1pm in Ettlingen in
◦
C.
4.2 Melville – Thermal Simulation for
Large Sceneries
Our second data set is provided by the City of
Melville, a local council located in Perth, Australia.
This council aims at sustainable and energy-efficient
urban development, for which, among others, stud-
ies investigating the influence of land usage on heat
islands are being carried out, see (Council of City
of Meville, 2017). For this purpose, heterogeneous
airborne sensor data, such as multispectral imagery,
a thermal infrared image and a LiDAR point cloud
as well as seven-years-old shapefile containing build-
ing outlines were available from the eponymous town.
We selected a residential area measuring 1 km × 2 km
and containing some 1500 buildings and many trees.
After all data was registered into the same coordinate
system, the steps mentioned in Section 2.2 were ap-
plied. Note that we used the sensor data for clas-
sification while we generated LoD0 building objects
from the building footprints contained in the shape-
files (Biljecki et al., 2016). We have not considered it
as a severe drawback that the shapefile was outdated
in some areas, since our main task here is to prove the
capability of the approach to simulate large scenes.
Moreover, those larger parts of the terrain that were
classified as buildings but not listed in the shapefile
were modeled as brick.
Considering the material classes needed for the
thermal simulation, we restrict ourselves to the ones
given in Table 2 where ground cover classes are re-
lated to the ground mesh only. Each semantic class
has been assigned: material parameters as listed in
Table 1, a specific core temperature, and a free con-
vection coefficient dependent on the environment (i.e.
the convective medium) and the material. Concerning
3D objects, we consider buildings and forest boxes.
In Figure 9, a detail of the city of Melville is
shown together with our classification and triangula-
Physically-based Thermal Simulation of Large Scenes for Infrared Imaging
61
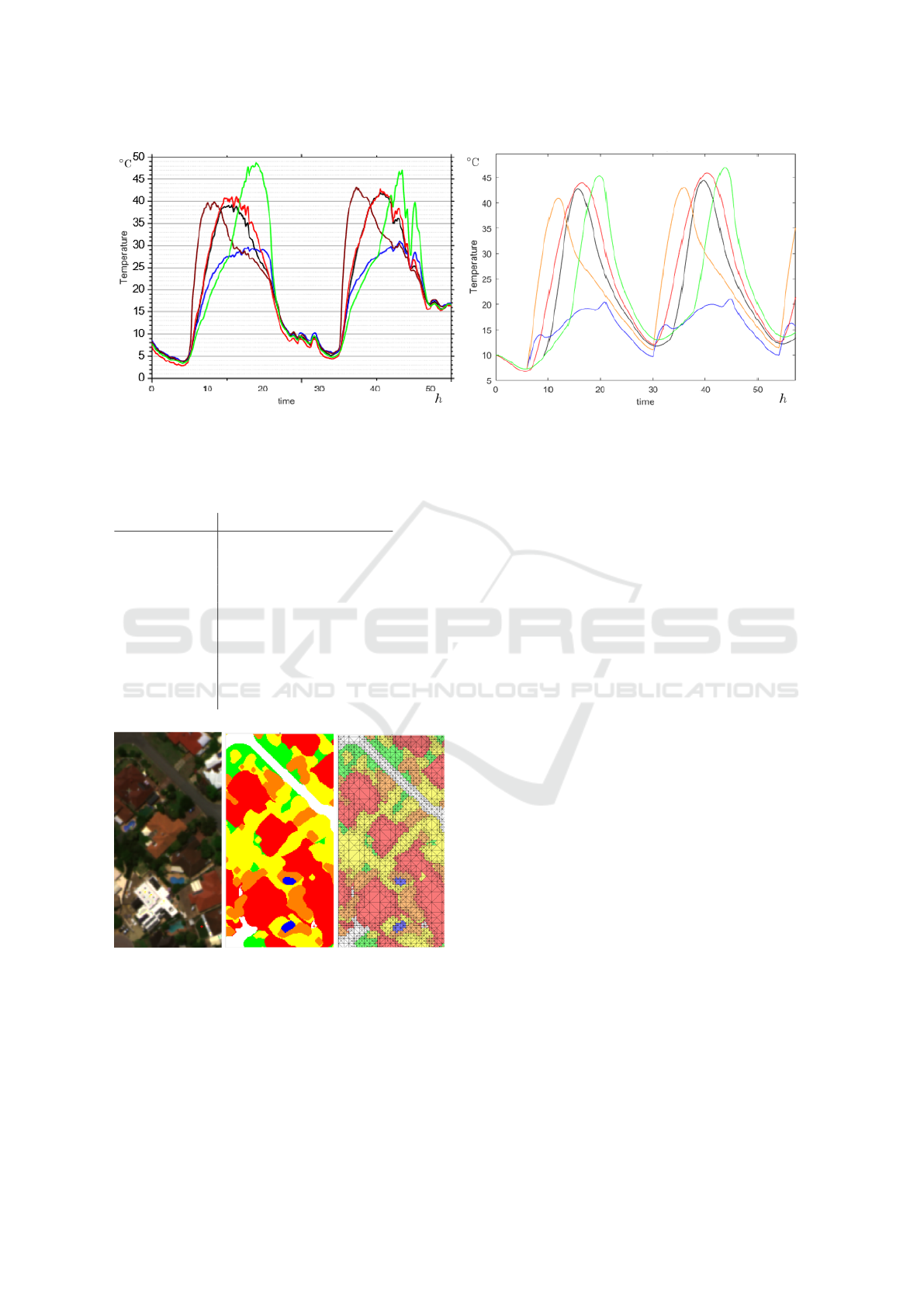
(a) Measured data (b) Simulated data
Figure 8: Measured and simulated temperatures for May 11 and 12, 2006, for thermistors 1 (black), 2 (blue), 3 (yellow), 4
(red) and 5 (green).
Table 2: Material classes of Melville data set.
Semantic Class color
Ground cover Street white
Soil orange
Grass green
Brick red
Tree yellow
Water blue
3D Object Building wall
Roof
Forest box wall
Forest box roof
(a) RGB-Image (b) Classification
(see Table 2)
(c) RTDQT
Figure 9: Generation of terrain mesh.
tion result of the ground.
In the simulation presented in the following, we
have chosen the forced convection to be neglected
by setting the wind velocity to zero, i.e. regard-
ing a windless scene. As further weather condi-
tions, we used the same as for the CUBI scenario.
The whole scene consists of 1313410 triangles, and
706405 points and 10 sets of material parameters. The
simulation terminated in 252 sec. for five day-night
cycles.
Figure 10 (a) shows our simulation result, i.e. the
resulting surface temperatures of the city of Melville
at the time 7h00 on a day in September. The struc-
ture of the city is clearly visible and the different ther-
mal behaviour of the materials appears realistic: the
streets are visible as warm areas and the areas with
vegetation are cooler. Figure 11 shows the surface
temperatures of the scene at noon in a slanted view,
so that the 3D structure becomes visible. Here, the
effect of thermal shadows is demonstrated. They are
visible on surfaces which are not illuminated by the
sun and therefore are exposed to less heating, i.e. the
surface temperature is cooler.
The thermal image of the city of Melville results
from several measurements during night time and al-
lows a first comparison between our simulation result
and actual sensor data. Figures 10(b) shows a smaller
region of our simulation result at nighttime and Fig-
ure 10(c) the corresponding thermal image. In direct
comparison, our heat simulation shows good agree-
ment with the thermal image. We have successfully
reproduced the strong signature of the streets during
night and the cooling effect by trees on the streets,
which can punctually be seen along the long road on
the left side of both images. Merging several trees
and modeling them as forest boxes proves to be con-
venient, e.g. the surrounding tree areas around the
large grass field return a reasonable surface temper-
ature. Differences between simulation and the ther-
mal image appear considering effects by shadow cast.
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
62

(a) Simulation result (topview) for
the city of Melville at 7h00
(b) Simulated Surface Temperatures (c) Thermal Infrared Image
Figure 10: Comparison between simulated temperatures and thermal infrared image.
Figure 11: Slanting view on the simulation results for the
city of Melville at noon. Areas not directly exposed to sun-
light heat up less and generate thermal shadows (circle).
Within the simulation, shadow casts lead to strong
cooling which is not present in the thermal sensor im-
age. Furthermore, building roofs show a considerably
lower temperature then in the simulation. We suspect
that this is due to the material properties, in particular
a low emissivity, which makes objects appear cooler
on thermal images than they actually are. Field mea-
surements might give more information about the ac-
tual roofing temperatures to enable an evaluation of
these differences.
5 CONCLUSIONS
In this paper, we have presented a thermal simula-
tion approach for large scenes in the framework of
a pipeline leading from raw sensor data to 3D en-
vironments rendered in the infrared spectrum. The
preceding work of the thermal simulation consists of
the material classification and mesh generation from
the sensor data. Given the triangulation, we define a
surface volume as simulation element for discretiza-
tion of the heat transfer equation. Our model results
in qualitatively good agreement between simulation
and ground truth data for small geometries such as
the CUBI object. Applied to a large data set using
the entire pipeline up to thermal simulation, we have
shown that our method efficiently leads to similar sur-
face temperatures as compared to a thermal image.
Outstanding signatures in the thermal image are rec-
ognizable in the simulation at a comparable point in
time. Furthermore, the simulation with time displays
the dependency of the solar irradiation and the result-
ing thermal shadows as we expected. Completing the
pipeline towards infrared rendering, where the heat
radiance is modeled, will lead to an optimized start-
ing point for comparison between thermal imaging
and simulation. Also, modeling the heat radiation in
future work will be a promising tool for urban heat
island consideration and other applications.
Physically-based Thermal Simulation of Large Scenes for Infrared Imaging
63

ACKNOWLEDGEMENTS
We express our deep gratitude to the City of Melville
and Dr. Petra Helmholz from Curtin University, Aus-
tralia, for the acquisition of the Melville data set as
well as Rebecca Ilehag from Karlsruhe Institute of
Technology, Germany, for data preparation. We thank
our colleagues Jonas Mispelhorn for providing the
OpenGL renderer and Dr. Jochen Meidow for read-
ing parts of the manuscript.
REFERENCES
Bartos, B. and Stein, K. (2015). FTOM-2D: a two-
dimensional approach to model the detailed thermal
behavior of nonplanar surfaces. In Target and Back-
ground Signatures, volume 9653, page 96530G. Inter-
national Society for Optics and Photonics.
Biljecki, F., Ledoux, H., and Stoter, J. (2016). An improved
LoD specification for 3D building models. Comput-
ers, Environment and Urban Systems, 59:25–37.
Breiman, L. (2001). Random forests. Machine learning,
45(1):5–32.
Bulatov, D., H
¨
aufel, G., Meidow, J., Pohl, M., Solbrig, P.,
and Wernerus, P. (2014). Context-based automatic
reconstruction and texturing of 3D urban terrain for
quick-response tasks. ISPRS Journal of Photogram-
metry and Remote Sensing, 93:157–170.
Council of City of Meville (2017). Urban forest strategic
plan 2017-2036: Plan a: City-controlled plan. Tech-
nical report, City of Melville, Perth, Australia.
Decaudin, P. and Neyret, F. (2004). Rendering forest scenes
in real-time. In EGSR04: 15th Eurographics Sympo-
sium on Rendering, pages 93–102. Eurographics As-
sociation.
Dewan, A. M. and Corner, R. J. (2014). Impact of land use
and land cover changes on urban land surface temper-
ature. In Dhaka Megacity, pages 219–238. Springer.
Feng, X. and Myint, S. W. (2016). Exploring the effect of
neighboring land cover pattern on land surface tem-
perature of central building objects. Building and En-
vironment, 95:346–354.
Gross, H. and Th
¨
onnessen, U. (2006). Extraction of lines
from laser point clouds. International Archives of
Photogrammetry, Remote Sensing and Spatial Infor-
mation Sciences, 36 (Part 3/W49):86–91.
H
¨
aufel, G., Bulatov, D., and Solbrig, P. (2017). Sensor data
fusion for textured reconstruction and virtual repre-
sentation of alpine scenes. In Earth Resources and
Environmental Remote Sensing/GIS Applications VIII,
volume 10428, page 1042805. International Society
for Optics and Photonics.
Ilehag, R., Bulatov, D., Helmholz, P., and Belton, D. (2018).
Classification and representation of commonly used
roofing material using multisensorial aerial data. In-
ternational Archives of the Photogrammetry, Remote
Sensing & Spatial Information Sciences, 42(1).
Johnson, K., Curran, A., Less, D., Levanen, D., Marttila,
E., Gonda, T., and Jones, J. (1998). MuSES: A new
heat and signature management design tool for virtual
prototyping. In Proc. of the 9th Annual Ground Target
Modelling and Validation Conference.
Kajiya, J. T. (1986). The Rendering Equation. In Proc.
of the 13th Annual Conference on Computer Graphics
and Interactive Techniques, SIGGRAPH ’86.
Lagouarde, J.-P., H
´
enon, A., Kurz, B., Moreau, P., Irvine,
M., Voogt, J., and Mestayer, P. (2010). Modelling
daytime thermal infrared directional anisotropy over
toulouse city centre. Remote Sensing of Environment,
114(1):87–105.
Lienhard IV, J. H. and Lienhard V, J. H. (2011). A heat
transfer textbook. Dover Publ., Mineola, NY, 4. ed.,
corr., rev. and updated edition.
Malaplate, A., Grossmann, P., and Schwenger, F. (2007).
Cubi: a test body for thermal object model validation.
In Infrared Imaging Systems: Design, Analysis, Mod-
eling, and Testing XVIII, volume 6543, page 654305.
International Society for Optics and Photonics.
Mar
´
echal, N., Gu
´
erin, E., Galin, E., M
´
erillou, S., and
M
´
erillou, N. (2010). Heat transfer simulation for mod-
eling realistic winter sceneries. In Computer Graphics
Forum, volume 29, pages 449–458. Wiley Online Li-
brary.
Pajarola, R. (2002). Overview of quadtree-based terrain tri-
angulation and visualization. Technical report, De-
partment of Information & Computer Science, Uni-
versity of California, Irvine.
Poglio, T., Savaria, E., and Wald, L. (2002). Outdoor scene
synthesis in the infrared range for remote sensing ap-
plications. In CISST’02: International Conference on
Imaging Science, Systems, and Technology. CSREA
Press, Athens, Ga, USA.
Siegel, R. and Howell, J. R. (1992). Thermal radiation heat
transfer. Francis & Taylor, Washington, DC, 3. ed.
edition.
Sonntag, D. (1990). Import new values of the physical con-
stants of 1986, vapour pressure formulations based on
the ITS-90, and psychrometer formulae. Z. Meterol,
70:340.
Xiong, B., Elberink, S. O., and Vosselman, G. (2014).
Building modeling from noisy photogrammetric point
clouds. ISPRS Annals of the Photogrammetry, Remote
Sensing and Spatial Information Sciences, 2(3):197–
204.
Xiong, X., Zhou, F., Bai, X., Xue, B., and Sun, C. (2016).
Semi-automated infrared simulation on real urban
scenes based on multi-view images. Optics Express,
24(11):11345–11375.
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
64
