Incorporating Plane-Sweep in Convolutional Neural Network Stereo

Imaging for Road Surface Reconstruction

Hauke Brunken and Clemens G

uhmann

Chair of Electronic Measurement and Diagnostic Technology, Technical University of Berlin,

Einsteinufer 17, 10587 Berlin, Germany

Keywords:

Stereo Vision, Neural Network, Plane Sweep, Pavement Distress.

Abstract:

Convolutional neural networks, which estimate depth from stereo pictures in a single step, have become state

of the art recently. The search space for matching pixels is hard coded in these networks and in literature is

chosen to be the disparity space, corresponding to a search in the cameras viewing direction. In the proposed

method, the search space is altered by a plane sweep approach, reducing necessary search steps for depth map

estimation of ﬂat surfaces. The described method is shown to provide high quality depth maps of road surfaces

in the targeted application of pavement distress detection, where the stereo cameras are mounted behind the

windshield of a moving vehicle. It provides a cheap replacement for laser scanning for this purpose.

1 INTRODUCTION

Knowledge about the road surface is useful in several

cases, such as road maintenance, driving assistance

systems and active suspension systems.

At present for the purpose of road maintenance,

specially equipped measuring vehicles are utilized,

which use laser scanners to generate a road proﬁle

(Eisenbach et al., 2017). Alternatively people are

send to observe and measure roads by hand. This is

costly and time consuming. As the road surface can

change quickly, for example when a pothole develops,

the gathered information becomes outdated.

Another subject are driving assistance or autono-

mous driving systems, where potholes should be ci-

rcumvented or the driving speed should be reduced

due to bad road conditions. Active suspension sys-

tems can utilize depth information to provide the best

driving comfort.

This work aims at solving the problem of recon-

structing the road surface ahead of a moving vehicle

by stereo vision. This is a difﬁcult task, as roads have

a low texture surface and surface defects produce little

change in elevation. The developed system could be

mounted on public vehicles, such as public transpor-

tation or garbage trucks in order to provide current

data for many roads with little effort. Changes in road

conditions can be detected early, which can lead to sa-

vings in repair costs. While laser scanners capture the

world serially, cameras can capture the entire image in

parallel. This is advantageous at high driving speeds,

as is the case with driver assistance or autonomous

driving systems.

The proposed method is an extension of neural

networks for disparity estimation by implementing

plane sweep stereo into the network. It is trained end-

to-end on data, which was created by a more traditi-

onal plane sweep approach. The ﬁnal network learns

from the training data and even outperforms the met-

hod it learned from in some cases.

Results are shown for the targeted application and

are compared to a laser scan.

2 RELATED WORK

Depth estimation from stereo images is a well-known

problem (Hartley and Zisserman, 2003), (Szeliski,

2011), (Ikeuchi, 2014). It can be broken down to ma-

tching pixels in left and right camera images. The

location of a point in 3D space can then be found by

triangulation. The corresponding pixel of a pixel in

one image lies on the epipolar line in the other image.

If the cameras are aligned horizontally, the epipolar

line is located in the same row in the second image as

the pixel in question in the ﬁrst image. Traditionally

this pixel matching procedure is divided into several

stages:

1. If the cameras are not (perfectly) aligned horizon-

784

Brunken, H. and Gühmann, C.

Incorporating Plane-Sweep in Convolutional Neural Network Stereo Imaging for Road Surface Reconstruction.

DOI: 10.5220/0007352107840791

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 784-791

ISBN: 978-989-758-354-4

tally, the pictures are rectiﬁed.

2. A similarity measure between each pixel in one

image and each pixel on the same horizontal line

in the other image is calculated.

3. The similarity measure is used to match pixels of

both images. Due to ambiguities, wrong matches

can easily occur if only the similarity measure is

taken into account. This makes an additional cost

function and complex optimization necessary.

Different similarity measures have been utilized. A

very efﬁcient one is a convolutional neural network,

which outperforms traditional methods like sum of

absolute differences, census transform and norma-

lized cross-correlation (Zbontar and LeCun, 2016).

This gave rise to the idea of integrating the second

and third steps into a single neural network. Diffe-

rent architectures thereof exist. In (Dosovitskiy et al.,

2015) a network for estimating optical ﬂow is propo-

sed. That means, a ﬁeld around a pixel in consecu-

tive frames of a video sequence needs to be searched.

If left and right pictures of a stereo camera are used

as input, the ﬂow corresponds to disparity. The idea

thus was modiﬁed for stereo images in (Mayer et al.,

2016), where a correlation layer is used to account

for the epipolar geometry. In (Kendall et al., 2017)

the idea of a cost volume is introduced. First, fea-

ture maps for left and right images are calculated in

the network. Then feature maps of different disparity

levels of one image are stacked on top of the feature

maps of the other image. This approach embeds the

epipolar geometry. In (Smolyanskiy et al., 2018) a

similar network with a semi-supervised training pro-

cedure is implemented, which can run near real-time.

Besides Flownet (Dosovitskiy et al., 2015), all

these methods search through disparity space, which

corresponds to a search in the cameras viewing di-

rection. This creates two problems in the targeted ap-

plication:

1. Since the cameras are mounted behind the winds-

hield, the angle between the viewing direction of

the cameras and the road is sharp. For the task of

depth estimation of the surface, many small steps

through disparity space are necessary to get a high

depth resolution of the surface.

2. The other problem is the rectiﬁcation of images.

To produce a high depth resolution, the baseline

between cameras has to be large. This in turn re-

quires the cameras to be tilted in, in order to get

an overlap of the images in the region of interest.

In this case, rectiﬁcation can result in a reduction

of quality, due to the required stretching and inter-

polation.

Both problems are solved by the plane sweep appro-

ach, which was ﬁrst introduced in (Collins, 1996):

A virtual plane is placed at arbitrary positions in 3D

space. Features of both images are projected onto the

plane and match if the plane’s position is correct. In

(Yang et al., 2003) this approach is used to warp entire

images for dense scene reconstruction.

In this work, a neural network is extended by a

plane sweep approach, in which feature maps are war-

ped by a plane homography inside the network. By

projecting the feature map of one camera onto the

plane and into the other camera, rectiﬁcation becomes

unnecessary, and, more importantly, by sweeping the

virtual plane from below to above the road surface,

the search space is reduced. The network is trained

on a dataset, which was created by a plane sweep ap-

proach in conjunction with semi global matching.

3 METHOD

The method described in this paper consists of an ex-

isting convolutional neural network for disparity esti-

mation, which is modiﬁed to estimate change in sur-

face elevation by a plane sweep approach. The plane

sweep direction is perpendicular to the road surface

and therefore a plane must be found which represents

the mean road surface. This plane is guessed initially

and reﬁned later on.

In this section ﬁrst the idea of plane sweep and

its usage is described. Next, the convolutional neu-

ral network on which this work is based on is brieﬂy

recapitulated. Subsequently the embedding of plane

sweep into this network is described. At the end it is

shown how the mean surface can be found.

3.1 Plane Sweep

The left camera image of a plane, that is parallel to

the x-y-plane, is calculated by the 2D homography

(Collins, 1996)

L,i

= K



L,1

L,2

L,3

+ t



. (1)

is the camera matrix. The camera location is given

by the columns of the rotation matrix r

L,{1,2,3}

and the

translation vector t

. z

is the distance between the x-

y-plane and the parallel plane.

To ﬁnd the plane parts of a pair of images was ta-

ken of, both images can be back projected onto virtual

planes i by the inverse homographies H

−1

L,i

and H

−1

R,i

where H

R,i

is the homography for the right camera. If

the plane is at the correct position for these parts of

the images, they will match on the virtual plane. This

Incorporating Plane-Sweep in Convolutional Neural Network Stereo Imaging for Road Surface Reconstruction

785

Leftimage

Rightimage

siamesenetworks

featuremap

network

3D

network

Depthmap

stack

feature

maps

featuremap

network

interpolation

&

regression

warpbyplane

homographies

4Dcostvolume

Figure 1: Feature maps are calculated by a Siamese network for both input images. One of them is transformed by a plane

homography and a 4D cost volume is created. Matching is done by the 3D network, which outputs the depth map.

idea was introduced in (Collins, 1996), where sparse

image features are back projected.

In this work dense feature maps are generated by

a neural network. The feature map of the left image is

back projected onto virtual planes and projected into

the right camera, where matching is performed by the

neural network. The back and forth projection is des-

cribed by

= H

R,i

· H

−1

L,i

. (2)

Performing the matching in the camera space instead

of the plane space has several advantages: Images –

or feature maps in this case – are not stretched much,

which is the case if the virtual plane is not parallel to

the camera. The shape of the cost volume stays the

same, no matter of the perspective the plane induces.

Besides, that way only the feature map of one image

has to be transformed.

3.2 Neural Network for Disparity

Estimation

Different architectures of neural networks for depth

estimation exist, as was laid out in Section 2. The

plane sweep extension can be added to all networks

which are based on the idea of a cost volume. Here

the work of (Chang and Chen, 2018) is incorporated,

as it is able to exploit global context information. By

creating image features with the help of spatial py-

ramid pooling, region-level features instead of pixel-

level features are introduced (Chang and Chen, 2018).

As roads have little texture, it is believed that region-

level features will improve the overall performance,

especially if cracks or other contexts are visible.

Their network consists of four parts: A Siamese

network that creates feature maps from input ima-

ges at a reduced resolution, concatenation of these

feature maps, creating a 4D cost volume, a 3D net-

work, which calculates the cost for each disparity

value for every location, upscaling by interpolation,

and a regression function. The feature map network

gets rectiﬁed 3-channel images as input with reso-

lution W × H (with times height) and creates F fe-

ature maps with resolution W /4 × H/4 per image.

The cost volume is assembled according to disparity

space. That means, for each considered disparity va-

lue, the feature maps of the reference image are stac-

ked on top of the shifted feature maps of the other

image. This produces a cost volume of dimension

W /4 × H/4 × D/4 x 2F. D is the number of consi-

dered disparity values. The 3D network converts the

4D cost volume into a 3D cost volume of dimension

W /4 × H/4 × D/4 by 3D convolutions, which is up-

scaled by trilinear interpolation to the original resolu-

tion of W × H × D. Now a regression function ﬁnds

the best ﬁtting disparity value by regressing over the

D values at every location. The regression function is

d =

max

∑

d=0

d · σ(−c

), (3)

where σ() is the softmax operation, d are the disparity

values, D

max

is the maximum disparity and c

is the

cost value.

3.3 Neural Network for Surface Depth

Map Estimation

In the proposed method the assembly of the cost vo-

lume is altered according to plane sweep. First P pla-

nes parallel to the road surface are proposed. The

right image is taken as reference, thus the left fea-

ture maps need to be warped by the induced homo-

graphies. For every proposed plane, the feature maps

of the reference image are stacked on top of the war-

ped feature map of the other image. This produces a

cost volume of dimension W/4 x H/4 x P x 2F. The

3D network and regression function are left unchan-

ged. The upscaling function changes, as that it does

not have to upscale the disparity (plane, respectively)

dimension. An overview of the method is shown in

Figure 1.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

786

Warping of the feature maps is accomplished by

inverse warping (Szeliski, 2011): Coordinates of

every pixel of the reference image are transformed by

the inverse of the plane induced homography (Equa-

tion 2). The result is a lookup table. The feature

maps of the left image are copied with the help of

this lookup table, which is ﬁrst rounded to the nearest

integer coordinate. As the neural network generates

features maps at a lower resolution compared to the

input images, the camera matrices have to be scaled

before applying Equation 2.

One might be tempted to use a more sophisticated

approach as in spatial transformer networks (Jader-

berg et al., 2015), where bilinear interpolation is used.

In our experiments this does not work. The neural

network has a large receptive ﬁeld (Chang and Chen,

2018), which, in conjunction with interpolation, pre-

sumably breaks the relation between an image pixel

and its corresponding value in the feature map. Du-

ring evaluation bilinear interpolation can be utilized.

Training is performed end-to-end on depth maps,

with the target being the index of the virtual planes.

The usage of the index is similar to the usage of dis-

parity in Section 3.2. That way, the network is inde-

pendent of the actual depth values and different plane

hypothesis can be proposed while training and evalu-

ating.

3.4 Locating the Mean Road Surface

As the plane sweep is conducted from below to above

the mean surface, its location has to be known in ad-

vance. An initial plane can be guessed, as the approx-

imate positions of the cameras in relation to the road

are known. The location is then reﬁned: A depth map

is created by the neural network and is then back pro-

jected to 3D space, resulting in a 3D point cloud in

the camera coordinate system. A grid of points is ex-

tracted as a subset to save some calculation time. A

plane, which best resembles the point cloud, is then

found by a random sample consensus (RANSAC) al-

gorithm (Fischler and Bolles, 1981). In that the mean

of the point cloud is subtracted. Singular value de-

composition is utilized, which directly gives the rota-

tion matrix from the camera coordinate system to the

plane coordinate system, in which the x-y-plane re-

sembles the mean surface. It is located in the center of

the road. The subtracted mean is the translation vec-

tor. To ﬁnd the ﬁnal r

{L/R},{1,2,3}

and t

{L/R}

, which

are used in Equation 1, the transformation between

camera centers and camera coordinate system has to

be accounted for.

To generate a bird’s-eye view later, it is useful

to place the camera coordinate system in the center

between the cameras. The rotation between camera

coordinate system and plane can then be composed

by a rotation around the x-axis, followed by a rotation

around the y-axis. Thus, the rotation matrix is disas-

sembled to Euler angles, the rotation around the z-axis

is set to 0 and the rotation matrix is reassembled. This

ensures that the birds-eye-view does not get rotated if

it is shown in the road coordinate system.

After locating the mean surface, the neural net-

work is evaluated a second time.

4 EXPERIMENTS

In the following section the system setup, the training

procedure and the evaluation is described.

4.1 System Setup

Two Basler acA1920-150uc global shutter color ca-

meras with 25 mm lenses are employed. The sen-

sors have an optical size of 2/3” with a resolution of

1920×1200 pixels. The pixel size is 4.8µm × 4.8 µm.

The cameras are mounted on a rig behind the winds-

hield of a vehicle. As the distance between cameras

and road is large (up to 13 m at the upper edge in Fi-

gure 2) and the depth resolution needs to be high (ele-

vation differences of a road are in the mm scale), the

baseline has to be as large as possible. Due to the ﬂat

geometry, a large baseline does not produce occlusi-

ons. The baseline is set to 1.08 m and camera height

above ground is 1.4 m. In order to have a large over-

lapping part in both pictures, cameras are tilted in by

◦

each. The angle between the camera rig and the

road is 13

◦

, in order to look across the hood. This

makes it possible to record an area of approximately

2m × 7m.

The aperture has a big inﬂuence on the depth of

ﬁeld. For the depth of ﬁeld to be large, it has to

be small. On the other hand the aperture inﬂuences

the required shutter time and thereby the motion blur,

thus it has to be large. Even at slow driving speeds the

motion blur predominates. For this reason, the aper-

ture is set to the smallest value of f/1.4 for images

taken while driving and to f/8.0 for standstill images.

As the windshield has an inﬂuence on calibration

parameters (Hanel et al., 2016), calibration is perfor-

med with the cameras in their ﬁnal position.

4.2 Training

The proposed convolutional neural network (refer-

red to as CNN in the following) is pretrained on the

KITTI 2015 dataset. Therefore, the cost volume in

Incorporating Plane-Sweep in Convolutional Neural Network Stereo Imaging for Road Surface Reconstruction

787

(a) (b) (c)

(d) (e) (f)

Figure 2: Static scene: a,d left and right image b,c depth map generated by SGM and CNN method (viewed from the right

camera perspective) e,f error between laser scan reference and SGM/CNN method. The circular part on the right and the

stripe on the left are artefacts of the laser scan. The distance between camera and the lower part of the image is 4.5m, between

camera and upper part 13.0m.

the network is assembled as described in Section 3.2.

Learned weights are saved and cost volume assembly

is switched to the plane sweep approach (Section 3.3).

Training is continued with data of the targeted appli-

cation. For the training set depth was extracted by a

stereo method, which is based on a plane sweep ap-

proach in conjunction with semi-global matching (the

method is referred to as SGM) and is out of scope of

this paper. It is based on the work in (Hirschm

uller,

2008). The location of the mean road surface is an

output of the earlier method and is also used for trai-

ning. The training dataset consists of 510 stereo ima-

ges, which were taken while driving. Another 20 still

stereo images were taken outside the vehicle.

Laser scans are not used for training because a suf-

ﬁciently large data set was not available and is difﬁ-

cult to obtain. Laser scanning and capture of stereo

images would have to take place simultaneously and

the relationship between scanner and camera would

have to be precisely known. This makes the measu-

rement complex and expensive equipment would be

necessary, especially for the measurements while dri-

ving. Thus, a stereo method is used.

The number of feature maps F is set to 32 and the

number of planes P to 64. Plane sweep is performed

from −30mm to +30 mm around the mean road sur-

face. An example of a training set composed of left

and right color images as input and a depth map as

output can be seen in Figure 2a, 2d and 2b (although

this particular example was used for validation only).

Training is performed on two NVidia GTX 1080

Ti graphics cards (both have 11 GB of memory) in

parallel mode. The model does not ﬁt into memory

in training mode if images with the full resolution of

1920 × 1200 pixels are employed. Thus, 256 × 256

pixel patches of the right image are randomly cho-

sen. The corresponding patch in the left image can be

calculated, as the planes which will be gone through

while sweeping are known in advance. The left image

patch is padded to 576 × 300 pixels in order to have

a uniform size for the learning batch. The principal

points in the camera matrices have to be adjusted ac-

cording to the patch locations. Batch size is set to 8.

In evaluation mode, when no gradients are required

and if intermediate results are deleted, the network

for full resolution images ﬁts into GPU memory of a

single card.

4.3 Evaluation

In order to interpret the results, ﬁrst the depth resolu-

tion of the camera system is investigated. The method

is then evaluated by a comparison against a laser scan

with standstill images. Afterwards, results from the

targeted application of pavement destress detection

while driving are shown.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

788

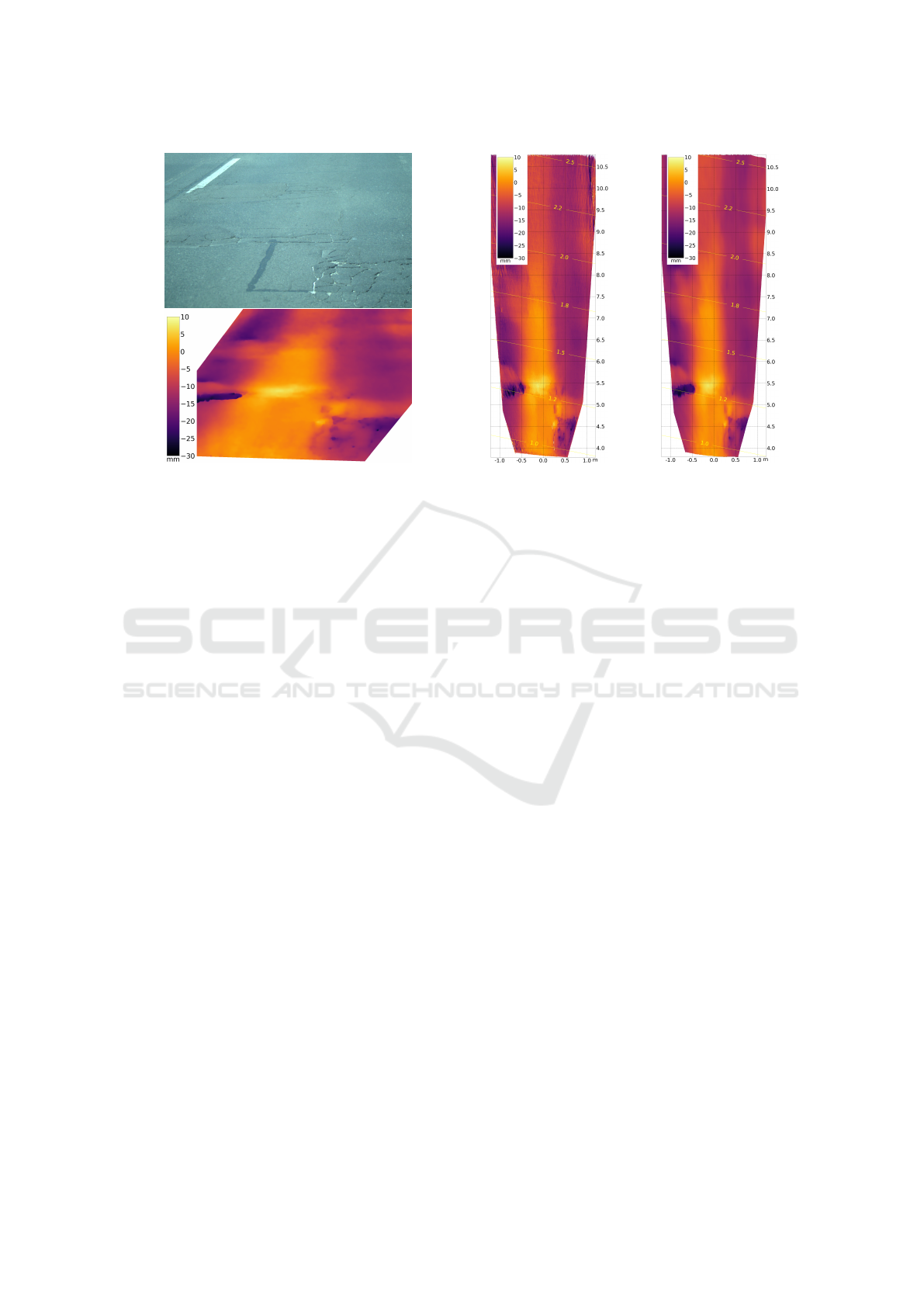
(a)

(b) (c)

Figure 3: (a) Right image, captured from behind the windshield of a moving car at 37km h

−1

and corresponding depth map

created with CNN method, (b) depth map from a bird’s-eye view with contour lines, indicating depth resolution in mm/pixel

created by SGM method and (c) created by CNN method.

4.3.1 Depth Resolution

For the aforementioned setup, the depth resolution is

calculated as follows: If the correct plane is known

for a pixel in the right camera image, the matching

pixel in the left camera image can be calculated by

the plane homography. If the plane is raised, the mat-

ching pixel will be shifted. The elevation of the plane

divided by the pixel shift is embraced as the resolu-

tion. It is shown as contour lines in Figures 3b and 3c

and in Figure 4 for the central line between cameras.

The exact resolution depends on the relation between

cameras and the mean surface.

4.3.2 Comparison Against Laser Scan

As a reference a laser scan was conducted. The scan-

ner (Z+F IMAGER 5006h) has a range uncertainty of

0.4mm and an uncertainty in vertical and horizontal

direction of 0.007

◦

. This sums up to a total maximal

uncertainty of 0.8 mm in the direction perpendicular

to the road surface in the area of interest. Due to the

high precision of the laser scanner, it is considered to

be the ground truth.

For comparison, the depth maps are projected to

3D space, where the distance to the point cloud of the

laser scanner can be calculated. This is accomplished

with the help of the software CloudCompare (GPL

software, 2017). Because the relation between ca-

mera and laser scanner coordinate system is unknown,

the compared point cloud is rotated and shifted until

both point clouds line up. Then a piecewise quadra-

tic function is ﬁtted through the reference point cloud

and the shortest distance to the compared point cloud

is calculated.

The result is shown for standstill images from the

right cameras perspective in Figure 2e and 2f for the

SGM and CNN methods. SGM refers to the method

which was used to create the training data and CNN

to the proposed method. Images were taken outside

the vehicle while standing still.

It can be seen that both methods are capable of

reconstructing the road surface with high precision.

The mean absolute error (MAE) is 1.1 mm for SGM

and 0.8 mm for the CNN method. The CNN method

did not just learn from the SGM method, it even out-

performs SGM in this example. SGM fails in parti-

cular regions, which can be seen in the upper left and

upper right corner, where CNN produces the correct

depth according to the error image (Figure 2f) and

SGM does not (Figure 2e). The reason presumably

is that in the CNN method region-level features are

employed (Section 3.2). The SGM method produces

correct results for most pixels, while some are wrong.

The correct pixels ﬁt the model, which is tried to be

learned by the neural network. The wrong pixels ap-

pear as noise. Since the correct pixel outweigh the

wrong pixels, the neural network is able to generalize

the correct and to reject the erroneous training data.

Figure 4 shows the MAE of horizontal lines in

bird’s-eye view (refer to Figure 3c) for Figure 2 and

the physical resolution as described in Section 4.3.1

for the central vertical line. The small MAEs of the

entire point clouds compared to the MAEs of hori-

Incorporating Plane-Sweep in Convolutional Neural Network Stereo Imaging for Road Surface Reconstruction

789

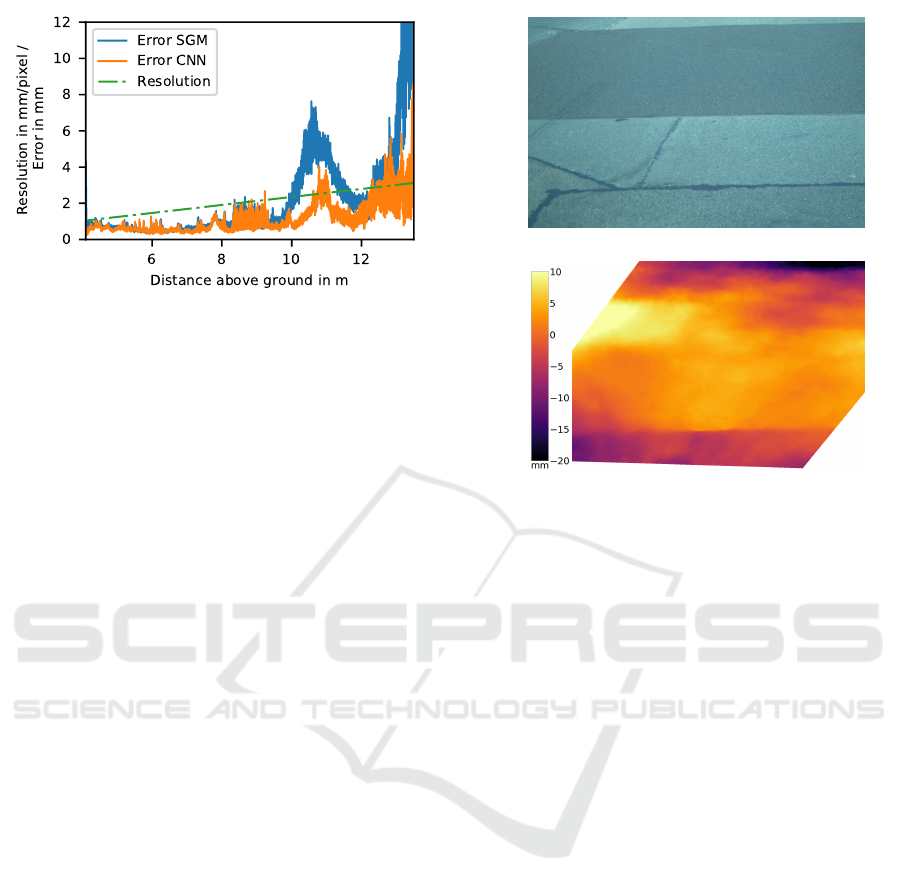
Figure 4: Errors of the SGM and CNN methods compared

to the laser scan are shown, which increase over distance

from the cameras. The physical depth resolution of the ste-

reo camera setup decreases over distance.

zontal lines shown in the graph are caused by the fact

that the density of the point cloud decreases over dis-

tance. Thus, there are more points with small errors

than with large errors. The mean of MAEs of hori-

zontal lines is 2.1 mm for SGM and 1.2mm for CNN.

The sudden increase of the error at 11 m is caused by

the circular artefact of the laser scan (Figure 2e and

2f) and the erroneous section of the SGM method in

the upper left (Figure 2e).

Compared to the physical resolution the errors are

very small, especially when they are close to the ca-

meras. The methods are capable of achieving sub-

pixel accuracy. The SGM method interpolates bet-

ween pixels by plane sweeping and image warping,

while the CNN method uses the regression function

(Equation 3). Another cause is the alignment of point

clouds (Section 4.3.2), which reduces the error artiﬁ-

cially.

4.3.3 Final Application

Figure 3 shows the right camera image and the cor-

responding depth maps from the cameras perspective

and from a bird’s-eye view. The images were ta-

ken from behind the windshield while driving at

37km h

−1

. A repair patch is visible (covering parts

of the lane mark), which is elevated from the road.

Closer to the camera on the left hand side a depres-

sion can be seen. In the lower right several cracks can

be extinguished. If one looks at the bird’s-eye view,

rutting is visible across the entire distance.

The CNN method (Figure 3c) is more robust than

the SGM method (Figure 3b), which can be seen

by looking at the lower left and upper right corners.

Overall the CNN method produces smoother depth

maps.

Figure 5 shows another example at a higher dri-

(a)

(b)

Figure 5: (a) Right image, captured from behind the winds-

hield of a moving car at 75 kmh

−1

and (b) corresponding

depth map created with the CNN method.

ving speed of 75km h

−1

. Although no laser scans are

available for images which were taken while driving,

the results are qualitatively correct. Please note that

the color scales cover different ranges in Figures 2, 3

and 5.

5 CONCLUSION

It was shown how convolutional neural networks for

disparity estimation can be adapted to predict depth

maps of ﬂat surfaces. Results are compared against a

laser scan and show high accuracy over large distan-

ces. The new method even outperforms the method it

learned from in some cases.

The proposed method proves to be very suita-

ble for the challenging task of road surface recon-

struction. It can be utilized to quickly scan road sur-

faces with little effort at driving speeds.

REFERENCES

Chang, J.-R. and Chen, Y.-S. (2018). Pyramid Stereo Ma-

tching Network. arXiv preprint arXiv:1803.08669,

page 9.

Collins, R. T. (1996). A space-sweep approach to true

multi-image matching. In Computer Vision and Pat-

tern Recognition, 1996. Proceedings CVPR’96, 1996

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

790

IEEE Computer Society Conference on, pages 358–

363. IEEE.

Dosovitskiy, A., Fischer, P., Ilg, E., Hausser, P., Hazirbas,

C., Golkov, V., van der Smagt, P., Cremers, D., and

Brox, T. (2015). Flownet: Learning optical ﬂow with

convolutional networks. In Proceedings of the IEEE

International Conference on Computer Vision, pages

2758–2766.

Eisenbach, M., Stricker, R., Seichter, D., Amende, K., De-

bes, K., Sesselmann, M., Ebersbach, D., Stoeckert, U.,

and Gross, H.-M. (2017). How to get pavement dis-

tress detection ready for deep learning? A systematic

approach. In 2017 International Joint Conference on

Neural Networks (IJCNN), pages 2039–2047, Ancho-

rage, AK, USA. IEEE.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: a paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Communications of the ACM, 24(6):381–395.

GPL software (2017). Cloudcompare 2.8.

Hanel, A., Hoegner, L., and Stilla, U. (2016). Towards the

Inﬂuence of a Car Windschield on Depth Calculation

with a Stereo Camera System. ISPRS - International

Archives of the Photogrammetry, Remote Sensing and

Spatial Information Sciences, XLI-B5:461–468.

Hartley, R. and Zisserman, A. (2003). Multiple view geome-

try in computer vision. Cambridge University Press,

Cambridge, UK; New York.

Hirschm

uller, H. (2008). Stereo Processing by Semiglobal

Matching and Mutual Information. IEEE Transacti-

ons on Pattern Analysis and Machine Intelligence,

30(2):328–341.

Ikeuchi, K., editor (2014). Computer Vision - A Reference

Guide. Springer US, Boston, MA.

Jaderberg, M., Simonyan, K., Zisserman, A., and others

(2015). Spatial transformer networks. In Advances in

neural information processing systems, pages 2017–

2025.

Kendall, A., Martirosyan, H., Dasgupta, S., Henry, P., Ken-

nedy, R., Bachrach, A., and Bry, A. (2017). End-

to-End Learning of Geometry and Context for Deep

Stereo Regression. arXiv:1703.04309 [cs]. arXiv:

1703.04309.

Mayer, N., Ilg, E., Hausser, P., Fischer, P., Cremers, D.,

Dosovitskiy, A., and Brox, T. (2016). A large dataset

to train convolutional networks for disparity, optical

ﬂow, and scene ﬂow estimation. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition, pages 4040–4048.

Smolyanskiy, N., Kamenev, A., and Birchﬁeld, S. (2018).

On the Importance of Stereo for Accurate Depth Es-

timation: An Efﬁcient Semi-Supervised Deep Neural

Network Approach. CoRR, abs/1803.09719.

Szeliski, R. (2011). Computer Vision. Texts in Computer

Science. Springer London, London.

Yang, R., Welch, G., and Bishop, G. (2003). Real-Time

Consensus-Based Scene Reconstruction Using Com-

modity Graphics Hardware. In Computer Graphics

Forum, volume 22, pages 207–216. Wiley Online Li-

brary.

Zbontar, J. and LeCun, Y. (2016). Stereo matching by

training a convolutional neural network to compare

image patches. Journal of Machine Learning Rese-

arch, 17(1-32):2.

Incorporating Plane-Sweep in Convolutional Neural Network Stereo Imaging for Road Surface Reconstruction

791