Non-rigid Shape Registration using Curvature Information

Albane Borocco and Beatriz Marcotegui

MINES ParisTech, PSL Research University, CMM - Centre for Mathematical Morphology,

35, rue St. Honore, 77305 Fontainebleau, France

Keywords:

Non-rigid Registration, Shape Registration, High Curvature, Industrial Quality Control.

Abstract:

This paper addresses a registration problem for an industrial control application: it meets the need to registrate

a model on an image of a ﬂexible object. We propose a non-rigid shape registration approach that deals with

a great disparity of the number of points in the model and in the manufactured object. We have developed a

method based on a classical minimization process combining a distance term and a regularization term. We

observed that, even if the control points fall on the object boundary, the registration failed on high curvature

points. In this paper we add a curvature-based term in order to improve the registration on object extremities.

We validate our approach on a real industrial application. The addition of this curvature term reduces by two

the error of the inner boundaries location on the previously problematic cases of our database.

1 INTRODUCTION

Manufacturing industry requires inspection tools for

controlling industrial processes. This control usually

relies on images of the manufactured objects and on a

prior knowledge of them. In our application the previ-

ous knowledge consists in the theoretical model in the

form of a set of boundaries of different object compo-

nents.

(a) model (b) manufactured object

Figure 1: Example of the data used.

Figure 1(a) shows a theoretical model from our

application. It contains the boudaries between the dif-

ferent object components. The visual appearance of

the inner parts (the textured appearance) is unknown.

Figure 1(b) shows an image of an object manufac-

tured according to this model. The segmentation of

the whole object is relatively easy. It is performed

by a marker-based watershed approach (Beucher and

Meyer, 1992). The segmentation result is overlayed in

red on ﬁgure 1(b). This step is out of the scope of this

paper. The automatic location of the inner boundaries

is much harder, as several object components have a

very similar visual appearance.

In order to control the quality of the manufac-

tured object, we need to perform the registration of

the model (2D shape) on the image of the object. This

registration relies on the external shape of the model

and the object image. The object is ﬂexible. A non-

rigid registration method of the model on the objects

image is required.

The main contribution of this paper is the inclu-

sion of a curvature term in a non rigid registration

framework that avoids spurious deformations in high

curvature zones. The approach is validated in an in-

dustrial context.

The rest of the paper is organized as follows. Sec-

tion 2 brieﬂy reviews the state of the art of registra-

tion methods, describes the principle of the selected

method that better ﬁts our requirements and discuss

its performances in different situations. Section 3 pro-

poses a solution that solves the observed problems. In

section 4 we validate our solution in a industrial con-

334

Borocco, A. and Marcotegui, B.

Non-rigid Shape Registration using Curvature Information.

DOI: 10.5220/0007354903340340

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 334-340

ISBN: 978-989-758-354-4

text. Qualitative and quantitative results are given. Fi-

nally section 5 concludes this paper.

2 REGISTRATION

The registration literature is very rich and offers many

different registration methods. Interesting surveys can

be found in: (Zitova and Flusser, 2003) (Sotiras et al.,

2013). We focus on the techniques relevant to our ap-

plication. Our model contains only the boundaries of

the object’s components and the visual appearance of

the inner parts is unknown. Thus image-based regis-

tration techniques are not suitable for our application.

Also the object is made of nearly incompressible

material and suffers only large scale deformations.

Thus, the inner parts move coherently with the object

boundary. Therefore we perform a shape registration

between the 2D model and the object external bound-

ary, and then apply the computed deformation to the

entire model. The same strategy is used by Peterlik

(Peterl

ık et al., 2017).

Our aim is then to register the model 2D shape

to shape of the manufactured object. Because of the

ﬂexible nature of our objects, we need a non-rigid 2D

shape registration. Many methods exist in the litera-

ture for this purpose.

Among them there are many well known methods

such as the ICP (Iterative Closest Point) method in-

troduced par Besl and McKay (Besl et al., 1992), but

even its variants later developed (Rusinkiewicz and

Levoy, 2001) (Pomerleau et al., 2013) are inappropri-

ate for cases where the sampling step is not uniform.

This is the case in our application, because the model

is discretized so that there are more points in areas

of strong curvature while the object boundary is regu-

larly sampled according to the resolution of the im-

age acquisition device. Also it is very sensitive to

the initialization step. Another widespread method

is the Coherent Point Drift (CPD) algorithm, (My-

ronenko and Song, 2010) (Myronenko et al., 2007).

It is a probabilistic method, for both rigid and non-

rigid point set registration that considers the align-

ment of two point sets as a probability density esti-

mation problem.

The method developed by Rouhani (Rouhani and

Sappa, 2012) is particularly suitable for our purpose.

Indeed, it can cope with the not even discretization

step of the model’s border. Also it exploits a quadratic

distance approximation which allows each iteration of

the algorithm to be linearly solved. Hence, the regis-

tration process has a fast convergence. Because of

those reasons we choose to use Rouhani’s method.

2.1 Principle of Rouhani’s Registration

Let us describe the Rouhani’s registration princi-

ple introduced in (Rouhani and Sappa, 2012). Let

S = {s

}

be the set of data points of the model shape

and C = {c

}

the points of the object boundary. The

registration is done by minimizing an error term in an

iterative process. This error relies on the sum of the

distance of points s

belonging to the model, to the

border of the object C:

SD(s

,C) =

− ρ

[(s

− c

)

]

+ [(s

− c

)

]

(1)

with s

the considered point belonging to the

model, c

the closest point to s

belonging to C, T

and N

, the unit tangent and outer normal at c

, d

the signed distance between s

and c

, ρ

, the curva-

ture radius at s

The use of this distance makes this registration

method it suitable for a different number of points on

registered shapes. Figure 2 shows an illustration of

the considered distance: In low curvature zones the

considered distance is close to the normal distance to

the shape, and so the minimizing process is not af-

fected by the different number of points. Whereas

in high curvature zones, the considered distance is

equivalent to the euclidean one.

Figure 2: Illustration of the considered distance.

A squared control lattice, P, is deﬁned and its de-

formation, L,is regularized by a global tension term ,

T (P), measured by its curvature over the whole do-

main:

T (P) =

Z Z

[kL

+ 2kL

+ kL

]dxdy (2)

with L, the vector ﬁeld representing the deforma-

tion of the control lattice.

In each iteration, we optimize the deformation

ﬁeld L in order to minimize the error E:

E = λT(P)+

∑

i=1

SD(L(s

),C) (3)

Non-rigid Shape Registration using Curvature Information

335

with L(s

) the position of s

after deformation of

the control lattice L, L(s

) is initialized as s

And λT (P) a regularity term in order to assure that

the local deformation is not too important.

λ represents the registration rigidity, and is auto-

matically tuned during the registration. It starts with

a high value ( λ = 10

), which intends to cope with

the alignment problem. Then, once the ratio of regis-

tration error between consecutive iterations is below

a given threshold, λ is divided by 10, until λ = 1.

Because of the chosen distance, the whole regis-

tration function in equation 3 is linear in terms of the

control lattice coordinates. The optimal control lattice

deformation is obtained by iterating the resolution of

a system of two linear equations. The reader is refered

to (Rouhani and Sappa, 2012) for a detailled descrip-

tion of this method.

The results obtained on our data using that method

are generally good: we observe that the external con-

tours coincide, but also, the internal ones, obtained by

the application of the deformation computed on the

external contour to the whole object, correspond to

the ones we observe in our objects, as it is shown in

ﬁgure 3.

Figure 3: Good registration results on objects 6 and 16 using

Rouhnani’s method (Rouhani and Sappa, 2012).

2.2 Problems Encountered

Using that method we have performed registration

of 2D shapes, obtained from the database (Ralph,

2009).The blue shape is the model that is registered

to another instance of the object, the red shape.

Figure 5 illustrates the results obtained after

Rouhani’s registration. We can observe that every

point of the model is, after registration, projected on

the contour of the image. Based on this observation,

it may be considered as a good result. However the

(a) object: dude 0 (b) model: dude 7

Figure 4: 2D Shapes used for registration.

(a) before registration (b) after Rouhani’s registra-

tion

zoom from 5(a)

(d) after Rouhani’s regis-

tration, zoom from 5(c)

Figure 5: Registration results on 2D Shapes: dude7 and

dude0.

contours do not actually coincide: If we connect the

dots, as shown in the ﬁgure 5(c), we observe that even

if the points were moved so that they belong to the

image contour after registration, the registration fails,

specially on the dude’s arms. We can observe that

phenomenon on the ﬁgure 5(d).

This phenomenon occurs because this registration

technique tends to minimize a criterion that is only

related to the distance between the model points and

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

336

the contours. In the case of the dude’s arms, the point

located at the end of the arm in the model is closer to

a point located in the forearm of the image than to the

extremity. This error appears mainly in high curvature

zones.

Figure 6: Mapping between model points and their location

after registration.

We also face this problem in our images. This phe-

nomenon can be observed in ﬁgure 6: the contours

coincide but there is a shift between them. The ﬁnal

error achieved by the algorithm is close to zero but the

registration still fails.

(a) model (b) registration of the model

on the object

Figure 7: Registration results on object 18: the deforma-

tion due to registration introduces non-physical curvatures

on the internal contours.

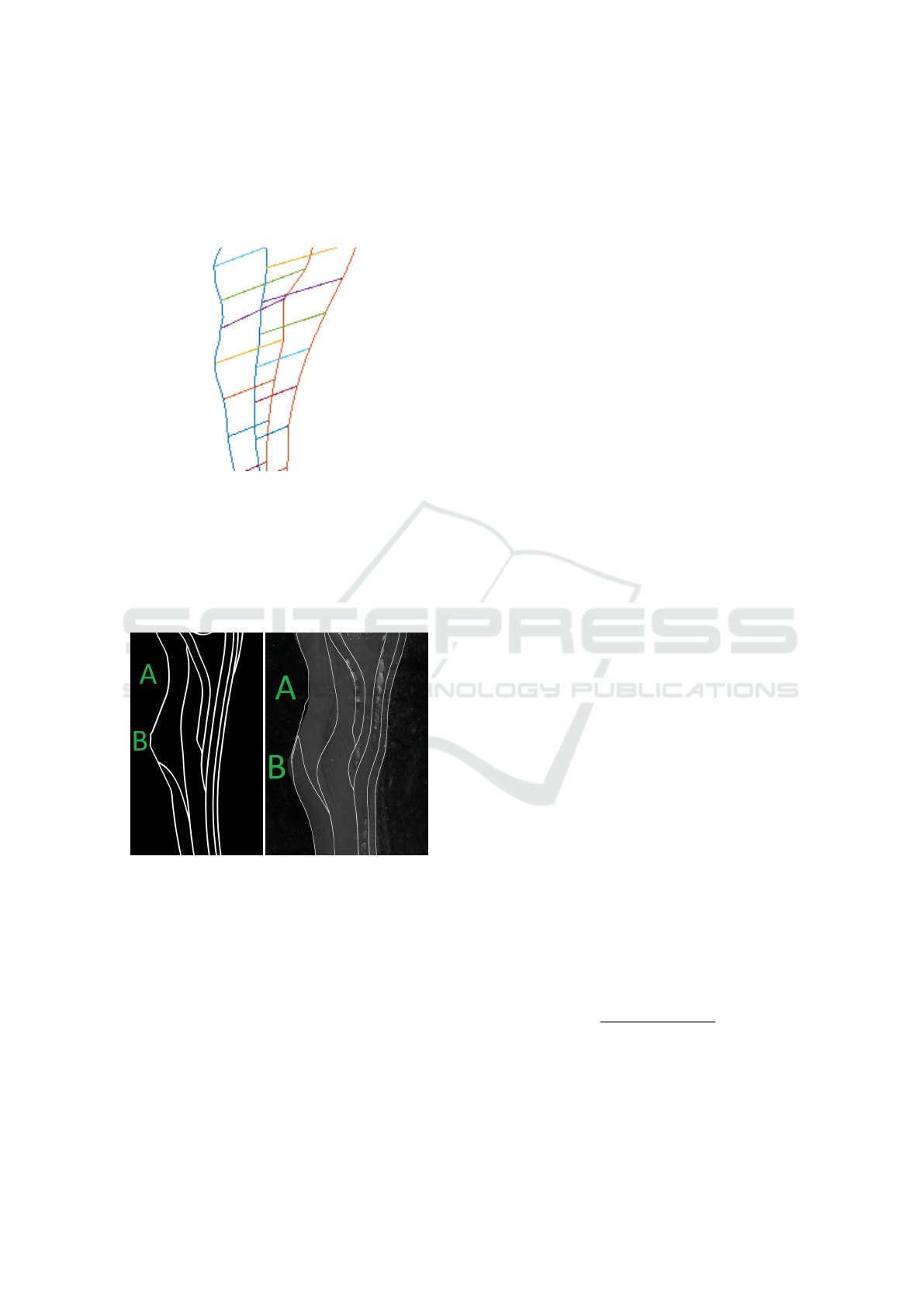
This is problematic in our case because it induces

distortion in the internal contours, as shown in ﬁgure

7. The observed distortions of the internal contours

are due to a shift between the obtained registration re-

sult and the expected one. This is in our case a major

mistake: such a distortion corresponds to a stretching

in the lower area (B) and a compression in the upper

area (A), as in ﬁgure 7, inducing a curvature in the in-

ternal contours. Those two physical transformations

could not happen in the case of nearly incompressible

material, and thereby this solution is not possible.

3 PROPOSED SOLUTION

Our solution relies in the fact that the distortion be-

tween the object and its model is global. Because of

that, high curvature zones present in the model will

remain in the object.

The solution we propose is to favor the pairing of

similar high curvature points by adding a term in the

error equation (3).

This term would avoid shifts between the con-

tours, but also prevent the case where model points

belong to the object’s contour after registration but the

contours do not coincide as seen on ﬁgure 5, which

happens mainly in high curvature zones.

First we detect high curvature points on the model.

We name them the characteristic points cp. Those

characteristic points are identiﬁed using the curvature

radius. For our experiment we deﬁned a point as high

curvature point if its curvature radius ρ

is the lo-

cal minimum of a zone where the curvature radius is

smaller than 50 pixels.

Then we detect high curvature points on the im-

age. By deﬁnition, high curvature points of the model

are also present in the object and no additional high

curvature points are created. Therefore we select the

same number of characteristic points N

as detected

in the model, within the high curvature points in the

image.

We match each characteristic point from the

model cp

to the closest characteristic point of the ob-

ject C(cp

We add a term in the error equation in order to

minimize the distance between characteristic points

of similar curvature.

E = λT (P)+

∑

i=0

i/∈cp

SD(L(s

),C)+

∑

i∈cp

µd(L(cp

),C(cp

))

(4)

with cp characteristic points, cp

being paired

with C(cp

), d the distance between those points and:

µ =

1 + |ρ

C(cp

) − ρ

(5)

with k, being a weight to give the curvature term

more or less impact, and ρ

and ρ

C(cp

)

being respec-

tive curvature radius. In our application we observed

experimentally that variations of this parameter has a

Non-rigid Shape Registration using Curvature Information

337

low sensitivity as long as it has values between 20 and

200. We decided to use k = 50.

Then as each iteration tends to reduce the global

error, the distance between those points will decrease.

4 EXPERIMENTAL RESULTS

4.1 Database

The study we conducted was for an industrial pur-

pose: an industrial partner provided us with images

of objects and the models according to which the ob-

jects were manufactured. Our database contains 80

images of size 14000 by 8000 pixels, of objects pro-

duced according to 31 different models.

In order for us to quantify the improvement on the

problematic cases of our obtained results, images of

objects with areas of strong curvature have been an-

notated by a specialist: we have a ground truth of the

real inner frontiers of the objects corresponding to 4

different models.

The method we’ve developed aims to be deployed

in factories, it must therefore must cope with a wide

variety of objects and models.

4.2 Results

Figure 8 compares the results between Rouhani’s

original method and our proposed improvement. We

observe that after Rouhani’s registration every point

of the model is projected on the image but that the

contours do not coincide.

Using our method, as the extremities of the arms

are high curvature points, those points are well regis-

tered.

Adding this constraint on high curvature points

improves the registration: in both cases every point of

the model is, after registration, projected on the con-

tour of the image, which leads to a small error term.

But the use of high curvature points pairing allows

contours to coincide even in high curvature zones.

This method improves the registration of the

model on the object produced: not deﬁning charac-

teristic points induces a shift between contours which

corresponds to a not physical deformation (cf. ﬁgure.

7), whereas those deformations do not occur with our

method cf. ﬁgure 9.

Figure 9 shows the performances of our method

on other problematic images. We observe on all the

objects that the inner borders are less curved using our

method in comparison with Rouhani’s method. These

(a) after Rouhani’s registra-

tion

(b) after our registration

ter Rouhani’s registration

(d) extremity of the arm

after our registration

Figure 8: Comparison of registration results on 2D Shapes

before and after adding the curvature term.

curvatures are not present in the model before regis-

tration, they where induced by the registration and do

not correspond to any physical deformation of the ob-

ject. Therefore our registration method improves the

registration.

The quantitative evaluation of the registration is

not easy. As illustrated hereinbefore, a perfect corre-

spondence of registered points is not a guarantee of

a perfect registration. In order to quantify the qual-

ity of the registration in an objective way, we intro-

duce a distance measure between the inner frontiers

of the object annotated by an expert, and their cor-

responding frontiers registered: To each point of the

registered inner frontier is associated the distance to

the closest point in the annotated frontiers.

As the objects are not perfect, even if the registra-

tion was perfect the inner contours in the image might

not correspond with those in the model. However, a

huge average distance between the annotated and the

registered frontiers reveals a failure in the registration.

The average distance to the ground truth is signif-

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

338

(a) object 18

(b) object 56

Figure 9: Comparaison of the results obtained before (left)

and after adding the curvature term (right) on objects 18, 56

and 75.

icantly lower for our result than for Rouhani’s result.

The quantitative evaluation of the results shown in ﬁg-

ure 9 are the following.

For object 18, shown in ﬁgure 9-a the average dis-

tance between the annotated and the registered fron-

tiers is 24.11 pixels using Rouhani’s method whereas

we obtain an average distance of 11.49 pixels using

our method. It corresponds to an improvement of 52

We obtain similar results for objects 56 and 75

shown in ﬁgures 9-b and 9-c. For object 56, be-

fore adding the curvature term, the average distance

to ground truth is 22.13, whereas with that term the

average distance is 12.53, which correspond to an im-

provement of 43%. Also for object 75, before adding

the curvature term, the average distance to ground

truth is 39.78, whereas with that term the average dis-

tance is 20.94, which correspond to an improvement

of 47%.

Over all the annotated objects, the mean distance

using Rouhani’s registration is 28.9 pixels, whereas

using our method we obtain an average distance of

14.2 pixels, wich corresponds to an improvement of

51%. Those results highlight the improvement made

by our method: the average distance on all annotated

objects is divided by 2.

By the use high curvature points pairing, this

method allows us to get better results: a curvature on

the inner contours is not induced by this registration.

The registered model’s contours are closer to the ob-

ject’s without any non physical deformation induced.

This method has been applied on our whole database

and similar results have been obtained.

5 CONCLUSION

This paper presents a method to cope with registration

mistakes of 2D shapes that are common in high curva-

ture regions. It is done by ﬁrst identifying and pairing

the high curvature points, then by adding a term that

favors the rapprochement of these pairs.

This method allows us to get better results that are

consistent with the physics inherent to the manufac-

tured object. It has been used in an industrial context,

and good results have been obtained on the set of im-

ages provided by the manufacturer. This method is

intended to be deployed in factories to allow a quality

control of the produced objects.

From the methodological point of view, we pro-

pose a non-rigid shape registration method, able to

handle correctly extremities registration. Our process

avoids signiﬁcant deformations of objects, that can

not be seen if we verify only the contour correspon-

dence.

REFERENCES

Besl, P. J., McKay, N. D., et al. (1992). A method for reg-

istration of 3-d shapes. IEEE Transactions on pattern

analysis and machine intelligence, 14(2):239–256.

Non-rigid Shape Registration using Curvature Information

339

Beucher, S. and Meyer, F. (1992). The morphologi-

cal approach to segmentation: the watershed trans-

formation. OPTICAL ENGINEERING-NEW YORK-

MARCEL DEKKER INCORPORATED-, 34:433–481.

Myronenko, A. and Song, X. (2010). Point set registra-

tion: Coherent point drift. IEEE transactions on pat-

tern analysis and machine intelligence, 32(12):2262–

2275.

Myronenko, A., Song, X., and Carreira-Perpin

an, M. A.

(2007). Non-rigid point set registration: Coherent

point drift. In Advances in Neural Information Pro-

cessing Systems, pages 1009–1016.

Peterl

ık, I., Courtecuisse, H., Rohling, R., Abolmaesumi, P.,

Nguan, C., Cotin, S., and Salcudean, S. (2017). Fast

elastic registration of soft tissues under large deforma-

tions. Medical Image Analysis.

Pomerleau, F., Colas, F., Siegwart, R., and Magnenat, S.

(2013). Comparing ICP variants on real-world data

sets. Autonomous Robots, 34(3):133–148.

Ralph, R. (2009). Mpeg-7 core experiment ce-shape-1 test

set.

Rouhani, M. and Sappa, A. D. (2012). Non-rigid shape

registration: A single linear least squares framework.

In European Conference on Computer Vision, pages

264–277. Springer.

Rusinkiewicz, S. and Levoy, M. (2001). Efﬁcient variants of

the ICP algorithm. In 3-D Digital Imaging and Mod-

eling, 2001. Proceedings. Third International Confer-

ence on, pages 145–152. IEEE.

Sotiras, A., Davatzikos, C., and Paragios, N. (2013). De-

formable medical image registration: A survey. IEEE

transactions on medical imaging, 32(7):1153–1190.

Zitova, B. and Flusser, J. (2003). Image registration

methods: a survey. Image and vision computing,

21(11):977–1000.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

340