Compensation of Simultaneous Orientation Contrast

in Superimposed Textures

Rudolf Netzel, Nils Rodrigues, Anja Haug and Daniel Weiskopf

Visualization Research Center (VISUS), University of Stuttgart, Germany

Keywords:

Simultaneous Contrast, Texture Orientation, Human Vision.

Abstract:

We propose a method that compensates the simultaneous orientation contrast in the visualization of superim-

posed textures. Such superposition plays a role in visualizations that overlay or enrich visual representations

of data with additional information. Our compensation method extracts the direction and frequency within the

input textures by using a Gabor ﬁlter bank. The foreground texture is then rotated to counterbalance the tilt

illusion. The rotation angle is determined by a model that adopts results of previous studies that measured the

inﬂuence of perceived contrast, direction, and frequency on the perceived tilt. The effectiveness of our method

is demonstrated for artiﬁcial stimuli and a typical example of scientiﬁc ﬂow visualization of multiple vector

ﬁelds.

1 INTRODUCTION

Visualization is used to generate graphical represen-

tations of data that are more understandable than the

source data in its original form. A multitude of dif-

ferent methods have been developed for a variety of

application domains, for instance, in ﬂow visualiza-

tion to make the structure of vector ﬁelds visible, or in

network visualization to show relationships between

elements represented as node-link diagrams. Such vi-

sualizations often suffer from visual clutter that could,

if not addressed properly, inﬂuence the perception and

thereby the interpretation of visualized data. This is

especially true when a post-processing step adds fur-

ther information to an existing visualization by super-

imposition.

A speciﬁc example of such a visualization is the

display of a ﬁrst vector ﬁeld through line integral con-

volution (LIC) and the overlay of arrow glyphs for a

second vector ﬁeld. Other examples of such overlays

are points of interest and routing instructions on top

of topological maps that help users to keep contextual

awareness. In general, this concept is related to the

topic of superimposing textures. In some cases, the

method of overlaying textures may produce perceptu-

ally inconsistent results. It is even possible that opti-

cal illusions are created that falsify the visualization.

In such scenarios, rendered graphics accurately depict

the source data, but human perception introduces ad-

ditional artifacts or distortions in addition to existing

(a) Hering illusion (b) Tilt illusion

Figure 1: Examples of visual illusions. In the Hering illu-

sion (a), two straight foreground lines (red) drawn on radial

lines in the background seem to bend outwards. The tilt illu-

sion (b) arises from a perfectly vertical texture (small inner

disk) on a background. Both shapes have a sinusoid texture,

but the foreground seems to have rotated counterclockwise.

graphical features.

One illusion that is very likely to appear in many

line-based visualizations is the tilt illusion. It results

in the perception of rotated or bent lines instead of

straight ones (Figure 1). It is difﬁcult to quantify the

effect for a general public, as it depends on viewing

distance, frequencies in the stimulus, orientation be-

tween back- and foreground, as well as individual hu-

man learning.

With this paper, we want to increase awareness of

such effects within the visualization community. It is

a relevant topic because it can occur when overlaying

textures or even in such simple cases where lines cross

Netzel, R., Rodrigues, N., Haug, A. and Weiskopf, D.

Compensation of Simultaneous Orientation Contrast in Superimposed Textures.

DOI: 10.5220/0007356800480057

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 48-57

ISBN: 978-989-758-354-4

(a) Image without compensation (b) Image with compensation

Figure 2: Example of a location-dependent compensation of the simultaneous orientation contrast (tilt illusion). The images

illustrate a disk (foreground texture) that is superimposed over a background texture. Both the background texture and disk

exhibit sinusoidal patterns. After the compensation, the disk in (a) appears no longer rotated in (b).

(Figure 1a). This is especially problematic when the

direction has to be estimated correctly, e.g., graph vi-

sualizations that use partial links (Becker et al., 1995).

For the remainder of this paper, we focus on il-

lusions caused by the simultaneous orientation con-

trast. We propose a method that allows us to compen-

sate the tilt illusion in speciﬁc cases: it takes as input

two superimposed textures and determines perceived

directions and frequencies of these textures utilizing

Gabor ﬁlters. Our method then compensates the tilt

illusion by rotating the overlaid texture in the opposite

orientation (Figure 2). We show examples of orienta-

tion contrast compensation for artiﬁcial stimuli and an

application from scientiﬁc visualization that we men-

tioned earlier: ﬂow visualization of two superimposed

vector ﬁelds, one shown by LIC, the other one shown

by arrow glyphs overlaid on top of the LIC image

(see Figure 7). Our model is capable of performing

a compensation for such stimuli, since it operates on

position-dependent data. Therefore, it can be applied

for, e.g., scientiﬁc visualizations with superimposed

textures.

2 RELATED WORK

When it comes to creating visualizations, there are

many factors that need to be considered, e.g., which

graphical primitives or color encoding should be used.

The visualization research community is very well

aware of the importance of human visual perception

in this context (Ware, 2012). In particular, there is

previous work on the role of attention (Healey and

Enns, 2012; Frintrop et al., 2010) and color (Zhou and

Hansen, 2016) for visualization.

However, there is less prior work that would quan-

tify the—possibly subtle—effects of the surrounding

on the actual visualization. A typical example is the

simultaneous contrast effect. Quite often this effect is

considered for color or luminance contrasts. For ex-

ample, the simultaneous color contrast has been con-

sidered in visualization techniques. This effect causes

the same color to be perceived differently depending

on its surrounding colors. Mittelst

adt et al. (2014)

developed an algorithm for the compensation of the

simultaneous color contrast by optimization of per-

ceived color. Here, the colors of a background and a

foreground texture are adjusted in an iterative process.

In each iteration, the background texture is evaluated

based on a color appearance model (iCAM) and ad-

justed accordingly. In subsequent work, Mittelst

adt

and Keim (2015) extended the approach to account

for interpersonal differences.

Another example is the compensation of per-

ceived motion in animated visualizations by Weiskopf

(2004). Differences in perceived speed are caused by

suboptimal motion perception for (almost) isolumi-

nant colors; and these differences are compensated by

data acquired through time-consuming user calibra-

tion. However, we are not aware of any previous vi-

sualization work that would compensate the perceived

direction of textures, which is the focus of our paper.

Researchers have studied the tilt illusion outside

the visualization context. Goodenough et al. (1979)

tackled it from the psychophysical side and tried to

ﬁnd the causes for errors in rod and frame tests. They

found that eye torsion and illusionary self-tilt do not

account for the total strength of the tilt-effect. In-

Compensation of Simultaneous Orientation Contrast in Superimposed Textures

stead, they suggested that simultaneous orientation

contrast is involved in the creation of errors in rod and

frame tests. Westheimer (1990) analyzed the effects

of distance, surrounding lines, time duration, and syn-

chronicity on orientation contrast for lines.

Research by Nothdurft (1991) shows that even

without overlaying images, orientation contrast can

create the perception of segmentation in ﬁelds of

lines. This might also be relevant for visualizations

where ﬁelds of arrows are superimposed on LIC im-

ages, as in our example in Section 5. Depending on

the difference on the perceived main direction of a

background and a foreground texture, the texture on

top could appear rotated and introduce areas of incon-

sistent ﬂow directions. Schwartz et al. (2009) detected

the patterns of tilt illusions in natural images with spa-

tially limited search ﬁelds and measured the perceived

tilt, but they did not perform any compensation. In

other research, it was shown that the spatial frequency

as well as the contrast has an inﬂuence of the per-

ceived tilt bias. To this end, Georgeson (1973) re-

ported the tilt bias for different spatial frequencies of

foreground and background texture. Durant and Clif-

ford (2006) studied the tilt effect by presenting fore-

ground and background asynchronously, while also

varying the contrast of both. Wei et al. (2013) mod-

eled simple cells as Gabor patches and used them to

identify line segments that seem to deform when lines

are crossing, but no compensation was performed.

Franceschiello et al. (2018) also used this model for

simple cells to derive a model that speciﬁcally com-

pensates Hering illusions.

In general, illusions, like the tilt illusion or il-

lusionary contours, are caused in the ﬁrst two lay-

ers (V1 and V2) in the visual cortex (Molotchnikoff

and Rouat, 2012; Carter, 2014). It was shown that

the receptive ﬁelds of so-called simple cells are in-

volved, which detect edges by overlapping receptive

ﬁelds and lateral inhibition. For our paper, we adopt

previous work and experiments in texture perception

and make them usable for visualization by deriving a

computational model for orientation compensation of

superimposed textures.

The superposition of visual elements, such as tex-

tures, plays an important role in visualization when-

ever there is more information to be shown than just

on a single 2D plot. A typical example is the combi-

nation of two surface displays (Bair and House, 2007;

Bair et al., 2009) or weaving of visual regions (Lu-

boschik et al., 2010). We are particularly interested in

the simultaneous display of multivariate or multiple

2D ﬂows in a single image (Kirby et al., 1999; Ur-

ness et al., 2006). For this, the overlay of two textures

is a useful and common approach since textures can

show ﬂow direction effectively. However, none of the

above previous papers considered simultaneous con-

trast effects in orientation perception.

3 METHOD

In this section, the compensation process for the si-

multaneous orientation contrast is described in more

detail. Our method relies on two textures as input:

one texture is a designated background texture, while

the other one is the foreground texture that is being

superimposed in order to provide, e.g., additional in-

formation at designated locations. The locations of

foreground textures are also an input for our method.

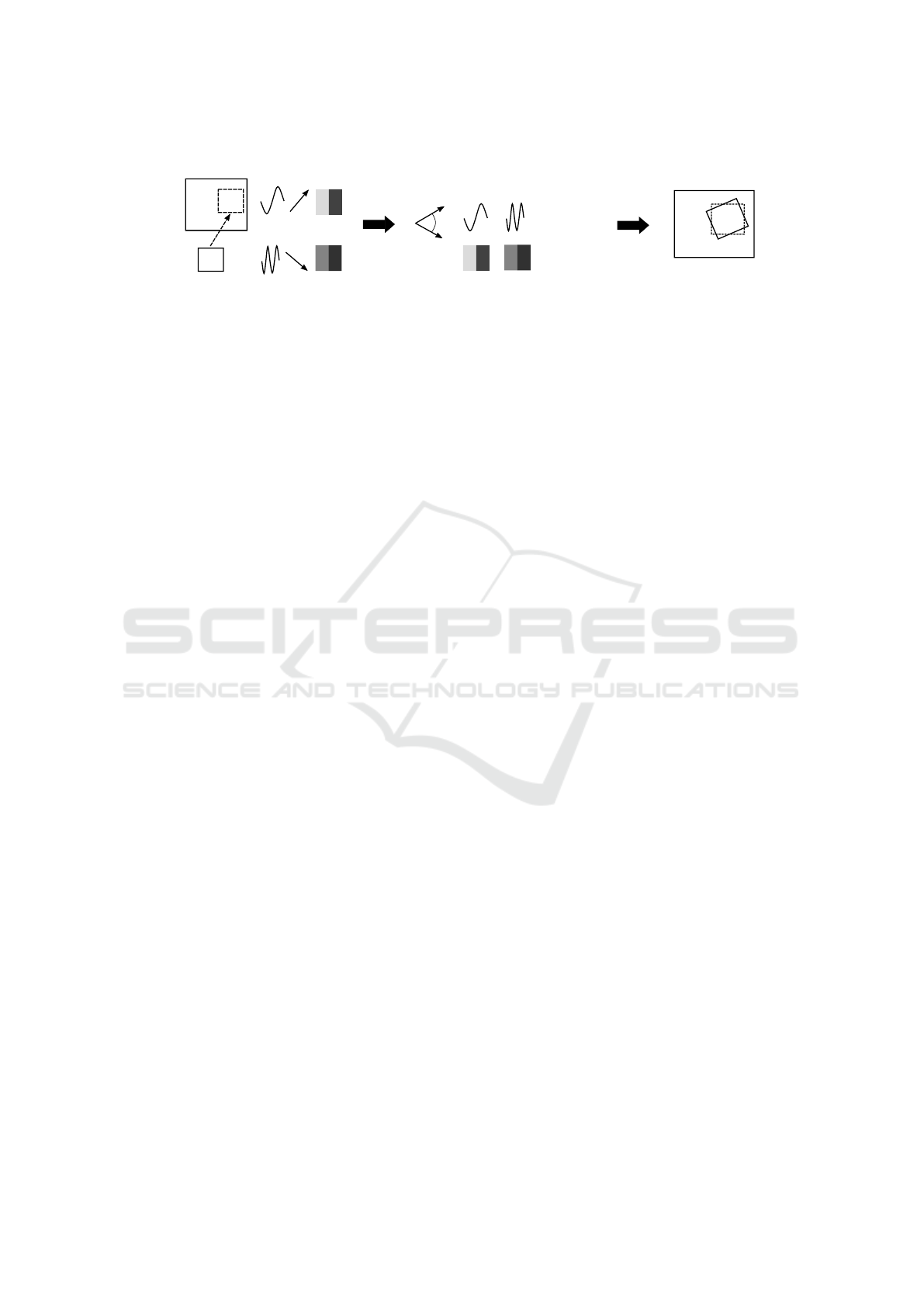
As depicted in Figure 3, the compensation pro-

cess consists of three parts: (1) input texture analysis

to retrieve characteristic values from the textures, (2)

computation of the tilt angle model that estimates per-

ceived orientation, and (3) the actual compensation of

the tilt bias by means of foreground rotation.

3.1 Input Texture Analysis

First, input textures have to be analyzed to perform

the compensation. Here, perceptually relevant char-

acteristic values are retrieved from the input textures:

direction, spatial frequency, and contrast. The con-

trast of the textures is deﬁned as the difference be-

tween the brightest and darkest texture point. We use

Gabor ﬁlters to retrieve frequency and direction in-

formation from the textures. These kinds of ﬁlters are

commonly used to imitate the frequency and direc-

tion perception in the human visual system (Palmer,

1999). Neurons and their associated receptive ﬁelds

in combination with lateral inhibition of neighboring

neurons form a pattern that is similar to that of Ga-

bor ﬁlters, which are generated by multiplying a 2D

sinusoidal function with a 2D Gaussian function or a

Hamming window. These ﬁlters are sensitive to the

direction and frequency deﬁned by a sinusoidal func-

tion.

Our computational model performs a convolution

of the input texture with these Gabor ﬁlters. The ﬁl-

tering result highlights edges that have properties sim-

ilar to those of the sinusoidal functions of the ﬁlters.

For our implementation, we create a ﬁlter bank for di-

rections between 0

◦

and 179

◦

, while the frequencies

are set to 2

cycles per degree with i ∈ 0, ..., 5 (assum-

ing a screen resolution of 1920 × 1200 and a view-

ing distance of 60 cm). This results in 1080 2D ﬁl-

ter responses. A sampling of the direction in 1

◦

steps

was performed to ensure that possible maxima are not

overlooked. Furthermore, the used tilt bias function

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

Texture analysis

Tilt angle model

Angle

Weights

= ω

frq

= ω

cont

Rotation

Figure 3: Steps for the compensation of the simultaneous orientation contrast. First, characteristic values are retrieved from

the foreground (FG) and background (BG) textures: direction, spatial frequency, and contrast. Then, the adjusted tilt bias

angle is determined; the original tilt bias angle is modiﬁed by taking into a count weights for the frequency and contrast. In

the ﬁnal step, the foreground object is rotated based into the opposite direction of the adjusted tilt bias.

was also derived with the same sampling. We aggre-

gate the scalar values of each such response to get

a single number that represents the total strength of

each ﬁlter. We used the default parameter for the spa-

tial frequency bandwidth (1 octave) that determines

the cutoff of the ﬁlter response as frequency content

in the input image doubles compared to the preferred

frequency. The default parameter is also used for the

spatial aspect ratio (0.5), which controls the ellipticity

of the Gaussian envelope. To make these representa-

tive scalar values comparable, they are normalized by

the size of their corresponding ﬁlter. The minimum

size of the ﬁlters was 53 × 53 pixels and the maxi-

mum size 209 × 209 pixels. Furthermore, to compute

the dominant direction and frequency, we need to ag-

gregate the previous results in two ways: we combine

all ﬁlter responses for each direction and all values

for each frequency. Figure 5 shows the result of such

a ﬁlter process for the ﬁrst case. We determine pri-

mary directions and frequencies based on the maxima

of the normalized responses.

It is important to note that Gabor ﬁltering leads to

a spatially dependent computation of the characteris-

tic values for the texture, i.e., angle, spatial frequency,

and contrast are not necessarily constant for the tex-

ture but may vary from location to location. While

many of the stimuli used in perception research may

have constant characteristic values across the whole

image, realistic examples from scientiﬁc visualization

will usually be spatially dependent.

3.2 Tilt Angle Model

In the second part, these characteristic values are used

to estimate the perceived angle tilt at the respective

location, i.e., the characteristic values are accessed

at the position where the foreground and background

textures coincide.

To this end, we adopt ﬁndings from previous stud-

ies and models from vision research and cast them

into a computable model. We determine an adjusted

tilt bias angle

bias

by multiplying the original tilt bias

angle α

bias

with weights for the inﬂuence of the spa-

tial frequency ω

frq

and the contrast ω

cont

bias

= α

bias

· ω

frq

· ω

cont

(1)

The values of α

bias

, ω

frq

, and ω

cont

are computed by

utilizing three functions that are based on previously

conducted studies about the effects of the tilt bias with

respect to differences of directions, frequencies, and

contrasts. The ﬁrst function approximates the original

tilt bias angle. The directional bias is deﬁned on the

interval [0;180] and is based on experimental results

of Schwartz et al. (2009).

We deﬁned the other two functions piecewise and

use them as weights for the inﬂuence of spatial fre-

quency (Georgeson, 1973) and contrast (Durant and

Clifford, 2006). Figure 4b shows how the inﬂuence

of frequency is deﬁned on [−3;0] and [0; 2] separately.

Weights for contrast are available for the input ranges

[−100;0] and [0; 100] (Figure 4c). They indicate that

the difference of frequency or contrast of the fore-

ground and background texture inﬂuence the effect of

tilt bias.

The inﬂuence of spatial frequency differences be-

tween foreground and background textures has an ex-

ponential drop-off in both positive and negative direc-

tions. For contrast differences, on the other hand, the

dependency of the weight function is approximately

linear for positive and negative values. Note that only

Georgeson (1973) conducted an experiment to explic-

itly measure the effect of spatial frequency, while Du-

rant and Clifford (2006) were interested in the after

effects of tilt illusions (delayed presentation of back-

ground or foreground texture). This included also the

simultaneous presentation of both textures, resulting

in four measurements that were used to approximate

the contrast weight function. Effects of tilt bias under

different conditions for artiﬁcial stimuli are depicted

in Figure 6 (images in the top row).

3.3 Foreground Rotation

In the last part,

bias

is ﬁnally used to compensate for

the tilt bias. We rotate the foreground texture around

Compensation of Simultaneous Orientation Contrast in Superimposed Textures

Diﬀerence between angles in degrees

-2.5

-2

-1.5

-1

-0.5

0.5

1.5

2.5

Tilt bias in degrees

20 40 60 80 100

120

140 160 1800

(a) Directional bias

-3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2

Spatial frequency background to foreground in octaves

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Weight

(b) Frequency weight function

-100 -80 -60 -40 -20 0 100

Background contrast relative to foreground contrast in %

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Weight

20 40 60 80

Figure 4: Bias functions used in our tilt angle model: (a) Approximated function of the measured tilt bias of Schwartz et al.

(2009); the blue part corresponds to positive angular differences in their work, magenta to negative differences. (b) Weights

for the detected spatial frequency of the foreground and the background texture; the weight is one if spatial frequency has

an inﬂuence, and zero if not; based on Georgeson (1973). (c) Weight for the contrast difference between the foreground and

background texture; the weight is one if the contrast has an inﬂuence, and zero if not; based on Durant and Clifford (2006).

(a) Superimposed images

0 20 40 60 80 100 120 140 160 180

0.5

1.5

2.5

#10

Background

Foreground

Combined

Filter direction

Filter response

(b) Responses of ﬁlters

Figure 5: Result of applying a Gabor ﬁlter bank on a super-

imposed image (a). The plot (b) shows the responses of the

ﬁlters in tested direction for the foreground, background,

and superimposed image. Maxima indicate the main direc-

tions.

its center point by the opposite of the adjusted tilt bias

angle.

This approach works quite well as long as the

foreground object covers a rather small area so that

the spatial coincidence between foreground and back-

ground can be uniquely determined. Furthermore, a

small object may just be rotated as a whole with-

out further considerations to be made. We leave the

extension of our method to large foreground objects

for future work: it may have to include nonlinear de-

formations of the foreground texture to accommodate

spatially varying tilt angles.

4 ARTIFICIAL STIMULI

During the development and reﬁnement of our com-

pensation method, we used a series of test images to

qualitatively rate the compensation. One series of test

images contained alternating black and white bars,

where both foreground and background texture had

a rectangular shape. Corners and edges of the fore-

ground textures might be useful for the visual sys-

tem to perform some kind of implicit compensation.

Hence, we used circular foreground textures in other

tests. Additionally, we employed sinusoidal functions

to generate striped textures. Related work often uses

such kinds of stimuli in the context of measuring the

tilt bias.

We went through several trial-and-error cycles to

detect and address problems with our preliminary

compensation model. The ﬁlter responses are one ex-

ample. At ﬁrst, they were noisy and it was not pos-

sible to detect a maximum, since the sizes of ﬁlters

were not considered. Therefore, we introduced a nor-

malization of ﬁlter responses.

Initial tests with textures of the same contrast

and spatial frequency yielded good results. However,

the method produced an overcompensation when we

changed the spatial frequency between foreground

and background. As described in the previous sec-

tion, weighting the compensation by the differences

in spatial frequency addressed this issue. For the same

reasons, a weight for the contrast difference was in-

troduced. We were able to prevent overcompensation

with these countermeasures. Results of successful

compensations for simple cases are depicted in Fig-

ure 6 (images on the bottom).

The test stimuli used so far are based on frequen-

cies and local contrasts that are constant across the

image. To further demonstrate the effects of tilt bias

and the results of our compensation method, we cre-

ated images that contain a broad range of frequency,

direction, and local contrast changes by using a J

ahne

test pattern (J

ahne, 2004). In such images, the spa-

tial frequency increases continuously from the center

until reaching a deﬁned maximum at the outer bor-

der. That makes the patterns point-symmetric and al-

lows for tests with a continuous range of directions.

So far, the stimuli have always been monochrome.

We continue without introducing color and calculate

the brightness of each point in the image using the

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

(a) No differences (b) Contrast difference (c) Frequency difference (d) Transparency

Figure 6: The tilt bias is inﬂuenced by the spatial frequency and contrast difference of the foreground and the background

texture. The effect is also present if transparency is used. This is shown in the top row. The bottom row depicts the same

images under the same conditions and after the compensation. In the bottom images of (a) and (d), the compensation was

not affected by the contrast and frequency weight. In (b) and (c), the weights reduced the amount of compensation. Viewing

distance about 20 cm.

function

g(x) =

· sin



|x|





tanh



− |x|





(2)

Here, x is the vector offset from the image center, |x|

the distance from the image center, r

is the maxi-

mum radius of the pattern in the image, and k

spec-

iﬁes the maximum instantaneous frequency. Further-

more, tanh can be seen as an approximation to a step

function, where r

is the location of the step and ω

is the width of the transition. The following parame-

ters were used to generate the test patterns: k

= 400, and ω = 40.

Figures 7 and 8 only use the lower half of the

ahne pattern, due to its symmetry. Arrows were

placed on a radial line to demonstrate the effects of

varying frequency and constant perceived direction of

the background texture. Furthermore, by arranging

arrows on circular paths, the impact of changing per-

ceived direction of the background texture and a con-

stant spatial frequency are shown. Figure 7a shows

the original image where some arrows seems to be ro-

tated by several degrees. This effect is compensated

in Figure 7b.

5 MULTIFIELD FLOW

VISUALIZATION

So far, our method was demonstrated only for artiﬁ-

cial stimuli. In this section, results of a compensation

for an example from scientiﬁc visualization are pre-

sented. In such a scenario, foreground textures might

be glyphs or other small graphical elements that are

superimposed over a background texture to provide

additional localized information.

We discuss a speciﬁc, yet typical example from

scientiﬁc ﬂow visualization: the simultaneous plot of

two 2D vector ﬁelds in a single image (Urness et al.,

2006). One of the vector ﬁelds may be visualized by

arrow glyphs that yield a coarse representation. A

complementary visualization is chosen for the other

vector ﬁeld and shown as background texture. Here,

we use a dense texture-based method in the form of

line integral convolution (LIC) (Cabral and Leedom,

1993). This method allows us to visualize ﬁne de-

tails of vector ﬁelds that might be hard to detect in

the coarse grids of glyphs. For more background on

texture-based ﬂow visualization, we refer to the sur-

vey paper by Laramee et al. (2004).

In such an example use case, the simultaneous ori-

entation contrast between the LIC background and the

glyph foreground can result in a tilt illusion. Mis-

Compensation of Simultaneous Orientation Contrast in Superimposed Textures

(a) Without compensation

(b) With compensation

Figure 7: Arrows are superimposed on a J

ahne test pattern. On the left side, for each arrow position, the frequency is

changing and the direction of the background texture is constant. On the right side, arrows are arranged on two circles leading

to a constant frequency and a varying direction. In a viewing distance of about 20 cm, some arrows seem to be tilted in (a).

This effect is compensated in (b). In (b), eight arrows are rotated clockwise (minimum 0.51

◦

, maximum 0.86

◦

, and average

0.69

◦

) and ﬁve arrows are rotated counterclockwise (minimum 0.36

◦

, maximum 2.28

◦

, and average 1.38

◦

perceptions in the orientation of superimposed ar-

rows can then lead to false readings of ﬂow direc-

tion. Therefore, compensation is crucial for a correct

interpretation of the vector ﬁelds. Figure 9a shows

an example without compensation. Here, an analyst

might have selected a region that is of interest and

manually placed arrows. For this example, we as-

sume that all glyphs should be perfectly horizontal.

Tilt bias from orientation contrast creates the appear-

ance of the lower three arrows going in slightly differ-

ent directions, while the upper ﬁve are not affected.

After compensation, all glyphs appear horizontal in

Figure 9b. The proposed method works on each ar-

row individually, i.e., the glyphs are rotated against

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

Figure 8: Arrows are superimposed on a J

ahne test pattern.

They are arranged on two circles, leading to a constant fre-

quency and a varying direction. When texture is rendered

with color, the tilt effect is less pronounced than in Fig-

ure 7a.

the tilt angle derived at the respective location on the

LIC background.

6 DISCUSSION

Our tests with different artiﬁcial stimuli show promis-

ing results and we were able to demonstrate that our

method can be applied in realistic scenarios from ﬂow

visualization. However, there are a few topics that re-

quire further investigation to improve the compensa-

tion and to test its validity.

The ﬁrst issue concerns the weight functions. Our

frequency weight seems to be reliable, since it is

based on the results of an experiment that speciﬁcally

tested the effects of frequency on the tilt bias. This is

not the case for the contrast weight. Here, we were

only able to use four measurements of an experiment

that measured the after effects of tilt illusions in the

case of a simultaneous appearance of fore- and back-

ground texture. In both cases, it would be beneﬁcial

to verify the results of the frequency experiment and

to improve the contrast weight function by conduct-

ing experiments with a more appropriate sampling of

the parameter space.

We based our method on the tilt bias of Schwartz

et al. (2009), who used measurements from Wes-

theimer (1990). In this original work, the author

conducted experiments using only vertically oriented

stimuli, but states on page 1914 that “there is no rea-

(a) Image without compensation

(b) Image with compensation

Figure 9: Arrows superimposed on background LIC tex-

tures that depict a vector ﬁeld. The three arrows at that bot-

tom of (a) are affected by the tilt illusion at a viewing dis-

tance of about 20 cm. In the compensated image (b), they

appear horizontal. In (b), four arrows are rotated clockwise

(0.76

◦

, 2.47

◦

, 0.08

◦

, and 1.71

◦

) and four arrows are rotated

counterclockwise (2.31

◦

, 0.96

◦

, 1.42

◦

, and 2.23

◦

son to believe that the ﬁndings [. . . ] would not apply

to other orientations”. However, viewing our test im-

ages vertically or horizontally can lead to the percep-

tion of varying degrees of the tilt illusion, depending

on the observer. This suggests the existence of an ad-

ditional parameter to the tilt effect and requires further

investigation.

Another aspect that is not addressed yet is the im-

pact of color on the tilt illusion. This was subject of

previous research (Clifford et al., 2003a; Lovegrove

and Over, 1973; Clifford et al., 2003b), where mea-

surements were taken with respect to color signals (L,

M, and S cone signals derived from RGB images) and

luminance. Color contrast can reduce the tilt effect, as

shown in Figure 8. Here, the tilt effect is weaker than

in Figure 7a. In the best case, Equation 1 might sim-

ply be extended by additional weight terms for the

inﬂuence of color. In the worst case, there could be

dependencies between color, contrast, and frequency

Compensation of Simultaneous Orientation Contrast in Superimposed Textures

that would need to be modeled.

The next topic that could be of relevance is to in-

corporate Gestalt laws into the compensation process.

For instance, horizontally aligned arrows on a virtual

horizontal line are less inﬂuenced by the tilt bias ac-

cording to our observations of initial tests. The human

visual system relies on certain expectations or makes

assumptions in the presence of geometric structures.

This issue is even more pronounced for large fore-

ground objects that may require nonlinear and spa-

tially dependent deformations for tilt compensation.

A related topic is the estimation of the dominant

frequency and direction. As described in Section 3,

the maximum response for direction and frequency

is currently utilized. However, Figure 5b shows that

there might be several distinct local maxima that

could be considered for compensation, in particular,

for large textures.

7 CONCLUSION

In this paper, we addressed the topic of visual illu-

sion effects; more speciﬁcally, the tilt illusion caused

by simultaneous orientation contrast. It is a relevant

topic within the ﬁeld of visualization, as it can occur

when overlaying textures or even in line renderings.

We have proposed an approach to compensate for

the tilt illusion in case of superimposed textures. This

is of practical relevance for visualization since su-

perimposed textures are commonly used for multi-

ﬁeld and other overlaid visualizations. To perform the

compensation, information about directions, frequen-

cies, and contrast are extracted from the input images.

Based on the results of prior experiments on the ef-

fects of the tilt illusion, we have approximated weight

functions for frequency and contrast, which are used

to avoid overcompensation. We demonstrate the re-

sults of our method for artiﬁcial stimuli and a realistic

scenario from ﬂow visualization.

In our example cases, the results are promising.

However, a misinterpretation of the visualization is

only prevented for speciﬁc stimuli, render sizes, view-

ing distances and subjects; all of which we cannot

control. While someone looks at the digital version

of this paper on a screen, someone else prints it with

or without scaling, holds it nearer to the eyes while

reading, etc. In short, there are still a number of top-

ics that need to be addressed. One of them is that our

efforts resulted in a compensation success that varies

between each individual person. More work is needed

to explore the effects of simultaneous orientation con-

trast. Our method might beneﬁt from additional ex-

periments to reﬁne the weight functions, the incorpo-

ration of color or Gestalt laws, and, ﬁnally, the han-

dling of secondary maxima in the weighting of per-

ceived directions and frequencies.

ACKNOWLEDGEMENTS

We would like to thank the German Research Foun-

dation (DFG) for ﬁnancial support within project B01

of SFB/Transregio 161.

REFERENCES

Bair, A. and House, D. H. (2007). Grid with a view: opti-

mal texturing for perception of layered surface shape.

IEEE Transactions on Visualization and Computer

Graphics, 13(6):1656–1663.

Bair, A., House, D. H., and Ware, C. (2009). Factors inﬂu-

encing the choice of projection textures for displaying

layered surfaces. In Proceedings of the 6th Symposium

on Applied Perception in Graphics and Visualization

(APGV), pages 101–108.

Becker, R. A., Eick, S. G., and Wilks, A. R. (1995). Visual-

izing network data. IEEE Transactions on Visualiza-

tion and Computer Graphics, 1(1):16–28.

Cabral, B. and Leedom, L. C. (1993). Imaging vector ﬁelds

using line integral convolution. In Proceedings of the

SIGGRAPH Annual Conference on Computer Graph-

ics and Interactive Techniques, pages 263–270.

Carter, R. (2014). The Brain. Dorling Kindersley Ltd.

Clifford, C. W., Pearson, J., Forte, J. D., and Spehar, B.

(2003a). Colour and luminance selectivity of spatial

and temporal interactions in orientation perception.

Vision Research, 43(27):2885 – 2893.

Clifford, C. W. G., Spehar, B., Solomon, S. G., Martin,

P. R., and Qasim, Z. (2003b). Interactions between

color and luminance in the perception of orientation.

Journal of Vision, 3(2).

Durant, S. and Clifford, C. W. G. (2006). Dynamics of the

inﬂuence of segmentation cues on orientation percep-

tion. Vision Research, 46(18):2934–2940.

Franceschiello, B., Sarti, A., and Citti, G. (2018). A neu-

romathematical model for geometrical optical illu-

sions. Journal of Mathematical Imaging and Vision,

60(1):94–108.

Frintrop, S., Rome, E., and Christensen, H. I. (2010). Com-

putational visual attention systems and their cognitive

foundations: a survey. ACM Transactions on Applied

Perception, 7(1):6:1–6:39.

Georgeson, M. A. (1973). Spatial frequency selectivity of a

visual tilt illusion. Nature, 245:43.

Goodenough, D. R., Oltman, P. K., Sigman, E., Rosso, J.,

and Mertz, H. (1979). Orientation contrast effects in

the rod-and-frame test. Perception & Psychophysics,

25(5):419–424.

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

Healey, C. G. and Enns, J. T. (2012). Attention and visual

memory in visualization and computer graphics. IEEE

Transactions on Visualization and Computer Graph-

ics, 18(7):1170–1188.

ahne, B. (2004). Practical Handbook on Image Process-

ing for Scientiﬁc and Technical Applications, Second

Edition. CRC Press, Inc.

Kirby, R. M., Marmanis, H., and Laidlaw, D. H. (1999).

Visualizing multivalued data from 2D incompressible

ﬂows using concepts from painting. In Proceedings of

the IEEE Visualization Conference, pages 333–340.

Laramee, R. S., Hauser, H., Doleisch, H., Vrolijk, B., Post,

F. H., and Weiskopf, D. (2004). The state of the art

in ﬂow visualization: dense and texture-based tech-

niques. Computer Graphics Forum, 23(2):203–222.

Lovegrove, W. and Over, R. (1973). Colour selectivity in

orientation masking and aftereffect. Vision Research,

13(5):895–901.

Luboschik, M., Radloff, A., and Schumann, H. (2010). A

new weaving technique for handling overlapping re-

gions. In Proceedings of the International Conference

on Advanced Visual Interfaces (AVI), pages 25–32.

Mittelst

adt, S. and Keim, D. A. (2015). Efﬁcient contrast ef-

fect compensation with personalized perception mod-

els. Computer Graphics Forum, 34(3):211–220.

Mittelst

adt, S., Stoffel, A., and Keim, D. A. (2014). Meth-

ods for compensating contrast effects in information

visualization. Computer Graphics Forum, 33(3):231–

240.

Molotchnikoff, S. and Rouat, J., editors (2012). Visual Cor-

tex - Current Status and Perspectives. InTech.

Nothdurft, H. (1991). Texture segmentation and pop-

out from orientation contrast. Vision Research,

31(6):1073–1078.

Palmer, S. E. (1999). Vision Science: Photons to Phe-

nomenology. MIT Press.

Schwartz, O., Sejnowski, T. J., and Dayan, P. (2009). Per-

ceptual organization in the tilt illusion. Journal of Vi-

sion, 9(4):19–19.

Urness, T., Interrante, V., Longmire, E., Marusic, I.,

O’Neill, S., and Jones, T. W. (2006). Strategies for

the visualization of multiple 2D vector ﬁelds. IEEE

Computer Graphics and Applications, 26(4):74–82.

Ware, C. (2012). Information Visualization: Perception for

Design. Morgan Kaufmann, third edition.

Wei, H., Ren, Y., and Li, B.-M. (2013). A collaborative

decision-making model for orientation detection. Ap-

plied Soft Computing, 13(1):302–314.

Weiskopf, D. (2004). On the role of color in the percep-

tion of motion in animated visualizations. In Proceed-

ings of the IEEE Visualization 2004 Conference, pages

305–312.

Westheimer, G. (1990). Simultaneous orientation con-

trast for lines in the human fovea. Vision research,

30(11):1913–1921.

Zhou, L. and Hansen, C. D. (2016). A survey of colormaps

in visualization. IEEE Transactions on Visualization

and Computer Graphics, 22(8):2051–2069.

Compensation of Simultaneous Orientation Contrast in Superimposed Textures