Energy-Based Visualization of 2D Flow Fields

Karsten Hanser, Stefan Meggendorfer, Peter H¨ugel, Florian Fallenb¨uche l, Haﬁz Muhammad Fahad

and Filip Sadlo

IWR, Heidelberg University, Im Neuenheimer Feld 205, H ei delberg, Germany

sadlo@uni-heidelberg.de

Keywords:

Flow Visualization, Bernoulli’s Principle, Energy Conversion.

Abstract:

In this paper, we present a novel approach for energy-based ﬂow visualization. Inspired by Bernoulli’s prin-

ciple, which is limited to steady inviscid ﬂow, we derive a set of energies whose sum is conserved along

pathlines in 2D time-dependent viscous ﬂow. We present an interactive approach for visual analysis based on

these quantities, as well as a compact color-coded representation. This enables effective analysis of energy

conversion along selected pathlines, as well as its spatial coherence. We exemplify the util ity of our approach

using results from computational ﬂuid dynamics and ﬂow in elastic porous media.

1 INTRODUCTION

Many problems in science and engineering require

vector ﬁeld rep resentations. A prominent example are

ﬂow problems, which are often addressed by compu-

tational ﬂuid dynamics (CFD) by means of numerical

solution of the Navier–Stokes (NS) equations.

There exists a wide spectrum of ﬂow visualization

techniques for analyzing vector ﬁeld s f rom CFD. On

the one hand, there are geometric approaches, such as

arrow glyphs a nd streamlines, which show the over-

all structure of a ﬂow, but fail at revealing underlying

physical mechanisms. On the other h a nd, there are

physically based approac hes, such as the λ

vortex

criterion, which often involve derivatives of the vec-

tor ﬁelds and sometimes additional q uantities such as

the pressure ﬁeld. Either way, most ﬂow visualization

techniques aim at a simpliﬁed representation of ﬂow,

often providing a “segmentation” into region s of si-

milar behavior or extraction of respective bou ndaries.

In this paper, we investigate the analysis of ﬂow

ﬁelds with regard to their immanent energies. We pre-

sent an approach that, on the one hand, enab les the

analysis of energy conversion in ﬂows for a better un-

derstandin g of the involved phy sical mechan isms. On

the other hand, our approach enables the identiﬁcation

of regions of physically similar b e havior with respect

to these energies. Our approach is in spired by Ber-

noulli’s principle, which, however, is ap plicable only

to inviscid stationary ﬂow. We extend it to viscous

time-dependent ﬂow, and derive from it a technique

for interactive visual analysis of ﬂow ﬁelds.

The contributions of this paper include:

• a set of energy quantities whose sum is conserved

along trajector ies, up to solver-induced err or,

• an approach to quantify that solver-induced e rror

and relate it to our quantities,

• an interactive exploration approach enabling de-

tailed analysis of energy conversion and the phy-

sical mechanisms along trajectories, and

• an approach to reveal the regions of qualitatively

similar behavior with respect to energy dynamics.

2 RELATED WORK

The most closely related work in the ﬁeld of ﬂuid

dynamics is Bernoulli’s Hydrodynamica (Bernou lli,

1738), which presents the concept later denoted Ber-

noulli’s principle, detailed in Section 3.

Previous work in the context of energy -based ﬂow

visualization includes proper orthogonal decomposi-

tion for separating different scales with respect to

energy (Pobitzer et a l., 2011), and a graph b ased ap-

proach , which focuses on the conversion and trans-

portation of internal and kinetic energy (Fernandes

et al., 2017). The focus of our work, in contrast, is

on decomposition, transport, and conversion of diffe-

rent energy types along pathlines.

Less closely re la ted are physically based criteria,

such as λ

(Jeong and Hussain, 1995 ) for vortex ex-

traction, and interaction betwe en shear ﬂow and vorti-

250

Hanser, K., Meggendorfer, S., Hügel, P., Fallenbüchel, F., Fahad, H. and Sadlo, F.

Energy-Based Visualization of 2D Flow Fields.

DOI: 10.5220/0007359602500258

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 250-258

ISBN: 978-989-758-354-4

ces (Schafhitzel et al., 2011; Sadlo et al., 2006). Other

approa c hes emp loy physical principles for visualizing

advection properties, such as schlieren ﬂow visuali-

zation (Brownlee et al., 2010) and virtual rheoscopic

ﬂuids (Barth a nd Burns, 2007).

3 BERNOULLI’S PRINCIPLE

Bernoulli presented in his early work on hydrodyna-

mics (Bernoulli, 1738) his prin ciple, which r elates ki-

netic, pressure, and potential energy. Assuming invis-

cid steady ﬂow, i.e., ﬂow that has zero viscosity and

no time dependency, his p rinciple states th a t energy is

conserved along streamlines, e.g., if velocity increa-

ses along a streamline, it implies a respective decrease

of pressure energy and/or potential energy. In other

words, it describes the tr ansformatio n of energy along

streamlines in ﬂuid ﬂow.

A streamline

(s) := x



(σ),t



dσ (1)

is obtain e d by solving a n initial value problem (IVP)

in a single time step t of the (potentially unsteady ) n -

dimensional vector ﬁeld u(x,t) deﬁned on a domain

Ω ⊆ R

, with x ∈ Ω and u ∈ R

. That is, one starts the

integration at a seed point x

∈ Ω with ξ

(0) = x

and in tegrate s a curve tangential to the vector ﬁeld

u(x,t) for a given duration s, keeping physical time t

ﬁxed. On the other hand, a p athline

(t) := x

u(ξ

(τ),τ) dτ (2)

is obtained by solving an IVP “including” physical

time, i.e., by starting integration at a seed point x

and

seed time t

, and integrating along th e time-dependent

vector ﬁeld u(x,t), that is, the integration parameter

is physical time t. Notice, that in steady vector ﬁelds,

streamlines and pathlines are identical.

According to Ber noulli’s principle, along such

a streamline in steady inviscid ﬂow, i.e., at each

point x = ξ

(s), the sum of kinetic energy

(x,t) :=

ku(x,t)k

, (3)

pressure energy

(x,t) :=

p(x,t)

, (4)

and potential energy

(x) := gh(x), (5)

stays con stant, i.e., E

(x,t) + E

(x) =

const., with pressure p(x,t), density of the ﬂuid ρ,

h(x) the height of point x, and gravity g.

(a) u(x,t) (b) E

(x,t)

(x,t) (d) E

(x,t)

(e) (f) ε(x,t)

Figure 1: Inviscid steady ﬂow past a back-facing step.

(a) Velocity magnitude (low-black; high-yellow), with stre-

amlines (white). (b) Kinetic energy E

(x,t) (low-black;

high-red) is not constant along streamlines, and neither is

pressure energy E

(x,t) (c) (low-black; high-blue). (d) To-

tal energy E

(x,t) = E

(x,t)+E

(x,t), however, is constant

up to small deviations. Isolines (red) of E

(x,t) and stream-

lines (white and gray) (e) deviate slightly due to inaccura-

cies of the simulation and derivative estimation, which we

quantify as solver error ε(x,t) (f) (0-black; 0.1-magenta).

Figure 1 illustrates the principle, at the example of

a simple inviscid (ν = 0) steady 2D ﬂow simulation

obtained with the G erris ﬂow solver (Popinet, 2007).

In this example (and the following), gravity has been

set to zero for simulation, resulting in zero potential

energy everywhere, i.e., there is only conversion be-

tween kinetic and p ressure energy here. Notice, that

the focus of this paper is ﬂow visualization, i.e., th e

input to our technique is the simulated ﬁelds u(x,t),

p(x,t), as well es density ρ and viscosity ν.

It is apparent that E

(x,t) (Figure 1(b)) is not uni-

form along the streamlines, and that neither is E

(x,t)

(Figure 1(c)). Nevertheless, their sum, which we de-

note total energy E

(x,t) := E

(x,t) + E

(x,t), is al-

most constant (Figure 1 (d)), as can be seen when

comparing the streamlin es to isolines of E

(x,t) (Fi-

gure 1(e)). The small deviations between stre amlines

and isolines of E

stem f rom inaccuracies of the simu-

lation and d erivative estimation during visualization.

To assess suc h inaccura cies, we derive a quan-

tity which we denote solver error ε(x,t) (Figure 1(f)).

Energy-Based Visualization of 2D Flow Fields

251

The numerical solver aims at solving the NS equation

Du(x,t)

= −

∇p(x,t)

+ ν∆u(x,t), (6)

with material derivative

Du(x,t)

∂u(x,t)

∂t

+ (∇u(x,t))u(x,t), (7)

density ρ, Laplacian ∆, an d kinematic viscosity ν.

However, due to in accuracies (non z ero solver resid u-

als, as well as potential inconsistencies between de -

rivative estimation in the solver and estimation du-

ring our visualization process), the left hand side is in

general not identical to the right hand side when the

terms of Equation 6 are computed from the simulated

ﬁelds u(x,t) and p(x,t). This motivates us to obtain ε

as the discrepancy between the two sides, i.e.,

ε(x,t) :=



Du(x,t)

∇p(x,t)

− ν∆u(x,t)



, (8)

normalized by µ, which is the average of the magni-

tude of Du(x,t)/Dt over the domain Ω:

µ :=

vol(Ω)

Ω



Du(x,t)



dΩ, (9)

with vol(Ω) being the volume (a rea) of the domain.

4 METHOD

The majority of ﬂuid dyn a mics pro blems involves

time dependency and necessitates nonzero viscosity,

which strongly limits the applicability of Bernoulli’s

principle. Our main aim in this work, is to ad-

dress both of these issues, i.e., to derive a concept

that en ables energy-based ﬂow visualization in time-

dependent viscous ﬂow. Where a s we formulate our

approa c h here for 2D ﬂows, its extension to 3D dom-

ains would be straightforward in large p arts.

4.1 Derivation of Energies

Let us start with a steady CFD simula tion of a ﬂow

around an obstacle. Again, gravity g was set to

zero for simulation, but in this case, the modeled

ﬂuid has nonzero kinematic viscosity ν, leading to

a wake behind the obstacle exh ibiting low veloci-

ties (Figure 2(a)). The kinetic energy ﬁeld E

(x,t)

(Figure 2(c)) and the pressure energy E

(x,t) (Fi-

gure 2(e)) can be easily computed according to Equ a-

tions 3 and 4 using the simula te d ﬁelds u(x,t) and

p(x,t). However, if these energies ar e summed up to

obtain the total energy E

(x,t), the resulting ﬁeld (Fi-

gure 2(g)) is not constant along streamlines, in con-

trast to the inviscid ca se from Section 3 (Figure 1(d)).

The rea son for this discr e pancy is the nonz ero vis-

cosity, which is violating the assumption s of Ber-

noulli’s principle. That is, velocity undergo e s diffu-

sion due to the viscosity (according to the rightmost

term ν∆u(x,t) in Equation 6). In other words, the

internal friction in the ﬂow “ tries to minimize” the

gradient of the velocity ﬁeld and thu s causes kinetic

energy to “diffuse”. The direction of this diffusion is

not constrained to directions along streamlines, and

therefore E

is, in general, no t constant along a stre-

amline in viscous ﬂow.

An interesting observation is, however, that since

the Navier–Stokes eq uation (Equation 6) represents

the materia l derivative of velocity u(x,t), it descri-

bes the acceleration of a ﬂuid parcel at location x and

time t. On the other hand, Bernoulli’s pr inciple invol-

ves the variation of k inetic energy E

along a stream-

line. The difference of kinetic energy be tween two

points s

and s

on such a strea mline has to equal

the total work between these points, and sin ce work

equals the integral of force along a path, we obtain

,t) = E

,t) +

Du(ξ

(s),t)

·ds, (10)

with x

= ξ

) and x

= ξ

) being the re-

spective positions on the streamline, and line ele-

ment ds := u(ξ

(s),t)ds. Notice th at E

is a speciﬁc

energy in Berno ulli’s formulation, and therefore we

do not need to multiply the material derivative with

density ρ to obtain E

,t). Notice also that since

pathlines and streamlines are ide ntical in steady ﬂow,

and since the Navier–Stokes equation also holds for

unsteady ﬂow, we can replac e in Equation 10 the stre-

amline ξ

by a pathline ξ

in this example (and in

general, as we will see la ter).

Altogether, Equation 10 provides an alternative

approa c h for computing E

(x,t), i.e., at time t, we

can start a pathline at point x, integrate it bac kward

in time (in reverse ﬂow direction) until time t

(with

< t), and evaluate th e line integral accordingly:

(x,t) = C

Du(ξ

x,t

(τ),τ)

·dτ

τ, (11)

with line element dτ

τ := u(ξ

x,t

(τ),τ)dτ, and pathline

x,t

(τ) := x +

u(ξ

x,t

(τ),τ) dτ (12)

with τ < t. C

is an integration constant, which needs

to be chosen. Notice that we denote our result in tegra-

ted kinetic energy

, in contrast to Bernoulli’s kinetic

energy E

Figure 2(d) shows

(x,t) for C

= 0, with re-

verse integration duratio n of 100 seconds. For this

integration duration, the pathlines either reach th e in-

let at the left boundary, or stay in the recirculation

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

252

(a) u(x,t)

(b)

(x,t)

(d)

(x,t)

(e) E

(x,t)

(f)

(x,t)

(g) E

(x,t)

(h)

(x,t)

Figure 2: Steady viscous ﬂow around obstacle, from left to right. (a) Velocity u(x) together with streamlines (w hit e). (b) In-

tegrated diffusion energy

(x), according to Equation 15, with two selected streamlines (gray). (c) Kinetic energy E

(x),

computed locally according to Equation 3. ( d) Integrated kinetic energy

(x) (Equation 11). (e) Pressure energy E

(x)

and (f) integrated pressure energy

(x,t) (Equation 14). (g) Total energy E

(x) is not conserved along streamlines, whereas

integrated total energy

is, i.e.,

= const. is our counterpart to Bernoulli’s principle for unsteady viscous ﬂow.

region right to the obstacle. Since the in le t velo-

city is constan t along the inlet, Figure 2(d) is, up

to an additive constant, identical to Figure 2(c ), ex-

cept for the region behind the obstacle. The reason

why

(x,t) in that region h as values different from

(x,t), is that setting C

= 0 there is not consistent

with setting C

= 0 at the inlet. While one co uld set

= E

(ξ

−

x,t

)), i.e., to the value of E

at the “up-

stream end” of the pathline, such an evaluation cannot

be ac hieved for our integrated diffusion energy intr o-

duced below. Therefore, we set C

= 0.

If we bring the right hand side of Equation 6 to

the left side, we have three terms on th e left hand side

that su m up to zero, i.e.,

Du(x,t)

∇p(x,t)

− ν∆u(x,t) = 0, (13)

or, in other words, thr ee terms whose sum is constant

along a pathline.

The same procedure as for

(x,t) can be car ried

out with respect to the pressure term, leading to the

integrated p ressure ene rgy

(x,t) = C

∇p(ξ

−

x,t

(τ),τ)

·dτ

τ. (14)

For the same reasons a s above, we set C

= 0, which

results in Figure 2(f).

In analogy, the third term of Equ a tion 13 moti-

vates to compute the energy difference between two

points along a pathline due to energy diffusion as:

(x,t) = C

−

ν∆u(ξ

−

x,t

(τ),τ)· dτ

τ, (15)

which we deno te integrated diffusion energy (Fi-

gure 2(b)). Notice that

cannot be obtained without

Energy-Based Visualization of 2D Flow Fields

253

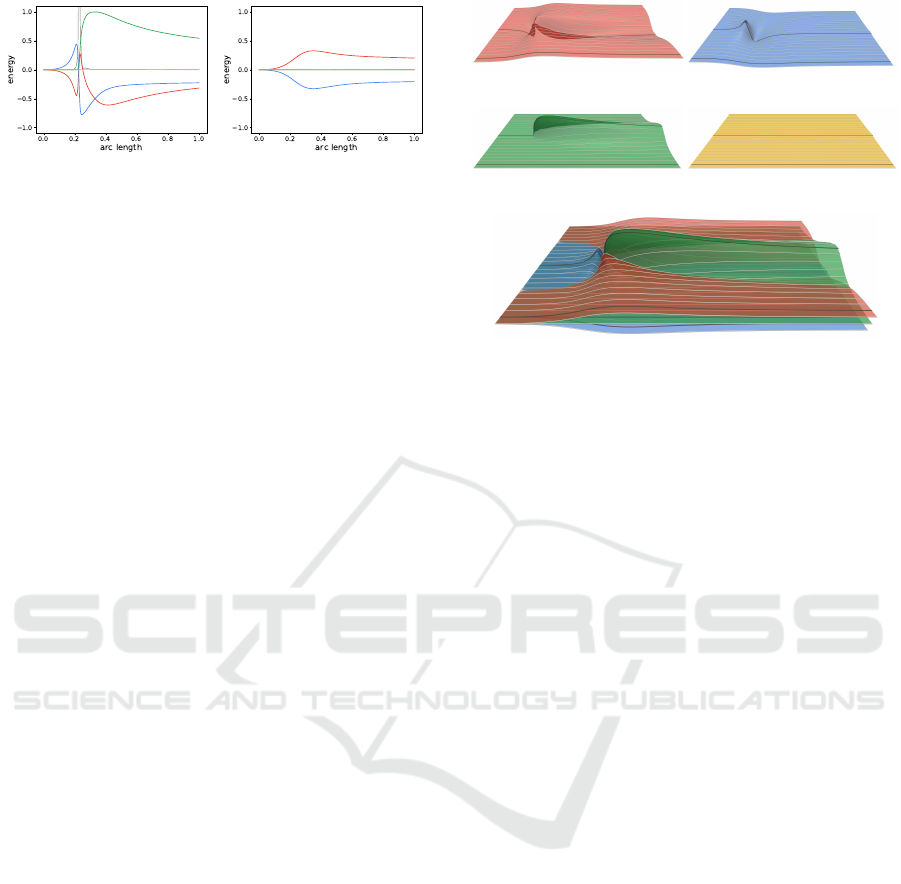
(a) (b)

Figure 3: 2D pathline plots, with

(red),

(blue),

(green),

(yellow), and ε (gray). ( a) Pl ot corresponding to

upper selected (gray) streamline in Figure 2. (b) Plot corre-

sponding to lower selected (gray) streamline in Fi gure 2.

integration, whereas E

and E

could. Nevertheless,

for consistency, we will work with

, and

Finally,

(x,t) :=

(x,t) +

(x,t),

our integrated total energy, is conserved along pathli-

nes, and represents the basis for our approach. It can

be seen as the counterpart to Bernoulli’s principle, for

unsteady viscous ﬂow. Figure 2(h) shows

, and one

can see that the ﬁeld is c onstant along pathlines, in

contrast to E

(Figure 2(g )).

4.2 2D Pathline Plots

To ease visual analysis of the variation (conversion)

of the energies

, and

along path lines, we

introdu ce 2D pathline plots. In these plots, a given

pathline represents the abscissa, parametrized by arc

length in ﬂow direction. Figure 3(a) shows th e plot fo r

the uppe r gray pathline (which is identical to a stre-

amline in this case) in Figure 2, whereas Figure 3(b)

shows the plot for the lower gray pathline in Figure 2.

In our implementation, the user can interactively seed

a pathline and explore the transformation of energy

along it by examining the respective plot in a linked

view. It can be seen how the energies are converted

and that

is indeed conserved .

The upper pathline (Figu re 3(a)) passes close by

the obstacle. Befor e the obstacle,

reduces an d

increases, indicating conversion from kinetic to pr es-

sure energy. Beh ind the obstacle (where the pathline

resides in the low-velocity wake),

is low but incre-

asing, while

is decaying almost at the same rate,

whereas

stays almo st constant. This in dicates that

kinetic energy is transported from the outside into this

region by diffusion, which means that that part of the

wake is accelerated due to viscosity, but inﬂuenced by

pressure only in close vicinity to th e obstacle.

Energy dynam ics alo ng the lower pathline (Fi-

gure 3( b)), on the other hand, is ba sically not af -

fected by viscosity. We identify from the pathline

plot that the ﬂow is ﬁrst accelerated due to conver-

sion from pressure energy to kin e tic energy, and la-

(a)

(b)

(c)

(d)

(e)

Figure 4: 3D pathline plots provide context for the 2D

pathline plots. The front gray pathline corresponds to Fi-

gure 3(b), whereas the farther one refers to the plot form

Figure 3(a). For more compact context, the surfaces can be

combined into a single view (e).

ter the ﬂow decelerates again, by transformin g kinetic

energy back to pressure energy.

4.3 3D Pathline Plots

Whereas the 2D pathline plots are an effective me-

ans for interactive analysis of energy dynamics al-

ong individual pathlines, they do not provide context,

i.e., they do not give information about the relation or

compariso n between different pathlines. To this end,

we introduce 3 D pathline p lots, as a complementary

technique that provides overview and context. We

construct these plots by computing a rake of pathlines

(i.e., a set of pa thlines seeded along a straight seeding

curve, e.g., as shown in Figure 2), generating the 2D

plot f or each of these pathlines, and then creating a

mesh betwe e n “adjace nt” curves of the same quantity.

That is, we take for each of the quantities

and

all arc-length parametrized cu rves, distribute

them evenly in “orthogonal” direction, and cre a te for

each of the quantities a triangle mesh. Figure 4(a)–(d)

shows an example for th e resulting surfaces. Notice

that in Figure 2, we show only every second pathline

that is used for generating the 3D plots, and for better

visibility, we additiona lly show only the lower half.

For improved context, the selected 2D pathline is

denoted b y a dark gray curve both in the 2D ﬁelds, as

well a s on the 3D plot surfaces. For more compact

overview, the resulting surfaces can also be merged

(Figure 4(e)), h owever, in that conﬁguration they rat-

her serve for context than for qualitative insights, due

to potential occlusion issues and clutter.

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

254

4.4 Energy Conversion Maps

Although the 3D pa thline plots provide g ood context

for interactive exploration by means of 2D pathline

plots, they exhibit several shortcomings for qualita-

tive or even quantitative analysis.

First, as mentioned above, their merged represen-

tation (Figure 4(e)) ten ds to suffer from occlusion and

visual clutter. Second, the fact tha t they do not re-

present the sp atial domain but instead a space that is

spanned by pathline arc length and pathline index hin-

ders interpretation. Third, we set the constants C

, and C

to zero, but any choice would be possi-

ble, which ma kes the “offset height” of the individual

pathline curves in the 3D pathline plot surfaces ba-

sically m e aningless, including their intersectio n (e.g.,

the intersection between the red and green manifold

in Fig ure 4(e )). Since the ﬁnal goal of o ur work is the

analysis of conversion of different ty pes of energy, it

is rather the rate of change of these energies along a

pathline that is of interest, than their value itself. This

motivates us to use material derivatives of

, and

for a more qualitative and quantitative analysis.

The mate rial derivative is a differentiation with re-

spect to tim e -dependent ﬂow, and it cap tures the rate

of change of a quantity, as “observed” alo ng a path-

line. Th us, the material derivative of

, and

gives us the amount of energy type per time unit that is

gained or lost by means of energy conversion along a

pathline. We could plot these derivatives again by me-

ans of the 3D pa thline plot approach (see Fig ure 5(a)

for an example). Whereas this would solve the issue

with the constants, since they vanish in the deriva-

tive, this representation would still suffer from occlu-

sion, visual clutter, and non -spatial domain. The re-

fore, we present energy conversion maps, our ﬁnal

component that complements our already presented

building blocks.

Our energy conversion maps are 2D RGB image s

in c ase of 2D ﬂow. For

, we compute its mate-

rial derivative D

(x,t)/Dt, determine the 5th per-

centile P

and the 95th percentile P

of the material

derivative, obtain the maximum P

of |P

| a nd |P

and then linearly map the material derivative to the

red channel, mapping −P

to zero red value and P

to full red value. Analogously, we map the material

derivative of

to the green channel, and the mate-

rial derivative of

to the blue channe l. This means,

that if all material derivatives are zero, this will result

in medium gray co lor. Figure 5(b) shows a respective

result, correspo nding to Figure 5(a).

The light blue region in front of the obstacle in

Figure 5(b), for example, corresp onds to conversion

of k inetic to pressure ene rgy. The o range region to

(a)

(b)

Figure 5: (a) 3D plot representation of material derivat ives

(red),

(blue), and

(green). (b) Energy conver-

sion map, mapping to red, green, and blue color channel.

the sides of the obstacle, on the othe r hand, indicates

conversion of pressure energy to kinetic energy. The

purple region behind the obstacle, i.e., in its wake, re-

presents conversion from diffusion energy to both ki-

netic and pressure energy. Finally, the greenish parts

on either side of the purple wake in dicate conversion

from kinetic and pressure energy to diffusion energy,

which means that the greenish regions “give” their

energy to the purple one via viscous interaction .

5 RESULTS

Having in place our overall technique, we will ap-

ply it now to different datasets. First, we exa-

mine a slightly time-dependent ﬂow around an obsta-

cle (Section 5.1), followed by a more unsteady case

exhibiting a K´arm´an vortex street (Section 5.2). Fi-

nally, we demonstrate that our approach is also ap-

plicable to advanced ﬂow problems, suc h as the ﬂow

through elastic porou s media (Section 5.3).

5.1 Slightly Unsteady Obstacle Flow

We now exam ine a CFD simulation tha t has been si-

mulated on the same geometry as the above steady

obstacle ﬂow, but with higher inlet velocity. As a

consequence, the ﬂow is slightly time-dependent, i.e.,

the wake behind the obstacle is “oscillating”. Fi-

gure 6(a) shows streamline s of a snapshot of the time-

dependent ﬂow, whereas Figure 6(b)–(e) show the

pathlines used for plot-b a sed visualization. Notice

that

, and

are not consistent with the

pathlines, since these ﬁelds are computed by a large

set of reverse-integrated pathlines started at each point

Energy-Based Visualization of 2D Flow Fields

255

(a) u(x,t)

(b)

(c)

(d)

(e)

(f) ε

Figure 6: Slightly unsteady obstacle ﬂow. (a) Velocity

magnitude with streamlines. (b) Integrated kinetic energy

with pathlines (white and gray). (c) Integrated pressure

energy. (d) Integrated diffusion energy. (e) Integrated to-

tal energy. (f) Solver error.

in space, as explained above, and therefore are loca-

ted at different space -time location. Nevertheless, a

look at the respective pathline plots (Figure 7(a) f or

the upper gray pathline an d Figure 7(b) fo r the lower

one) reveals that

is still conserved very well along

these pathlines. A closer inspection of Figure 7(a) re-

veals that

slightly increases when the pathline pas-

ses the obstacle. This is consistent w ith higher va-

lues of the solver error ε the re. Overall, investiga-

ting the 3D pathline plots (Figure 7(c)–(g)) and the

energy conversion m ap (Figure 7(h)) reveals that this

ﬂow is still similar to the steady one from Section 4,

and tha t our a pproach works equally well with pathli-

nes in time-depe ndent ﬂow.

5.2 K

arm

an Vortex Street

This example is the result of increasing the inlet velo-

city even more, resultin g in K´arm´an vortex sh edding.

As can be seen from the different energy ﬁelds and

the comparison between streamlines (Figure 8(a)) and

pathlines (Figure 8(b)–(e )), this dataset is substan-

tially time-dependent. Furthermore, it exhibits lar-

ger solver erro r ε (Figure 8(f)) than the one from

Section 5.1. This larger error leads to a lower level

of energy conservation at the obstacle, as c a n be seen

from the variation of

in the 2D pathline plot for

the uppe r pathline (Figure 9(a)). In contrast, energy

is well conserved for the lower pathline (Figure 9(b)),

consistent with the lower solver err or in that region.

The energy conversion map (Figure 9(h)) reveals

that the area around the vortex shedding is domina-

ted by c onversion from kinetic to pressure energy

(light blue ), and back fr om pressure energy to kine-

tic energy (orange). Close to the Lagrangian coherent

(a) (b)

(c)

(d)

(e)

(f)

(g)

(h)

Figure 7: Slightly unsteady obstacle ﬂow. 2D pathline plot

for upper ( a) gray pathline from Figure 6(b) and lower (b)

one. 3D pathline plots (c)–(g). (h) Energy conversion map

reveals similarity with steady example from Section 4.

structures (ridges in the reverse ﬁnite-time Lyapunov

exponent ﬁeld (Figure 9(i)), computed for the same

integration time as our energies), our approach in dica-

tes conversion from kinetic and pressure energy to dif-

fusion energy (green) , and b ack from diffusion energy

to kine tic and pressure energy (purple). This may

indicate, similar to the case from Figure 5(b), that

energy is transported via viscous mechanisms (diffu-

sion). Besides that, the dark blue regions indicate co n-

version from kinetic and diffusion energy to pressure

energy, and the yellow regions back from pressure to

kinetic and diffusion energy, also re la ting to viscous

effects. Nevertheless, a more deta iled analysis and va-

lidation regarding the impact of ε has to be subject to

future work.

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

256

(a) u(x,t)

(b)

(c)

(d)

(e)

(f) ε

Figure 8: K´arm´an dataset. (a) Velocity magnitude with

streamlines (white). Kinetic (b), pressure (c), diffusion (d),

and total energy (e). Solver error (f) is considerably higher

compared to the slightly unsteady case (Figure 6(f)).

5.3 Elastic Porous Flow

Our last example is a simulation of a ﬂow through an

elastic porous medium. In this case, it is the solution

of the consolidation mode l of Biot, which averages

the porous medium to macroscopic scale. The setup,

which is quadratic in rest state, exhibits three diffe-

rent permeabilities (Figure 11(a)). The upper and lo-

wer boundaries are non-pe rmeable, the left boundary

is a velocity inlet, and the right boundary serves as a

“valve”, i.e., the permeability is very low during the

ﬁrst phase, and high during the second phase. As a

consequence, the material is ﬁrst “inﬂated”, and starts

releasing the ﬂuid after the inﬂow has been stopped

and the right boundary has been “opened”.

Since this example consists of an elastic porous

medium, within which e nergy can be stored as pres-

sure and deformation, we replace the material deriva-

tive of ene rgies by the time derivative, i.e., we focus

on the ma te rial instead of the ﬂow through the mate-

rial. Also, due to the used simulation model, we do

not need to take into account diffusion caused by vis-

cosity. Thus, diffusion energy from above is replaced

by deformation energy, which we compute a s

k∇d(x,t) + (∇d(x,t))

⊤

|∇· d(x,t)|

dx,

(16)

with displacement ﬁeld d(x,t) and cell C of the grid.

Figure 10(a)–(c) shows the ﬁrst phase o f the pro-

cess for kinetic energy, (f)–(h ) for pressure energy,

and (k)–(m) deformation energy. Accordingly, (c) –(e)

shows the second phase for kinetic e nergy, (h) –(j) for

pressure energy, and (m)–(o) for deformation energy.

Figure 11(b) d epicts energy dynamics at the c e nter.

(a) (b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Figure 9: K´arm´an ﬂ ow. 2D pathline plots (a) and (b) reveal

that energy conservation is violated close to the obstacle due

to high solver error (Figure 8(f)) in that region. 3D pathline

plots (c)–(g) r eﬂect energy dynamics of vortex shedding.

(h) Energy conversion map. (i) Finite-time Lyapunov expo-

nent ﬁeld, for comparison (low-black; high-cyan).

The th ree ph a ses and respective energy conversions

are clearly visible in the plo t. It is appar ent that du-

ring the inﬂation phase, kinetic en e rgy is higher at

the inlet, whereas during the outﬂow ph ase, kinetic

energy is larger at the o utlet. Interestingly, pressure

energy as well as deformation energy a re larger at the

inlet in both phases. The energy conversion maps (Fi-

gure 10(p)–(t)), based on the time derivative, reveal

Energy-Based Visualization of 2D Flow Fields

257

(a) (b) (c) (d) (e) (f) (g) (h) (i) (j)

(k) (l) (m) (n) (o) (p) (q) (r) (s) (t)

Figure 10: Elastic porous ﬂow. (a)–(e) Kinetic energy, (f)–(j) pressure energy, (k)–(o) deformation energy, and (p)–(t) re-

spective energy conversion maps, each wi th respective streamlines.

(a) (b)

Figure 11: Elastic porous ﬂow. (a) High (blue), medium

(gray), and very low (red) permeability. (b) Plot of ki-

netic (red), pressure (blue), deformation (green), and to-

tal (yellow) energy over time, at the center of the domain.

that during the ﬁrst phase, energy conversion is low

(close to gray colors), whereas at the start of the se-

cond phase, one can see conversion from pressure and

deformation energy to k inetic energy, in p articular at

the outlet. During the second p hase, we observe that

the region that converts deformation and pressure into

kinetic energy shrinks from righ t to left.

6 CONCLUSION

We presented a counterpart to Berno ulli’s principle,

which describes the conservation a nd co nversion of

energy alon g streamlines in inviscid ﬂow. By exten-

ding the concept to time-dependent ﬂow and accou n-

ting for viscous effects, w e established a basis for the

visualization o f energy dynamics in ﬂow ﬁelds. We

presented an interactive exploration approach based

on our concept, complemented it with a direct visu-

alization approach of e nergy conversion, and demo n-

strated its utility using simple examples. As future

work, we would like to further investigate the proper-

ties of our appro ach using additional examples, and

extend it to 3D ﬂow ﬁelds and other types of energy.

ACKNOWLEDGEMENTS

The research lea ding to these results has been done

within the Transregional Collaborative Research Cen-

ter SFB / TRR 16 5 “Waves to Weather” funded by the

German Science Foundation (DFG).

REFERENCES

Barth, W. and Burns, C. (2007). Virtual rheoscopic ﬂuids

for ﬂow visualization. IEEE Transactions on Visuali-

zation and Computer Graphics, 13(6):1751–1758.

Bernoulli, D. (1738). Hydrodynamica, sive de viribus et

motibus ﬂuidorum commentarii. Opus academicum ab

auctore, dum Petropoli ageret, congestum.

Brownlee, C., Pegoraro, V., Shankar, S., McCormick, P.,

and Hansen, C. (2010). Physically-based interactive

schlieren ﬂow visualization. In Proc. IEEE Paciﬁc Vi-

sualization Symposium 2010, pages 145–152.

Fernandes, O., Frey, S. , and Ertl, T. (2017). Transportation-

based visualization of energy conversion. In P roc.

IVAPP 2017, volume 3, pages 52–63.

Jeong, J. and Hussain, F. (1995). On the identiﬁcation of a

vortex. Journal of Fluid Mechanics, 285(69):69–94.

Pobitzer, A., Tutkun, M., Andreassen, O., Fuchs, R., Pei-

kert, R., and Hauser, H. (2011). Energy-scale aware

feature extraction for ﬂow visualization. Computer

Graphics Forum, 30(3):771–780.

Popinet, S. (2007). The Gerris ﬂow solver. In Rencontres

Mondiales du Logiciel Li bre, July.

Sadlo, F., Peikert, R., and Sick, M. (2006). Visualization

tools for vorticity transport analysis i n incompressible

ﬂow. IEEE Transactions on Visualization and Com-

puter Graphics, 12(5):949–956.

Schafhitzel, T., Baysal, K., Vaaraniemi, M., Rist, U.,

and Weiskopf, D. (2011). Visualizing the evolution

and interaction of vortices and shear layers in time-

dependent 3D ﬂow. IEEE Transactions on Visualiza-

tion and Computer Graphics, 17(4):412–425.

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

258