
Fast View Synthesis with Deep Stereo Vision
Tewodros Habtegebrial
1
, Kiran Varanasi
2
, Christian Bailer
2
and Didier Stricker
1,2
1
Department of Computer Science, TU Kaiserslautern, Erwin-Schrdinger-Str. 1, Kaiserslautern, Germany
2
German Research Center for Artificial Intelligence, Trippstadter Str. 122, Kaiserslautern, Germany
Keywords:
Novel View Synthesis, Convolutional Neural Networks, Stereo Vision.
Abstract:
Novel view synthesis is an important problem in computer vision and graphics. Over the years a large number
of solutions have been put forward to solve the problem. However, the large-baseline novel view synthesis pro-
blem is far from being ”solved”. Recent works have attempted to use Convolutional Neural Networks (CNNs)
to solve view synthesis tasks. Due to the difficulty of learning scene geometry and interpreting camera mo-
tion, CNNs are often unable to generate realistic novel views. In this paper, we present a novel view synthesis
approach based on stereo-vision and CNNs that decomposes the problem into two sub-tasks: view dependent
geometry estimation and texture inpainting. Both tasks are structured prediction problems that could be ef-
fectively learned with CNNs. Experiments on the KITTI Odometry dataset show that our approach is more
accurate and significantly faster than the current state-of-the-art.
1 INTRODUCTION
Novel view synthesis (NVS) is defined as the problem
of rendering a scene from a previously unseen camera
viewpoint, given other reference images of the same
scene. This is an inherently ambiguous problem due
to perspective projection, occlusions in the scene, and
the effects of lighting and shadows that vary with a
viewpoint. Due to this inherent ambiguity, this can be
solved only by learning valid scene priors and hence,
is an effective problem to showcase the application of
machine learning to computer vision.
In the early 1990s, methods for NVS were propo-
sed to deal with slight viewpoint changes, given ima-
ges taken from relatively close viewpoints. Then NVS
can be performed through view interpolation (Chen
and Williams, 1993), warping (Seitz and Dyer, 1995)
or rendering with stereo reconstruction (Scharstein,
1996). There are a few methods proposed over the ye-
ars to solve the problem of large-baseline NVS (Chau-
rasia et al., 2013), (Zitnick et al., 2004), (Flynn et al.,
2016), (Goesele et al., 2010), (Penner and Zhang,
2017). Some methods are based on structure from
motion (SFM) (Zitnick et al., 2004), which can pro-
duce high-quality novel views in real time (Chaura-
sia et al., 2013), but has limitations when the input
images contain strong noise, illumination change and
highly non-planar structures like vegetation. These
methods need to preform depth synthesis for poorly
reconstructed areas in SFM, which is challenging for
intricate structures. In contrast to these methods, neu-
ral networks can be trained end-to-end to render NVS
directly (Flynn et al., 2016). This is the paradigm we
follow in this paper.
Many recent works have addressed end-to-end
training of neural networks for NVS (Dosovitskiy
et al., 2015), (Tatarchenko et al., 2016), (Zhou et al.,
2016), (Yang et al., 2015). These methods typi-
cally perform well under a restricted scenario, where
they have to render geometrically simple scenes.
The state-of-the-art large-baseline view synthesis ap-
proach that works well under challenging scenarios
is DeepStereo, introduced by Flynn et. al. (Flynn
et al., 2016). DeepStereo generates high-quality no-
vel views on the KITTI dataset (Geiger et al., 2012),
where older SFM based methods such as (Chaura-
sia et al., 2013) do not work at all. This algorithm
uses plane-sweep volumes and processes them with a
double tower CNN (with color and selection towers).
However, processing plane-sweep volumes of all re-
ference views jointly imposes very high memory and
computational costs. Thus, DeepStereo is far slower
than previous SFM based methods such as (Chaurasia
et al., 2013).
In this work we propose a novel alternative to
DeepStereo which is two orders of magnitude fas-
ter. Our method avoids performing expensive cal-
culations on the combination of plane-sweep volu-
792
Habtegebrial, T., Varanasi, K., Bailer, C. and Stricker, D.
Fast View Synthesis with Deep Stereo Vision.
DOI: 10.5220/0007360107920799
In Proceedings of the 14th Inter national Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 792-799
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Two sample renderings from the KITTI dataset (Geiger et al., 2012), using our proposed method. Images are
rendered using four neighbouring views. From left to right, the median baseline between consecutive input views increases
from 0.8m to 2.4m.
mes of reference images. Instead, we predict a proxy
scene geometry for the input views with stereo-vision.
Using forward-mapping (section 3.3), we project in-
put views to the novel view. Forward-mapped images
contain a large number of pixels with unknown color
values. Rendering of the target view is done by ap-
plying texture inpainting on the warped-images. Our
rendering pipeline is fully-learnable from a sequence
of calibrated stereo images. Compared to DeepStereo,
the proposed approach produces more accurate results
while being significantly faster. The main contributi-
ons of this paper are the following.
• We present a novel view synthesis approach based
on stereo-vision. The proposed approach decom-
poses the problem into proxy geometry prediction
and texture inpainting tasks. Every part of our
method is fully learnable from input stereo refe-
rence images.
• Our approach provides an affordable large-
baseline view synthesis solution. The proposed
method is faster and even more accurate than
the current state-of-the-art method (Flynn et al.,
2016) . The proposed approach takes seconds to
render a single frame while DeepStereo (Flynn
et al., 2016) takes minutes.
2 RELATED WORK
Image based rendering has enjoyed a significant
amount of attention from the computer vision and
graphics communities. Over the last few decades, se-
veral approaches of image-based rendering and mo-
delling were introduced (Chen and Williams, 1993),
(Seitz and Dyer, 1995), (Seitz and Dyer, 1996),
(Adelson et al., 1991), (Scharstein, 1996). Fitzgib-
bon et. al. (Fitzgibbon et al., 2005) present a solu-
tion that solves view synthesis as texture synthesis by
using image-based priors as regularization. Chaura-
sia et. al. (Chaurasia et al., 2013), presented high-
quality view synthesis that utilizes 3D reconstruction.
Recently, Penner at. al. (Penner and Zhang, 2017)
presented a view synthesis method that uses soft 3D
reconstruction via fast local stereo-matching similar
to (Hosni et al., 2011) and occlusion aware depth-
synthesis. Kalantari et. al. (Kalantari et al., 2016)
used deep convolutional networks for view synthesis
in light-fields.
Encoder-decoder Networks have been used in ge-
nerating unseen views of objects with simple geo-
metric structure, (e.g. cars, chairs, etc) (Tatarchenko
et al., 2016), (Dosovitskiy et al., 2015). However, the
renderings generated from encoder-decoder architec-
tures are often blurry. Zhou et al. (Zhou et al., 2016),
used encoder-decoder networks to predict appearance
flow, rather than directly generating the image. Com-
pared to direct novel view generating methods (Tatar-
chenko et al., 2016), (Dosovitskiy et al., 2015), the
appearance-flow based method produces crispier re-
sults. Nonetheless, the appearance flow based also
fails to produce any convincing results in natural sce-
nes.
Flynn et. al. (Flynn et al., 2016), proposed the
first CNN based large baseline novel view synthe-
sis approach. DeepStereo has a double-tower(color
and selection towers) CNN architecture. DeepSte-
reo takes a volume of images projected using multiple
depth planes, known as plane-sweep volume as input.
The color-tower produces renderings for every depth
plane separately. The selection-tower estimates pro-
babilities for the renderings computed for every depth
plane. The output image is then computed as a weig-
hted average of the rendered color-images. DeepSte-
reo generates high-quality novel views from a plane
sweep volume generated from few(typically 4) refe-
rence views. To the best of our knowledge, Deep-
Stereo is the most accurate large-baseline method,
Fast View Synthesis with Deep Stereo Vision
793

proven to be able to generate accurate novel views
of challenging natural scenes. Recently, monocular
depth prediction based view synthesis methods have
been proposed (Liu et al., 2018), (Yin et al., 2018).
Despite being fast, these works produce results with
significantly lower quality compared to multiview ap-
proaches such as DeepStereo (Flynn et al., 2016).
Conv
3
Conv
16
Conv
3
Conv
16
Pool
2,2
Pool
2,2
Up
sample
Res
32
Conv
48
Res
32
DepthConcat
RenderedView
DepthPrediction ForwardMappingReferenceViews
UnseenView
CameraPose
(a)Proxygeometryestimationandviewwarping
(b)Textureinpainting
(a) Sample view-warping
Figure 2: Illustration of our novel view synthesis approach.
in the first stage(a), we begin by estimating dense depth
maps from the input reference stereo pairs using an unsu-
pervised stereo-depth prediction network. Estimated depth
maps are used to project input views to the target view via
Forward-mapping, shown in Equation 7. As shown in (b),
the output novel view is rendered with the texture inpainting
applied on the forward mapped views.
3 PROPOSED METHOD
In this section we discuss our proposed view
synthesis approach. Our aim is to generate
the image X
t
of a scene from a novel vie-
wpoint, using a set of reference stereo-pairs
{{X
1
L
,X
1
R
},{X
2
L
,X
2
R
},...,{X
V
L
,X
V
R
}}
1
and their po-
ses {P
1
,P
2
,...,P
V
} w.r.t the target view. The pro-
posed method has three main stages, namely proxy
scene geometry estimation, forward-mapping and tex-
ture inpainting. As shown in Figure 2 the view synt-
hesis is performed as follows: first, a proxy scene ge-
ometry is estimated as a dense depth map. The es-
timated depth map is used to forward-map the input
1
subscripts L and R indicate left and right views, re-
spectively
views to the desired novel viewpoint. Forward map-
ping (described in section 3.3) leads to noisy images
with a large number of holes. The final rendering is,
therefore, generated by applying texture inpainting on
the forward-mapped images. Both the depth estima-
tion and texture inpainting tasks are learned via con-
volutional networks. Components of our view synthe-
sis pipeline are trainable using a dataset that contains
a sequence of stereo-pairs with known camera poses.
3.1 Depth Prediction Network
We train a convolutional network to estimate depth
from an input stereo pair. The training set for the
depth prediction CNN is generated by sampling M
stereo pairs from our training set. The proposed
network is composed of the following stages: feature
extraction, feature-volume aggregation and feature-
volume filtering. Architecture-wise our network is
similar to GCNet (Kendall et al., 2017). However,
there are several key differences, including the
fact that our network is trained in an unsupervised
manner. Similar to our depth prediction network, a
recent work (Zhong et al., 2017) also investigates
learning stereo disparity prediction without using
ground truth data.
3.2 Feature Extraction
Generating robust feature descriptors is an important
part of stereo matching and optical flow estimation
systems. In this work we extract image-features using
a convolutional network. Applying the fully convo-
lutional network (Table 1) on left and right stereo-
images, we extract features F
L
and F
R
.
Feature-volume Generation
Features F
L
and F
R
are aggregated into feature-
volumes V
L
and V
R
for the left and right images, re-
spectively. Feature volumes are data structures that
are convenient for matching features. Feature volume
V
L
is created by concatenating F
L
with F
R
translated
at different disparity levels d
i
∈ {d
1
,d
2
,...d
D
}. V
L
=
[(F
L
,F
d
1
R
),(F
L
,F
d
2
R
),...,(F
L
,F
d
D
R
)]
2
Similarly, V
R
is created by translating F
L
and concatenating it with
F
R
.
2
We used (X,Y) to denote concatenating X and Y across
the first dimension and we use [ X and Y] to denote stacking
X and Y , which creates a new first dimension
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
794

Table 1: Details of the feature extraction stage. In the first entry of the third row, we use res 1 to res 9, as a shorthand
notation for a stack of 9 identical residual layers.
Layers
Kernel
size
Stride
Input
channels
Output
channels
Nonlinearity
conv 0 5x5 2x2 32 32 ReLU
res 1 to res 9 3x3 1x1 32 32 ReLU + BN
conv 10 3x3 1x1 32 32 -
Feature-volume Filtering
Generated feature volumes aggregate left and right
image features at different disparity levels. This stage
is posed with the task of computing pixel-wise proba-
bilities over disparities from feature volumes. Since
V
L
and V
R
are composed of features vectors spanning
3-dimensions (disparity, image-height, and image-
width) it is convenient to use 3D convolutional layers.
3D convolutional layers are able to utilize neighbor-
hood information across the above three axes. The
3D-convolutional encoder-decoder network used in
this work is similar to Kendal et. al. (Kendall et al.,
2017).
Let’s denote the output of applying feature-
volume filtering on V
L
and V
R
as C
L
and C
R
, respecti-
vely. C
L
and C
R
, are tensors represent pixel-wise dis-
parity ”confidences”. In order to convert confidences
into pixel-wise disparity maps, a soft-argmin function
is used. C
L
and C
R
represent negative of confidence,
hence, we use soft-argmin, instead of soft-argmax.
The soft-argmin operation (Equation 1) is a differen-
tiable alternative to argmin (Kendall et al., 2017). For
every pixel location, soft-argmin first normalizes the
depth confidences into a proper probability distribu-
tion function. Then, disparities are computed as the
expectation of the disparity under the normalized dis-
tributions. Thus applying soft-argmin on C
L
and C
R
gives disparity maps D
L
and D
R
, respectively.
P
L
(i,x,y) =
e
−C
L
(i,x,y)
∑
D
j=1
e
−C
L
( j,x,y)
D
L
(x,y) =
D
∑
i=1
disp(i) ∗ P
L
(i,x,y)
(1)
The estimated disparities D
L
,D
R
are disparities
that encode motions of pixels between the left and
right images. We convert the predicted disparities into
a sampling grid in order to warp left image to the
right image (and vice versa). Once sampling grid is
created we apply bi-linear sampling (Jaderberg et al.,
2015) to perform the warping. Denoting the bi-linear
sampling operation as Φ, the warped left and right
images could be expressed as
˜
X
L
= Φ(X
R
,D
L
) and
˜
X
R
= Φ(X
L
,D
R
), respectively.
Disparity Estimation Network Training Objective
Our depth prediction network is trained in unsu-
pervised manner by minimizing a loss term which
mainly depends on the photometric discrepancy be-
tween the input images {X
L
,X
R
} and their respective
re-renderings {
˜
X
L
,
˜
X
R
}. Our network minimizes, the
loss term L
T
which has three components: a photo-
metric discrepancy term L
P
, smoothness term L
S
and
left-right consistency term L
LR
, with different weig-
hting parameters λ
0
,λ
1
, and λ
2
.
L
T
= λ
0
L
P
+ λ
1
L
LR
+ λ
2
L
S
(2)
Photometric discrepancy term L
P
is a sum of an
L1 loss and a structural dissimilarity term based on
SSIM (Wang et al., 2004) with multiple window si-
zes. In our experiments we use S = {3,5,7}. N in
Equation 3 is the total number of pixels.
L
P
=
λ
p
1
N
(||
˜
X
L
− X
L
||
1
+ ||
˜
X
R
− X
R
||
1
)+
λ
p
s
N
∑
s∈S
(SSIM
s
(
˜
X
L
,X
L
) + SSIM
s
(
˜
X
R
,X
R
))
(3)
Depth prediction from photo-consistency is an ill-
posed inverse problem, where there are a large num-
ber of photo-consistent geometric structures for a gi-
ven stereo pair. Imposing regularization terms en-
courages the predictions to be closer to the physically
valid solutions. Therefore, we use an edge-aware
smoothness regularization term L
S
in Equation 5 and
left-right consistency loss (Godard et al., 2016) Equa-
tion 4. L
LR
is computed by warping disparities and
comparing them to the original disparities predicted
by the network.
L
LR
= ||
˜
D
L
− D
L
||
1
+ ||
˜
D
R
− D
R
||
1
where
˜
D
L
= Φ(D
R
,D
L
) and
˜
D
R
= Φ(D
L
,D
R
)
(4)
Smoothness term L
S
forces disparities
D
L
and D
R
to have small gradient magnitudes
in smooth image regions. However, the term allows
large disparity gradients in regions where there are
strong image gradients.
L
S
=∇
x
D
L
e
(−∇
x
X
L
)
+ ∇
y
D
L
e
(−∇
y
X
L
)
+
∇
x
D
R
e
(−∇
x
X
R
)
+ ∇
y
D
R
e
(−∇
y
X
R
)
3
(5)
Fast View Synthesis with Deep Stereo Vision
795

Bilinear sampling, Φ allows back-propagation of
error (sub-)gradients from the output such as
˜
X s back
to the input images X s and disparities Ds. There-
fore, it is possible to use standard back-propagation
to train our network. Formal derivations for the back-
propagation of gradients via a bilinear sampling mo-
dule could be found in (Jaderberg et al., 2015).
3.3 Forward Mapping
(a) Sample view-warping
(b) Close-up view of warped and target images
Figure 3: View-warping with forward mapping.
We apply our trained stereo depth pre-
dictor on the V input stereo pairs
{{X
1
L
,X
1
R
},{X
2
L
,X
2
R
},...,{X
V
L
,X
V
R
}} and gene-
rate disparities for the left camera input views,
{D
1
L
,D
2
L
,...D
V
L
}. The right stereo views are used
only for estimating disparities. Forward mapping
and texture inpainting are done only on the images
from the left camera. In this section, unless specified
otherwise, we refer the images from left camera as
the input images/views and we drop the subscripts L
and R.
Forward-mapping projects input views to the
target-view using their respective depth-maps. The
predicted disparities of the input views could be con-
verted to depth values. Depth Z
i
w,h
for a pixel at loca-
tion (w,h) in the i − th input view, can be computed
from the corresponding disparity D
i
w,h
, as follows:
Z
i
w,h
=
f
x
∗ B
D
i
w,h
(6)
where K is the intrinsic camera matrix, B is the base-
line, and f
x
is focal length.
3
∇
x
is gradient w.r.t x, similarly ∇
y
is gradient w.r.t y
The goal of forward mapping is to project the in-
put views to the target view, t. Given the relative pose
between the input-view i and target-view as a transfor-
mation matrix P
i
= [R
i
|T
i
], pixel p
i
h,w
(pixel location
{h,w} in view i) will be forward mapped as follows,
to a pixel location p
t
x,y
on the target view:
x
0
,y
0
,z
0
∼ KP
i
Z
i
h,w
K
−1
[h,w,1]
T
x =
x
0
/z
0
and y =
y
0
/z
0
(7)
Following a standard forward projection Equa-
tion 7, the reference input frames {X
1
,X
2
,...,X
V
}
are warped to the target view {W
1
,W
2
,...,W
V
}.
As shown in Figure 3, forward-mapped views have
a large number of pixel locations with unknown color
values. These holes are created for various reasons.
First, forward-mapping is a one-to-one mapping of
pixels from the input views to the target view. This
creates holes as it doesn’t account for zooming in ef-
fects of camera movements, which could lead to one-
to-many mapping. Moreover, occlusion and rounding
effects lead to more holes. In addition to holes, some
warped pixels have wrong color values due to inaccu-
racies in depth prediction.
3.4 Texture Inpainting
The goal of our texture inpainting network is to learn
generating the target view X
t
from the set of warped
input views {W
1
,W
2
,...,W
V
}. This is a structu-
red prediction task where the input and output images
are aligned. Due to the effects mentioned above in
section 3.3, texture mapping results in noisy warped
views, see Figure 3. Forward-mapped images W
i
s
contain two kinds of pixels: noisy-pixels, those with
unknown (or wrong) color values and good-pixels,
those with correct color value. Ideally we would like
to hallucinate the correct color value for the noisy
pixels while maintaining the good pixels.
The architecture of our proposed inpainting net-
work is inspired by Densely Connected (Huang et al.,
2017) and Residual (He et al., 2016) network archi-
tectures. Details of the network architecture are pre-
sented in Table 2. The network has residual layers
with long range skip-connections that feed features
from early layers to the top layers, similar to Den-
seNets (Huang et al., 2017). The architecture is de-
signed to facilitate flow of activations as well as gra-
dients through the network. The texture inpainting
network is trained by minimizing L1 loss between the
predicted novel views and the original images.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
796

Table 2: Texture inpainting network architecture. The network is mainly residual, except special convolution layers which
could be used as input and output layers.
Block Layer Input
Input,Out.
channels
Output size
Block 0 conv 0 warped views 4*4,32 H, W
Block 0 res 1 conv 0 32,32 H, W
Block 1 res 2 pool(res 1), pool(warped views) 32+16, 48 H/2, W/2
Block 1 res 2 to res 7 (repeat res 2, 5 times) res 2 48 ,48 H/2, W/2
Block 1 res 8 res 7 48 ,48 H/2, W/2
Block 2 conv 9 upsample(res 8), res 1 48+32,48 H, W
Block 2 res 10 conv 9 48, 48 H, W
Block 2 res 11 res 10 48, 48 H,W
Block 3 conv 12 res 11 48, 16 H,W
Block 3 output conv 12 16, 3 H,W
(a) Rendering with our approach and DeepStereo (Flynn
et al., 2016)
(b) Close-up view of warped and target images
Figure 4: Rendering of a sample scene for qualitative eva-
luation. Close-up views show that preserves the geometric
structure better than DeepStereo and textitDeepStereo has
ghosting where the traffic sign is replicated multiple times.
Our rendering resembles the target except for slight amount
of blur.
4 EXPERIMENTS
We tested our proposed approach on the KITTI (Gei-
ger et al., 2012) public computer vision benchmark.
Our approach has lower rendering error than the cur-
rent state-of-the-art (Flynn et al., 2016) (see Table 3).
Qualitative evaluation also show that out method bet-
ter preserves the geometric details of the scene, shown
in Figure 4.
Network Training and Hyper-parameters. The
depth predictor loss term has three weighting para-
meters: λ
0
for photometric loss, λ
1
for left-right con-
sistency loss and λ
2
for local smoothness regulariza-
tion. The weighting parameters have to be set pro-
perly, wrong weights might lead trivial solutions such
as a constant disparity output for every pixel. The
weighting parameters used in our experiments are the
following: λ
0
= 5, λ
1
= 0.01, λ
2
= 0.0005. The pho-
tometric loss is also a weighted combination of l1 loss
and SSIM losses with different window sizes. These
weighting factors are set to be λ
1
P
= 0.2, λ
3
P
= 0.8,
λ
5
P
= 0.2 and λ
7
P
= 0.2. As discussed in section 3. the
depth-prediction and texture inpainting networks are
trained separately. We train the networks with back-
propagation using Adam optimizer (Kingma and Ba,
2014), with mini-batch size 1 and learning rate of
0.0004. The depth prediction network is trained for
200,000 iterations and the inpainting network is trai-
ned for 1 Million iterations.
Dataset
We evaluate our proposed method on the publicly
available KITTI Odometry Dataset (Geiger et al.,
2012). KITTI is an interesting dataset for large-
baseline novel view synthesis. The dataset has a large
number of frames recorded in outdoors sunny urban
environment. The dataset contains variations in the
scene structure (vegetation, buildings, etc), strong il-
lumination changes and noise which makes KITTI a
challenging benchmark.
The dataset contains around 23000 stereo pairs di-
vided into 11 sequences (00 to 10). Each sequence
Fast View Synthesis with Deep Stereo Vision
797
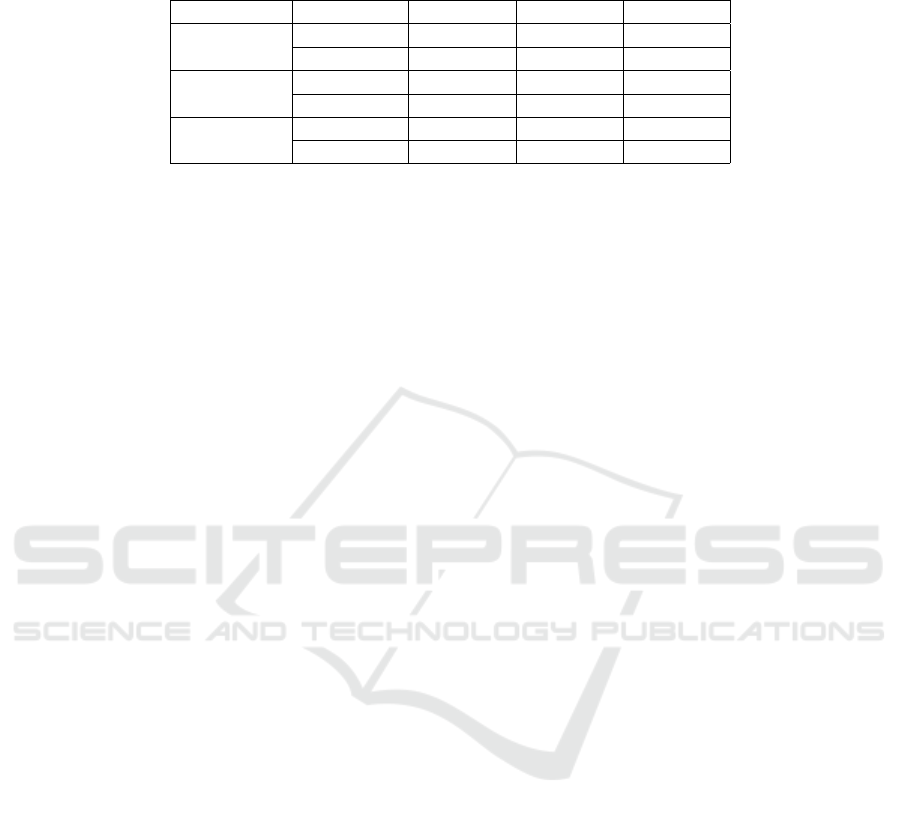
Table 3: Quantitative evaluation of our method against DeepStereo. We used our texture inpainting network with residual
blocks as shown in Table 2. Our approach outperforms DeepStereo (Flynn et al., 2016) in all cases. Each row shows the
performance of a method that is trained on a specific input camera spacing and tested on all three spacings.
Spacing Method Test 0.8 m Test 1.6 m Test 2.4 m
Train 0.8 m
Ours 6.66 8.90 12.14
DeepStereo 7.49 10.41 13.44
Train 1.6 m
Ours 6.92 8.47 10.38
DeepStereo 7.60 10.28 12.97
Train 2.4 m
Ours 7.47 8.73 10.28
DeepStereo 8.06 10.73 13.37
contains a set of images captured by a stereo camera,
mounted on top of car driving through a city. The ste-
reo camera captures frames every ≈ 80 cms. In order
to make our results comparable to DeepStereo (Flynn
et al., 2016), we hold out sequence 04 for validation,
sequence 10 for test and used the rest for training. In
our experiments, 5 consecutive images are used, with
the middle one is held out as target and the other 4
images are used as reference. Tests are done at diffe-
rent values of spacing between consecutive images.
Taking consecutive frames gives spacing of around
0.8 m. Sampling every other frame give a spacing
of ≈ 1.6m and every third frame gives ≈ 2.4m spa-
cing. The error metric used to evaluate performance
of rendering methods a mean absolute brightness er-
ror, computed per pixel per color channel.
Results
Table 3 shows the results of our proposed approach
compared to DeepStereo (Flynn et al., 2016), on the
KITTI dataset. Our approach outperforms DeepSte-
reo in all spacings of the input views, while being sig-
nificantly faster. In Figure 4, sample renderings are
shown for a qualitative evaluation of our approach and
DeepStereo. As shown in the lowest two rows of Fi-
gure 4, renderings of DeepStereo suffer from ghosting
effects due to cross-talk between different depth pla-
nes, which led to the replicated traffic sign and noisy
bricks(as could be seen in the close-up views).
We performed tests to compare our texture inpain-
ting architecture against the so called UNet architec-
ture (Ronneberger et al., 2015). Furthermore, in or-
der to evaluate the significance of the texture inpain-
ting stage, we measured the accuracy of our system
when the texture inpainting stage is replaced by sim-
ple median filtering scheme applied on the warped
views. In an ablation test, we found out that our in-
painting network achieves lower error than a com-
monly used architecture called UNet (Ronneberger
et al., 2015)(error 6.66 vs 7.08). A test performed to
investigate the effect of using residual layers instead
of convolutional layers shows that residual layers give
slightly better performance (error 6.66 vs 6.70).
Timing. During the test phase, at a resolution of
528 ×384, our depth prediction stage and the forward
mapping take 6.08 seconds and 2.60 seconds (for four
input neighbouring views), respectively. The texture
rendering takes takes 0.05 seconds. Thus, the total
time adds up to 8.73 seconds, per frame. This is much
faster than DeepStereo which takes 12 minutes to ren-
der a single frame of resolution 500 × 500. Our expe-
riments are performed on a multi-core cpu machine
with single Tesla V100 GPU.
5 CONCLUSION AND FUTURE
WORK
We presented a fast and accurate novel view synthe-
sis pipeline based on stereo-vision and convolutional
networks. Our method decomposes novel view synt-
hesis into, view-dependent geometry estimation and
texture inpainting problems. Thus, our method uti-
lizes the power of convolutional neural networks in
learning structured prediction tasks.
Our proposed method is tested on a challenging
benchmark, where most existing approaches are not
able to produce reasonable results. The proposed
approach is significantly faster and more accurate
than the current state-of-the-art. As part of a future
work, we would like to explore faster architectures to
achieve real-time performance.
ACKNOWLEDGEMENTS
This work was partially funded by the BMBF project
VIDIETE(01IW18002).
REFERENCES
Adelson, E. H., Bergen, J. R., et al. (1991). The plenoptic
function and the elements of early vision.
Chaurasia, G., Duchene, S., Sorkine-Hornung, O., and
Drettakis, G. (2013). Depth synthesis and local warps
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
798

for plausible image-based navigation. ACM Transacti-
ons on Graphics (TOG), 32(3):30.
Chen, S. E. and Williams, L. (1993). View interpola-
tion for image synthesis. In Proceedings of the 20th
annual conference on Computer graphics and inte-
ractive techniques, pages 279–288. ACM.
Dosovitskiy, A., Tobias Springenberg, J., and Brox, T.
(2015). Learning to generate chairs with convolutio-
nal neural networks. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 1538–1546.
Fitzgibbon, A., Wexler, Y., and Zisserman, A. (2005).
Image-based rendering using image-based priors. In-
ternational Journal of Computer Vision, 63(2):141–
151.
Flynn, J., Neulander, I., Philbin, J., and Snavely, N. (2016).
Deepstereo: Learning to predict new views from the
world’s imagery. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 5515–5524.
Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we re-
ady for autonomous driving? the kitti vision bench-
mark suite. In Computer Vision and Pattern Recogni-
tion (CVPR), 2012 IEEE Conference on, pages 3354–
3361. IEEE.
Godard, C., Mac Aodha, O., and Brostow, G. J. (2016).
Unsupervised monocular depth estimation with left-
right consistency. arXiv preprint arXiv:1609.03677.
Goesele, M., Ackermann, J., Fuhrmann, S., Haubold, C.,
Klowsky, R., Steedly, D., and Szeliski, R. (2010). Am-
bient point clouds for view interpolation. In ACM
Transactions on Graphics (TOG), volume 29, page 95.
ACM.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resi-
dual learning for image recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 770–778.
Hosni, A., Bleyer, M., Rhemann, C., Gelautz, M., and
Rother, C. (2011). Real-time local stereo matching
using guided image filtering. In Multimedia and Expo
(ICME), 2011 IEEE International Conference on, pa-
ges 1–6. IEEE.
Huang, G., Liu, Z., Weinberger, K. Q., and van der Maaten,
L. (2017). Densely connected convolutional networks.
In Proceedings of the IEEE conference on computer
vision and pattern recognition, volume 1, page 3.
Jaderberg, M., Simonyan, K., Zisserman, A., et al. (2015).
Spatial transformer networks. In Advances in neural
information processing systems, pages 2017–2025.
Kalantari, N. K., Wang, T.-C., and Ramamoorthi, R. (2016).
Learning-based view synthesis for light field cameras.
ACM Transactions on Graphics (TOG), 35(6):193.
Kendall, A., Martirosyan, H., Dasgupta, S., Henry, P., Ken-
nedy, R., Bachrach, A., and Bry, A. (2017). End-to-
end learning of geometry and context for deep stereo
regression. arXiv preprint arXiv:1703.04309.
Kingma, D. P. and Ba, J. (2014). Adam: A method for sto-
chastic optimization. arXiv preprint arXiv:1412.6980.
Liu, M., He, X., and Salzmann, M. (2018). Geometry-aware
deep network for single-image novel view synthesis.
arXiv preprint arXiv:1804.06008.
Penner, E. and Zhang, L. (2017). Soft 3d reconstruction
for view synthesis. ACM Transactions on Graphics
(TOG), 36(6):235.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:
Convolutional networks for biomedical image seg-
mentation. In International Conference on Medical
image computing and computer-assisted intervention,
pages 234–241. Springer.
Scharstein, D. (1996). Stereo vision for view synthesis.
In Computer Vision and Pattern Recognition, 1996.
Proceedings CVPR’96, 1996 IEEE Computer Society
Conference on, pages 852–858. IEEE.
Seitz, S. M. and Dyer, C. R. (1995). Physically-valid view
synthesis by image interpolation. In Representation
of Visual Scenes, 1995.(In Conjuction with ICCV’95),
Proceedings IEEE Workshop on, pages 18–25. IEEE.
Seitz, S. M. and Dyer, C. R. (1996). View morphing. In
Proceedings of the 23rd annual conference on Com-
puter graphics and interactive techniques, pages 21–
30. ACM.
Tatarchenko, M., Dosovitskiy, A., and Brox, T. (2016).
Multi-view 3d models from single images with a con-
volutional network. In European Conference on Com-
puter Vision, pages 322–337. Springer.
Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P.
(2004). Image quality assessment: from error visi-
bility to structural similarity. IEEE transactions on
image processing, 13(4):600–612.
Yang, J., Reed, S. E., Yang, M.-H., and Lee, H. (2015).
Weakly-supervised disentangling with recurrent trans-
formations for 3d view synthesis. In Advances in
Neural Information Processing Systems, pages 1099–
1107.
Yin, X., Wei, H., Wang, X., Chen, Q., et al. (2018). Novel
view synthesis for large-scale scene using adversarial
loss. arXiv preprint arXiv:1802.07064.
Zhong, Y., Dai, Y., and Li, H. (2017). Self-supervised lear-
ning for stereo matching with self-improving ability.
arXiv preprint arXiv:1709.00930.
Zhou, T., Tulsiani, S., Sun, W., Malik, J., and Efros, A. A.
(2016). View synthesis by appearance flow. arXiv
preprint arXiv:1605.03557.
Zitnick, C. L., Kang, S. B., Uyttendaele, M., Winder, S., and
Szeliski, R. (2004). High-quality video view interpo-
lation using a layered representation. In ACM tran-
sactions on graphics (TOG), volume 23, pages 600–
608. ACM.
Fast View Synthesis with Deep Stereo Vision
799
