Critical Parameter Consensus for Efficient Distributed Bundle
Adjustment
Zhuohao Liu
1
, Changyu Diao
2,3
, Wei Xing
1
and Dongming Lu
1,3
1
College of Computer Science and Technology, Zhejiang University, Hangzhou, China
2
Cultural Heritage Institute, Zhejiang University, Hangzhou, China
3
Key Scientific Research Base for Digital Conservation of Cave Temples,
Zhejiang University, State Administration for Cultural Heritage, China
Keywords:
Structure from Motion, Distributed Bundle Adjustment, Consensus, Block Partitioning, Biclustering.
Abstract:
We present a critical parameter consensus framework to improve the efficiency of Distributed Bundle Adjus-
tment (DBA). Existing DBA methods are based solely on either camera consensus or point consensus, often
resulting in excessive local computation time or large data transmission overhead. To address this issue, we
jointly partition points and cameras, and perform the consensus on both overlapping cameras and points. Our
joint block partitioning method first initializes a non-overlapping block partition, maximizing local problem
constraints and ensuring a uniform partition. Then overlapping cameras and points are added in a greedy
manner to maximize the partition score that quantifies the efficiency of DBA for local blocks. Experimental
results on public datasets show that we can achieve better computational efficiency without loss of accuracy.
1 INTRODUCTION
Structure-from-Motion (SfM) relies on Bundle Ad-
justment (BA) to minimize re-projection errors to op-
timize the final camera poses and scene point positi-
ons (Triggs et al., 2000; Agarwal et al., 2011; Frahm
et al., 2010) in multi-view 3D reconstruction pipeline.
Time and memory requirements for BA increase dra-
matically as the size of the BA problem grows. On the
other hand, with the convenience of Internet image
acquisition and the popularity of aerial equipment
such as UAV, the scale of reconstruction increases
continually. The high demand for resources by BA
solves makes it a major computational bottleneck for
the multiview 3D reconstruction.
Distributed Bundle Adjustment (DBA) (Eriksson
et al., 2016; Zhang et al., 2017; Ramamurthy et al.,
2017) is an iterative computing framework that uti-
lizes out-of-core parallelism. The original BA pro-
blem is divided into multiple subproblems with over-
lappings and distributed to local computing nodes. In
each iteration, each node solves a much smaller BA
problem. Different local overlap parameters are fu-
sed in the primary node and are then returned to the
worker nodes. The iterative process converges to a lo-
cal optimal solution of the original problem. Subpro-
blems require much less computation time and me-
mory. The DBA’s memory requirements are determi-
ned by subproblems and the total computation time t
is given by,
t = (t
s
+t
o
) × N
it
(1)
In addition to the time t
s
required for solving subpro-
blems, the data transfer of the overlapping parameters
results in transmission overhead t
o
, and N
it
is the num-
ber of iterations.
Block partitioning methods relate the total compu-
tation time t in three aspects: the scale of the largest
subproblem, the number of overlapping parameters,
and the local constraints, which correspond to t
s
, t
o
,
N
it
, respectively. The classical LM method for sol-
ving the BA problem exhibits a quadratic convergence
rate. However, the consensus framework on which
the DBA framework is based does not converge faster
than linear. Therefore, to accelerate overall conver-
gence, it is necessary to improve the local problem
constraint and use local optimization as much as pos-
sible to obtain better results. Based on these three as-
pects, the correlation between partitioning and com-
putational efficiency can be quantified, and a partitio-
ning metric function is proposed.
Under the block partitioning metric, the solution
of the optimal partitioning is actually a constrained
graph-partitioning problem. The constraint is that all
observation points are covered in at least one sub-
800
Liu, Z., Diao, C., Xing, W. and Lu, D.
Critical Parameter Consensus for Efficient Distributed Bundle Adjustment.
DOI: 10.5220/0007361108000807
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 800-807
ISBN: 978-989-758-354-4
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

block. Each parameter may be in any block, and so
there are exponential possible solutions. We propose
to perform block partitioning by a joint division of
points and cameras, and so the consensus will use a
portion of points and cameras that are critical over-
lapping parameters.
2 RELATED WORK
2.1 DBA
DBA divides the original high complexity BA pro-
blem into smaller subproblems. Optimizing subpro-
blems with no overlap can improve the accuracy of
local reconstruction (Zhu et al., 2014) but the solution
is not globally optimal. The consensus-based frame-
work was first proposed by Eriksson et al. (Eriks-
son et al., 2016), which is constructed as a Douglas-
Rachford splitting problem and converges to the lo-
cal minimum of the original BA problem. Zhang et
al. (Zhang et al., 2017) formulated the DBA problem
based on the alternating direction method of multi-
pliers (ADMM) and further refined the proof of con-
vergence. However, different block partitioning can
result in varied performance. Our method is also ba-
sed on the consensus framework and we focus on im-
proving the efficiency of DBA by exploring how to
partition the partitioning of subproblems.
2.2 Block Partitioning
Block partitioning methods in the multi-view 3D re-
construction pipeline can basically be divided into
two categories. The first one is point-based cluste-
ring. Based on the density, accuracy, and spatial prox-
imity of points, the adjacency graph (Zhu et al., 2014)
can be established. Then points are iteratively divided
into many parts. However, a large number of points
can make division a difficult task. Another category
includes image-based clustering methods. Kushal et
al. (Kushal and Agarwal, 2012) partitioned cameras
based on the Canonical Views algorithm (Simon et al.,
2007). A camera arrangement matrix can be obtained
according to clustering results, which is then used as
a pre-conditioner to ensure the stability of the normal
equation. The cluster method involves no overlapping
parameters. However, for a valid block partitioning in
DBA, overlapping parameters are required for con-
sensus across different blocks. In the pre-processing
step of dense reconstruction, Furukawa et al. (Furuk-
awa et al., 2010) hierarchically divided images to ens-
ure that the number of local images does not exceed a
predefined value. In addition, they added overlapping
images to the cluster to ensure that scene points are
well reconstructed. Although the local problem size
constraint can be satisfied, the number of local pro-
blems is not known before computation. In the case of
the approximate geometry of the known scene, image
clustering and scene segmentation can be combined
with (Zhang et al., 2015). For reconstruction methods
that are based on depth map, each image finds adja-
cent images (Mostegel et al., 2018; Mostegel et al.,
2016) and naturally forms a partition. The number of
such partitions is equal to the number of images and
the result of the partitioning can have a high degree of
overlap.
At present, there are few studies on the block
partitioning method for DBA. Block partitioning can
have a significant impact on efficiency because it de-
termines the data transmission overhead and local
computation time, and can also result in varied num-
ber of iterations. Existing methods perform point
clustering and add all visible images of points to local
blocks (Zhang et al., 2017), or add all visible points of
images to local blocks after image clustering. (Eriks-
son et al., 2016). The former introduces a large num-
ber of overlapping points. Since the number of points
is generally much larger than the number of images,
it will increase the data transmission overhead. Ne-
arly all points will present in each block when images
see a large portion of scene points. The latter increa-
ses the local optimization time since the computation
time of the local optimization is mainly determined
by the number of cameras.
3 CONSENSUS FRAMEWORK
3.1 ADMM Algorithm
Consensus framework for DBA can be constructed
based on DR Splitting or ADMM, which are mat-
hematically equivalent (Giselsson and Boyd, 2014).
The introduction below is based on ADMM. Consi-
der an optimization problem for univariate and multi-
objectives,
min
x
f (x) =
Σ
N
i=1
f
i
(x) (2)
where x ∈ R
n
, f
i
is the ith objective term. Solving
the problem in a distributed system requires that the
objective terms can be processed separately. By intro-
ducing the local variable x
i
∈ R
n
and the global vari-
able z, this problem can be rewritten as a constrained
problem, written as
min
x
Σ
N
i=1
f
i
(x
i
)
s.t.x
i
= z,i = 1,...,N
(3)
Critical Parameter Consensus for Efficient Distributed Bundle Adjustment
801

master
worker
distribute local block data
collect local update result
worker
(a)
p
1
𝑪
1
𝑪
2
𝑪
3
𝑪
4
p
2
p
3
p
4
p
5
p
6
0
(b)
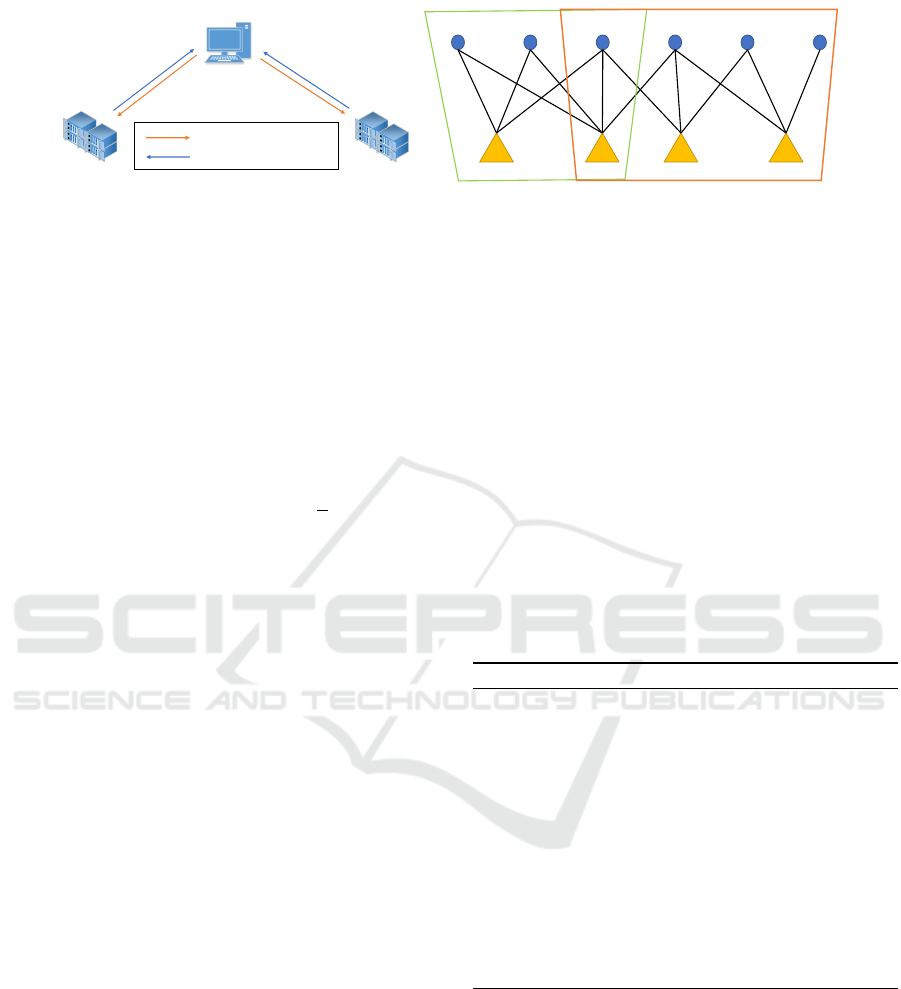
Figure 1: (a) Our consensus framework consists of a master node and K worker nodes (K=2 in the figure). In each iteration,
worker nodes optimizes local problems and passes results to the master node, which is transferred back to the working node
after the master node’s consensus computation. (b) An example of block partitioning. Each point is visible by multiple
cameras. The line between the point and the visible camera represents an observation. Block partition divides the visibility
graph into multiple subgraphs, which have overlapping cameras or 3D points for consensus.
The constraint is that all local variables are consistent,
and this problem is also known as a global consensus
problem.
The above constrained problem can be further
transformed into an unconstrained one through the
augmented Lagrangian method.
L
ρ
(x,y,z) =
N
Σ
i=1
( f
i
(x
i
) + y
T
i
(x
i
− z)+
ρ
2
k
x
i
− z
k
2
2
)
(4)
where x = x
1
,...,x
N
, ρ > 0 is the penalty parameter.
When ρ = 0, the above formula becomes the standard
Lagrangian form, and y
i
is the estimation of the La-
grange multiplier.
The ADMM algorithm iteratively optimizes
x
1
,...,x
N
, y, z. In the t + 1 iteration,
x
t+1
k
= argmin
x
k
L
ρ
(x
k
,y,z
t
) (5)
w
t+1
= argmin
w
L(x
t+1
k
,w,y
t
k
) =
K
Σ
k=1
x
t+1
k
(6)
y
t+1
k
= y
t
k
+ ρ(x
t+1
k
− w
t+1
) (7)
The iterations proceed until the difference between
the local variable and the global variable (the primal
residual) as well as the amount of change of the global
variable (the dual residual) are smaller than a given
threshold value.
3.2 Consensus for DBA
The original BA problem corresponds to f (x) in
ADMM in DBA. BA jointly optimizes camera pa-
rameters C = {C
1
,C
2
,...,C
m
} and sparse 3D scene
point coordinates by minimizing reprojection errors
P = {P
1
,P
2
,...,P
n
}:
argmin
C,P
f (C,P) = arg min
C,P
m
∑
i=1
n
∑
j=1
(v
ip
Π(C
i
,P
j
) − x
i j
)
2
(8)
Where v
i j
∈ {0, 1} is the visibility between the camera
C
i
and the 3D point P
j
and . The projection operator
Π(·) can project the given 3D point X
j
to the camera
C
i
. The projected point must coincide with observati-
ons o
i j
.
The objective function is the sum of multiple re-
projection errors and can be easily represented as
multiple objective terms. The parameter (C,P) to be
optimized corresponds to x in the formula 2. Suppose
that there is a block partitioning P = {(C
k
,P
k
)} and
(C
i
,P
i
) corresponds to x
i
, so that
f (C,P) =
Σ
N
k=1
f
k
(C
k
,P
k
) (9)
Algorithm 1: DBA: Processing by worker node k.
1: repeat
2: wait
3: until receive block data in P
k
from master node
4: initialize y
k
= 0
5: repeat
6: update y
k
as Equation 7
7: update x
k
as Equation 5
8: send overlap parameters in x
k
to master node
9: repeat
10: wait
11: until
12: receive the updated z
t+1
k
from master node
13: until termination
The above ADMM-based consensus framework
can be implemented in a star-topology distributed sy-
stem with one master node and multiple worker no-
des, as shown in Figure 1(a). The processings in the
master node and worker nodes are shown in the Algo-
rithm 2 and Algorithm 1, respectively.
Because the projection operator is non-linear, f (x)
is a non-convex function. According to the theo-
rem in (Zhang et al., 2017), f (x) must additionally
satisfy the ∇ f (x) local Lipshitz continuous condition.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
802

Algorithm 2: DBA: Processing by master node.
1: compute block splitting P
2: for all block P
k
∈ P do
3: send block data in P
k
to worker node k
4: end for
5: initialize iteration count t ← 0
6: repeat
7: repeat
8: wait
9: until
10: receive overlapping parameter updates from
all workers
11: compute w
t+1
in parameter consensus as
Equation 6
12: broadcast w
t+1
k
to all worker nodes
13: t ← t + 1
14: until termination
15: retrieve non-overlapping parameters from all
workers.
Specifically, 1) The gradient of the distortion function
must be Lipshitz continuous 2) Parameterization of
rotation requires Lipshitz continuous. Therefore, the
angle-rotation axis representation can be used in the
projection operator, while the over-parameterized re-
presentation of such rotation of the quaternion cannot.
3) The scene depth is greater than d
min
> 0.
4 BLOCK PARTITIONING FOR
EFFICIENT BA
4.1 Objective of Block Partitioning
In the DBA consensus framework, the block partitio-
ning results will be used to construct multi-objective
functions, which can include any combination of re-
projection error summations. The points and camera
parameters involved in a single objective function are
in the same block. Figure 1(b) illustrates an exam-
ple of block partitioning in which the triangle repre-
sents the camera and the circle represents the three-
dimensional point. If there is a line between the point
and the camera, there is an observation.
Suppose a block partitioning method divides the
original objective function into K objective functions.
Their sum must be equal to the original target and
each observation must appear in at least one block.
When the same observation occurs in multiple blocks,
the objective function must be reweighted.
P = {(C
k
,P
k
,O
k
)}s.t.∪
K
k=1
O
k
= O (10)
where 1 ≤ k ≤ K, C
k
⊂ C, P
k
⊂ P, O
k
is a collection of
observations corresponding to the camera and points
in the block. In the BA problem, points and came-
ras are related to each other. A simple partition with
no overlap will discard some observations, resulting
in the loss of the original information. In order to in-
clude all observations, there must be overlapping pa-
rameters. Therefore, block partitioning is a partitio-
ning problem with overlap. To take full advantage of
hardware resources, we set the number of partitions
to a fixed value, which can be determined based on,
for example, the number of cores.
Any block partitions that satisfy the constrain can
make the consensus converge in the end. However,
different partitions will affect their computational ef-
ficiency. We score block partitions based on three fac-
tors that determine the efficiency of DBA.
• Largest Subproblem Size. A larger block con-
tains more parameters and requires more time for
local optimization. Different BA solvers can pos-
sess different time complexity. For example, in
the BA solver without Schur complement, the
number of points is much larger than in the ca-
meras, which determines the computation time.
Cameras weigh much more if the camera para-
meters are first solved using Schur complement.
Here we consider both the points and the came-
ras. The LSS score is determined by the average
of the local point and the camera’s proportion of
all points and cameras.
LSS = 1 − (|C
i
|/m +|P
i
|/n)/2 (11)
• Data Transfer Overhead. The total amount of
data transmission can be computed based on pa-
rameterization. We normalize this score based on
the maximum size of possible overlapping para-
meters, and so the final DTO score is given by
DTO = 1 − (a
c


˜
C


+ a
p


˜
P


− a
t
)/((K − 1)a
t
)
(12)
• Local Coverage. Predicting how well a scene
is reconstructed is actually determined by several
aspects, such as visibility, angles, and distances.
Here, we simplify the problem by measuring only
the visibility as follows,
LC =
∑
K
k=1
(
∑
|C
k
|
i=1
V
k
i,:
/V
i
0
,:
+
∑
|P
k
|
j=1
V
k
:, j
/V
:, j
0
)/2K
(13)
To compare different methods more conveniently,
a numerical value for the classification method is re-
quired. We use a weighted average method to com-
bine the three metrics. The three values are not di-
rectly comparable, and their importance will also vary
Critical Parameter Consensus for Efficient Distributed Bundle Adjustment
803

depending on the network condition, computation re-
source, etc.
F
bs
= (w
1
LSS +w
2
DTO + w
3
LC)/(w
1
+ w
2
+ w
3
).
(14)
In the next section, we introduce our block partiti-
oning method.
4.2 Partitioning Method
Block partitioning is actually a graph partitioning pro-
blem on a bipartite graph, with each edge in at least
in one partition. Our goal is to determine a block par-
tition with a good partition score and improve the ef-
ficiency of DBA.
For a given number of divisions K, each point or
camera may be in any of the divisions, and so there are
((m + n)
K
) possible partitions in total. The proposed
block partitioning method consists of two steps. First,
the constraint that all observations must be covered is
relaxed and we find an initial non-overlapping parti-
tion. Then overlapping parameters are added to sa-
tisfy the constraints.
4.2.1 Biclustering-based Initialization
Biclustering (Dhillon, 2001) is a method of simulta-
neously clustering rows and columns of a matrix at
the same time. It is very similar to Normalized
Cut (Shi and Malik, 2000) and maximizes the inter-
block spacing and intra-block correlation while ensu-
ring uniform division. The difference is that bicluster
can be used directly for different adjacency matrices
for rows and columns. We compute the number of
observations in a block as
vis(C
k
,P
k
) =
∑
c
i
∈C
k
,p
j
∈P
k
v
i j
(15)
Then the association between a block and other
blocks can be expressed as cut
cut(C
k
,P
k
) = vis(C
k
,P
k
c
) + vis(C
k
c
,P
k
), (16)
the degree of association within the block is within,
within(C
k
,P
k
) = 2vis(C
k
,P
k
) + cut(C
k
,P
k
) (17)
Then the goal of the final optimization is
f
bc
(P) =
∑
K
k=1
cut(C
k
,P
k
)/within(C
k
,P
k
) (18)
This problem can be solved by the spectral met-
hod. By solving the SVD decomposition of the vi-
sibility matrix, each parameter is represented as a
K dimension vector. The sparsity of the visibility
graph makes the SVD decomposition easy to com-
pute. Then a K-means algorithm clusters the vectors
and the parameters into K blocks.
Figure 2: Initialization of block partitioning based on bi-
clustering. Rows, columns, and elements represent came-
ras, 3D points, and observations, respectively. We reorga-
nized the 3D points and camera index values based on their
labels. Points and cameras in the same block will form a
block in the visible view.
After biclustering, we reorganize them based on
the point index of the point and camera. When the
corresponding camera and point appear in the same
block, it is also assigned to this block. As can be seen
from Figure 3, aggregation occurs in the observations
in the different blocks. Intuitively, our partitioning
method hopes to ensure that the size of the block is
as uniform as possible, thereby reducing the largest
block, and reducing the local optimization time of the
largest block, thereby optimizing the local calculation
time. It is also necessary to reduce the number of ob-
servation points that are not on the diagonal block as
much as possible. For a point that is not on the dia-
gonal block, the coverage of the point and the camera
will be reduced. In the block partition metric function,
it is expressed as a reduction in the objective function.
We have initialized a partition with no overlap, and
there is a need for overlap in the DBA so that consen-
sus can be achieved.
4.2.2 Critical Parameter Voting
The initial non-overlapping parameter partitioning
does not cover all observations. The set of all obser-
vations O is equal to the union of the uncovered obser-
vations O
−
and the set of observed observations O
+
,
O
−
∪ O
+
= O . For o
i j
∈ O
−
, L
i
represents the block
where C
i
is located, and M
j
represents the block of P
j
.
In a valid block partition, O
−
=
/
0. Each parameter
in the initialization has its own block, so L
i
6=
/
0 and
P
j
6=
/
0. We use the triplet op = (k, i, b) to represent an
operation that adds a parameter to the block, where k
is the index of the block, 1 <= k <= K. Flag b speci-
fies the operation adds a camera or a point and i repre-
sents the index of the point or the camera. Then for
each o
i j
, the set of candidate operations corresponds
to is S
i j
. The set of all candidate operations is S. There
will be overlaps in the set of candidate operations for
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
804

different observations.
In this step, our goal is to obtain a set of operations
that cover all the observations and maximize the par-
titioning function. This is a combinatorial optimiza-
tion problem. We propose a greedy strategy to calcu-
late the sequence of operations, Q = op
1
,op
2
,...,op
q
.
Each operation picks the best action, making it the
largest variable for the split metric. Each add ope-
ration changes the block partition and its evaluation,
and so an add operation can be evaluated based on the
amount of score change.
f
v
(op) = ∆ f
bc
(19)
The scores of all candidate operations must to be
calculated when the parameters are added. There are
three main aspects involved in evaluating a single ope-
ration. Add a camera or point to a block, and the
transmission overhead increase is fixed, For a local
maximum block, it changes only when it corresponds
to the current largest block. The change in coverage
of a point depends on the number of points added.
Although the cost of a single operation is easy to cal-
culate, the number of points and cameras can be very
large because of large-scale problems. It is compu-
tationally infeasible to score all candidate operations
each time an operation is added. Therefore, we first
vote on these operations by adding the number of ob-
servations to obtain a smaller candidate set S. In addi-
tion, the addition will change the existing block par-
tition and will also affect the score of the next add
operation. Therefore, we compute the first K batch
operations each time, which improves efficiency. So
our final voting algorithm is shown in the Algorithm
3.
Algorithm 3: Critical Parameter Voting Algorithm.
Input: visibility graph V , number of blocks K
Output: block splitting P
1: Initialize a non-overlapping block splitting P
with biclustering as in Section 4.2
2: repeat
3: Initialize candidate operations set Q =
/
0
4: for all o
i j
that not in any block do
5: Q
i j
← candidate adding operation for o
i j
6: Q ← Q ∪ Q
i j
7: end for
8: Vote all the operations in Q as Equation 19
9: Sort operations with descending order by vo-
ting score
10: Perform min(N
batch
,|Q
+
|) operations in Q
with largest voting score
11: Update block splitting P
12: until Q =
/
0
Although the cost of a single operation is easy to
calculate, because the number of points and cameras
can be very large in large-scale problems, a single
operation will have an impact on the ratings of sub-
sequent operations. We calculate a batch operation
each time to improve computational efficiency.
5 EXPERIMENT
5.1 Dataset and Experiment Platform
We conducted experiments on the BAL public dataset
(Agarwal et al., 2010). The dataset statistics are pre-
sented in Table 1. Scenes in the dataset have different
sizes and initial reprojection errors. We also recorded
the runtime of the traditional BA method for a single
iteration.
Table 1: Dataset statistics. Different data sets have different
numbers of images, 3D points, 2D observations. The table
also shows the iteration time t
BA
.
dataset N
c
N
p
N
o
t
BA
ladybug s 49 7k 31k 0.29
trafalgar 257 65k 226k 1.4
ladybug 1723 157k 679k 4.9
venice 1778 994k 5.00M 31
final 13682 4456k 29M 279
The experiments are performed on a star-shaped
topology distributed platform of several workstations.
One of the workstations is the master node, and the
others are working nodes. Each node has an 8-core
3.6 GHz Intel i7-4770k CPU with 16GB memory.
The master node and the working node communi-
cate through the LAN, and the maximum transferring
speed between two nodes is about 100MB/s.
In the local problem solver, DBA is a meta-
algorithm for BA problems. In our consensus frame-
work, we use the iterative Schur algorithm in Goo-
gle’s Ceres Solver to solve the BA subproblem. The
iterative method accelerates the solution of the linear
equation in the Schur complement method.
Ceres Solver is implemented in C++, and we call
its interface directly in Python based on Cython. The
block partitioning and the consensus operation on the
master node are implemented in Python, and the data
transfer is directly based on socket. Setting of the
weight in the block partition evaluation must be car-
ried out according to the actual situation. For exam-
ple, the weight of DTO is related to data transmission
rate. The weight of LSS and LC depends on the com-
puting power of the node.
Critical Parameter Consensus for Efficient Distributed Bundle Adjustment
805

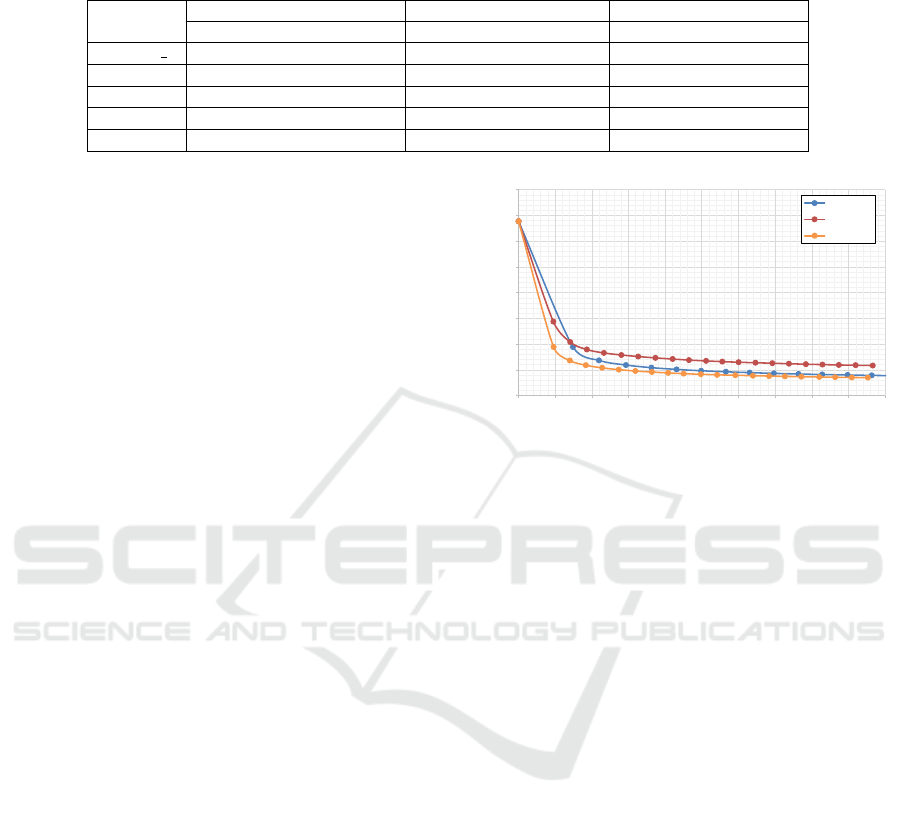
Table 2: Comparison of PC (Eriksson et al., 2016), CC (Zhang et al., 2017),and our CPC on partitioning metrics. The three
partitioning metrics are LSS, DTO and LC, which correspond to the maximum block size of the block partition, the number
of overlapping parameters, and the proportion of local visible points, respectively.
Dataset
PC (Eriksson et al., 2016) CC (Zhang et al., 2017) Our CPC
LSS DTO LC LSS DTO LC LSS DTO LC
ladybug s 0.284 0.210 0.919 0.250 0.995 0.780 0.292 0.924 0.935
ladybug 0.313 0.305 0.813 0.250 0.981 0.760 0.322 0.837 0.945
trafalgar 0.652 0.761 0.570 0.437 0.988 0.676 0.756 0.985 0.797
venice 0.884 0.953 0.930 0.504 0.969 0.512 0.923 0.995 0.988
final 0.679 0.694 0.832 0.437 0.995 0.647 0.726 0.987 0.923
5.2 Experimental Results
For each data set, the number of partitions is chosen
based on the size of the data set. We compare the
impact of different partitioning methods on DBA effi-
ciency based on three aspects: local computing time,
data transmission overhead and local coverage. Our
DBA method is referred as Critical Parameter Con-
sensus (CCP) to distinguish between existing Camera
Consensus (CC) method and Point Consensus (PC)
method. According to the partition metrics in Section
4, the three aspects correspond to the size of the lar-
gest block divided by the block, the amount of over-
lapping parameter transmission, and the coverage of
the partial block. Table 2 presents the comparison of
different block partitioning methods on the partitio-
ning metric. Our approach combines point and ca-
mera information and optimize LSS and LC during
the voting process. It can be seen from the table that
our method is superior to other methods in local cal-
culation time and coverage.
In terms of data transmission, the CC method is
slightly better than other methods. The number of
points is usually much larger than the number of ca-
meras, and so adding only the camera will obviously
bring more overlapping parameters. The time taken
for data transmission is actually related to the time
of data transmission. In an extreme network environ-
ment, the CC method can be adopted to reduce the
time overhead caused by data transmission. In addi-
tion, our method can change the weight according to
the actual situation, and changing weight to use more
overlapping cameras can achieve similar effects using
the CC method.
The values of LSS and DTO are the ratio of the
maximum subproblem size and the overlap parameter,
respectively, and their effects on transmission over-
head and computation time are relatively straightfor-
ward. The value of LC affects the speed at which the
DBA converges. We compare the convergence rates
of different methods through experiments, as shown
in Figure 3. Our CPC method exhibits the highest LC
value and the fastest convergence. In addition, we can
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 2 4 6 8 10 12 14 16 18 20
mean reprojection error (pix.)
Time (s)
PC
CC
Our CPC
Figure 3: Comparison of the convergence rates of different
partitioning methods on the ladybug dataset. The horizontal
axis is the time spent and the vertical axis is the average
reprojection error.
also observe from the table that greater local coverage
will also make the final reprojection error smaller.
Using more partitions will make the local problem
smaller, and so the local calculation time is small,
which increases the number of overlapping parame-
ters and reduce the local coverage. Increasing the
number of partitions will reduce the calculation time,
but as the number of partitions increases, the effi-
ciency increase will be less significant.
We also recorded the iteration time and correspon-
ding reprojection error of the traditional BA method
and different DBA methods. On smaller data set, the
actual computation time of a traditional BA is less
than the computation time of the DBA. The compu-
tational overhead in the DBA is significant when the
problem size is small. On a larger data set, DBA
demonstrates computational efficiency advantage be-
cause the local computation time is much smaller, ma-
king up for the disadvantages of data overhead and
convergence speed. DBA also uses less memory, and
so when a memory bottleneck exists, DBA is a better
choice than traditional BA methods.
6 CONCLUSION
In this paper, we have studied how to use both points
and cameras information in block partitioning to im-
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
806

prove the consensus framework for DBA. Our intui-
tion about this problem is that by properly assigning
the parameters in local blocks, the three indicators
LSS, DTO and LC that determines the total compu-
tation time can be balanced. We propose to biclus-
ter the visibility graph to initialize a non-overlapping
partition first, and then select the overlapping para-
meters that are critical for consensus using a scoring
scheme. Experimental results on multiple datasets
show that our joint block partitioning based critical
parameter consensus method is more efficient than ca-
mera consensus and point consensus. The final mean
projection error is comparable since our block parti-
tioning also guarantees the visibility information in
local blocks.
Future Work. In the current study, the local compu-
tation is performed synchronously, which means that
all worker nodes must wait for the largest block to
complete the computation. We plan to experiment
with the asynchronous consensus framework (Zhang
and Kwok, 2014) to further improve the performance
of DBA. In addition, we hope to use more computing
nodes and test larger datasets to further explore the
potential of our consensus framework.
ACKNOWLEDGEMENTS
This work is supported by the Key R&D Program of
Zhejiang Province, China (No. 2018C03051).
REFERENCES
Agarwal, S., Furukawa, Y., Snavely, N., Simon, I., Curless,
B., Seitz, S. M., and Szeliski, R. (2011). Building
rome in a day. Commun. ACM, 54(10):105–112.
Agarwal, S., Snavely, N., Seitz, S. M., and Szeliski, R.
(2010). Bundle adjustment in the large. In European
Conference on Computer Vision, pages 29–42.
Dhillon, I. S. (2001). Co-clustering documents and words
using bipartite spectral graph partitioning. In Procee-
dings of the seventh ACM SIGKDD international con-
ference, pages 269–274. ACM.
Eriksson, A., Bastian, J., Chin, T.-J., and Isaksson, M.
(2016). A consensus-based framework for distributed
bundle adjustment. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 1754–1762.
Frahm, J. M., Fitegeorgel, P., Gallup, D., Johnson, T., Ragu-
ram, R., Wu, C., Jen, Y. H., Dunn, E., Clipp, B., and
Lazebnik, S. (2010). Building rome on a cloudless
day. In European Conference on Computer Vision,
pages 368–381.
Furukawa, Y., Curless, B., Seitz, S. M., and Szeliski, R.
(2010). Towards internet-scale multi-view stereo. In
Computer Vision and Pattern Recognition (CVPR),
2010 IEEE Conference on, pages 1434–1441. IEEE.
Giselsson, P. and Boyd, S. (2014). Linear convergence
and metric selection for douglas-rachford splitting and
admm. IEEE Transactions on Automatic Control,
62(2):532–544.
Kushal, A. and Agarwal, S. (2012). Visibility based precon-
ditioning for bundle adjustment. In Computer Vision
and Pattern Recognition, pages 1442–1449.
Mostegel, C., Fraundorfer, F., and Bischof, H. (2018). Pri-
oritized multi-view stereo depth map generation using
confidence prediction. ISPRS Journal of Photogram-
metry and Remote Sensing.
Mostegel, C., Rumpler, M., Fraundorfer, F., and Bischof, H.
(2016). Using self-contradiction to learn confidence
measures in stereo vision. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion, pages 4067–4076.
Ramamurthy, K. N., Lin, C.-C., Aravkin, A. Y., Pankanti,
S., and Viguier, R. (2017). Distributed bundle adjust-
ment. In ICCV Workshops, pages 2146–2154.
Shi, J. and Malik, J. (2000). Normalized cuts and image
segmentation. IEEE Transactions on pattern analysis
and machine intelligence, 22(8):888–905.
Simon, I., Snavely, N., and Seitz, S. M. (2007). Scene sum-
marization for online image collections. In IEEE In-
ternational Conference on Computer Vision, pages 1–
8.
Triggs, B., Mclauchlan, P. F., Hartley, R. I., and Fitzgibbon,
A. W. (2000). Bundle adjustment a modern synthesis.
Lecture Notes in Computer Science, 1883(1883):298–
372.
Zhang, R. and Kwok, J. T. (2014). Asynchronous distribu-
ted admm for consensus optimization. In Internatio-
nal Conference on International Conference on Ma-
chine Learning, pages II–1701.
Zhang, R., Li, S., Fang, T., Zhu, S., and Quan, L. (2015).
Joint camera clustering and surface segmentation for
large-scale multi-view stereo. In Proceedings of the
IEEE International Conference on Computer Vision,
pages 2084–2092.
Zhang, R., Zhu, S., Fang, T., and Quan, L. (2017). Dis-
tributed very large scale bundle adjustment by global
camera consensus. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 29–38.
Zhu, S., Fang, T., Xiao, J., and Quan, L. (2014). Local re-
adjustment for high-resolution 3d reconstruction. In
Proceedings of the IEEE Conference on Computer Vi-
sion and Pattern Recognition, pages 3938–3945.
Critical Parameter Consensus for Efficient Distributed Bundle Adjustment
807