
Performance Evaluation of Real-time and Scale-invariant
LoG Operators for Text Detection
Dinh Cong Nguyen
1,2
, Mathieu Delalandre
1
, Donatello Conte
1
and The Anh Pham
2
1
Tours University, Tours City, France
2
Hong Duc University, Thanh Hoa, Vietnam
{nguyendinhcong, phamtheanh}@hdu.edu.vn
Keywords:
Text Detection, LoG, Blobs, Key-points, Real-time, Estimators, DoG, Fast Gaussian Filtering, Scale-space,
Stroke Model, Groundtruthing, Performance Characterization, Repeatability.
Abstract:
This paper presents a state-of-the-art and a performance evaluation of real-time text detection methods, ha-
ving particular focus on the family of Laplacian of Gaussian (LoG) operators with scale-invariance. The
computational complexity of operators is discussed and an adaptation to text detection is obtained through
the scale-space representation. In addition, a groundtruthing process and a characterization protocol are pro-
posed, performance evaluation is driven with repeatability and processing time. The evaluation highlights a
near-exact approximation with real-time operators at one to two orders of magnitude of execution time. The
real-time operators are adapted to recent camera devices to process high resolution images. Perspectives are
provided for operator robustness, optimization and characterization of the detection strategy.
1 INTRODUCTION
Text processing in natural images is a core topic in
the fields of image processing and pattern recognition.
Recent state-of-the-arts on methods and international
contests can be found in (Ye and Doermann, 2015)
and (Gomez et al., 2017), respectively. A key pro-
blem is to make these methods being time efficient so
that they can be embedded into devices (e.g. smartp-
hone, tablet, smart camera) to support a real-time pro-
cessing (Yang et al., 2015; Girones and Julia, 2017;
Deshpande and Shriram, 2016).
The real-time systems in the literature (Gomez
and Karatzas, 2014; Liu et al., 2014; Yang et al.,
2015; Girones and Julia, 2017) apply the strategy of
two stages composing of detection and recognition.
The detection stage localizes the text components at a
low complexity level and groups them into text candi-
date regions before classification. The goal is to get a
perfect recall for the detection with a maximum pre-
cision for optimization of the recognition. The two-
stage strategy differs from the end-to-end strategy,
that applies a direct template/feature matching with
classification using high-level models for text (Neu-
mann and Matas, 2016).
The text elements in natural images present spe-
cific shapes with elongation, orientation and stroke
width variation, etc. as shown in Figure 1. This ma-
kes difficult to the detection problem. Hence, various
approaches have been investigated in the literature to
design real-time and robust methods.
Figure 1: Example of text elements/characters in images,
extracted from (de Campos et al., 2009).
The published works drive the text processing as a
blob detection problem with the maximally stable ex-
tremal regions (MSER) (Yang et al., 2015; Deshpande
and Shriram, 2016) and the LoG-based operators (Liu
et al., 2014; Girones and Julia, 2017).
MSER looks for the local intensity extrema and
applies a watershed-like segmentation algorithm. The
operator is rotation, scale and affine-invariant. It
can be processed at a linear complexity (Salahat
and Qasaimeh, 2017). It performs well with back-
ground/foreground regions but is sensitive to blurring.
Alternative to MSER is the Laplacian of Gaus-
sian (LoG) operator. The LoG operator is also a blob
detector. Similar to MSER, it can be made rotation,
344
Nguyen, D., Delalandre, M., Conte, D. and Pham, T.
Performance Evaluation of Real-time and Scale-invariant LoG Operators for Text Detection.
DOI: 10.5220/0007361503440353
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 344-353
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Table 1: The symbols used in the paper.
Symbols Meaning Symbols Meaning
Continuous/discrete domain ∇
2
Laplacian
f An image function/raster b Estimator
g A Gaussian function/operator k Parameter to control approximation between LoG, DoG
Π A step function/box filter ϖ The stroke model function σ
s
= ϖ(w)
w Stroke width parameter with w ∈ [w
min
,w
max
] Discrete domain
a Signal amplitude λ Weighting parameter
β,α Thresholding parameters ω
2
Size of operator (width × height)
⊗ The global convolution product (σ
0
...σ
m
) A filter bank including (m + 1) discrete filters
Continuous domain n Number of box filters
σ, σ
s
The standard deviation, optimum scale for stroke detection N Size of image
h, h
s
, h
e
Response with the stroke model, h
s
/h
e
the stroke/edge optimums O Complexity
g
xx
(either y) Second partial derivative of the g function r, ε Radius of region, overlap error
scale and contrast-invariant. However, it is less sensi-
tive to blurring and can be tuned as a stroke detector.
As a general trend, the operator ensures a better cha-
racterization of text elements.
The LoG operators can be made real-time and
competitive with respect to MSER. At the best of
our knowledge, the real-time property of LoG ope-
rators has been explored only for spatial filtering and
scale-invariance. The operators, which are contrast-
invariant (Miao et al., 2016) or generalized (Kong
et al., 2013), cannot fit with the real-time constraint.
This paper gives an overview and a performance
evaluation of real-time and scale-invariant LoG ope-
rators for text detection. Adaptation to text detection
is achieved by the scale-space representation. Per-
formance evaluation analyzes the impact of real-time
operators for text detection with their parameters and
gives a comparison in term of time processing.
The organization of the remainder of the paper is
as follows. Section 2 gives the state-of-the-art. Then,
performance evaluation of operators is discussed in
section 3. At last, section 4 will conclude and propose
some perspectives. Table 1 provides the meaning of
the main symbols used in the paper.
2 STATE-OF-THE-ART
2.1 Introduction
The LoG operator is defined as the Laplacian of Gaus-
sian, and then derived from the Gaussian function.
The Gaussian function, in a multivariate form, is gi-
ven in Eq. (1) with a vectorial notation.
g(p|µ,Σ) =
1
(2π)
n
2
p
|Σ|
e
−
1
2
(p−µ)
T
Σ
−1
(p−µ)
(1)
In the two dimensional case, n = 2, p is a point
and µ a mean. Σ is the diagonal covariance matrix
with Σ
−1
the inverse and |Σ| the determinant, where
the σ
x
,σ
y
parameters in Σ are the standard deviations
for the dimensions x, y. Considering σ
x
= σ
y
= σ, µ
null and a scalar notation, the Gaussian function Eq.
(1) becomes Eq. (2).
g(x,y,σ) =
1
2πσ
2
e
−
x
2
+y
2
2σ
2
(2)
The LoG is a compound operator resulting of the
Laplacian ∇
2
of g(x,y,σ) as Eq. (3).
∇
2
g(x,y,σ) = g
xx
(x,y,σ) + g
yy
(x,y,σ)
=
1
2πσ
4
x
2
+ y
2
σ
2
−2
e
−
x
2
+y
2
2σ
2
(3)
The LoG-filtered image h(x,y) Eq. (4) is obtained
by the global convolution ⊗ between the initial image
f (x,y) and the LoG operator ∇
2
g(x,y,σ).
h(x,y) = ∇
2
g(x,y,σ) ⊗ f (x,y) (4)
As illustrated in Figure 2, the response of the LoG
operator Eq. (4) is dependent on the σ parameter. At
a low value, the operator focuses its response to ed-
ges that can be detected with zero-crossing. When σ
increases, a peak at the blob location appears in the
response. Due to noise, the peak is thresholded to get
the blob components. The blob centroid is obtained
with a non-maximum suppression in the local neig-
hborhood. The corresponding key-point is expressed
with the centroid coordinates and a radius having a
normal value r =
√
2σ for a circular blob.
However, this peak value relies on the correla-
tion between σ and the size of the blob, and a wrong
scale can result in a missed detection. To deal with
this problem, the standard approach is to handle the
operator in the scale-space domain with a filter bank
(σ
0
,...,σ
m
). This requires a specific approach for op-
timization to bound the number of filters and to handle
them in a time efficient way.
Another constraint is the processing time for filte-
ring. The convolution product of Eq. (4) has a com-
plexity O(Nω
2
) with N the image size (in pixels) and
ω
2
the size (width × height) of the LoG filter. The
size of the filter is dependent on the σ parameter such
as we have ω = 6σ for a full coverage. This leads to a
Performance Evaluation of Real-time and Scale-invariant LoG Operators for Text Detection
345
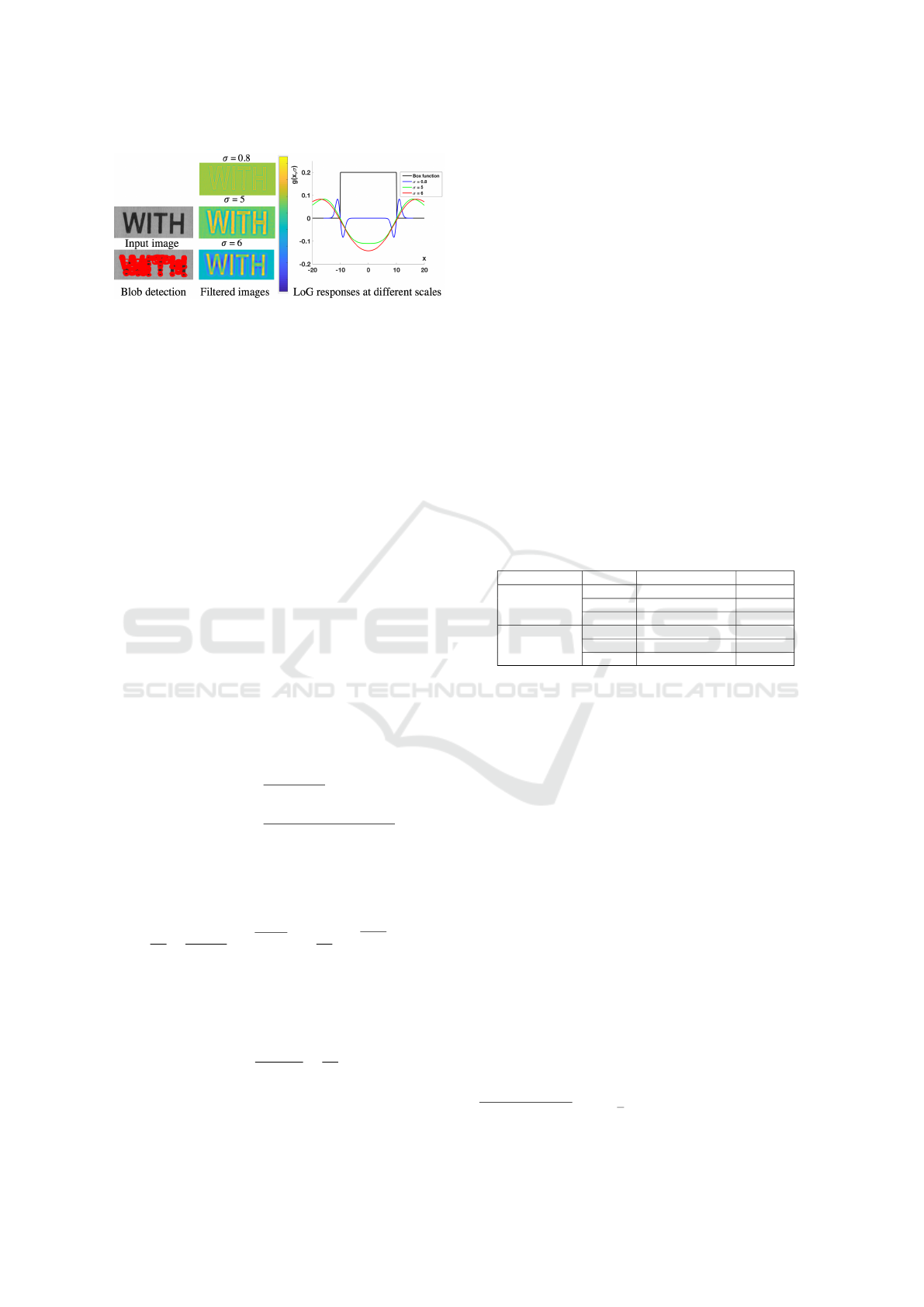
Figure 2: Text detection with a LoG operator with different
values for the σ parameter.
large processing time making the operator little com-
patible with a real-time use-case. To cope with this
problem, several contributions have been proposed in
the literature for reformulation and approximation of
the LoG operator.
We will discuss the different optimization issues
in next sections.
2.2 Fast LoG Filtering
The standard approach to accelerate the LoG filtering
is to reformulate the LoG function into a Difference of
Gaussian (DoG) function and then to approximate the
DoG function with a fast Gaussian filtering method.
The DoG function is defined from the heat equa-
tion Eq. (5) (Lindeberg, 1994). In Eq. (5), the norma-
lization of the LoG function Eq. (3) with a scale para-
meter σ gives the derivative of the Gaussian function
in the scale-space domain. The left term of Eq. (5)
can be reformulated as a local derivative, with k a pa-
rameter and a step offset δ
σ
= (k −1)σ. The approxi-
mation of the derivative in this equation gets better as
δ
σ
goes to 0 when k comes to 1.
σ∇
2
g(x,y,σ) =
∂g(x,y,σ)
∂σ
≈
g(x,y,kσ) −g(x, y, σ)
(k −1)σ
(5)
With reformulation of Eq. (5), the LoG function
can be approximated by mean of a DoG as Eq. (6),
g(x,y,kσ
2
) −g(x,y,σ
2
) ≈ (k −1)σ
2
∇
2
g(x,y,σ)
=
1
2π
1
(kσ
2
)
2
e
−
x
2
+y
2
2(kσ
2
)
2
−
1
σ
2
2
e
−
x
2
+y
2
2σ
2
2
(6)
with a normalization factor (k −1)σ
2
. Considering
σ
1
= kσ
2
, the relation among σ,σ
1
,σ
2
is formulated
as Eq. (7) (Gonzalez and Woods, 2007).
σ
2
=
σ
2
1
σ
2
2
σ
2
1
−σ
2
2
ln
σ
2
1
σ
2
2
(7)
The DoG function is computed with two Gaus-
sian filters. With convolution, the Gaussian filtering
can be implemented in separable way at a complexity
O(Nω). When ω is large, it is still a time consuming
task. Several methods have been proposed in the li-
terature to accelerate the Gaussian filtering and make
it independent of the filter size at a complexity O(N).
These methods attempt to improve computational ef-
ficiency in the expense of accuracy. They are referred
as fast Gaussian filtering methods. They enter in an
estimator cascade methodology where LoG ≈DoG ≈
d
DoG, with
d
DoG a DoG estimator.
Survey with performance evaluation can be found
in (Charalampidis, 2016; Elboher and Werman,
2012). Two main categories have been investigated
including the box and recursive-based filters. The se-
lection of a suitable method depends on the applica-
tion use-case which is supposed to be solved in term
of a good trade-off between speed and accuracy. The
Table 2 gives a global comparison of the methods.
Table 2: Time optimization and accuracy of fast Gaussian
filterings: (SII) Stacked Integral Image (VYV) Vliet Young
Verbeek (KII) Kernel Integral Image (TCF) Truncated Co-
sine Functions (+++) best case (+) medium case.
Category Methods Time optimization Accuracy
Box ++ +++
Box filter SII +++ ++
KII + +
Deriche ++ ++
Recursive filter TCF +++ +++
VYV + ++
For illustration, we will give here the box filte-
ring method (Kovesi, 2010; Fragoso et al., 2014). As
shown in the Table 2, the method is referred as the top
accurate box-based filters and being competitive with
the recursive filters. The box filtering method sums up
averaging filtering to approximate a Gaussian filter, as
Eq. (8) with a desired standard deviation.
b
g(x,y,σ) =
n
∑
i=1
λ
i
Π
i
(x,y) (8)
In Eq. (8) Π
i
(x,y) is a box filter function having
a predefined size with a value 1 if (x, y) are located
inside the box, 0 otherwise. The λ
i
parameters weight
the box filters Π(x, y). n is the number of box filters
that can be fixed between 4 to 6 for a good trade-off
between optimization and robustness (Kovesi, 2010).
From Eq. (8), it becomes possible to approximate
the DoG operator by
d
DoG in Eq. (9) with two sets of
box filter functions. As the k parameter in Eq. (5) is
supposed to be low
1
, a similar number of filters can
1
In practice, k ∈]1,
√
2].
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
346
be applied for estimation of the two Gaussian kernels.
d
DoG =
b
g(x,y,kσ) −
b
g(x,y,σ)
=
n
∑
i=1]
λ
i
Π
i
(x,y) −
n
∑
j=1
λ
j
Π
j
(x,y) (9)
The DoG-filtered image is achieved by the global
convolution Eq. (10) between the input image f (x, y)
and the DoG estimators
d
DoG.
(
b
g(x,y,kσ) −
b
g(x,y,σ)) ⊗ f (x,y)
=
b
g(x,y,kσ) ⊗ f (x, y) −
b
g(x,y,σ) ⊗ f (x,y)
=
n
∑
i=1
λ
i
Π
i
(x,y) ⊗ f (x,y) −
n
∑
j=1
λ
j
Π
j
(x,y) ⊗ f (x,y)
(10)
Obviously, the Π
i
(x,y) ⊗ f (x, y) products of Eq.
(10) can be obtained with integral image at a com-
plexity O(N). As a result, approximation of the DoG
operator could be achieved with 2n accesses to the in-
tegral image, it is therefore parameter free.
A core problem with the Gaussian kernel approx-
imation is to fix the n, Π
i
(x,y), λ
i
parameters of Eq.
(8). The approach used in the literature (Bhatia et al.,
2010; Fragoso et al., 2014) is the minimization of the
Mean Square Error (MSE) Eq. (11). This minimi-
zation can be achieved by any appropriate numerical
methods for regression. In (Fragoso et al., 2014), the
LASSO algorithm is used to solve the problem.
MSE =
∑
(x,y)∈[0,w]
(g(x,y) −
b
g(x,y))
2
(11)
2.3 Scale-space Representation
As discussed in section (2.1), the stroke detection is
dependent on the scale parameter σ. To deal with this
problem, the standard approach is to deploy a filter
bank at different scales (σ
0
,...,σ
m
). This is referred as
the scale-space representation in the literature (Lowe,
2004; Nilufar et al., 2012), which is counted on the
used operator and the considered detection problem.
We will have a particular focus here on the DoG ope-
rator for stroke detection.
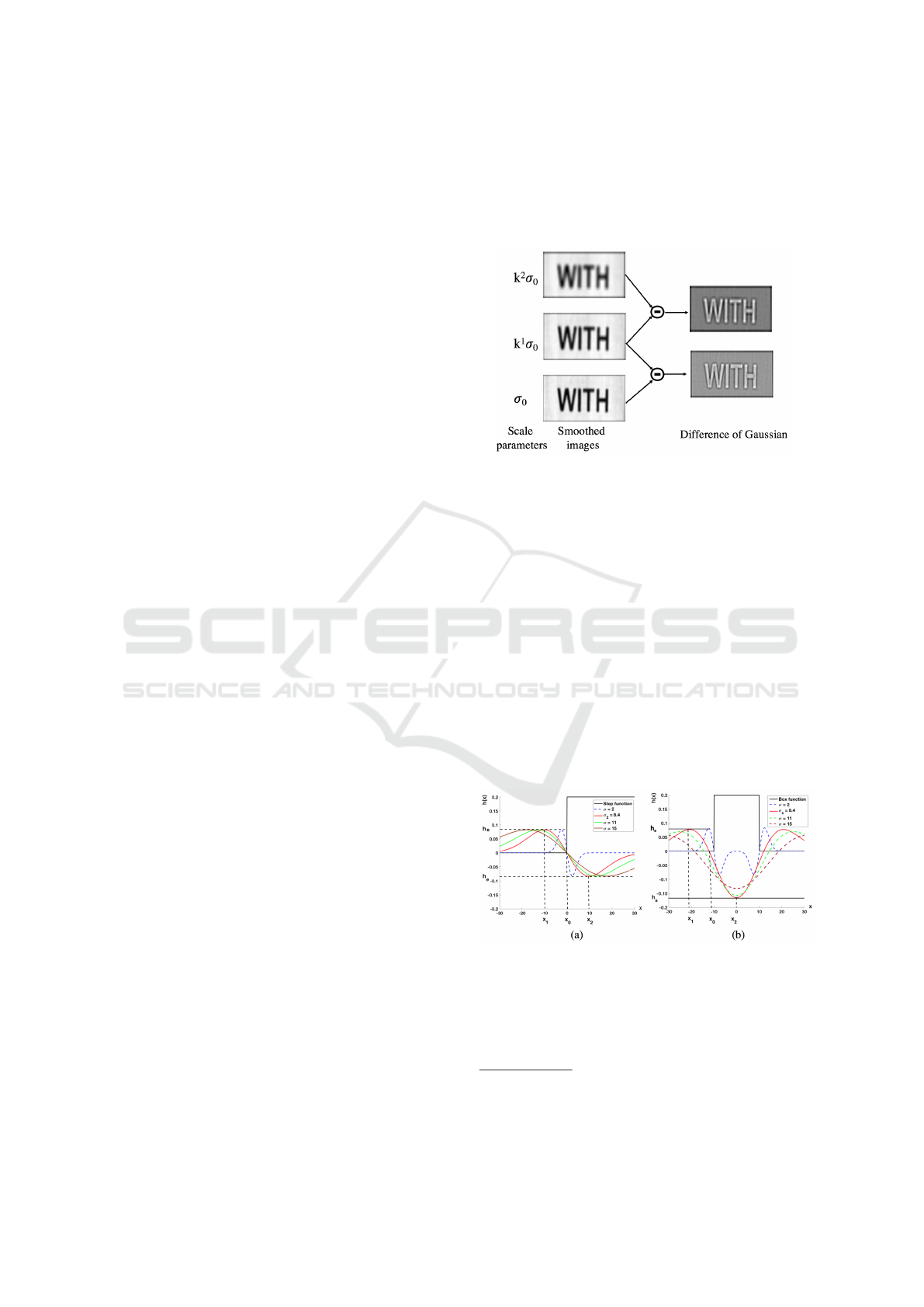
A time-efficient approach for construction of the
scale-space responses with DoG has been proposed
in the SIFT descriptor (Lowe, 2004). It was applied
in several papers for text detection (Mao et al., 2013;
Risnumawan et al., 2014). The approach is illustra-
ted in Figure 3. The input image is convolved with a
set of (m + 1) Gaussian filters having different scales
(σ
0
,...,σ
m
). Each scale is fixed as σ
i
= k
i
σ
0
. The k
parameter is set to ensure a doubling of σ
0
at a 2
1/m
value. The DoG product is obtained by comparison of
adjacent image scales, that reduces by half the needed
filters. For optimization purposes, the overall process
is applied with a small set of filters (e.g. 5) and repea-
ted in a closed-loop way, where a re-sampling is used
at any loop
2
. The overall computation is then greatly
reduced.
Figure 3: Scale-space representation of (Lowe, 2004).
The approach of (Lowe, 2004) considers an expo-
nential model for the scale-space representation. For
stroke detection, contributions in the literature sug-
gest a linear model where the parameter σ is able to
be derived from the stroke width parameter w. This is
presented as the stroke model (Liu et al., 2014).
The Figure 4 illustrates the model. The general
idea is to look for the convolution response between a
LoG-based operator and a stroke signal modeled as an
unit step function. We can express then the null cases
with the derivatives to get the minimum/maximum of
the convolution product. Assuming that these mini-
mum/maximum are located at the center of the stroke
w/2, we can present the standard deviation σ as a
function σ = ϖ(w).
Figure 4: LoG responses at different scales to (a) a step
function (b) a boxcar function of size w = 21.
Assuming the image signal as a function
3
a ⊗
Π(x), where Π(x) is the step function Eq. (12) and a
as the signal amplitude, the convolution product with
2
Additional optimization is achieved with successive
convolutions, we will report the reader to (Lowe, 2004).
3
For simplification, considering the 1D case.
Performance Evaluation of Real-time and Scale-invariant LoG Operators for Text Detection
347

the LoG operator ∇
2
g(x) is given in Eq. (13).
Π(x
0
−x) =
(
0 x < x
0
1 otherwise.
(12)
h(x
0
) = a(Π ⊗∇
2
g)(x
0
)
= a
Z
+∞
−∞
Π(x
0
−x)∇
2
g(x)dx (13)
As Π(x
0
−x) is located at x
0
, the convolution pro-
duct Π(x
0
−x) ⊗∇
2
g(x) over x equals the summation
∇
2
g(x) centered at x
0
. With normalization and ap-
proximation of ∇
2
g(x) as given in Eq. (6), the Eq.
(13) is reformulated into Eq. (14).
(k −1)σ
2
h(x
0
)
≈
Z
+∞
−∞
a(g(x
0
−x,σ
1
) −g(x
0
−x,σ
2
))dx (14)
From the derivative of Eq. (14) with a reformula-
tion into Eq. (6), the local extremal optimum is obtai-
ned as Eq. (15) with the k parameter.
x
1,2
= ±kσ
r
2lnk
k
2
−1
(15)
As given in Eq. (15) and illustrated in Figure 4
(a), it can be seen that the x
1,2
locations are dependent
on the σ parameter. While bringing x
2
= x
0
+w/2 the
center of the stroke and goes to Eq. (15), we can get
the optimum scale σ
s
Eq. (16).
σ
s
= ϖ(w) =
w
2k
r
k
2
−1
2lnk
(16)
As illustrated in Figure 4 (b), two responses h
e
,h
s
appear within the model at the x
1,2
locations with σ
s
.
The response h
e
characterizes the edge of the
stroke. It is obtained with Eq. (17) while brin-
ging σ
s
Eq. (16) back to Eq. (14), and approxi-
mating the Gaussian integral at any location in Eq.
(14) with a er f (x) Gaussian error function er f (x) =
2
√
π
R
x
0
e
−t
2
dt. For notation simplification, the Eq. (17)
is given by considering x
0
= 0.
h
e
=
a
2
er f
k
r
lnk
k
2
−1
!
−er f
r
lnk
k
2
−1
!!
(17)
A peak response h
s
appears at the middle of the
stroke w/2. This response decreases while shifting
the scaling parameter σ around the σ
s
optimum Fi-
gure 4 (b). However, no mathematical formulation for
h
s
was proposed in the model. This results from the
proposed proof that interpolates the stroke response
from a step function. At the best of our knowledge,
Figure 5: LoG responses at different signal amplitudes and
widths of the box function with k =
√
2.
the h
s
formulation has been never investigated in the
literature. Simulation reveals a value h
s
that is inde-
pendent of the scale parameter σ and proportional to
the signal amplitude a, as illustrated in Figure 5.
The optimization within the scale-space conside-
ring the stroke model is attained while applying an
optimal quantization σ
s
= ϖ(w) of Eq. (16) with
w ∈ [w
min
,w
max
] as a discrete value. The size of the
filter bank is then correlated to the stroke width gap
of the considered detection problem such as we have
m = w
max
−w
min
. With a DoG formulation, this re-
quires 2(m + 1) Gaussian kernels for detection.
3 PERFORMANCE EVALUATION
3.1 Introduction
We present in this section a performance evaluation
of the real-time LoG operators with the used dataset,
groundtruth and characterization protocol.
Several datasets are available for performance
evaluation of text detection such as the ICDAR Ro-
bust Reading Competition 2017 and the COCO-text
datasets (Gomez et al., 2017; Nayef et al., 2017).
These datasets target performance evaluation of text
detection where the groundtruth is given at the word
level. They are not adapted for characterization of de-
tectors at the pixel level. For this specific purpose,
we have developed a semi-automatic groundtruthing
process, as given in Figure 6.
This semi-automatic groundtruthing process tar-
gets near optimum parameters for scale-invariant LoG
filtering. The parameters are fixed with a closed-loop
methodology by an expert user, while inspecting the
visual quality of the filtered images. The process ap-
plied no hand-made modification of the ground-truth,
just a control of the parameters. This task uses a prior
segmentation of character images. We have applied
to a subset of the public Chars74K dataset (de Cam-
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
348

pos et al., 2009), as presented in Figure 1 and Table
3. This subset has been extracted from full images
captured at a low resolution. Our overall process uses
four main components C
1
,C
2
,C
3
and C
4
.
Figure 6: Semi-automatic process for groundtruthing.
• C
1
controls the scale-space. For groundtruthing,
we applied a brute-force strategy with a filter bank
σ
0
,...,σ
m
having a large size m+ 1 = 101 at regu-
lar scale intervals. The minimum and maximum
values w
min
,w
max
have been fixed as heuristics by
an expert user.
• C
2
fixes the operator response. The LoG ope-
rator with a normalization (k − 1)σ
2
is applied
for groundtruthing allowing a direct comparison
with the real-time estimators. The responses are
computed at all scales and locations, a maximum
h(x,y) is selected.
• C
3
,C
4
control the response. The selection of a
key-point is done with a threshold β fixed by
the expert user such as we obtain a key-point if
h(x,y) > β. The thresholding is applied after a
non-maximum suppression (NMS) step as com-
mon for blob detection with the LoG operator
(Lindeberg, 1994). As the operator response is
dependent on the background/foreground ampli-
tude a, an estimation ˆa is obtained with the met-
hod of (Otsu, 1979) in C
4
and applied for normali-
zation in C
2
before C
3
. For the sake of evaluation,
we store for each key-point the optimum response
h
s
(x,y) and scale σ
s
(x,y).
Table 3: The subset of character images in the Chars74K
dataset (de Campos et al., 2009).
Images 7705
Classes 62
Size (Kpixel) 0.3K-10K
[w
min
,w
max
] [5, 30]
Resolution of full images 640 x 480 (VGA)
For characterization, the repeatability criteria is
used as a regular metric for local detectors (Rey-Otero
et al., 2014a). ((x
r
,y
r
,r
r
)
re f
,(x
t
,y
t
,r
t
)
test
) are refe-
rence and test key-points describing circular regions
of radius r
r
, r
t
respectively. (x
t
,y
t
,r
t
)
test
is taken un-
der approximation of (x
r
,y
r
,r
r
)
re f
. The two regions
will be considered as repeated if they respect an over-
lap error ε Eq. (18). For the need of evaluation,
we have fixed the computation of the radius with the
stroke model of Eq. (16), while fixing r = w/2.
1 −
|(x,y,r)
test
∩(x,y,r)
re f
|
|(x,y,r)
re f
∪(x,y,r)
test
|
≤ ε (18)
A global repeatability score indicates how the key-
points in the reference feature map are repeated in the
test feature map. We denote n
r
and n
t
as the numbers
of key-points in the two maps, respectively. The repe-
atability score is estimated as ratio between number
of repeated key-points over minimal of (n
r
,n
t
).
Experimentally, the global repeatability score of
a detector is computed as an average of repeatability
scores of all character images in the dataset. We relax
the value of the parameter ε to achieve a ROC −like
curve of the global repeatability score. In most publis-
hed benchmarks (Rey-Otero et al., 2014a), the para-
meter ε is set in range [0.3,1] where the value ε = 0.4
is the maximum overlap error tolerated.
The operator responses depend on several aspects
as the estimation methods and parameters, the scale-
space representation or the signal amplitude. For a de-
tailed analysis, particular characterization tasks must
be defined. For this specific purpose, we deployed
the architecture of our groundtruthing process Figure
6 and relaxed the components C
1
to C
4
. The Table 4
details our overall protocol.
• The tasks 1 to 4 evaluate the real-time operators.
• The tasks 5, 6 describe the robustness under con-
ditions of low resolution and illumination change.
• The task 7 gives the time processing.
We distinguish these different tasks thereafter.
Table 4: The characterization protocol.
Task C
1
C
2
k C
3
Groundtruth Brute-force
1
ˆa
σ
2
(k −1)∇
2
g None β
Task 1 Brute-force
1
ˆa
(g
1
−g
2
) k ∈]1,
√
3] β
Task 2 Brute-force
1
ˆa
( ˆg
1
− ˆg
2
) k ≈1 β
Task 3
Stroke model
1
ˆa
(g
1
−g
2
)
k ≈1 β
SIFT
Task 4 Stroke model
1
ˆa
( ˆg
1
− ˆg
2
) k ≈1 β
Task 5 Stroke model
1
ˆa
(g
1
−g
2
) k ≈1 β
Task 6 Brute-force (g
1
−g
2
) k ≈1 α
Task 7
SIFT g
1
−g
2
k ≈1 αStroke model g
1
−g
2
Stroke model ˆg
1
− ˆg
2
3.2 LoG Estimators (Tasks 1, 2)
The characterization tasks 1, 2 are related to the LoG
approximation with a DoG and a fast Gaussian filte-
ring method, as discussed in section (2.2). For a fair
Performance Evaluation of Real-time and Scale-invariant LoG Operators for Text Detection
349
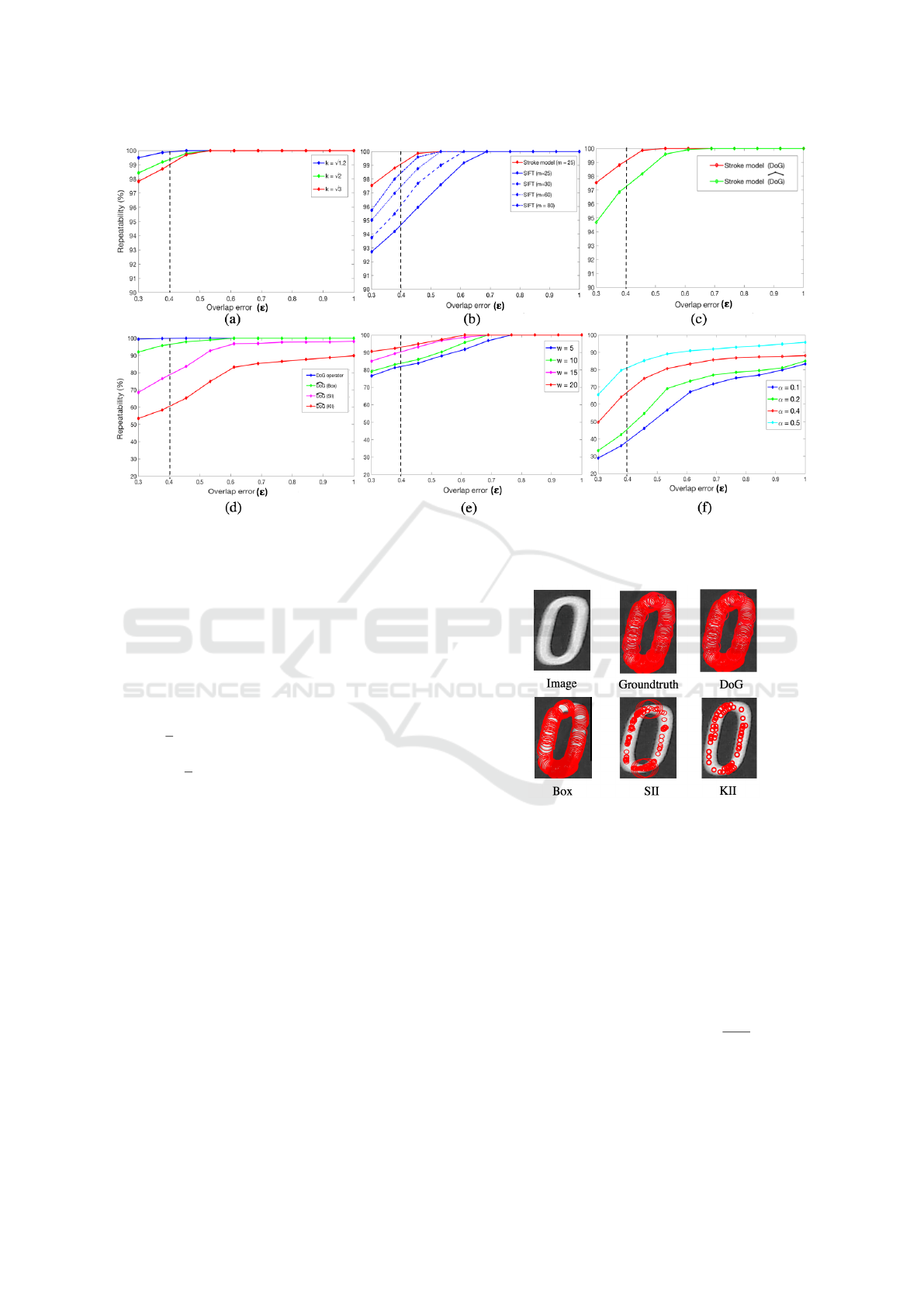
Figure 7: Repeatability score of (a) DoG with different values for the k parameter (b) the stroke model against the SIFT
descriptor (c) the stroke model based on the DoG and
d
DoG operators (d) DoG estimators based on the Box, SII, KII methods
(e) operator responses for low scale characters (f) DoG responses without normalization.
evaluation, we have controlled the scale-space in a
brute-force way and applied normalization to the ope-
rator response, as done for groundtruthing. By this
way, the obtained performances will only characterize
the distortion introduced by the LoG approximation.
The results for DoG approximation are given with
repeatability as a ROC-like curve Figure 7 (a). The
DoG approximation has almost none impact for low
k ∈]1,
√
2]. We observe less than 1% of error in the re-
peatability score at ε = 0.4. Distortions start to appear
with k >
√
3.
To characterize the fast Gaussian filtering, we
have selected representative methods for medium,
strong and best accuracy in Table 2. The box method
has been set with n = 5 and selection of Π
i
(x,y),λ
i
pa-
rameters with the method of (Fragoso et al., 2014). In
the Figure 7 (d), the methods with a low accuracy in-
troduce several degradations in the detection results,
whereas the box method results in less than 5% of
repeatability error at ε = 0.4. The Figure 8 gives a
comparison of a detection result among the operators.
3.3 Scale-space Representation (Task 3)
At this stage, we compare the SIFT descriptor and
the stroke model for the scale-space representation,
as presented in section (2.3). We have driven two cha-
racterization sub-tasks to compare the representations
at a same level of complexity and repeatability.
Figure 8: Detection results with different operators.
Characterization with Complexity. the size m + 1
of the bank filter and the σ parameters are fixed with
Eq. (16) of the stroke model using the character
widths of the dataset Table 3. Considering w ∈ [5,30],
we have obtained a size of m + 1 = 26 filters with
σ ∈ [2.3, 14.3] requiring 52 Gaussian kernels for a
DoG implementation. For a same complexity, we
have taken into account a similar number of Gaussian
filters for SIFT resulting in 52 scales with the archi-
tecture of Figure 3. Taking into account the relation
σ
max
= k
2(m+1)
σ
min
for the scale-space control within
the descriptor, we have achieved k =
√
1.06. This va-
lue for k has been applied in the stroke model too for
a similar LoG approximation.
As shown in Figure 7 (b), the stroke model (m =
25) with DoG outperforms the SIFT descriptor (m =
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
350

25) with a gap of 5% repeatability scores at ε = 0.4.
This results from the model and Eq. (16) that guaran-
tee optimum responses of filters at scales σ
s
conside-
ring a discrete representation of the stroke widths.
Characterization with Repeatability. in this step
we have analyzed the complexity overhead with the
SIFT descriptor at the same level of repeatability. Si-
milar to the previous characterization task, we have
fixed σ ∈ [2.3,14.3] as low and high optimum scale
values for detection. We have increased the number
of Gaussian filters m + 1 while reducing the k para-
meters within the equation σ
max
= k
2(m+1)
σ
min
to re-
ach an equal repeatability score with the stroke model.
Figure 7 (b) presents the results, where the SIFT des-
criptor reaches a near-exact approximation (less than
1% of difference between the repeatability scores) at
m = 80 for ε = 0.4.
3.4 Real-time Operator (Task 4)
From this task, we have applied a characterization
protocol to achieve end-to-end real-time detector. We
have set the operator with the stroke model for the
scale-space representation, a top accurate method for
fast Gaussian filtering with a low value k =
√
1.2 for
an optimum approximation. Figure 7 (c) gives the re-
peatability scores. This highlights the performance of
the detector that has a near-exact approximation of a
DoG filter with 2% of error within the repeatability
scores at ε = 0.4.
3.5 Low Resolution (Task 5)
As highlighted in the tasks 1 to 4, a closely perfect ap-
proximation of the scale-invariant LoG operator can
be achieved with a real-time method. A real-time ope-
rator is designed to accomplish a near-exact approxi-
mation with 2% of error at ε = 0.4. However, this re-
sult is attained from low resolution images (640×480)
where characters expose from small size w
min
= 5.
We analyze here the degradation found by the low
resolution. As detailed in section (3.1), our ground-
truth is given with a map σ
s
(x,y) including the scales
σ
s
for the optimum responses h
s
. Rather than compu-
ting a repeatability score covering all the scales, we
have selected the responses at a targeted scale σ
i
to
get a map σ
i
(x,y) Eq. (19). A same process is done
for detection.
σ
i
(x,y) =
(
1 σ
s
(x,y) = σ
i
0 otherwise.
(19)
A similar protocol to the task 1 has been applied with
k =
√
1.2 for a strong approximation. By this way, the
protocol characterizes the distortion introduced by the
low resolution only.
As shown in Figure 7 (e), several degradations
emerge for the low scale characters w ≤ 15. This is
due to the quantification noise, that produces false de-
tections and miss cases given in Figure 9. As general
trend, near to 15% of improvement can be achieved
for the repeatability scores while shifting w
min
from 5
to 20. Considering the image resolution of the data-
set, a recommendation is to shift to a full HD capture
to get images at sizes (1920×1080) or higher. This
will guarantee a robust repeatability at w
min
≈ 20.
Figure 9: Detection at low and high resolution.
3.6 Illumination Change (Task 6)
As discussed in section (3.1) and Figure 6, we have
driven our characterization tasks 1 to 5 with a norma-
lization parameter 1/ ˆa for contrast-invariance. Ho-
wever, within a real-life detection this parameter is
unknown. This can result in several degradations of
detector performances when important illumination
changes appear in the images. Our task 6 clarifies
this aspect, where the operator has been applied wit-
hout normalization. We have used a protocol similar
to the task 1 but with a low parameter k =
√
1.2. Com-
pared with the previous tasks, we have fixed another
thresholding parameter α taking into account the un-
normalized responses.
Figure 7 (f) provides the results where major dis-
tortions emerge. For an optimum detection, α must
set high enough to filter out the false positives. In that
case the low contrast images raise false negative re-
sults and miss detections as depicted in Figure 10.
Figure 10: Detection results without contrast normalization
(FD) false detections (MC) miss cases.
This points out the performance limits of the de-
tection due to the illumination changes. This intro-
duces a 20% error as an average in the repeatability
Performance Evaluation of Real-time and Scale-invariant LoG Operators for Text Detection
351
score at ε = 0.4. The design of a contrast-invariant
LoG operator is a key topic the in literature as a recent
work in (Miao et al., 2016). However, the proposed
methods cannot fit with a real-time constraint. As the
method of (Miao et al., 2016) is 4 to 5 slower com-
pared to the DoG operator. At the best of our know-
ledge, real-time and contrast-invariant LoG operators
have been never investigated in the literature.
3.7 Time Processing (Task 7)
Next to the characterization of detection results, we
have evaluated the processing time of the different
methods. We have compared the DoG operators des-
cribed in task 3 with the end-to-end real-time opera-
tor of the task 4. This results in three methods given
in Table 5. The goal here is to analyze the opera-
tors while applying optimization in the spatial and/or
scale-space domains. The time processing depends
on the complexity of operators and their parameters.
As concluded in the tasks 1 to 5, we have fixed
• n = 5 for the Gaussian approximation (tasks 1, 2),
• w ∈ [5, 30] with σ ∈ [2.3,14.3] and m = 25,80 for
optimum detection within the scale-space repre-
sentations at low resolution (task 3),
• image resolutions with the VGA, HD and full HD
modes to handle the low resolution (task 5).
Table 5: DoG operators for text detection (RT) real-time
(SM) stroke model (Conv) convolution with separability
(SS) scale-space (Comp) complexity.
VGA
(640× 480)
HD
(1280× 720)
Full HD
(1920× 1080)
Methods Filter SS Comp m w m w m w
DoG Conv SIFT O(Nω ×m) 80 [5,30] 106 [9,53] 158 [13,79]
RT-DoG Conv SM O(Nω ×m) 25 [5,30] 44 [9,53] 66 [13,79]
RT-
d
DoG Box SM O(N ×m) 25 [5,30] 44 [9,53] 66 [13,79]
We provide first in Table 6 the numbers of requi-
red low-level CPU operations for each of the met-
hods, as done in the literature (Elboher and Werman,
2012). The left part of table gives the formulations
with parameters, whereas the right part provides the
total amount of operations with the parameter values.
Table 6: Arithmetic operations per pixel for the operators.
Number of operations per pixel (in thousands)
Methods
Parameters
(+) + (∗)
Use-cases
VGA (Char74K) HD Full HD
DoG 2
∑
m
i=0
(2ω
i
+ 2ω
i
) 25.89K 61.02K 133.57K
RT-DoG 2
∑
m
i=0
(2ω
i
+ 2ω
i
) 10.3K 31.8K 70.4K
RT-
d
DoG 2(m + 1)(4n + n) 1.3K 2.25K 3.35K
We acquire one to two orders of magnitude of exe-
cution time with optimization in the spatial and scale-
space domains, where one order is obtained with the
fast Gaussian filtering method. The complexity of
operators are O(Nω), O(N) respectively, the RT-
d
DoG
operator performs well as the image resolution raises.
The Table 7 gives the processing times. All the
methods have been implemented at a same level of
parallelism for a fair comparison with a single thread
and auto-vectorization (Mitra et al., 2013). These re-
sults fit with the parameters given in Table 6 conside-
ring the additional time to get the integral image for
the RT-
d
DoG operator and the difference between the
pipelines for vectorization.
With multithreading, the operators can support a
regular frame rate even with a HD, full HD capture.
Let’s note that a near time 3 acceleration factor could
be acquired for all the methods, while applying hand
optimized intrinsic functions (Mitra et al., 2013). Ho-
wever, this approach makes the code CPU depen-
dent that raises portability constraints. The overall
complexity could be shifted to a sublinear level with
spatial and scale-space sampling (Lowe, 2004; Rey-
Otero et al., 2014b), that introduces other degradati-
ons and constraints.
Table 7: Time processing of operators in (ms) performing
with the C++ on a Mac- OS 2.2 GHz Intel Core i7 system.
Methods DoG RT-DoG RT-
d
DoG
Threads 1 1 1
VGA 988 437 164
Processing time (ms) HD 8058 4135 857
Full HD 42170 21630 3190
4 CONCLUSIONS
The real-time LoG operators with one to two orders
of magnitude of execution time are given. Adaptation
to text detection is attained through the scale-space
representation. They can support for modern camera
devices because of their ability to perform efficiently
with high resolution images.
As perspectives, the real-time operators are not
robust to illumination changes. This is a crucial
problem for text detection, real-time methodologies
for contrast-invariance should be investigated (Miao
et al., 2016). Additional optimization could be propo-
sed with sampling in the spatial and scale-space dom-
ains. This requires specific models linked to detection
problems (Rey-Otero et al., 2014b).
This work gives a performance evaluation at the
detector level. The characterization for full text de-
tection must be addressed, for an objective compari-
son with other real-time detectors.
A further issue is to characterize the two-stage and
end-to-end strategy. Real-time operators target a per-
fect recall for detection for search-space reduction.
They can result in a large optimization when used as
input of a template/feature matching method. Indeed,
such a method requires GPU support and low resolu-
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
352

tion images to fit with a real-time constraint (Liao
et al., 2017).
REFERENCES
Bhatia, A., Snyder, W., and Bilbro, G. (2010). Stacked inte-
gral image. In International Conference on Robotics
and Automation (ICRA). 1530–1535.
Charalampidis, D. (2016). Recursive implementation
of the gaussian filter using truncated cosine functi-
ons. In Transactions on Signal Processing (TSP).
64(14):3554–3565.
de Campos, T., Babu, B., and Varma, M. (2009). Character
recognition in natural images. In International Con-
ference on Computer Vision Theory and Applications
(VISAPP).
Deshpande, S. and Shriram, R. (2016). Real time text de-
tection and recognition on hand held objects to assist
blind people. In International Conference on Auto-
matic Control and Dynamic Optimization Techniques
(ICACDOT). 1020–1024.
Elboher, E. and Werman, M. (2012). Efficient and accurate
gaussian image filtering using running sums. In In-
ternational Conference on Intelligent Systems Design
and Applications (ISDA),. 897–902.
Fragoso, V., Srivastava, G., Nagar, A., and Li, Z. (2014).
Cascade of box (cabox) filters for optimal scale space
approximation. In Conference on Computer Vision
and Pattern Recognition Workshops (CVPRW). 126–
131.
Girones, X. and Julia, C. (2017). Real-time text localization
in natural scene images using a linear spatial filter. In
International Conference on Document Analysis and
Recognition (ICDAR). 1:1261–1268.
Gomez, L. and Karatzas, D. (2014). Mser-based real-time
text detection and tracking. In International Confe-
rence on Pattern Recognition (ICPR). 3110–3115.
Gomez, R., Shi, B., Gomez, L., Numann, L., and Veit, A.
(2017). Icdar2017 robust reading challenge on coco-
text. In International Conference on Document Ana-
lysis and Recognition (ICDAR). 1435-1443.
Gonzalez, R. and Woods, R. (2007). Image processing.
Kong, H., Akakin, H., and Sarma, S. (2013). A gene-
ralized laplacian of gaussian filter for blob detection
and its applications. In Transactions on cybernetics.
43(6):1719–1733.
Kovesi, P. (2010). Fast almost-gaussian filtering. In In-
ternational Conference on Digital Image Computing:
Techniques and Applications (DICTA). 121–125.
Liao, M., Shi, B., Bai, X., Wang, X., and Liu, W. (2017).
Textboxes: A fast text detector with a single deep neu-
ral network. In AAAI,4161–4167.
Lindeberg, T. (1994). Scale-space theory: A basic tool for
analysing structures at different scales. In Journal of
Applied Statistics. 21.224–270.
Liu, Y., Zhang, D., Zhang, Y., and Lin, S. (2014). Real-time
scene text detection based on stroke model. In Inter-
national Conference on Pattern Recognition (ICPR).
3116–3120.
Lowe, D. (2004). Distinctive image features from scale-
invariant keypoints. In International Journal of Com-
puter Vision (IJCV). 60(2):91–110.
Mao, J., Li, H., Zhou, W., Yan, S., and Tian, Q. (2013).
Scale based region growing for scene text detection.
In International Conference on Multimedia Retrieval
(ICMR). 1007–1016.
Miao, Z., Jiang, X., and Yap, K. (2016). Contrast invari-
ant interest point detection by zero-norm log filter. In
Transactions on Image Processing (TIP). 25.(1):331–
342.
Mitra, G., Johnston, B., and Rendell, A. (2013). Use of
simd vector operations to accelerate application code
performance on low-powered arm and intel platforms.
In International Symposium on Parallel & Distributed
Processing, Workshops (IPDPSW). 1107–1116.
Nayef, N., Yin, F., Bizid, I., Choi, H., and Feng, Y. (2017).
Icdar2017 robust reading challenge on multi-lingual
scene text detection and script identification-rrc-mlt.
In International Conference on Document Analysis
and Recognition (ICDAR). 1:1454–1459.
Neumann, L. and Matas, J. (2016). Real-time lexicon-
free scene text localization and recognition. In Tran-
sactions on Pattern Analysis and Machine Intelligence
(PAMI). 38(9):1872–1885.
Nilufar, S., Ray, N., and Zhang, H. (2012). Object detection
with dog scale-space: a multiple kernel learning ap-
proach. In Transaction on Image Processing (TIP).
21(8):3744–3756.
Otsu, N. (1979). A threshold selection method from gray-
level histograms. IEEE, 9(1): 62–66.
Rey-Otero, I., Delbracio, M., and Morel, J. (2014a). Com-
paring feature detectors: A bias in the repeatability
criteria, and how to correct it. arXiv:1409.2465.
Rey-Otero, I., Morel, J., and Del, M. (2014b). An analy-
sis of scale-space sampling in sift. In International
Conference on Image Processing (ICIP). 4847–4851.
Risnumawan, A., Shivakumara, P., and Chan, C. (2014).
A robust arbitrary text detection system for natural
scene images. In Expert Systems with Applications.
41.18:8027–8048.
Salahat, E. and Qasaimeh, M. (2017). Recent advances
in features extraction and description algorithms: A
comprehensive survey. In International Conference
on Industrial Technology (ICIT). 1059–1063.
Yang, H., Wang, C., Che, X., Luo, S., and Meinel, C.
(2015). An improved system for real-time scene text
recognition. In International Conference on Multime-
dia Retrieval (ICMR). 657–660.
Ye, Q. and Doermann, D. (2015). Text detection and recog-
nition in imagery: A survey. In Transactions on Pat-
tern Analysis and Machine Intelligence (PAMI). 37.7:
1480-1500.
Performance Evaluation of Real-time and Scale-invariant LoG Operators for Text Detection
353
