
Lagged Transfer Entropy Analysis to Investigate Cardiorespiratory
Regulation in Newborns during Sleep
Nicolò Pini
1,2,*
a
, Maristella Lucchini
1,2,*
b
, William P. Fifer
2
c
,
Nina Burtchen
3
and Maria G. Signorini
1
d
1
Dipartimento di Elettronica, Informazione e Bioingegneria, Politecnico di Milano, 20133 Milano, Italy
2
Department of Psychiatry, Columbia University College of Physicians & Surgeons, 10032 New York, U.S.A.
3
Department of Psychosomatic Medicine and Psychotherapy, University of Freiburg, 79106 Freiburg, Germany
mariagabriella.signorini@polimi.it,
Keywords: Transfer Entropy, Cardiorespiratory Regulation, Multivariate Modelling, Sleep Regulation, Autonomic
Nervous System.
Abstract: The autonomic nervous system (ANS) acts modulating the cardiac and respiratory systems by means of the
sympathetic and parasympathetic branches. In this work, we propose to employ Transfer Entropy (TE) with
the aim of disambiguating the contributions of the two branches over cardiorespiratory regulation in newborns
during sleep. Specifically, we computed TE on the original time series representative of the two subsystems,
namely Heart Rate Variability (HRV) and Respiration (RESP). Furthermore, we employed a lagged version
of the two original signals to derive a TE estimation capable of providing and insight on the short-term
memory between the two systems. Results show the information transfer quantified by TE
RESP→RR
decaying
rapidly as the shift between the two time series increases. On the other hand, TE
RR→RESP
exhibits a slower but
prolonged interaction, which lasts over numerous lags. The novel approach presented in this work affords the
potential to assess infants’ ANS development in terms of the quantification of cardiorespiratory control
functioning.
1 INTRODUCTION
Sleep is a central activity in humans across all ages.
The maturation of sleep is one of the most important
physiological processes occurring during the first
year of life and is particularly rapid during the
first six months after birth. A human infant shows
prolonged and characteristic epochs of stable
behavior, called behavioral states. Many
physiological variables are inter-related and mutually
influencing during the state cycles and change their
properties at the transition (Prechtl, 1974).
During sleep, autonomic nervous system (ANS)
acts to modulate heart rate variability (HRV) and
respiration, accordingly to sleep states (SS).
*Both authors contributed equally to this manuscript
a
https://orcid.org/0000-0002-0839-6033
b
https://orcid.org/0000-0002-7968-7196
c
https://orcid.org/0000-0002-6936-9303
d
https://orcid.org/0000-0002-9391-9846
In the last few decades, knowledge about the
mechanisms underlying cardiorespiratory
interactions as a function of sleep states has grown
(Berntson et al., 1993; Loewy and Spyer, 1990)
underlying the complex linear and nonlinear interplay
between the cardiac and respiratory systems.
Nonetheless, a full characterization of such
interaction is still pending and the investigation of
sympatho-vagal interaction and its role in
cardiorespiratory regulation needs further
elucidation.
Cardiorespiratory interaction investigation relies
on a joint analysis of HRV and respiration signals.
HRV is a non-invasive, indirect, but reliable
measure of ANS functioning. It is ideally suited for
Pini, N., Lucchini, M., Fifer, W., Burtchen, N. and Signorini, M.
Lagged Transfer Entropy Analysis to Investigate Cardiorespiratory Regulation in Newborns during Sleep.
DOI: 10.5220/0007363301390146
In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 139-146
ISBN: 978-989-758-353-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
139

tracking changes in cardiovascular autonomic control
in subjects at rest as well as during physiological
challenges (Schipke et al., 1999). Many studies have
demonstrated the ability of HRV measures and
derived parameters to characterize autonomic profiles
and perform risk stratification (Farrell et al., 1991;
Huikuri and Stein, 2013). In the perinatal field HRV
has been particularly successful in the assessment of
newborn infants for whom standard protocols
designed for adults requiring cooperation are
unfeasible (Galland et al., 2000; Harper et al., 1976;
Lucchini et al., 2016b).
In order to integrate the respiratory signal for a
bivariate approach, many signal processing
approaches have been proposed, using either linear
(e.g., cross-spectral analysis) or non-linear methods
(e.g., mutual information) to model the
interrelationship between HR and respiration signal
(Frasch et al., 2007; Kluge et al., 1988; Lucchini et
al., 2016a). Nonetheless, all the aforementioned
techniques are lacking the capability of providing
information on the directionality of such
relationships.
Transfer Entropy (TE) was developed to precisely
address this issue. The main focus of this
methodology is on tracking the information flow
between two given systems. Specifically, TE can
enhance the quantification of the directional coupling
between HRV and respiration providing insight on
the relative contribution of the sympathetic and
parasympathetic regulatory influences (Schreiber,
2000). In the context of biological time series, TE has
been utilized to test the effect of age and gender on
cardiorespiratory interaction complexity (Nemati et
al., 2013), characterize tilt response (Faes et al., 2012;
Porta et al., 2015), and highlight the importance of
information storage, transfer and modification in
interacting dynamical systems (Caţaron and Andonie,
2018; Faes et al., 2013a; Valenza et al., 2018).
In this paper we propose to employ TE
methodology to characterize cardiorespiratory
interaction during sleep in newborn infants. The
novelty we introduce in this work is the computation
of TE on time series shifted at various lags, to assess
the short-term memory of one system with respect to
the other. This approach provides further information
on the relationship between the cardiac and
respiratory systems at different time lags and thus
better characterization of the different role of the
sympathetic and parasympathetic branches of ANS,
which are known to operate on different time frames
and scales. We are searching for indices that could
ultimately be used as early markers of regulatory
alterations or malfunctions in the cardiorespiratory
mechanisms, potentially leading to infant distress.
2 MATERIALS AND METHODS
2.1 Subjects and Data Collection
The results presented in this paper are based on the
analysis of a dataset of 157 newborns, whose
gestational age at birth varies from 38 to 40 weeks
(mean±std: 39.03±0.80).
None of the enrolled infants had been admitted to
the Neonatal Intensive Care Unit nor had any major
illness, congenital abnormalities or known genetic
disorders. Mothers were at least 18 years of age and
displayed no evidence of major illness or psychiatric
disorders during the pregnancy.
Data collection was performed at Columbia
University Medical Center, upon mothers’ consent
and approval of the Institutional Review Board of the
New York State Psychiatric Institute and of the
Columbia University Medical Center.
Electrocardiography (ECG) and respiration signals
were recorded non-invasively at a sampling rate of
500 Hz and 200 Hz respectively, by means of three
leads on the chest in standard positions (RA, RL, LL,
DATAQ Instruments) and by a respiratory inductance
belt around the infant abdomen (Ambulatory
Monitoring Inc., Ardsley, NY, USA).
During the study, infants were sleeping supine and
sleep states were classified into active sleep (AS) and
quiet sleep (QS) by an automated algorithm (Isler et
al., 2016) and further validated by expert clinicians
(Stefanski et al., 1984).
2.2 Signal Pre-Processing
R wave peaks were detected on the ECG employing
the Pan-Tompkins algorithm (Pan and Tompkins,
1985). An adaptive filter was then applied to remove
ectopic beats or artifacts, preserving the beat-to beat
sequence. Respiration signals were band-pass filtered
in the interval 0.05-3.5 Hz and were then resampled
at the time of occurrence of R peaks. The RR series
was then defined so that RR(n), is time interval
between the n-th R peak and the successive one at
time (n+1)-th. Similarly, the n-th sample of
resampled respiration series RESP(n) is obtained by
resampling the original respiration series at the onset
of the n-th R peak which coincides with the time
previously defined for RR(n) as schematically shown
in Figure 1.
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
140

Figure 1: Schematic representation of RR and RESP series
extraction starting from ECG and respiration signals.
Within the same sleep state, segments of 300
consecutive RR intervals (RR) and 300 respiration
samples (RESP) were identified. The resulting series,
RR(n) and RESP(n) with n=1,…,300, were
normalized to zero mean and unit variance to be
employed for further analysis. The segments length
was chosen based on previous studies, reporting 300
samples series as appropriate for a reliable Transfer
Entropy (TE) estimation (Faes et al., 2014, 2011;
Lucchini et al., 2017). Each subject had at least one
segment in either AS or QS and 17 of them presented
both states during the study. The total number of
analyzed segments was 174, 79 in AS and 77 in QS.
2.3 Transfer Entropy
Since its definition by Schreiber (Schreiber, 2000),
TE has been vastly described as a powerful tool to
unveil information transfer between subsystems
(Faes et al., 2013b; Vicente et al., 2011). The method
incorporates the notion of directional and causal
information exchange in a model-free framework,
bridging its applicability towards short and
experimental datasets as in this context.
The traditional formulation for TE considers a set
of M interacting dynamical systems and aims at
quantifying the information flow from a source
system X to a target system Y, conditioned to the
remaining M-2 systems. In the context of this work,
the number M of subsystems is equal to 2, namely the
cardiac and respiratory systems, represented by the
time series RR and RESP respectively.
Denoting x
n
, y
n
as the stochastic variables
representing the states of the processes X and Y at time
t, and x
1:n
, y
1:n
the vectors of their respective past
states, TE is defined as reported in Equation 1:
(1)
where the sum incorporates all states visited by the
subsystems.
It appears clear that the formulation of TE can be
also written in terms of difference between two
Conditional Entropy (CE) terms, as expressed in
Equation 2:
(2)
It becomes evident that, regardless the formulation,
TE quantifies the information provided by the past of
the process X about the present of the process Y, that
is not already provided by the past of Y.
An open issue regarding TE estimation is the
quantification and disambiguation of instantaneous
effects, namely addressing the information flow
x
n
→y
n
. Instantaneous causality has been reported to
have impact on TE computation and various
approaches to address it have been proposed in
literature. In this work, compensated Transfer
Entropy (cTE) as formulated by Faes et al. (Faes et
al., 2013) has been computed. The method assimilates
instantaneous effects with the past states (x
1:n
becomes
x
n
) if causally meaningful. On the other
hand, in case of non causal meaningful interaction,
instantaneous effects are considered as a conditioning
factor (x
n
plays a role analogous to y
1:n-1
). In the latter
case, the present state of the source is compensated to
have instantaneous causality removed from TE
computation.
Figure 2: Schematic workflow of the steps for TE
estimation starting from the RR series and resampled
respiration signal.
OUTPUT results: TE
RR→RESP
and TE
RESP→RR
Statistical significance check by surrogate series
Estimation by Nearest Neighbor (NN) method
Definition of probability density function for
RR(n), RESP(n), and their interrelationship
Non Uniform Embedding (NUE) reconstruction
based on information reduction criterion
Quantification and disambiguation of istantaneous
effects
INPUT series: RR(n) and RESP(n)
Lagged Transfer Entropy Analysis to Investigate Cardiorespiratory Regulation in Newborns during Sleep
141

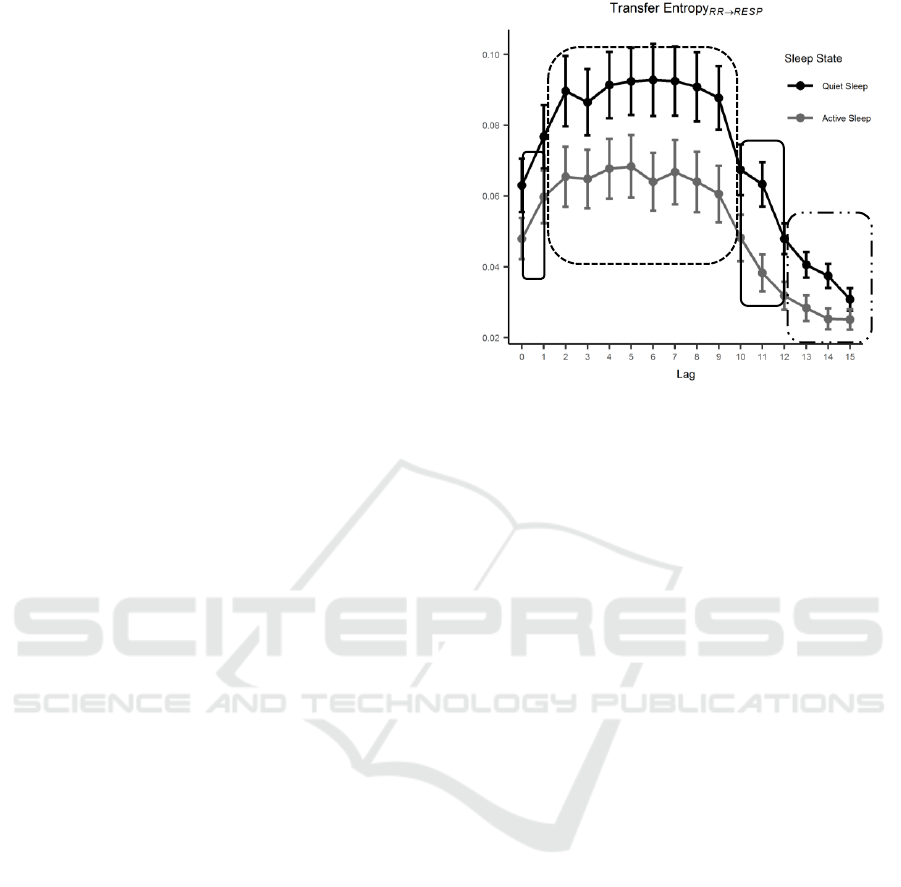
Figure 3: TE
RR→RESP
distributions as a function of lag and grouped based on sleep state. TE increases from lag equal to 0 and
remains stable to higher values for intermediate lags. From lag 9 on, TE decreases due to a vanishing mutual influence between
the two series.
In the context of TE computed upon series of short
length, as for physiological time series, the
reconstruction of the vector of past states and the
estimation of probability density functions are
crucial. Regarding the reconstruction of vector of the
past states, the basic idea is to optimize the time-delay
embedding based on a sequential procedure capable
of selecting a reduced subset of components which
better describe the destination process, allowing the
inclusion of the present state. It is important to
underline that the presented selection procedure is
based on information reduction given the assumption
that joint probabilities are insensitive to temporal
ordering of components. This procedure, called non
uniform embedding procedure is explained in details
in (Faes et al., 2013). In this word, the maximum
number of candidates L is set to 10 and the resulting
embedding vector is denoted as V
k
.
The final step towards TE estimation relies on the
definition of probability density functions to
approximate the interrelationship between X and Y
from a single realization of the two processes. The
estimation of terms in Equation 1 is based on
previously defined embedding vectors (V
k
) only and
it employs a Nearest Neighbor (NN) estimator.
Considering NN estimator, it is possible to rewrite
Equation 2 as follows:
(3)
where is V
Y
denotes the relevant visited states by the
subsystem Y only. Terms in Equation 3 are estimated
based on the formulation reported in (Montalto et al.,
2014).
The combination of non uniform embedding and
NN estimator (NN NUE) has been reported to be
optimal for the selection of candidates in the context
of TE estimation (Kugiumtzis, 2013).
Furthermore, the statistical significance of
computed TE is assessed using surrogate data
implemented by time shift procedure. In this work,
the number of employed surrogate series is equal to
100 and the maximum allowed time shift is set to 20
samples. The threshold employed for the definition of
a significant TE value is set above the 95
th
percentile
of surrogate series distribution.
Figure 2 reports the workflow of TE computation
starting from the original time series RR(n) and
RESP(n) to obtain both TE
RR→RESP
and TE
RESP→RR
.
2.4 Lagged Transfer Entropy
In this work, a novel approach to quantify the short-
term memory effect of two interacting systems
starting from the notion of TE is proposed. The new
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
142
approach lies its foundations on the previously
described TE implementation, yet it considers several
lagged versions of the original series. Supposing to
quantify TE
X→Y
at lag value equal to one, the target
series is shifted forward of a quantity equal to one
sample so that x(n) is now aligned with y(n-1).
The lagged version of TE proposed in this work
aims at quantifying the information provided by the
past of X on the shifted portion of the process Y, that
is not already provided by the past of Y.
The underlying idea is the quantification of the
source series effects on the target and the
quantification of the short memory effect between the
two. In this work, the maximum allowed value for the
lag between RR and RESP series is set to 15, which
corresponds to 15 beats. The choice of maximum lag
equal to 15 beats is related to the physiological
imping effect of sympathetic and parasympathetic
systems on cardiac and respiratory systems, as well as
the operational cardiac and breathing frequencies in
newborns (Frasch et al., 2007).
2.5 Statistical Analysis
The significance of TE measures was assessed by
performing a two-way ANOVA testing separately the
two directionalities, namely TE
RR→RESP
and
TE
RESP→RR
and as fixed factor the sleep state (AS vs
QS) and lag values ranging from 0 to 15. The
covariates included in the model were infant’s sex
(Sex), mode of delivery (MoD) and hours of life
(HoL) from delivery to time of the study assessment.
Significance is reported for main effects as well as
interactions between independent variables. Post-hoc
tests were performed to assess significant differences
between pairs of lags and to disambiguate interaction
effects among fixed factors.
3 RESULTS
3.1 TE Directionality from RR to
RESP
The analysis of TE in the directionality RR→RESP
reports a significant between-subjects effect for both
fixed factors, SS and lag (p<0.001 and p<0.001), but
no interaction effect between the two. Moreover,
covariates included in the model are no significant in
explaining the behavior of TE with exception for HoL
(p<0.001).
The amount of significant TE estimates, based on
surrogate testing, progressively decreases as a
function of lag moving from the non-lagged version
Figure 4: TE
RR→RESP
distributions as a function of lag and
grouped based on SS. Error bars represent 95% confidence
interval (CI) of the derived distributions. TE increases from
lag equal to 0 and remains stable to higher values for
intermediate lags. From lag 9 on, TE decreases due to a
vanishing mutual influence between the two series.
of the two signals to lag=15. The non-significant
estimates are on average 15 over 174 in the lag
interval 0-12 and they further increase up to an
average of 62 from lag 12 to 15. The TE values for
each lag and grouped based on SS are reported in
Figure 3.
The results for the post-hoc test performed on the
independent factor lag are graphically shown in
Figure 4. Circles enclose groups of lags among which
no significant differences are found. The influence of
RR modulation over respiration is significantly
increasing when comparing the instantaneous effect
(lag = 0) with respect to the two signals lagged by one
beat. This increase in TE
RR→RESP
stays stable over 8
lags to then decrease and return to values similar to
the result for lag equal to zero. Lags from 12 to 15 are
statistically different from the previous ones, yet their
distributions are obtained by a reduced poll of TE
values due to lack of significant TE estimates after
performing surrogate check. TE values are
consistently lower for AS compared to QS and this is
independent from the lags. Nevertheless, higher lags
exhibit a flatter trend possibly as a consequence of
more hampered and inconsistent TE estimates.
Lagged Transfer Entropy Analysis to Investigate Cardiorespiratory Regulation in Newborns during Sleep
143

Figure 5: TE
RESP→RR
distributions as a function of lag and
grouped based on SS for the proposed restricted model. TE
progressively decreases from lag 0 to lag 3 with a more
pronounced trend in QS.
3.2 TE Directionality from RESP to RR
In contrast to the behavior previously reported for the
directionality RR→RESP, RESP→RR
analysis
shows a TE decrease as lags are progressively
increasing from 0 to 15. In this context, significant
between-subjects effects for both SS and lag are
reported, p<0.001 and p<0.001 as well as an
interaction effect of SS*Lag, p<0.001.
It is remarkable to notice that no differences in TE
distributions are found comparing each pairs of lags
from lag 3 to lag 15. It is possible to assimilate the
described lag interval to a unique class towards the
aim of avoid over-representing similar class
distributions in the successive statistical analysis.
Furthermore, surrogate testing procedure excludes an
average of 66 TE values from lag 4 to lag 15 but only
around 30 from 0 to 3. Given these considerations, the
statistical results reported for TE
RESP→RR
are extracted
by considering lags from 0 to 3 only, as reported in
Figure 5. The ANOVA performed on this restricted
number of lags is consistent with the results obtained
considering all computed lags. Significant between-
subjects effects for SS and lag are reported, p<0.001
and p<0.001 and SS*Lag p<0.001. No significance
for covariates is found.
As a general consideration, regardless SS,
TE
RESP→RR
decreases as lags increase with a marked
drop between lag 0 to lag 1. Post-hoc test on the factor
lag reports significant differences when comparing
pairs of lags with exception in the comparison of lag
equal to 2 versus lag equal to 3. SS-related changes of
TE are similar to what previous reported for
TE
RR→RESP
even if such slope decrease is less marked
and flatter when passing from TE in AS vs TE in QS.
Given the reported interaction between fixed factors
(SS*Lag), simple main effects were tested. The
results indicate that differently from TE
RR→RESP
, SS
differences are mainly driven by lags.
4 DISCUSSION AND
CONCLUSIONS
For healthy full-term newborns, as the cohort
investigated in this work, sleep constitutes the
predominant state, with an average prevalence of AS
over QS. ANS modulation over either the cardiac and
respiratory systems is strongly dependent upon sleep
state dynamics, thus its regulation is indeed
responsible for the generation and modulation of
cardiorespiratory patterns. Investigation of the
functional organization of these neurophysiological
systems is extremely challenging, due to their
intrinsic complexity and the necessity to access them
by means of noninvasive recordings only.
Fortunately, the analysis of HRV, breathing and their
coupling provide an optimal set of noninvasive
functional probes of the behavior of cardiorespiratory
systems.
In this paper we deepened the investigation
presented in Lucchini et al. (Lucchini et al., 2017).
Our previous investigation focused on the traditional
TE estimation and highlighted a predominant
information transfer in QS vs AS regardless the sleep
state, with a stronger TE gap when considering the
directionality from RESP to RR (TE
RESP→RR
).
In this present work, the use of the lagged series
allowed us to gain insight on the temporal
relationships between systems as a function of
increasing lags providing a transferrable link to the
beat scale. As a matter of fact, results show that the
information transfer from RESP to RR (TE
RESP→RR
)
decays rapidly as the shift between the time series
increases. The statistical significance of TE
estimation progressively decreases for increasing
lags, consolidating the hypothesis that the mutual
influence of RR over RESP is rather transient and acts
on a very short scale. On the other hand, considering
the directionally from RR to RESP (TE
RR→RESP
), the
maximum information transfer between the
subsystems requires an average of 2 beats to activate
but it remains stable for a longer period of
approximately 8 or 9 beats.
Findings considering the unlagged (lag=0) TE
estimates reported in this work are in accordance with
the TE results previously reported in Lucchini et al.
(Lucchini et al., 2017) for the same cohort of
newborns. TE values in QS are on average higher
with respect to TE in AS, regardless the considered
directionality and sleep state.
Coming to the findings obtained by employing the
lagged version of TE, results might suggest that
different information transfer directionality are in fact
driven by one of the two autonomic branches of the
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
144

ANS (Hoyer et al., 2005) respectively. As a matter of
fact, the sympathetic branch intervenes on a slower
time scale, but its effect last longer in the target
system, whereas the parasympathetic has a punctual
yet rapidly vanishing action. Given these
considerations, it is possible to speculate that that the
vagal system is possibly more implicated in the
directionality from RESP to RR while the
sympathetic in the opposite directionality. The latter
assumption is based on the behavior of TE
RR→RESP
showing higher TE values for intermediate lags up to
the point of reaching almost comparable values to the
maximum information transfer for TE
RESP→RR
.
In sum, we have provided a noninvasive
characterization of the sleep state effects on
cardiorespiratory regulation in newborns, by
employing a measure of TE capable of quantifying
both linear and nonlinear aspect of the
interrelationship between the cardiac and respiratory
system. The novel approach of lagged TE was
capable of highlighting interactions occurring on
different time scales and possibly related to the
activation of the two autonomic branches. The
proposed interpretation of TE related findings is also
consistent with previous works, modelling the
interrelationship between the two branches of ANS
and cardiorespiratory regulation (Ataee et al., 2012).
In the specific context of this work, information flow
between HR and respiration is increased in QS with
respect to AS, indicating that in such sleep state more
information is exchanged between the cardiac and the
respiratory systems on average. This approach to the
quantification of cardiorespiratory interactions
affords the potential for early assessment of infant
development of bidirectional control between
physiological systems providing a more
comprehensive framework of investigation rather
than studying the two signals on their own.
Lastly, the proposed approach could facilitate
early risk assessment for neurophysiological
disorders such as Sudden Infant Death Syndrome
(SIDS) by tracking adverse profile of information
exchange between the two systems, thus exposing
infants to greater risk for a variety of pathology
involving the malfunction of cardiorespiratory
controlling mechanism.
ACKNOWLEDGEMENTS
The writing of this manuscript was supported by the
Sackler Institute of Developmental Psychobiology at
Columbia University and by National Institute of
Health grants NIH Grants R37 HD32774 (WPF) and
T32 MH018264 (NB). This publication was also
supported by the National Center for Advancing
Translational Sciences, National Institutes of Health,
through Grant Number UL1TR001873. The content
is solely the responsibility of the authors and does not
necessarily represent the official views of the NIH.
REFERENCES
Ataee, P., Belingard, L., Dumont, G.A., Noubari, H.A.,
Boyce, W.T., 2012. Autonomic-cardiorespiratory
regulation: A physiology-based mathematical model.
Proc. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. EMBS
3805–3808.
Berntson, G.G., Cacioppo, J.T., Quigley, K.S., 1993.
Respiratory sinus arrhythmia: Autonomic origins,
physiological mechanisms, and psychophysiological
implications. Psychophysiology 30, 183–196.
Caţaron, A., Andonie, R., 2018. Transfer Information
Energy: A Quantitative Indicator of Information
Transfer between Time Series. Entropy 20, 323.
Faes, L., Marinazzo, D., Montalto, A., Nollo, G., 2014.
Lag-specific transfer entropy as a tool to assess
cardiovascular and cardiorespiratory information
transfer. IEEE Trans. Biomed. Eng. 61, 2556–2568.
Faes, L., Montalto, A., Nollo, G., Marinazzo, D., 2013a.
Information decomposition of short-term
cardiovascular and cardiorespiratory variability.
Comput. Cardiol. (2010). 40, 113–116.
Faes, L., Nollo, G., Porta, A., 2011. Information domain
approach to the investigation of cardio-vascular, cardio-
pulmonary, and vasculo-pulmonary causal couplings.
Front. Physiol. 2.
Faes, L., Nollo, G., Porta, A., 2012. Non-uniform
multivariate embedding to assess the information
transfer in cardiovascular and cardiorespiratory
variability series. Comput. Biol. Med. 42, 290–297.
Faes, L., Nollo, G., Porta, A., 2013b. Compensated transfer
entropy as a tool for reliably estimating information
transfer in physiological time series. Entropy 15, 198–
219.
Farrell, T.G., Bashir, Y., Cripps, T., Malik, M., Poloniecki,
J., Bennett, E.D., Ward, D.E., Camm, A.J., 1991. Risk
stratification for arrhythmic events in postinfarction
patients based on heart rate variability, ambulatory
electrocardiographic variables and the signal-averaged
electrocardiogram. J. Am. Coll. Cardiol. 18, 687–697.
Frasch, M.G., Zwiener, U., Hoyer, D., Eiselt, M., 2007.
Autonomic organization of respirocardial function in
healthy human neonates in quiet and active sleep. Early
Hum. Dev. 83, 269–277.
Galland, B.C., Hayman, R.M., Taylor, B.J., Bolton, D.P.G.,
Sayers, R.M., Williams, S.M., 2000. Factors Affecting
Heart Rate Variability and Heart Rate Responses to
Tilting in Infants Aged 1 and 3 Months. Pediatr. Res.
48, 360–368.
Harper, R.M., Hoppenbrouwers, T., Sterman, M.B.,
McGinty, D.J., Hodgman, J., 1976. Polygraphic studies
Lagged Transfer Entropy Analysis to Investigate Cardiorespiratory Regulation in Newborns during Sleep
145

of normal infants during the first six months of life. I.
Heart rate and variability as a function of state. Pediatr.
Res. 10, 945–951.
Hoyer, D., Pompe, B., Chon, K.H., Hardraht, H., Wicher,
C., Zwiener, U., 2005. Mutual information function
assesses autonomic information flow of heart rate
dynamics at different time scales. IEEE Trans. Biomed.
Eng. 52, 584–592.
Huikuri, H. V., Stein, P.K., 2013. Heart rate variability in
risk stratification of cardiac patients. Prog. Cardiovasc.
Dis. 56, 153–159.
Isler, J.R., Thai, T., Myers, M.M., Fifer, W.P., 2016. An
automated method for coding sleep states in human
infants based on respiratory rate variability. Dev.
Psychobiol. 58, 1108–1115.
Kluge, K. a, Harper, R.M., Schechtman, V.L., Wilson, a J.,
Hoffman, H.J., Southall, D.P., 1988. Spectral analysis
assessment of respiratory sinus arrhythmia in normal
infants and infants who subsequently died of sudden
infant death syndrome. Pediatr. Res. 24, 677–682.
Kugiumtzis, D., 2013. Direct-coupling information
measure from nonuniform embedding. Phys. Rev. E -
Stat. Nonlinear, Soft Matter Phys. 87.
Loewy, A.D., Spyer, K.M., 1990. Central Regulation of
Autonomic Functions. Oxford Univ. Press.
Lucchini, M., Fifer, W.P., Ferrario, M., Signorini, M.G.,
2016a. Feasibility study for the assessment of cardio-
respiratory coupling in newborn infants. In:
Proceedings of the Annual International Conference of
the IEEE Engineering in Medicine and Biology
Society, EMBS. pp. 5509–5512.
Lucchini, M., Fifer, W.P., Sahni, R., Signorini, M.G.,
2016b. Novel heart rate parameters for the assessment
of autonomic nervous system function in premature
infants. Physiol. Meas. 37, 1436–1446.
Lucchini, M., Pini, N., Fifer, W.P., Burtchen, N., Signorini,
M.G., Lucchini, M., Pini, N., Fifer, W.P., Burtchen, N.,
Signorini, M.G., 2017. Entropy information of
cardiorespiratory dynamics in Neonates during sleep.
Entropy 19, 225.
Montalto, A., Faes, L., Marinazzo, D., 2014. MuTE: A
MATLAB toolbox to compare established and novel
estimators of the multivariate transfer entropy. PLoS
One 9.
Nemati, S., Edwards, B.A., Lee, J., Pittman-Polletta, B.,
Butler, J.P., Malhotra, A., 2013. Respiration and heart
rate complexity: Effects of age and gender assessed by
band-limited transfer entropy. Respir. Physiol.
Neurobiol. 189, 27–33.
Pan, J., Tompkins, W.J., 1985. A Real-Time QRS Detection
Algorithm. IEEE Trans. Biomed. Eng. BME-32, 230–
236.
Porta, A., Faes, L., Marchi, A., Bari, V., De Maria, B.,
Guzzetti, S., Colombo, R., Raimondi, F., 2015.
Disentangling cardiovascular control mechanisms
during head-down tilt via joint transfer entropy and self-
entropy decompositions. Front. Physiol. 6, 1–14.
Prechtl, H.F.R., 1974. The behavioural states of the
newborn infant (a review). Brain Res. 76, 185–212.
Schipke, J.D., Pelzer, M., Arnold, G., 1999. Effect of
respiration rate on short-term heart rate variability. J.
Clin. Basic Cardiol. 2, 92–95.
Schreiber, T., 2000. Measuring information transfer. Phys.
Rev. Lett. 85, 461–464.
Stefanski, M., Schulze, K., Bateman, D., Kairam, R.,
Pedley, T., Masterson, J., James, L.S., 1984. A scoring
system for states of sleep and wakefulness in term and
preterm infants. Pediatr. Res.
Valenza, G., Faes, L., Citi, L., Orini, M., Barbieri, R., 2018.
Instantaneous Transfer Entropy for the Study of
Cardiovascular and Cardiorespiratory Nonstationary
Dynamics. IEEE Trans. Biomed. Eng. 65, 1077–1085.
Vicente, R., Wibral, M., Lindner, M., Pipa, G., 2011.
Transfer entropy-a model-free measure of effective
connectivity for the neurosciences. J. Comput.
Neurosci. 30, 45–67.
BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing
146
