
Generative Adversarial Networks as an Advanced Data Augmentation
Technique for MRI Data
Filippos Konidaris, Thanos Tagaris, Maria Sdraka and Andreas Stafylopatis
School of Electrical and Computer Engineering, National Technical University of Athens,
Iroon Polytexneiou 9, Zografou Campus 15780, Athens, Greece
Keywords:
Generative Adversarial Networks, Deep Learning, MRI, Data Augmentation, ADNI, Alzheimer’s Disease.
Abstract:
This paper presents a new methodology for data augmentation through the use of Generative Adversarial Net-
works. Traditional augmentation strategies are severely limited, especially in tasks where the images follow
strict standards, as is the case in medical datasets. Experiments conducted on the ADNI dataset prove that
augmentation through GANs outperforms traditional methods by a large margin, based both on the validation
accuracy and the models’ generalization capability on a holdout test set. Although traditional data augmenta-
tion did not seem to aid the classification process in any way, by adding GAN-based augmentation an increase
of 11.68% in accuracy was achieved. Furthermore, by combining traditional with GAN-based augmentation
schemes, even higher accuracies can be reached.
1 INTRODUCTION
Over the past years, there has been a rapid deve-
lopment in the field of Computer Vision, especially
through techniques involving Deep Learning. A trend
has emerged, where models achieving state-of-the-art
performances are becoming deeper and more com-
plex. An explanation might be that the most important
benchmark each new Deep Neural Network must pass
is the annual ImageNet Large Scale Visual Recogni-
tion Challenge (ILVRC) (Russakovsky et al., 2015),
which requires the models to be trained on an immen-
sely large dataset (i.e. millions of images). However,
performance on this challenge does not always trans-
late well to real world applications, as they rarely in-
clude such a large dataset.
Training a deep model on insufficient data usu-
ally results in overfitting, because a model of high
capacity is capable of “memorizing” the training set.
Multiple methods have been shown to alleviate this
problem, but none so effectively to be used exclusi-
vely. These techniques can be split into two broad
categories: regularization techniques, aiming to limit
the model’s capacity (e.g. dropout, parameter norm
penalties) and data augmentation techniques, attemp-
ting to increase the size of the dataset (Kuka
ˇ
cka et al.,
2018). In practice, most models benefit from a mul-
Github repo: https://github.com/filippos1994/Gan mri
aug
titude of these techniques. This study mostly focuses
on the latter category.
Data augmentation has proven to be very effective
and is adopted universally in the field of deep lear-
ning, e.g. (Ciresan et al., 2010), (Vasconcelos and
Vasconcelos, 2017). It is in fact so effective that it is
being used even in tasks that involve large amounts
of data (Wu et al., 2015). The most common forms
of augmentation include horizontal and vertical flips,
affine transformations (e.g. scaling, translating, rota-
ting), brightness/contrast adjustments and filter appli-
cations (e.g. blurring, sharpening). The goal of such
transformations is to obtain a new image that contains
the same semantic information as the original.
While augmentation most certainly helps neural
networks learn and generalize more effectively, it
also has its drawbacks. In most cases, augmenta-
tion techniques are limited to minor changes on an
image, as more “heavy” augmentations might damage
the image’s semantic content. Furthermore, the forms
of augmentation one can use differ from problem to
problem, making their application ad-hoc and empi-
rical. For instance, medical images have to be mildly
augmented as they follow strict standards (i.e. they
are centered, their orientation and intensity vary little
from image to image and many times they are late-
rally/horizontally asymmetric) (Hussain et al., 2017).
Finally, augmentation techniques are applied on one
image at a time and thus are unable to gather any
48
Konidaris, F., Tagaris, T., Sdraka, M. and Stafylopatis, A.
Generative Adversarial Networks as an Advanced Data Augmentation Technique for MRI Data.
DOI: 10.5220/0007363900480059
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 48-59
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

information from the rest of the dataset. This paper
proposes a novel technique that overcomes said limi-
tations and is capable of augmenting any given data-
set with realistic, high-quality images generated from
scratch.
Generative Adversarial Networks (GANs) (Good-
fellow et al., 2014) are a family of unsupervised neu-
ral networks most commonly used for image genera-
tion. Each GAN is composed of two networks: a ge-
nerator and a discriminator, competing against each
other in a two-player minimax game. These models
have proven to be capable of creating realistic images
and will serve as the basis of this study.
2 RELATED WORK
Generative Adversarial Networks have been success-
fully used in the past for data augmentation. For
example, (Antoniou et al., 2017) and (Wang et al.,
2018) use custom GAN architectures in a low-data
setting achieving consistently better results than tra-
ditionally augmented classifiers, while (Perez and
Wang, 2017) devise a novel pipeline called Neural
Augmentation which, through style transfer techni-
ques, aims at generating images of different styles,
performing equally as good as traditional augmenta-
tion schemes in a subsequent classification task. Ad-
ditionally, (Neff, 2018) proposes a generative model
which learns to produce pairs of images and their re-
spective segmentation masks in order to assist a U-
Net segmentation model, proving that in simpler da-
tasets networks trained with a mix of synthetic and
real images stay competitive with networks trained on
strictly real data using standard data augmentation.
One field in which data augmentation is especi-
ally important is that of medical imaging, where the
lack of available public data is a ubiquitous problem
since access to individual medical records is hea-
vily protected by legislation and appropriate consent
must be given. In most cases this process is hinde-
red by bureaucracy and/or high costs, while the re-
sulting collection is greatly imbalanced towards nor-
mal subjects. Several authors employ Machine Le-
arning techniques to learn directly from the available
data and surpass the state-of-the art in problems as
diverse as generating benchmark data, image norma-
lization, super resolution, or cross-modality synthesis
(Frangi et al., 2018).
The medical field has only recently started adop-
ting GAN-based methodologies for synthesizing ima-
ges (Yi et al., 2018). In particular (Bentaieb and
Hamarneh, 2018) and (Shaban et al., 2018) propose
GAN-based style transfer approaches to stain nor-
malization in histopathology images, with quite in-
teresting results in various datasets. For tackling seg-
mentation tasks, various authors have proposed cus-
tom GAN architectures and pipelines which are ad-
versarially trained to produce proper segmentation
masks from a given medical image dataset (Shin
et al., 2018), (Dai et al., 2017), (Xue et al., 2017).
Regarding image translation between modes, (Dar
et al., 2018) synthesize T2-weighted brain MRI ima-
ges from T1-weighted ones, and vice versa, using a
Conditional GAN model. Finally, many authors, such
as (Frid-Adar et al., 2018) and (Costa et al., 2018),
have attempted to generate counterfeit medical ima-
ges in order to increase the size of the training set of
different deep learning models, a task more closely
related to the one examined in this paper.
Supplementary to all of the above efforts, our ap-
proach aims to exploit the superior performance of
GANs for the benefit of medical image classifica-
tion. We explore the impact of GAN-assisted data
augmentation on the diagnosis of Alzheimer’s Dise-
ase through non-invasive MRI scans and our critic is
a robust CNN model designed to classify among Alz-
heimer’s patients and healthy controls.
3 GENERATIVE ADVERSARIAL
NETWORKS
A Generative Adversarial Network is composed of
two networks, the generator and the discriminator.
The generator accepts a noise vector as input and pro-
duces fake data, which are then fed, along with real
ones, to the discriminator, whose goal is to distinguish
which distribution the samples originate from. Con-
versely, the generator’s goal is to learn the real dis-
tribution without witnessing it, in order to make its
output indistinguishable from real samples. Both net-
works are trained simultaneously and adversarially,
until an equilibrium is reached.
In order to combat instability issues during trai-
ning, the Earth Mover’s or Wasserstein distance was
used, partially because it leads to convergence for a
much broader set of distributions, but mostly because
its value is directly correlated to the quality of the ge-
nerated data. (Arjovsky et al., 2017). The resulting
formulation of the game is presented in eq. (1), where
D is the set of 1-Lipschitz functions.
min
G
max
D∈D
E
x∼P
r
[D(x)] − E
z∼P
z
[D(G(z))] (1)
The discriminator’s 1-Lipschitz constraint was
initially achieved by clipping its weights by an ar-
bitrary value (WGAN). It was later shown that this
Generative Adversarial Networks as an Advanced Data Augmentation Technique for MRI Data
49
technique led to sub-optimal behaviour, which could
be ameliorated with the inclusion of a gradient pen-
alty term to the discriminator’s loss function, as
shown in eq. (2), calculated on a random interpola-
tion point between the real and the fake samples (P
ˆx
)
(Gulrajani et al., 2017). The resulting architecture
(WGAN-GP) is the one used in the current work.
L = E
z∼P
z
[D(G(z))] − E
x∼P
r
[D(x)] +
+ λ E
ˆx∼P
ˆx
[(k∇
ˆx
D( ˆx)k
2
− 1)
2
]
(2)
4 PROPOSED AUGMENTATION
METHODOLOGY
The main goal of this study was to produce realistic
images for each of the classes on-demand. To achieve
this, a framework was designed where a single GAN
was trained on each of the classes. For this purpose, a
GAN architecture of sufficient capacity to understand
and model the underlying distributions of each of the
classes had to be selected. A GAN that satisfies the
above goal should, after training, be able to produce
realistic images of the class it was trained upon.
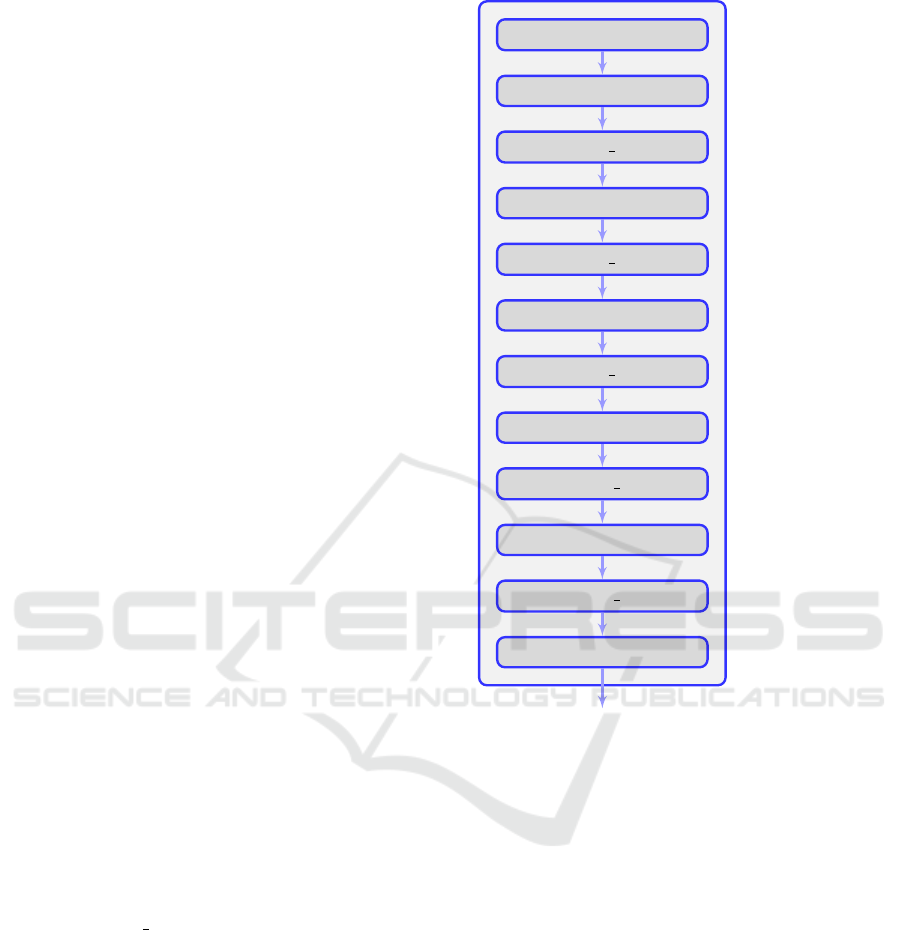
4.1 Generator
An architecture with 11 layers and more than 15 mil-
lion trainable parameters was selected as the genera-
tor of the network. The architecture is depicted in
Figure 1.
The input of the generator is a vector of 128
random values in the [0, 1) range, sampled from a uni-
form distribution. Following the input is a Fully Con-
nected (FC) layer with 6 · 5 · 512 = 15360 neurons.
The output of the FC layer is then transformed into a
3D volume, which can be thought of as a 6 × 5 image
with 512 channels. The subsequent layers are regular
2D convolutions (Conv) and 2D transposed convolu-
tions (Conv trans up), sometimes referred to as “de-
convolution” layers. A 5 × 5 sized kernel and ‘same’
padding were selected for both types of layers, while
a stride of 2 was selected for the transposed convolu-
tions. This results in the doubling of the spatial di-
mensions of its input.
All layers apart from the last are activated by a
“Leaky ReLU” function. The final layer has a hy-
perbolic tangent (tanh) activation function, because
its output needs to be bounded in order to be able to
output an image. A tanh function was preferred over
a sigmoid function because it is centered around 0,
which helps during training (LeCun et al., 1998).
Finally, after five alternations of convolution and
transposed convolution layers (each of which doubles
Input (128)
Dense (6 · 5 · 512)
Conv trans up (512)
Conv (256)
Conv trans up (256)
Conv (128)
Conv trans up (128)
Conv (64)
Conv trans up (64)
Conv (32)
Conv trans up (32)
Conv (1)
Input (128)
FC (6 · 5 · 512)
Conv trans up (512)
Conv (256)
Conv trans up (256)
Conv (128)
Conv trans up (128)
Conv (64)
Conv trans up (64)
Conv (32)
Conv trans up (32)
Conv (1)
0
1.981.440 + 61.440
6.554.112 + 2048
3.277.056 + 1024
1.638.656 + 1024
819.328 + 512
409.728 + 512
204.864 + 256
102.464 + 256
51.232 + 128
25.632 + 128
801
Figure 1: On the left is the architecture of the network’s
generator. The size of each layer can be seen after its name.
On the right, the number of parameters (trainable + batch
normalization) of each layer is presented.
the size of its input), an image with a resolution of (6·
2
5
× 5 · 2
5
) = (192 × 160) and 1 channel is produced.
4.2 Discriminator
The discriminator is a regular CNN architecture ai-
med towards binary classification. The one used in
the present study consists of 11 layers and around 9.5
million trainable parameters and can be seen in Figure
2.
The input to the discriminator is a single-channel
192 × 160 image. This image is then passed five ti-
mes through alternating layers of convolutions with a
stride of 1 and 2 respectively; the latter are used for
sub-sampling as there are no pooling layers present
in the architecture. The final two layers are FC ones.
All layers in the network are activated by a “Leaky
ReLU” , besides the last one which has no activation
function.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
50
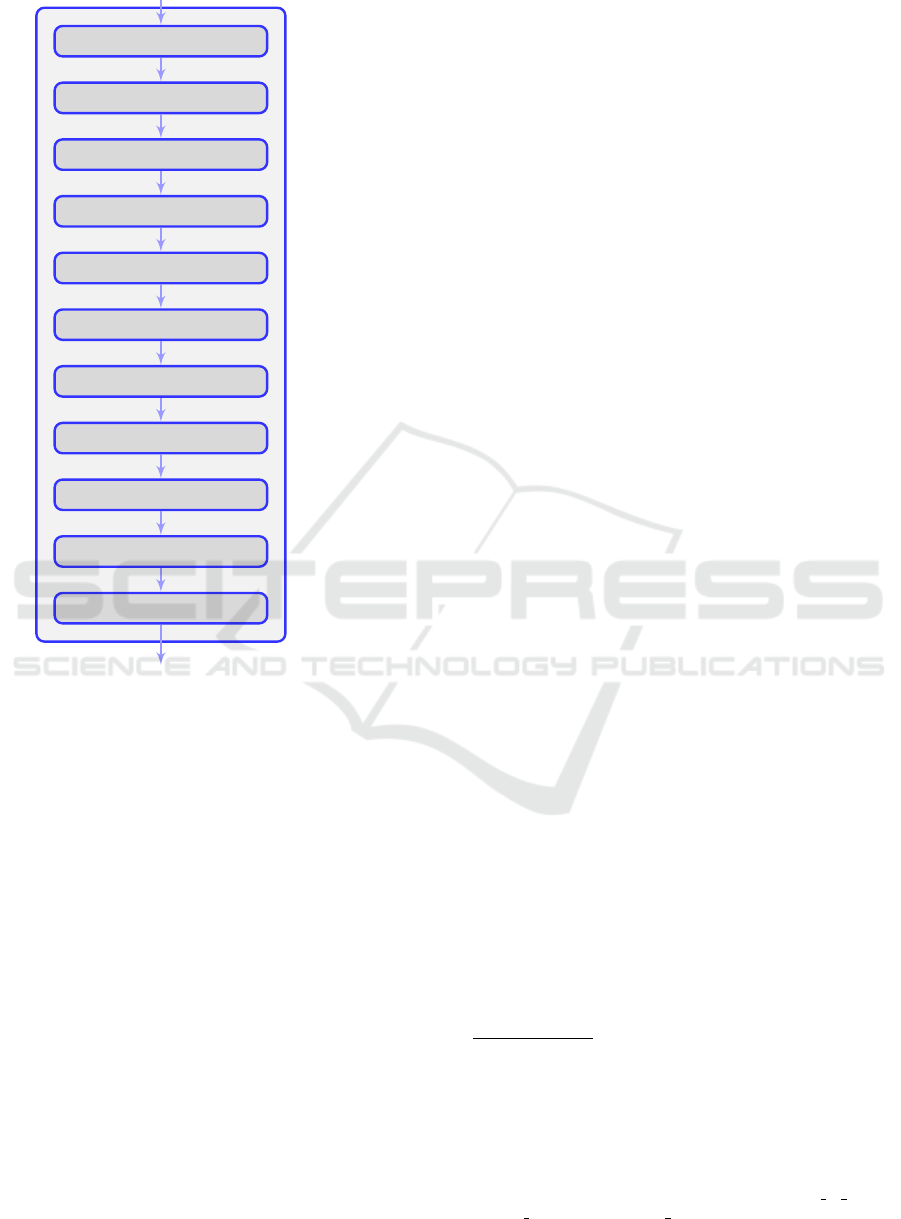
Conv (32)
Conv down (64)
Conv (64)
Conv down (64)
Conv (64)
Conv down (128)
Conv (128)
Conv down (128)
Conv (128)
Dense (512)
Dense (1)
(192, 160, 1)
Conv (32)
Conv down (64)
Conv (64)
Conv down (64)
Conv (64)
Conv down (128)
Conv (128)
Conv down (128)
Conv (128)
FC (512)
FC (1)
832
51.264
102.464
102.464
102.464
204.928
409.728
409.728
409.728
7.864.832
513
Figure 2: The architecture of the network’s discriminator
is depicted on the left. The size of each layer can be seen
after its name. The number of parameters of each layer is
presented on the right of the Figure.
5 APPLICATION
For an experimental validation of the effectiveness
of the proposed methodology, an application was
selected where traditional augmentation techniques
were ineffective. One of the most troublesome dom-
ains for data augmentation is medical imaging, since
biological constraints pose great limitations on the vi-
sual transformations that can be applied without da-
maging the semantic content of the data.
5.1 Dataset
To fully test and evaluate our approach, we experi-
mented on the Alzheimer’s Disease Neuroimaging
Initiative (ADNI)
1
dataset (Petersen et al., 2010).
Alzheimer’s disease (AD) is an irreversible neurode-
generative disease that results in loss of memory and
mental function (thinking, planning, judgment) cau-
sed by the permanent deactivation of neuronal synap-
ses. It is the sixth-leading cause of death in the Uni-
ted States and the most common cause of dementia
among people over the age of 65, yet no prevention
methods or cures have been discovered (Alzheimer’s
Association, 2018).
The ADNI was launched in 2003 as a public-
private partnership, led by Principal Investigator Mi-
chael W. Weiner, MD. The primary goal of ADNI has
been to test whether serial magnetic resonance ima-
ging (MRI), positron emission tomography (PET), ot-
her biological markers, and clinical and neuropsycho-
logical assessment can be combined to measure the
progression of mild cognitive impairment (MCI) and
early Alzheimer’s disease (AD). It has grown to in-
clude data from over 300 patients with AD, over 850
patients with mild cognitive impairment (MCI) and
over 350 normal control subjects (NC).
5.1.1 Patient Selection
In our study we selected a subset of the ADNI image
data which only included scans of normal (NC) and
AD patients, ignoring MCI subjects to aim for the hig-
hest variance between classes. In addition, since Alz-
heimer’s disease causes obvious damage in the brain
tissue, such as shrinkage of the hippocampus and ce-
rebral cortex and enlargement of ventricles, we utili-
zed only the T1 MRI images available. To account
for imbalance between the two classes, 58% of cont-
rol subjects was randomly chosen, ending up with 152
AD patients and 101 NC subjects.
5.1.2 Preprocessing
All images downloaded from the ADNI database
were already preprocessed according to the official
ADNI acquisition protocol (Jack Jr et al., 2008). Ad-
ditional preprocessing steps were taken to facilitate
model training, such as removal of 40 − 45% of the
images at the beginning of the sequence and 25%
at the end of the sequence, and resizing them to
1
Data used in preparation of this article were obtai-
ned from the Alzheimer’s Disease Neuroimaging Initia-
tive (ADNI) database (adni.loni.usc.edu). As such, the
investigators within the ADNI contributed to the design
and implementation of ADNI and/or provided data but did
not participate in analysis or writing of this report. A
complete listing of ADNI investigators can be found at:
http://adni.loni.usc.edu/wp-content/uploads/how to apply
/ADNI Acknowledgement List.pdf
Generative Adversarial Networks as an Advanced Data Augmentation Technique for MRI Data
51

192 × 160 with Lanczos interpolation. Finally, we
randomly divided the dataset into training, validation
and test sets, keeping intact the sequence of each pa-
tient so that every patient appears in only one of the
aforementioned sets. Table 1 shows the distribution
of images (and patients) among classes.
We should note here that in our initial experi-
ments we randomly shuffled and split all images wit-
hout preserving each patient’s sequences; this allowed
the models to identify key features in each subject’s
head’s morphology and achieve a perfect score on the
test set (i.e. for each test set image, the model had
been trained on another from the same patient). Be-
cause of this, the study of the models’ generalization
on new, unseen patients, which is a necessary require-
ment for all medical applications, became infeasible.
Table 1: Image distribution for the ADNI dataset. The re-
spective number of patients is enclosed in parentheses.
training validation test
AD 25,154 (134) 1,975 (12) 1,399 (6)
NC 24,298 (86) 2,343 (9) 2,139 (6)
5.2 Experimental Framework
In order to measure the effectiveness of the proposed
methodology, the following experiment was devised:
Firstly, a Deep Neural Network architecture, capa-
ble of achieving a satisfactory performance on classi-
fying the two categories (i.e. AD, NC), was selected.
This network was trained on the aforementioned data-
set with (II) and without (I) the use of traditional aug-
mentation techniques. Afterwards, artificial images
were added to the training data, forming a composite
dataset, which was again used to train the same net-
work with (IV) and without (III) the use of traditional
augmentation. The four combinations are depicted in
Table 2 for better clarity.
Table 2: The four experiments conducted. The use of GANs
for data augmentation is represented by the horizontal axis
and the use of traditional augmentation techniques on the
vertical axis. The two experiments on the bottom row (i.e.
III and IV) will be referred to as “composite data” experi-
ments.
augmentation
NO YES
GAN
NO I II
YES III IV
The goal of the study was to prove that the mo-
del trained with data augmentation through the use of
GANs (III) outperforms the one without (I). Moreo-
ver, the use of GANs (III) was compared to traditio-
nal augmentation techniques (II), while the impact of
both forms of augmentation (IV) was also examined.
Several metrics were used to evaluate the perfor-
mance of our experiments (i.e. accuracy, precision,
recall, f1), but for simplicity only the accuracy sco-
res will be presented. Since the datasets are highly
balanced, the rest of the metrics fall in line and con-
sequently were considered redundant.
5.2.1 Classification Model
For the classification task we used the popular Res-
Net architecture (He et al., 2016) with 18 layers. The
architecture concluded with a singe FC layer with a
softmax activation function. One parameter we expe-
rimented on was the use of dropout (Srivastava et al.,
2014), which was applied on FC layer; three diffe-
rent dropout rates were examined: 0% (which is equi-
valent to no dropout), 25% and 50%. Every model
was trained from scratch on the available images after
dataset normalization was applied. The models were
trained for a total of 100 epochs with the Adam opti-
mization algorithm (Kingma and Ba, 2014).
5.2.2 Traditional Augmentation Techniques
Due to the nature of our dataset we could only apply
a limited range of visual transformations. In particu-
lar, we sequentially applied: a) horizontal flip with
a given probability, b) brightness adjustment within
90%−110% of the original values, with the same pro-
bability, c) scaling to 90%−110% of the original size,
translation by −5 to +5 percent per axis and rotation
by −5 to +5 degrees, again with the same probabi-
lity. Higher values for this probability correspond to
larger deformations for each image. The probability
will be addressed with the symbol p and will illustrate
the “strength” of the augmentation. For all transfor-
mations, the discarded pixels were all padded with 0
(i.e. the intensity of the background). The whole pro-
cedure is shown in Algorithm 1. In our experiments
we tried probability values (p) of 0.25 and 0.5.
Algorithm 1: Traditional augmentation algorithm.
1: procedure AUGMENT(img, p)
2: with probability p:
3: img ← FlipHorizontally(img)
4: with probability p:
5: img ← Ad justBrightness(img, (0.9, 1.1))
6: with probability p:
7: img ← Scale(img, (0.9, 1.1))
8: img ← Translate(img, (−5, +5))
9: img ← Rotate(img, (−5, +5))
10: return img
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
52
5.2.3 GAN Augmentation
In our GAN models we used a batch size of 32, the
Adam optimizer, Wasserstein loss and gradient pen-
alty (with weight = 10 as in the original paper).
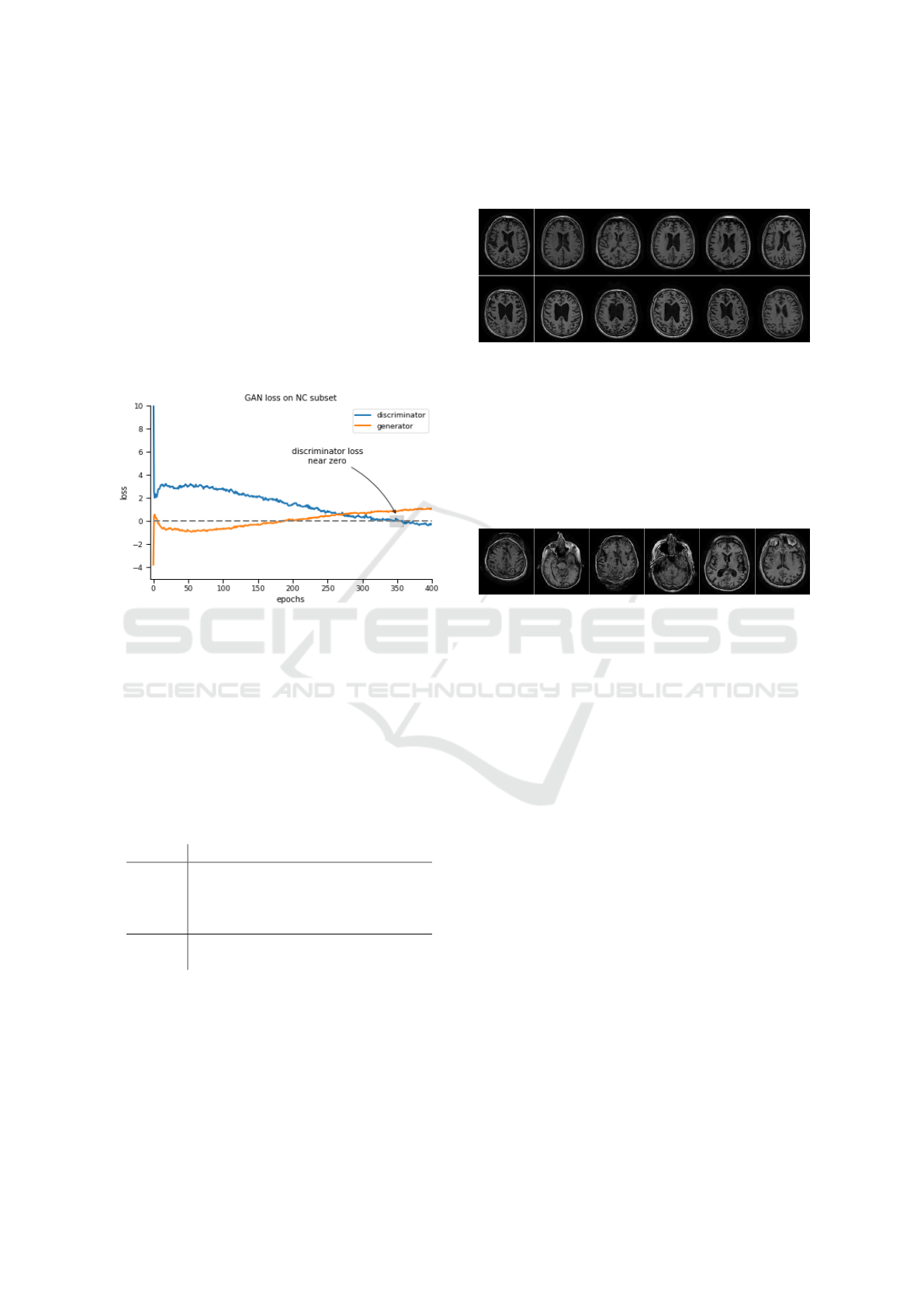
The condition upon which training was termina-
ted required the loss of the discriminator to reach 0,
at which point it is unable to distinguish between real
and fake images. This was reached after around 350
epochs, as can be seen in Figure 3, which depicts the
training losses of the GAN trained on the subset of
ADNI control subjects (i.e. NC). The AD subset exhi-
bited similar training loss curves.
Figure 3: The loss of the GAN trained on the NC subset.
After they were fully trained, the GANs were tas-
ked of producing 50, 000 fake images for each class.
These were combined with the images from the ori-
ginal dataset to form eight separate composite data-
sets, each with a different ratio of fake/real images
(i.e. 25%, 50%, 75%, 100%, 125%, 150%, 175% and
200%). Table 3 shows the statistical characteristics of
all eight composite training sets.
Table 3: Statistics of composite training sets for different
fake/real image ratios.
0% 25% 50% 75%
mean 35.317 35.240 35.200 35.121
std 44.920 44.826 44.783 44.709
100% 125% 150% 175% 200%
35.118 35.089 35.073 35.050 35.035
44.686 44.669 44.640 44.626 44.610
The generated images impacted the statistical me-
asures very slightly, testament of how well the GANs
modeled the distribution of the training sets.
5.3 Empirical Evaluation
In this section we present a number of images produ-
ced by the trained generator in order to demonstrate
our model’s potential. Most generated images proved
to be of extremely high quality (Fig. 4) and showed
all traits of a real MRI scan.
Figure 4: Comparison between real samples (leftmost ima-
ges) from the two classes (NC top, AD below) and their five
most lookalike GAN-created samples, in left-to-right order.
The images were found using an unsupervised, 5-Nearest
Neighbors model.
In Fig. 5 we demonstrate a few cases where the
generator failed to synthesize meaningful images, but
fortunately these mishaps constitute a very small part
of our final composite data.
Figure 5: Some non-realistic looking samples.
Finally, with the additional assistance of a speci-
alized radiologist, we concluded that the overall qua-
lity of the synthetic images was sufficient for use in
the subsequent experiments.
6 RESULTS
Two methods were used for evaluating the results of
the four experiments. The first, which we will refer
to as the “runtime evaluation” involved the validation
set, while the second involved the test set and is refer-
red to as the “generalization analysis”. The first was
used to select the best model regarding both the epoch
and hyper-parameters with which it achieves its best
performance, while the second served to produce an
unbiased estimate of the performance of the models.
6.1 Runtime
During training, at the end of each epoch, every model
was evaluated on the validation set. This procedure
was used to select the best hyper-parameters and to
study the convergence of the models. The accuracy at
the end of each epoch was stored for all experiments
and when plotted can illustrate how the models’ per-
formance improves during training. Because of the
Generative Adversarial Networks as an Advanced Data Augmentation Technique for MRI Data
53
high oscillations some models experience, the graphs
were “smoothed” through a moving average. After
training, weights of the epoch at which each model
achieved its highest validation accuracy were stored.
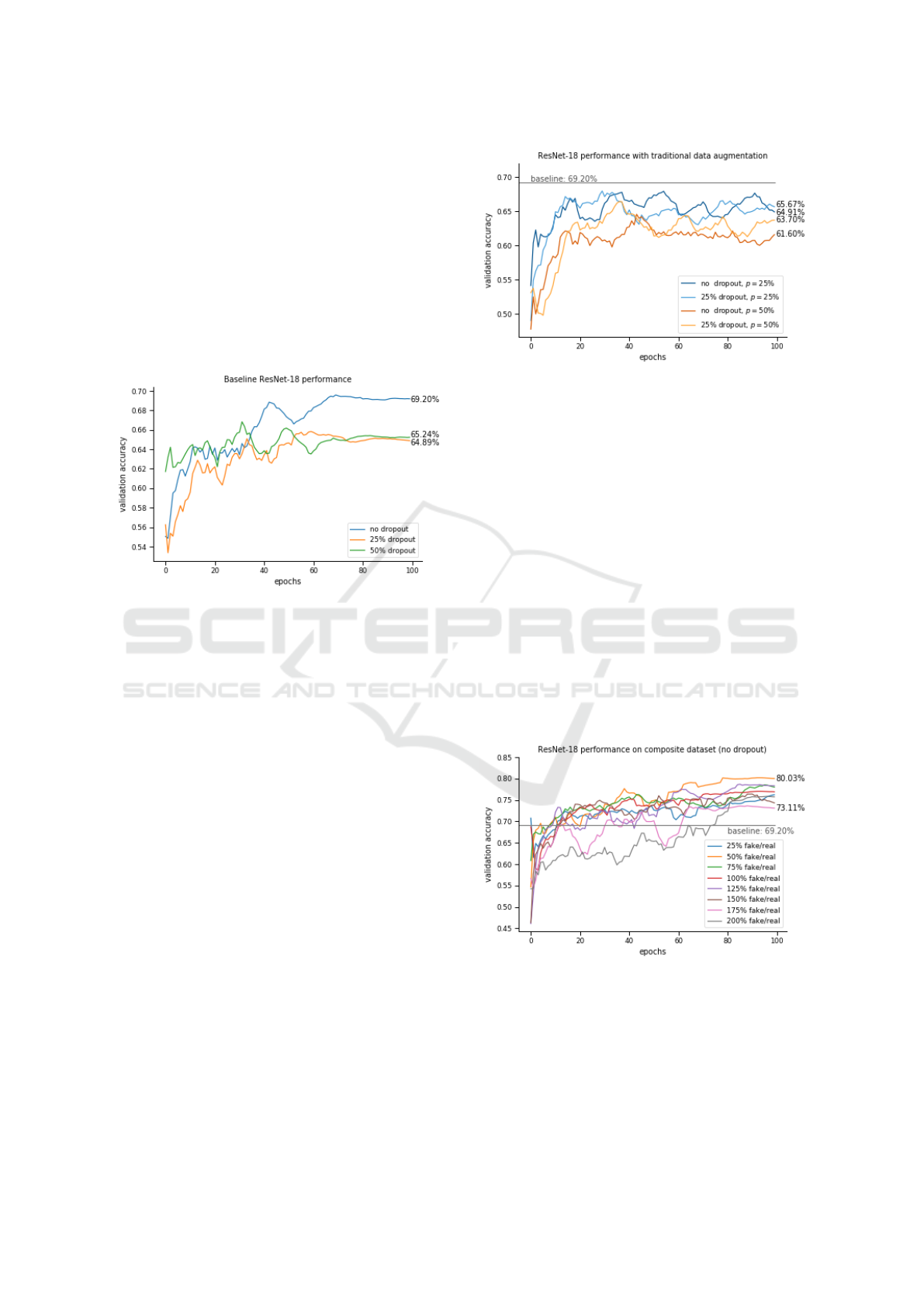
6.1.1 I. Baseline Experiments
This experiment aimed at establishing a baseline for
future experiments. Three different dropout probabi-
lities were tested, 0% (which corresponds to no dro-
pout), 25% and 50%. The results can be seen in Fi-
gure 6.
Figure 6: ResNet-18 trained on the ADNI dataset without
any form of augmentation. This will be used as a baseline
for the next experiments.
The best model (i.e. the ones with no dropout)
achieved an accuracy of 69.2%. This will serve as the
“baseline” for subsequent runs. The addition of dro-
pout appeared to deteriorate the model’s performance
by around 4%.
6.1.2 II. Traditional Augmentation
After establishing the baseline, the next step was to
study how the addition of traditional augmentation
techniques affect the performance of the models. The
augmentors used are described in Section 5.2.2. Fi-
gure 7 depicts the runtime performance of two models
(i.e. one with 25% dropout probability and one wit-
hout dropout) on the augmented dataset. While the
model without dropout clearly outperformed the ot-
hers, its use was re-evaluated during this experiment,
as the regularization effect might be beneficial on not
so ideal data.
While augmentation usually improves a model’s
performance, in the present experiment it did not, ap-
parent by the fact that not a single model reached the
baseline set by the previous experiment. One expla-
nation could be that MR images have a very strict for-
mat. Even the mildest augmentation strategies pro-
ved counter-productive for the classification task. The
Figure 7: ResNet-18 trained on the ADNI dataset with tradi-
tional forms of augmentation. Two different network archi-
tectures were examined for two different values of p. The
baseline from the previous experiment is represented by a
straight line.
best model in this experiment was the one without
dropout and with a 25% augmentation probability,
which converged to an accuracy of 65.67%.
From the figure it is also apparent that augmenta-
tion impairs the model’s convergence, evident by the
heavy oscillations in the curves.
6.1.3 III. Composite Data
The main goal of this study was to evaluate the per-
formance of a CNN trained on a dataset augmented by
images generated from a GAN. In order to determine
the ideal amount of artificial images to be added to the
original dataset, 8 experiments were run, described in
Section 5.2.3. These results are depicted in Figure 8.
Figure 8: ResNet-18 trained on the ADNI dataset augmen-
ted with GAN generated images. 8 different datasets were
used with different ratios of fake/real images. All architec-
tures here do not make use of any dropout. The baseline is
represented by a straight line.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
54
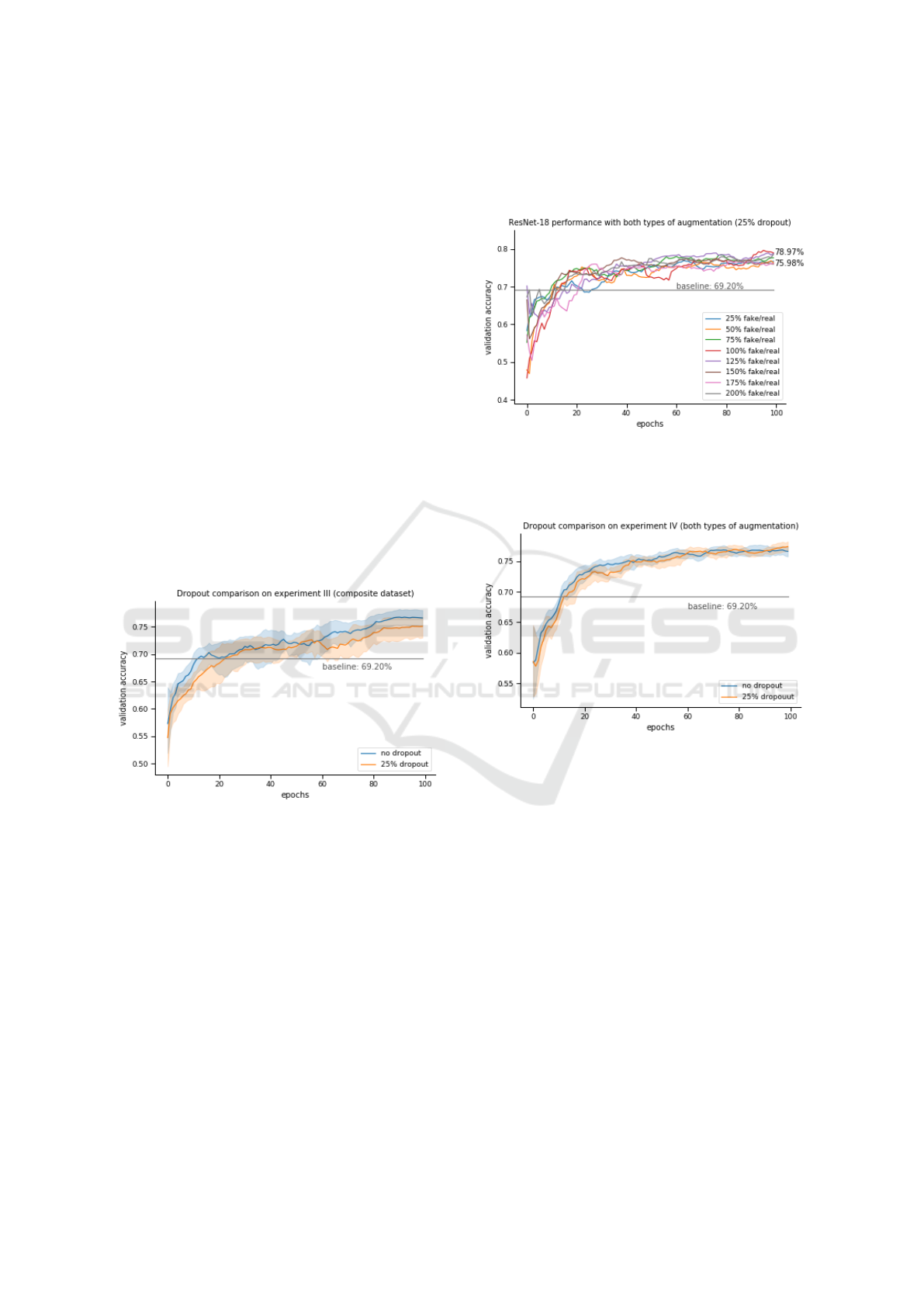
Every single one of the runs outperforms the ba-
seline, proving that GANs can be effectively used as
data augmentors, even in tasks where traditional aug-
mentation techniques are ineffective. The best ratio
(i.e. 50%) scores more than 10% higher than the ba-
seline.
Another thing to note is that performing data aug-
mentation with GAN-generated images does not hea-
vily impact the convergence of the models, as was the
case with traditional augmentation techniques. Even
with the increase in the size of the dataset, almost all
models had converged by epoch 80. In contrast most
traditional data augmentation runs (Figure 7) hadn’t
converged even through the full length of the experi-
ment (100 epochs).
The optimal ratio appears to be somewhere bet-
ween 50 and 125 percent; the best score was 80.03%
from the model trained with a 50% fake/real ratio.
Further tests were run with the use of dropout with
the probability of 25%. While these were worse than
those without dropout, they confirmed the best ratio.
Figure 9 compares the two tests; the thick line repre-
sents the mean of all 8 scores of each test, while the
error band stretches from the best to the worst.
Figure 9: Each of the two tests (i.e. dropout 0% and 25%)
represent 8 runs with different fake/real image ratios. The
thick line follows the mean of all 8 runs, while the error
band covers the distance from the best to worst model. The
baseline is represented by a straight line.
Both tests score much higher than the baseline,
while models that didn’t use dropout outperform the
others.
6.1.4 IV. Composite Data with Traditional
Augmentation
Finally, the combination of both types of augmen-
tation (i.e. traditional and GAN-based) was exami-
ned. The best model this time proved to be the one
with 25% dropout and a 100% fake/real ratio, scoring
78.97%. Contrary to previous experiments, dropout
proved useful in this case. The models trained with
25% dropout, p = 25% and eight different fake/real
ratios are depicted in Figure 10.
Figure 10: ResNet-18 trained on eight different composite
datasets with different fake/real ratios. All models were trai-
ned with 25% dropout and p = 25%. The baseline is repre-
sented by a straight line.
Figure 11: Each of the two tests (i.e. dropout 0% and 25%)
represent 8 runs with different fake/real image ratios. The
thick line follows the mean of all 8 runs, while the error
band covers the distance from the best to worst model. All
models are trained with a 25% dropout probability. The
baseline is represented by a straight line.
The models with 25% dropout fared slightly better
than the ones without, as seen in Figure 11.
Another comparison could be made involving the
two experiments trained on composite datasets, i.e.
one with (IV) and one without (III) the use of traditi-
onal data augmentation. Figure 12 shows the two best
categories of experiments III and IV.
While the addition of traditional augmentation
techniques did manage to assist in the convergence of
the models, the best model was still the one from ex-
periment III. Because there was uncertainty on whet-
her or not the models had fully converged, their trai-
ning was continued for another 100 epochs. After 200
epochs, two more models managed to reach over 80%
validation accuracy: these were the models from ex-
Generative Adversarial Networks as an Advanced Data Augmentation Technique for MRI Data
55
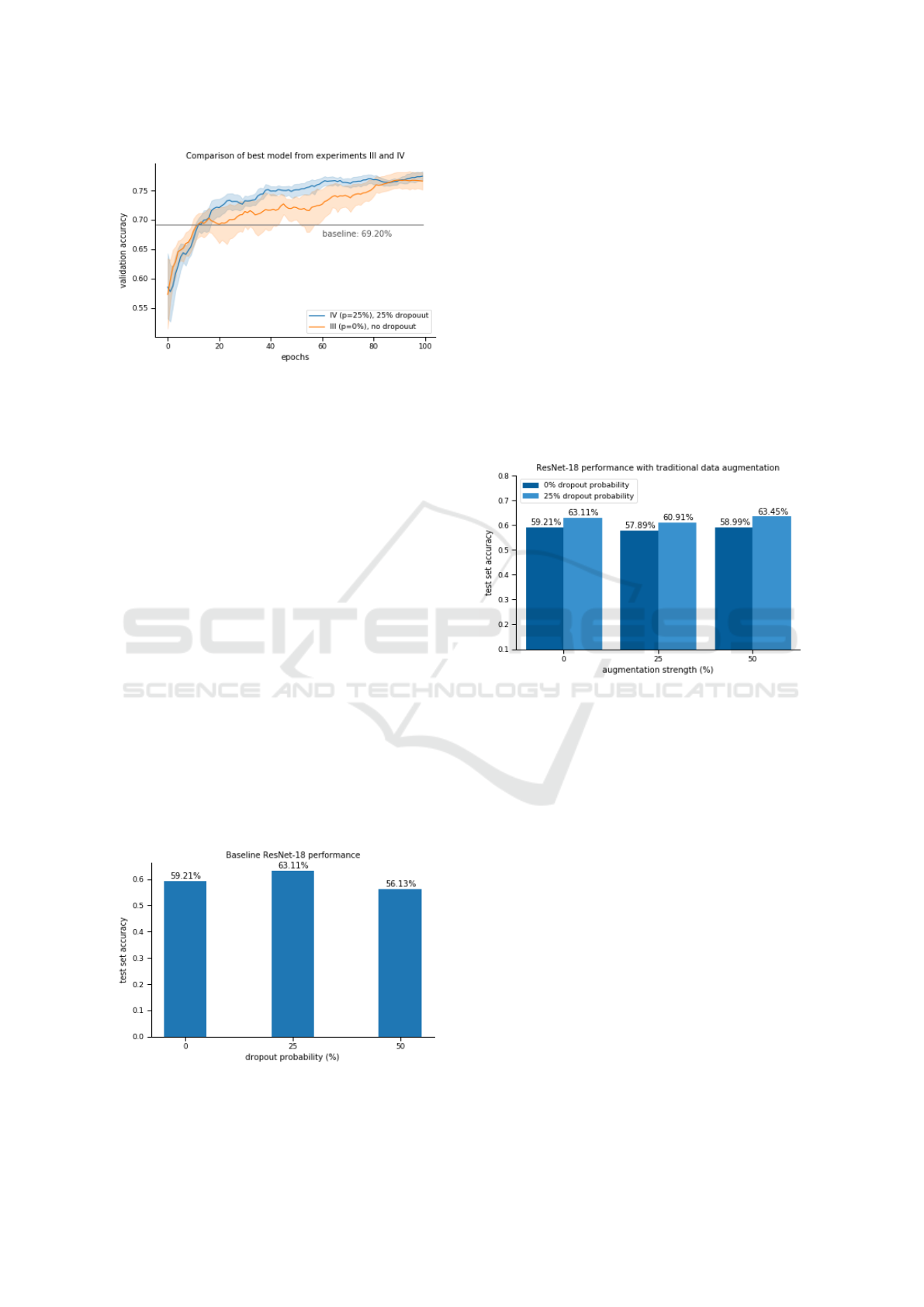
Figure 12: The best runs from experiments III and IV. The
8 runs from experiment III are without any dropout, while
the 8 runs from experiment IV are with 25% dropout.
periment IV, with p = 25%, a dropout probability of
25% and fake/real ratios of 125% and 150% respecti-
vely. This proves that models trained with “strong”
augmentations can be effective, but require more trai-
ning time.
6.2 Generalization
After training the models and evaluating them on the
validation set to identify (a) the best hyper-parameters
and (b) the epoch that it achieves its best performance,
these “best” models were further evaluated on the test
set. Because the hyper-parameter and epoch selection
was done on the validation set, there is a chance that
these led to an overfit of the models on that set. The
test set was meant to evaluate the models one last
time, as objectively as possible.
6.2.1 I. Baseline Experiments
Figure 13 shows the effect of dropout on the models
trained without any form of augmentation.
Figure 13: Three ResNet-18 architectures with different
dropout probabilities were evaluated. 0% dropout is the
same as not using dropout at all.
The first thing to note is that the scores are lower
than the corresponding ones on the validation set, es-
pecially the one that didn’t use dropout. This could
be a consequence of overfitting on the validation set.
In any case, the test set results are considered to be
more reliable. The use of dropout appears to benefit
the results on the test set, which would make sense if
any overfit was taking place. The best model proved
to be the one with a 25% dropout probability, which
achieved an accuracy of 63.11%. This will serve as
the baseline throughout the rest of the experiments.
6.2.2 II. Traditional Augmentation
The second experiment involved the use of traditio-
nal augmentation techniques; the results are shown in
Figure 14.
Figure 14: Two different values of p were tested (i.e. 25%
and 50%). The first two bars (with p = 0%) represent
the previous experiment where no augmentation was used.
They are considered to be the baseline.
Again, the use of dropout benefited the models,
which seems to confirm our previous hypothesis of
overfitting. Data augmentation appears to have little
to no effect, regardless its probability. Nevertheless
the best model was the one with 25% dropout proba-
bility and p = 50%, with a score of 63.45%.
6.2.3 III. Composite Data
For the third experiment, the models were trained on
the eight composite datasets. The results can be seen
in Figure 15.
Almost all of the models that used the composite
data outperformed the baseline. These results fall in
line with those from Section 6.1.3. The best model
was the one with a 25% dropout probability and a
50% fake/real ratio, scoring 72.81%; an increase of
15.4% over the baseline model’s performance.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
56
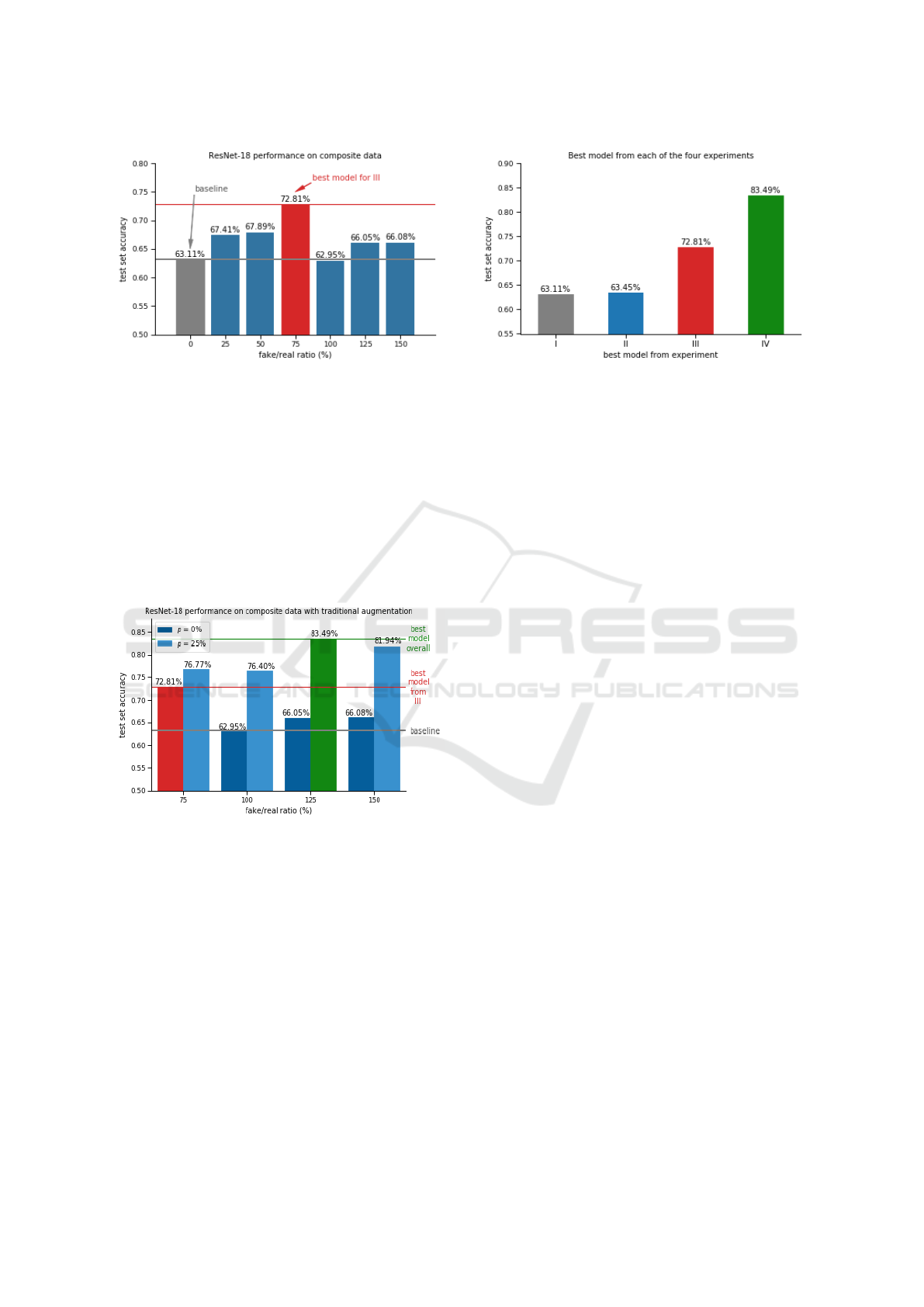
Figure 15: The models in this experiment were trained on
six composite datasets with different ratios of fake/real ima-
ges. Again the first one represents the accuracy scored by a
model trained on the original dataset (baseline result).
6.2.4 IV. Composite Data with Traditional
Augmentation
Finally, traditional augmentation techniques were
used on the composite dataset. The models were eva-
luated with and without the use of dropout.
The results are illustrated in Figure 16.
Figure 16: The models in this experiment were trained on
six composite datasets with different ratios of fake/real ima-
ges. Again the first one represents the accuracy scored by a
model trained on the original dataset (baseline result).
Augmentation appeared to improve the results by
a large margin, in contrast to what it did in the base-
line experiment. This is discussed further in Section
6.3.
The best model was the one with a 125% fake/real
ratio, which achieved the best overall accuracy of
83.49%. An increase of 14.7% and 32.3% over the
best model from experiment III and the baseline, re-
spectively.
Figure 17 compares the best scoring models from
each of the 4 experiments. Both models that were trai-
ned on composite datasets (i.e. III and IV), performed
Figure 17: The best performing model from each of the four
experiments is presented here. While traditional augmenta-
tion (II) didn’t help the baseline model’s performance (I),
the use of GAN-generated images (III) did. By combining
traditional and GAN augmentation schemes (IV), the best
overall score was achieved.
much better than those trained on the original dataset
(i.e. I and II). While traditional augmentation didn’t
help the baseline model (I) it did help the one trained
on the composite dataset (III). A possible explanation
is discussed in the following section.
6.3 Discussion
The benefit of augmenting the dataset with GAN-
produced images is obvious from the experiments on
both the validation (Sec. 6.1) and the test sets (Sec.
6.2). Most importantly, they increase the accuracy of
the models without impacting their convergence.
The main question that arises is why does traditio-
nal data augmentation seem to work on the composite
and not on the original data. A possible explanation
would be that, even though the original dataset is an
acceptable 50, 000 images, these were obtained from
a mere 220 subjects. This results in the dataset ha-
ving a low variance regarding the shapes and forms
of the heads depicted in the images (i.e. the same
patient will produce similar images from visit to vi-
sit). Traditional augmentation strategies would either
heavily alter each image, confusing the model or, in
our case, be so subtle that it simply won’t improve its
performance. The images introduced by GANs howe-
ver don’t correspond to a real patient, so each image’s
characteristics are unique to the dataset, increasing its
variance, and thus possibly giving meaning to traditi-
onal augmentation techniques.
7 CONCLUSION
This paper presents a novel methodology for data aug-
mentation with the use of Generative Adversarial Net-
Generative Adversarial Networks as an Advanced Data Augmentation Technique for MRI Data
57

works. It involves training a GAN for each of the clas-
ses of the original dataset and then using it to produce
a number of synthetic images.
The use of a powerful generative model for pro-
ducing images has many advantages over traditional
augmentation schemes. The most important are the
quality of the produced images and the capability of
generalizing beyond the limits of the original dataset
to produce new patterns. The proposed technique is
especially useful in low-variance datasets where the
images follow a very strict format.
To study the impact of this augmentation strategy,
four experiments were conducted. First, a CNN ar-
chitecture was trained on a large dataset to form a
baseline (I). Afterwards the same model was trained
with traditional (II) and the proposed GAN augmen-
tation technique (III). Finally, the use of both forms
of augmentation on the same dataset was examined
(IV). The models were trained on MR images from
the ADNI dataset to classify patients with AD from
NC subjects.
The models trained with the proposed GAN aug-
mentation methodology (III) outperform the ones
with a traditional one (II) by a large margin. In fact,
because of the nature of the images, the traditional
techniques offered no improvement over the baseline
experiment (I). The final experiment, which combi-
ned both forms of augmentation (IV) outperformed
the rest, showing that while traditional augmentation
could not function on its own, it synergizes well with
GAN augmentation.
Because of the success of the present experiment,
multiple future research directions could be spawned.
An obvious choice is to experiment with different ar-
chitectures for further improvements on the data qua-
lity, either within the WGAN-GP framework by utili-
zing a more powerful discriminator, or by using a ne-
wer, more sophisticated framework that leads to im-
proved experimental performance, such as the Auxi-
liary Classifier GANs by (Odena et al., 2016) or the
Progressive Growing GANs by (Karras et al., 2017).
A different research direction is to use GANs as
a way to improve performance on imbalanced data-
sets. Instead of discarding surplus data or repeating
the same images, a GAN could be trained on the least
populous classes and then generate synthetic data. If
trained correctly, there could be a non-trivial increase
in performance.
ACKNOWLEDGEMENTS
The Titan X Pascal graphics card used for this rese-
arch was donated by the NVIDIA Corporation.
Data collection and sharing for this project was
funded by the Alzheimer’s Disease Neuroimaging
Initiative (ADNI) (National Institutes of Health Grant
U01 AG024904) and DOD ADNI (Department of De-
fense award number W81XWH-12-2-0012). ADNI
is funded by the National Institute on Aging, the Na-
tional Institute of Biomedical Imaging and Bioengi-
neering, and through generous contributions from the
following: AbbVie, Alzheimer’s Association; Alz-
heimer’s Drug Discovery Foundation; Araclon Bio-
tech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb
Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan
Pharmaceuticals, Inc.; Eli Lilly and Company; Eu-
roImmun; F. Hoffmann-La Roche Ltd and its affi-
liated company Genentech, Inc.; Fujirebio; GE He-
althcare; IXICO Ltd.; Janssen Alzheimer Immunot-
herapy Research & Development, LLC.; Johnson &
Johnson Pharmaceutical Research & Development
LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso
Scale Diagnostics, LLC.; NeuroRx Research; Neuro-
track Technologies; Novartis Pharmaceuticals Corpo-
ration; Pfizer Inc.; Piramal Imaging; Servier; Takeda
Pharmaceutical Company; and Transition Therapeu-
tics. The Canadian Institutes of Health Research is
providing funds to support ADNI clinical sites in Ca-
nada. Private sector contributions are facilitated by
the Foundation for the National Institutes of Health
(www.fnih.org). The grantee organization is the Nort-
hern California Institute for Research and Education,
and the study is coordinated by the Alzheimer’s Ther-
apeutic Research Institute at the University of Sout-
hern California. ADNI data are disseminated by the
Laboratory for Neuro Imaging at the University of
Southern California.
REFERENCES
Alzheimer’s Association (2018). Alzheimer’s disease facts
and figures. Alzheimer’s & Dementia, 14(3):367–429.
Antoniou, A., Storkey, A., and Edwards, H. (2017). Data
augmentation generative adversarial networks. arXiv
preprint arXiv:1711.04340.
Arjovsky, M., Chintala, S., and Bottou, L. (2017). Wasser-
stein gan. arXiv preprint arXiv:1701.07875.
Bentaieb, A. and Hamarneh, G. (2018). Adversarial stain
transfer for histopathology image analysis. IEEE
Transactions on Medical Imaging, 37(3):792–802.
Ciresan, D. C., Meier, U., Gambardella, L. M., and Schmid-
huber, J. (2010). Deep big simple neural nets excel on
handwritten digit recognition. CoRR, abs/1003.0358.
Costa, P., Galdran, A., Meyer, M. I., Niemeijer, M.,
Abr
`
amoff, M., Mendonc¸a, A. M., and Campilho,
A. (2018). End-to-end adversarial retinal image
synthesis. IEEE Transactions on Medical Imaging,
37(3):781–791.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
58

Dai, W., Doyle, J., Liang, X., Zhang, H., Dong, N., Li, Y.,
and Xing, E. P. (2017). SCAN: structure correcting
adversarial network for chest x-rays organ segmenta-
tion. CoRR, abs/1703.08770.
Dar, S. U. H., Yurt, M., Karacan, L., Erdem, A., Erdem,
E., and C¸ ukur, T. (2018). Image synthesis in multi-
contrast MRI with conditional generative adversarial
networks. CoRR, abs/1802.01221.
Frangi, A. F., Tsaftaris, S. A., and Prince, J. L. (2018).
Simulation and synthesis in medical imaging. IEEE
Transactions on Medical Imaging, 37(3):673–679.
Frid-Adar, M., Diamant, I., Klang, E., Amitai, M., Gold-
berger, J., and Greenspan, H. (2018). Gan-based
synthetic medical image augmentation for increased
CNN performance in liver lesion classification. CoRR,
abs/1803.01229.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A., and Ben-
gio, Y. (2014). Generative adversarial nets. In Advan-
ces in neural information processing systems, pages
2672–2680.
Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V., and
Courville, A. C. (2017). Improved training of wasser-
stein gans. CoRR, abs/1704.00028.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resi-
dual learning for image recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 770–778.
Hussain, Z., Gimenez, F., Yi, D., and Rubin, D. (2017).
Differential data augmentation techniques for medical
imaging classification tasks. In AMIA Annual Sympo-
sium Proceedings, volume 2017, page 979. American
Medical Informatics Association.
Jack Jr, C. R., Bernstein, M. A., Fox, N. C., Thompson,
P., Alexander, G., Harvey, D., Borowski, B., Britson,
P. J., L. Whitwell, J., Ward, C., et al. (2008). The alz-
heimer’s disease neuroimaging initiative (adni): Mri
methods. Journal of Magnetic Resonance Imaging:
An Official Journal of the International Society for
Magnetic Resonance in Medicine, 27(4):685–691.
Karras, T., Aila, T., Laine, S., and Lehtinen, J. (2017). Pro-
gressive growing of gans for improved quality, stabi-
lity, and variation. CoRR, abs/1710.10196.
Kingma, D. P. and Ba, J. (2014). Adam: A method for
stochastic optimization. CoRR, abs/1412.6980.
Kuka
ˇ
cka, J., Golkov, V., and Cremers, D. (2018). Regulari-
zation for deep learning: A taxonomy.
LeCun, Y. A., Bottou, L., Orr, G. B., and M
¨
uller, K.-
R. (1998). Efficient backprop. In Neural networks:
Tricks of the trade, pages 9–48. Springer.
Neff, T. (2018). Data augmentation in deep learning using
generative adversarial networks. Master’s thesis, Graz
University of Technology, Graz, Austria,.
Odena, A., Olah, C., and Shlens, J. (2016). Conditional
image synthesis with auxiliary classifier gans. arXiv
preprint arXiv:1610.09585.
Perez, L. and Wang, J. (2017). The effectiveness of data
augmentation in image classification using deep lear-
ning. CoRR, abs/1712.04621.
Petersen, R. C., Aisen, P., Beckett, L., Donohue, M., Gamst,
A., Harvey, D., Jack, C., Jagust, W., Shaw, L., Toga,
A., et al. (2010). Alzheimer’s disease neuroimaging
initiative (adni) clinical characterization. Neurology,
74(3):201–209.
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh,
S., Ma, S., Huang, Z., Karpathy, A., Khosla, A.,
Bernstein, M., Berg, A. C., and Fei-Fei, L. (2015).
ImageNet Large Scale Visual Recognition Challenge.
International Journal of Computer Vision (IJCV),
115(3):211–252.
Shaban, M. T., Baur, C., Navab, N., and Albarqouni, S.
(2018). Staingan: Stain style transfer for digital histo-
logical images. CoRR, abs/1804.01601.
Shin, H.-C., Tenenholtz, N. A., Rogers, J. K., Schwarz,
C. G., Senjem, M. L., Gunter, J. L., Andriole, K., and
Michalski, M. (2018). Medical Image Synthesis for
Data Augmentation and Anonymization using Gene-
rative Adversarial Networks. ArXiv e-prints.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. (2014). Dropout: a simple way
to prevent neural networks from overfitting. The Jour-
nal of Machine Learning Research, 15(1):1929–1958.
Vasconcelos, C. N. and Vasconcelos, B. N. (2017). Incre-
asing deep learning melanoma classification by clas-
sical and expert knowledge based image transforms.
CoRR, abs/1702.07025.
Wang, Y., Girshick, R. B., Hebert, M., and Hariharan,
B. (2018). Low-shot learning from imaginary data.
CoRR, abs/1801.05401.
Wu, R., Yan, S., Shan, Y., Dang, Q., and Sun, G. (2015).
Deep image: Scaling up image recognition. arXiv pre-
print arXiv:1501.02876.
Xue, Y., Xu, T., Zhang, H., Long, L. R., and Huang, X.
(2017). Segan: Adversarial network with multi-scale
$l
1$ loss for medical image segmentation. CoRR,
abs/1706.01805.
Yi, X., Walia, E., and Babyn, P. (2018). Generative Adver-
sarial Network in Medical Imaging: A Review. ArXiv
e-prints.
Generative Adversarial Networks as an Advanced Data Augmentation Technique for MRI Data
59
