Visual Growing Neural Gas for Exploratory Data Analysis

Elio Ventocilla and Maria Riveiro

School of Informatics, University of Sk

ovde, Sk

ovde, Sweden

Keywords:

Growing Neural Gas, Dimensionality Reduction, Multidimensional Data, Visual Analytics, Exploratory Data

Analysis.

Abstract:

This paper argues for the use of a topology learning algorithm, the Growing Neural Gas (GNG), for provi-

ding an overview of the structure of large and multidimensional datasets that can be used in exploratory data

analysis. We introduce a generic, off-the-shelf library, Visual GNG, developed using the Big Data framework

Apache Spark, which provides an incremental visualization of the GNG training process, and enables user-

in-the-loop interactions where users can pause, resume or steer the computation by changing optimization

parameters. Nine case studies were conducted with domain experts from different areas, each working on

unique real-world datasets. The results show that Visual GNG contributes to understanding the distribution

of multidimensional data; ﬁnding which features are relevant in such distribution; estimating the number of k

clusters to be used in traditional clustering algorithms, such as K-means; and ﬁnding outliers.

1 INTRODUCTION

Exploratory data analysis (EDA) is “a detective work”

for ﬁnding and uncovering patterns (Tukey, 1977).

It is process engaged by users “without heavy de-

pendence on preconceived assumptions and models”

about the data (Goebel and Gruenwald, 1999). Doing

EDA can be as simple as opening and reading a data

ﬁle in a text editor, or as complex as running multi-

ple Machine Learning (ML) algorithms over a dataset.

While doing EDA, a data scientist’s ﬁrst approach to

a dataset may be driven towards having an overview

of the structure of the data. That is, a view on how

data is distributed in the multidimensional space. The

exploratory steps following the overview might then

be driven towards understanding the given structure,

i.e., answering why some data points are close to each

other and why others are far apart.

Traditional visualization techniques such as scat-

ter plots or scatter plot matrices, can provide the de-

sired overview without needing too much data pre-

processing. However, these techniques are, when

used on their own, limited to the size and/or the di-

mensionality of a dataset (Spence, 2007; Munzner,

2014). ML techniques for hierarchical or density ba-

sed clustering, can overcome these dimensionality li-

mitations, while providing means to visualize data

structure using dendograms or reachability plots (RP).

These plots are, nevertheless, limited to the size of the

dataset, since they visually encode every data point.

An example ML method that is capable of compres-

sing large multidimensional datasets into a ﬁxed num-

ber of representative units is the Self-organizing Map,

SOM, (Kohonen, 1997). Through the U-Matrix plots,

it is possible to visualize these units even if they are

in a high-dimensional space. This visual representa-

tion, however, can be argued not to be as intuitive as a

scatter plot for depicting the structure of the data, and

moreover, the dimension of the U-matrix grid needs

to be established beforehand.

An ML technique which provides the compression

beneﬁts of SOMs is the Growing Neural Gas (GNG)

(Fritzke, 1995). GNG is a topology learning algo-

rithm which starts with two representative units and

grows as it builds a topological representation of data.

Its growth can be limited to a given number of units

and the resulting topological network can be plotted

using graphs. In this paper, we argue that GNG can

provide a complementary perspective of the structure

of large multidimensional datasets for EDA, and that

its potential has been somewhat overlooked by the Vi-

sual Analytics (VA) community.

The effective use of GNG can, as it happens with

other ML algorithms, be hindered by the complexity

that it might represent to users in terms of ease and ef-

fective use, as well as outcome interpretation. This is

often referred to as a black-box problem (Bertini and

Lalanne, 2010; van Leeuwen, 2014; Holzinger, 2016;

Ribeiro et al., 2016), where the learning process and

the ﬁtted model do not readily lend themselves to user

Ventocilla, E. and Riveiro, M.

Visual Growing Neural Gas for Exploratory Data Analysis.

DOI: 10.5220/0007364000580071

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 58-71

ISBN: 978-989-758-354-4

view and interpretation. Indeed, model visualization

for exploration, understanding and evaluation is still

an open challenge in many VA applications, see, e.g.,

Andrienko et al. (2018).

In this paper, we introduce a Visual Analytics

(VA) library to support data structure analysis through

the use of GNG. The solution provides a two dimensi-

onal, incremental overview of the GNG training pro-

cess by displaying partial versions of the generated

topology. Force-directed graphs (FDG) are used to

project the topology onto the two-dimensional plane,

while other visual cues such as nodes’ sizes and dis-

tances are applied to facilitate the interpretation of the

distribution and density of the data. The implemen-

tation leverages from the Apache Spark framework

for deployment over Big Data. User interaction is

enabled during the GNG training so that the process

can be paused, resumed or steered by changing opti-

mization parameters. Details about the trained GNG

units can be seen in a coordinated Parallel Coordina-

tes (PC) plot view. Our implementation is generic in

the sense that it is not tailored to a speciﬁc domain.

The main target users are data scientists as deﬁned by

Kaggle

: “someone who uses code to analyze data”.

The library was evaluated in a qualitative manner

through nine case studies with domain users from dif-

ferent academic areas, who ﬁtted well the data scien-

tist proﬁle. Their feedback was mainly positive, with

observations for improvement. To the best of our kno-

wledge, this is the ﬁrst visually interactive library for

GNG which is not domain-bound, whose visual repre-

sentation gives an overview of data structure regard-

less of its size or dimensionality, and whose format is

aimed at users under the previously given deﬁnition.

In summary, our concrete contributions are:

• a set of visual encodings for a two dimensio-

nal representation of the data distribution, density,

and class – in the case of labeled data – using

GNG topologies, which is applicable to any data

set regardless of size and dimensionality.

• a VA library for GNG which integrates with

the Apache Zeppelin environment and the Apa-

che Spark framework, thus enabling its use in Big

Data analysis.

• the results of a usability evaluation through nine

case studies assessing the usability of the VA li-

brary, and its contributions to GNG interpretabi-

lity and insight gain.

Section 2 is dedicated to reviewing related vi-

sual techniques and ML algorithms, as well as rela-

https://spark.apache.org [Accessed March 2018]

https://www.kaggle.com/surveys/2017 [Accessed Sep-

tember 2018]

ted work. Section 3 describes the GNG algorithm.

We present and justify our design choices for spatial

layout, color, and interaction in terms of known per-

ceptual principles and relevant references in section

4; section 5 describes the Visual GNG library deploy-

ment and usage. Section 6 provides a summary of the

case studies that showcase the use of Visual GNG and

evaluate its usability. Finally, we discuss the results

of the evaluations carried out, and the challenges as-

sociated to the use of Visual GNG in section 7 and we

ﬁnish with conclusions.

2 BACKGROUND AND RELATED

WORK

Visual techniques such as scatter plots or scatter plot

matrices can, without much data pre-processing, pro-

vide an overview of a dataset’s structure. Their ef-

fectiveness, however, can be limited by the dimen-

sionality of the data, i.e., the more dimensions, the

higher the user cognitive load (Spence, 2007). Ot-

her techniques such as RadViz (Hoffman et al., 1997),

Star plots (SP) (Kandogan, 2000) and Parallel Coordi-

nates (PC) (Inselberg and Dimsdale, 1990), deal bet-

ter with multidimensional data. Their effectiveness,

nevertheless, can still be limited by data size. The

amount of information conveyed by PC plots, for ex-

ample, depletes when too many data points are plot-

ted (Munzner, 2014).

PC is widely used for analyzing multivariate data

(a book dedicated entirely to this topic is, for instance,

Inselberg (2009)). PC has been applied in multiple

and very disparate application areas for the analysis

of multidimensional data; state-of-the-art reports that

review their usage and related research are, e.g., Das-

gupta et al. (2012); Heinrich and Weiskopf (2013); Jo-

hansson and Forsell (2016). PC has been noted to pro-

vide better support for the visualization of data featu-

res, than that of data points as units (Spence, 2007);

a property which aimed at leveraging in our solution,

as later described.

Machine Learning

ML techniques can generalize the complexity of the

data by means of dimensionality reduction, den-

sity estimation and clustering. Dimensionality re-

duction algorithms such as principle component ana-

lysis (PCA) (Hotelling, 1933) and the t-Distributed

Stochastic Neighbor Embedding (t-SNE) (Maaten

and Hinton, 2008), can project the data from mul-

tiple dimensions to a two dimensional space, hence,

Visual Growing Neural Gas for Exploratory Data Analysis

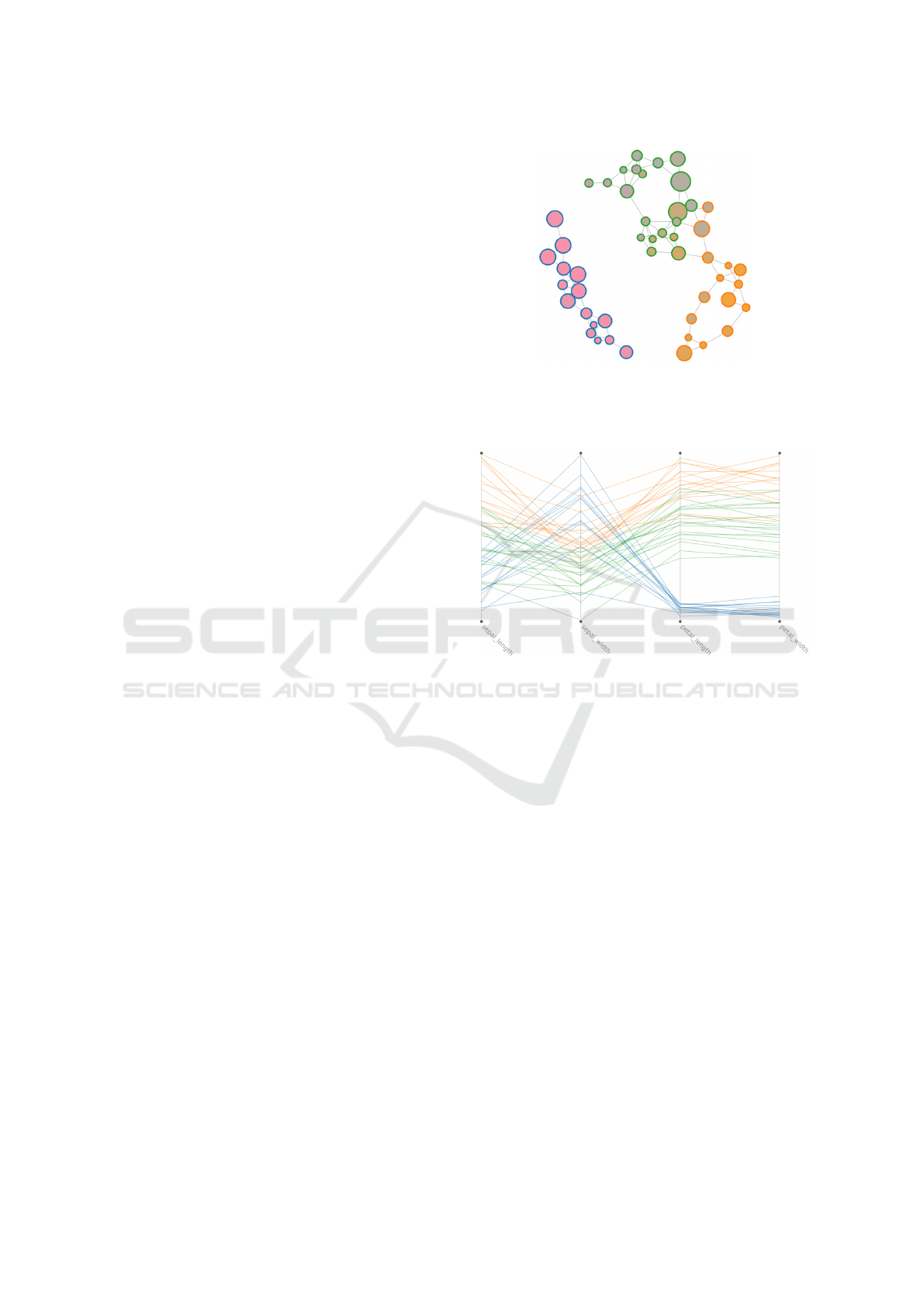
Figure 1: Evolution of a Growing Neural Gas model, ﬁtted to the E-MTAB-5367 (transcriptome dynamics) dataset, over

10000 iterations. Node ﬁll color depicts the value of p15081 CEL, the ﬁrst feature in the dataset, as given by each prototype.

Pink represent lower values, while orange higher. Node size encodes density, i.e., amount of data points represented by a

unit. Edge length encodes Euclidean distance between prototypes. The ﬁnal graph on the right represents the structure of the

dataset in terms of data distribution and density, as seen by GNG. The topology suggests incremental changes in the values of

the data points, instead of drastic ones; the antenna-looking nodes on the top suggest the existence of out-of-norm data points.

enabling the use traditional scatter plots even for mul-

tidimensional data. Of these two, t-SNE has proven

to be specially powerful for visualizing the structure

of multidimensional data (Maaten and Hinton, 2008).

The technique, however, can be costly in terms of

time and resources when plotting large datasets. Furt-

hermore, it is non-deterministic, thus, precluding the

replication results.

Other ML techniques that provide means for plot-

ting an overview of data structure are hierarchi-

cal clustering (HC) algorithms, SOMs (Kohonen,

1997) and the density-based clustering algorithm,

OPTICS (Ankerst et al., 1999).

HC algorithms create trees of nested partitions

where the root represents the whole dataset, each leaf

a data point, and each level in between a partition or

cluster. The resulting tree of an HC algorithm can be

plotted using dendograms, a tree-like structure where

the joints of its branches are depicted at different heig-

hts based on a distance measure. The OPTICS algo-

rithm has a similar logic to that of HC algorithms in

the sense that data points are brought together one by

one. A key difference is that OPTICS sorts the data

points in a way that can later be visualized using a re-

achability plot (RP), where valleys can be interpreted

as clusters and hills as outliers. Dendograms and RPs

depict every data point, thus making them susceptible

to the size of a dataset as well.

One of the most widely used neural-based algo-

rithms in visualization applications is the SOM (Ko-

honen, 1997). SOM takes a set of n-dimensional trai-

ning vectors as input and clusters them into a smal-

ler set of n-dimensional nodes, also known as model

vectors. These model vectors tend to move toward

regions with a high training data density, and the ﬁ-

nal nodes are found by minimizing the distance of

the training data from the model vectors. The output

from a SOM can be plotted using a U-Matrix, which

is a two-dimensional arrangement of – commonly –

mono-colored hexabins. The opacity color of each bin

is then varied based on a distance value between mo-

del vectors: the more opaque the higher the distance

and vice versa. SOMs have been used in multiple ap-

plications, e.g., feature learning (Vanetti et al., 2013),

ﬂow mapping (Guo, 2009), trajectory and trafﬁc ana-

lysis (Schreck et al., 2009; Riveiro et al., 2008).

Interpretable and Interactive ML

In the intersection between HCI and ML is found

considerable research where the focus is on user in-

teraction with, and interpretation of, ML techniques

(Amershi et al., 2013). The dialog between user and

algorithm for solving problems is appealing for many

reasons, for instance, to integrate valuable expert kno-

wledge that may be hard to encode directly into com-

putational models, to help resolve existing uncertain-

ties as a result of error that may arise from automa-

tic ML or to build trust by making humans invol-

ved in the modeling or learning processes (Boukhelifa

et al., 2018). Thus, human and machine collaborate

to achieve a task, whether this is to classify objects, to

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

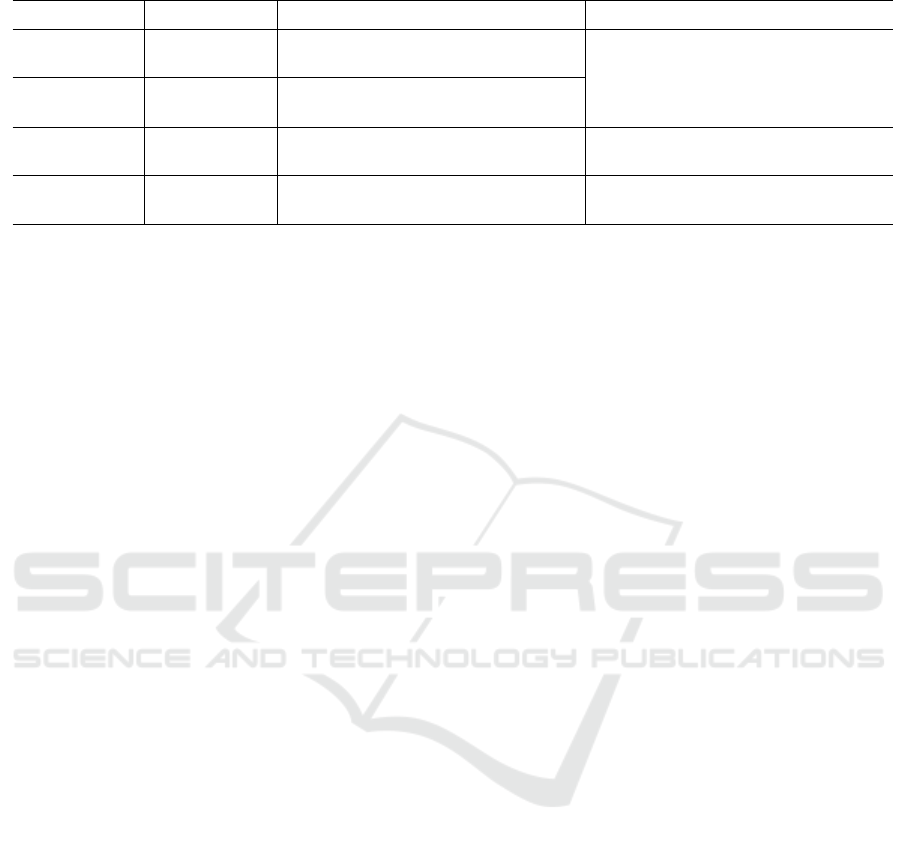
Table 1: Summary of visual encodings used in Visual GNG.

ATTRIBUTE ENCODING VALUE GIVEN BY

TASK SUPPORT

Similarity Edge length

Distance (e.g., Euclidean) between

units’ prototypes.

Identiﬁcation of cluster patterns and

outliers.

Density Node size

Number of times a unit has been

closest to an input signal.

Distribution Node ﬁll color

Prototypes’ value representation for a

given dataset feature.

Identiﬁcation of informative features.

Class

Node stroke

color

Label value of the last input signal a

unit was closest to.

Identiﬁcation of class distribution.

ﬁnd interesting data projections or patterns, or to de-

sign creative artworks (Boukhelifa et al., 2018). Users

can be involved in different phases (Ventocilla et al.,

2018) such as in feature selection, optimization, mo-

del training, output reﬁnement and evaluation.

3 GROWING NEURAL GAS

GNG is described as an incremental neural network

that learns topologies (Fritzke, 1995). It constructs

networks of nodes and edges as a means to des-

cribe the distribution of data points in the multi-

dimensional space. GNG, unlike other clustering al-

gorithms (e.g., K-means, SOM), grows during the le-

arning process and does not require users to deﬁne

a number of k centroids. Such a dynamic property

has been noted as advantageous over other clustering

algorithms (Heinke and Hamker, 1998; Prudent and

Ennaji, 2005).

The algorithm starts with two connected neurons

(units), each with a randomly initialized reference

vector (prototype). Samples (signals) from the data

are taken and fed, one by one, to the algorithm. For

each input signal the topology adapts by moving the

unit which is closest, and its direct neighbors, towards

the signal itself. Closeness, in this case, is given by

the Euclidean distance between a unit’s prototype and

the signal. New units are added to the topology every

λ signals, in between the two neighboring units with

the highest accumulated error. A unit’s error cor-

responds the squared distance between its prototype

and previous signals. Edges (i.e., connections bet-

ween units), on the other hand, are added between the

two closest units to an input signal, at every iteration,

and are removed when their age surpasses a threshold.

Edges are aged in a linear manner at every iteration,

and are only reset when they already connect the two

closest units to a signal.

Heinke and Hamker (1998) benchmarked diffe-

rent neural-based algorithms and found GNG having

the best performance. Their comparison criteria were

based on “classiﬁcation error, the number of training

epochs, and sensitivity toward variation of parame-

ters”. The adaption capabilities of GNG are demon-

strated in Sledge and Keller (2008). Applications

of GNG are found in literature related to clustering

and classiﬁcation problems, for instance, Daszykow-

ski et al. (2002); Costa and Oliveira (2007); Palomo

and L

opez-Rubio (2017).

GNG has not, to the best of our knowledge, been

used for visual exploration of multidimensional data-

sets or used in VA-related research.

4 VISUAL ENCODINGS

The ﬁrst contribution of this paper is a set of visual en-

codings for a two dimensional representation of data

distribution, density, and class. A summary of the vi-

sual encodings is given in Table 1.

FDGs were used to project GNG topological con-

structions onto a two dimensional plane. An FDG

usually simulates two forces (Munzner, 2014): a re-

pulsion force which pushes nodes away from each

other, and an attraction force which pulls connected

nodes close together. Force-directed placement algo-

rithms usually start with nodes at random positions

and then gradually moves them until an equilibrium

between the forces is reached.

The reasons for using FDGs to visually encode a

GNG topology are (1) the seamless visual mapping it

entails, where GNG units can be represented by nodes

in the graph, and (2) their connections as edges; FDGs

are free from data-bound spatial constraints, i.e., free

from mapping data to x/y coordinates for creating a

layout; attraction forces provide means for depicting

distance relations and, therefore, clusters; and they

can be interacted with without losing structure nor

distances by re-heating the placement algorithm when

nodes are dragged.

Visual Growing Neural Gas for Exploratory Data Analysis

Figure 2: (a) Zeppelin paragraph exemplifying the use of the Visual GNG library; ﬁgures (b) to (f) depict a sequence of the

evolution of the GNG model of the Iris dataset; (g) shows the GNG model with nodes colored by prototypes’ values for petal

width. Nodes in (f) are colored by sepal width. Calling the display() method in (a) displays the visual elements for system

feedback and user control of the learning process.

Prototype Similarity

GNG, by deﬁnition, connects units which have si-

milar prototypes. With FDGs it is possible to furt-

her highlight similarities between units’ prototypes

by means of attraction. That is, the more similar the

prototypes are, the closer their representative nodes

will be and vice versa. Similarity can be based on a

distance measure between prototypes (e.g., Euclidean

distance).

PC can be used as a detailed view of the prototy-

pes so users can corroborate the similarity between

nodes. By plotting units’ prototypes in PC, and by ha-

ving it as a coordinated juxtaposed view to the FDG,

the user can explore where the similarities – and dis-

similarities – between prototypes exist. Coordination

can be static and/or interactive. Static coordination

can, for example, be based on color, where the color

ﬁll of a node in FDG is also employed for the stroke

color of its corresponding line in PC. Interactive coor-

dination, on the other hand, can be achieved through

linked highlighting, e.g., increasing a line’s width in

PC, when the user hovers over its corresponding node

in the FDG (e.g., Figs. 4 and 3).

Our solution encodes similarity by constraining

attraction of nodes based on the Euclidean distance

of their prototypes. We made use of the D3js force-

directed layout library, which is a Javascript frame-

work for the development data-drive, web-based user

interfaces. A method called linkDistance, which

takes a value in pixels, enables such a distance con-

straint between the nodes when running the placement

algorithm. We scale the Euclidean distance between

units’ prototypes to a deﬁned range of pixels:

dscale(e

g f

) =

g f

− E

min

max

− E

min

∗ (b − a) + a

Where e

g f

is the Euclidean distance between units

g and f ; variables a and b are the minimum and max-

imum pixel lengths; and E

min

and E

max

the minimum

and maximum Euclidean distances in the topology.

To avoid overlapping nodes we set a = r

+ r

where

r represents the radius of nodes g and f respectively.

The maximum length, on the other hand, is given by

b = m

+ k where m denotes a maximum node radius

and k a constant. The values for these two are arbi-

trary, 15 and 50 pixels respectively.

Nodes (a), (b) and (c) in Figure 4 present an ex-

ample of prototypes similarity. The edge connecting

nodes (c) and (b) is shorter compared to the edge bet-

ween nodes (a) and (b). This suggests that prototypes

in (c) and (b) have a smaller Euclidean distance than

that of prototypes in (a) and (b). This can be veriﬁed

by looking at their representations in the PC plot in Fi-

gure 5. Highlighted lines in PC correspond to highlig-

hted nodes in the FDG, i.e., line (a) in PC represents

node’s (a) prototype in FDG and so on. Highlighting

in the PC plot is done by increasing line width from

1 pixel to 3, and by demoting other lines by lowering

their opacity from 100% to 25%.

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

Data Density

The density of the data in the multi-dimensional space

can be estimated during the execution of the GNG,

and be visually encoded in the size of the nodes.

A way for estimating the density of the data with

GNG is to count the number of times a unit has been

selected as the closest to an input signal. The more

times a unit is closest to a signal, the more data points

it will potentially represent. We say potentially be-

cause a unit might move away from some data points

as it moves towards an input signal; moreover, new

units added to the model might take fractions of regi-

ons that were covered by old units. As a way for im-

proving the density estimation – and the model – we

removed units with low utility (i.e., obsolete units), as

proposed in Fritzke (1995), after a maximum number

of units has been reached. This way, new units are ad-

ded in more representative places in later iterations.

Not doing so will, based on our trails, increase the

chances of having topologies with empty units (i.e.,

prototypes that do not represent any data point).

In our solution nodes vary in size based on how

frequent each has been the closest (the winner) to an

input signal. A node’s size, in this case, is encoded

through radius – which is also pixel-based. The win-

ning frequency is mapped to a radius also linearly:

rscale(c

) =

−C

min

max

−C

min

∗ (m − n) + n

Where c

is the winning frequency count of unit g;

min

and C

max

are the minimum and maximum win-

ning frequencies in the topology, and n is the mini-

mum pixel radius. We give n an arbitrary value of 5

pixels. Taking that the maximum radius is given by

m, then nodes’ radius can vary from 5 pixels to 15.

Looking at Figure 4, it is possible to see that node

(d) has the lowest estimated density of all highlighted

nodes.

Data Distribution

Hints on how the data is distributed in the multi-

dimensional space can be given by encoding how a

prototype represents the value of a dataset’s feature.

More speciﬁcally, by mapping the value represented

by each prototype, for a user-selected feature, to the

ﬁll color of its corresponding node. Figures 2 (f) and

(g) represent an example where ﬁll color in (f) is de-

ﬁned by prototypes’ value for ‘sepal length’, whereas

in (g) by prototypes’ value for ‘petal width’. Such an

encoding can help users determine the importance of

a feature on the distribution of the data. The color

scale selected for this purpose should be one which

allows a user to identify where the lowest and highest

values of a given feature are found in the topology.

The selection of a proper color scale could also help

users identify outliers in the data.

In addition to encoding feature values as ﬁll color,

classiﬁcation values (labels) can be visually represen-

ted in the color stroke of the nodes. This is in the

case of working with labeled data. Assigning a la-

bel to a unit is possible by taking the label of the last

input signal it has been closest to. Having a visual

cue on how classiﬁcations are distributed within the

topological model can help users comprehend the dif-

ferences between instances of different classes, and

the similarities between those of the same.

Our solution uses the colors suggested by Spence

and Efendov (2001) to ﬁll the color of the nodes, ba-

sed on prototypes’ values for a given data feature:

pink denotes the lowest values, gray average values

and orange the higher. The intention, as stated Spence

et al., is for the highest and lowest values to “pop out”.

Figures 2 (f) and (g) are examples of two different co-

lor ﬁlls. Nodes in (f) are colored based on the values

of sepal width, whereas in (g) colors are based on pe-

tal width. By looking at (f) and (g), it is possible to see

that petal width describes the distribution of the data

better than sepal width. Iris of type Setosa are repre-

sented by all pink nodes in (g), but by a mix of colors

(orange, gray and pink) in (f). Moreover, the color

shift from orange to gray – i.e., a smooth change from

large to average petal width – in the larger network

in (g) corresponds to, on the orange side, iris of type

Virginica and, on the gray side, Versicolor. This color

shift does not occur in (f).

5 VISUAL GNG LIBRARY

The second contribution of this paper is an off-the-

shelf Visual GNG library

for Apache Zeppelin

, a

web-based notebook system for data-driven program-

ming. Zeppelin enables, among other things, writing

and executing Scala and SQL code, it provides access

to the Apache Spark framework for Big Data analy-

sis and provides built-in charts such as scatter plots,

bar, and line charts. In this section, we explain how to

deploy the library and its interactive capabilities.

The off-the-shelf format of the library requires

that a dependency to the library is added to the Zep-

pelin Spark interpreter as described in Ventocilla and

Riveiro (2017), before it can be deployed. We as-

A version can be found here: https://www.his.se/om-

oss/Organisation/Personalsidor/Elio-Ventocilla/

https://zeppelin.apache.org [Accessed August 2018]

Visual Growing Neural Gas for Exploratory Data Analysis

sume the dependency has been added for the follo-

wing steps.

To deploy Visual GNG the user needs to – in a

Zeppelin notebook – import the library, create an in-

stance of VisualGNG and then call the display()

method (see Figure 2 (a)). Importing the library gi-

ves the user access the VisualGNG class. Creating

an instance of it requires the user to provide the data

that will be used in the learning process (i.e., a Spark

DataFrame). In the example given in Figure 2 (a),

the data is represented by variable data, while the

VisualGNG instance is represented by the variable

gng. We make use of the Iris dataset (Blake and Merz,

1998) in the example.

Figure 3: Parallel coordinates plot of GNG prototypes cor-

responding to nodes in Figure 4 (f). Stroke color is based

on the prototypes’ values for sepal width.

Calling the display() method on the gng varia-

ble shows the following elements: an execution but-

ton for running and pausing the GNG learning pro-

cess; a drop down element Parameters for user access

to optimization parameters; a drop-down list Color by

for selecting the data feature by which the ﬁll of the

nodes are colored; a status text describing the current

state in terms of iterations, number of edges and no-

des; and two connected nodes, as that is the initial

state of the GNG model.

Clicking on the execution button changes its text

to Pause, and starts the learning process in the back-

ground. Updates to the FDG are made every λ num-

ber iterations, i.e., every time a new unit is added to

the model. Figures 2 (b) to (f) show the evolution

of the GNG model at different iterations steps for the

Iris dataset. It is possible to see here how the topo-

logy splits into two networks: a small one represen-

ting one type of iris, and the bigger one representing

the two other types. This is an expected outcome for

the Iris dataset. Two types of iris (Virginica and Versi-

color), with many shared characteristics, became part

of a single network (the big one); whereas the other

Figure 4: Force-directed graph of the GNG model generated

from the Iris dataset. Highlighted nodes correspond to those

selected by the user. The visual encoding for highlighting

nodes is done by demoting non-selected nodes with a lower

opacity.

Figure 5: Parallel coordinates plot of the GNG prototypes

generated from the Iris dataset. Highlighted lines corre-

spond to nodes selected by the user in the FDG (see Figure

4).

type of iris (Setosa), which has more remarkable dif-

ferences from the other two, developed a network of

its own (the small one).

To visualize the resulting prototypes in a PC plot

the user can, in another Zeppelin paragraph, call the

method parallelCoordinates() of the gng varia-

ble (see Figure 3).

User Interactions

Interactive features are described in two parts: those

regarding system feedback and user control on the le-

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

arning process, and those regarding user exploration

for interpretation.

Feedback and Control

System feedback and user control features are descri-

bed based on M

uhlbacher et al. (2014) types of user

involvements (TUI): execution feedback, result feed-

back, execution control, and result control.

Execution feedback regards information the sy-

stem gives the user about an ongoing computation.

Visual GNG provides two types of execution feed-

back: aliveness (i.e., whether computations are un-

der progress or something failed) and absolute pro-

gress (i.e., “information about the current execution

phase”). Aliveness is given by the text in the execu-

tion button (Run, Pause and Done). Absolute progress

is given in the status text, through which the user is

informed about the number of iterations executed so

far.

Result feedback regards information the system

gives to the user about intermediate results of an on-

going computation. Visual GNG provides feedback

about structure-preserving intermediate results, i.e.,

partial results that are “structurally equivalent” to the

ﬁnal result. Such feedback is given by updating the

FDG when units and connections are added to, or re-

moved from, the model. These updates are reﬂected

by reheating the force-directed placement so that the

FDG layout is recomputed, with model updates taken

account.

Execution control involves user interactions that

have an impact on an ongoing computation. Visual

GNG enables this type of control through the execu-

tion button. By clicking on it, the user can start the

optimization, pause it and resume it. If the user wis-

hes to reset the optimization to zero, it is possible to

do so by rerunning the Zeppelin paragraph. It is also

possible for the user to execute different instances of

VisualGNG in different paragraphs within the same

notebook. This can prove convenient when compa-

ring results for different parameter settings.

Result control deﬁnes user interactions that have

an impact on the ﬁnal result. This type of user invol-

vement is often referred to as steering (Mulder et al.,

1999). In Visual GNG the user can steer the learning

process by changing learning parameters in the Para-

meters drop-down element. Changes to the learning

parameters can be done before and during the lear-

ning process.

Interaction for Interpretation

Other types of interactive features are aimed at hel-

ping the user explore to interpret the ﬁtted – or parti-

Figure 6: Force-directed graph of the GNG model genera-

ted from the Iris dataset. Nodes in gray and lower opacity

correspond to those ﬁltered out in PC (Figure 7). Selected

nodes remain highlighted even when ﬁltered.

Figure 7: Parallel coordinates plot of the GNG prototypes

generated from the Iris dataset. Lines in gray and lower opa-

city correspond to prototypes ﬁltered by the lower boundary

of petal width.

ally ﬁtted – topology. Three types of interactive fea-

tures were implemented for this purpose: linked high-

lighting, ﬁltering and K-Means clustering.

Linked highlighting takes place when the user ho-

vers over a node in the FDG. By doing so, its corre-

sponding prototype in the PC plot is highlighted, i.e.,

the width of the line is increased while the opacity of

other lines is reduced. Hovering out returns the pro-

totype line to its previous visual encoding. Clicking

on the node will make the line to remain highligh-

ted even when hovering out (Figure 3), and will also

demote all other non-selected nodes in the FDG by

decreasing their opacity (Figure 4). This interactive

feature aims at facilitating the interpretation of what

a prototype represents (i.e., the feature values of the

data points it represents), and also how prototypes dif-

ferentiate from each other. More speciﬁcally, it faci-

litates answering the question of what is the general

proﬁle of the data points in a given region of the topo-

Visual Growing Neural Gas for Exploratory Data Analysis

logy? And, why do they belong to that region and not

to another?

Filtering, on the other hand, is triggered by drag-

ging up and down feature boundaries in the PC plot

(Figure 7). Dragging feature boundaries will cause

prototype lines with values outside the boundaries, as

well as their corresponding nodes in the FDG (Figure

6), to be demoted with gray color and lower opacity.

Filtering allows users to see which areas in the GNG

network have prototypes with a given proﬁle.

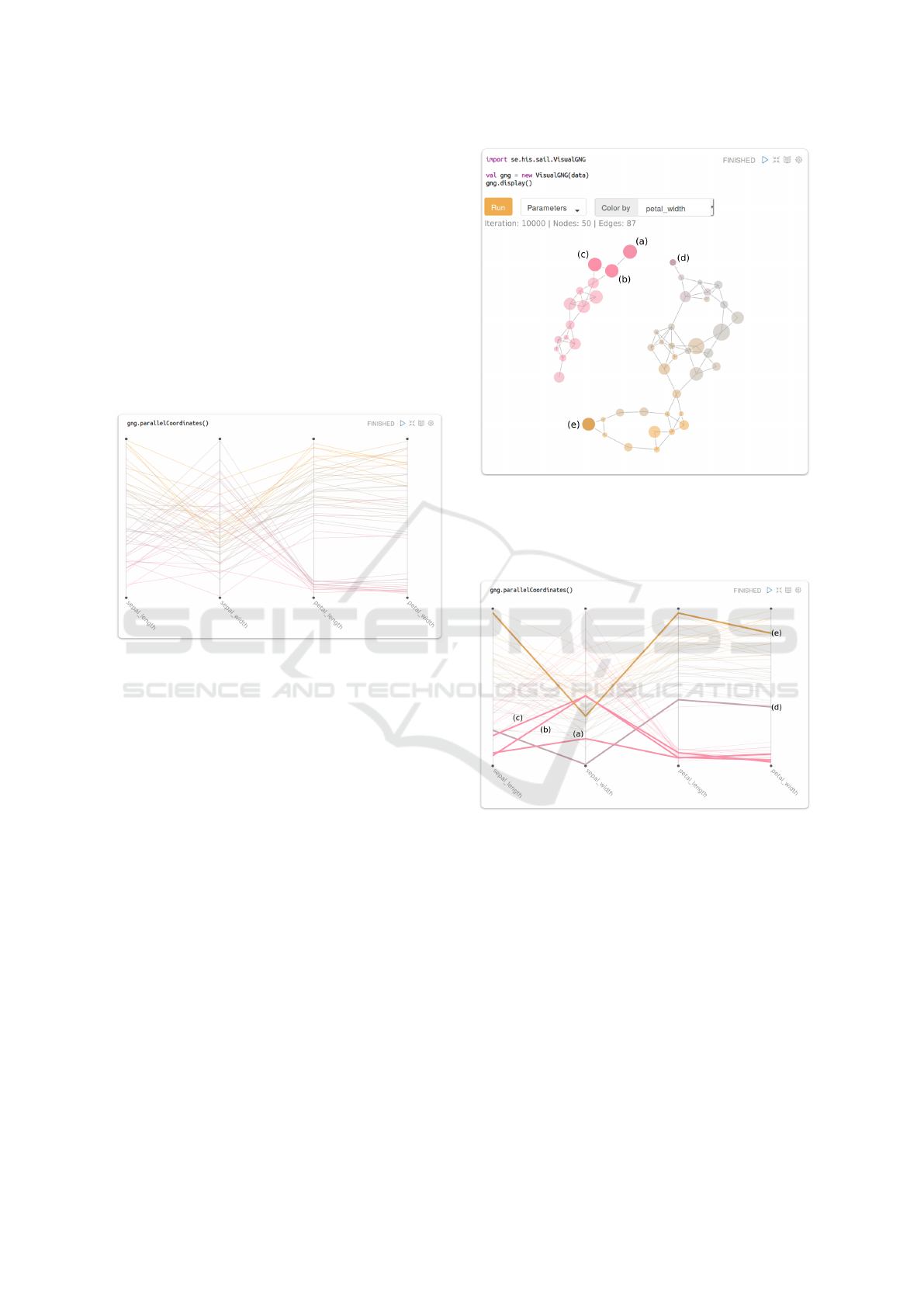
K-Means clustering can be called through the

kmeans(k) method of the gng variable. By provi-

ding a number of k, the system will run K-Means over

the prototypes in the GNG model. In other words, it

will group prototypes into k clusters, as given by K-

Means. The results are then depicted in the FDG by

coloring the stroke of the nodes based on their assig-

ned cluster (Figure 8). Prototypes in PC are also co-

lored based on the corresponding cluster (Figure 9).

Calling kmeans again with another k value will reco-

lor nodes and lines based on the new cluster assign-

ments. This allows fast testing of different k values

with visual feedback on the cluster distributions, re-

gardless of the size and dimensionality of the data.

6 CASE STUDIES

The third contribution is the results of nine case

studies carried to investigate the capabilities of Vi-

sual GNG. The participants of the empirical evaluati-

ons were data scientists from the following academic

areas: three from bioinformatics, one from biomedi-

cine, two from engineering, one from game research,

and two from general data science and machine lear-

ning. One was a master student, one a Ph.D. candi-

date, two were post-docs and ﬁve principal investiga-

tors (PI).

Each case study was arranged in four stages: (a)

preliminary questions about user domain, expertise,

type of data and analysis tools employed in their

daily work; (b) familiarization with the technology

using two examples, each with a different dataset; (c)

thinking-aloud user analysis of domain data with Vi-

sual GNG; (d) and, ﬁnally, wrap up questions on user

experience during (c). All four stages were carried

individually and followed a semi-structured interview

format (the interview guide was devised according to

descriptions by Patton (2005)), at each participant’s

ofﬁce, with an approximate duration of one hour. A

Zeppelin server was set up so that users would have

access to it from their own workstations. Three no-

tebooks were created for each study: two for the ex-

amples used in stage (b) and the other for the domain

Figure 8: Force-directed graph of the GNG model genera-

ted from the Iris dataset. Stroke color of the nodes (green,

blue and orange) are based on the classiﬁcation made by

K-means (for K = 3).

Figure 9: Parallel coordinates plot of the GNG prototypes

generated from the Iris dataset. Stroke color of the lines

(green, blue and orange) is based on a classiﬁcation made

by K-means (for K = 3).

data of stage (c). Two datasets from the UCI reposi-

tory (Blake and Merz, 1998) were used in the exam-

ples: the Wine Quality dataset and the Breast Cancer

Wisconsin (Diagnostic) dataset.

Each of the notebooks used in stage (b) and (c)

had a predeﬁned layout with seven paragraphs, each

with code for a speciﬁc task: (1) load data, (2) view

data, (3) deploy Visual GNG, (4) display PC, (5) run

K-means, (6) compute predictions, and (7) see pre-

dictions. The idea of the predeﬁned notebooks was

to overcome knowledge gaps related to Zeppelin, the

Scala programming language, and Spark. By doing

so, the focus of the case studies was delimited – to

the largest possible extent – to the usability of the Vi-

sual GNG library. Thus, users did not need to write

code during the sessions and only needed to run the

paragraphs. We did, however, intervene in a few ca-

ses to help users remove features used in the training

dataset, or to set a given feature as a label.

To ensure consistency, the ﬁrst author of this paper

was the administrator of all the case studies with the

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

participants. Field notes were taken during the sessi-

ons and all impressions were written on the same day.

Responses from the ﬁrst stage (a) gave a general

proﬁle of the participants. Their experience in ana-

lyzing data varied from 2 to 10 years. All said to

commonly deal numeric and structured data in CSV

format. Participants from Bioinformatics said to also

have categorical and temporal data, and that their raw

data usually came in a platform-speciﬁc format (.CEL

ﬁles). Commonly used tools for analysis were R Stu-

dio, MATLAB and Excel. Two participants also men-

tioned the use of Python and two others SPSS. When

asked about what they usually looked for in the data,

ﬁve (5) participants responded informative features

(for clustering or classiﬁcation), ﬁve (5) groups or

clusters, two (2) outliers, one (1) anomalies, and four

(4) patterns in time series.

At the beginning of stage (b), users were given

an introduction to the different technologies involved,

i.e., Zeppelin, Scala, Spark and GNG. They were then

briefed on the use of the Visual GNG library by going

through the Wine Quality notebook example. The

brieﬁng took into account: the purpose of each para-

graph, how to execute them, how to run Visual GNG,

the meaning of the visual encodings, and, ﬁnally, the

supported user interactions. Once done with the Wine

Quality example, we let the users run the Breast Can-

cer notebook on their own.

Stage (c) was the main part of the study where

users explore their own data with the Visual GNG li-

brary.

Participants from bioinformatics made use of

two publicly available datasets: E-MTAB-5367 on

“Transcriptomics during the differentiation of human

pluripotent stem cells to hepatocyte-like cells”

(see

Figure 1), and GSE52404 on “The effects of chronic

cadmium exposure on gene expression in MCF7 bre-

ast cancer cells”

. The participant from biomedicine

made use of data from samples taken from patients

with two different conditions. The game researcher

used preprocessed data from heart and video recor-

dings of subjects playing games, which aimed at in-

ducing boredom and stress. An engineer made used

maintenance related data, while the other made use of

data associated with clutches. The two in general data

science and ML used data from measurements in steel

production and results from a topic modeling techni-

que used on telecomunications-related data, respecti-

vely. All datasets came in a CSV format with numeric

values. Some had categorical values which where, ac-

https://www.ebi.ac.uk/arrayexpress/experiments/E-

MTAB-5367/ [Accessed September 2018]

https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc

=GSE52404 [Accessed September 2018]

cording to the participants, unimportant for clustering

and, therefore, could be dropped. Datasets varied in

size (e.g. 46, 16436, 33297 up to 70523 instances)

and dimensionality (e.g., 7, 58, 758 and above 2000

features).

We asked participants to think aloud as they were

performing their analysis. Some, however, got im-

merse in the process and forgot to explain their acti-

ons, in which case, we asked questions every now and

then following participant observation protocols. Du-

ring their exploratory analysis, most users looked for

clusters, features which were important for a given

classiﬁcation and outliers. Common interactions with

Visual GNG were hovering and clicking on nodes to

see their centroids in PC, and changing nodes’ color

based on different features. A few of the users would

also try running K-means as well as re-running GNG

with different parameters (e.g., using fewer nodes).

The ﬁnal stage (d) involved structured interview

questions regarding usability (is the library easy to

use? is it helpful for EDA?), interpretability (is it

helpful for understanding the model / the parameters

/ the learning process?) and insight (were you able

to gain new understanding of the data?). We used a

1 to 5 Likert scale for questions on usability and in-

terpretability, where 1 was a negative perception (i.e.,

not easy, not helpful) and 5 a positive (very easy, very

helpful), and yes or no for insight. Comments were

encouraged for all answers.

Results on usability and interpretability can be

seen in Figure 10. Feedback related to usability was

mainly positive, with eight out of nine users answe-

ring both questions with rates of either four (4) or ﬁve

(5). Interpretability, on the other hand, received more

neutral or negative feedback (i.e., ratings of three or

less): ﬁve users did not ﬁnd the tool very helpful for

Figure 10: Answers from nine participants on a 1 to 5 Li-

kert scale about Visual GNG in terms of usability (Easy to

use, Helpful for EDA) and interpretability (helpful for un-

derstanding the model / the parameters / the learning pro-

cess). One (1) represents a negative user perception (not

easy, not helpful) and ﬁve (5) a positive (very easy, very

helpful).

Visual Growing Neural Gas for Exploratory Data Analysis

understanding the GNG model, six did not ﬁnd it very

helpful for understanding the GNG learning parame-

ters, and eight did not ﬁnd it very helpful for under-

standing the GNG learning process.

Answers on insight had four (4) yes and ﬁve (5)

no. Those with a positive answer said to have gained

new insights in the form of: relevant features for pre-

diction and classiﬁcation, estimated number of clus-

ters, data scatteredness and variations in certain (gene

data) samples. The others who gave a negative ans-

wer made the following comments: three said they

needed more time to analyze the data; one said that

new insight was not gained but that previous ﬁndings

were conﬁrmed; one said that the data (results from

a topic modeling technique) were not appropriate for

the clustering made by GNG.

To conclude we asked the users whether they

would consider making use of Visual GNG again and

for which purpose. Eight answered positively stating

that they would use Visual GNG again for clustering,

feature engineering, visualization and/or ﬁnding out-

liers.

7 DISCUSSION

In this paper, we argue that GNG can provide ana-

lysts with a useful perspective of the data structure in

spite of its size or dimensionality, and that its effective

use can be facilitated through VA. To sustain our ar-

gument, we developed a proof-of-concept as an off-

the-shelf artifact called Visual GNG, and conducted

nine case studies with real-world datasets to evaluate

its usability and its contribution to GNG interpretation

and insight gain.

Due to the large size of many current datasets, a

common problem with graphs is visual clutter. Node-

link diagrams, like the ones generated by GNG, pro-

vide an intuitive way to represent graphs; neverthe-

less, visual clutter quickly becomes a problem when

graphs comprised of a large number of nodes and

edges (Holten and van Wijk, 2009), which is why,

sometimes, matrix-based representations are used as

alternatives (see Van Ham (2003); Ghoniem et al.

(2004); Holten and van Wijk (2009)). The same clut-

tering problems are seen in PC when a large number

of data points are plotted (Zhou et al., 2008; Mun-

zner, 2014). Visual GNG, however, leverages from

GNGs capability to compress and generalize the data

to a limited number of nodes, thus reducing the risks

of visual clutter in both FDG and PC. This compres-

sion feature is also key for letting users test different k

values for K-Means, while providing fast visual feed-

back on the results. The same concept can be exten-

ded to other clustering techniques, such as, DBSCAN

or to hierarchical clustering methods such as Ward Jr

(1963). This would allow user-driven assessment on

the behavior of different techniques on the same da-

taset. The exploratory process of deﬁning the number

of k could also be complemented with clustering me-

trics such as the Silhouette.

The results from the empirical evaluation show

that Visual GNG has the potential to be used in the

exploration and analysis of large, multidimensional

data through the proposed visual encodings. In most

cases, Visual GNG proved to be useful, and most par-

ticipants agreed that our implementation was easy to

use, was helpful for EDA and that they would use it

again. It is, however, interesting to see that in spite of

this, many did not ﬁnd it helpful for understanding the

models produced by GNG, the learning parameters,

and/or the GNG learning process. A user commented

in this regard saying that, in order to understand the

model and the learning parameters, it is important to

understand the algorithm itself, and that the animated

growth of the model shown in the FDG did not ex-

plain much about it. This is a reasonable argument

which probably justiﬁes why many users gave low

scores to the understanding of the learning process.

Just visually representing the model in a FDG will

say very little of the learning process itself – which

is composed of several steps and rules. Understan-

ding the learning process, however, might not always

be of interest as it was mentioned by two users. One

of them stated that “what’s happening to my data” is

the main driver in the exploratory analysis process,

and that the learning process itself was not a priority.

This leaves an open question on when it is important

for data scientists to understand the inner workings of

an algorithm (currently, there are a lot of discussions

about this issue in the ML and HCI communities), and

how it can be facilitated through VA. In general, the

challenges associated to model visualization and inte-

raction for validation, reﬁnement and evaluation have

been highlighted by several works, e.g., Andrienko

et al. (2018); Lu et al. (2017); Endert et al. (2017).

During the case studies we ran into an unfores-

een challenge: many participants had preconceived

expectations of what to ﬁnd. Most had already ana-

lyzed their data with other tools and techniques and,

therefore, had certain expectations on what to look

for and what could be found. In one case a parti-

cipant said to be looking for ﬁve clusters previously

seen through other techniques, and was somewhat di-

sappointed for not ﬁnding them with Visual GNG. In

another case a participant started to actively look for

outliers that were encountered in previous analyses.

Such cases correspond to conﬁrmatory data analysis

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

and not exploratory (Tukey, 1977), and can be linked

as well to negative reasoning enhancement tendencies

(humans have a tendency to seek information which

supports their hypothesis and ignore negative infor-

mation). To avoid these situations, we could present

the participants with unknown or not previously ana-

lyzed data, but that is a challenge of its own. Another

option might also be to use public data from parti-

cipants’ domains but, would their engagement be the

same? Tukey (1977) states that attitude in the analysis

of data is a key factor that deﬁnes EDA. The most sen-

sible solution we see, for a strict evaluation of EDA,

are longitudinal studies.

GNG does not come without limitations. One is

that it does not handle discrete variables. GNG re-

lies on the Euclidean distance, a metric that does not

always produce meaningful values for variables such

as, e.g., gender. A solution is to pre-process data

using a one-hot-encoder, where each value of a dis-

crete variable becomes a variable itself, and where the

values each can take are zero (0) or one (1). Another

aspect to take into consideration is that GNG might

overﬁt if the number of units is close to the number of

data points. Such conditions can result in a GNG mo-

del with many small detached networks, where some

units do not represent any data point. This can be sol-

ved by reducing the maximum number of units crea-

ted in the ﬁtting process.

8 CONCLUSIONS

Exploratory data analysis tasks are usually inte-

ractive, where analysts employ various support met-

hods and tools to fuse, transform visualize and com-

municate ﬁndings. Frequently, due to the ill-deﬁned

nature of these tasks, unsupervised ML techniques are

employed for EDA. However, neural-based clustering

techniques, such as the GNG, that learn topologies

from the data providing thus, complementary views

on it, have been overlooked by the VA and HCI com-

munities.

In this paper, we suggested the use of Visual GNG

for EDA, using FDG for representing the topological

models derived by the GNG and PC for showing a

detailed representation of units’ prototypes. Hence,

the major contributions of this paper are (1) a two-

dimensional visual representation of data using GNG

and FDGs, regardless of the dimensionality of the

data, (2) a generic (non-domain bound) off-the-shelf

VA library for GNG, and (3) nine case studies for the

evaluation of the library in regards usability, GNG in-

terpretability and insight gain.

The qualitative feedback from expert data scien-

tists in the case studies carried out indicate that Vi-

sual GNG is easy to use and useful for EDA. Eight

out of nine participants showed interest in using the

library again for the purpose of ﬁnding groups and

relevant features. These are subjective results with

limited external validity. Carrying studies on gene-

ral (non-domain speciﬁc) EDA, with a larger external

validity, remains a challenge in terms of tasks and me-

trics, and will be considered in future work.

REFERENCES

Amershi, S., Cakmak, M., Knox, W. B., Kulesza, T., and

Lau, T. (2013). IUI workshop on interactive machine

learning. In Proc. Companion Publication Int. Conf.

on Intelligent User Interfaces, pages 121–124. ACM.

Andrienko, N., Lammarsch, T., Andrienko, G., Fuchs, G.,

Keim, D., Miksch, S., and Rind, A. (2018). Vie-

wing visual analytics as model building. In Computer

Graphics Forum. Wiley Online Library.

Ankerst, M., Breunig, M. M., Kriegel, H.-P., and Sander, J.

(1999). Optics: Ordering points to identify the clus-

tering structure. In Proc. of the 1999 ACM SIGMOD

Int. Conf. on Management of Data, pages 49–60, New

York, NY, USA. ACM.

Bertini, E. and Lalanne, D. (2010). Investigating and re-

ﬂecting on the integration of automatic data analysis

and visualization in knowledge discovery. SIGKDD

Explor. Newsl., 11(2):9–18.

Blake, C. and Merz, C. (1998). UCI repository of ma-

chine learning databases. Irvine, CA: University of

California, Department of Information and Computer

Science. https://archive.ics.uci.edu/ml/datasets.html.

Boukhelifa, N., Bezerianos, A., and Lutton, E. (2018). Eva-

luation of interactive machine learning systems. arXiv

preprint arXiv:1801.07964.

Costa, J. A. F. and Oliveira, R. S. (2007). Cluster analy-

sis using growing neural gas and graph partitioning.

In Neural Networks, 2007. IJCNN 2007. International

Joint Conference on, pages 3051–3056. IEEE.

Dasgupta, A., Chen, M., and Kosara, R. (2012). Concep-

tualizing visual uncertainty in parallel coordinates. In

Computer Graphics Forum, volume 31, pages 1015–

1024. Wiley Online Library.

Daszykowski, M., Walczak, B., and Massart, D. L. (2002).

On the optimal partitioning of data with k-means, gro-

wing k-means, neural gas, and growing neural gas.

Journal of chemical information and computer scien-

ces, 42(6):1378–1389.

Endert, A., Ribarsky, W., Turkay, C., Wong, B., Nabney, I.,

Blanco, I. D., and Rossi, F. (2017). The state of the art

in integrating machine learning into visual analytics.

In Computer Graphics Forum, volume 36, pages 458–

486. Wiley Online Library.

Fritzke, B. (1995). A growing neural gas network learns to-

pologies. In Tesauro, G., Touretzky, D. S., and Leen,

T. K., editors, Advances in Neural Information Pro-

cessing Systems 7, pages 625–632. MIT Press.

Visual Growing Neural Gas for Exploratory Data Analysis

Ghoniem, M., Fekete, J.-D., and Castagliola, P. (2004). A

comparison of the readability of graphs using node-

link and matrix-based representations. In IEEE Symp.

on Information Visualization, INFOVIS, pages 17–24.

Goebel, M. and Gruenwald, L. (1999). A survey of

data mining and knowledge discovery software tools.

SIGKDD Explor. Newsl., 1(1):20–33.

Guo, D. (2009). Flow mapping and multivariate visualiza-

tion of large spatial interaction data. IEEE Transacti-

ons on Visualization and Computer Graphics, 15(6).

Heinke, D. and Hamker, F. H. (1998). Comparing neural

networks: a benchmark on growing neural gas, gro-

wing cell structures, and fuzzy artmap. IEEE Tran-

sactions on Neural Networks, 9(6):1279–1291.

Heinrich, J. and Weiskopf, D. (2013). State-of-the-art of

parallel coordinates. In Eurographics (STARs), pages

95–116.

Hoffman, P., Grinstein, G., Marx, K., Grosse, I., and Stan-

ley, E. (1997). Dna visual and analytic data mi-

ning. In Proceedings. Visualization ’97 (Cat. No.

97CB36155), pages 437–441.

Holten, D. and van Wijk, J. J. (2009). A user study on visu-

alizing directed edges in graphs. In Proceedings of the

SIGCHI Conference on Human Factors in Computing

Systems, pages 2299–2308. ACM.

Holzinger, A. (2016). Interactive machine learning for he-

alth informatics: when do we need the human-in-the-

loop? Brain Informatics, 3(2):119–131.

Hotelling, H. (1933). Analysis of a complex of statistical

variables into principal components. Journal of edu-

cational psychology, 24(6):417.

Inselberg, A. (2009). Parallel coordinates. In Encyclopedia

of Database Systems, pages 2018–2024. Springer.

Inselberg, A. and Dimsdale, B. (1990). Parallel coordina-

tes: A tool for visualizing multi-dimensional geome-

try. In Proc. of the 1st Conf. on Visualization, pages

361–378, Los Alamitos, CA, USA. IEEE Computer

Society Press.

Johansson, J. and Forsell, C. (2016). Evaluation of parallel

coordinates: Overview, categorization and guidelines

for future research. IEEE Transactions on Visualiza-

tion and Computer Graphics, 22(1):579–588.

Kandogan, E. (2000). Star coordinates: A multi-

dimensional visualization technique with uniform tre-

atment of dimensions. In Proceedings of the IEEE

Information Visualization Symposium, volume 650,

page 22.

Kohonen, T. (1997). Self-Organizing Maps. Springer series

in information sciences. Berlin: Springer, 2 edition.

Lu, Y., Garcia, R., Hansen, B., Gleicher, M., and Maciejew-

ski, R. (2017). The state-of-the-art in predictive visual

analytics. In Computer Graphics Forum, volume 36,

pages 539–562. Wiley Online Library.

Maaten, L. v. d. and Hinton, G. (2008). Visualizing data

using t-sne. Journal of machine learning research,

9(Nov):2579–2605.

uhlbacher, T., Piringer, H., Gratzl, S., Sedlmair, M., and

Streit, M. (2014). Opening the black box: Strategies

for increased user involvement in existing algorithm

implementations. IEEE Transactions on Visualization

and Computer Graphics, 20(12):1643–1652.

Mulder, J. D., van Wijk, J. J., and van Liere, R. (1999). A

survey of computational steering environments. Fu-

ture Generation Computer Systems, 15(1):119 – 129.

Munzner, T. (2014). Visualization analysis and design.

CRC Press.

Palomo, E. J. and L

opez-Rubio, E. (2017). The gro-

wing hierarchical neural gas self-organizing neural

network. IEEE Transactions on Neural Networks and

Learning Systems, 28(9):2000–2009.

Patton, M. Q. (2005). Qualitative research. Wiley Online

Library.

Prudent, Y. and Ennaji, A. (2005). An incremental growing

neural gas learns topologies. In Proc. IEEE Int. Joint

Conf. on Neural Networks, volume 2, pages 1211–

1216.

Ribeiro, M. T., Singh, S., and Guestrin, C. (2016). ”Why

should i trust you?”: Explaining the predictions of any

classiﬁer. In Proc. of the 22nd ACM SIGKDD Int.

Conf. on Knowledge Discovery and Data Mining, pa-

ges 1135–1144, New York, NY, USA. ACM.

Riveiro, M., Falkman, G., and Ziemke, T. (2008). Impro-

ving maritime anomaly detection and situation awa-

reness through interactive visualization. In 11th Int.

Conf. on Information Fusion, pages 1–8. IEEE.

Schreck, T., Bernard, J., Von Landesberger, T., and Kohl-

hammer, J. (2009). Visual cluster analysis of trajec-

tory data with interactive kohonen maps. Information

Visualization, 8(1):14–29.

Sledge, I. J. and Keller, J. M. (2008). Growing neural gas

for temporal clustering. In Pattern Recognition, 2008.

ICPR 2008. 19th International Conference on, pages

1–4. IEEE.

Spence, I. and Efendov, A. (2001). Target detection in

scientiﬁc visualization. Journal of Experimental Psy-

chology: Applied, 7(1):13–26.

Spence, R. (2007). Information Visualization: Design for

Interaction. Pearson/Prentice Hall.

Tukey, J. W. (1977). Exploratory data analysis, volume 2.

Reading, Mass.

Van Ham, F. (2003). Using multilevel call matrices in large

software projects. In IEEE Symposium on Information

Visualization, INFOVIS 2003, pages 227–232. IEEE.

van Leeuwen, M. (2014). Interactive data exploration using

pattern mining, pages 169–182. Springer Berlin Hei-

delberg, Berlin, Heidelberg.

Vanetti, M., Gallo, I., and Nodari, A. (2013). Unsupervi-

sed feature learning using self-organizing maps. In

Proceedings of the International Conference on Com-

puter Vision Theory and Applications - Volume 1: VI-

SAPP, (VISIGRAPP 2013), pages 596–601. INSTICC,

SciTePress.

Ventocilla, E., Helldin, T., Riveiro, M., Bae, J., Boeva, V.,

Falkman, G., and Lavesson, N. (2018). Towards a

taxonomy for interpretable and interactive machine le-

arning. In IJCAI/ECAI. Proc. of the 2nd Workshop

on Explainable Artiﬁcial Intelligence (XAI-18), pages

151–157.

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

Ventocilla, E. and Riveiro, M. (2017). Visual analytics solu-

tions as ‘off-the-shelf’ libraries. In 21st International

Conference Information Visualisation (IV).

Ward Jr, J. H. (1963). Hierarchical grouping to optimize an

objective function. Journal of the American statistical

association, 58(301):236–244.

Zhou, H., Yuan, X., Qu, H., Cui, W., and Chen, B. (2008).

Visual clustering in parallel coordinates. Computer

Graphics Forum, 27(3):1047–1054.

Visual Growing Neural Gas for Exploratory Data Analysis