Visual Exploration Tools for Ensemble Clustering Analysis

Sonia Fiol-Gonz

alez

, Cassio F. P. Almeida

1,2

, Ariane M. B. Rodrigues

, Simone D. J. Barbosa

and H

elio Lopes

Departamento de Inform

atica, Pontif

ıcia Universidade Cat

olica do Rio de Janeiro, Bazil

ENCE - Instituto Brasileiro de Geograﬁa e Estat

ıstica, Rio de Janeiro, Brazil

Keywords:

Clustering, Ensemble Methods, Ensemble Visualization, Uncertainty Visualization, Co-association Matrix.

Abstract:

Uncertainty Analysis is essential to support decisions, and it has been gaining attention in both visualization

and machine learning communities —in the latter case, mainly because ensemble methods are becoming a

robust approach in several applications. In particular, for unsupervised learning, there are several ensemble

clustering methods that generate a co-association matrix, i.e., a matrix whose element (i, j) represents the

estimated probability that the given sample pair is on the same cluster. This work studies the following

decision problem: “Given a similarity function, which groups of elements of a set form robust clusters?”

Robust here means that all elements of each cluster are connected with a probability within a given interval.

Our main contribution is a prototype that helps decision makers, through visual exploration, to have insights to

solve this task. To do so, we provide visual tools for ensemble clustering analysis. Such tools are grounded in

the co-association matrix generated by the ensemble. With these tools we are better equipped to recommend

the group of elements that form each cluster, considering the uncertainty generated by ensemble clustering

methods.

1 INTRODUCTION

Uncertainty Analysis is an active area of research:

it helps decision makers through the quantiﬁcation

of uncertainties in relevant variables (Ghanem et al.,

2017). One way to perform this quantiﬁcation is

to randomly generate an ensemble of possible out-

comes of the given decision problem. Nowadays, the

large amount of computer resources available makes

such ensemble generation possible (Cunha Jr et al.,

2014). The visual analysis of the generated en-

sembles emerges as an important visualization chal-

lenge (Obermaier et al., 2014). This paper deals with

uncertainty visualization in the context of ensemble

clustering analysis.

It is now common to have ensemble classiﬁers in

supervised learning. They combine the outputs of

multiple classiﬁers with the purpose of improving the

classiﬁcation accuracy (Dietterich, 2000). Likewise,

ensemble clustering methods in unsupervised learn-

ing combine multiple partitions to provide better clus-

tering of the data set (Vega-Pons and Ruiz-Shulcloper,

2011). Several ensemble clustering methods generate

a co-association matrix, which is a matrix where each

(i, j) element represents the estimated probability that

the given sample pair is on the same cluster (Fred and

Jain, 2005). These methods can also generate a stan-

dard deviation for each pair, which also represents an

estimated uncertainty.

Objective and Contributions. This work aims to

help decision makers to obtain insights to answer

the following question: “Given a similarity function,

which groups of elements of a dataset form robust

clusters?” By robust we mean that all elements of

each cluster are connected with a probability in a

given interval.

To achieve our goal, we provide a visual tool for

ensemble clustering analysis. Grounded in the co-

association matrix generated by the ensemble, such

tool supports us in recommending the group of ele-

ments that form each cluster, considering the uncer-

tainty generated by ensemble clustering methods. The

tool includes: variations over heatmaps to visualize

the co-association matrices, violin plots of the silhou-

ette of each group in the ﬁnal partition, network and

edge bundling to visualize the relationships between

datapoints, a scatter plot of a 2D projection, and a

map, when the data is georeferenced.

Paper Outline. The paper is structured as follows:

Section 2 brieﬂy describes related works on ensemble

clustering visualization; Section 3 presents the char-

acteristics of the visual exploration tool of ensemble

Fiol-González, S., Almeida, C., Rodrigues, A., Barbosa, S. and Lopes, H.

Visual Exploration Tools for Ensemble Clustering Analysis.

DOI: 10.5220/0007366302590266

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 259-266

ISBN: 978-989-758-354-4

259

results; Section 4 describes some analyses of a real-

world use case with the tool and conclusions are given

in Section 5.

2 RELATED WORK

Ensemble Clustering. Ensemble clustering com-

bines multiple clustering results from the same dataset

into a ﬁnal partition (Vega-Pons and Ruiz-Shulcloper,

2011; Xu and Tian, 2015; Huang et al., 2015). It is

considered a difﬁcult task because cluster labels are

symbolic, so it is also necessary to solve a correspon-

dence problem.

Among the most popular clustering ensemble

techniques we ﬁnd methods based on co-association

matrices. Iam-On et al. present two new similarity

matrices, which are empirically evaluated and com-

pared against the standard co-association matrix on

six datasets using four different combination meth-

ods and six clustering validity criteria (Iam-On et al.,

2008). The Evidence Accumulation matrix (EAC)

method (Fred and Jain, 2005) is based on a co-

association technique for extracting a consensus clus-

tering from a clustering ensemble. An extension of

EAC is the Weighted Evidence Accumulation matrix

(WEAC) (Huang et al., 2015), which includes weights

to penalize low quality clustering and agglomera-

tive methods to obtain the consensus partition. An-

other option is the Probability Accumulation (PA)

method (Wang et al., 2009), a clustering aggregation

scheme that uses a correlation matrix based on clus-

ter size. The Ensemble Clustering Matrix Completion

(ECMC) method, proposed by (Yi et al., 2012), is ro-

bust to uncertainties in the data. The Robust Spectral

Ensemble Clustering (RSEC) learns a robust repre-

sentation for the co-association matrix through low-

rank constraint, which reveals the cluster structure of

a co-association matrix and captures various noises in

it (Tao et al., 2016).

The recent Locally Weighted Ensemble Clus-

tering method is an ensemble clustering approach

based on ensemble-driven cluster uncertainty estima-

tion and local weighting co-association matrix strat-

egy; it applies two novel consensus functions to con-

struct the ﬁnal partitions (Huang et al., 2018). An-

other example is a novel committee-based cluster-

ing method composed of three stages (Fiol-Gonzalez

et al., 2018): (i) generating the clustering ensemble by

combining feature selection strategies and clustering

methods varying the number of clusters to generate

multiple scenarios; (ii) combining the results of the

multiple clustering scenarios generated to produce a

co-association matrix; and (iii) creating sets of parti-

tions using the co-association matrix and then select-

ing the ﬁnal partition based on the best performance

using the silhouette coefﬁcient.

Visual Analysis of Ensembles. Due to their com-

plexity and size, ensembles provide challenges in data

management, analysis, and visualization (Potter et al.,

2009). Wang et al. reported a survey on visualiza-

tion techniques and analytic tasks involving ensemble

data (Wang et al., 2018). They organize ensemble vi-

sualization techniques research into a pipeline, where

ensemble data go to through a statistical aggregation

step before visualization, a visual composition step

after visualization, or a combination of both. In other

words, these visualization techniques can be applied

to get an overview of the entire ensemble or to com-

pare the relationships between a small number of sce-

narios.

There are some tools to help visualize ensemble

data. Ensemble-Vis links views built from means and

standard deviations, using color and overlaid contours

to view the complete ensemble dataset (Potter et al.,

2009). IPFViewer combines small multiples views at

multiple hierarchical levels to analyze hierarchical en-

semble data (Thurau et al., 2014). Hao et al. apply

ensemble visualization techniques in a network secu-

rity analysis environment to produce a network en-

semble visualization system (Hao et al., 2015). These

techniques can cluster trafﬁc with similar behavior

and identify trafﬁc with unusual patterns, facilitating

the analysis of relationships between alerts and trafﬁc

ﬂow.

Inspired by the related work and by the fact that

it is possible to combine clustering results to improve

the ﬁnal partition, we want to visualize this ﬁnal parti-

tion to understand its internal structure. We therefore

address the following research questions:

• RQ1: How to visualize the ﬁnal partition of a

combination of clustering results?

• RQ2: Given a ﬁnal partition, how to visualize its

internal structure?

• RQ3: How to visualize the co-association matrix

and uncertainty matrix from which the ﬁnal parti-

tion was generated?

• RQ4: How to visually identify whether the pat-

terns detected in the co-association matrix con-

form to the groups in the ﬁnal partition?

• RQ5: How is it possible to identify the probabil-

ity of obtaining connected components that agree

with the ﬁnal partition groups?

• RQ6: How to compare the ﬁnal partition with

other possible solutions (clusterings)?

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

260

3 VISUAL EXPLORATION TOOL

OF ENSEMBLE RESULTS

This section proposes some visual exploration tools of

the co-association matrix, to facilitate the understand-

ing of the ensemble clustering result. There are sev-

eral ensemble methods to construct the co-association

matrix (Berikov, 2016; Lin et al., 2017; Fiol-Gonzalez

et al., 2018). Among these, we selected Fiol et al.’s

committee-based clustering method to generate the

ensemble, because their algorithm generates as out-

put the following matrices (see Section 2):

• Co-association matrix (CM), where the position

(i, j) contains the probability that elements i and

j are in the same cluster.

• Partitions Silhouette matrix (PSM), where the po-

sition (i, j) contains a tuple with the silhouette

value and the cluster id (< sil,cl

id >) for element

i in partition j. The ﬁnal partition is identiﬁed by

an index f , where 0 ≤ f ≤ ncol(PSM).

The algorithm also generates a third matrix based

on the CM to complement the uncertainty information

in the overview task:

• Standard Deviation matrix (STD CM), where the

position (i, j) contains the uncertainty (std) asso-

ciated to the same element in the co-association

matrix.

We propose to use some visualization techniques

to assist in analytic tasks involving ensemble cluster-

ing data. Wang et al. reported six visual analytic tasks

that cover most of the ensemble visualization litera-

ture, from which we chose three, as follows:

1. Overview: visual summary of ensemble data and

overall uncertainty information.

2. Comparison: visual identiﬁcation of the differ-

ence between two members.

3. Clustering: grouping of members or ensemble ob-

jects by similarity.

Based on these analytic tasks we deﬁned three design

goals for our visual exploration tool. We had to ex-

trapolate the tasks from ensemble data members or

object dimensions to ensemble clustering dimensions.

The three main design goals are:

G1: Provide a visual representation of ensemble

clustering (clustering task).

G2: Provide a visual summary of the ﬁnal parti-

tion and uncertainty information (overview task).

G3: Support a visual identiﬁcation of the differ-

ences between groups (comparison task).

In the next subsections we explain in detail the so-

lutions proposed for each design goal.

The tool was developed using the R script

language (R Core Team, 2018) and the

shiny (Chang et al., 2018), plotly (Sievert, 2018),

leaflet (Cheng et al., 2018), visNetwork (Almende

B.V. et al., 2018), edgebundleR (Tarr et al., 2016)

packages. We chose R because we wanted to test

quickly and easily different possibilities of visualiza-

tions and different datasets. We are already working

on the development of the solutions presented here in

a more robust tool using Python (Van Rossum and

Drake, 2003).

Our design consists of coordinated multiple

views (Scherr, 2008), where views are displayed side-

by-side and changes in one view affect the others. In

fact, this solution is preferable when compared to sin-

gle view because it can display different facets of the

clustering ensemble information while avoiding vi-

sual clutter. Basically, the interaction area of the tool

consists of three linked parts (Figure 1): A) conﬁ-

dence ﬁltering; B) CM and related information; and

C) group relationship, connections, 2D data points

representation, and geospatial information.

The threshold in region A is a pair < min, max >

(0 ≤ min ≤ max ≤ 1) of parameters the user can de-

ﬁne. This ﬁltering acts directly on the other parts (B

and C), producing a clearer representation of the de-

sired data and a better deﬁnition of patterns in the CM.

The histogram next to the threshold represents the dis-

tribution of the CM. By manipulating the threshold, it

is possible to identify the percentage of binds (< i, j >

pairs) that would remain after ﬁltering.

By using the ensemble method results, we can use

the conﬁdence interval of the probability of each bind

to propose three new approaches for ﬁltering connec-

tions, as follows:

• Traditional Interval Filter: Takes into account

the estimated probability of the bind. We accept

the connection of the pair as true if the probability

that the pair is on the same cluster is within the

interval threshold.

• Weak Interval Filter: Veriﬁes whether the conﬁ-

dence interval intersects the given threshold inter-

val.

• Strong Interval Filter: Only accepts a pair as

connected if the entire conﬁdence interval of the

bind is included in the threshold interval.

The conﬁdence interval was constructed using the

Gaussian probability distribution with signiﬁcance

level α (CM

i, j

±z

ST D

i, j

√

n, where n is the num-

ber of scenarios in the ensemble). These intervals

are related to uncertainty and they represent the range

of potential values of the true connection probability.

Using the strong ﬁlter, we only select binds with con-

Visual Exploration Tools for Ensemble Clustering Analysis

261

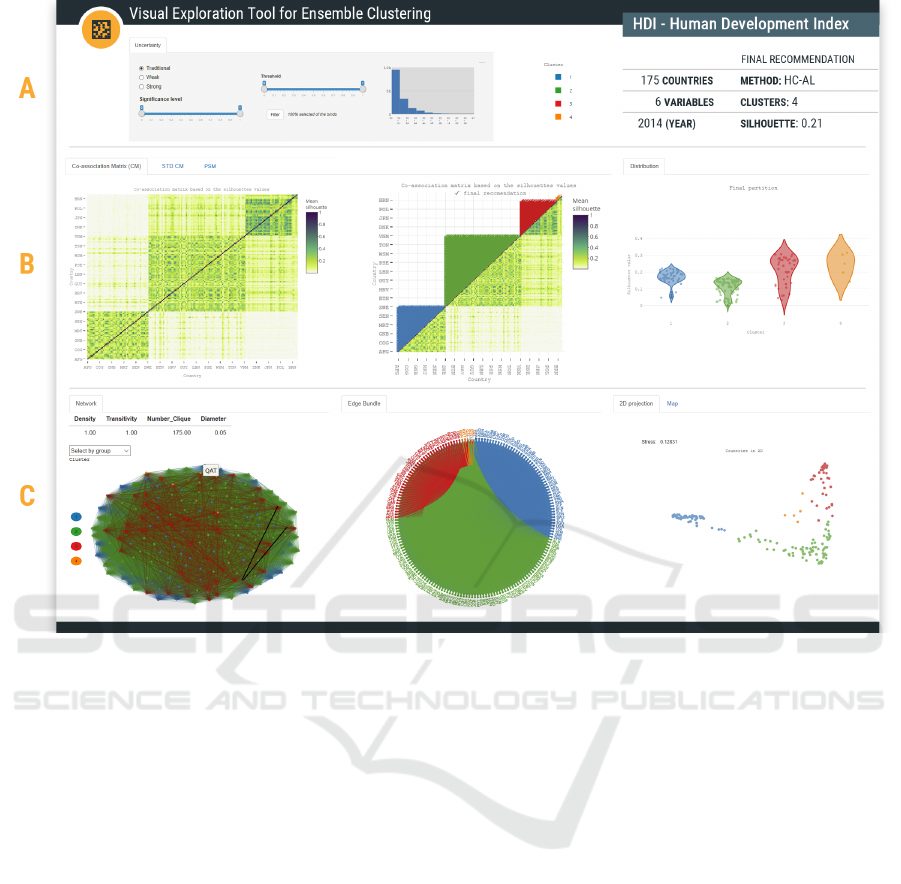
Figure 1: Visualization components of the tool.

ﬁdence intervals within thresholds. In other words,

there is a very small chance that the threshold does

not contain the actual bind value. In the weak case, it

is sufﬁcient that the chance that the threshold contain-

ing the actual bind value is greater than zero.

We use colors to represent clusters. They serve as

a visual aid to relate the different views, except for the

heat map visualizations, which have their own color

scale. The right-hand side of region A displays some

information about the dataset and the ﬁnal partition.

Region B is divided into two parts. The left-hand

side groups in tabs the four co-association matrices

and the silhouette value of all possible recommenda-

tions. The right-hand side shows the probability den-

sity of the silhouette of each group.

Region C includes four views: (i) a network com-

ponent to visualize how each data point connects with

the others; (ii) an edge bundling component that al-

lows to view each network connection separately;

(iii) the 2D spatial projection of each data point; and

(iv) the map component to identify how each group is

organized geographically (if applicable).

To achieve G1 (visual representation of an ensem-

ble clustering), we chose three ways to visually rep-

resent clusters: cluster colors across all groups, a 2D

projection through scatter plots, and a map.

2D Projection. To represent the similarity degree

of the data points and the ﬁnal partition, we use

a Multidimensional Scaling (MDS) projection tech-

nique (Kruskal and Wish, 1978). We project each

data point in two dimensions using scatter plots. To

evaluate the quality of the projection, we inform the

measure of the stress (see Figure 1, region C).

Each point of the 2D projection represents a mem-

ber of the ﬁnal partition and can be recognized by

the color corresponding to its cluster. In this way, we

can visualize a representation of the dispersion of the

points inside and between clusters, allowing to evalu-

ate the quality of the ﬁnal partition.

Map. Georeferenced objects, such as neighborhoods,

cities, and countries, are visualized in a map to easily

analyze whether adjacent elements belong to the same

cluster. When one clicks on a region, it shows a pop-

up with the region name and the cluster number. This

allows domain experts to recognize whether the ﬁnal

partition is in line with their experience.

Together, the 2D projection and map representa-

tions answer RQ1 (How to visualize the ﬁnal partition

of a combination of clustering results?).

To achieve G2 (visual summary of the ﬁnal par-

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

262

tition and overall uncertainty information), we chose

heat maps, because they convey an overview of the

behavior of datapoints. We represent four types of

matrices in heat maps. Associated with them, the

graph and the edge bundling provide an overview of

the relationship between the datapoints.

Heat Map. We used the heat map to represent the CM

in its traditional form (Wilkinson and Friendly, 2009),

and the uncertainty matrix, adapted with scatter plots.

This visualization compacts large amounts of infor-

mation into a small space to bring out coherent pat-

terns in the data. Each matrix has its symmetric and

lower triangular variation. The data are sorted using

the cluster numbers from the ﬁnal partition in order to

form the patterns corresponding with the clusters in

the heat map.

When representing the CM as a heat map it is pos-

sible to notice that all the values in the main diagonal

are 1 (dark color), i.e., representing the probability of

the element being in the same cluster as itself. Con-

versely, pairs with value 0 (light color) mean that the

two elements have no binds, i.e., they never appear

in the same cluster. By hovering over each cell of

the matrix, a tooltip with information about the pair

of binds appears: the pair’s name, relationship value,

group, and standard deviation (in the case of the un-

certainty matrix).

Symmetric Co-association Matrix: There are spe-

ciﬁc patterns with rectangular shape (henceforth

blocks) formed around the main diagonal in the heat

map, containing the elements belonging to the same

cluster. Visualizing the data in this way (see Figure 1-

B) allows users to ﬁnd darker regions, have an idea of

the cohesion of groups, identify and count the blocks

in the result. In Figure 1-B one can see three blocks.

We can see the same pattern in all four representations

of the matrix, but it is more evident here.

Lower Triangular Co-association Matrix: The

lower part of this matrix represents the same infor-

mation as the previous one. At the upper part, we

map the clusters according to the ﬁnal partition (see

Figure 1-B). It is helpful when we cannot ﬁnd well-

deﬁned patterns in the symmetric matrix (e.g., the red

cluster in Figure 1-B). This feature helps us answer

RQ4 (How to visually identify whether the patterns

detected in the co-association matrix conform to the

groups in the ﬁnal partition?).

STD CMs: In this view, instead of painting the entire

matrix cell, we use circles whose size is proportional

to the standard deviation value. The smaller the circle

size, the lower the uncertainty associated with the pair

of binds. The color remains the same as in the other

heatmaps.

The set of matrices provides an overview of the

aggregate ensemble, allowing to analyze the proba-

bility of two data points falling in the same cluster

in the multiple combinations and to know the uncer-

tainty associated with that probability. This allows us

to answer RQ3 (How to visualize the co-association

matrix and uncertainty matrix from which the ﬁnal

partition was generated?).

Graph. To visualize the CM in a graph, one can de-

ﬁne a complete undirected weighted graph as G <

V,E > where V are the elements of the dataset and

E are the edges connecting each two elements. The

weight of an edge is equal to the probability with

which the two elements are together in the explored

scenarios. Visually, the size of each node corresponds

to its degree (number of nodes with which it is con-

nected). When an edge is selected, the tool shows the

probability associated with its pair of nodes.

This third section (see Figure 1-C) shares the

threshold of the previous sections: setting a thresh-

old range disables the edges with weights outside of

the range, allowing to decompose the fully connected

graph in separate connected components. This visual-

ization enhances the study of components containing

elements of different clusters, allowing users to no-

tice the nodes which tend to be isolated even with low

thresholds, to analyze the articulation points (repre-

sented with a thicker border) of the graph in depth;

and to obtain an overview of some graph statistics,

such as diameter, density, transitivity, and the number

of cliques. In addition, the edges of the diameter in

each connected component are presented in a differ-

ent way, e.g., edge in red color (see Figure 1-C).

Hierarchical Edge Bundling. Hierarchical edge

bundling is a ﬂexible and generic method that can

be used in conjunction with existing tree visualiza-

tion techniques. Low bundling strength mainly pro-

vides low-level, node-to-node connectivity informa-

tion, whereas high bundling strength provides high-

level information (Holten, 2006).

At ﬁrst glance, it allows identifying the number

of items per group. If an item is selected, we may

quickly see the related items (i.e., items that share an

edge with the selected one) and whether they are in

the same group or not. If all the elements linked to

it are in the same group (i.e., represented in the same

color), the group is very cohesive.

As we modify the threshold, we can see the con-

nections increasing or decreasing (both in the graph

and in the edge bundling), which allows us to iden-

tify values in which related components are formed.

This way we can answer RQ5 (How is it possible to

identify the probability of obtaining connected com-

ponents that agree with the ﬁnal partition groups?).

Finally, to achieve G3 (visual identiﬁcation of dif-

Visual Exploration Tools for Ensemble Clustering Analysis

263

ferences between groups), we use violin plots super-

imposed by a dot chart for each group, placed side

by side. Violin plots summarize density shapes into

a single plot of the data within each group, allow-

ing comparison between groups (Hintze and Nelson,

1998). Inside each violin it is possible to identify the

amount of data points per group. Hovering over each

violin shows a tooltip with the interquartile informa-

tion. This way we can answer RQ2 (Given a ﬁnal

partition, how to visualize its internal structure?)

Scatter Plot for PSM shows the silhouette values for

each possible partition, as well as the ﬁnal partition.

The triangle markings shows the silhouette value in

the ﬁnal partition: an upward triangle indicating that

the silhouette value is above the average for that data

point, and the downward triangle otherwise. This al-

lows us to answer RQ6 (How to compare ﬁnal parti-

tion with other possible solutions (clusterings)?).

4 USE CASE

The publicly available Human Development Index

(HDI)

was createdas part of the United Nations pro-

gram, among other objectives, to compare and char-

acterize the countries according to their development

level. The online data are organized by year, and for

each year it contains a set of features to compute the

index. The 175 countries are classiﬁed in four groups:

very high, high, medium, and low, but we only use this

information to verify our clustering. We used the fol-

lowing variables to build the dataset: Infant mortality

rate (per 1,000 live births) - 2013, Gross national in-

come (GNI) per capita (2011 PPP$) - 2014, Labour

force participation rate (% ages 15 and older) - 2013,

Mean years of schooling - 2014, Expected years of

schooling - 2014 and Life expectancy at birth - 2014.

The goal is to obtain a ﬁnal partition using the en-

semble method. We use the following parameters:

K varying from 2 to 28; Sequential Forward Selec-

tion and Sequential Backward Selection as feature se-

lection methods; and K-means, K-medoids and Hi-

erarchical Clustering with Average Link (HC-AL) as

clustering methods to create the ensemble. To obtain

the ﬁnal partition we used the K-medoids and HC-AL

methods. We used α = 0.05 to create the conﬁdence

interval.

Results. The method proposed 4 clusters with a sil-

houette around 0.21 and using HC-AL. Figure 1 B-2

shows the CM generated from the aggregate ensemble

and the ﬁnal partition of the method.

Human Development Index: https://goo.gl/so6LpE last

visited in September, 2018

The orange cluster contains the very high coun-

tries, such as QAT (Qatar), ARE (United Arab

Emirates), KWT (Kuwait), SGP (Singapore), BRN

(Brunei Darussalam), but with the highest GNI. The

other very high countries are located in the red clus-

ter. The high countries are in the green cluster and the

poor countries are in the blue cluster. The countries

with medium development are mixed in the green and

blue clusters. We can see the clusters in the world

map (Figure 1C-3).

In the symmetric representation of CM (Figure

1B-1), we have four well deﬁned blocks. The fourth

cluster (in orange) is the smallest one, with only 5

data points. We can see it most clearly in Figure

1B-2. These blocks are ﬁlled with green dots, while

the connection with the elements in other blocks are

mostly in yellow, so the connection within the clus-

ter is stronger than outside it. In order to highlight

this fact, the threshold was set to 0.30 with traditional

ﬁlter. This conﬁguration results in 8.2% of all con-

nections.

In the ﬁnal partition, the blue group and the green

group have the smallest ranges of the silhouette values

(see Figure 1 B-3), while the red group has the largest

range, which matches the variation in the CM (see

Figure 1 B-1).

With a 0.40 threshold and weak ﬁlter, the groups

have more intra-connections, as well as some connec-

tions between the groups, mixing different groups in

the same connected component (see Figure 2b, dot-

ted outline). This conﬁguration results in 5.0% of all

connections. The selected connected component (in

red, green and blue) has 103 countries represented on

the map (see Figure 4a). The countries in blue are

IND (India), NAM (Namibia), and STP (Sao Tome

and Principe), and they have a medium HDI. This case

is less restrictive, with more heterogeneous countries

and a range of HDI from 0.51 to 0.94.

With a 0.40 threshold and traditional ﬁlter (ﬁgure

omitted for brevity), the elements looks sparse, but

the green and red dots are still joined by an articu-

lation point (node POL-Poland in red). Most of the

countries in the green subgroup (see Figure 4b) have

a high HDI. This conﬁguration results in 3.8% of all

connections, i.e., 1.2% fewer than when ﬁltered with

the weak ﬁlter. The selected connected component (in

red and green) has 50 countries.

With a 0.40 threshold and strong ﬁlter, the graph

looks more cohesive (see Figure 3). This conﬁgura-

tion results in 3.0% of all connections, i.e., 2.0% and

0.8% fewer than when ﬁltered with the weak and tra-

ditional ﬁlters, respectively. The selected connected

component (in red) has 33 countries, and all of them

have very high HDI ranging from 0.82 to 0.94. Strong

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

264

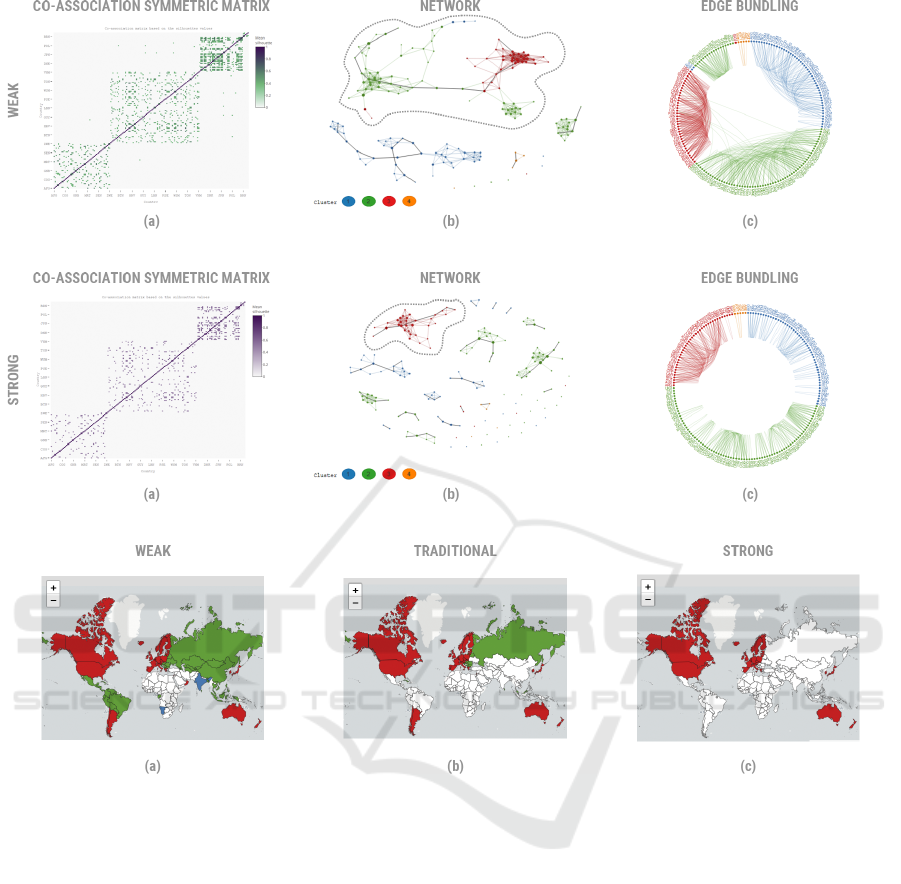
Figure 2: Visualization of the ﬁnal partition for the HDI dataset with a threshold of [0.40;1] and weak ﬁlter.

Figure 3: Visualization of the ﬁnal partition for the HDI dataset with a threshold of [0.40;1] and strong ﬁlter.

Figure 4: Visualization of the selected connected components for the HDI dataset with a threshold of [0.40;1].

ﬁlters are good to identify more cohesive groups.

5 CONCLUSIONS

This work proposed a visual tool prototype that sup-

ports the exploration of different aspects of a dataset.

It is a useful tool to deeply analyze the connection

between the elements, characterize the instances, and

locate them on a map. This is an interesting approach

for spatial analysis, where the number of elements is

reduced. With all the results, the proposed research

goals were accomplished. Although we tested the ap-

proach with different datasets, we could only present

here one of them.

Our ﬁrst step in this work was to explore different

types of visualizations to assist in the analysis of the

ﬁnal partition. Our next step is to evaluate our tool

in an empirical study to identify: (i) different insights

that analysts gain when interacting with the visualiza-

tions; (ii) possible interaction design enhancements

of the tool; and (iii) new features that could allow a

deeper and more comprehensive analysis.

ACKNOWLEDGEMENTS

We thank Conselho Nacional de Desenvolvimento

Cient

ıﬁco e Tecnol

ogico (CNPq) for partially ﬁnanc-

ing this research.

REFERENCES

Almende B.V., Thieurmel, B., and Robert, T. (2018). vis-

Network: Network Visualization using ’vis.js’ Li-

Visual Exploration Tools for Ensemble Clustering Analysis

265

brary. R package version 2.0.3.

Berikov, V. (2016). Cluster ensemble with averaged co-

association matrix maximizing the expected margin.

In DOOR (Supplement), pages 489–500.

Chang, W., Cheng, J., Allaire, J., Xie, Y., and McPherson,

J. (2018). shiny: Web Application Framework for R.

R package version 1.1.0.

Cheng, J., Karambelkar, B., and Xie, Y. (2018). leaﬂet:

Create Interactive Web Maps with the JavaScript

’Leaﬂet’ Library. R package version 2.0.1.

Cunha Jr, A., Nasser, R., Sampaio, R., Lopes, H., and

Breitman, K. (2014). Uncertainty quantiﬁcation

through the monte carlo method in a cloud com-

puting setting. Computer Physics Communications,

185(5):1355–1363.

Dietterich, T. G. (2000). Ensemble methods in machine

learning. In International workshop on multiple clas-

siﬁer systems, pages 1–15. Springer.

Fiol-Gonzalez, S., Almeida, C., Barbosa, S., and Lopes, H.

(2018). A novel committee–based clustering method.

In International Conference on Big Data Analytics

and Knowledge Discovery, pages 126–136. Springer.

Fred, A. L. and Jain, A. K. (2005). Combining multiple

clusterings using evidence accumulation. IEEE Trans-

actions on Pattern Analysis & Machine Intelligence,

(6):835–850.

Ghanem, R., Higdon, D., and Owhadi, H. (2017). Hand-

book of uncertainty quantiﬁcation. Springer.

Hao, L., Healey, C. G., and Hutchinson, S. E. (2015). En-

semble visualization for cyber situation awareness of

network security data. In 2015 IEEE Symposium on

Visualization for Cyber Security (VizSec), pages 1–8.

IEEE.

Hintze, J. L. and Nelson, R. D. (1998). Violin plots: a box

plot-density trace synergism. The American Statisti-

cian, 52(2):181–184.

Holten, D. (2006). Hierarchical edge bundles: Visualiza-

tion of adjacency relations in hierarchical data. IEEE

Transactions on visualization and computer graphics,

12(5):741–748.

Huang, D., Lai, J.-H., and Wang, C.-D. (2015). Combining

multiple clusterings via crowd agreement estimation

and multi-granularity link analysis. Neurocomputing,

170:240–250.

Huang, D., Wang, C.-D., and Lai, J.-H. (2018). Locally

weighted ensemble clustering. IEEE transactions on

cybernetics, 48(5):1460–1473.

Iam-On, N., Boongoen, T., and Garrett, S. (2008). Reﬁning

pairwise similarity matrix for cluster ensemble prob-

lem with cluster relations. In International Confer-

ence on Discovery Science, pages 222–233. Springer.

Kruskal, J. B. and Wish, M. (1978). Multidimensional Scal-

ing, volume 31.

Lin, Z., Yang, F., Lai, Y., Gao, X., and Wang, T. (2017).

A scalable approach of co-association cluster ensem-

ble using representative points. In Automation (YAC),

2017 32nd Youth Academic Annual Conference of

Chinese Association of, pages 1194–1199. IEEE.

Obermaier, H., Joy, K. I., et al. (2014). Future challenges

for ensemble visualization. IEEE Computer Graphics

and Applications, 34(3):8–11.

Potter, K., Wilson, A., Bremer, P.-T., Williams, D., Dou-

triaux, C., Pascucci, V., and Johnson, C. R. (2009).

Ensemble-vis: A framework for the statistical visual-

ization of ensemble data. In Data Mining Workshops,

2009. ICDMW’09. IEEE International Conference on,

pages 233–240. IEEE.

R Core Team (2018). R: A Language and Environment for

Statistical Computing. R Foundation for Statistical

Computing, Vienna, Austria.

Scherr, M. (2008). Multiple and coordinated views in in-

formation visualization. Trends in Information Visu-

alization, 38:1–8.

Sievert, C. (2018). plotly for R.

Tao, Z., Liu, H., Li, S., and Fu, Y. (2016). Robust spec-

tral ensemble clustering. In Proceedings of the 25th

ACM International on Conference on Information and

Knowledge Management, pages 367–376. ACM.

Tarr, G., Bostock, M., and Patrick, E. (2016). edgebundleR:

Circle Plot with Bundled Edges. R package version

0.1.5.

Thurau, M., Buck, C., and Luther, W. (2014). Ipfviewer a

visual analysis system for hierarchical ensemble data.

In Information Visualization Theory and Applications

(IVAPP), 2014 International Conference on, pages

259–266. IEEE.

Van Rossum, G. and Drake, F. L. (2003). Python language

reference manual. Network Theory United Kingdom.

Vega-Pons, S. and Ruiz-Shulcloper, J. (2011). A survey of

clustering ensemble algorithms. International Jour-

nal of Pattern Recognition and Artiﬁcial Intelligence,

25(03):337–372.

Wang, J., Hazarika, S., Li, C., and Shen, H.-W. (2018). Vi-

sualization and visual analysis of ensemble data: A

survey. IEEE transactions on visualization and com-

puter graphics.

Wang, X., Yang, C., and Zhou, J. (2009). Clustering aggre-

gation by probability accumulation. Pattern Recogni-

tion, 42(5):668–675.

Wilkinson, L. and Friendly, M. (2009). The history of

the cluster heat map. The American Statistician,

63(2):179–184.

Xu, D. and Tian, Y. (2015). A comprehensive survey

of clustering algorithms. Annals of Data Science,

2(2):165–193.

Yi, J., Yang, T., Jin, R., Jain, A. K., and Mahdavi, M.

(2012). Robust ensemble clustering by matrix com-

pletion. In 2012 IEEE 12th International Conference

on Data Mining, pages 1176–1181. IEEE.

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

266