Weighted Linear Combination of Distances within Two Manifolds for 3D

Human Action Recognition

Amani Elaoud

, Walid Barhoumi

1,2

, Hassen Drira

and Ezzeddine Zagrouba

Universit

e de Tunis El Manar, Institut Sup

erieur d’Informatique, Research Team on Intelligent Systems in Imaging and

Artiﬁcial Vision (SIIVA), LR16ES06 Laboratoire de Recherche en Informatique, Mod

elisation et Traitement de l’Information

et de la Connaissance (LIMTIC), 2 Rue Bayrouni, 2080 Ariana, Tunisia

Universit

e de Carthage, Ecole Nationale d’Ing

enieurs de Carthage (ENICarthage),

45 Rue des Entrepreneurs, 2035 Tunis-Carthage, Tunisia

IMT Lille Douai, Univ. Lille, CNRS, UMR 9189 – CRIStAL – Centre de Recherche en Informatique Signal et Automatique

ezzeddine.zagrouba@fsm.rnu.tn

Keywords:

3D Human Action, Temporal Modeling, Grassmann Manifold, Special Orthogonal Group, Weighted Distance,

Human Skeleton.

Abstract:

Human action recognition based on RGB-D sequences is an important research direction in the ﬁeld of com-

puter vision. In this work, we incorporate the skeleton on the Grassmann manifold in order to model the

human action as a trajectory. Given the couple of matched points on the Grassmann manifold, we introduce

the special orthogonal group SO(3) to exploit the rotation ignored by the Grassmann manifold. In fact, our

objective is to deﬁne the best weighted linear combination between distances in Grassmann and SO(3) man-

ifolds according to the nature of action, while modeling human actions by temporal trajectories and ﬁnding

the best weighted combination. The effectiveness of combining the two non-Euclidean spaces was validated

on three standard challenging 3D human action recognition datasets (G3D-Gaming, UTD-MHAD multimodal

action and Florence3D-Action), and the preliminary results conﬁrm the accuracy of the proposed method

comparatively to relevant methods from the state of the art.

1 INTRODUCTION

In recent years, human action recognition has become

a popular research ﬁeld due to its wide applications

in many areas, such as video surveillance (Han

et al., 2018), robot vision (Marinoiu et al., 2018) and

gaming (Wang et al., 2017). In fact, visual analysis of

human activities has a long history in computer vision

research and it has already been surveyed in many

papers ((Weinland et al., 2011), (Ye et al., 2013) and

(Wang et al., 2018)). Nevertheless, most of the works

focused on detecting and analyzing human actions

from the information acquired via RGB sensors

((Poppe, 2010) and (Ramanathan et al., 2014)).

However, there are still some challenging problems

within RGB videos, such as illumination change

and occlusion. For these reasons, extracting useful

information from RGB-D data is attracting more

attention, particularly due to the increasing evolution

of 3D sensors. In fact, various types of modern sen-

sors; such as motion capture systems, stereo cameras

and depth sensors; are nowadays widely used to ob-

tain the 3D data. Indeed, motion capture systems

usually utilize optical sensing of markers (e.g. Mo-

Cap: http://mocap.cs.cmu.edu/). For instance, (Gupta

et al., 2014) provided video sequences that were used

for action recognition via non-linear circulant tem-

poral encoding. Moreover, (Natarajan and Nevatia,

2008) presented a method based on MoCap data for

recognizing known human actions, under several vari-

ations in view and scale. Furthermore, the stereo cam-

eras are based on 3D data obtained via infrared stereo

sensors. As an example, an action recognition method

using body joint-angle features, extracted from stereo

cameras, was introduced in (Uddin et al., 2011). Sim-

ilarly, (Han and Lee, 2013) used stereo cameras to

collect motion data while constructing a 3D skeleton

model to detect the critical unsafe actions of work-

ers. On the other side, the depth sensors (e.g. Mi-

crosoft Kinect://www.xbox.com/en-US/kinect/) offer

Elaoud, A., Barhoumi, W., Drira, H. and Zagrouba, E.

Weighted Linear Combination of Distances within Two Manifolds for 3D Human Action Recognition.

DOI: 10.5220/0007369006930703

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 693-703

ISBN: 978-989-758-354-4

693

cost-effective real-time 3D data. These sensors have

prompted intensive research efforts on 3D human

action recognition thanks to the extra dimension of

depth. In fact, the information given by depth maps is

insensitive to background clutter and includes rich 3D

structural information of the scene. In particular, the

depth information from Kinect cameras can be effec-

tively analyzed to better locate and extract the body

joints, which form the human skeleton. Indeed, the

3D skeleton data is demonstrating a high performance

in real-world applications in gaming (Fanfarelli et al.,

2018) and computer vision research (Lun and Zhao,

2015). In the next section (c.f. Sect. 2), we will dis-

cuss the state of the art on human action recognition

using 3D data with a focus on the recent development

within Kinect-based recognition methods.

The importance of several methods which tend

to process and classify time is proved in the liter-

ature (Anirudh et al., 2015). Independently of the

used cameras, two ways have been proposed for ac-

tion recognition. One way is to model actions as se-

quences of poses, such as the method of (Agrawal

et al., 2018), which had as an input a sequence of

human poses. This method investigated a gesture

recognition by motion augmentation model. More-

over, the work of (Zanﬁr et al., 2013) proposed to de-

ﬁne a set of moving pose descriptors while consid-

ering position, speed and acceleration information of

body joints. The other way is to use temporal-based

methods, while adapting notably the Dynamic Time

Warping (DTW) (Sakoe and Chiba, 1978) in order to

match temporal sequences. In fact, DTW allows bet-

ter modeling of variations within model sequences for

action recognition. For instance, an evolution algo-

rithm was applied in (Chaaraoui et al., 2014) to se-

lect an optimal subset of joints for action representa-

tion and classiﬁcation, while using DTW for sequence

matching. More recently, (Mitchel et al., 2018) in-

troduced a fast dynamic time warping for human ac-

tion recognition. This was performed by deﬁning ad-

equate procedures for applying the Globally Optimal

Reparameterization Algorithm (GORA) to character-

ize and compare signals in the form of real trajectories

and video sequences.

In this work, we are particularly interested in rec-

ognizing different actions that can appear in various

ﬁelds, such as sports (Mora and Knottenbelt, 2017)

and daily activities (Sung et al., 2012). The major

contribution of this work can be summarized as fol-

lows. We model the 3D human action as a weighted

linear combination on the Grassmann and SO(3) man-

ifolds. Indeed, we present an accurate approach for

action recognition based on measuring the similar-

ity between trajectories. Since the Grassmann man-

ifold ignores the rotation, which can prevent the good

progress of the action recognition, we propose to inte-

grate the special orthogonal SO(3), as a second man-

ifold, in order to solve the problem of invariance

against rotation. Firstly, we calculate the distance

on the Grassmann manifold after applying Grassmann

projection while modeling the human motion as a tra-

jectory on the Grassmann manifold. For the couples

of points that were matched in the Grassmann mani-

fold, we calculate the relative 3D rotations by intro-

ducing special orthogonal group SO(3) to exploit the

rotation ignored by the Grassmann manifold. Thus,

we obtain two distances: one on the Grassmann mani-

fold and a second one on the special orthogonal group

SO(3). Then, we combine these two distances while

testing different weights to ﬁnd the best weighted lin-

ear combination according to the nature of action,

such as an action contains or not a rotation.

The rest of this paper is organized as follows. In

section 2, we brieﬂy present the related work on hu-

man action recognition from RGB-D data captured by

Kinect sensor. In section 3, we suggest to apply a

weighted linear combination between the two man-

ifolds (Grassmann and SO(3)) in order to deal with

accurate 3D human action recognition. Then, in sec-

tion 4, we show experimental results to demonstrate

the effectiveness of the proposed method. Finally, we

present conclusions and future work in section 5.

2 RELATED WORK

In this section, we brieﬂy review the related work

on 3D human action recognition using the data cap-

tured from Kinect sensing devices (Han et al., 2013).

In fact, RGB-D data acquired by Kinect sensor for

human motion analysis comprises three modalities

(RGB, depth and skeleton). Thus, according to the

used data among these given by Kinect, we can dis-

tinguish three different categories of methods: depth-

based methods, skeleton-based methods and hybrid

methods.

As an example of depth-based methods, (Chen et al.,

2015a) used Depth Motion Maps (DMMs) to capture

the motion cues of actions and Local Binary Patterns

(LBPs) to represent the features. Similarly, (Chen

et al., 2016) presented a real-time method for hu-

man action recognition based on depth motion maps.

Moreover, descriptors for depth maps were proposed

using a histogram capturing the distribution of the

surface normal orientation in the 4D volume of time

(Oreifej and Liu, 2013). Otherwise, (Yang and Tian,

2014) clustered hypersurface normals in a depth se-

quence to form the polynormal for extracting the lo-

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

694

cal motion and shape information. Space-Time Oc-

cupancy Patterns (STOP) were also proposed as de-

scriptors for classifying human action from depth se-

quences (Vieira et al., 2012).

Differently to RGB and depth data, skeleton data

contains human representation with the locations of

human key joints in the 3D space leading to the emer-

gence of many recent works on 3D action recognition

(Li et al., 2017). For example, (Xia et al., 2012) ap-

plied histograms of 3D joint locations in skeleton esti-

mation from Kinect sensors. Similarly, (Thanh et al.,

2012) extracted the 3D joint positions for convert-

ing skeletons into histograms. Recently, (Du et al.,

2015) proposed Hierarchical Recurrent Neural Net-

work (HRNN) for skeleton-based action recognition.

Furthermore, learning discriminative trajectorylet de-

tector sets were adapted for capturing dynamic and

static information of the skeletal joints (Qiao et al.,

2017). More recently, (Hou et al., 2018) used Con-

volutional Neural Networks (ConvNets) to learn the

spatio-temporal information of a skeleton sequences.

In (Chen and Forbus, 2017), action recognition from

skeleton data was performed via analogical gener-

alization over qualitative representations. (Ghojogh

et al., 2018) utilized the temporal position of skele-

tal joints and the Fisherpose method in order to create

a feature vector for recognizing the pose of the body

in each frame. Moreover, an image classiﬁcation ap-

proach was presented in (Li et al., 2018) to transform

the 3D skeleton videos to color images.

With Hybrid methods for 3D human action recog-

nition, the idea is to beneﬁt from many types of data

(RGB + skeleton (Shahroudy et al., 2014), depth +

skeleton (Elmadany et al., 2018), RGB + depth (Oﬂi

et al., 2013)) in order to optimize the recognition

accuracy. For example, (Zhu et al., 2013) incorpo-

rated RGB images and skeleton sequences while ex-

tracting Spatio-Temporal Interest Points (STIP) from

RGB images, as well as distances between skele-

ton joints, for human action recognition. Differently,

(Ohn-Bar and Trivedi, 2013) combined skeletal fea-

tures with additional depth-based features. Moreover,

(Shahroudy et al., 2016) proposed heterogeneous set

of depth- and skeleton- based features for multipart

learning to recognize the actions in depth videos. In

a recent work, (Rahmani and Bennamoun, 2017) in-

troduced a learning model for view-invariant appear-

ance representation of human body-parts while com-

bining features from depth and skeleton data. In (Bakr

and Crowley, 2018), human actions were recognized

by using RGB and depth descriptors that were com-

puted around motion trajectories. However, most of

hybrid methods are suffering with the long computa-

tional time.

Generally, manifold-based representations per-

form success with the skeletal data such that a skele-

ton is represented using a ﬁnite number of salient

points. The 3D skeleton data encodes human body

as an articulated system of rigid segments connected

by joints. To easily manipulate this number of land-

marks, it can be effectively processed using the geom-

etry of non-Euclidean spaces, what gives rise to the

notion of manifolds performing dimensionality reduc-

tion (Cherian and Sra, 2017). Thus, manifold anal-

ysis has been extensively considered in many com-

puter vision applications (Efros and Torralba, 2016),

such as face recognition (Harandi et al., 2011), track-

ing (Hu et al., 2018) and action recognition (Chen

et al., 2018). In particular, the issue of 3D human ac-

tion recognition has been recently studied with using

skeleton manifolds. For example, (Amor et al., 2016)

focused on exploiting the skeletons for 3D action

recognition in the Kendall’s shape space (Kendall,

1984). Similarly, (Tanfous et al., 2018) incorporated

dictionary learning to the Kendall’s shape space cod-

ing of 3D skeletal sequences. In the Grassmann man-

ifold, (Slama et al., 2015) analyzed human motion

by modeling 3D body skeletons over non-Euclidean

spaces. In (Rahimi et al., 2018), a kernelized Grass-

mann manifold learning method was proposed us-

ing multigraph embedding method. Differently, other

works proposed to extract 3D geometric relationships

from skeleton joints with feature representation on

the Lie group (Vemulapalli et al., 2014). Further-

more, the Lie group structure was incorporated into a

deep network architecture to learn more appropriate

Lie group features for skeleton-based action recog-

nition (Huang et al., 2017). Otherwise, (Devanne

et al., 2015) demonstrated the beneﬁt of temporal evo-

lution of skeleton joints into a Riemannian manifold.

For instance, the works of (Meng et al., 2015) and

(Meng et al., 2018) presented a Riemannian analysis

of the distance trajectories for a real-time human ac-

tion recognition.

3 PROPOSED METHOD

The skeleton sequences represent a sparse represen-

tation of human action videos. It has been proved

previously that this sparse representation is still

representative of the human action. In order to deal

with undesirable variability of skeleton sequences,

we propose ﬁrstly to model this variability as group

action on underlying space representing the data.

Then, we compare the quotient spaces resulting of

action of this group. Thus, we consider the skeleton

sequences as trajectories in the Stiefel manifold

Weighted Linear Combination of Distances within Two Manifolds for 3D Human Action Recognition

695

(the set of k-dimensional orthonormal bases in R

where (k < n)). The rotation will be later removed

on quotient spaces of Stiefel manifold by the action

of the rotation group SO(3). The resulting quotient

space will model the skeleton independently of the

rotation in R

and thus it will make the comparison

of skeletons invariant to the rotation (this will be de-

tailed in section 3.1). Moreover, the ignored rotations

will be considered by another metric by modeling

the rotations between corresponding skeletons in the

SO(3). We will show in section 3.2 the metrics that

consider the rotation of the skeletons while detailing

the fusion of these complementary metrics. Before

that, we start our discussion by the deﬁnition of the

underlying manifolds. In fact, the special orthogonal

group SO(n) is a matrix Lie group formed by the set

of all n × n rotation matrices. It is obtained (1) by

considering the subset of orthogonal matrices with a

determinant equals to +1.

SO(n) =



Y ∈ R

n×n

/ Y

Y = I and det(Y ) = 1



(1)

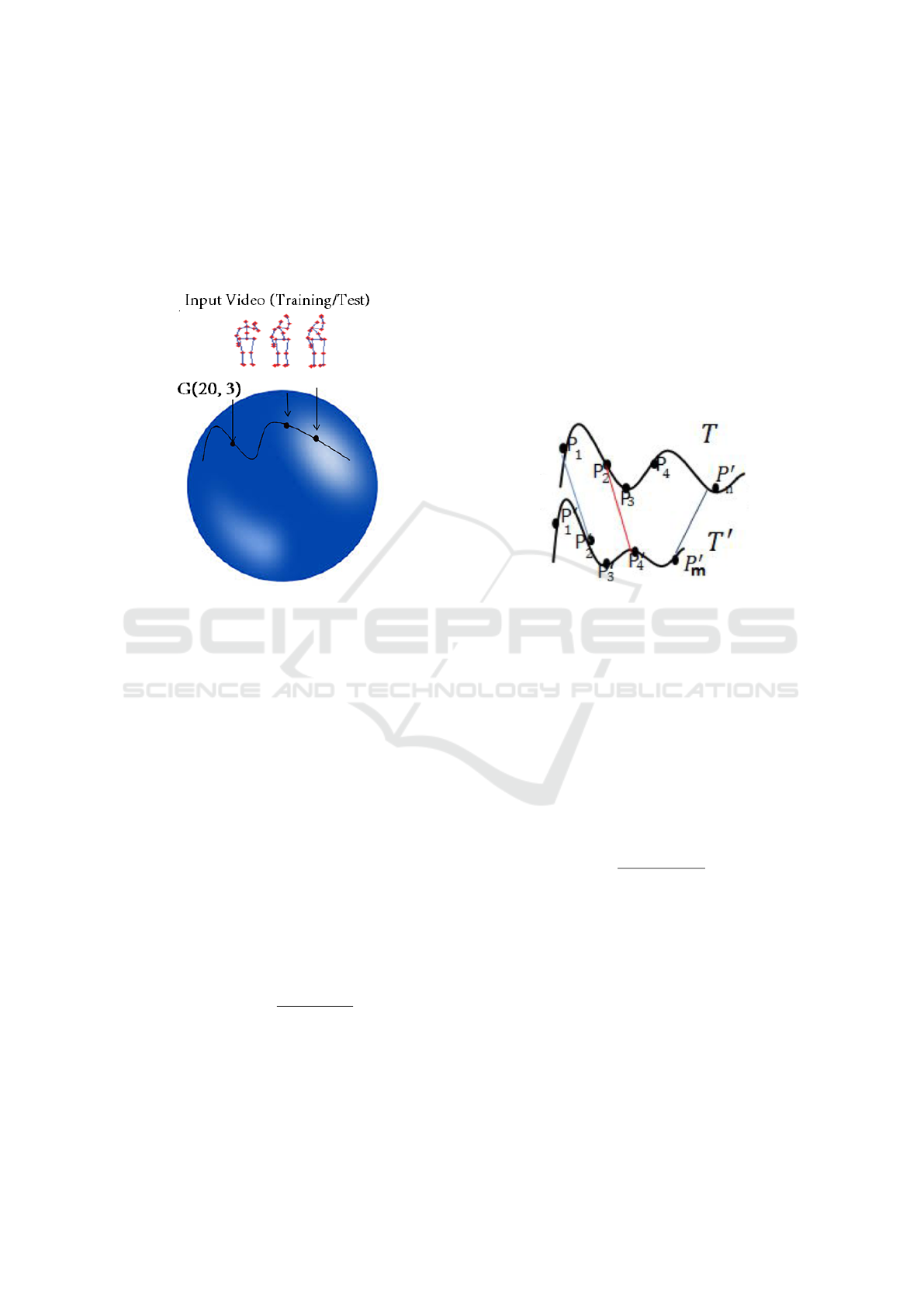
Figure 1: Outline of the proposed method.

Stiefel manifold is the set of k-dimensional

orthonormal bases in R

where (k < n). It is a

quotient space of the special orthogonal group SO(n),

given by V (R

) = SO(n)/SO(n − k). In particular,

Grassmann manifold G(R

) is deﬁned as the set of

k-dimensional linear subspaces of R

. It is a quotient

space of Stiefel manifold V (R

), represented by

V (R

)/SO(k). Given P

and P

, P

∈ G(20,3))

two matrices of size n × k with orthonormal columns,

the distance on the Grassmann manifold (2) is the

geodesic distance, which is deﬁned as the length of

shortest curve in the manifold.

Dis

Grass

) =

∑

l=1

(2)

where θ denotes the principal angle between the two

subspaces P

and P

3.1 Comparison in Grassmann

Manifold

The proposed method has as input the skeleton se-

quence of the studied test person and the skeletons

of all persons in the training set. Since the used se-

quences are with different sizes, our objective is to

compare the input test sequence T

with all composed

training set T

...T

in order to identify the most similar

one to T

among T

...T

. The sequence motion is rep-

resented by two trajectories as illustrated in Figure 1.

In fact, the proposed method starts by the comparison

of the trajectories on the Grassmann manifold. To do

this, each frame in the skeleton sequence is modeled

by a point in the trajectory (Figure 2). Indeed, the pro-

jection of skeleton data on the Grassmann manifold

is mainly performed using Singular Value Decompo-

sition (SVD)-based orthogonalization (Elaoud et al.,

2017). In fact, all data points on the Grassmann man-

ifold are projected on R

(for Kinect V1, since 20

landmarks are given with each skeleton). Each frame

in a skeleton sequence motion is modeled by a matrix

of size 20 × 3, where l ∈ {1,...,n} and n denotes

the number of frames in the studied sequence. We cal-

culate the distance on the Grassmann manifold Dist

for one trajectory sequence of test T

with all trajec-

tories sequences of training T

(3) in order to obtain

the closest distance. We use the DTW algorithm that

resolves the problem of temporal alignment and mea-

sures the similarity between sequences varied in time.

Thus, DTW allows action comparison to ﬁnd the best

warping point between two sequences with different

sizes. It is worth noting that the Grassmann manifold

is characterized by ignoring rotation, what motivated

to resort also to special orthogonal group.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

696

Dist

) =

∑

l=1

Dist

Grass

(l), T

(l))

∑

l=1

(3)

where T

is training trajectory and T

is test trajec-

tory.

Figure 2: Grassmann Projection.

3.2 Comparison in Special Orthogonal

Group SO

The second used representation in this work is on the

special orthogonal group SO(3), which provides the

difference of rotation between two skeletons with 3D

joints. In our case, it is a 3-dimensional subspace

that provides a 3×3 rotation matrix deﬁned on SO(3).

Thereafter, we obtain a trajectory composed of differ-

ence of rotations. We apply the distance on SO(3), for

couple of points already matched on the Grassmann

manifold (5). For example, in Figure 3 we calculate

the difference of rotation for the point P

and the point

that are matched on the Grassmann manifold in or-

der to consider the ignored rotation for this couple of

points. For any two skeletons, a difference of rota-

tion is a point in SO(3) and the distance on SO(3) can

be deﬁned by the Frobenius norm of a matrix of rota-

tion N (difference of rotation between the two studied

skeletons) (4).

||N||

Trace(N

N) (4)

Furthermore, the distance Dist

is the sum of the

Frobenius norm of the matrix of rotation. We use the

distance on SO(3) for one trajectory sequence of test

with all trajectories sequences of training T

...T

(5). By this way, the Grassmann manifold was used

to match points within the two studied trajectories T

and T

while evaluating the similarity of test trajectory

by using the rotation distance invariant Dist

. Then,

the couple of matched points are processed on SO(3)

in order to evaluate the similarity by using Dist

consider the rotation difference. Lastly, the two dis-

tances will be linearly combined to produce ﬁnal sim-

ilarity between T

and T

Dist

) =

∑

l=1

Dist

(l), T

(l))

∑

l=1

||N(l)||

(5)

Figure 3: Matching on the Grassmann manifold.

3.3 Weighted Linear Combination

We propose herein to combine the distance Dist

the Grassmann manifold with the distance Dist

SO(3) to ﬁnd a trade-off between these two manifolds

considering the assessment of similarity between two

trajectories according to the nature of their actions

(including rotation or not). Firstly, we start by nor-

malizing the distances D (Dist

and Dist

) within

the testing and training data in order to bring all new

values D

into the range [0, 1] while restricting the

range of values (6).

D − Dmin

Dmax − Dmin

(6)

Then, we test different values of each distance

weight, α and 1 − α, on the training set in order to

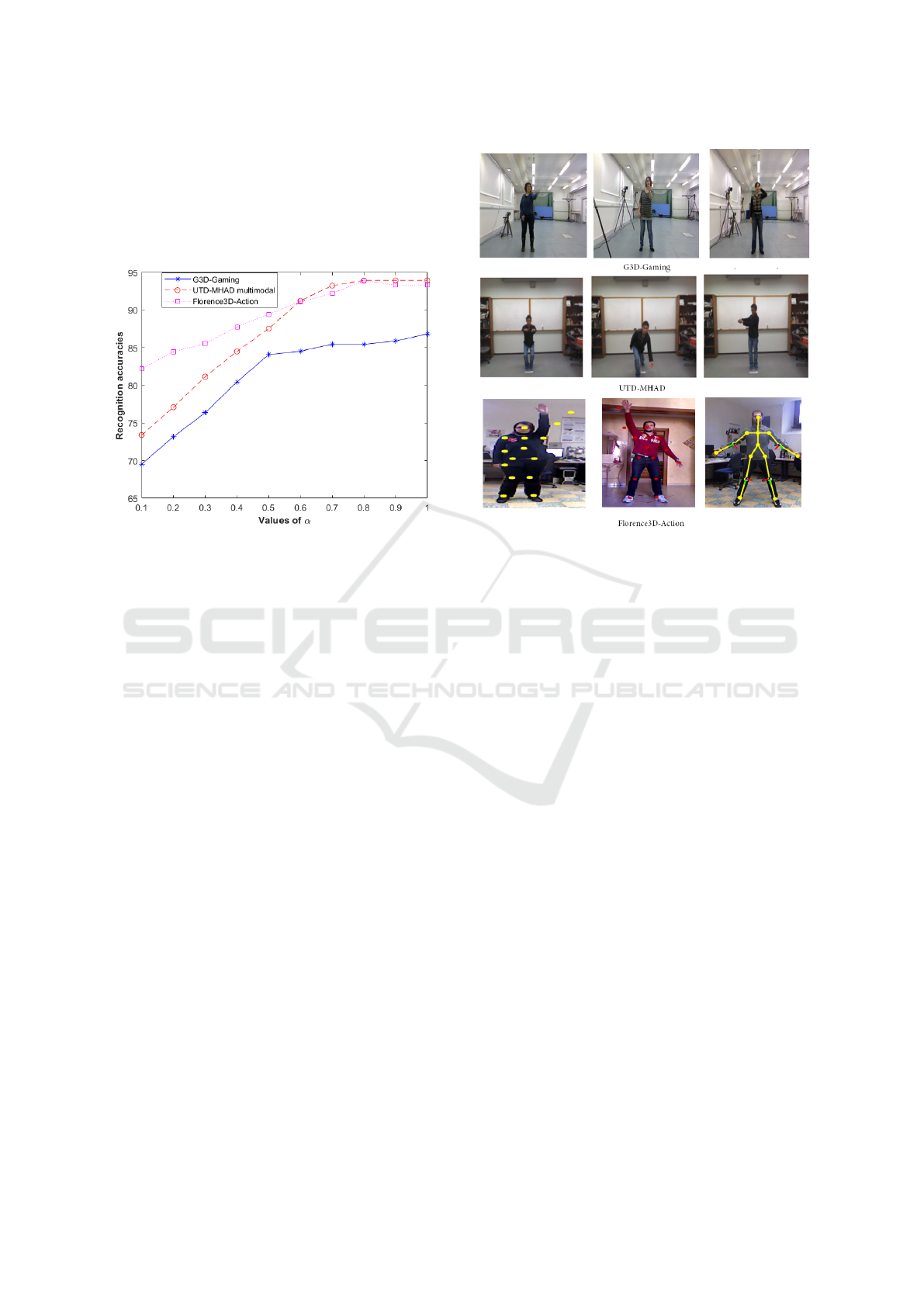
ﬁnd the best weighted linear combination (Figure 4).

The selection of the tested values of α is strongly

depending on the nature of the studied actions (7).

For example, if the action does not contain a rotation,

α has a value that is equal to 1. Then, the deﬁned

weighted linear combination is applied on the test

set in order to recognize the input action. Indeed, to

recognize an unknown test trajectory T

, a classiﬁ-

cation by the nearest neighbour distance is used to

decide the nature of the action within the sequence

(7). This step is driven by a decision rule for the

Weighted Linear Combination of Distances within Two Manifolds for 3D Human Action Recognition

697

dataset while ﬁnding the weight that maximizes the

recognition action accuracy.

arg min

16l≤n

Dist(T

(7)

where, Dist = α.Dist

+ (1 − α).Dist

Figure 4: The recognition accuracies with different values

of α.

4 RESULTS

To demonstrate the effectiveness of the proposed 3D

action recognition method, we used three standard

3D human action datasets (Figure 5): G3D-Gaming,

UTD-MHAD multimodal action and Florence3D-

Action. The ﬁrst benchmark, G3D-Gaming dataset

(Bloom et al., 2012), contains 10 subjects performing

20 different gaming motions (e.g. golf swing, tennis

swing forehand, tennis swing backhand, tennis serve,

throw bowling ball. . . ). Each subject repeats every

action more than two times. This dataset is collected

using Kinect V1 camera with a skeleton of 20 joints.

Thus, the G3D-Gaming dataset is composed of 663

gaming motions sequences.

For comparison purpose, we followed the same

evaluation setting of (Vemulapalli and Chellapa,

2016) and (Huang et al., 2017) for this dataset. In-

deed, we used the cross-subject test setting, in which

ﬁve subjects were used for training and ﬁve other sub-

jects were used for testing. All the reported results

for G3D-Gaming dataset were averaged over ten dif-

ferent random combinations of training and test sub-

jects. Besides, the recognition accuracy is deﬁned by

the average of the 20 actions within the testing set.

The second used dataset is UTD-MHAD multimodal

action (Chen et al., 2015b), which contains 27 actions

performed by 8 subjects (4 females and 4 males) such

that each subject performs each action 4 times. Thus,

Figure 5: A sample of the datasets used.

this dataset includes 861 data sequences collected us-

ing Kinect V1 camera and a wearable inertial sensor,

with 3D locations of 20 joints. In fact, it illustrates

various actions that cover sport actions (e.g. “bowl-

ing”, “tennis serve” and “baseball swing”...), hand

gestures (e.g. “draw X”, “draw triangle”, and “draw

circle”. . . ), daily activities (e.g. “knock on door”, “sit

to stand” and “stand to sit”. . . ) and training exer-

cises (e.g. “arm curl”, “lung” and “squat”. . . ). Like-

wise (Wang et al., 2016) and (Chen et al., 2015b), the

cross-subject protocol was adopted. The data from

the subject numbers 1, 3, 5, 7 were used for the train-

ing while the subject numbers 2, 4, 6, 8 were used

for the testing. The third used dataset is Florence3D-

Action (Seidenari et al., 2013) that illustrates actions,

which have been captured using a Kinect V1 camera,

while being performed by 10 subjects. In fact, each

subject repeats every action two or three times for a

total of 215 action sequences. It includes nine activi-

ties, namely wave, drink from a bottle, answer phone,

clap, lace, sit down, stand up, read watch, bow. For

this dataset, we followed the cross-subject test setting

in which half of the subjects was used for the training

and the remaining half was used for the testing.

The obtained results were numerically compared

with methods that adopted skeletal representations

among the aforementioned datasets. Indeed, for the

G3D-Gaming dataset, the proposed method was com-

pared with three methods that are based on skele-

ton manifolds. In fact, the two ﬁrst compared meth-

ods used pairwise transformations of skeletal joints

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

698

on Lie group using learning methods (Vemulapalli

et al., 2014), (Vemulapalli and Chellapa, 2016) and

the last method employed deep learning, also on Lie

Groups, for skeleton-based action recognition (Huang

et al., 2017). Furthermore, while using UTD-MHAD

multimodal action dataset, we compared the sug-

gested method against the two works of (Chen et al.,

2015b) and (Wang et al., 2016). In these works, ac-

tion recognition based on joint trajectory maps was

incorporated using convolutional neural networks in

(Wang et al., 2016), and, in addition to the skeleton

data, depth and inertial sensor data were integrated in

(Chen et al., 2015b). For Florence3D-Action dataset,

we compared the suggested method against Rieman-

nian representations, namely (Vemulapalli and Chel-

lapa, 2016) that proposed trajectories on Lie groups

and (Tanfous et al., 2018) that represented the mo-

tion of skeletal shapes as trajectories on the Kendall’s

shape.

It is worthy noting that we tested different values

of α with the training set to extract the best weighted

linear combination. For the dataset G3D-Gaming

dataset, we found that the best recognition accuracy

was recorded when the value of α is equal to 1, since

the actions within this dataset do not contain rota-

tions. Then, we applied this weighted linear combi-

nation on the testing set to perform action recogni-

tion. In fact, this combination provides 100% accu-

racy for 13 actions (’PunchRight’,’PunchLeft’, ’Kick-

Right’, ’KickLeft’, ’Defend’, ’TennisServe’, ’Walk’,

’Run’, ’Climb’, ’Crouch’, ’Steer’, ’Flap’ and ’Clap’)

thanks to the accurate modeling information exploita-

tion in the proposed method. However, the worst re-

sult was 50% for the ’GolfSwing’ action (Figure 6).

Indeed, ’GolfSwing’ was frequently confused with

’PunchRight’. This is probably due to the fact that

the skeleton motions of the two actions are too sim-

ilar. In Table 1, we show that the proposed method

outperforms the state of the art methods with value

of accuracy 93% against 87.23% with (Vemulapalli

et al., 2014), 87.95% with (Vemulapalli and Chellapa,

2016) and 89.10% with (Huang et al., 2017).

While validating using the UTD-MHAD dataset,

we tried different values of α with the training set and

we observed a growth in performance with value of α

equals to 0.9. We applied this combination on the set

of test and 18 actions (’Clap’, ’Throw’, ’Arm cross’,

’Basketball shoot’, ’Draw X’, ’Draw circle’, ’Bowl-

ing’, ’Boxing’, ’Arm curl’, ’Push’, ’Catch’, ’Pickup

and throw’, ’Jog’, ’Walk’, ’Sit to stand’, ’Stand to sit’,

’Lunge’, ’Squat’) were well distinguished with val-

ues of the recognition accuracy equal to 100%. How-

ever, the worst value was 84.65% for the ’Draw cir-

cle counter clockwise’ action. The main confusions

Figure 6: Recognition rate of the proposed method for the

G3D-Gaming dataset.

concern very similar actions of ’Draw circle counter

clockwise’ and ’Draw circle (clockwise)’ (Figure 7).

Table 2 demonstrates that the proposed method out-

performs the state of the art methods with value of

95.37% against 79.10% for (Wang et al., 2016) and

85.10% for (Chen et al., 2015b).

Figure 7: Skeleton sequence comparison for the ’Draw cir-

cle (clockwise)’ action (ﬁrst row) and ’Draw circle counter

clockwise’ action (second raw) from the UTD-MHAD

dataset.

With the Florence3D-Action dataset, the best

value of α is equal to 1. This combination provided

100% accuracy for four actions (’clap’, ’light place’,

’sit down’, ’stand up’). However, the worst result was

Weighted Linear Combination of Distances within Two Manifolds for 3D Human Action Recognition

699

Table 1: Comparison of the recognition accuracy (Acc) of the proposed method against the state of the art methods using the

G3D-Gaming dataset.

Method Acc (%)

(Vemulapalli et al., 2014): skeleton on Lie group 87.23

(Vemulapalli and Chellapa, 2016): skeleton on Lie group 87.95

(Huang et al., 2017): skeleton on Lie group + deep learning 89.10

Proposed Method: skeleton on SO(3) + Grassmann 93

Table 2: Comparison of the recognition accuracy (Acc) of the proposed method against the state of the art methods using the

UTD-MHAD dataset.

Method Acc (%)

(Wang et al., 2016): skeleton + convolutional neural networks 79.10

(Chen et al., 2015b): Depth + skeleton 85.10

Proposed Method: skeleton on SO(3) + Grassmann 95.37

Table 3: Comparison of the recognition accuracy (Acc) of the proposed method against the state of the art methods using the

Florence3D-Action dataset.

Method Acc (%)

(Vemulapalli and Chellapa, 2016) skeleton on Lie groups 91.4

(Tanfous et al., 2018) skeleton + Kendall’s shape 93.04

Proposed Method: skeleton on SO(3) + Grassmann 92.59

Figure 8: Recognition rate of the proposed method for the

UTD-MHAD dataset.

78% for the ’answer phone’ action (Figure 9). The

recorded results (Table 3) proved that our method out-

performs the state of the art methods with value of

92.59% against 91.4% for (Vemulapalli and Chellapa,

2016). But, we performed less well against (Tan-

fous et al., 2018) with value of 93.04%. This con-

ﬁrms once again the relevance of adopting the ge-

ometry of manifolds for dealing with 3D human ac-

tion recognition. Nevertheless, for making a statisti-

cal decision and comparing the studied methods while

performing solid argument that is supported by sta-

tistical analysis, we used the p-value (or probability

value). In fact, a level of 0.05 indicates that a 5%

risk is used as the cutoff for signiﬁcance. If the p-

value is lower than 0.05, we reject the null hypothe-

sis that there is no difference between the two com-

pared methods and we conclude that a signiﬁcant dif-

ference exists (i.e. below 0.05 it is signiﬁcant; over

0.05 it is not signiﬁcant). In our case, we recorded a

signiﬁcant difference with p-value below 0.05 for the

two datasets G3D-Gaming and UTD-MHAD multi-

modal. However, there are no signiﬁcant difference

for Florence3D-Action dataset, with a p-value over

0.05 against (Wang et al., 2016) as well as against

(Tanfous et al., 2018).

Figure 9: Recognition rate of the proposed method for the

Florence3D-Action dataset.

5 CONCLUSION

Human action recognition from RGB-D (Red, Green,

Blue and Depth) is one of the most active research

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

700

topics in computer vision and has attracted increas-

ing attention in computer vision in recent years due

to the advantages of depth information over conven-

tional RGB video, typically, being insensitive to il-

lumination changes and reliable to estimate body sil-

houette and skeleton. In this paper, we presented an

effective 3D human action recognition with skeleton

information provided by a RGB-D sensor (Kinect).

In fact, we had presented a framework for human

action recognition using trajectories’ comparison us-

ing analysis of two distances within two manifolds.

This framework offers the possibility to measure the

similarity trajectories of actions by ﬁnding the best

weighted linear combination between the Grassmann

manifold and the SO(3) manifold. Moreover, the

nearest neighbour classiﬁcation and the DTW were

performed to achieve the action recognition. We

showed how this modeling can be effectively used for

action recognition on three publicly available 3D ac-

tion datasets. In fact, the proposed method outper-

forms the state of the art methods, although that it

does not assume any prior knowledge with large vari-

ations among the actions. For future work, we would

like to extend the framework to other applications (e.g

re-identiﬁcation...) while considering other underly-

ing manifolds (e.g Kendall...). Moreover, to improve

the current results, we can combine depth and skele-

ton data since the skeleton alone can be insufﬁcient

to distinguish sophisticated actions and the estimated

positions by Kinect generally suffer some noise ef-

fects.

REFERENCES

Agrawal, R., Joshi, A., and Betke, M. (2018). Enabling

early gesture recognition by motion augmentation.

In Proceedings of the 11th PErvasive Technologies

Related to Assistive Environments Conference, pages

98–101. ACM.

Amor, B. B., Su, J., and Srivastava, A. (2016). Action

recognition using rate-invariant analysis of skeletal

shape trajectories. volume 38, pages 1–13. IEEE.

Anirudh, R., Turaga, P., Su, J., and Srivastava, A. (2015).

Elastic functional coding of human actions: From

vector-ﬁelds to latent variables. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition, pages 3147–3155.

Bakr, N. A. and Crowley, J. (2018). Histogram of ori-

ented depth gradients for action recognition. In The

Computing Research Repository (CoRR), pages 1801–

09477.

Bloom, V., Makris, D., and Argyriou, V. (2012). G3d: A

gaming action dataset and real time action recogni-

tion evaluation framework. In Computer Vision and

Pattern Recognition Workshops (CVPRW), 2012 IEEE

Computer Society Conference on, pages 7–12. IEEE.

Chaaraoui, A. A., Padilla-L

opez, J. R., Climent-P

erez, P.,

and Fl

orez-Revuelta, F. (2014). Evolutionary joint

selection to improve human action recognition with

rgb-d devices. Expert systems with applications,

41(3):786–794.

Chen, C., Jafari, R., and Kehtarnavaz, N. (2015a). Action

recognition from depth sequences using depth motion

maps-based local binary patterns. In Applications of

Computer Vision (WACV), 2015 IEEE Winter Confer-

ence on, pages 1092–1099. IEEE.

Chen, C., Jafari, R., and Kehtarnavaz, N. (2015b). Utd-

mhad: A multimodal dataset for human action recog-

nition utilizing a depth camera and a wearable inertial

sensor. In Image Processing (ICIP), 2015 IEEE Inter-

national Conference on, pages 168–172. IEEE.

Chen, C., Liu, K., and Kehtarnavaz, N. (2016). Real-

time human action recognition based on depth mo-

tion maps. Journal of real-time image processing,

12(1):155–163.

Chen, K. and Forbus, K. D. (2017). Action recognition from

skeleton data via analogical generalization. In Proc.

30th International Workshop on Qualitative Reason-

ing.

Chen, X., Weng, J., Lu, W., Xu, J., and Weng, J. (2018).

Deep manifold learning combined with convolutional

neural networks for action recognition. IEEE trans-

actions on neural networks and learning systems,

29(9):3938–3952.

Cherian, A. and Sra, S. (2017). Riemannian dictionary

learning and sparse coding for positive deﬁnite matri-

ces. IEEE transactions on neural networks and learn-

ing systems, 28(12):2859–2871.

Devanne, M., Wannous, H., Berretti, S., Pala, P., Daoudi,

M., and Del Bimbo, A. (2015). 3-d human action

recognition by shape analysis of motion trajectories

on riemannian manifold. IEEE transactions on cyber-

netics, 45(7):1340–1352.

Du, Y., Wang, W., and Wang, L. (2015). Hierarchical recur-

rent neural network for skeleton based action recog-

nition. In Proceedings of the IEEE conference on

computer vision and pattern recognition, pages 1110–

1118.

Efros, A. and Torralba, A. (2016). Guest editorial: Big data.

International Journal of Computer Vision, 119(1):1–

Elaoud, A., Barhoumi, W., Drira, H., and Zagrouba, E.

(2017). Analysis of skeletal shape trajectories for

person re-identiﬁcation. In International Conference

on Advanced Concepts for Intelligent Vision Systems,

pages 138–149. Springer.

Elmadany, N. E. D., He, Y., and Guan, L. (2018). In-

formation fusion for human action recognition via

biset/multiset globality locality preserving canonical

correlation analysis. IEEE Transactions on Image

Processing, 27(11):5275–5287.

Fanfarelli, J. R., McDaniel, R., and Crossley, C. (2018).

Adapting ux to the design of healthcare games and ap-

plications. Entertainment Computing, 28:21–31.

Weighted Linear Combination of Distances within Two Manifolds for 3D Human Action Recognition

701

Ghojogh, B., Mohammadzade, H., and Mokari, M. (2018).

Fisherposes for human action recognition using kinect

sensor data. IEEE Sensors Journal, 18(4):1612–1627.

Gupta, A., Martinez, J., Little, J. J., and Woodham, R. J.

(2014). 3d pose from motion for cross-view action

recognition via non-linear circulant temporal encod-

ing. In Proceedings of the IEEE conference on com-

puter vision and pattern recognition, pages 2601–

2608.

Han, J., Shao, L., Xu, D., and Shotton, J. (2013). Enhanced

computer vision with microsoft kinect sensor: A re-

view. volume 43, pages 1318–1334. IEEE.

Han, S. and Lee, S. (2013). A vision-based motion capture

and recognition framework for behavior-based safety

management. Automation in Construction, 35:131–

141.

Han, Y., Zhang, P., Zhuo, T., Huang, W., and Zhang,

Y. (2018). Going deeper with two-stream convnets

for action recognition in video surveillance. Pattern

Recognition Letters, 107:83–90.

Harandi, M. T., Sanderson, C., Shirazi, S., and Lovell,

B. C. (2011). Graph embedding discriminant analy-

sis on grassmannian manifolds for improved image set

matching. In Computer Vision and Pattern Recogni-

tion (CVPR), 2011 IEEE Conference on, pages 2705–

2712. IEEE.

Hou, Y., Li, Z., Wang, P., and Li, W. (2018). Skeleton op-

tical spectra-based action recognition using convolu-

tional neural networks. IEEE Transactions on Circuits

and Systems for Video Technology, 28(3):807–811.

Hu, H., Ma, B., Shen, J., and Shao, L. (2018). Man-

ifold regularized correlation object tracking. IEEE

transactions on neural networks and learning systems,

29(5):1786–1795.

Huang, Z., Wan, C., Probst, T., and Van Gool, L. (2017).

Deep learning on lie groups for skeleton-based action

recognition. In Proceedings of the 2017 IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 6099–6108. IEEE computer Society.

Kendall, D. G. (1984). Shape manifolds, procrustean met-

rics, and complex projective spaces. Bulletin of the

London Mathematical Society, 16(2):81–121.

Li, B., He, M., Cheng, X., Chen, Y., and Dai, Y. (2017).

Skeleton based action recognition using translation-

scale invariant image mapping and multi-scale deep

cnn. arXiv preprint arXiv:1704.05645.

Li, B., He, M., Dai, Y., Cheng, X., and Chen, Y. (2018).

3d skeleton based action recognition by video-domain

translation-scale invariant mapping and multi-scale

dilated cnn. Multimedia Tools and Applications, pages

1–21.

Lun, R. and Zhao, W. (2015). A survey of applications and

human motion recognition with microsoft kinect. In-

ternational Journal of Pattern Recognition and Artiﬁ-

cial Intelligence, 29(05):1555008.

Marinoiu, E., Zanﬁr, M., Olaru, V., and Sminchisescu,

C. (2018). 3d human sensing, action and emotion

recognition in robot assisted therapy of children with

autism. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition, pages

2158–2167.

Meng, M., Drira, H., and Boonaert, J. (2018). Distances

evolution analysis for online and off-line human ob-

ject interaction recognition. Image and Vision Com-

puting, 70:32–45.

Meng, M., Drira, H., Daoudi, M., and Boonaert, J. (2015).

Human-object interaction recognition by learning the

distances between the object and the skeleton joints.

In Automatic Face and Gesture Recognition (FG),

2015 11th IEEE International Conference and Work-

shops on, volume 7, pages 1–6. IEEE.

Mitchel, T., Ruan, S., Gao, Y., and Chirikjian, G. S. (2018).

The globally optimal reparameterization algorithm:

an alternative to fast dynamic time warping for action

recognition in video sequences. The Computing Re-

search Repository (CoRR), pages 1807–05485.

Mora, S. V. and Knottenbelt, W. J. (2017). Deep learning

for domain-speciﬁc action recognition in tennis. In

Computer Vision and Pattern Recognition Workshops

(CVPRW), 2017 IEEE Conference on, pages 170–178.

IEEE.

Natarajan, P. and Nevatia, R. (2008). View and scale in-

variant action recognition using multiview shape-ﬂow

models. In Computer Vision and Pattern Recognition,

2008. CVPR 2008. IEEE Conference on, pages 1–8.

IEEE.

Oﬂi, F., Chaudhry, R., Kurillo, G., Vidal, R., and Bajcsy, R.

(2013). Berkeley mhad: A comprehensive multimodal

human action database. In Applications of Computer

Vision (WACV), 2013 IEEE Workshop on, pages 53–

60. IEEE.

Ohn-Bar, E. and Trivedi, M. (2013). Joint angles similari-

ties and hog2 for action recognition. In Proceedings of

the IEEE conference on computer vision and pattern

recognition workshops, pages 465–470.

Oreifej, O. and Liu, Z. (2013). Hon4d: Histogram of ori-

ented 4d normals for activity recognition from depth

sequences. In Proceedings of the IEEE conference on

computer vision and pattern recognition, pages 716–

723.

Poppe, R. (2010). A survey on vision-based human action

recognition. Image and vision computing, 28(6):976–

990.

Qiao, R., Liu, L., Shen, C., and van den Hengel, A. (2017).

Learning discriminative trajectorylet detector sets for

accurate skeleton-based action recognition. Pattern

Recognition, 66:202–212.

Rahimi, S., Aghagolzadeh, A., and Ezoji, M. (2018). Hu-

man action recognition based on the grassmann multi-

graph embedding. Signal, Image and Video Process-

ing, pages 1–9.

Rahmani, H. and Bennamoun, M. (2017). Learning action

recognition model from depth and skeleton videos. In

The IEEE International Conference on Computer Vi-

sion (ICCV).

Ramanathan, M., Yau, W.-Y., and Teoh, E. K. (2014). Hu-

man action recognition with video data: research and

evaluation challenges. IEEE Transactions on human-

machine systems, 44(5):650–663.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

702

Sakoe, H. and Chiba, S. (1978). Dynamic programming

algorithm optimization for spoken word recognition.

IEEE transactions on acoustics, speech, and signal

processing, 26(1):43–49.

Seidenari, L., Varano, V., Berretti, S., Bimbo, A., and Pala,

P. (2013). Recognizing actions from depth cameras as

weakly aligned multi-part bag-of-poses. In Proceed-

ings of the IEEE Conference on Computer Vision and

Pattern Recognition Workshops, pages 479–485.

Shahroudy, A., Ng, T.-T., Yang, Q., and Wang, G. (2016).

Multimodal multipart learning for action recognition

in depth videos. IEEE transactions on pattern analy-

sis and machine intelligence, 38(10):2123–2129.

Shahroudy, A., Wang, G., and Ng, T.-T. (2014). Multi-

modal feature fusion for action recognition in rgb-d

sequences. In Communications, Control and Signal

Processing (ISCCSP), 2014 6th International Sympo-

sium on, pages 1–4. Citeseer.

Slama, R., Wannous, H., Daoudi, M., and Srivastava, A.

(2015). Accurate 3d action recognition using learn-

ing on the grassmann manifold. Pattern Recognition,

48(2):556–567.

Sung, J., Ponce, C., Selman, B., and Saxena, A. (2012).

Unstructured human activity detection from rgbd im-

ages. In Robotics and Automation (ICRA), 2012 IEEE

International Conference on, pages 842–849. IEEE.

Tanfous, A. B., Drira, H., and Amor, B. B. (2018). Coding

kendall’s shape trajectories for 3d action recognition.

In IEEE Computer Vision and Pattern Recognition.

Thanh, T. T., Chen, F., Kotani, K., and Le, H.-B. (2012).

Extraction of discriminative patterns from skeleton se-

quences for human action recognition. In Computing

and Communication Technologies, Research, Innova-

tion, and Vision for the Future (RIVF), 2012 IEEE

RIVF International Conference on, pages 1–6. IEEE.

Uddin, M. Z., Thang, N. D., Kim, J. T., and Kim, T.-S.

(2011). Human activity recognition using body joint-

angle features and hidden markov model. volume 33,

pages 569–579. Wiley Online Library.

Vemulapalli, R., Arrate, F., and Chellappa, R. (2014). Hu-

man action recognition by representing 3d skeletons

as points in a lie group. In Proceedings of the IEEE

conference on computer vision and pattern recogni-

tion, pages 588–595.

Vemulapalli, R. and Chellapa, R. (2016). Rolling rotations

for recognizing human actions from 3d skeletal data.

In Proceedings of the IEEE Conference on Computer

Vision and Pattern Recognition, pages 4471–4479.

Vieira, A. W., Nascimento, E. R., Oliveira, G. L., Liu, Z.,

and Campos, M. F. (2012). Stop: Space-time occu-

pancy patterns for 3d action recognition from depth

map sequences. In Iberoamerican congress on pattern

recognition, pages 252–259. Springer.

Wang, P., Li, W., Ogunbona, P., Wan, J., and Escalera, S.

(2018). Rgb-d-based human motion recognition with

deep learning: A survey. Computer Vision and Image

Understanding.

Wang, P., Li, Z., Hou, Y., and Li, W. (2016). Action

recognition based on joint trajectory maps using con-

volutional neural networks. In Proceedings of the

2016 ACM on Multimedia Conference, pages 102–

106. ACM.

Wang, P., Wang, S., Gao, Z., Hou, Y., and Li, W. (2017).

Structured images for rgb-d action recognition. In

Proceedings of the IEEE Conference on Computer Vi-

sion and Pattern Recognition, pages 1005–1014.

Weinland, D., Ronfard, R., and Boyer, E. (2011). A sur-

vey of vision-based methods for action representation,

segmentation and recognition. Computer vision and

image understanding, 115(2):224–241.

Xia, L., Chen, C.-C., and Aggarwal, J. K. (2012). View

invariant human action recognition using histograms

of 3d joints. In Computer vision and pattern recogni-

tion workshops (CVPRW), 2012 IEEE computer soci-

ety conference on, pages 20–27. IEEE.

Yang, X. and Tian, Y. (2014). Super normal vector for activ-

ity recognition using depth sequences. In Proceedings

of the IEEE conference on computer vision and pat-

tern recognition, pages 804–811.

Ye, M., Zhang, Q., Wang, L., Zhu, J., Yang, R., and Gall,

J. (2013). A survey on human motion analysis from

depth data. In Time-of-ﬂight and depth imaging. sen-

sors, algorithms, and applications, pages 149–187.

Springer.

Zanﬁr, M., Leordeanu, M., and Sminchisescu, C. (2013).

The moving pose: An efﬁcient 3d kinematics descrip-

tor for low-latency action recognition and detection.

In Proceedings of the IEEE international conference

on computer vision, pages 2752–2759.

Zhu, Y., Chen, W., and Guo, G. (2013). Fusing spatiotem-

poral features and joints for 3d action recognition. In

Proceedings of the IEEE Conference on Computer Vi-

sion and Pattern Recognition Workshops, pages 486–

491.

Weighted Linear Combination of Distances within Two Manifolds for 3D Human Action Recognition

703