Indexing k-mers in Linear-space for Quality Value Compression

Yoshihiro Shibuya

1,2

and Matteo Comin

Department of Information Engineering, University of Padua, via Gradenigo 6B, Padua, Italy

Laboratoire d’Informatique Gaspard-Monge (LIGM), University Paris-Est Marne-la-Vall´ee,

Bˆatiment Copernic - 5, bd Descartes, Champs sur Marne, France

Keywords:

k-mers, Indexing, Quality Score, Read Compression.

Abstract:

Many bioinformatics tools heavily rely on k-mer dictionaries to describe the composition of sequences and

allow for faster reference-free algorithms or look-ups. Unfortunately, naive k-mer dictionaries are very mem-

ory inefﬁcient, requiring very large amount of storage space to save each k-mer. This problem is generally

worsened by the necessity of an index for fast queries. In this work we discuss how to build an indexed linear

reference containing a set of input k-mers, and its application to the compression of quality score in FASTQ

ﬁles. Most of the entropy of sequencing data lies in the quality scores, and thus they are difﬁcult to compress.

Here, we present an application to improve the compressibility of quality values while preserving the infor-

mation for SNPs calling. We show how a dictionary of signiﬁcant k-mers, obtained from SNPs databases and

multiple genomes, can be indexed in linear space and used to improve the compression of quality value.

Availability: the software is freely available at https://github.com/yhhshb/yalff.

1 INTRODUCTION

The compression of DNA is usually as simple as as-

signing a two bit encoding to each of the four bases.

This encoding achieve almost similar results to stan-

dard lossless compressors (Malysa et al., 2015). On

the other hand, the quality values, produced by se-

quencing technologies, span a wider range of values,

and when compressed they can sum up to about 70%

of the total space to encode a FASTQ ﬁle (Greenﬁeld

et al., 2016). Quality valuesare usually encoded using

the Phred system (Ewing et al., 1998). Quality val-

ues are often essential for assessing sequence quality,

mapping reads to a reference genome, detecting muta-

tions for genotyping, assembling genomic sequences,

reads clustering (Comin et al., 2014; Comin et al.,

2015) and comparison (Schimd and Comin, 2016).

Quality scores are more difﬁcult to compress due

to a larger alphabet (63-94 in original form) and in-

trinsically have a higher entropy (Yu et al., 2015).

With lossless compression algorithms and entropy en-

coders reaching their theoretical limits and delivering

only moderate compression ratios (Bonﬁeld and Ma-

honey, 2013), there is a growing interest to develop

lossy compression schemes to improve compressibil-

ity further.

To further reduce the ﬁle sizes, Illumina proposed

a binning method to reduce the number of differ-

ent quality values from 42 to 8 (Illumina8bin, 2011).

With this proposal, Illumina opened the doors for al-

lowing lossy compression of the quality values. An-

other approach called P-Block (C´anovas et al., 2014)

involves local quantization so that a representative

quality score replaces a contiguous set of quality

scores that are within a ﬁxed distance of the represen-

tative score. Similarly, the R-Block (C´anovas et al.,

2014) scheme replaces contiguous quality scores that

are within a ﬁxed relative distance of a representa-

tive score. Other lossy approaches improve com-

pressibility and preserve higher ﬁdelity by minimiz-

ing a distortion metric such as mean-squared-error

or L1-based errors (Qualcomp and QVZ) ((Malysa

et al., 2015) (Ochoa et al., 2013)). The drawback

of lossy compression of quality values is that down-

stream analysis could be affected by the loss in-

curred with this type of compression. This could

be the case for the above methods that process only

the string of quality scores, without considering the

DNA sequence associated to the read. However, (Yu

et al., 2015), (Ochoa et al., 2017) and (Greenﬁeld

et al., 2016) showed that quality values compressed

with more advanced methods could achieve not only

a better performance in downstream analyses than

Illumina-binnedquality values, but even better perfor-

mance than the original quality values in some cases

because these methods remove noise from the data.

Shibuya, Y. and Comin, M.

Indexing k-mers in Linear-space for Quality Value Compression.

DOI: 10.5220/0007369100210029

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 21-29

ISBN: 978-989-758-353-7

The most promising methods are those using both

sequence and quality information. Leon (Benoit et al.,

2015) constructs a reference from the input reads in

the form of a bloom ﬁlter compressed de-Bruijn graph

and then maps each nucleotide sequence as a path in

the graph. If a base is covered by a sufﬁciently large

number of k-mers from the reference its quality is

set at a ﬁxed high value. Among the most interest-

ing tools, Quartz (Yu et al., 2015), similarly to Leon,

relies on an external reference to decide if a given

nucleotide is wrong or not. This reference database

is implemented as list of 2497777428 k-mers stored

explicitly, that requires 24GB when gzipped. Simi-

larly, GeneCodeq (Greenﬁeld et al., 2016) also has

a list of k-mers as ground truth, but the algorithm

involved during quality compression, i.e. smooth-

ing, is more complex than Quartz. Each base has

its associated error probability recalculated using a

Bayesian framework and the smoothing takes place

only if the new quality is greater than the old one.

Both Quartz (Yu et al., 2015) and GeneCodeq (Green-

ﬁeld et al., 2016) require a machine with at least

32GB of RAM, because of the size of the reference

database. In (Shibuya and Comin, 2018) we have pro-

posed a method for quality value compression based

on a single reference genome. However, the authors

of (Yu et al., 2015) demonstrated that the use of sig-

niﬁcant k-mers coming from multiple genomes or

SNPs databases, are beneﬁcial for quality score com-

pression and SNPs calling. Hence, in this paper we

explore the use of multiple sources of mutations, i.e.

SNP databases, for quality value compression.

The most common procedure to obtain a reference

list of k-mers from a set of sequences is by a k-mer

counting procedure. Most of the existing implemen-

tations rely on some hashing scheme. The hashing

usually involves a simple application of a hash func-

tion to each k-mer to obtain a numeric value which

is then used to access a hash table where the actual

counters are kept. There exist efﬁcient implementa-

tions of hashing functions which focus on optimizing

and accelerating the generation of the hash value by

using the previous computed hash like in (Mohamadi

et al., 2016) or (Girotto et al., 2018b; Girotto et al.,

2018a). On the other hand, a very fast implementation

of a hash table can be found in Jellyﬁsh (Marc¸ais and

Kingsford, 2011) which uses a lock-free table allow-

ing access from multiple threads if they do not collide

in the same bucket for writing operations. Another ap-

proach is found in (Rizk et al., 2013) and involves the

use of minimizers, a type of Locality Sensitive Hash-

ing to efﬁciently group similar k-mers into buckets.

The next step usually involves some sort of sort-

ing and indexing for allowing fast retrieval of some

particular k-mer (or its neighbors) and link this infor-

mation to the position in the original sequence. This

step is necessary whenever the counting procedure is

the ﬁrst step of a more complex pipeline. It is not so

uncommon for some applications to index a sequence

using the positions of each of its k-mers (Greenﬁeld

et al., 2016; Shajii et al., 2016). While this approach

is advantageous when a proper counting of the k-mers

is required it is not necessary in general when the ﬁnal

goal is to support set queries and/or retrieval of a spe-

ciﬁc sequence or its position inside the original string.

For this purpose, it is generally possible to strip a dic-

tionary of k-mers of the counters to obtain a smaller

representation. Unfortunately, even in the hypothe-

sis of removing all the under-represented k-mers and

all counters, the space required by a full table is still

high. For example, LAVA (Shajii et al., 2016) uses

a databases of k-mers extracted from dbSNP (Sherry

et al., 2001), because of the large size of this database

it requires 60GB of ram. In fact, for a DNA sequence

of length n the potential number of k-mers is n−k+ 1

each of length k for a total amount of space in the or-

der of O(k(n− k + 1)) = O(kn) bytes.

If the k-mer table has to be transmitted a naive

solution would be to compress it using a standard

compressor such as

gzip

. This procedure only

works for moving the database from one place to an-

other because to fully restore its functionality it must

be decompressed anyway. Another question is how

efﬁcient the standard compressors (or an two bit en-

coding) are in reducing the size of the table. What

is the best way to compress a set of k-mers? Is

it possible to use them for an optimal compression

scheme removing redundancy and exploiting the pe-

culiar structure of each k-mer and its relation with the

others?

To answer this question in this work we analyze a

particular application of k-mer dictionaries, that is the

compression of quality scores. In this work we inves-

tigate how to construct a linear string, or set of strings,

that contains all input k-mers. In particular we will

consider a special set of k-mers extracted from pop-

ular SNPs databases like dbSNP (Sherry et al., 2001)

or Affymetrix Genome-Wide Human SNP Array 6.0.

In the following sections we present an application of

a reassembly procedure to reduce a dictionary of k-

mers into a set of sequences guaranteed to contain all

the k-mers. This procedure will allow us to store the

whole dictionary in linear form reducing the mem-

ory requirements from O(kn) to O(n) without losing

information. For querying the resulting dictionary we

will index it with the FM-Index, and use the FM-index

for quality value compression.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

2 METHODS

The main insights in order to reduce the size of the

dictionary is that most of the information carried by a

k-mer stored explicitly is redundant. This intuition is

easily explained by recalling the k-mer counting pro-

cedure itself. All the k-mers counted comes from a

set sequences and the counting procedure is only nec-

essary to remove the wrong ones. There is no need

to keep the k-mers explicitly stored to answer simple

yes/no queries over their set. Given two consecutive

k-mers it is possible to reassemble them into a single

(k+1)-mer thus reducing the storage requirement by

k-1 bases.

2.1 Dictionary Reassembly

There exists two methods to build a dictionary string

comprising all the k-mers needed for quality smooth-

ing. The ﬁrst is a k-mer counting procedure followed

by an assembly (Figure 1 top left). If the counting is

performed on a set of real datasets of reads then a ﬁl-

tering of the k-mers whose counter is below a certain

threshold might be required to prevent false positives

to be used as ground truth, as in (Yu et al., 2015). The

ﬁlter is effective only if the datasets used have a very

high coverage, leading to increased memory and time

requirements for this step.

The reassembly step can be carried out on almost

all dictionaries regardless of the tools used to gener-

ate them, leading to a linear sequence, or set of se-

quences, that contains all the input k-mers. This re-

quirement is what makes this step different from a

common de-novo assembly where the k-mers that do

not align well with the graph are discarded leading

to k-mers not present in the ﬁnal reconstructed se-

quence. In general, this procedure will output more

than one sequence because of the uniqueness of each

k-mer in the resulting strings. Some redundantk-mers

could allow for the concatenation of multiple contigs

into one. The strings obtained are generally stored

into a simple FASTA ﬁle where the identiﬁers can

lead to unwanted memory usage especially if there

are a very large number of short contigs. The mem-

ory requirements can worsening during the indexing

of the FASTA ﬁle by adding information to account

for the boundaries of each sequence. Simply con-

catenating each conting to each other produce k-1

spurious k-mers for each junction which might be a

source of potential false-positives during the applica-

tion of quality value compression. The software used

to perform this step is the greedy ProphAsm assem-

bler (ProphAsm) used in the Prophyle metagenomic

suite (Bˇrinda, 2016; Bˇrinda et al., 2017). In contrast

to the similar software BCalm (Chikhi et al., 2016) it

doesn’t stop at each discordant new k-mer producing

less and longer contigs.

If the previous method does not lead to a signiﬁ-

cant reduction of space compared to an already avail-

able reference genome (Figure 1 bottom left) then

the latter one can be the right choice. The previ-

ous method of construction will probably lead to a

set of strings very similar to the reference genome of

the organism even when applied in an optimal setting

(when the k-mers can be aligned into few contigs).

It is true that a counting procedure involving many

sequences will include many variants in the ﬁnal dic-

tionary string but nonetheless it is very convenient to

use a reference genome directly.

Both method can be extended for accounting for

known lists of SNPs. The ﬁrst one can include ad-

ditional k-mers during the counting procedure and

reassembly the whole dictionary back into a string.

These additional k-mers can be extracted from a list

of known SNPs, like in LAVA (Shajii et al., 2016),

where for each SNP we can we take the k-mers that

overlap with the SNP with the reference allele re-

placed by the alternate. If the starting point is an al-

ready assembled set of dictionary strings it is possible

to simply add the relevant k-mers at the end of one

contig by concatenation or by maintaining the list of

known SNPs as is and load it together with the refer-

ence string. This work uses the ﬁrst method because

as described in the Results section the realigned dic-

tionary contains signiﬁcant k-mers coming from mul-

tiple human genomes, extracted from dbSNP (Sherry

et al., 2001) and Affymetrix Genome-Wide Human

SNP Array 6.0.

The problem of indexing a set of reference se-

quences in minute space, while providing full search

capability, has been widely studied and efﬁcient data

structure are now available. The data structure cho-

sen for this purpose is the FM-Index (Ferragina and

Manzini, 2000; Ferragina and Manzini, 2005) which

is based on the Burrows-Wheeler transform (BWT)

(Burrows and Wheeler, 1994) of a sequence. The

FM-index, and its variants, are now at the basis of

many algorithms in the ﬁeld of sequence analysis. For

example, one of the most used tool for reads map-

ping, BWA (Li and Durbin, 2010), is based on the

FM-index and it requires as input the FM-index of the

reference genome. For its simplicity, its relative easy

installation and its widespread usage, we decided to

use the BWA for indexing and querying our list of

sequences. The FM-index will be used to search for

k-mers. The procedure to retrieve the position of a

k-mer is the enhanced backward search algorithm de-

scribed in (Li and Durbin, 2009), that is also able to

Indexing k-mers in Linear-space for Quality Value Compression

Figure 1: Examples of dictionary string construction. The ﬁrst method employs a k-mer counting procedure, the second one

uses an already available reference genome and other reference sequences. Additional information, e.g. regarding SNPs data,

can be included in the dictionary string by concatenation. In the last step the dictionary string is indexed using an FM-Index.

Figure 2: An example of quality smoothing by YALFF including both mismatches with the k-mers DB and low quality values.

account for mismatches. In our case we will search if

a k-mer is present in the reference genome with up to

one mismatch.

In our work for compressing quality scores

(Shibuya and Comin, 2018) the use of BWA also had

the collateral advantage of not requiring a separate

indexed FASTA for compression instead sharing the

same indexed reference genome for reads alignments.

In this work the indexed sequences are not equivalent

to a reference genome, but instead they represent a

set of k-mers that uniquely identiﬁes known variants

from dbSNP and Affymetrix SNPs databases.

2.2 Quality Value Compression based

on k-mers

We evaluate the quality of the k-mers dictionary for

the compression of quality values. This work extends

our previous work on YALFF (Shibuya and Comin,

2018) where we presented a novel algorithm for com-

pressing quality strings without losing precision dur-

ing SNPs calling. The main differences are in the ref-

erence sequence used for compression. In (Shibuya

and Comin, 2018) we compress a FASTQ ﬁle using

always a single reference genome (i.g. HG38), while

in this study we build a sequence dictionary based

on a set of signiﬁcant k-mers that appear in multiple

genomes coming from the 1000 Genome Project, the

dbSNP, and the Affymetrix SNPs databases. To keep

the paper self-contained here we brieﬂy describe the

YALFF algorithm.

The method YALFF employs a dictionary of k-

mers to assess if a base of a read is correct. A reads is

decomposed into its constituent k-mers and they are

searched in the reference dictionary. Given a base of

the read, if all k-mers that cover the base are found

in the dictionary then we assume that the base is cor-

rect and thus we can modify (smooth) the correspond-

ing quality score to a ﬁxed high value, see Figure

2 for an example. In the ﬁrst version of YALFF,

the database against which the k-mers are checked

is the well known human reference genome

hg38

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

the form of a BWA index. A summary of the algo-

rithm is illustrated in Figure 3. The threshold should

be chosen depending on if it is necessary to avoid as

much distortion as possible or if compression is con-

sidered much more important. As a rule of thumb

a higher threshold maintains more quality values un-

changed but this leads to an increase in the entropy of

the output ﬁle. A good value found for this study was

a quality value equal to the character ’ (apex) which

corresponds to a probability of error of 0.25119.

Quartz (Yu et al., 2015) is another FASTQ com-

pressor which explicitly stores all the k-mers in a

hash table. Quartz requires 25GB of RAM whereas

YALFF only need 5.7GB. The k-mer counting pro-

cedure used to build the default database of Quartz

was performed on multiple NGS reads coming from

different individuals of the 1000 Genome Project and

therefore contains more signiﬁcant k-mers compared

to the simple reference genome. Similarly in LAVA

(Shajii et al., 2016), the authors use two popular

SNPs databases like dbSNP (Sherry et al., 2001) and

Affymetrix Genome-Wide Human SNP Array to se-

lect a set of k-mers that uniquely identify these muta-

tions. Here, we will use these set of k-mers instead of

a single reference genome.

All subsequent results use k equal to 32, the length

used by other studies (Yu et al., 2015; Greenﬁeld

et al., 2016; Shibuya and Comin, 2018). 32 has been

chosen because the k-mers should be long enough

to ensure that the number of all possible k-mers is

much larger than the number of unique k-mers in the

genome, so as to ensure incidental collisions between

unrelated k-mers are rare. Also, k-mer length should

ideally be a multiple of four, since a 4bp length DNA

sequence can be represented by a single byte and dis-

criminating between forward and reverse strand is not

important in this application (it is only required a

yes/no response to a query). A 32-mer satisﬁes these

constraints (Yu et al., 2015; Greenﬁeld et al., 2016);

it is represented by a single 64-bit integer, with a rel-

atively low probability of containing more than one

sequencing error with Illumina sequences, as well as

resulting in few k-mer collisions.

2.3 Datasets, Pipeline and Parameters

The dataset used in this study is a set of real reads

(NA12878) from the 1000 Genomes Project (Con-

sortium, 2012). Only the two paired end archives

were used (namely SRR622461

1.ﬁlt.fastq.gz and

SRR622561

2.ﬁlt.fast.gz) for the evaluation, while

the third containing unpaired reads were discarded.

For validation, we used an up-to-date high-quality

genotype annotation generated by the Genome in a

Bottle Consortium (Zook et al., 2014). The GIAB

gold standard contains validated genotype informa-

tion for NA12878, from 14 sequencing datasets with

ﬁve sequencing technologies, seven read mappers and

three different variant callers. To measure accuracy,

we use loci in the SNP list which are also genotyped

in the GIAB gold standard (so called high conﬁdent

regions) (SNPs, 2018). This dataset has been widely

used for benchmarking in other papers (Yu et al.,

2015; Shajii et al., 2016),

One of the dictionary string used as a reference

is the human genome reference FASTA ﬁle

hg38.fa

downloaded from (HG38, 2018). The other k-mers

databases are generated from dbSNPs (Sherry et al.,

2001) and Affymetrix Genome-Wide Human SNP

Array 6.0. Although YALFF can be run on a normal

laptop the ProphAsm assembler requires a powerful

computer to load all the k-mers it needs to reassem-

bly. For this reason all tests were performed on a

14 lame blade cluster DELL PowerEdge M600 where

each lame is equipped with two Intel Xeon E5450 at

3.00 GHz, 16GB RAM and two 72GB hard disk in

RAID-1 (mirroring).

The basic idea is to compare the compression re-

sults for the given dataset using both the original

reference genome and the re-assembled dictionary

of k-mers of dbSNPs and Affymetrix Genome-Wide

Human SNP Array with YALFF’s algorithm. The

performance evaluation of the smoothing procedure

alone compares the number of retrieved SNPs from

a smoothed FASTQ to the ground truth associated to

the original dataset, with each set of variants (stored

in the output VCF ﬁle) compared against the consen-

sus set of variants. Each evaluation comprises three

metrics: Precision, Recall and F-Measure. Once these

parameters have been computed for using both dictio-

naries they can be compared each other to assess how

the additional variants inside the k-mers database can

inﬂuence a smoothing algorithm and the linear repre-

sentation of the k-mers set. The genotyping pipeline

is implemented as a single bash script which uses

bwa

mem

for alignments,

bcftools

for SNP calling and

rtgplot

for evaluation.

The exact commands are reported for each pro-

gram used outside the evaluation pipeline:

• ./print quartz dict dec200.bin.sorted | prophasm -

k 32 -i - -o <Output FASTA>

• cat <Input ﬁle> | ./YALFF -d hg38.fa -g \’ -t 1 >

Where

print quartz dict

is a simple utility

written in C that prints each k-mer of Quartz’s binary

dictionary to the standard output.

Indexing k-mers in Linear-space for Quality Value Compression

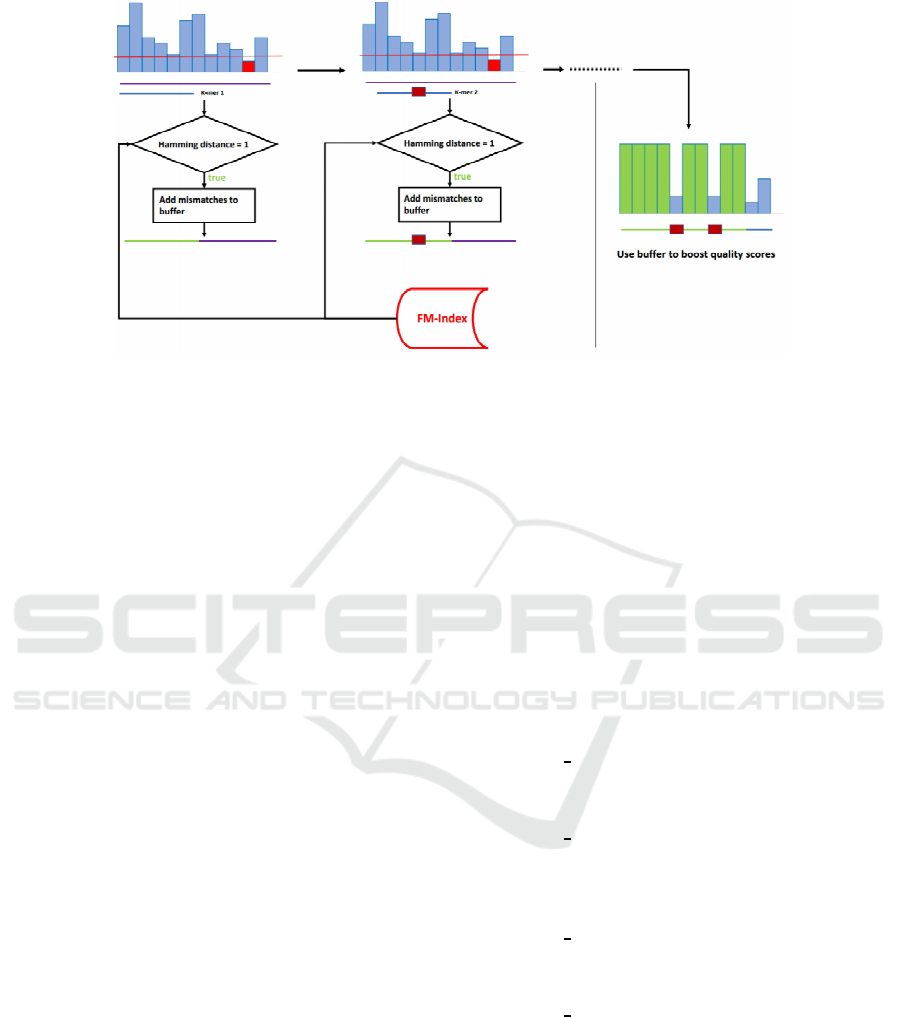
Figure 3: Diagram of YALFF’s inner workings.

3 RESULTS

In this section the effects of the different k-mers

databases are compared in terms of genotyping accu-

racy and compression of the database itself and the

input FASTQ ﬁles. In order to give some context

to the measurements related to the unprocessed input

and Quartz are also reported from the YALFF paper.

3.1 Effects on Genotyping Accuracy

The performance evaluation of the algorithms com-

pares the number of retrieved SNPs from a smoothed

ﬁle to the ground truth. The latter comes with the

original dataset and contains a set of variants val-

idated using the genetic information of the parents

whose child is the individual providing the source of

the dataset. Each set of variants is stored in a VCF ﬁle

analyzable with the software described before.

The benchmarking tools output the following val-

ues:

• True Positives (T.P.): All those variants that are

both in the consensus set and in the set of called

variants.

• False Positives (F.P.): All those variants that are in

the called set of variants but not in the consensus

set.

• False Negatives (F.N.): All those variants that are

in the consensus set but not in the set of called

variants.

These values are used to compute the following

three metrics:

• Recall: This is the proportion of called variants

that are included in the consensus set; that is, R =

T.P./(T.P. + F.N.),

• Precision: This is the proportion of consensus

variants that are called by the variant calling

pipeline; that is, P = T.P./(T.P. + F.P.).

• F-Measure: The harmonic mean of precision and

recall; that is, F − Measure = 2∗ (P∗ R)/(P+ R)

The following abbreviations are used in each ta-

ble:

• None: The original FASTQ ﬁles without any fur-

ther modiﬁcation.

• Quartz: The result of smoothing the original input

dataset with Quartz and its standard k-mers dic-

tionary.

• YALFF

hg38: The result of smoothing the origi-

nal input dataset with YALFF and the hg38 refer-

ence genome as a database of k-mers.

• YALFF Affy: YALFF when using the re-

assembled database of signiﬁcant k-mers from

Affymetrix Genome-Wide Human SNP Array

6.0.

• YALFF dbSNPs: YALFF when using the re-

assembled database of signiﬁcant k-mers from db-

SNPs.

• YALFF All: YALFF when using the reassem-

bled database of k-mers from hg38, dbSNPs

and Affymetrix Genome-Wide Human SNP Ar-

ray 6.0.

In Table 1 are reported the results on the genotyp-

ing accuracy for the various tools.

Table 1 illustrates that Quartz is the most aggres-

sive in terms of raw numbers. Compared to the origi-

nal dataset it tends to add a very large number of True

Positives and False Positives while greatly decreas-

ing the False Negatives. This overall behavior would

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

Table 1: Comparison of the number of True Positives, False

Positives and False Negatives found by the SNP calling

pipeline after smoothing the input reads with the various

methods.

Method T.P. F.P. F.N.

None 2588159 219803 1493731

Quartz 2661218 237820 1420672

YALFF hg38 2603620 221368 1478264

YALFF Affy 2610302 222017 1471583

YALFF dbSNP 2645734 222820 1436155

YALFF All 2652457 224616 1429433

be more than adequate if well calibrated, but unfortu-

nately it tends to degrade the Precision. On the other

hand, the algorithm of YALFF

hg38 is more conser-

vative with a better precision and a lower number of

false positives, preferring to maintain as much as ﬁ-

delity to the original as possible (see, Table 2).

We can observe that although YALFF

hg38

has a smaller F-Measure compared to Quartz, the

use of more informative k-mers dictionaries, e.g.

YALFF

dbSNP and YALFF All, increases the F-

measure to comparable values. In particular, these

two k-mers dictionaries appear to be only one that can

improve the precision with respect to the unprocessed

input. In summary, we can preserve an higher preci-

sion and a smaller number of false positives on SNP

calling. This is very important in many medical ap-

plications where false positives should be avoided.

Table 2: Equivalent representation of Table 1 in terms of

Precision, Recall and F-Measure.

Method Precision Recall F-Measure

None 0.9217 0.6341 0.7513

Quartz 0.9180 0.6520 0.7624

YALFF hg38 0.9216 0.6378 0.7539

YALFF Affy 0.9216 0.6395 0.7551

YALFF dbSNP 0.9223 0.6482 0.7613

YALFF All 0.9219 0.6498 0.7623

The reassembled dictionary of signiﬁcant k-mers

allows YALFF to inherit some characteristics of its

rival. This can be easily noticed by looking at the

increased recall. The larger is the k-mers database,

the betters is the recall, reching its maximum with

YALFF

All. Unfortunately, the precision does not

follow a similar behavior, where YALFF

dbSNP is

the best performing. The difference between the two

smoothing algorithms account for the remaining dif-

ferences, with Quartz being much more permissive

in the deﬁnition of a modiﬁable quality value with

YALFF being more conservative.

3.2 Effects on Compression

Another criteria of evaluation is the ability of the dif-

ferent tools to improve the compressibility of quality

values. The effect on compression can be seen in last

column of Table 3.

Table 3: The compression ratios are deﬁned as

uncompressed size

compressed size

obtained by compressing the resulting

smoothed FASTQ using

gzip

, where the uncompressed

size is 42GB. The size of the k-mer dictionary is also re-

ported.

Method Index [GB] Compression ratio

None 0 4.617

Quartz 19 6.925

YALFF hg38 5.26 7.147

YALFF Affy 5.11 7.133

YALFF dbSNP 6.27 7.241

YALFF All 6.7 7.402

First, we can observe that the processed FASTQ

ﬁle is more compressible than the original ﬁle. This

is expected as all methods tend to reduce the entropy

of quality values. The compression ratio of YALFF

is generally higher that Quartz, even if using just the

hg38 genome as reference. Moreover, if more ad-

vanced k-mer dictionaries are used, then the compres-

sion ratio increases even further.

The most evident advantage of using a com-

pressed index is the huge reduction of the dictio-

nary size meaning less RAM used during execution.

Quartz needs a powerful computer to run with large

amount of memory, at least 32GB of RAM, whereas

YALFF requires about 6-7GB of RAM, depending on

the k-mers dictionary. It must be noted that it is pos-

sible to reassemble all the unique k-mers in the hg38

reference into a more compact form. This solution

is not shown here because it is exactly equivalent in

terms of performances to the standard hg38 dictio-

nary which is more straightforward to compute, not

involving the reassembly step. The only advantage

is a reduced dimension of the k-mer dictionary from

5.26 GB to 5.09 GB.

The second advantage is the ability to store a large

number of additional variations in linear space. For

example, the total number of SNPs reported in the

popular dbSNPs and AffymetrixSNPs are about 13M.

We have shown that the hg38 and all these 13M mu-

tations can be indexed with as little as 6.7GB.

3.3 Running Time

While the reassembly of multiple k-mers into a sin-

gle linear reference allows for reduced memory con-

Indexing k-mers in Linear-space for Quality Value Compression

sumption and the possibility to use widespread index-

ing algorithms such as the FM-Index it also comes

with reduced query speeds. The poor locality of suc-

cinct data structures, to which the FM-Index belongs,

introduces a less efﬁcient use of the cache. This may

impact the execution time of YALFF making it about

1.3x times slower than Quartz. This problem can

be mitigated using some optimization tricks such as

using multiple cores or extending a match on a k-

mer to search the neighbors on the linear sequence

effectively reducing the number of accesses to the

database.

4 CONCLUSIONS AND FUTURE

WORK

This work has demonstrated the feasibility of com-

bining a reassembly procedure with a string indexing

algorithm to produce a very compact dictionary of k-

mers which works as drop-in replacements whenever

static k-mer hash tables are needed. Given a SNPs

database, like dbSNPs or Affymetrix SNPs, it is pos-

sible to ﬁnd a set of k-mers that are uniquely associ-

ated to a SNP. This set of k-mers can be efﬁciently

compressed into a string dictionary and used for qual-

ity value compression. These k-mers dictionaries are

more informative than a single reference genome and

they show better performance in terms of compres-

sion ratio and accuracy of genotyping, while keeping

low memory requirements.

Future directions of research are the construction

of a dynamic FM-Index with the ability to add and

remove k-mers without recomputing the whole struc-

ture, another interesting problem is how to speed-up

the search queries reducing cache misses. In the ﬁeld

of metagenomic read classiﬁcation most methods are

based on k-mers indexes (Girotto et al., 2017; Mar-

chiori and Comin, 2017; Qian et al., 2018), and only

recently the FM-index has been applied (Bˇrinda et al.,

2017), similarly the discovery of SNPs without map-

ping based on FM-index has been proposed only re-

cently (Prezza et al., 2018). We believe that the use of

FM-index will be beneﬁcial in other alignment-free

applications like pan-genomics.

REFERENCES

Benoit, G., Lemaitre, C., Lavenier, D., Drezen, E., Dayris,

T., Uricaru, R., and Rizk, G. (2015). Reference-free

compression of high throughput sequencing data with

a probabilistic de Bruijn graph. BMC Bioinformatics,

16:288.

Bˇrinda, K. (2016). Novel computational techniques for

mapping and classifying Next-Generation Sequencing

data. PhD thesis, Universit´e Paris-Est.

Bˇrinda, K., Salikhov, K., Pignotti, S., and Kucherov, G.

(2017). Prophyle: a phylogeny-based metagenomic

classiﬁer using the burrows-wheeler transform. Poster

at HiTSeq 2017.

Bonﬁeld, J. K. and Mahoney, M. V. (2013). Compression

of fastq and sam format sequencing data. Plos one.

Burrows, M. and Wheeler, D. J. (1994). A block-sorting

lossless data compression algorithm. Technical report,

Digital Equipment Corporation.

Chikhi, R., Limasset, A., and Medvedev, P. (2016). Com-

pacting de bruijn graphs from sequencing data quickly

and in low memory. Bioinformatics, 32(12):i201–

i208.

C´anovas, R., Moffat, A., and Turpin, A. (2014). Lossy com-

pression of quality scores in genomic data. Bioinfor-

matics, 30(15):2130–2136.

Comin, M., Leoni, A., and Schimd, M. (2014). Qcluster:

Extending alignment-free measures with quality val-

ues for reads clustering. In Brown, D. and Morgen-

stern, B., editors, Algorithms in Bioinformatics, pages

1–13, Berlin, Heidelberg. Springer Berlin Heidelberg.

Comin, M., Leoni, A., and Schimd, M. (2015). Clustering

of reads with alignment-free measures and quality val-

ues. Algorithms for Molecular Biology, 10(1):1–10.

Consortium, T. . G. P. (2012). An integrated map of ge-

netic variation from 1,092 human genomes. Nature,

491(7422):56–65.

Ewing, B., Hillier, L., Wendl, M. C., and Green, P. (1998).

Base-Calling of Automated Sequencer Traces Using-

Phred. I. Accuracy Assessment. Genome Research,

8(3):175–185.

Ferragina, P. and Manzini, G. (2000). Opportunistic Data

Structures with Applications. In Proceedings of the

41st Annual Symposium on Foundations of Computer

Science, FOCS ’00, pages 390–, Washington, DC,

USA. IEEE Computer Society.

Ferragina, P. and Manzini, G. (2005). Indexing Compressed

Text. J. ACM, 52(4):552–581.

Girotto, S., Comin, M., and Pizzi, C. (2017). Higher re-

call in metagenomic sequence classiﬁcation exploiting

overlapping reads. BMC Genomics, 18(10):917.

Girotto, S., Comin, M., and Pizzi, C. (2018a). Efﬁcient

computation of spaced seed hashing with block index-

ing. BMC Bioinformatics, 19(15):441.

Girotto, S., Comin, M., and Pizzi, C. (2018b). Fsh: fast

spaced seed hashing exploiting adjacent hashes. Al-

gorithms for Molecular Biology, 13(1):8.

Greenﬁeld, D. L., Stegle, O., and Rrustemi, A. (2016).

GeneCodeq: quality score compression and improved

genotyping using a Bayesian framework. Bioinfor-

matics (Oxford, England), 32(20):3124–3132.

HG38 (2018). Human reference genome (hg38). http://

hgdownload.cse.ucsc.edu/goldenpath/hg38/bigZips/.

Illumina8bin (2011). Quality scores for next-generation se-

quencing, illumina inc. Technical report, Illumina Inc.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

Li, H. and Durbin, R. (2009). Fast and accurate short read

alignment with Burrows-Wheeler transform. Bioin-

formatics (Oxford, England), 25(14):1754–1760.

Li, H. and Durbin, R. (2010). Fast and accurate long-read

alignment with Burrows-Wheeler transform. Bioin-

formatics (Oxford, England), 26(5):589–595.

Malysa, G., Hernaez, M., Ochoa, I., Rao, M., Ganesan, K.,

and Weissman, T. (2015). QVZ: lossy compression

of quality values. Bioinformatics (Oxford, England),

31(19):3122–3129.

Marc¸ais, G. and Kingsford, C. (2011). A fast, lock-free

approach for efﬁcient parallel counting of occurrences

of k-mers. Bioinformatics, 27(6):764–770.

Marchiori, D. and Comin, M. (2017). Skraken: Fast and

sensitive classiﬁcation of short metagenomic reads

based on ﬁltering uninformative k-mers. In Pro-

ceedings of the 10th International Joint Conference

on Biomedical Engineering Systems and Technologies

- Volume 3: BIOINFORMATICS, (BIOSTEC 2017),

pages 59–67. INSTICC, SciTePress.

Mohamadi, H., Chu, J., Vandervalk, B. P., and Birol, I.

(2016). nthash: recursive nucleotide hashing. Bioin-

formatics, 32(22):3492–3494.

Ochoa, I., Asnani, H., Bharadia, D., Chowdhury, M., Weiss-

man, T., and Yona, G. (2013). QualComp: a new lossy

compressor for quality scores based on rate distortion

theory. BMC bioinformatics, 14:187.

Ochoa, I., Hernaez, M., Goldfeder, R., Weissman, T., and

Ashley, E. (2017). Effect of lossy compression of

quality scores on variant calling. Brieﬁngs in Bioin-

formatics, 18(2):183–194.

Prezza, N., Pisanti, N., Sciortino, M., and Rosone, G.

(2018). Detecting Mutations by eBWT. In Parida,

L. and Ukkonen, E., editors, 18th International Work-

shop on Algorithms in Bioinformatics (WABI 2018),

volume 113 of Leibniz International Proceedings in

Informatics (LIPIcs), pages 3:1–3:15, Dagstuhl, Ger-

many. Schloss Dagstuhl–Leibniz-Zentrum fuer Infor-

matik.

ProphAsm. Compressing k-mer sets via assembling con-

tigs. https://github.com/prophyle/prophasm.

Qian, J., Marchiori, D., and Comin, M. (2018). Fast and

sensitive classiﬁcation of short metagenomic reads

with skraken. Communications in Computer and In-

formation Science, 881:212–226.

Rizk, G., Lavenier, D., and Chikhi, R. (2013). Dsk: k-mer

counting with very low memory usage. Bioinformat-

ics, 29(5):652–653.

Schimd, M. and Comin, M. (2016). Fast comparison of

genomic and meta-genomic reads with alignment-free

measures based on quality values. BMC Medical Ge-

nomics, 9(1):41–50.

Shajii, A., Yorukoglu, D., William Yu, Y., and Berger,

B. (2016). Fast genotyping of known snps

through approximate k-mer matching. Bioinformat-

ics, 32(17):i538–i544.

Sherry, S. T., Ward, M.-H., Kholodov, M., Baker, J., Phan,

L., Smigielski, E. M., and Sirotkin, K. (2001). dbsnp:

the ncbi database of genetic variation. Nucleic Acids

Research, 29(1):308–311.

Shibuya, Y. and Comin, M. (2018). Better quality score

compression through sequence-based quality smooth-

ing. 15th Annual Meeting of the Bioinformatics Italian

Society. Submitted to BMC Bioinformatics.

SNPs (2018). List of known variants of the sample na12878.

ftp://ussd-ftp.illumina.com/2017-1.0/hg38.

Yu, Y. W., Yorukoglu, D., Peng, J., and Berger, B. (2015).

Quality score compression improves genotyping ac-

curacy. Nature Biotechnology, 33(3):240–243.

Zook, J. M., Chapman, B., Wang, J., Mittelman, D., Hof-

mann, O., Hide, W. A., and Salit, M. L. (2014). Inte-

grating human sequence data sets provides a resource

of benchmark snp and indel genotype calls. Nature

Biotechnology, 32:246–251.

Indexing k-mers in Linear-space for Quality Value Compression