
Latest Advances in Solving the All-Pairs Suffix Prefix Problem
Maan Haj Rachid
a
Department of Oncology-Pathology, Science for Life Laboratory, Karolinska Institutet, Stockholm, Sweden
Keywords:
All-Pairs Suffix-Prefix, Overlaps, Genome Assembly.
Abstract:
Finding the overlaps between sequences that are generated by Next Generation Sequencing (NGS) technology
is a time- and space-consuming step in building a string graph in genome assembly. The problem is known
in computer science as all-pairs suffix prefix (APSP). The problem has been tackled since 1992 and several
solutions were presented to solve it. While some of them achieve optimal theoretical time consumption, they
have a very high space-consumption in addition to being practically slow due to a raised constant factor. Some
other recent solutions practically consume much less space and time to solve APSP despite their adaptations
to techniques and data structures which don’t have optimal worst-case asymptotic complexity.
Other few researches tackled the approximate version of the overlap problem hoping to avoid error-detecting
stages in genome assembly. These solutions used the same data structures which were employed to solve
APSP in addition to some advanced techniques in order to address the complexity of approximate matching.
In this work, we evaluate these recent algorithms, in terms of time and space, in both exact and approximate
formats. Our results show that FastAPSP has the best time-consumption unless the size of the data set is large.
The high space demand of such large data sets would favor the usage of SOF and Readjoiner. Our experiments
also show that AOF is, in general, faster than FM unless the data set is small and repetitive. In addition, it can
handle large data sets that cannot be processed by FM.
1 INTRODUCTION
The emergence of the Next Generation Sequencing
(NGS) technology created a new computational chal-
lenge. In the context of de novo genome assembly, the
overwhelming number of reads (sequences) which are
produced by NGS requires further processing in order
to create the string graph. A string graph is a graph
in which nodes represent reads while edges represent
overlaps between reads. When a string graph is cre-
ated, a path which passes through every node exactly
once is sought. Such path is called a Hamilton path.
An assembler which builds a string graph is called
an overlap-based genome assembler. An alternative
choice is to build a de Bruijn graph which requires
solving an easier problem, namely the Euler path. An
Euler path is a path which passes through every edge
in the graph exactly once. The nodes in a de Bruijn
graph are k-mers obtained from the sequences where
k is less than the length of one sequence.
Finding overlaps between sequences is the ini-
tial time- and space-consuming step that is required
to build the string graph. Finding overlaps is well-
a
https://orcid.org/0000-0002-6380-209X
known in literature as all-pairs suffix-prefix (APSP).
For a group of sequences G = S
1
,S
2
,...S
k
, finding a
solution for APSP is to find the longest suffix-prefix
matching for every ordered pair in G.
Gusfield et al. (Gusfield et al., 1992) presented an
optimal solution for APSP using a generalized suffix
tree (GST). A suffix tree of a text T is a data structure
in which each suffix in T is represented by a path from
the root to a leaf. The high space-consumption of suf-
fix tree motivated Ohlebusch and Gog (Ohlebusch and
Gog, 2010) to present a practically better solution in
terms of time and space using a generalized enhanced
suffix array (GESA). An ESA is a suffix array and an
LCP (longest common prefix) array. A Suffix array of
a text T with a size of n is an array of size n containing
the text positions of lexicographically sorted suffixes
of T . An LCP array is an array of size n containing
the lengths of the longest common prefixes of every
two consecutive lexicographically sorted suffixes of
T . The word ”Generalized” is used to indicate that
the data structure is created from one string that is
built by concatenating all reads (sequences) together
and separating every two reads with a distinct separa-
tor.
174
Rachid, M.
Latest Advances in Solving the All-Pairs Suffix Prefix Problem.
DOI: 10.5220/0007369801740181
In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 174-181
ISBN: 978-989-758-353-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

The usage of compressed versions of these data
structures in some works such as (Simpson and
Durbin, 2012), (Haj Rachid et al., 2014b) and
(Haj Rachid et al., 2014a) offered low space-
consumption solutions for APSP, however, it had
a dramatic slowdown effects. Despite the optimal
time complexity of GST and ESA, it has been real-
ized that these solutions have high constants when
solving APSP. Accordingly, practical solutions such
as Readjoiner (Gonnella and Kurtz, 2012) and SOF
(Haj Rachid and Malluhi, 2015) are practically faster
solutions and consume much less space than GST and
GESA.
Tustumi et al (Tustumi et al., 2016) revisited OG
solution using ESA and improved the time (2.6 times
faster) and the space (15% less) consumptions. The
work of (Louza et al., 2016) presented a technique to
parallelize ESA’s new technique. The presented par-
allelization achieved superior speed–up over the se-
quential version, however, Readjoiner and SOF have
better time and space consumptions.
Lim and Park (Lim and Park, 2017) recently pre-
sented a solution which uses the same data structure
that is utilized in SOF in addition to other few auxil-
iary data structures. The presented solution uses ad-
vanced algorithmic techniques for the matching step
in order to achieve fast running time. The time con-
sumption is dramatically improved over SOF with an
expected higher space-consumption than SOF. They
called their algorithm FastAPSP.
While most researches tackled APSP when build-
ing a de novo overlap-based assembler, a few of
them such as (V
¨
alim
¨
aki, Niko and Ladra, Susana and
M
¨
akinen, Veli, 2012) tackled the approximate ver-
sion of the overlap problem. Valimaki et al. used a
compressed suffix array (FM index (Ferragina et al.,
2004b)) with the backward backtracking technique to
find approximate overlaps. The technique is also en-
hanced by suffix filters which were introduced and
improved by (K
¨
arkk
¨
ainen, Juha and Na, Joong Chae,
2007) and (Kucherov, Gregory and Tsur, Dekel, 2014)
respectively.
Such direction can save the time required to de-
tect and to correct errors in the input reads. The
work of (Haj Rachid, Maan, 2017) utilizes pigeonhole
principle in finding approximate overlaps and it con-
sumes less time and space than (V
¨
alim
¨
aki, Niko and
Ladra, Susana and M
¨
akinen, Veli, 2012). However,
only Hamming distance was used in the experiments
which extremely limits the usability of the presented
tool as processing genomic data requires handling in-
sertions/deletions in addition to mismatches.
1.1 Our Contribution
• We extend the algorithm presented in (Haj
Rachid, Maan, 2017) to handle edit distance. We
call the new tool AOF (Approximate Overlap
Finder).
• We compare the time and the space consumptions
for 4 recent algorithms to solve APSP.
• We also analyze the performance and the space-
consumption for two solutions for approximate
APSP.
2 PRELIMINARIES
An input read (sequence) is a string of character over
an ordered alphabet Σ={A,C,G,T}. In this work, k de-
notes the number of input reads, n is the total length of
all strings, m is the minimal length of an overlap and
h is the threshold of mismatches/deletions/insertions.
2.1 Approximate Matching
An approximate matching between two strings can
be expressed by the edit distance. The edit distance
between strings S
1
, S
2
is defined as the minimum
number of insertions, deletions and replacements of
symbols to transform string S
1
into S
2
(Levenshtein,
Vladimir I, 1966). Hamming distance is another way
to describe an approximate match. The Hamming dis-
tance between strings S
1
and S
2
is the number of mis-
matching symbols between strings S
1
and S
2
. A string
S
1
is an approximate match to S
2
, if the edit distance
(or the Hamming distance) between the two strings is
≤ h, where h is the threshold of insertions, deletions
and replacements (or only replacements when Ham-
ming distance is used) to transform S
1
to S
2
.
2.2 Dynamic Programming
Dynamic programming was first presented by Bell-
man (Bellman, Richard, 1954). The basic idea is
to break the problem down into its basic blocks, re-
solve the sub problems, and record the results in a
two-dimensional array A. We initialize A[0, j] = j and
A[i,0]= i. For j>0 and i>0, A[i, j] can be calculated
as follows:
A[i, j] = Min
A[i, j − 1] + 1 ,
A[i − 1, j] + 1
A[i − 1, j − 1] +Comp(S
1
[i],S
2
[ j])
where Comp(S
1
[i],S
2
[ j])=0, if S
1
[i],S
2
[ j] are
Latest Advances in Solving the All-Pairs Suffix Prefix Problem
175
matched, and 1 otherwise. We assume that the gap
penalty is 1.
Needleman and Wunsch (Needleman, Saul B and
Wunsch, Christian D, 1970) used dynamic program-
ming to find an optimal global alignment and to cal-
culate the edit or Hamming distance. An alignment
for two DNA, RNA or protein sequences is a way
of arranging the two sequences to identify regions of
similarity that may be a consequence of functional,
structural, or evolutionary relationships between them
(Gollery, Martin, 2005). In global alignment, we
attempt to align every character in every sequence,
while local alignment only targets regions of similar-
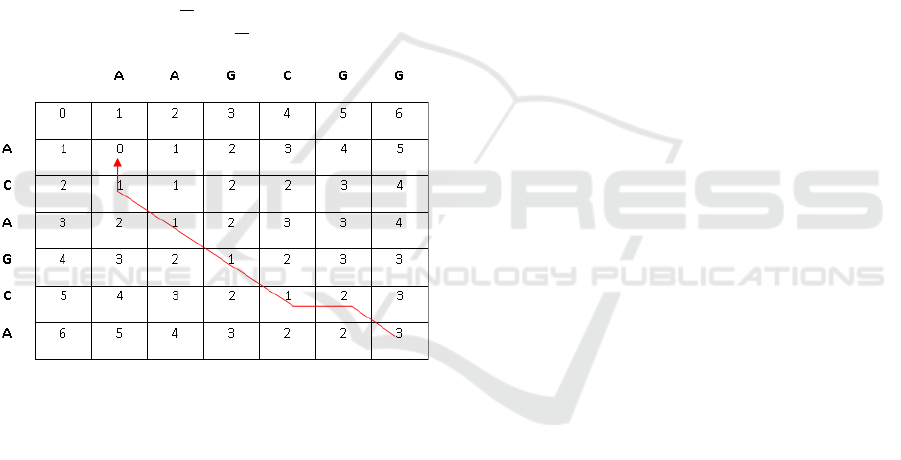
ity. Figure 1 demonstrates the procedure for finding
edit distance and then executing a technique called
backtracing in order to find the global alignment. The
two sequences are aligned as follows:
A AGCGG
ACAGC A
Figure 1: Finding edit distance for two sequences using dy-
namic programming. A backtracing technique is used to
derive the alignment between the two sequences (shown in
red). We assume that gap penalty is 1, mismatch penalty is
1, and matching reward is 0.
2.3 Pigeonhole Principle
The principle is based on the idea that if an
approximate match between two strings with the
same length does exist using at most h inser-
tions/deletions/mismatches, then if we divide each
of the two strings into h+1 parts of the same length
(the last part in both strings may be longer than the
other parts if the length of a string is not divisible
by h + 1), at least one part in one of them will ex-
actly match the corresponding part in the other string.
Many softwares such as Blast (Wu, Thomas D and
Nacu, Serban, 2010) uses such concept to take advan-
tage of extremely fast online and offline exact match-
ing algorithms to find candidates (seeds) for approxi-
mate matching. When a candidate is found, the time-
consuming dynamic programming technique is ap-
plied to validate this matching.
2.4 Approximate All-Pair Suffix-Prefix
(AAPSP)
We define a solution for AAPSP as follows. For a
group of sequences G, the target is to find all suffix-
prefix matchings which have a minimal length of m
and require at most h insertions/deletions/mismatches
(or only mismatches when Hamming distance is used)
for every ordered pair in G.
3 STUDIED TOOLS
Our selection for the studied tools was based on meet-
ing three requirements:
• The tool has been presented recently as a state-of-
the-art, in terms of space or time consumptions, to
find overlaps.
• The tool supports multi-threading.
• The time and space consumptions for finding the
overlaps using the tool can be isolated if the tool
also performs other tasks such as building a string
graph or executing an assembly algorithm.
3.1 Exact Overlap
3.1.1 Readjoiner
Readjoiner (Gonnella and Kurtz, 2012) is a complete
overlap-based assembler which takes sequences as
an input, filters them, then assembles them in three
phases:
• Overlap: finds overlaps and builds the string
graph.
• Layout: finds the locations of the reads with re-
spect to each other.
• Consensus: constructs the sequence.
To find overlaps, Readjoiner first creates buckets
based on reads prefixes. The initial target is to dis-
tribute all suffixes of all reads on their correspond-
ing buckets. In order to reduce the number of candi-
date suffixes in each bucket, Readjoiner creates filters
(P and Q) which are built using the first k
1
and the
last k
2
characters of the k-mer of every prefix in ev-
ery read, where k
1
,k
2
, and k are parameters. In each
bucket, knowing that each bucket contains suffixes
BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms
176

which positively passed the ”P and Q” checks and
cannot match prefixes from other buckets, Readjoiner
then finds overlaps using the algorithm presented in
(Ohlebusch and Gog, 2010). Finding overlaps can be
isolated in Readjoiner from the rest of the pipeline.
3.1.2 String Overlap Finder (SOF)
SOF uses a compact prefix tree to solve APSP
(Haj Rachid and Malluhi, 2015). A compact prefix
tree for a group of strings G is a tree in which ev-
ery string in G is represented by a path from the root
to a leaf. The idea is to test every suffix in every
read by seeking a path for it in the tree. If a path
p from the root down to a node matches a suffix Su,
then Su represents a suffix-prefix match. SOF finds
all suffix-prefix matches for every ordered pair in the
input strings. To find only the longest suffix-prefix
match, it uses an additional two-dimensional array to
store results.
Readjoiner is faster and consumes less space than
SOF when a single thread is used. In addition, SOF
has a degraded performance when the reads are long.
However, SOF has, in general, better time and space
consumptions in multi-threading environments. In
addition, SOF utilizes more threads than Readjoiner
and handles large data sets (Haj Rachid and Malluhi,
2015).
3.1.3 Enhanced Suffix Array
Tustumi et al. (Tustumi et al., 2016) revisited Ohle-
busch and Gog technique to solve APSP using GESA.
An additional array P with a length k (number of
strings) has been added in order to include the posi-
tion of every complete string in GESA. The new tech-
nique is based on scanning GESA in a different way
(from bottom to top) for each segment in GESA us-
ing the new auxiliary data structure which ultimately
excludes many suffixes from processing and accord-
ingly saves time. Experimental results show that the
time and space consumptions have improved over
OG algorithm. The new algorithm also outperforms
Readjoiner but only when m is small (≤ 5). The par-
allelized version of their new algorithm demonstrates
better scalability than SOF on the multi-core system
(Louza et al., 2016).
3.1.4 FastAPSP
FastAPSP employs the same data structure which
SOF utilizes, however, it uses an advanced algorith-
mic technique in the matching step instead of the
brute force processing of every suffix in SOF. The new
technique can be summarized as categorizing suffixes,
based on their lengths, in three different cases and
avoiding processing them (matching a path in the tree)
whenever possible. In order to do that, FastAPSP uses
additional auxiliary data structures.
FastAPSP is remarkably faster than SOF and
Readjoiner when enough space is available (Lim,
2018). In addition, it can find only the largest suf-
fix prefix match without the need of two-dimensional
array of size k
2
. Nevertheless, FastAPSP consumes
more space than SOF which may limit its ability to
handle large data sets.
3.2 Approximate Overlap
3.2.1 FM With Backtracing
An FM-index is a compressed full-text sub string in-
dex based on the Burrows-Wheeler transform (Bur-
rows and Wheeler, 1994). It was created by Paolo Fer-
ragina and Giovanni Manzini(Ferragina et al., 2004a).
The Burrows-Wheeler transform (BWT) rearranges
a character string into runs of similar characters.
This is useful for compressing a string that has runs
of repeated characters by techniques such as move-
to-front transform and run-length encoding (Bentley
et al., 1986). (V
¨
alim
¨
aki, Niko and Ladra, Susana and
M
¨
akinen, Veli, 2012) utilizes FM with the backward
backtracking technique to find approximate overlaps.
3.2.2 AOF: Finding Edit-Distance-Based
Approximate Overlaps using Pigeonhole
Principle
The work of (Haj Rachid, Maan, 2017) explains a
technique to find approximate overlaps between se-
quences using pigeonhole technique. However, Ham-
ming distance was used to define an approximate
overlap. We show how to use the same principle to
find approximate overlaps using edit distance.
Let m be a minimal length for an overlap (i.e., a
suffix-prefix match with a length <m will not be con-
sidered). If suffix S is an approximate suffix-prefix
match with a threshold h, then its prefix of length m
has to have an edit distance ≤h when aligned with a
prefix of length m of some read. Accordingly, if the
prefix of S with size m is divided into h+1 parts of
equal length, then one of these parts exactly matches
a corresponding part of a prefix p of some read r with
the same size m.
Let S be a candidate for an approximate overlap
(i.e., one of its parts of equal length exactly matches
a corresponding part in a prefix of a read). Let j
1
, j
2
be the starting character and the ending character of
the matching part in S respectively. We first globally
align the prefix of S which is ending with the character
Latest Advances in Solving the All-Pairs Suffix Prefix Problem
177

Figure 2: Solving approximate all-pairs suffix-prefix using
pigeonhole principle. Since the black portion in S
i
is the
second part in the suffix, we look for it in index 2. Two
matches are found. Threshold h is 3 in this example, ac-
cordingly, we have 4 indices.
S[ j
1
-1] with its corresponding part in prefix p. If the
edit distance for this alignment is smaller than h, then
we also globally align the suffix of S which is starting
from the character S[ j
2
+1] in S with its corresponding
part in prefix p. Accordingly, the technique can be
summarized as follows:
• Divide the prefix of length m for each read into
h+1 parts of equal length (except the last part
which may be longer if m is not divisible by h+1).
Accordingly, we have k(h+1) parts.
• Add each part p from each read r to an index
which has entries of type hkey, Li where L is a
list of reads. Accordingly, if p is already in the
index, r will be added to an existed entry (in its L
list), otherwise, a new entry hp, {r}i will be added
to the index.
• Every suffix S in every read where |S|≥m will be
tested. This is done by dividing the prefix of S of
size m into h+1 parts of equal length and search-
ing for each part in the index. If a part p has a
hit at position i in the index, we investigate ev-
ery read r
1
in L
i
. Using dynamic programming,
we globally align all characters that precede p in
S with their corresponding characters in r
1
. If the
threshold h is not exceeded, we also globally align
all characters after p in S with their corresponding
characters in r
1
. If the end of S is reached with-
out exceeding the threshold, then S is reported as
an approximate overlap between r (the read which
contains S) and r
1
. Figure 2 explains the tech-
nique.
Time complexity for this technique is O(n
2
). The
performance clearly correlates negatively with the
number of hits. The index may contain (h+1)k en-
tries. All entries may have up to (h+1)k values (in all
L lists). Therefore, the space complexity is bounded
by the size of the text which is O(n log σ) where n is
the total length of all reads and σ is the size of the
alphabet.
4 EXPERIMENTAL RESULTS
4.1 Experimental Setup
4.1.1 Exact Overlap
We compare the time and space consumptions for
the latest four parallelized solutions for APSP: Read-
joiner (RJ), SOF, ESA, and FastAPSP. All tools can
output the overlaps using the format hv,w,ovi where
v and w are reads and ov is the size of the over-
lap. Our six datasets, shown in table 1, are obtained
from PubMed with sizes ranging from 42MB up to
32 GB. We ran our experiments on a machine run-
ning Linux Ubuntu with 2.6 GHZ CPU, 32 GB RAM,
and 8 threads.
4.1.2 Approximate Overlap
The source code for AOF can be downloaded from
https://github.com/maanrachid/AOF. We analyze the
performance of two algorithms to find approximate
overlaps: FM and AOF. Both tools support multi-
threading and provide the user the ability to specify
m, h, and the type of distance (edit/Hamming).
Our experiments were run on an 8-threads ma-
chine with 8 GB RAM and a CPU of 2.6 GHZ.
We used randomly-generated and real data sets.
Randomly-generated data is created using a program
which asks the user for n and k then generates k ran-
dom sequences with a total length of n. Real data
sets were obtained from PubMed and Citrus genome
database. Their details are shown in table 2. We com-
pare the time and space consumptions of AOF and
FM (V
¨
alim
¨
aki, Niko and Ladra, Susana and M
¨
akinen,
Veli, 2012). We run AOF with mismatch penalty of 1,
gap penalty of 1 and a match score of 0. Edit distance
is used in all experiments.
4.2 Discussion
4.2.1 Exact Overlap
Table 3 show that both time and space consumptions
for parallelized ESA are extremely high when com-
pared with the other three solutions. FastAPSP has
BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms
178

Algorithm 1: Solving AAPSP using pigeonhole principle.
1: psize ←m/(h + 1)
2: for Every read r in input reads do
3: for Every candidate suffix S in r do
4: for Every part p of length psize in S’s prefix of size m do
5: if p is found in position i in the index then
6: for Every read r
1
found in L
i
do
7: Globally align all characters before p with their corresponding characters in r
1
8: if threshold is not exceeded then
9: Globally align all characters after p with their corresponding characters in r
1
until the end of S is reached
10: end if
11: if threshold is not exceeded then
12: Report S as a suffix-prefix match between r and r
1
13: Apply back-tracing
14: Report the alignment.
15: end if
16: end for
17: end if
18: end for
19: end for
20: end for
Table 1: Data sets used in testing four solutions for APSP.
Data Set n k m
Streptococcus Mitis (SRR007326) 42M 156,310 40
HIV (SRR5760188) 62.4M 320,739 40
E.coli (SRR2244250) 302.3M 502,172 40
Salmonella (SRR2007640) 1.2G 2,508,609 40
Exome Human Genome (SRR866986) 9.8G 53,603,681 40
Female Human Genome (SRR098909) 32.7G 161,962,055 80
Table 2: n is the total size. k is the number of sequences. m is the minimal length of an overlap.
Data Set n (MB) k m
Random 1 1 10,000 30
Random 2 2.5 20,000 30
Random 3 5 50,000 30
Streptococcus Mitis (SRR007326) 42 156,310 60
Citrus Trifoliata 46 62,344 60
Citrus Sinensis 154 208,909 70
E. Coli (SRR2244250) 302 502,172 80
the best time-consumption in most of the cases (4 out
of 6), however its space consumption is always higher
than SOF and Readjoiner, which may be the reason
for FastAPSP’s termination in the last two large data
sets (9.8 and 32.7 GB). SOF and Readjoiner have
the best space-consumption. SOF consumes less time
than Readjoiner in all cases and processes all data sets
without a termination.
4.2.2 Approximate Overlap
We first investigate the impact of the minimal length
of an overlap m on the performance. Figure 3 shows
that FM has the same performance for all different
values of m, while m clearly affects AOF’s perfor-
mance. While the two applications start with close
results, SOF’s performance improves dramatically
when m increases.
Latest Advances in Solving the All-Pairs Suffix Prefix Problem
179

Table 3: Time and space consumptions for all 4 solutions: Readjoiner, ESA, SOF, FastAPSP.
Data Set Readjoiner SOF ESA FastAPSP ReadJoiner SOF ESA FastApsp
Time Time Time Time Space Space Space Space
SRR007326 2 0,3 76 0,2 21 38 944 71
SRR5760188 T 167 1,320 65 T 68 7,100 212
SRR2244250 77 33 T 13 438 238 T 636
SRR2007640 337 200 900 100 474 726 7,200 5,900
SRR866986 T 1,885 T T T 10,034 T T
SRR098909 T 14,153 T T T 31,219 T T
Table 4: T indicates a termination due to high space consumption. h is the maximum number of errors (mis-
matches/insertions/deletions). m is the minimal length for an overlap.
Data m h=1 h=2 h=3 h=1 h=2 h=3
Set AOF AOF AOF FM FM FM
Random 1 30 0.06 0.1 7 1 36 324
Random 2 30 0.1 0.8 43 10 194 2,520
Random 3 30 0.3 2.7 180 17 228 2,880
Streptococcus Mitis 60 22 56 137 171 1545 T
Citrus Trifoliata 60 282 870 2171 127 1,020 T
Citrus Sinensis 70 55 290 1,029 T T T
E. Coli 80 4,021 34,800 168,000 T T T
Table 5: T indicates a termination due to high space consumption.
Data Set AOF FM
Random 1 9 MB 141 MB
Random 2 15 MB 540 MB
Random 3 23 MB 691 MB
Streptococcus Mitis 93 MB 5.1 GB
Citrus Trifoliata 290 MB 6.8 GB
Citrus Sinensis 850 MB T
E. Coli 750 MB T
Figure 3: Performance of FM and AOF using different min-
imal overlap values (m) on random data with different data
set sizes. Number of mismatches is 3 in all tests. Logarith-
mic scale is used.
This is expected. When the length of the piece
which will be searched for in the index increases,
fewer matches are expected. Since we have less hits,
dynamic programming will be applied less often and
the time consumption improves.
Table 4 demonstrates the performances of AOF
and FM (V
¨
alim
¨
aki, Niko and Ladra, Susana and
M
¨
akinen, Veli, 2012) using different values for h
(the threshold for mismatches/deletions/insertions) on
both random and real data. Since random cases have
a few or almost no matches, AOF runs faster than FM
while FM has better performance with small genomic
and repetitive data due to increasing the number of
hits. Despite the slowdown of AOF with genomic
data, it is clear that it can handle large cases which
cause a terminating error when run with FM.
Table 5 clearly explains the cause of termination.
AOF consumes much less space than FM. Accord-
ingly, FM could not handle several cases due to its
high space consumption. AOF can be an appropriate
solution in a machine with limited resources.
BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms
180

5 CONCLUSION
FastAPSP is the right choice for solving APSP when
data sets are relatively small or space-consumption is
not a big concern. In such cases, Readjoiner could
be an excellent choice for relatively small data sets
in a single-core machine. In other circumstances,
SOF could be a favorable choice. We present AOF
as a space-efficient tool which enables genome as-
sembler’s engineer to handle the overlap problem es-
pecially in machines with limited resources using
both Hamming distance and edit distance. Unlike
FM, AOF’s time consumption improves dramatically
when minimal length of an overlap (m) increases. De-
spite the fact that AOF is slower than FM in handling
some small genomic data sets, AOF can process large
data sets which cannot be handled by FM due to the
high space-consumption.
REFERENCES
Bellman, Richard (1954). The theory of dynamic program-
ming. Technical report, DTIC Document.
Bentley, J. L., Sleator, D. D., Tarjan, R. E., and Wei, V. K.
(1986). A locally adaptive data compression scheme.
Communications of the ACM, 29(4):320–330.
Burrows, M. and Wheeler, D. J. (1994). A block-sorting
lossless data compression algorithm. Technical report,
Digital SRC Research Report.
Ferragina, P., Manzini, G., M
¨
akinen, V., and Navarro, G.
(2004a). An alphabet-friendly fm-index. In Interna-
tional Symposium on String Processing and Informa-
tion Retrieval, pages 150–160. Springer.
Ferragina, P., Manzini, G., Veli, M., and Navarro, G.
(2004b). An alphabet-friendly FM-index. In SPIRE,
pages 150–160.
Gollery, Martin (2005). Bioinformatics: Sequence and
genome analysis, david w. mount. cold spring harbor,
ny: Cold spring harbor laboratory press, 2004, 692
pp., paperback. isbn 0-87969-712-1. Clinical Chem-
istry, 51(11):2219–2219.
Gonnella, G. and Kurtz, S. (2012). Readjoiner: a fast and
memory efficient string graph-based sequence assem-
bler. BMC Bioinformatics, 13:82.
Gusfield, D., Landau, G., and Schieber, B. (1992). An effi-
cient algorithm for the all pairs suffix-prefix problem.
Inf. Process. Lett., 41(4):181–185.
Haj Rachid, M. and Malluhi, Q. (2015). A practical
and scalable tool to find overlaps between sequences.
BioMed research international, 2015.
Haj Rachid, M., Malluhi, Q., and Abouelhoda, M. (2014a).
A space-efficient solution to find the maximum over-
lap using a compressed suffix array. In MECBME.
Haj Rachid, M., Malluhi, Q., and Abouelhoda, M. (2014b).
Using the Sadakane compressed suffix tree to solve
the all-pairs suffix prefix problem. BioMed Research
International.
Haj Rachid, Maan (2017). Two efficient techniques to find
approximate overlaps between sequences. BioMed
Research International, 2017.
K
¨
arkk
¨
ainen, Juha and Na, Joong Chae (2007). Faster filters
for approximate string matching. In ALENEX. SIAM.
Kucherov, Gregory and Tsur, Dekel (2014). Improved fil-
ters for the approximate suffix-prefix overlap problem.
In International Symposium on String Processing and
Information Retrieval, pages 139–148. Springer.
Levenshtein, Vladimir I (1966). Binary codes capable of
correcting deletions, insertions, and reversals. In So-
viet physics doklady, volume 10, pages 707–710.
Lim, J. (2018). A Practical Algorithm for the All-Pairs
Suffix-Prefix Problem. PhD thesis.
Lim, J. and Park, K. (2017). A fast algorithm for the all-
pairs suffix–prefix problem. Theoretical Computer
Science, 698:14–24.
Louza, F. A., Gog, S., Zanotto, L., Araujo, G., and Telles,
G. P. (2016). Parallel computation for the all-pairs
suffix-prefix problem. In International Symposium on
String Processing and Information Retrieval, pages
122–132. Springer.
Needleman, Saul B and Wunsch, Christian D (1970). A
general method applicable to the search for similari-
ties in the amino acid sequence of two proteins. Jour-
nal of molecular biology, 48(3):443–453.
Ohlebusch, E. and Gog, S. (2010). Efficient algorithms
for the all-pairs suffix-prefix problem and the all-
pairs substring-prefix problem. Inf. Process. Lett.,
110(3):123–128.
Simpson, J. and Durbin, R. (2012). Efficient de novo as-
sembly of large genomes using compressed data struc-
tures. Genome research, 22(3):549–556.
Tustumi, W. H., Gog, S., Telles, G. P., and Louza, F. A.
(2016). An improved algorithm for the all-pairs
suffix–prefix problem. Journal of Discrete Algo-
rithms, 37:34–43.
V
¨
alim
¨
aki, Niko and Ladra, Susana and M
¨
akinen, Veli
(2012). Approximate all-pairs suffix/prefix overlaps.
Information and Computation, 213:49–58.
Wu, Thomas D and Nacu, Serban (2010). Fast and snp-
tolerant detection of complex variants and splicing in
short reads. Bioinformatics, 26(7):873–881.
Latest Advances in Solving the All-Pairs Suffix Prefix Problem
181
