
Attribute Grammars for Incremental Scene Graph Rendering
Harald Steinlechner, Georg Haaser, Stefan Maierhofer and Robert F. Tobler
VRVis Research Center, Austria
Keywords:
Scenegraph, Attribute Grammar, Rendering Engine, Domain-Specific-Languages, Incremental Evaluation.
Abstract:
Scene graphs, as found in many visualization systems are a well-established concept for modeling virtual
scenes in computer graphics. State-of-the-art approaches typically issue appropriate draw commands while
traversing the graph. Equipped with a functional programming mindset we take a different approach and uti-
lize attribute grammars as a central concept for modeling the problem domain declaratively. Instead of issuing
draw commands imperatively, we synthesize first class objects describing appropriate draw commands. In or-
der to make this approach practical in the face of dynamic changes to the scene graph, we utilize incremental
evaluation, and thereby avoid repeated evaluation of unchanged parts. Our application prototypically demon-
strates how complex systems benefit from domain-specific languages, declarative problem solving and the
implications thereof. Besides from being concise and expressive, our solution demonstrates a real-world use
case of self-adjusting computation which elegantly extends scene graphs with well-defined reactive semantics
and efficient, incremental execution.
1 INTRODUCTION
In Computer Graphics the standard approach for re-
presenting virtual scenes in memory is the so-called
scene graph. It is a directed acyclic graph with leaf
nodes typically representing geometries in a scene
and internal nodes used to organize geometries into
groups, and associate various attributes. Examples for
such attributes are transformation nodes (called Trafo
for short) to place the geometries at different positions
in the scene or shader nodes to associate material pro-
perties with geometries. An example of a simple table
modeled as a scene graph is given in Fig. Figure 1.
!"#$#%&#$'#()*+)
Trafo
Shader
Trafo
table top
Shader
Group
Trafo Trafo Trafo Trafo
table leg
Figure 1: Table modeled using a scene graph. Shader no-
des are used for specifying different material and lighting
properties for wooden legs and the table top made of glass.
In order to create an image of a scene given its repre-
sentation as a scene graph, appropriate commands to
the underlying graphics hardware need to be issued.
Operationally, each graphics command modifies the
implicit graphics state (or GPU memory) in order to
set the stage for performing the actual draw com-
mand. In the scene graph, each node type represents a
type of state change to the rendering state. Transfor-
mation nodes for example, modify the transformation
matrices of the underlying graphics implementation
machinery (e.g. write data to GPU memory), whereas
shader nodes activate the appropriate shader code in
the graphics implementation that will be used to com-
pute the color when a specific object is determined to
be visible at a given pixel.
By traversing the scene graph from its root to the
geometry nodes at the leaves in a depth first man-
ner, and maintaining a traversal state containing the
current value of all possible attribute types (e.g. the
current transformation value, the current shader va-
lue, etc.), it is fairly simple to submit the appropriate
graphics commands for generating a visual represen-
tation. Most current rendering engines are based on
this traversal scheme.
In this paper we propose to utilize attribute gram-
mars (Knuth, 1968) as the formalism for describing
scene graph semantics. Whereas attribute grammars
in their original form where introduced to compute
static or dynamic semantics of languages, we use
them to compute render objects (describing complete
render state) on the structure of scene graphs. The de-
clarative nature of this representation has a number of
advantages to procedural and object-oriented imple-
mentations that are today’s standard.
W
¨
orister et al. (W
¨
orister et al., 2013) already
Steinlechner, H., Haaser, G., Maierhofer, S. and Tobler, R.
Attribute Grammars for Incremental Scene Graph Rendering.
DOI: 10.5220/0007372800770088
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 77-88
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
77

used incremental attribute grammar evaluation as mo-
tivation for the incremental update mechanism of so-
called render caches, a flat and optimized runtime re-
placement for scene graph parts. In contrast to our
work, which builds on general purpose incremental
evaluation and allows arbitrary dynamism, they use
a hand-written traversal to generate render caches on
specific points in the scene graph and use a depen-
dency index to update caches on value changes, e.g.
transformation changes.
In addition to composability (Swierstra, 2005),
another vital advantage of attribute grammars is their
well-founded declarative dataflow via attributes. At-
tribute grammars are well understood and allow for
a wide range of optimizations such as fusing traver-
sals (Swierstra et al., 1999) and incremental evalua-
tion (Reps et al., 1983). Our main contributions are:
• We show that attribute grammars can be used
to model scene graphs elegantly and concisely
(Section 2.2), while maintaining extensibility in
terms of data and operations
1
. By just adding a
new type and necessary semantic functions (equa-
tions defining only the necessary attributes for the
new node type, see Figure 3) scene graph sys-
tems can be extended easily for specific domains.
Due to its declarative nature, our system allows
for much shorter (in terms of code length) imple-
mentations and is easier to understand, since for
example, attributes do not need to be passed ex-
plicitly.
• Attribute grammar semantics need to be light-
weight and flexible in order to easily integrate
with existing applications, infrastructure and data
processing modules. To that end we introduce an
embedded domain-specific language (EDSL) for
authoring syntax and semantics of attribute gram-
mars (Section 2.2).
• For highly dynamic data, we extend our system
with incremental evaluation of dynamic values.
In contrast to previous work, we use no speciali-
zed algorithm for incremental evaluation of attri-
bute grammars, but base our algorithm on recent
advances in the field of self-adjusting computa-
tion (Acar et al., 2002; Acar, 2005; Hammer et al.,
2014).
Incremental evaluation is exposed via another
EDSL (similarly to LINQ to SQL (Meijer et al.,
2006; Syme, 2006)), which automatically gene-
rates a dependency graph while executing code.
The underlying implementation (Hammer et al.,
1
note that the visitor pattern does not provide this exten-
sibility due to the expression problem (Wadler, 1998; Tor-
gersen, 2004)
2014) takes care of external input modifications
(e.g. mouse moves) and re-executes only code
paths affected by those changes. This is called
change propagation and takes away the burden of
explicitly handling changes and updates.
While hardware-accelerated rendering is roughly
linear in the number of objects, traversal quickly
becomes a bottleneck in non-trivial scene graphs,
resulting in bad utilization of GPU resour-
ces (W
¨
orister et al., 2013). Furthermore, traver-
sal cost is proportional to the number of scene
graph nodes, i.e. intermediate nodes used for fac-
toring sub-graphs degrade performance of rende-
ring even more. Although this is an inherent pro-
blem for scene graphs, due to incremental evalu-
ation we pay for intermediate nodes only once at
construction instead of each frame (Section 4.2).
Finally, incremental evaluation of render objects
goes hand in hand with work recently published
in the field of high-performance rendering (see
Section 2.3), works for arbitrary changes and re-
quires no manual placement of render caches.
In our evaluation, we show that attribute gram-
mars combined with incremental computation in-
deed solve aforementioned problems in an elegant
way and with promising performance characteristics
(Section 4). The incremental approach allows to track
changes and perform low level GPU optimizations
such as command buffer (Khronos Group, 2016) re-
recording only when necessary. Moreover, we think
that this work is a step towards filling the gap bet-
ween low-level optimizations for efficient rendering
and domain specific languages for scene representa-
tion and interaction (see Figure 4).
To summarize, the aim of this paper is to show
the excellent interplay between attribute grammars,
recent advances on incremental computation and ad-
vances in high-performance rendering.
2 OUR APPROACH:
SELF-ADJUSTING AND
SIDE-EFFECT FREE SCENE
GRAPHS
The remainder of this paper is structured as follows:
Section 2.1 shows how to compute a set of render ob-
jects, which later can be updated incrementally.
In Section 2.2 we use attribute grammars to com-
pute a set of render objects declaratively. Section 2.3
shows how to update sets of render objects incremen-
tally. Sections 3.1 and 3.2 introduce EDSLs for autho-
ring attribute grammars and incremental computati-
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
78

ons. Finally, we put everything together (Section 3.3),
evaluate and contrast our approach to related work
(Section 4) and explain tradeoffs.
2.1 Computing Render Objects
!"#$%&'()(*+,&*-."#/01234
!"#$%&'()(*+5%#6*"1111234
!"#$%&'()"*76*"1111111234
!"#$%&'()(*+,&*-."#/01234
)))
8&(+191
11:*76*";<=*'+
>
?1
11:*76*";<=*'+
@
?
1131A
/0"1"01&71"*76*";<=*'+(B
11!"#$%&'()(*+,&*-."#/01"0)."#/0
11!"#$%&'()(*+5%#6*"1"0)5%#6*"
11!"#$%&'()"*76*"1"0)!*0C*+"D
Render all objects:
traverse with
sideeffects
compute
RenderObjects
Figure 2: Traditional scene graph traversal issues graphics
commands while traversing. In functional programming by
contrast, we compute a set of render objects (purely functio-
nal) which can later be interpreted in order to issue graphics
commands to the graphics hardware.
The basic concept of our approach is to com-
pute values representing draw commands instead of
issuing many small graphics commands while traver-
sing a scene graph (see Fig. 2). For each leaf node
we compute a render object which captures all argu-
ments required for issuing an appropriate draw call.
This flattens the scene graph to a list and eliminates
traversal overhead. In the last step, render objects are
mapped to concrete GPU graphics commands, which
can be directly issued to the GPU batch-style, elimi-
nating more overhead.
2.2 The Scene Graph Grammar
Scene graphs typically use shared leaf nodes in or-
der to reuse the same geometry in different contexts,
i.e. with different attributes. A desk, to give a tri-
vial example, might use a shared instance of the table
leg for all table legs, rendered with different spatial
transformations (see Fig. 1). Traditionally, attribute
grammars operate on tree-like structures. Semantics
for shared nodes however, need to be computed on
each path, so attribute grammars naturally carry over
to graphs, when instancing attributes per path.
The main point of our approach is to use attri-
bute grammars for modeling scene graph semantics,
solving the task of computing sets of render objects
purely declaratively. Fig. 3 gives attribute grammar
equations for computing a set of render objects. Note
that, in practice render objects need to capture the
transitive closure of arguments required for rendering
(not only shaders).
Group
Shader
Geometry
Shader
Geometry
shader
0
shader
1
geometry
0
geometry
1
shader
0
shader
1
{ Render
Object
0
}
{ Render
Object
1
}
{ Render
Object
0
}
{ Render
Object
1
}
{ RenderObject
0,
RenderObject
1
}
child0
child1
inh SEM shader:
| Group child0.shader = this.shader;
child1.shader = this.shader;
| Shader child.shader = this.shader
syn SEM RenderObjects:
| Group this.RenderObjects =
child0.RenderObjects ∪
child1.RenderObjects
| Shader this.RenderObjects = child.RenderObjects
| Geometry this.RenderObjects =
{ create RenderObject( this.shader,
this.geometry ) }
Figure 3: Attribution of a simple scene graph (top). Shader
nodes propagate provided shader values (shader
0
,shader
1
)
downwards, thus defining an inherited attribute. Geometry
nodes produce rendering output by constructing a render
object given its local geometry instance as well as the inher-
ited shader attribute. Group nodes compute the union render
object set, which in turn propagates towards the root node.
This upward propagation makes sets of rendering objects
a synthesized attribute. The text definition (bottom) shows
attribute grammar equations in style of UUAGC (Swierstra
et al., 1999) and reads as such: shader is an inherited attri-
bute (flows downwards), e.g. for binary groups, the child‘s
surface attribute is defined as the surface value valid at this
point. RenderObjects is a synthesized attribute (is compu-
ted for sub graph, computed towards root), e.g. for geome-
try nodes, a render object set is computed by querying the
inherited attributes shader and the geometry data contained
in the geometry node itself.
2.3 Self-adjusting Computation for
Reactive Scene Graphs
Attribute grammars allow for purely functional eva-
luation of scene graph semantics. Still, the synthesi-
zed set of render objects is immutable and needs to be
recomputed periodically, if input attributes or scene
graph properties change.
Incremental computation, which has been investi-
gated for a long time (e.g. Ramalingam and Reps (Ra-
malingam and Reps, 1993) provide an extensive sur-
vey), is a solid foundation for updating program out-
puts incrementally, given some changes in its in-
puts. Although various approaches for incremental
evaluation of attribute grammars have been proposed
(e.g. (Reps et al., 1983; Hudson, 1991)), we aim for a
more general approach, which composes cleanly with
incremental algorithms outside the domain of the at-
Attribute Grammars for Incremental Scene Graph Rendering
79

adaptively
compute
render objects
incrementalSet+{+
++++RenderObject
1
,+
++++RenderObject
2
,…+
}
High performance
low-level optimizations
(e.g. GPU render cache)
this paper
Figure 4: Given the input scene graph, we compute the
set of render objects and the underlying dependency graph.
Whenever the input graph is modified, we automatically
map those changes to changes in the incrementally main-
tained set of render objects. Subsequently, the incremental
set can be used to optimize and issue graphics commands
to the graphics hardware (e.g. using command lists (Jeff
et al., 2015) or vulkan command buffers (Khronos Group,
2016) which only need to be re-recorded whenever the set
changes).
tribute grammar semantics.
To our rescue, Acar et al. introduced adaptive
functional programming (Acar et al., 2002), a frame-
work for incremental evaluation of arbitrary (purely)
functional programs. In their library, they support
meta operations, for modifying inputs for adaptive
computations. In a subsequent step, all output values
are made consistent again by selective re-execution
of affected parts, determined by the dynamic depen-
dency graph. Their approach is particularly well sui-
ted for our use case, since minimal modification of se-
mantic functions yields incremental versions thereof
and the change propagation composes with other al-
gorithms implemented in their framework.
In our work, we use an implementation of adap-
tive functional programming by lifting all dynamic
values into modifiable cells and modify all semantic
functions to work adaptively, by utilizing combinators
operating on these cells.
As a result, we synthesize render objects once and
update the resulting set adaptively (see Figure 4). This
not only solves efficiency issues for scene graph tra-
versal as updates can be performed in O(∆) instead of
O(n), where ∆ is the size of the change and n is the to-
tal size of the scene, but also provides huge potential
for optimizing execution of graphics commands. The
incremental set of render objects can be subscribed
for changes and combined with low level optimiza-
tions such as command lists in OpenGL (Jeff et al.,
2015) or command buffers (Khronos Group, 2016),
which only need to be re-recorded when the incre-
mental set was modified, or other whole-scene opti-
mization methods, such as the incremental rendering
VM (Haaser et al., 2015), were applied (see Fig. 4).
To summarize, our method adheres to the follo-
wing concepts:
Separation of Effects. We keep rendering traversals
pure (no side-effects) by synthesizing a set of ren-
der objects including all parameters required for
rendering in a subsequent step.
Declarative Formulation. By utilizing attribute
grammars, our formulation is purely declarative.
Furthermore, by using inherited and synthesized
attributes we have clean semantics for data-flow
within scene graphs.
Incremental Evaluation. Above concepts allow for
a clean and concise implementation of scene
graphs. At first glance, the high-level abstraction
has intrinsic cost when compared to hand-tuned
traversals. However, this high abstraction pro-
vides opportunity for optimization. In fact, by
utilizing adaptive functional programming and
our declarative formulation, we can significantly
speed up rendering by uncoupling rendering per-
formance from scene structure: as we exactly
know which parts of a computation have not chan-
ged, we can safely reuse previously calculated va-
lues.
3 IMPLEMENTATION
Our implementation is part of a visual computing re-
search platform and is used in several research pro-
totypes, as well as for industrial projects. It targets
.NET Core and is written mostly in F# and C#. Note
that, our DSL for incremental evaluation uses F#’s
Computation expressions (Petricek and Syme, 2014),
which considerably improves readability, and mainte-
nance of dependency graphs is completely transparent
to the user.
3.1 An EDSL for Scene Graphs
Usually, attribute grammar systems automatically ge-
nerate executable code out of an attribute grammar
description (e.g. Utrecht University Attribute Gram-
mar Compiler (Swierstra et al., 1999), JastAdd (Ek-
man and Hedin, 2007)).
As an alternative, embedded domain-specific lan-
guages (EDSLs) have been proposed for authoring at-
tribute grammars (Sloane et al., 2010). In contrast
to generators, well-foundedness checks, such as un-
defined attributes, are hard to implement in embed-
ded languages. Viera and Swierstra introduced an
embedding in Haskell, which performs static ana-
lysis (type checking) of attribute grammar definiti-
ons (Viera et al., 2009).
Since we aim for interoperability with existing
code we utilize an embedded domain specific lan-
guage written in F#. Our implementation is entirely
dynamic and supports on-demand extensions of data
types and semantic functions. To accomplish this, we
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
80

scan for classes with specific annotations and regis-
ter their member functions in a global table. On the
API side, we use overloaded operators for accessing
inherited and synthesized attributes. For querying at-
tributes we use dynamically typed overloads of the ?
operator. The signature is given in Figure 5, while the
implementation can be found online
2
. Those opera-
tors are dynamically typed, i.e. the result type can be
any type, but in practice, type inference works notably
well as attribute lookups typically appear in rich type
contexts and using an attribute implicitly declares its
actual type. This is similar to having auto variables
in C++ code.
Our implementation is rather naive. When compu-
ting a synthesized attribute, we successively look for
matching semantic functions and traverse downwards
while maintaining a stack of parent nodes. When
computing the value of an inherited attribute, we se-
arch up through this path until we find the proper se-
mantic function.
For encoding the syntax we use an object-oriented
encoding. In this setting, each production becomes
a separate class. This way we can easily add further
productions later (simply by inheriting the base class).
While for scene graphs we need to compute a set of
render objects, we first present a toy example compu-
ting the sum of a linked list, in order to get familiar
with syntax and semantics of our DSL. For reference,
the grammar for linked lists in EBNF can be written
as follows (here we use the ‘:‘ operator as separator
for list items
3
):
hlisti ::= hnili
| hintegeri : hlisti
Consider the purely functional implementation of a
linked list in C# (which models the list syntax in an
object oriented manner):
public interface List {} // base interface for all lists
// class for linked list nodes (value and next pointer)
public class Cons : List
{
public int Value; public List Rest;
public Cons(int value, List rest){
Value = value; Rest = rest;
}
}
public class Nil : List {} // the the end of the list.
The F# version (to get familiar with the syntax) looks
like this:
type List = interface end // introduce syntactic form.
// in grammar notation, add a production: List :=
Cons(v,xs),→
type Cons(v : float, xs : List) =
2
Our implementation extended with real world con-
cerns such as thread safety, can be found at https://
aardvark-community.github.io/ag-for-scenegraphs
3
the syntactic expression would be: 1 : 2 : nil,
the C# equivalent: new Cons(1,new Cons(2,Nil())),
the F# version: Cons(1,Cons(2, Nil()))
interface List
member x.Rest = xs
member x.Value = v
// in grammar notation, add a production: List := Nil()
type Nil() = interface List
The attribute grammar for computing the sum of a list
can be written using equations operating on the syn-
tactic nodes (in UUAGC syntax, as used in Figure 3):
syn SEM List:
| Nil this.Sum = 0
| Cons this.Sum =
this.Value + this.Rest.Sum
The definition for the synthesized attribute Sum reads
as follows: For empty lists (Nil), the sum is zero. For
Cons cells, we add the list value and the synthesized
attribute computed for the tail of the list. By utilizing
the dynamically typed question-mark operator as de-
fined in Figure 5 the synthesized attribute Sum can be
described as such:
[<Semantic>] // the attribute grammar implementation looks
for semantic attributes,→
type SumSem() =
// each member corresponds to an equation in the
attribute grammar.,→
member x.Sum(cons : Cons) =
cons.Value + cons.Rest?Sum()
member x.Sum(nil : Nil) = 0
Note the similarity of the equations and our domain
specific language implementation. Again, for clarity
the C# version would look like:
[<Semantic>]
public class SumSem {
public int Sum(Cons cons) {
return cons.Value + queryInhAttribute(cons.Rest,'Sum');
}
public int Sum(Nil nil) { return 0; }
}
The translation to C# reveals the implementation
technique we use. Each question-mark operator trig-
gers the resolution of the queried attribute. Note that
there is huge optimization potential, since the under-
lying traversals can be fused together and inherited
attributes can be passed efficiently (Reps et al., 1983;
Hudson, 1991) and inherited attributes can be compu-
ted while traversing downwards (Rosendahl, 1992).
Similarly, inherited attributes which in traversal-
based scene graph systems need to be tediously pas-
sed via traversal state objects can be accessed at any
point in semantic functions. The underlying evalu-
ating scheme automatically builds the necessary tra-
versal functions.
3.2 Computation Expressions for
Adaptive Computations
Although theory and implementation of incremental
evaluation frameworks is outside the scope of this pa-
per, we give a short overview.
Typically, variables in functional programming
languages are immutable and thus cannot be chan-
ged after initialization. Most (functional) languages
Attribute Grammars for Incremental Scene Graph Rendering
81

(
*
Queries some node for the attribute attribName. As convention for function types (unit-> 'a) we query synthesized
attributes, where non-function types can be used for querying inherited attributes (in F# generic arguments are written as
lowercase letters with tick ' prefix), e.g.,→
let a : AttribType = node?AttribName // Compute inherited attribute `AttribName` on some node:
let b : AttribType = node?AttribName() // Compute synthesized attribute `AttribName` on some node:
*
)
val ( ? ) : node:obj -> attribName : string -> 'a
(
*
Assignes an attribute to some syntactic entity, usage: node.Child?Attribute <- someValue
*
)
val ( ?<- ) : node:obj -> attribName : string -> unit
Figure 5: F# operations as entry-points for accessing attributes dynamically. Note, that these special operators are provided
by the F# language and can be overloaded (similar to overloading << in C++). While ? is binary, ?<- is a ternary operator,
which can be used for overloading assignments. The operators also have special treatment in the compiler, since at call-site
the user applies identifiers while at definition side those identifiers are bound to strings.
type ref<'a>() =
member x.SetValue (v : 'a) = // sets internal value to v
member x.GetValue () = // reads current value of reference
(like dereference the value),→
// read only reference type.
type aref<'a> =
// One method to compute content of type 'a.
abstract member GetValue : unit -> 'a
// changeable, dependency aware input reference (e.g. user
input is stored in CRefs),→
type cref<'a>() =
// sets internal value to v and propagate changes in the
dependency graph,→
member x.SetValue (v : 'a) = ..
interface aref<'a> with ...// implementation
type aset<'a> =
abstract member GetSet : unit -> set<'a>
type cset<'a>() =
member x.Add (v : 'a) = // add v to the set
member x.Rem (v : 'a) = // remove v from the set
Figure 6: API for reference cells and mutable sets (top) and
dependency aware, i.e. adaptive versions (bottom).
however provide explicit data types for dealing with
mutable cells (often called ref cells). Similarly to
explicit reference cells, a central concept for incre-
mental computation is to wrap modifiable data into a
special type, called aref<’a> where ’a is the type
contained in the cell
4
. With this mechanism all wri-
tes and reads can be enriched in order to maintain a
dependency graph underneath. Those datatypes we
refer to as adaptive data-structures. Our examples in
this paper use adaptive references (often called modi-
fiable in the literature). We distinguish between two
kinds of adaptive references:
• adaptive references (aref), which represent a de-
pendency tracked cell which is part of the depen-
dency graph and describes either an intermediate
result or the final result of an adaptive computa-
tion.
• changeable references (cref), which represent a
dependency tracked cell but can be modified ex-
ternally (i.e. has a public setter).
Although such adaptive references are sufficient to
track modifications in arbitrary data-structures, it is
4
in F#, generic parameters are written in lowercase let-
ters with tick (’) prefix
module Mod =
let map (f : 'a -> 'b) (a : aref<'a>) : aref<'b> = ...
let bind (f : 'a -> aref<'b>) (a : aref<'a>) : aref<'b> = ..
// creates readonly adaptive cell
let constant (v : 'a) : aref<'a> = ..
// creates changeable input cell
let init (v : 'a) : cref<'a> = ..
module CSet =
let init (l : list<'a>) : cset<'a> = // construct and
initialize with l,→
Figure 7: Operators for adaptive references.
Figure 8: Dependency graph construction for let b = map
f a. The map operator creates an output cell and adds a de-
pendency graph edge into a’s edge list. Whenever a gets
modified we mark all successors to be out-of-date (have in-
consistent value). Each time the user requests the actual
value of an aref, the value needs to be recomputed as effi-
ciently as possible (and the out-of-date flags cleared again).
often more efficient to provide special purpose imple-
mentations of standard data-structures such as, e.g.
lists and sets (Acar et al., 2010). Since sets are in-
dispensable in our use case we use a special purpose
implementation (for transparency, an explicit sort-key
needs to added to render objects) called aset and
cset respectively. Stub implementations for mutable
datatypes (reference and set) and their adaptive coun-
terpart are shown in Figure 6.
The types cref<’a> and cset<’a> can be chan-
ged externally and trigger change propagation in the
system. The types aref<’a> and aset<’a> serve as
read only views on dependency graphs. For adap-
tive references there is one single additional opera-
tion (bind) required to describe arbitrary adaptive
functional programs. Given an input cell of type
aref<’a> and a function of type ’a -> aref<’b>
the bind operator computes an output reference of
type aref<’b>. This operation allows to dynamically
switch between dependencies depending on the cur-
rent value of an adaptive reference. A less expres-
sive version of this operator is map which maps values
of type aref<’a> to aref<’b> by applying the map-
ping function of type ’a -> ’b. The signature for the
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
82

Figure 9: Computation expressions provide a convenient
way to write adaptive functions, even for more complex sce-
narios such as dynamic dependencies, where the value of
another aref switches between dependency graph variants.
most common operators is given in Figure 7 with the
map operator depicted in Figure 8.
Our internal implementation is based on out-of-
date marking, similar to Hudon’s lazy change propa-
gation strategy (Hudson, 1991). For re-evaluation we
use eager out-of-date marking paired with lazy eva-
luation, based on the approach of (Hammer et al.,
2014). For details on the implementation of such a
framework we refer to the literature, e.g. (Acar et al.,
2002; Acar, 2005; Acar et al., 2010; Hammer et al.,
2014).
Inspired by Carlssons’s monadic approach to self-
adjusting computation (Carlsson, 2002), we use mo-
nads in order to make programming with incremental
algorithms easier. To this end, we use F#’s compu-
tation expressions (Petricek and Syme, 2014) which
provide syntactic expansion for monadic computati-
ons similarly to Haskell’s do-notation (Peyton Jones
et al., 2003) or LINQ (Bierman et al., 2007). Most es-
sentially, let! corresponds to monadic bind, which
in our case reads the value of an aref<’a> and com-
putes a new one in its continuation.
Subsequently, we provide signatures in order to
make our examples work and refer to our open source
implementation for details. A computation expression
builder for adaptive computations of our implementa-
tion can be defined as such:
type Builder() =
member x.Bind(m : aref<'a>, f : 'a -> aref<'b>) =
Mod.bind f m
member x.Return (v : 'a) =
Mod.constant v :> aref<_>
member x.ReturnFrom(m : aref<'a>) = m
member x.Zero() = Mod.constant ()
Figure 10 (top) gives an example for aref’s with ex-
panded code (middle), and the dependency graph for
a slightly extended example is shown in Figure 9.
In contrast to the do-notation which operates on
monadic operations, computation expressions allow
to overload practically all F# language constructs ma-
king them a perfect fit for providing first class support
for lists (e.g. for loops). An example demonstrating
adaptive sets (aset) and computation expression buil-
der syntax is given in Figure 10 (bottom).
type Builder() = ... // defines syntactic translation
// instantiate computation expression builder
let adaptive = Builder()
let test () =
// creates an aref cell initialized with 1.
let a = Mod.init 1
let plus1 =
adaptive { // starts an adaptive block
// adaptively reads value a into value a'
let! a' = a
// returns (a'+1) and writes the result to plus1.
return 'a + 1
}
assert 2 = plus1.GetValue() // force evaluates plus1 to 2
a.SetValue(2) // changes a to 2
assert 3 = plus1.GetValue() // force now evaluates plus1 to 3
let a = Mod.init 1
let b = Mod.init 2
let plus =
adaptive {
let! currentA = a // adaptively read a
let! currentB = b // currentA has type int.
return currentA + currentB // ordinary integer addition
}
let plusDesugared = // the same as plus
Mod.bind (fun currentA ->
Mod.bind (fun currentB ->
currentA + currentB
) b
) a
let aset = SetBuilder()
// construct changeable set given a F# list
let changeableSet = CSet.init([1,2,3])
let mapped = aset {
// use overloaded `for` syntax defined in builder
for x in changeableSet do
// aset provides an implementation of yield which
// emits a value into resulting the adaptive set
yield x + 1
}
mapped.GetSet() => {2,3,4}
// as side effect modify the input set
changeableSet.Add 4
// force the output, observe updated output
mapped.GetSet() => {2,3,4,5}
Figure 10: Computation expression builder example for
aref’s (top), a simple example comparing the builder ver-
sion with the expanded variant of the same code (middle)
and an example involving aset’s (bottom).
3.3 Putting Everything Together
Our attribute grammar implementation is based on
an object-oriented encoding for specifying syntax.
Given ISg (Interface for Scene graphs) being the
base type for all scene graph nodes, productions
have the form: ISg := Render | Group (..) |
TrafoApp (..).... In our OOP encoding the root
production (ISg) can be defined as follows:
(
*
emtpy base interface for all scene graph nodes
*
)
type ISg = interface end
The terminal production ISg := RenderNode can be
described as:
(
*
introduces class RenderNode implementing ISg interface
*
),→
type Render() = interface ISg
One common pattern in scene graphs is to use appli-
cators to apply a value to a given sub-graph:
type IApplicator<'a>(value : aref<'a>, child : aref<ISg>) =
member x.Value = value
member x.Child = child
interface ISg
Attribute Grammars for Incremental Scene Graph Rendering
83

[<Semantic>] (
*
runtime attribute which makes members
available as ag rules to used by the system
*
),→
type RenderJobs() =
// create a render object using the local transformation
let createRenderJob (n : Render) (t : Trafo3d) : RenderObject = ....
// defines a member RenderObject for type RenderObject
member sem.RenderObjects(node : Render) =
aset {
// queries inherited attribute Trafo
let! trafo = node?Trafo
// create a draw call and yield it into the set
yield createRenderJob node trafo
}
member sem.RenderObjects( g : Group) : aset<RenderObject> =
aset {
// incrementally loop over sub scene graph set
for x in g.children do
// Compute synth. attribute for the child
let ro = x?RenderObjects()
// yield the computed set of render objects
yield! ro
}
// ddefault rule for all nodes of type IApplicator<'a>
member x.RenderObjects(app : IApplicator<'a>):aset<RenderObject>=
aset {
let! child = app.Child // adaptively read the sub
yield! child?RenderObjects()
}
member x.Trafo( trafo : TrafoApp) : unit =
// applies local trafo to its sub graph
// i.e. `assigns` the inherited attribute
trafo.Child?Trafo <- trafo.Value
Figure 11: Semantic functions for synthesizing render ob-
jects from a scene graph.
Let us now define a node which applies a transforma-
tion (as aref since it should be changeable) to a sub-
graph (i.e. the production ISg := Transform ISg)
and a group node with an arbitrary number of child-
ren:
type TrafoApp(value : aref<Trafo3d>, child : aref<ISg>) =
inherit IApplicator<Trafo3d>(value,child)
type Group = { children : aset<ISg> }
with interface ISg
The semantics for synthesizing render objects is gi-
ven in Figure 11. All semantic functions have type
aset<RenderObject> reflecting the fact that their re-
sult is an adaptive computation yielding a set of ren-
der objects. The rule for Trafo assigns an aref con-
taining the applied transformation to its modifiable
children.
3.4 Extensibility: Adding Operations
As an example for adding operations, we extend the
system with the ability to compute the bounding box
of an ISg. In object-oriented design, this additional
method would require to modify all implementations
(see the expression-problem (Wadler, 1998)). In con-
trast, our approach is extensible regarding operations
and Figure 12 shows an example implementation. For
leaf nodes we simply return the object space bounding
box, lifted into a modifiable by utilizing the adaptive
builder. For group nodes, we internally use an adap-
tive version of the fold function for combining the
bounding boxes adaptively. For applicators we simply
[<Semantic>]
type BoundingBoxSem() =
member x.BoundingBox(r : Render) =
adaptive {
return r.BoundingBox
}
member x.BoundingBox(app : IApplicator<'a>) : aref<BoundingBox> =
adaptive {
let! child = app.Child
return child?BoundingBox()
}
member x.BoundingBox(trafo : TrafoApp) : aref<BoundingBox> =
adaptive {
let! child = trafo.Child
let! childBB = child?BoundingBox()
let! trafo = trafo.Value
return transform trafo childBB
}
member x.BoundingBox(g : Group) : aref<BoundingBox> =
combineBoundingBox g.children
Figure 12: Semantics for bounding box computation. No-
des of type TrafoApp are handled explicitly in order to
transform the computed bounding box, while others are
handled implicitly by the IApplicator function.
compute the bounding box for the child and return the
result, while for transformation nodes, we compute
the bounding box of the child graph and transform it
appropriately.
3.5 Extensibility: Adding Nodes
Let us now extend the system with a new node which
toggles between a high-quality and a simplified repre-
sentation of the scene. Figure 13 shows the new node
and specialized semantics for existing synthesized at-
tributes, like bounding boxes and render objects.
Note that, not all types need to be handled here,
since unrelated nodes, such as TrafoApp are au-
tomatically handled by the semantic function for
IApplicator previously defined.
4 EVALUATION AND
DISCUSSION
The evaluation of our system is twofold. Firstly, does
our approach really provide a valid solution to scene
graph programming and how does it compare to ex-
isting systems? Secondly, since our implementation
focuses on a succinct implementation and a clean se-
paration of data and semantics, we are interested in
actual run-time performance.
4.1 Comparison to Related Work
Our new approach solves the following problems that
are typical in current systems:
Modularity. Most rendering systems using scene
graph traversal are implemented in an object-oriented
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
84

type LevelOfDetail =
{ simple : aref<ISg>; // represent low quality version of the contained sub graph (fast rendering)
// note that, in order to allow dynamic changes for those sub graphs,
// we use aref<ISg> instead of plain ISg.
detailed : aref<ISg>; // represent high quality version of the contained sub graph (slow rendering)
useSimple : BoundingBox -> bool // given the world space bounding box of the child graph, compute whether simple
} with interface ISg // is sufficient (i.e. the object is far enough so that a simple rendering suffices)
[<Semantic>]
type LodSemantic() =
member x.BoundingBox( lod : LevelOfDetail) = adaptive { return! lod.simple?BoundingBox() }
member x.RenderObjects( lod : LevelOfDetail ) : aset<RenderObject> =
aset {
let! low = lod.simple // read the simple version adaptively
let! box3d = low?BoundingBox() // adaptively synthesize bounding box attribute for the child
match lod.useSimple box3d with // apply lod decision function
| true -> yield! low?RenderObjects() // synthesize render jobs for low
| false -> let! high = lod.detailed // adaptively read detailed child graph
yield! high?RenderObjects() // synthesize render jobs for high
}
Figure 13: Extending the scene graph with a new node type for specifying level-of-detail syntactically. Note that, we do not
need to add semantic functions for unrelated nodes such as TrafoApp, since the previously defined semantic function for
IApplicator covers this case.
style, where each node needs to implement all neces-
sary methods for scene graph management and traver-
sal, e.g. OpenSceneGraph (Burns and Osfield, 2004).
Adding scene graph nodes can be easily accomplis-
hed, but adding new operations usually is fairly in-
tricate, e.g. for the visitor pattern all implementati-
ons need to be modified. Our declarative definition
of both scene graph structure and attributes, makes it
simple to add both nodes and operations.
Communication. Via attributes, our approach intrin-
sically supports declarative data-flow between seman-
tically related nodes, without the need for using ad
hoc mechanisms, such as user-defined global state.
Dynamism. Another source of complexity in many
systems is dynamic data, ubiquitous in many visua-
lization tasks. Tobler introduced a separate, seman-
tic scene graph in order to allow dynamic changes in
an associated rendering scene graph, which needs to
be explicitly implemented (Tobler, 2011). Our incre-
mental evaluation EDSL provides an automatic solu-
tion for this idea by implicitly tracking changes to all
inherited and synthesized attributes.
Efficiency. As scene graph traversal quickly becomes
a bottleneck for large scenes (W
¨
orister et al., 2013),
systems either directly optimize scene graphs by ap-
plying persistent transformations for compacting the
graph (Strauss and Carey, 1992), or use caching in or-
der to reduce traversal overhead (Durbin et al., 1995;
W
¨
orister et al., 2013). Instead of fighting symptoms,
our approach effectively decouples runtime cost from
scene graph complexity via incremental evaluation.
This greatly reduces or, in absence of change, even
eliminates traversal overhead.
Interopability. Most visualization systems require
developers to convert all domain-specific data into
framework-specific structures. This is costly in terms
of runtime and memory. Our system allows to di-
rectly leverage existing types and data structures wit-
hout modification by specifying application-specific
semantic functions instead of implementing a pre-
defined set of functions or interfaces. As an exam-
ple, consider the assimp library
5
with its own scene
graph, which has been integrated into our system
by providing semantic functions interacting with the
compiled types in the assimp library.
4.2 Performance
Our proposed incremental system has runtime com-
plexity proportional to change O(∆) as opposed to
O(n) in traversal-based systems. Asymptotically, we
therefore outperform classical non-incremental sys-
tems independent of implementation technique or op-
timizations. In practice, this holds true only for rea-
sonable scenes which change gradually over time.
When discussing tradeoffs of our system, we need
to distinguish the two main sources of overhead. First,
incremental evaluation requires to maintain a depen-
dency graph, and second, attributes need to be resol-
ved at runtime, involving a dictionary lookup.
Clearly, after initialization, the overhead is zero
for static scenes. If no dependencies change, no ree-
valuation takes place and no attributes need to be
computed. With increasing size of change, we expect
change propagation cost to increase, and eventually to
reach a point where the cost of maintaining the depen-
dency graph outweighs its benefit. Thus, the fraction
of change per frame seems to be the parameter best
describing the tradeoffs in our system.
We compare three different implementations to
better understand when this crossover occurs. 1. An
optimized implementation of classical scene graph
5
The open asset import library http://assimp.
sourceforge.net
Attribute Grammars for Incremental Scene Graph Rendering
85
traversal. We use the semantic scene graph as it is clo-
sest with respect to extensibility and expressiveness.
2. Our system. 3. Our system, but with hard-wired at-
tribute grammar evaluation in order to separate over-
head from incremental evaluation and to simulate an
optimal attribute grammar implementation.
For 1 we measure the time to perform the up-
date and traverse the scene without executing rende-
ring specific code. This effectively simulates an un-
derlying zero-overhead graphics API and GPU driver.
For 2 and 3 we update the scene and loop over the
set of render objects. In each case we measure the
average runtime over 30 update/loop cycles. Note,
that at startup, we once perform a dry run to avoid
measuring unrelated JIT initialization costs.
In order to adequately test the limits of our appro-
ach, we created two test setups deliberately introdu-
cing maximum stress in the two main components of
our system.
First we investigate the performance of the incre-
mental system regarding to value changes in an artifi-
cial test scene with 9000 leaf nodes, each with its own
transformation node as well as a group node on top.
The benchmark shows (see Figure 14) that chan-
ging values in the scene graph indeed is roughly pro-
portional to the number of value changes and the in-
volved overheads seem reasonable. Beside from run-
time costs we measured approximately factor 4 in
memory footprint, mostly for storing the dependency
graph.
Figure 14: Runtime in ms for varying number of changes
(from no change, to modifying all 9000 transformations).
For a fair comparison, our system performs updates and
loops over the resulting aset, thus for 0 updates, we still
spend some milliseconds in that loop. The manually tuned
traversal version tracks dependencies, but the incremental
change propagation algorithm directly manipulates trans-
formation values of the render objects, involving no addi-
tional overhead. As it turns out the incremental evaluation
system performs well for this task and outperforms the clas-
sic traversal based approach since its runtime is proportional
to size of the change.
Note that attribute grammar evaluation incurs no
overhead in this setting. Furthermore, since due to
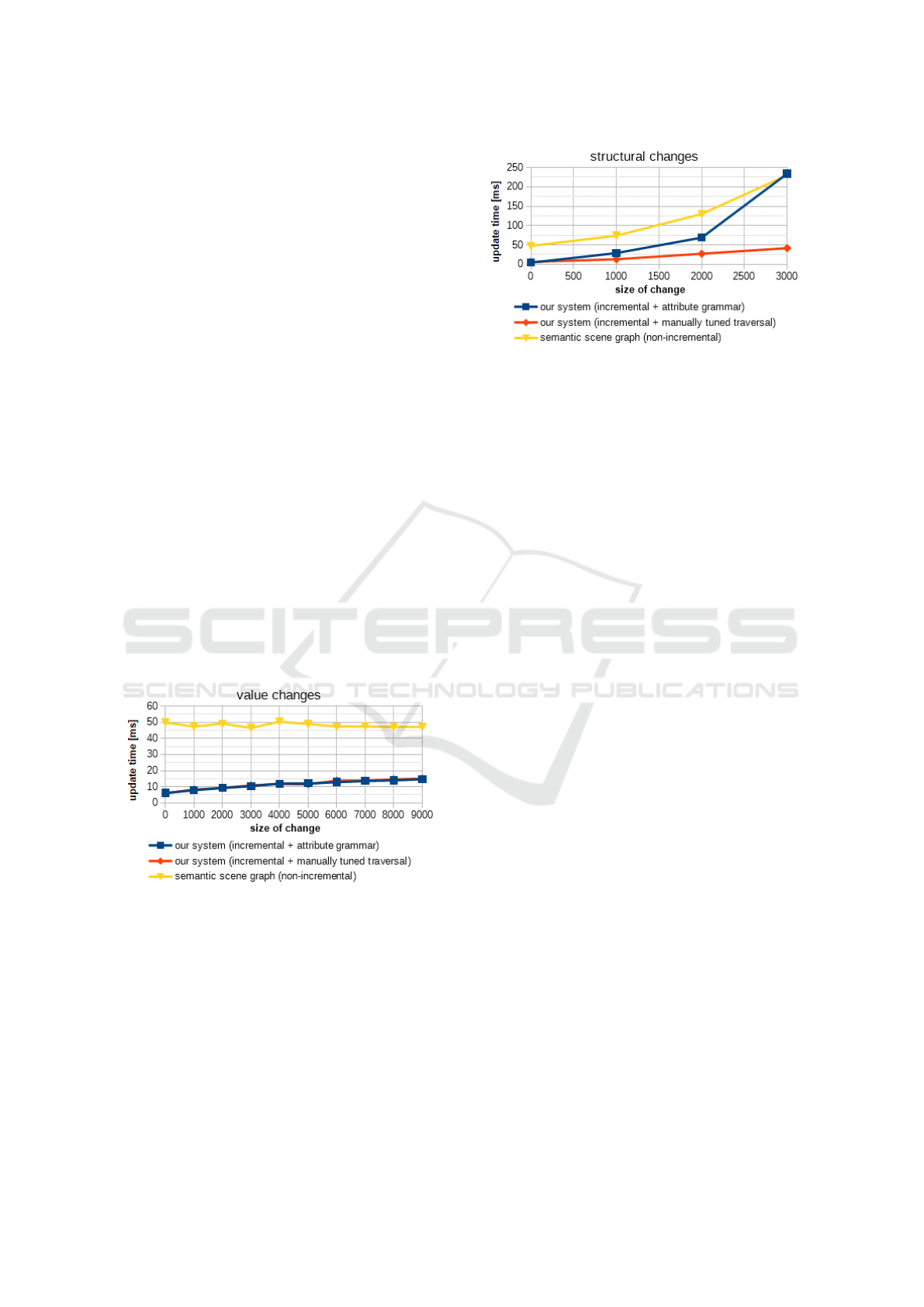
Figure 15: Runtime in ms for varying size of structural
change (removed and created nodes) for a scene with 9000
leaf nodes. Starting at 3000 changes per frame, i.e. one
third of the scene, reevaluation takes longer than simply tra-
versing the scene using the semantic scene graph approach.
With the manually tuned traversal, which tracks dependen-
cies but only handles required attributes, i.e. does not re-
solve attributes at runtime, the cost of our naive implemen-
tation becomes apparent. In a nutshell, our general but naive
implementation pays off as long as less than one third of the
scene is replaced per frame.
incremental evaluation value changes directly modify
the affected data (transformation values of render ob-
jects in our case), no attributes need to be computed.
Thus, for value changes, in contrast to traversal based
approaches, we only pay traversal cost once on con-
struction instead of each frame. Although such va-
lue changes are the most frequent change in many use
cases, often the scene changes modify not only va-
lues within the scene graph but also its structure (e.g.
new characters spawn in a game scene). Although less
frequent, we need to analyze this type of change. In
another test setup, instead of modifying the transfor-
mation values within the scene we modify whole sub-
graphs and replace old parts with new scene graphs
(see Figure 15). Although the attribute grammar eva-
luation incurs significant cost, almost one third of the
scene can be modified until traditional scene graph
implementations perform better. Although this is an
artificial setting and scenes typically change gradu-
ally (typically not one third of the scene is replaced in
one frame), the cost is not neglectable. A better attri-
bute grammar implementation could improve on that,
but in practice this worst-case rarely happens and the
advantages outweigh the cost in most use cases.
Although our system performs reasonable for ty-
pical workloads with semi-static scenes, we see furt-
her potential for optimization.
The most promising being low level optimiza-
tions enabled by incremental change tracking. By
using callbacks from the dependency graph, ope-
rations such as re-recording command lists/buffers
could be triggered much more targeted. Moreover
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
86

this work should motivate and enable research in
connecting methods particularly developed for high-
performance rendering (e.g. (W
¨
orister et al., 2013;
Haaser et al., 2015)) with domain specific languages
for scene and interaction specification (e.g. Vega-
lite’s grammar (Satyanarayan et al., 2017)). Anot-
her interesting research direction might be to con-
nect declarative scene descriptions to shader-centered
methods as recently explored by He et al. (He et al.,
2017).
4.3 Experience and Future Work
Clean concepts and semantics are noble goals. Our
experience with the system shows that a declarative
approach greatly reduces application complexity wit-
hout sacrificing expressiveness and performance and
that attribute grammars give structure to computer
graphics problems. In previous versions of our system
we used conventional scene graph implementations,
and it was crucial for our new approach to compose
with existing code and not to alienate developers with
too many tools and abstraction layers. In retrospect
we find that our new implementation is much smaller,
while having many more features, is easier to work
with and easier to extend. In the future we would like
to improve our naive attribute grammar implementa-
tion with native code generation in order to push even
more towards high-performance rendering.
5 CONCLUSIONS
Although concepts from computer language theory
are applicable to a wide range of use cases, we see sur-
prisingly little interdisciplinary work in this regard.
In this paper, we demonstrated a non-trivial applica-
tion of attribute grammars and self-adjusting compu-
tation in the field of visual computing. As our evalu-
ation shows, this approach solves a number of typical
problems of state-of-the-art scene graph systems in a
clean and well-founded manner.
ACKNOWLEDGEMENTS
We would like to thank Robert F. Tobler for all his
contributions — rest in peace.
VRVis is funded by BMVIT, BMDW, Styria, SFG
and Vienna Business Agency in the scope of CO-
MET - Competence Centers for Excellent Technolo-
gies (854174) which is managed by FFG.
REFERENCES
Acar, U. A. (2005). Self-adjusting computation. PhD thesis,
Carnegie Mellon University, Pittsburgh, PA, USA.
Acar, U. A., Blelloch, G., Ley-Wild, R., Tangwongsan, K.,
and Turkoglu, D. (2010). Traceable data types for
self-adjusting computation. In Proc. of the 2010 ACM
SIGPLAN conference on Programming language de-
sign and implementation, PLDI ’10, pages 483–496,
New York, NY, USA. ACM.
Acar, U. A., Blelloch, G. E., and Harper, R. (2002). Adap-
tive functional programming. In Proceedings of the
29th ACM SIGPLAN-SIGACT symposium on Prin-
ciples of programming languages, POPL ’02, pages
247–259, New York.
Bierman, G. M., Meijer, E., and Torgersen, M. (2007). Lost
in Translation: Formalizing Proposed Extensions to
C#. SIGPLAN Not., 42(10):479–498.
Burns, D. and Osfield, R. (2004). Open Scene Graph A:
Introd., B: Examples a. Applications. In Proc. of the
IEEE Virtual Reality 2004, VR ’04, page 265, Wa-
shington.
Carlsson, M. (2002). Monads for incremental computing.
In Proc. of the 7th ACM SIGPLAN internat. conf. on
Func. progr., ICFP ’02, pages 26–35, New York.
Durbin, J., Gossweiler, R., and Pausch, R. (1995). Amorti-
zing 3D Graphics Optimization Across Multiple Fra-
mes. In Proceedings of the 8th Annual ACM Sym-
posium on User Interface and Software Technology,
UIST ’95, pages 13–19, New York.
Ekman, T. and Hedin, G. (2007). The JastAdd system —
modular extensible compiler construction. Sci. Com-
put. Program., 69(1-3):14–26.
Haaser, G., Steinlechner, H., Maierhofer, S., and Tobler,
R. F. (2015). An Incremental Rendering VM. In Proc.
of the 7th Conference on High-Performance Graphics,
HPG ’15, pages 51–60, New York, NY, USA. ACM.
Hammer, M. A., Phang, K. Y., Hicks, M., and Foster, J. S.
(2014). Adapton: Composable, demand-driven in-
cremental computation. In Proceedings of the 35th
ACM SIGPLAN Conference on Programming Lan-
guage Design and Implementation, PLDI ’14, pages
156–166, New York.
He, Y., Foley, T., Hofstee, T., Long, H., and Fatahalian, K.
(2017). Shader components: Modular and high per-
formance shader development. ACM Trans. Graph.,
36(4):100:1–100:11.
Hudson, S. E. (1991). Incremental attribute evaluation: a
flexible algorithm for lazy update. ACM Trans. Pro-
gram. Lang. Syst., 13(3):315–341.
Jeff, B., Wallez, C., Tavenrath, M., Kilgard, M., Em-
mons, J., and Ludwig, T. (2015). NVidia com-
mand list. https://www.khronos.org/registry/OpenGL/
extensions/NV/NV command list.txt. accessed Oct
‘18.
Khronos Group, I. (2016). Vulkan 1.0 specifica-
tion. https://www.khronos.org/registry/vulkan/specs/
1.0/pdf/vkspec.pdf. accessed Oct ‘18.
Knuth, D. E. (1968). Semantics of context-free languages.
Mathematical systems theory, 2:127–145.
Attribute Grammars for Incremental Scene Graph Rendering
87

Meijer, E., Beckman, B., and Bierman, G. (2006). Linq:
Reconciling object, relations and xml in the .net fra-
mework. In Proceedings of the 2006 ACM SIGMOD
International Conference on Management of Data,
SIGMOD ’06, pages 706–706, New York, NY, USA.
ACM.
Petricek, T. and Syme, D. (2014). The F# Computation
Expression Zoo. In Proceedings of Practical Aspects
of Declarative Languages, PADL 2014.
Peyton Jones, S. et al. (2003). The Haskell 98 Language and
Libraries: The Revised Report. Journal of Functional
Programming, 13(1):0–255.
Ramalingam, G. and Reps, T. (1993). A categorized bi-
bliography on incremental computation. In Proc. of
the 20th ACM SIGPLAN-SIGACT symposium on Prin-
ciples of programming languages, POPL ’93, pages
502–510, New York.
Reps, T., Teitelbaum, T., and Demers, A. (1983). Incre-
mental context-dependent analysis for language-based
editors. ACM Trans. Program. Lang. Syst., 5(3):449–
477.
Rosendahl, M. (1992). Strictness analysis for attribute
grammars. In Proceedings of the 4th International
Symposium on Programming Language Implementa-
tion and Logic Programming, PLILP ’92, pages 145–
157, London, UK, UK. Springer-Verlag.
Satyanarayan, A., Moritz, D., Wongsuphasawat, K., and
Heer, J. (2017). Vega-lite: A grammar of inte-
ractive graphics. IEEE Trans. Visualization & Comp.
Graphics (Proc. InfoVis).
Sloane, A. M., Kats, L. C. L., and Visser, E. (2010). A pure
object-oriented embedding of attribute grammars.
Electron. Notes Theor. Comput. Sci., 253(7):205–219.
Strauss, P. S. and Carey, R. (1992). An object-oriented 3D
graphics toolkit. In Proc. of the 19th annual confe-
rence on Computer graphics and interactive techni-
ques, SIGGRAPH ’92, pages 341–349, New York.
Swierstra, S., Azero Alcocer, P., and Saraiva, J. (1999). De-
signing and implementing combinator languages. In
Swierstra, S., Oliveira, J. N., and Henriques, P. R.,
editors, Advanced Functional Programming, volume
1608 of Lecture Notes in Computer Science, pages
150–206. Springer Berlin Heidelberg.
Swierstra, W. (2005). Why Attribute Grammars Matter. The
Monad.Reader, 4.
Syme, D. (2006). Leveraging .NET Meta-programming
Components from F#: Integrated Queries and Inter-
operable Heterogeneous Execution. In Proceedings
of the 2006 Workshop on ML, ML ’06, pages 43–54,
New York, NY, USA. ACM.
Tobler, R. F. (2011). Separating semantics from rendering:
a scene graph based architecture for graphics applica-
tions. Vis. Comput., 27(6-8):687–695.
Torgersen, M. (2004). The Expression Problem Revisited,
pages 123–146. Springer Berlin Heidelberg.
Viera, M., Swierstra, S. D., and Swierstra, W. (2009). Attri-
bute grammars fly first-class: how to do aspect orien-
ted programming in Haskell. In Proc. of the 14th
ACM SIGPLAN Int. Conf. on Functional program-
ming, ICFP ’09, pages 245–256, New York.
Wadler, P. (1998). Email, Discussion on the Java Genericity
mailing list.
W
¨
orister, M., Steinlechner, H., Maierhofer, S., and Tobler,
R. F. (2013). Lazy Incremental Computation for Ef-
ficient Scene Graph Rendering. In Proc. of the 5th
High-Performance Graphics Conference, HPG ’13,
pages 53–62, New York.
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
88
