Gene Set Overlap: An Impediment to Achieving High Speciﬁcity in

Over-representation Analysis

Farhad Maleki and Anthony J. Kusalik

Department of Computer Science, University of Saskatchewan, Saskatoon, Saskatchewan, Canada

Keywords:

Gene Expression, Gene Set Analysis, Gene Set Enrichment, Gene Set Overlap, Speciﬁcity.

Abstract:

Gene set analysis methods are widely used to analyze data from high-throughput “omics” technologies. One

drawback of these methods is their low speciﬁcity or high false positive rate. Over-representation analysis is

one of the most commonly used gene set analysis methods. In this paper, we propose a systematic approach to

investigate the hypothesis that gene set overlap is an underlying cause of low speciﬁcity in over-representation

analysis. We quantify gene set overlap and show that it is a ubiquitous phenomenon across gene set databases.

Statistical analysis indicates a strong negative correlation between gene set overlap and the speciﬁcity of over-

representation analysis. We conclude that gene set overlap is an underlying cause of the low speciﬁcity. This

result highlights the importance of considering gene set overlap in gene set analysis and explains the lack of

speciﬁcity of methods that ignore gene set overlap. This research also establishes the direction for developing

new gene set analysis methods.

1 INTRODUCTION

High-throughput “omics” technologies have been

widely used to investigate biological questions that

require screening of a large number of biomolecules.

The main challenge facing these technologies is ana-

lyzing the generated data to gain biological insight.

An RNA-Seq experiment, for example, may sug-

gest several hundred genes as being differentially ex-

pressed. Manual interpretation of such a large set of

genes is impractical and susceptible to investigator

bias toward a hypothesis of interest.

Gene set analysis is a well-established computa-

tional approach to gain biological insight from data

resulting from high-throughput gene expression ex-

periments (Huang et al., 2009). It relies on the as-

sumption that most biological processes are the con-

sequence of a coordinated activity of a group of genes.

Therefore, the primary goal of gene set analysis is

to detect concordant changes in expression patterns

of predeﬁned groups of genes, referred to as gene

sets. Members of a given gene set often share a com-

mon biological function or attribute. MSigDB (Liber-

zon et al., 2011), GeneSigDB (Culhane et al., 2011),

GeneSetDB (Araki et al., 2012), Go-Elite (Zambon

et al., 2012), and Enrichr (Kuleshov et al., 2016)

are among the most widely used gene set databases.

These databases have been generated from vari-

ous sources including GO (Ashburner et al., 2000),

KEGG (Kanehisa et al., 2016), Reactome (Joshi-Tope

et al., 2005), and BioCarta (Nishimura, 2001).

Often gene set analysis methods report a large

number of gene sets as being differentially enriched,

where the majority of the reported gene sets are bi-

ologically irrelevant or uninformative (Tarca et al.,

2013). The rapid growth of the size of gene set

databases is intensifying this issue. Consequently,

gaining biological insight from the results of gene set

analysis is becoming more challenging and prone to

investigator biases in favour of a hypothesis of inter-

est. For example, Araki et al. used GeneSetDB to an-

alyze a list of 79 differentially expressed Affymetrix

probe sets (Araki et al., 2012) resulting from an ex-

periment where endothelial cells were induced to un-

dergo apoptosis (Johnson et al., 2004). After cor-

rection for multiple hypothesis testing, they reported

1694 gene sets as statistically signiﬁcant, i.e. differ-

entially enriched. Interpreting this large number of

gene sets is challenging.

Understanding the factors contributing to low

speciﬁcity in gene set analysis helps in choosing

methods that are more robust against these factors.

Such an understanding also facilitates interpreting the

results of gene set analysis methods and accelerates

the development of new methods that address these

contributing factors to achieve higher speciﬁcity with-

182

Maleki, F. and Kusalik, A.

Gene Set Overlap: An Impediment to Achieving High Speciﬁcity in Over-representation Analysis.

DOI: 10.5220/0007376901820193

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 182-193

ISBN: 978-989-758-353-7

out sacriﬁcing sensitivity and accuracy.

Speciﬁcity of gene set analysis methods in the

absence of differential expression of genes has been

studied. Tarca et al. (Tarca et al., 2013) investigated

the speciﬁcity of sixteen gene set analysis methods in

the absence of differential expression and showed that

even when there is no differential expression, some

gene set analysis methods produce a large number

of false positives. However, their approach cannot

be used to assess the speciﬁcity of a gene set analy-

sis method in the presence of differentially expressed

genes.

Overlap between gene sets has been suggested

as being responsible for the low speciﬁcity of gene

set analysis methods. To deal with overlap between

gene sets, PADOG (Tarca et al., 2012) assigns lower

weights to genes that belong to more than one gene

set. For a given gene g, this weight is negatively

correlated with the number of gene sets containing

g. TopGO (Alexa et al., 2006) is another attempt

to deal with gene set overlap. It considers that

Gene Ontology (GO) terms are organized as a di-

rected acyclic graph encoding a hierarchy of general-

to-more-speciﬁc terms. This structure leads to com-

monality between the genes corresponding to a child

node and those of its parent(s). TopGO proposes a

gene elimination and a gene down-weighting proce-

dure to decorrelate the GO graph structure resulting

from these relations. MGSA (Bauer et al., 2010)

utilises a Bayesian approach that considers the over-

lap between GO categories to reduce the number of

false positives. SetRank (Simillion et al., 2017) is an-

other attempt at reducing the number of false positives

by considering the overlap between gene sets.

Parallel to the development of gene set analysis

methods, various gene set databases have been de-

veloped. The prevailing trend in developing gene set

databases has been introducing more gene sets and in-

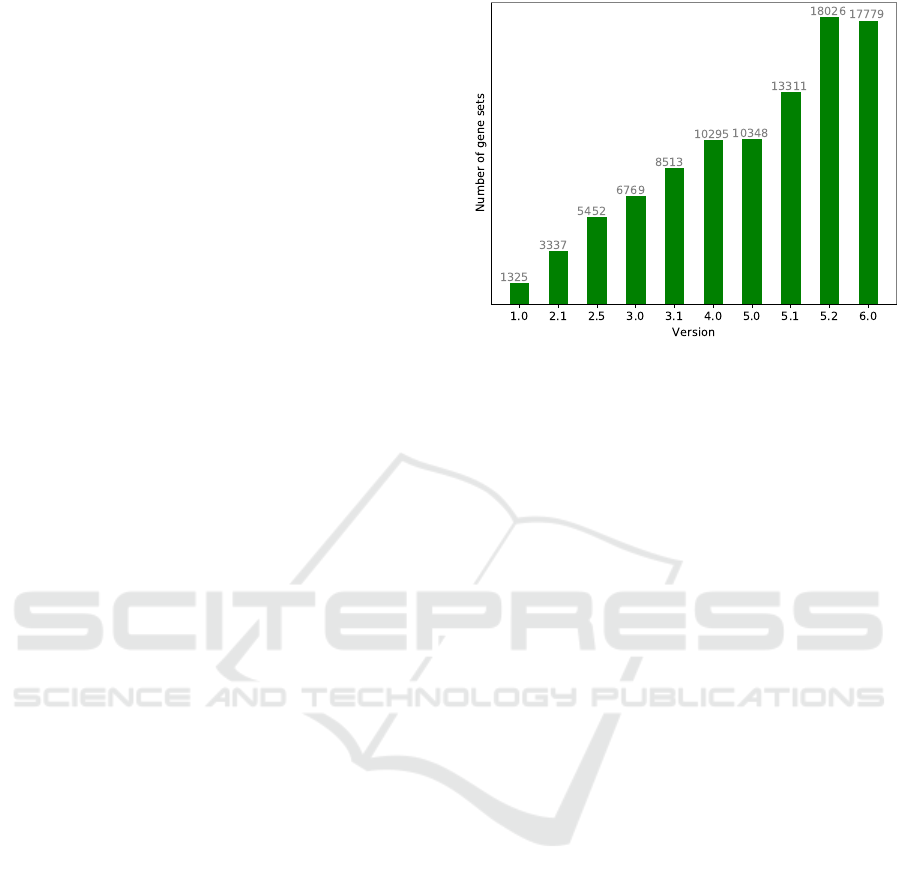
creasing database size. Figure 1 illustrates the growth

of MSigDB across its versions. This gene set database

has been designed for gene set analysis in human,

and its current version includes gene sets from various

sources such as GO, KEGG, Reactome, and BioCarta.

This gene set database has undergone a 13-fold in-

crease in the number of gene sets compared to its ﬁrst

version. Given the limited number of known genes

for human, this steep growth leads to an increase in

the number of gene sets overlapping with each other.

To the best of our knowledge, there is no system-

atic study of the effect of gene set overlap on the re-

sults of gene set analysis. In this paper, we investigate

the hypothesis that gene set overlap plays a prominent

role in the lack of speciﬁcity of over-representation

analysis (ORA), which is one of the most widely used

Figure 1: The number of gene sets in different versions of

MSigDB.

gene set analysis methods (Draghici et al., 2003).

The rest of the paper is organised as follows. In

Section 2, we brieﬂy describe ORA. In Section 3,

we show that gene set overlap is a ubiquitous phe-

nomenon in gene set databases; we use quantita-

tive measures to visualize gene set overlap in Gene-

SetDB (Araki et al., 2012), GeneSigDB (Culhane

et al., 2010), and MSigDB (Liberzon et al., 2011),

which are well-established gene set databases. In Sec-

tion 4, using these quantitative measures, we intro-

duce a methodology to study the effect of gene set

overlap on the speciﬁcity of ORA. In Section 5, we

describe the experimental results; using the method-

ology introduced in Section 4, we statistically investi-

gate the effect of gene set overlap on the speciﬁcity

of ORA by assessing the correlation between gene

set overlap and speciﬁcity. In Section 6, we discuss

the implication of gene set overlap and the challenges

it entails. We also provide suggestions for develop-

ing and evaluating gene set analysis methods. Finally,

Section 7 offers a short summary and conclusion.

2 OVER-REPRESENTATION

ANALYSIS

Many algorithms have been proposed and used for

gene set analysis, of which ORA is one of the most

widely used. Due to its simplicity, well-established

underlying statistical model, and ease of implementa-

tion, ORA is available through many tools (Beißbarth

and Speed, 2004), (Berriz et al., 2003), (Boyle et al.,

2004), (Jiao et al., 2012), (Maere et al., 2005), (Wang

et al., 2017), (Wrobel et al., 2005), (Young et al.,

2005), (Zeeberg et al., 2003), (Zeeberg et al., 2005),

(Zhang et al., 2005). This method deﬁnes a concor-

Gene Set Overlap: An Impediment to Achieving High Speciﬁcity in Over-representation Analysis

183

Table 1: Representation of ORA as a contingency table.

Each cell contains a count of genes satisfying the condition

given by the row and column.

Genes ∈ L Genes /∈ L Total

Genes ∈ G

k −n

Genes ∈ G

kLk −n

(n − kG

k) -

(kLk −n

)

n −kG

Total kLk n −kLk n

dant change in expression pattern of members of a

given gene set as a change that is unlikely to happen

by chance. It also quantiﬁes the concept of change

as the number of differentially expressed genes in a

pairwise comparison of phenotypes, e.g. “cancerous”

versus “non-cancerous”.

ORA can be outlined as follows (Dr

aghici et al.,

2003). Suppose that data analysis for an experiment

using a high-throughput technology predicts a set of

differentially expressed genes L, and that the inter-

section of L and a given gene set G

contains n

genes.

In addition, assume that the set of background genes,

i.e. all genes with a non-zero probability of being dif-

ferentially expressed, contains n genes. For example,

the background genes in a microarray study can be

the set of all genes represented on the arrays. Denote

the background set as U. Let G

refer to the comple-

ment of G

with respect to U, i.e. all genes in U but

not in G

. Given L, G

, and U, ORA assesses whether

the number of differentially expressed genes in G

more than what it should be just by chance, i.e. it is

over-represented. Table 1 represents ORA as a con-

tingency table, where k• k is the cardinality operator.

Assuming that genes are selected using a sim-

ple random sampling approach, ORA can be mod-

eled using a hypergeometric distribution (Dr

aghici

et al., 2003). Accordingly, the probability of hav-

ing n

genes from G

among differentially expressed

genes, i.e. L, is as follows:

f (n

;n,kG

k,kLk) =







n−kG

kLk−n





kLk



(1)

In addition, Fisher’s exact test can be used to

examine the signiﬁcance of the association between

genes in G

and genes in L. The p-value can be cal-

culated for over-representation of G

based on Equa-

tion 2.

p =

∑

j=n

f ( j; n,kG

k,kLk)

= 1 −

−1

∑

j=0

f ( j; n,kG

k,kLk) (2)

3 OVERLAP IN GENE SET

DATABASE

ORA, as with other gene set analysis methods, re-

lies on availability of a gene set database. Gene set

databases are developed by collecting genes that are

manually or computationally inferred to share a com-

mon biological function or attribute. The availabil-

ity of a priori knowledge through public repositories

such as GO (Ashburner et al., 2000), KEGG (Kane-

hisa et al., 2016), and OMIM (Hamosh et al., 2002)

makes it possible to develop gene set databases. There

are many publicaly available gene set databases in-

cluding L2L (Newman and Weiner, 2005), Signa-

tureDB (Shaffer et al., 2006), CCancer (Dietmann

et al., 2010), GeneSigDB (Culhane et al., 2010),

GeneSetDB (Araki et al., 2012), and MSigDB (Liber-

zon et al., 2011). The latter three are widely used for

gene set analysis.

MSigDB is the gene set database integrated with

GSEA (Subramanian et al., 2005). MSigDB acquires

gene sets through manual curation and computational

methods (Liberzon et al., 2011). As a meta-database,

MSigDB extracts gene sets from several sources in-

cluding GO (Ashburner et al., 2000), KEGG (Kane-

hisa et al., 2016), Reactome (Joshi-Tope et al., 2005),

and BioCarta (Nishimura, 2001).

GeneSigDB is another database of gene sets ex-

tracted from published experimental expression stud-

ies of genes, proteins, or miRNAs. GeneSigDB relied

on PubMed searches to collect papers relevant to a set

of search terms mainly focused on cancer, lung dis-

ease, development, immune cells, and stem cells. To

develop the database, the authors downloaded the rel-

evant papers and then manually transcribed gene sets

from them or their supplementary documents.

GeneSetDB, as another meta-database, is a collec-

tion of 26 public databases focused on pathways, phe-

notypes, drugs, gene regulation, or Gene Ontology.

The primary focus of GeneSetDB is human, although

it supports mouse and rat using computationally in-

ferred homology (Araki et al., 2012).

3.1 Gene Set Overlap and ORA: A

Hypothetical Example

To show how overlap of gene sets can affect the re-

sults of ORA, in this section we present a hypothet-

ical example. Suppose that in a high-throughput ex-

periment, the expression activity of 10000 genes has

been measured. After conducting the experiment and

performing single gene analysis, 100 genes have been

predicted as being differentially expressed. Consider

gene sets A, B, and C as illustrated in Figure 2, where

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

184

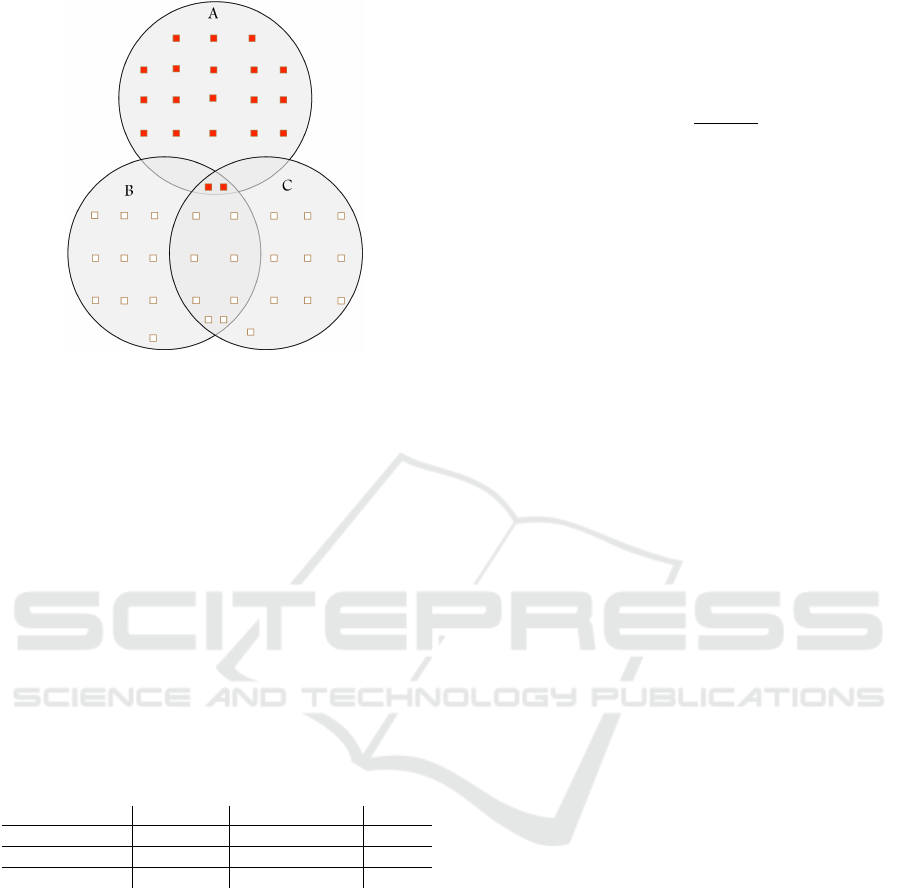
Figure 2: A hypothetical example: gene set overlap leading

to lack of speciﬁcity of ORA. Each circle represents a gene

set. Rectangles coloured in red and white represent differ-

entially expressed and non-differentially expressed genes,

respectively. Gene set B (and also C) is predicted as being

differentially enriched by ORA solely due to partial overlap

with A, a truly differentially enriched gene set.

gene sets are depicted as circles, and genes belonging

to each gene set are depicted as rectangles. In each

gene set, genes predicted as being differentially ex-

pressed are coloured in red and the rest of the genes

are coloured in white. As shown in Figure 2, all genes

in A have been predicted as being differentially ex-

pressed. Table 2 illustrates the contingency table for

over-representation of B.

Table 2: The contingency table for the over-representation

of B. DE stands for differentially expressed and Non-DE

stands for non-differentially expressed.

DE Genes Non-DE Genes Total

Genes in B 2 18 20

Genes not in B 98 9882 9980

Total 100 9900 10000

According to Fisher’s exact test, B is predicted as

being differentially enriched with a 95% conﬁdence

level (p-value = 0.0167). This result is primarily due

to the overlap between A and B. This example sug-

gests that gene set overlap can lead to a lack of speci-

ﬁcity in gene set analysis methods.

In this paper, we use GeneSigDB version 4, Gene-

SetDB for Human (downloaded on February 2, 2018),

and MSigDB version 6.0, unless stated otherwise.

3.2 Measuring Gene Set Overlap

To study gene set overlap and its effect on the speci-

ﬁcity of ORA, we use the Jaccard coefﬁcient to quan-

tify the overlap between two gene sets. We then use

this quantitative measure to visualize gene set overlap

in MSigDB, GeneSetDB, and GeneSigDB.

For given sets A and B, the Jaccard coefﬁcient is

deﬁned as follows:

J(A,B) =

kA ∩ Bk

kA ∪ Bk

(3)

The Jaccard coefﬁcient is a value between 0 and 1,

where J(A,B) = 0 means that there is no overlap be-

tween A and B; J(A,B) = 1 means that there is a com-

plete overlap between A and B, i.e. A = B; and other

values (0 < J(A,B) < 1) represent partial overlaps be-

tween A and B. The Jaccard index can be used to

quantify the overlap between two sets; for example, it

can be used to measure the overlap between two gene

sets from a gene set database or the overlap between

a gene set and a set of differentially expressed genes

resulting from a gene expression study. Hereafter, we

refer to Jaccard index as overlap score.

For a given set of genes L

and a gene set database

G, we deﬁne the overlap coefﬁcient, or overlap score,

of L

with respect to G as follows:

O(L

,G) =

∑

∈G

J(L

) (4)

This measure is representative of the cumulative over-

lap of L

with all gene sets in the gene set database G.

For the sake of brevity, whenever gene set database G

can be inferred from the context, we use the phrase

“overlap score of L

” to refer to O(L

,G). Note that

O(L

,G), which is the summation of overlap between

and each gene set in the gene set database G, should

not be mistaken with overlap between two sets of

genes. The latter is calculated using the Jaccard in-

dex (Equation 3).

3.3 Visualization of Gene Set Overlap

We visualize a gene set database as a graph, where

each gene set G

is represented as a vertex v

, and

there is an edge between two vertices v

and v

J(G

) > 0; the value of J(G

) is used as the

weight for this edge. Since the Jaccard coefﬁcient

is symmetric, the graph deﬁned using this measure

is an undirected graph. Due to the sheer number of

overlapping gene sets, such a graph has a large num-

ber of edges. To visualize substantial overlaps be-

tween gene sets, we only show overlap scores greater

than or equal to 0.5, while retaining all vertices. In

other words, in all graph visualizations in this paper,

an edge between two vertices v

and v

indicates that

their corresponding gene sets, i.e. G

and G

, share

at least half of their genes. The “hairballs” in Fig-

ure 3 and also Figures 6 and 7 (in the Appendix)

are due to the existence of a large number of edges,

Gene Set Overlap: An Impediment to Achieving High Speciﬁcity in Over-representation Analysis

185

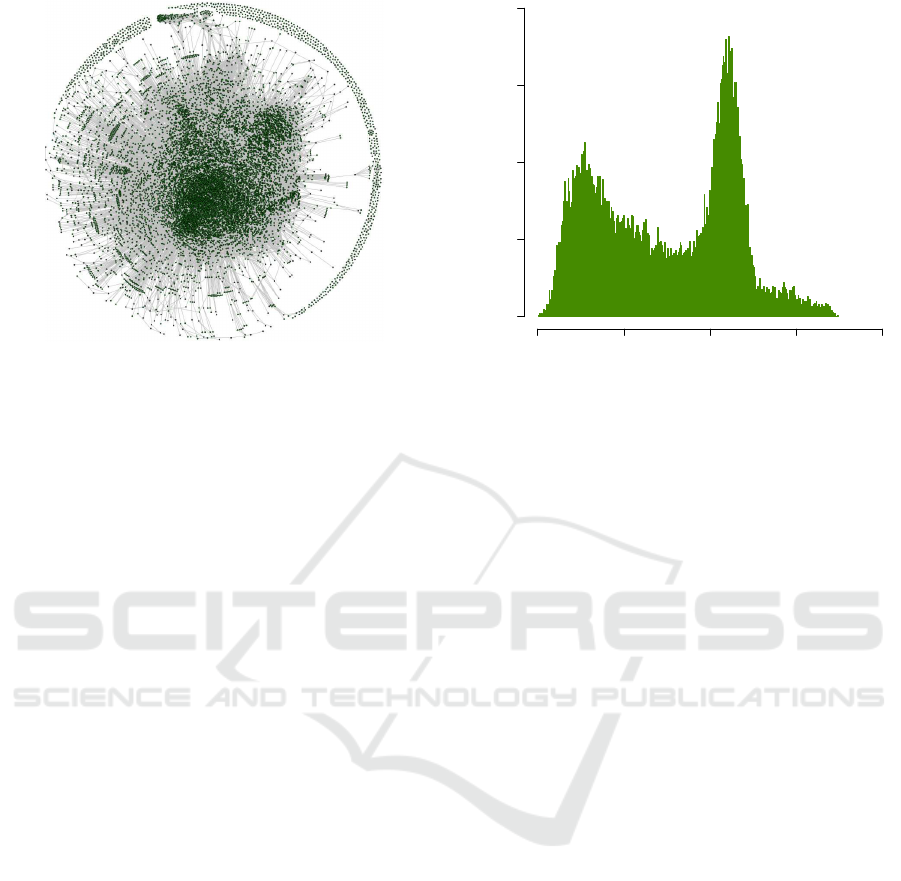
Figure 3: The graph representing the overlap between gene

sets in MSigDB. In this graph, each vertex represents a gene

set in MSigDB, and each edge represents an overlap with

Jaccard coefﬁcient greater than or equal to 0.5 between two

gene sets (see Equation 3). The “hairball” is the result of a

large number of gene sets with a substantial overlap (≥ 0.5)

with each other.

i.e. pairs of gene sets with a substantial amount of

overlap. These graphs highlight the existence of gene

set overlap as a ubiquitous phenomenon in gene set

databases. The graph visualization can be generated

using Fruchterman Reingold layout (Fruchterman and

Reingold, 1991) in Gephi (version 0.9.2) (Bastian

et al., 2009).

To further visually inspect the gene set overlap in

a given gene set database G, we use a frequency plot.

For each gene set G

in G, we calculate f

= k{G

J(G

) > 0 ( j 6= i) and G

∈ G}k. f

is the number

of gene sets G

( j 6= i) in G with a non-zero overlap

with G

. After calculating f

values for all G

in G,

we use a frequency plot to show the distribution of

values. Figure 4 and also Figures 8, and 9 (in the

Appendix) illustrate the distribution of f

values for

MSigDB, GeneSetDB, and GeneSigDB, respectively.

These ﬁgures are in agreement with Figure 3, 6, and

7 and show the prevalence of gene set overlap in the

aforementioned gene set databases.

Figure 4 suggests that overlap scores in MSigDB

follow a multimodal distribution. This can be at-

tributed to the fact that MSigDB is a meta-database

that extracts gene sets from several sources including

GO, KEGG, Reactome, and BioCarta. A compelling

result revealed by Figure 4 is that majority of gene

sets in MSigDB have at least a non-zero overlap with

more than 1000 other gene sets in MSigDB (out of a

total of 17778 gene sets). Also, there is no gene set in

MSigDB without overlap with some other gene set(s).

Finally, there are gene sets that overlap with the ma-

jority of gene sets in MSigDB. For example, the gene

Frequency

0 5000 10000 15000 20000

0 50 100 150 200

Figure 4: A frequency plot for f

values in MSigDB illus-

trates the prevalence of gene set overlap. For each gene set

in a gene set database G (MSigDB here), f

is the number

of gene sets G

( j 6= i) in G with J(G

) > 0.

set associated with the “cellular response to organic

substance” GO term (GO:0071310) has one non-zero

overlap with 17292 gene sets. This gene set is asso-

ciated with a general GO term and therefore overlaps

a large number of gene sets including the gene sets

deﬁned using relatively more speciﬁc GO terms.

4 METHODOLOGY

Evaluation of ORA using a quantitative measure

such as speciﬁcity requires a gold standard dataset for

which the differentially enriched gene sets are a pri-

ori known. Such a gold standard does not exist. In

this section, we propose a methodology for a quanti-

tative evaluation of the effect of gene set overlap on

the speciﬁcity of ORA in the absence of such a gold

standard dataset.

To perform ORA, a single gene analysis method

must be conducted to predict the set of differentially

expressed genes. This set serves as one of the in-

puts to ORA. In practice, often noise and biological

variability introduce errors—i.e. false positives and

false negatives—in the result of single gene analysis.

In the context of single gene analysis, false positives

are genes that are not differentially expressed but pre-

dicted as being so, and false negatives are genes that

are differentially expressed but predicted as not being

such. False negatives in single gene analysis may re-

duce the sensitivity of ORA, while false positives may

reduce the speciﬁcity. To avoid the interference of the

single gene analysis errors in the study of gene set

overlap and its effect on the speciﬁcity of ORA, we

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

186

assume that differentially expressed genes have been

identiﬁed correctly; also, this is the same assumption

that ORA relies on. Therefore, to perform the quan-

titative evaluation, a scenario in which all genes in a

given gene set have been accurately detected as being

differentially expressed is considered.

To deal with the absence of a gold standard

dataset, in this paper the following procedure is used

to identify the true enrichment status of gene sets.

Given a gene set database G = {G

| 1 ≤ j ≤ m} and

, a set of differentially expressed genes, and a ﬁxed

parameter γ, for each gene set G

∈ G we consider G

as being truly differentially enriched if at least 100×γ

percent of its members are differentially expressed

genes, i.e.

∩L

≥ γ. Otherwise, G

is considered

as not being truly differentially enriched. γ serves as

a threshold; since there is no consensus about such a

threshold value, we repeat the main experiments for a

wide range of values for γ, and we show that regard-

less of the value chosen for γ the results are consis-

tent. In the rest of the paper, the set of truly differ-

entially enriched and truly nondifferentially enriched

gene sets are denoted by T

(γ) and T

−

(γ), respec-

tively, and are deﬁned as follows:

(γ) = {G

∈ G |

∩ L

≥ γ} (5)

−

(γ) = {G

∈ G |

∩ L

< γ} (6)

Hereafter, for the sake of brevity, we avoid writing

the parameter γ; for example, we refer to T

(γ) and

−

(γ) as T

and T

−

respectively.

Given γ and L

, Equations 5 and 6 determine the

true enrichment status of all gene sets in G. Knowing

the true enrichment status of gene sets, we run ORA.

The parameters (inputs) for running ORA are: a list of

differentially expressed genes L

, a signiﬁcance level

α, a background set U, and a gene set database G =

: 1 ≤ j ≤ m}.

In this research, the experiments were conducted

using python version 3.6.2. To implement ORA,

the ﬁsher exact method from the stats module of

scipy version 0.19.1 was used. Also, the Benjamini-

Hochberg FDR adjustment for multiple comparisons

was performed using the multipletests method (with

method parameter equal to fdr bh) from statsmodels

version 0.8.0.

For each gene set G

in G, ORA calculates a p-

value p

. After calculating p

,.. ., p

—the p-values

corresponding to the over-representation of gene sets

,.. .,G

in G according to Equation 2—the Ben-

jamini-Hochberg FDR adjustment (Dr

aghici, 2016)

for multiple comparisons is applied. All gene sets

with an adjusted p-value less than α are predicted as

signiﬁcant, i.e. being differentially enriched. G

deﬁned as the set of all such signiﬁcant gene sets. G

includes both true positives and false positives. G

−

is deﬁned as the set of all nonsigniﬁcant gene sets,

i.e. G

−

= G − G

. G

−

includes both true negatives

and false negatives. For the given value of γ, true

positives (TP

), false positives (FP

), true negatives

(TN

), and false negatives (FN

) are identiﬁed based

on Equations 7, 8, 9, and 10.

T P

= T

∩ G

(7)

= G

− T

(8)

T N

= T

−

∩ G

−

(9)

= G

−

− T

−

(10)

Using these values, speciﬁcity (SPC

) is calculated ac-

cording to Equation 11.

SPC

kT N

k + kFP

(11)

To be able to gain insight that is unbiased toward a

single set L

, this process is repeated many times, each

time with a different L

. We denote the set of all L

L = {L

| 1 ≤ i ≤ l}.

Algorithm 1 (see the Appendix) illustrates the

methodology for conducting the experiment. In each

iteration of the algorithm, i.e. the outer loop, a gene

set L

from L is used, and the process is repeated for

all gene sets in L. In addition, for each set L

∈ L, the

overlap score of L

with respect to gene set database

G, i.e. O(L

,G), is calculated according to Equa-

tion 4. Having overlap score and speciﬁcity measure

for each L

∈ L, the relationship between overlap and

the speciﬁcity of ORA can be assessed using statisti-

cal methods (see Section 5).

5 EXPERIMENTAL RESULTS

To study the effect of gene set overlap on the speci-

ﬁcity of ORA using Algorithm 1, MSigDB—one of

the most widely used gene set databases devoted to

gene set analysis—was used as the gene set database

G. Since ORA requires a list (set) of differentially

expressed genes as input, Algorithm 1 requires a col-

lection of such lists (denoted as L in the algorithm).

ImmuneSigDB (Godec et al., 2016) version 6.0 was

used to provide such a collection. ImmuneSigDB

contains lists of differentially expressed genes, each

created by identifying differentially expressed genes

in a dataset extracted from Gene Expression Omnibus

(GEO) (Edgar et al., 2002). Therefore, each list in

ImmuneSigDB represents a set of differentially ex-

pressed genes derived from a high-throughput study.

Gene Set Overlap: An Impediment to Achieving High Speciﬁcity in Over-representation Analysis

187

To investigate the association between gene set

overlap and the speciﬁcity of ORA results, ﬁrst the

overlap score O(L

,G) was calculated for each list L

in ImmuneSigDB. In this experiment, a signiﬁcance

level α = 0.05 and γ values equal to 0.1, 0.2, 0.3, 0.4,

0.5, 0.6, 0.7, 0.8, 0.9, and 0.99 were used. For each

value of γ, Algorithm 1 was run to calculate SPC

cor-

responding to each L

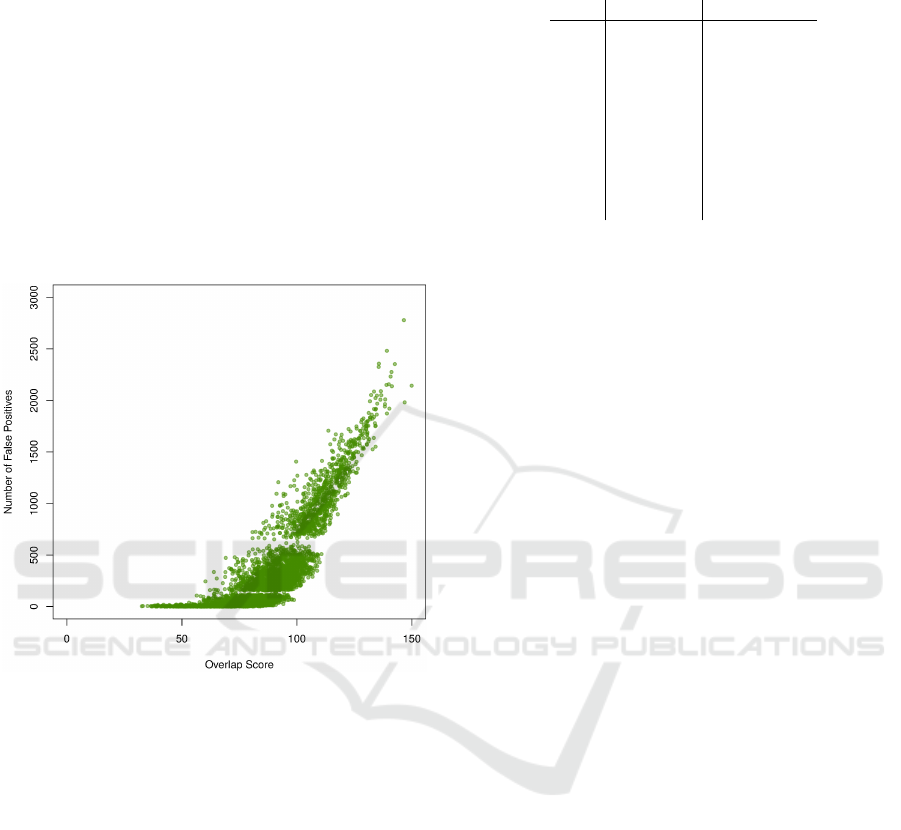
∈ L. Figure 5 illustrates the

relationship between gene set overlap and the num-

ber of false positives for γ = 0.5. As overlap score in-

creases, we observe an increase in the number of false

positives and therefore a decline in the speciﬁcity. We

observed the same pattern for all the aforementioned

values of γ.

Figure 5: Number of false positives increases as overlap

score increases (γ = 0.5). A similar pattern was observed

for other values of γ.

To study the relationship between gene set over-

lap and the speciﬁcity of ORA, we used a statistical

test of correlation. Choosing a proper test of corre-

lation requires assessment of the normality assump-

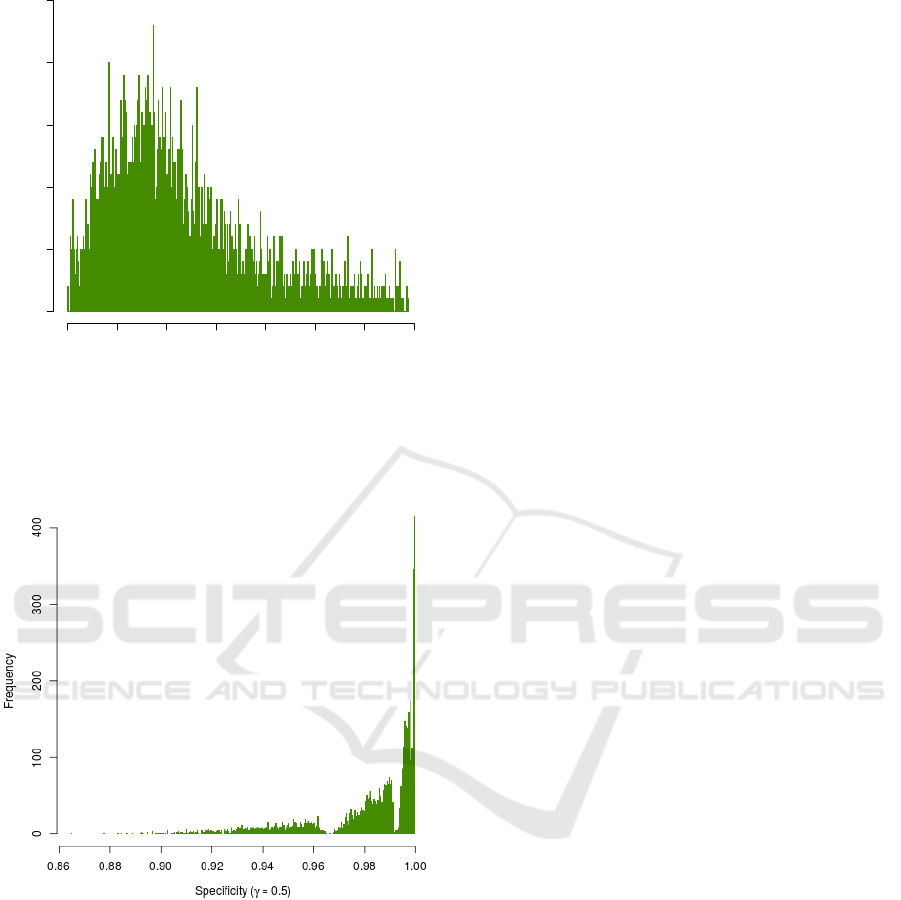
tion. To test the null hypothesis that speciﬁcity values

are normally distributed, we used the Shapiro-Wilk

test (Shapiro and Wilk, 1965). Table 4 shows the test

results for the aforementioned values of γ. Consid-

ering those results, as conﬁrmed by the histogram in

Figure 10 (see Appendix), we concluded that speci-

ﬁcity values are not normally distributed. Therefore,

a Spearman’s rank correlation coefﬁcient test, a non-

parametric test, was conducted for each value of γ to

test the null hypothesis that there is no correlation be-

tween speciﬁcity and overlap scores. Table 3 shows

the result of this test for various values of γ. Con-

sidering these results, we concluded that there is a

strong negative correlation between gene set overlap

and speciﬁcity of ORA.

Table 3: The result of Spearman rank correlation tests for

different values of γ. All p-values are less than 0.0000001.

γ r

p-value

0.10 -0.884064 <0.0000001

0.20 -0.880628 <0.0000001

0.30 -0.879913 <0.0000001

0.40 -0.879589 <0.0000001

0.50 -0.879366 <0.0000001

0.60 -0.879301 <0.0000001

0.70 -0.879302 <0.0000001

0.80 -0.879301 <0.0000001

0.90 -0.879307 <0.0000001

0.99 -0.879307 <0.0000001

6 DISCUSSION

In this research, we proposed a systematic approach

for evaluating the speciﬁcity of over-representation

analysis. Using the proposed method, we demon-

strated that there is a signiﬁcant negative correlation

between the speciﬁcity of ORA and gene set overlap.

In other words, gene set overlap increases the number

of false positives, i.e. gene sets incorrectly predicted

as being differentially enriched. The increase in the

number of false positives makes interpreting the re-

sults of ORA difﬁcult and prone to investigator biases

toward a hypothesis of interest. It also hinders repro-

ducibility of gene set analysis results.

We also showed that gene set overlap is a ubiq-

uitous phenomenon across gene set databases. The

existence of multifunctional genes is one contributor

to this phenomenon. Multifunctional genes are genes

associated with several molecular functions or bio-

logical processes; therefore, they appear in several

gene sets, contributing to gene set overlap. Multi-

functional genes are commonplace; for example, Pri-

tykin et al. (Pritykin et al., 2015) identiﬁed 2517 mul-

tifunctional genes in the human genome. As a conse-

quence, gene set overlap is an integral characteristic

of gene set databases. Another factor contributing to

the prevalence of gene set overlap in databases that

deﬁne some (or all) of their gene sets based on GO is

the child-parent relationship between GO terms. GO

terms are organized as a directed acyclic graph; each

node represents a GO term; and each edge between

two nodes represents a parent-child relationship be-

tween terms, with the child term being more speciﬁc

than its parent term(s). Therefore, gene sets derived

from GO terms that are involved in such child-parent

relationships share common genes; this, in turn, con-

tributes to the existence of gene set overlap.

Being an integral part of gene set databases, gene

set overlap should be considered in the design and

evaluation of gene set analysis methods. However,

many gene set analysis studies have used simulated

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

188

collections of non-overlapping gene sets for method

evaluation and comparison (Ackermann and Strim-

mer, 2009), (Efron and Tibshirani, 2007), (Nam and

Kim, 2008). Therefore, gene set overlap and its ef-

fect on the outcome of gene set analysis methods have

been overlooked. We suggest using datasets that ac-

count for overlap as a requirement in the evaluation of

gene set analysis methods.

Although many gene set analysis methods and

tools have been developed, there are very few meth-

ods that consider gene set overlap. For example,

PADOG is an attempt for addressing gene set over-

lap that leads to a small number of false positives

(has high speciﬁcity), but its sensitivity has been re-

ported to be lower than that of other gene set anal-

ysis methods (see Table S2 from the work by Tarca

et al., 2013). SetRank is another gene set analysis

method designed with gene set overlap in mind to in-

crease speciﬁcity (Simillion et al., 2017). The authors

of SetRank claimed that due to a lower number of

false positives, the signiﬁcant results reported by this

method are more reliable than other methods. There-

fore, it may be a viable solution for the lack of speci-

ﬁcity of gene set analysis methods. A rigorous evalu-

ation of the speciﬁcity and sensitivity of this method

is suggested as future research.

The existence of gene set databases that accurately

represent biological processes and functions is essen-

tial to the success of gene set analysis. Increasing the

size of gene set databases by depositing more gene

sets has been the common trend in developing gene

set databases. The increase in the number of gene

sets has introduced more gene set overlap, which in

turn leads to a higher false positive rate. There is a

need to focus on quality rather than sheer quantity in

developing gene set databases. We suggest further re-

search on the quality control of gene set databases.

Another suggestion for improving the speciﬁcity

of current methods is to exclude irrelevant or unin-

formative gene sets before conducting gene set analy-

sis. Considering the size of gene set databases, ﬁlter-

ing these gene sets is laborious and, if done manually,

prone to investigator bias toward gene sets considered

“relevant”. Developing a computational approach for

ﬁltering irrelevant or uninformative gene sets would

be worthwhile.

In the proposed method for evaluating ORA, we

considered scenarios with only one differentially en-

riched gene set. In practice, a speciﬁc phenotype

may be the result of altering several biological pro-

cesses or functions, i.e. multiple gene sets. We ex-

pect that the differential enrichment of several gene

sets intensiﬁes the extent to which gene set overlap

reduces speciﬁcity. In other words, we expect to see a

larger number of false positives compared to the situ-

ation considered in this work. The proposed method

is capable of handling scenarios with several differ-

entially enriched gene sets. Also, Algorithm 1 can be

used seamlessly with sensitivity or accuracy instead

of speciﬁcity.

Since the input to ORA is a list of differentially

expressed genes, we utilized ImmuneSigDB (Godec

et al., 2016) for evaluating ORA. However, some

gene set analysis methods require an expression ma-

trix that represents expression level of genes under

study across control and case samples. The proposed

methodology is capable of evaluating such gene set

analysis methods. To do so, the only requirement is

developing expression proﬁles with the differentially

enriched gene set(s) encoded in expression values.

Therefore, our methodology can be used as a system-

atic approach to study speciﬁcity, sensitivity, and ac-

curacy of other gene set analysis methods. For exam-

ple, we suggest the study of the relationship between

gene set overlap and the speciﬁcity of GSEA (Sub-

ramanian et al., 2005), which is another well-estab-

lished gene set analysis method, as future work.

In the absence of gene set overlap, gene set anal-

ysis is a trivial problem, as many methods have

achieved high speciﬁcity when being evaluated (by

their authors) using simulated gene set databases with

non-overlapping gene sets. If gene set overlap was

considered in the evaluation of these methods, the

lack of speciﬁcity of many gene set analysis methods

would be obvious. For example, assume a gene set

analysis method that uses average expression value of

genes within a gene set (in control versus case sam-

ples) to predict the enrichment status of a gene set.

Also assume that there is a single differentially ex-

pressed gene that appears in 100 gene sets. Such a

method would report all 100 gene sets as being differ-

entially enriched, while most of these gene sets might

be biologically irrelevant. Therefore, we strongly rec-

ommend considering gene set overlap in any attempt

for evaluating gene set analysis using simulated data.

7 CONCLUSION

In this paper, we proposed a systematic approach to

study the effect of gene set overlap on the result of

ORA (over-representation analysis). Using the pro-

posed method and statistical analysis, we showed

that there is a signiﬁcant negative correlation between

gene set overlap and speciﬁcity of ORA. We quanti-

ﬁed gene set overlap and showed that it is a ubiquitous

phenomenon across gene set databases. The proposed

approach for the study of the relationship between

Gene Set Overlap: An Impediment to Achieving High Speciﬁcity in Over-representation Analysis

189

gene set overlap and speciﬁcity of ORA can easily

be used to investigate the effect of gene set overlap on

different gene set analysis methods using quantitative

measures such as speciﬁcity, sensitivity, and accuracy.

Considering the effect of gene set overlap on the re-

sults of ORA, it is essential to develop and use meth-

ods that address gene set overlap and achieve higher

speciﬁcity without sacriﬁcing sensitivity in the pre-

diction of differentially enriched gene sets. Due to

the lack of gold standard datasets, where the differ-

entially enriched gene sets are known a priori, sim-

ulated datasets have been widely used for evaluation

of gene set analysis methods. The databases used in

these studies are often a collection of non-overlapping

gene sets of the same size. This setting is substantially

different from a real gene set database where gene

set overlap is common. By completely ignoring gene

set overlap, some methods achieve high speciﬁcity on

simulated data but behave inadequately when work-

ing in real settings. We strongly recommend that the

use of non-overlapping datasets be avoided for evalu-

ation of gene set analysis methods.

REFERENCES

Ackermann, M. and Strimmer, K. (2009). A general modu-

lar framework for gene set enrichment analysis. BMC

Bioinformatics, 10(1):47.

Alexa, A., Rahnenf

uhrer, J., and Lengauer, T. (2006). Im-

proved scoring of functional groups from gene expres-

sion data by decorrelating go graph structure. Bioin-

formatics, 22(13):1600–1607.

Araki, H., Knapp, C., Tsai, P., and Print, C. (2012). Gene-

setdb: A comprehensive meta-database, statistical and

visualisation framework for gene set analysis. FEBS

Open Bio, 2:76 – 82.

Ashburner, M., Ball, C. A., Blake, J. A., Botstein, D.,

Butler, H., Cherry, J. M., Davis, A. P., Dolinski, K.,

Dwight, S. S., Eppig, J. T., Harris, M. A., Hill, D. P.,

Issel-Tarver, L., Kasarskis, A., Lewis, S., Matese,

J. C., Richardson, J. E., Ringwald, M., Rubin, G. M.,

and Sherlock, G. (2000). Gene ontology: tool for the

uniﬁcation of biology. Nature Genetics, 25(1):25–29.

Bastian, M., Heymann, S., and Jacomy, M. (2009). Gephi:

an open source software for exploring and manipu-

lating networks. In Proceedings Of The Third Inter-

national Conference On Weblogs And Social Media

(ICWSM), volume 8, pages 361–362.

Bauer, S., Gagneur, J., and Robinson, P. N. (2010). Going

bayesian: model-based gene set analysis of genome-

scale data. Nucleic Acids Research, 38(11):3523–

3532.

Beißbarth, T. and Speed, T. P. (2004). GOstat: ﬁnd statisti-

cally overrepresented gene ontologies within a group

of genes. Bioinformatics, 20(9):1464–1465.

Berriz, G. F., King, O. D., Bryant, B., Sander, C., and Roth,

F. P. (2003). Characterizing gene sets with funcasso-

ciate. Bioinformatics, 19(18):2502–2504.

Boyle, E. I., Weng, S., Gollub, J., Jin, H., Botstein,

D., Cherry, J. M., and Sherlock, G. (2004). GO::

Termﬁnder—open source software for accessing gene

ontology information and ﬁnding signiﬁcantly en-

riched gene ontology terms associated with a list of

genes. Bioinformatics, 20(18):3710–3715.

Culhane, A. C., Schr

oder, M. S., Sultana, R., Picard, S. C.,

Martinelli, E. N., Kelly, C., Haibe-Kains, B., Ka-

pushesky, M., St Pierre, A.-A., Flahive, W., et al.

(2011). GeneSigDB: a manually curated database and

resource for analysis of gene expression signatures.

Nucleic Acids Research, page D1060–D1066.

Culhane, A. C., Schwarzl, T., Sultana, R., Picard, K. C., Pi-

card, S. C., Lu, T. H., Franklin, K. R., French, S. J.,

Papenhausen, G., Correll, M., and Quackenbush, J.

(2010). Genesigdb—a curated database of gene ex-

pression signatures. Nucleic Acids Research, 38(suppl

1):D716–D725.

Dietmann, S., Lee, W., Wong, P., Rodchenkov, I., and

Antonov, A. V. (2010). CCancer: a bird’s eye view

on gene lists reported in cancer-related studies. Nu-

cleic Acids Research, 38(suppl 2):W118–W123.

aghici, S. (2016). Statistics and data analysis for mi-

croarrays using R and bioconductor. CRC Press.

Draghici, S., Khatri, P., Martins, R. P., Ostermeier, G. C.,

and Krawetz, S. A. (2003). Global functional proﬁling

of gene expression. Genomics, 81(2):98–104.

aghici, S., Khatri, P., Martins, R. P., Ostermeier, G. C.,

and Krawetz, S. A. (2003). Global functional proﬁling

of gene expression. Genomics, 81(2):98–104.

Edgar, R., Domrachev, M., and Lash, A. E. (2002). Gene

expression omnibus: Ncbi gene expression and hy-

bridization array data repository. Nucleic Acids Re-

search, 30(1):207–210.

Efron, B. and Tibshirani, R. (2007). On testing the signiﬁ-

cance of sets of genes. The Annals of Applied Statis-

tics, pages 107–129.

Fruchterman, T. M. and Reingold, E. M. (1991). Graph

drawing by force-directed placement. Software: Prac-

tice and experience, 21(11):1129–1164.

Godec, J., Tan, Y., Liberzon, A., Tamayo, P., Bhattacharya,

S., Butte, A. J., Mesirov, J. P., and Haining, W. N.

(2016). Compendium of immune signatures identiﬁes

conserved and species-speciﬁc biology in response to

inﬂammation. Immunity, 44(1):194–206.

Hamosh, A., Scott, A. F., Amberger, J., Bocchini, C., Valle,

D., and McKusick, V. A. (2002). Online mendelian

inheritance in man (omim), a knowledgebase of hu-

man genes and genetic disorders. Nucleic Acids Res,

30(1):52–55.

Huang, D. W., Sherman, B. T., and Lempicki, R. A. (2009).

Bioinformatics enrichment tools: paths toward the

comprehensive functional analysis of large gene lists.

Nucleic Acids Research, 37(1):1–13.

Jiao, X., Sherman, B. T., Huang, D. W., Stephens, R.,

Baseler, M. W., Lane, H. C., and Lempicki, R. A.

(2012). David-ws: a stateful web service to fa-

cilitate gene/protein list analysis. Bioinformatics,

28(13):1805–1806.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

190

Johnson, N. A., Sengupta, S., Saidi, S. A., Lessan, K.,

Charnock-Jones, S. D., Scott, L., Stephens, R., Free-

man, T. C., Tom, B. D., Harris, M., et al. (2004). En-

dothelial cells preparing to die by apoptosis initiate

a program of transcriptome and glycome regulation.

The FASEB journal, 18(1):188–190.

Joshi-Tope, G., Gillespie, M., Vastrik, I., D’Eustachio, P.,

Schmidt, E., de Bono, B., Jassal, B., Gopinath, G.,

Wu, G., Matthews, L., et al. (2005). Reactome: a

knowledgebase of biological pathways. Nucleic Acids

Research, 33(suppl 1):D428–D432.

Kanehisa, M., Sato, Y., Kawashima, M., Furumichi, M., and

Tanabe, M. (2016). Kegg as a reference resource for

gene and protein annotation. Nucleic Acids Research,

44(D1):D457–62.

Kuleshov, M. V., Jones, M. R., Rouillard, A. D., Fernandez,

N. F., Duan, Q., Wang, Z., Koplev, S., Jenkins, S. L.,

Jagodnik, K. M., Lachmann, A., McDermott, M. G.,

Monteiro, C. D., Gundersen, G. W., and Ma’ayan, A.

(2016). Enrichr: a comprehensive gene set enrich-

ment analysis web server 2016 update. Nucleic Acids

Research, 44(W1):W90–W97.

Liberzon, A., Subramanian, A., Pinchback, R., Thor-

valdsd

ottir, H., Tamayo, P., and Mesirov, J. P. (2011).

Molecular signatures database (MSigDB) 3.0. Bioin-

formatics, 27(12):1739–1740.

Maere, S., Heymans, K., and Kuiper, M. (2005). BiNGO: a

cytoscape plugin to assess overrepresentation of gene

ontology categories in biological networks. Bioinfor-

matics, 21(16):3448–3449.

Nam, D. and Kim, S.-Y. (2008). Gene-set approach for ex-

pression pattern analysis. Brieﬁngs in Bioinformatics,

9(3):189–197.

Newman, J. C. and Weiner, A. M. (2005). L2L: a sim-

ple tool for discovering the hidden signiﬁcance in mi-

croarray expression data. Genome Biology, 6(9):R81.

Nishimura, D. (2001). Biocarta. Biotech Software & Inter-

net Report: The Computer Software Journal for Sci-

entists, 2(3):117–120.

Pritykin, Y., Ghersi, D., and Singh, M. (2015). Genome-

wide detection and analysis of multifunctional genes.

PLOS Computational Biology, 11(10):e1004467.

Shaffer, A. L., Wright, G., Yang, L., Powell, J., Ngo, V.,

Lamy, L., Lam, L. T., Davis, R. E., and Staudt, L. M.

(2006). A library of gene expression signatures to il-

luminate normal and pathological lymphoid biology.

Immunological Reviews, 210(1):67–85.

Shapiro, S. S. and Wilk, M. B. (1965). An analysis

of variance test for normality (complete samples).

Biometrika, 52(3/4):591–611.

Simillion, C., Liechti, R., Lischer, H. E., Ioannidis, V., and

Bruggmann, R. (2017). Avoiding the pitfalls of gene

set enrichment analysis with setrank. BMC Bioinfor-

matics, 18(1):151.

Subramanian, A., Tamayo, P., Mootha, V. K., Mukher-

jee, S., Ebert, B. L., Gillette, M. A., Paulovich, A.,

Pomeroy, S. L., Golub, T. R., Lander, E. S., et al.

(2005). Gene set enrichment analysis: A knowledge-

based approach for interpreting genome-wide expres-

sion proﬁles. Proceedings of the National Academy of

Sciences, 102(43):15545–15550.

Tarca, A. L., Bhatti, G., and Romero, R. (2013). A

comparison of gene set analysis methods in terms of

sensitivity, prioritization and speciﬁcity. PloS One,

8(11):e79217.

Tarca, A. L., Draghici, S., Bhatti, G., and Romero, R.

(2012). Down-weighting overlapping genes improves

gene set analysis. BMC Bioinformatics, 13(1):136.

Wang, J., Vasaikar, S., Shi, Z., Greer, M., and Zhang,

B. (2017). Webgestalt 2017: a more comprehen-

sive, powerful, ﬂexible and interactive gene set enrich-

ment analysis toolkit. Nucleic Acids Research, pages

W130–W137.

Wrobel, G., Chalmel, F., and Primig, M. (2005). goCluster

integrates statistical analysis and functional interpre-

tation of microarray expression data. Bioinformatics,

21(17):3575–3577.

Young, A., Whitehouse, N., Cho, J., and Shaw, C. (2005).

Ontologytraverser: an R package for GO analysis.

Bioinformatics, 21(2):275–276.

Zambon, A. C., Gaj, S., Ho, I., Hanspers, K., Vranizan,

K., Evelo, C. T., Conklin, B. R., Pico, A. R., and Sa-

lomonis, N. (2012). Go-elite: a ﬂexible solution for

pathway and ontology over-representation. Bioinfor-

matics, 28(16):2209–2210.

Zeeberg, B. R., Feng, W., Wang, G., Wang, M. D., Fojo,

A. T., Sunshine, M., Narasimhan, S., Kane, D. W.,

Reinhold, W. C., Lababidi, S., et al. (2003). GoMiner:

a resource for biological interpretation of genomic and

proteomic data. Genome Biology, 4(4):R28.

Zeeberg, B. R., Qin, H., Narasimhan, S., Sunshine, M.,

Cao, H., Kane, D. W., Reimers, M., Stephens,

R. M., Bryant, D., Burt, S. K., et al. (2005). High-

Throughput GoMiner, an ‘industrial-strength’ integra-

tive gene ontology tool for interpretation of multiple-

microarray experiments, with application to studies of

common variable immune deﬁciency (CVID). BMC

Bioinformatics, 6(1):1.

Zhang, B., Kirov, S., and Snoddy, J. (2005). WebGestalt:

an integrated system for exploring gene sets in various

biological contexts. Nucleic Acids Research, 33(suppl

2):W741–W748.

APPENDIX

Table 4: The result of Shapiro-Wilk tests for different values

of γ. All p-values are less than 0.0000001.

γ W-Statistic p value

0.10 0.783470 <0.0000001

0.20 0.773921 <0.0000001

0.30 0.771523 <0.0000001

0.40 0.770568 <0.0000001

0.50 0.770193 <0.0000001

0.60 0.769961 <0.0000001

0.70 0.769868 <0.0000001

0.80 0.769840 <0.0000001

0.90 0.769828 <0.0000001

0.99 0.769821 <0.0000001

Gene Set Overlap: An Impediment to Achieving High Speciﬁcity in Over-representation Analysis

191

Algorithm 1: Calculation of speciﬁcity of ORA.

Input:

G = {G

| 1 ≤ j ≤ m}: A gene set database

L = {L

| 1 ≤ i ≤ l}: A set of differentially

expressed gene lists

U: A set of genes used as background set

for ORA

α : The signiﬁcance level

γ : The threshold value used for identifying

true positives

Output:

Speciﬁcity value corresponding to

each L

∈ L

i = 1

while i ≤ l do

j = 1

while j ≤ m do

= ORA(G

,U)

j = j + 1

end while

Calculate p

ad justed

as the adjusted p-value corre-

sponding to p

, where (1 ≤ j ≤ m)

← {G

| p

ad justed

< α and 1 ≤ k ≤ m}

−

= G − G

Calculate T

(γ) and T

−

(γ) using Equations 5

and 6

Calculate TP

, FP

, TN

, and FN

using Equa-

tions 7, 8, 9, and 10

Calculate SPC

using Equation 11

i = i + 1

end while

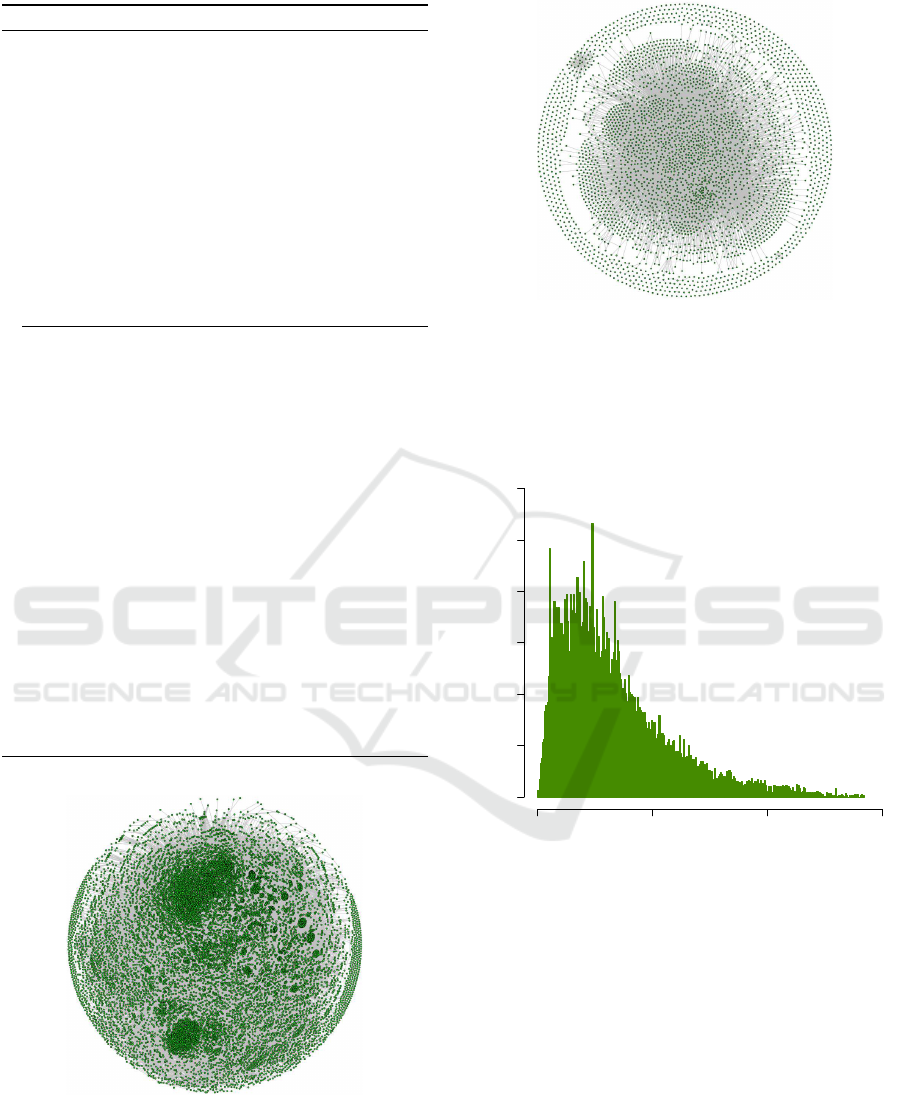
Figure 6: The graph representing the overlap between gene

sets in GeneSetDB. In this graph, each vertex represents a

gene set in GeneSetDB, and each edge represents an overlap

with Jaccard coefﬁcient greater than or equal to 0.5 between

two gene sets. The “hairball” is the result of a large number

of gene sets with a substantial overlap (≥ 0.5) with each

other.

Figure 7: The graph representing the overlap between gene

sets in GeneSigDB. In this graph, each vertex represents a

gene set in GeneSigDB, and each edge represents an overlap

with Jaccard coefﬁcient greater than or equal to 0.5 between

two gene sets. The “hairball” is the result of a large number

of gene sets with a substantial overlap (≥ 0.5) with each

other.

Frequency

0 5000 10000 15000

0 50 100 150 200 250 300

Figure 8: A frequency plot for f

values in GeneSetDB il-

lustrates the prevalence of gene set overlap. For each gene

set G

in a gene set database G (GeneSetDB here), f

is the

number of gene sets G

( j 6= i) in G with a non-zero overlap

with G

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

192

Frequency

0 500 1000 1500 2000 2500 3000 3500

0 5 10 15 20 25

Figure 9: A frequency plot for f

values in GeneSigDB il-

lustrates the prevalence of gene set overlap. For each gene

set G

in a gene set database G (GeneSigDB here), f

is the

number of gene sets G

( j 6= i) in G with a non-zero overlap

with G

Figure 10: The histogram of the speciﬁcity values (γ = 0.5).

Obvious deviation of the histogram from a bell-shaped

curve suggests that the speciﬁcity values are not normally

distributed. A similar pattern was observed for other values

of γ.

Gene Set Overlap: An Impediment to Achieving High Speciﬁcity in Over-representation Analysis

193