Polyp Shape Recovery using Vascular Border from Single Colonoscopy

Image

Hiroyasu Usami

, Yuji Iwahori

, M. K. Bhuyan

, Aili Wang

, Naotaka Ogasawara

and Kunio Kasugai

Department of Computer Science, Chubu University, Kasugai, Japan

Department of Electronics and Electrical Engineering, Indian Institute of Technology Guwahati, Guwahati, India

Higher Education Key Lab., Harbin University of Science and Technology, Harbin, China

Department of Gastroenterology, Aichi Medical University, Nagakute, Japan

{nogasa, kuku3487}@aichi-med-u.ac.jp

Keywords:

Shape from Shading, Lambertian Surface, Specular Removal, U-net, RANSAC, Colonoscopy.

Abstract:

The shape and size of a colonic polyp is a biomarker that correlates with its risk of malignancy and guides its

clinical management. It is the most accurate method for detecting polyps of all sizes, and it allows biopsy of

lesions and resection of most polyps, and it is considered nowadays as the gold standard for colon screening.

However, there are still open challenges to overcome, such as the reduction of the missing rate. Colonoscopy

images usually consist of nonrigid objects such as a polyp, and no approaches have been proposed to recovery

shape and absolute size from a single image. Hence, it is a challenging topic to reconstruct polyp shape using

computer vision technique. This paper proposes a polyp shape retrieval method based on Shape from Shading

(SFS), and this research contributes to mitigating constraint for applying SFS to the single colonoscopy image

using vascular border information. Experiments conﬁrmed that the proposed method recovered approximate

polyp shapes.

1 INTRODUCTION

A polyp guideline for the diagnosis, treatment,

and surveillance for patients with colorectal polyps

published originally in 1993(Bond, 1993), and it

has been developing following evidence-based(Force,

1989)(Winawer et al., 1997)(Byers et al., 1997). The

guideline indicates that the shape and size of a colo-

nic polyp is a biomarker that correlates with its risk of

malignancy and guides its clinical management.

Endoscopy images usually consist of nonrigid ob-

jects such as a polyp so that applying photoclinometry

based recovery approach is reasonable for the issue

mentioned earlier. Shape from Shading (SFS)(Horn,

1989) is as one valuable approach based on photocli-

nometry. SFS uses the intensity of images directly to

reconstruct the target object surface orientation from

a single image. Some approaches (Iwahori et al.,

2015)(Wu et al., 2010) reconstructed 3D shape from

colonoscopy image based on SFS. The paper(Iwahori

et al., 2015) proposed a polyp recovery approach

using both photometric and geometric constraints as-

suming one light source colonoscopy. Another ap-

proach(Usami et al., 2016) reconstructed polyp shape

considering more actual colonoscopy, which has two

light sources, and it used a neural network to modify

the obtained surface gradients. In case of besides tar-

geting polyp, the paper (Wu et al., 2010) proposed a

3D shape recovery method for an artiﬁcial spine.

SFS and colonoscopy image are compatible on the

ﬁrst sight, but there are constraints for applying SFS

to colonoscopy image. Those approaches need some

parameters like a depth Z from colonoscopy lens to

the surface, and surface reﬂectance coefﬁcient C Furt-

hermore, those approaches assume the whole surface

which has same the C and the Lambertian surface.

This research contributes mitigating constraint for ap-

plying SFS to the colonoscopy regardless of genera-

ting Lambertian image processing based on vascula-

ture structure and its border. The outline of this pa-

per is as follows. Firstly, an assumed observation sy-

stem and photometric constraints are introduced. In

the next, preprocessing and approaches which obtai-

ning parameters using vascular are described for po-

lyp shape retrieval. In the experiment, evaluation is

conducted using actual colonoscopy images. Finally,

104

Usami, H., Iwahori, Y., Bhuyan, M., Wang, A., Ogasawara, N. and Kasugai, K.

Polyp Shape Recovery using Vascular Border from Single Colonoscopy Image.

DOI: 10.5220/0007379101040111

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 104-111

ISBN: 978-989-758-353-7

conclude the proposed approach and discuss future

works in conclusion.

2 ALGORITHM

The proposed approach assumes an observation sy-

stem of two light source colonoscopy for polyp shape

recovery, and consists of following steps.

Step0. Assume an observation system of two light

source colonoscopy.

Step1. Estimate the camera parameters by con-

ducting camera calibration.

Step2. Conduct specular highlight removal.

Step3. Conduct blood vessel extraction using U-net.

Step4. Obtain depth Z and reﬂectance coefﬁcient

C of blood vessels by estimating its horizontal

plane, and using its geometric structure.

Step5. Obtain depth Z and reﬂectance coefﬁcient

C of intestinal-inner-walls using borders between

blood vessels and optimization.

2.1 Observation System of Two Light

Source Colonoscopy

The observation system of the colonoscopy is assu-

med to be a point light source and perspective pro-

jection. According to the actual environment of the

colonoscopy, two light point sources are assumed as

shown in Fig.1.

Figure 1: Observation System of Two Light Sources En-

doscope.

Here, let the coordinate of the center of the lens

be (0,0,0), let both light source coordinate be s

(a, b, 0) and s

= (c, d, 0), let f be focal length, let

each distance from light source to surface be l

and

. Let n be the normal surface vector. Image intensity

E and reﬂectance coefﬁcient C can be denoted Eq.(1)

following illuminance inverse square law.

E = C(

n · s

) (1)

Eq.(1) can be denoted using depth Z from the lens

to the surface as following equations. Normal vector

n on arbitrary point of diffuse reﬂectance surface can

be represented Eq.(2).

n =

(p, q, −1)

+ q

+ 1

(2)

Here, let each p, q be surface gradient.

(p, q) = (

∂Z

∂X

∂Z

∂Y

) (3)

Let arbitrary surface point be X , Y, Z, l

and l

can

be represented

(a − X)

+ (b −Y)

+ Z

(4)

(c − X)

+ (d −Y )

+ Z

(5)

Both light source vector s

and s

on arbitrary

point of diffuse reﬂectance surface can be denoted as

follows.

(a − X, b −Y, −Z)

(a − X)

+ (b −Y)

+ Z

(6)

(c − X, d −Y, −Z)

(c − X)

+ (d −Y )

+ Z

(7)

World coordinate X, Y are represented by Eq.(8)

X =

Z, Y =

Z (8)

Substituting Eq.(2)-Eq.(8) into Eq.(1), E and C

can be denoted using Z as Eq.(9).

E =

+ q

+ 1

−p(a −

Z) − q(b −

Z) + Z



(a −

+ (b −

+ Z



−p(c −

Z) − q(d −

Z) + Z



(c −

+ (d −

+ Z



(9)

The proposed method reconstructs the 3D shape from

colonoscopy images postulated in the observation

model. This Eq.(9) is used to solve each C of the

blood vessel and the intestinal-inner-wall (Based on

Eq.(16) and Eq.(26)).

Polyp Shape Recovery using Vascular Border from Single Colonoscopy Image

105

2.2 Camera Calibration

Camera parameters of the colonoscopy are estima-

ted. Estimating camera parameters of the colo-

noscopy is performed using multiple images of chec-

kerboard taken by colonoscopy following existing ca-

mera calibration techniques(Zhang, 2000)(Heikkila

and Silv

en, 1997). Fig.(2) shows examples of chec-

ker board image which taken by an colonoscopy is as

shown in Fig.(2).

Figure 2: Examples of Checker Board.

Furthermore, positions of two light source on co-

lonoscopy S

= (a, b, 0) and S

= (c, d, 0) are estima-

ted by conducting optimization for a know sphere ob-

ject image taken by the colonoscopy.

2.3 Specular Highlight Removal

The spectral energy distribution of the light reﬂected

from the surface can be denoted as the product of the

spectral energy distribution of the illumination and

the surface reﬂectance. Following the dichromatic re-

ﬂection model (Shafer, 1985), the reﬂected light can

be separated into two components specular and dif-

fuse reﬂection. Specular components affect the result

of shape recovery under SFS approach and, frequently

arise on the colonoscopy image. The paper (Tchou-

lack et al., 2008) proposed the specular components

removal method on colonoscopy image by conducting

the in-painting process to specular components. Mo-

diﬁed region by in-painting process lacks the surface

information.

The diffuse color component has a characteris-

tic that the maximum fraction of the diffuse color

component in diffuse local patches in color images

changes smoothly. Hence specular components can

be removed by following this characteristic. Furt-

hermore, the proposed approach obtains depth Z and

reﬂectance coefﬁcient C based using the border bet-

ween blood vessels and intestinal-inner-walls. Specu-

lar components removal process should be done wit-

hout removing the border between blood vessel and

intestinal-inner-walls since the border information is

used when reﬂectance coefﬁcient C is estimated sepa-

rately at each region around the border. The propo-

sed approach removes specular components introdu-

cing bilateral ﬁlter based on the method(Yang et al.,

2010)(Yang et al., 2015).

2.4 Blood Vessel Segmentation

The proposed approach obtains depth Z and reﬂec-

tance coefﬁcient C using blood vessel information.

As segmentation methods, some methods were propo-

sed (Carreira and Sminchisescu, 2011)(Uijlings et al.,

2013)(Ronneberger et al., 2015). In this case, the de-

sired output should include localization, i.e., a class

label is supposed to be assigned to each pixel, and

segmentation method should be applicable to vascu-

lature structure. This paper proposes a method based

on the U-net architecture(Ronneberger et al., 2015).

The network architecture of the proposed method

is shown in Fig.3. The network architecture was con-

structed with less down sampling layers because the

resolution of the targeted colonoscopy images is not

high.

Figure 3: Network Architecture.

The loss function is the cross-entropy and the neu-

ral network employees the stochastic gradient des-

cent for optimization. The activation function after

each convolutional layer is the Rectiﬁer Linear Unit

(ReLU) and dropout of 0.2 are used between two con-

secutive convolutional layers.

2.5 Obtaining Depth Z and Reﬂectance

Coefﬁcient C

The parameters Z and C for shape recovery under SFS

approach are obtained by estimating blood vessel ho-

BIOIMAGING 2019 - 6th International Conference on Bioimaging

106

rizontal plane locally with considering a horizontal

plane in the observation system.

2.5.1 Estimation of the Horizontal Plane

The horizontal planes of columnar forms against lens

can be obtained by considering the continuity of

width from columnar centerline to both end of edge.

The columnar width cropped by the horizontal plane

against lens as shown in Fig.4 continues while the

cropped region are horizon against lens. The hori-

zontal planes of blood vessel can be obtained locally

based on this property. The procedure of obtaining

the horizontal plane is as follows.

Here, for the explicit description of the algorithm,

Fig6 to Fig.9 show the procedure using an example of

colonoscopy image with partial blood vessel.

Step1 Extract a blood vessel region in Fig.6 from the

original image in Fig.5.

Step2 Extract centerline of the blood vessel by per-

forming line thinning processing as shown in

Fig.7.

Step3 Extract edge of blood vessel using morpho-

logy operation as shown in Fig.8.

Step4 Draw a line orthogonal to the centerline and

crop the line by both end of edge. Finally, extract

continuous regions where the cropped line has the

same width as shown in Fig.9.

Figure 4: Horizontal Plane of Columnar against lens.

Figure 5: Original Image.

Figure 6: Example of Extrac-

ted Blood Vessel Region.

Figure 7: Example of Line

Thinning Processing.

Figure 8: Example of Edge

Extraction.

Figure 9: Example of Estimation of Horizontal Plane.

2.5.2 Estimation of Blood Vessel Z and C

Fig.10 shows an observation model for obtaining

depth parameter Z of the blood vessel using its ho-

rizontal plane.

The depth Z from the colonoscopy lens can be cal-

culated using the model with respect to the estimated

horizontal plane of the blood vessel. The procedure

for calculating parameter Z is described below.

Figure 10: Observation System of Horizontal Plane.

From 4LOI

∼ 4LS

and ∠LS

is an external

angle of 4LS

, ∠LS

can be obtained by Eq.(10).

∠LS

= π − ∠LI

O (10)

From 4LOI

∼ 4LS

,4LS

can be expressed

from Eq.(11) and Eq.(12).

∠LS

= ∠LI

O (11)

Polyp Shape Recovery using Vascular Border from Single Colonoscopy Image

107

∠S

= π − ∠LS

− ∠LS

(12)

Similarly, ∠L S

can be obtained from Eq.(13).

∠LS

= π −

− ∠S

(13)

The hypotenuse from the lens L to the center of

the suture center S

in 4LS

, the distance LS

can

be obtained from Eq.(14). Here, the distance P

the same as the radius of blood vessel.

cos∠LS

(14)

The distance from the lens L to the surface of the

blood vessel P

can be obtained from Eq.(15). Here,

is the same as the radius of blood vessel.

= LS

− P

(15)

From 4LZP

∼ 4LOI

, the depth Z can be obtai-

ned from Eq.(16).

Z = LP

sin∠LI

O (16)

Here, each surface gradient parameter p, q is

obtained stand for the xz plane and the yz plane re-

spectively. The gradient surface parameter p is obtai-

ned from a gradient of orthogonal line to the line pas-

sing L = (0, 0) and P

= (

Z, Z) on the xz plane. The

gradient of the line passing L and P

is obtained from

Eq.(17)

(17)

The surface gradient p can be obtained from the ort-

hogonal line to the obtained gradient from Eq.(17) as

shown in Eq.(18)

p = −

(18)

The gradient surface parameter q is obtained from

a gradient of orthogonal line to the line passing L =

(0, 0) and P

= (

Z, Z) on the yz plane. The gradient

of the line passing L and P

is obtained from Eq.(19)

(19)

The surface gradient q can be obtained from the ort-

hogonal line to the obtained gradient from Eq.(19) as

shown in Eq.(20)

q = −

(20)

Finally, substituting obtained Z, p, q and image

intensity E to Eq.(9), C of the blood vessel is obtai-

ned. Here, horizontal plane sections where the same

width continues more than 6 tracing the center line of

medical suture were adapted as horizontal plane secti-

ons, and calculate MEAN and STD of both Z and C

for each section, then, C is selected by the following

process. C is conﬁrmed in order from the section

where the continuous section of the same width re-

gion is long and Z with less STD is obtained, and

MEDIAN of C, where the outlier value is not obtai-

ned and with the low value of STD, is selected, and

Smirnov-Grubbs test(Grubbs et al., 1950) was used

for outliers.

2.5.3 Estimation of Intestinal-inner-wall Z and C

Assuming the blood vessel and the intestinal-inner-

wall have continuous surface, intestinal-inner-wall

parameters Z and C are derived by using the boundary

surface as shown in Fig.11.

Figure 11: Boundary Surfaces between Blood Vessel and

Intestinal-Inner-Wall.

Here, the red color in the ﬁgure is deﬁned as

a blood vessel region and Known point. Let an

intestinal-inner-wall neighboring the blood vessel be

a Trial point. Let a blood vessel point located x axis

be a Known point K

. Let a blood vessel point lo-

cated y axis be a Known point K

A depth Z of a Trial point Z

can be represen-

ted using its surface gradient (p, q) and a Z of Known

point as shown in Eq.(21). Here, ∆X = X

− X

, ∆Y =

−Y

= Z

+ p∆X + q∆Y (21)

Each ∆X, ∆Y denotes a distance of x axis and y

axis respectively on the world coordinate system per-

spective projection as shown in Eq.(22).

= Z

+ p



− x



+ q



− y



(22)

Solving Eq.(22) for Z, Eq.(23) can be obtained.



1 − px

− qy



= Z



1 − px

− qy



(23)

Let Z

be Z

expect

, the Z

expect

can be denoted as

shown in Eq.(24)

expect

( f − px

− qy

)

f − px

− qy

(24)

BIOIMAGING 2019 - 6th International Conference on Bioimaging

108

Finally, deﬁne f (p, q, a, b, c, d, f , Z) as Eq.(25)

using Eq.(9), the surface reﬂectance coefﬁcient C

of intestinal-inner-wall is estimated by optimization

using RANSAC (Fischler and Bolles, 1981) and

Eq.(26). Here, let p and q be surface gradient, let

each light source coordinate be a, b, c, d, let f be fo

focal length, let Z be the calculated depth and let E

be each real intensity E.

f (p, q, a, b, c, d, f , Z) =

+ q

+ 1

−p(a −

Z) − q(b −

Z) + Z



(a −

+ (b −

+ Z



−p(c −

Z) − q(d −

Z) + Z



(c −

+ (d −

+ Z



(25)

opt

= arg min

∑

i=1

||E

−C f (p, q, a, b, c, d, f , Z)||

(26)

3 EXPERIMENT

3.1 Camera Calibration

The result of camera calibration is shown in Table.1.

The colonoscopy inner parameters as focal length,

principal point and radial distortion were obtained by

performing camera calibration.

Here, two parameters were obtained respectively

because of aspect ratio.

Table 1: Result of Estimation.

Parameter Result of Calibration

Focal length (pixels)

[ 718.7447 + / - 0.8387,

718.3827 + / - 0.8654 ]

Principal point (pixels)

[ 879.0439 + / - 0.4669,

533.5813 + / - 0.4240 ]

Radial distortion

[ - 0.3913 + / - 0.0010,

0.1178 + / - 0.0008 ]

Positions of two light source on colonoscopy were

estimated using sphere object image taken by the co-

lonoscopy. Positions of two light source estimated are

= (a : −5.001, b : 1.996, 0) and S

= (c : 5.001, d :

1.996.0).

3.2 Blood Vessel Extraction

The vessel probability of each pixel was obtained by

averaging multiple predictions to improve the perfor-

mance. With a stride of 5 pixels in both height and

width, multiple consecutive overlapping patches were

extracted in each test image. Then, the vessel proba-

bility was obtained for each pixel by averaging pro-

babilities over all the predicted patches covering the

pixel.

Evaluation was done using masked images crea-

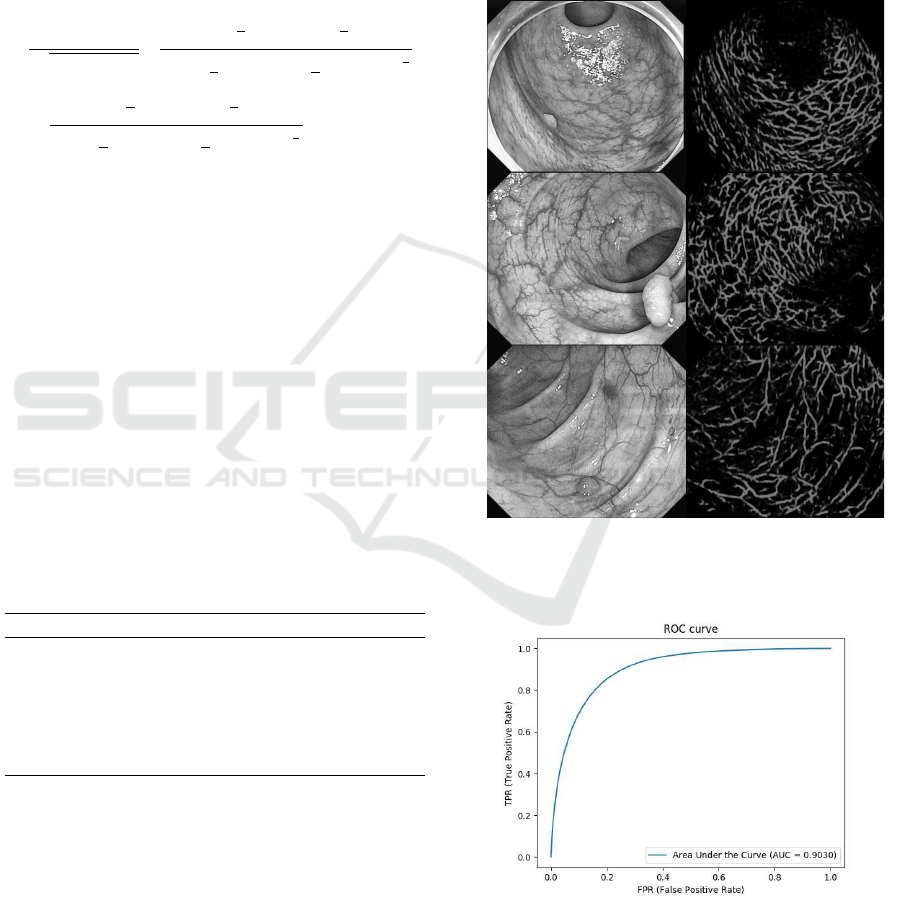
ted by manual drawing as ground truth. Fig.12 shows

the results of colon blood vessel detection and overall

accuracy of the prediction was 0.8432.

Figure 12: Example of Prediction Results.

Fig.13 shows the Area Under the ROC curve

(AUC ROC) of the evaluation, and AUC was 0.9030.

Figure 13: AUC ROC.

From the result of blood vessel extraction, the pro-

posed method extracted blood vessel region accura-

tely.

Polyp Shape Recovery using Vascular Border from Single Colonoscopy Image

109

3.3 Polyp Shape Reconstruction

Using blood vessel information and obtained parame-

ters, polyp shape recovery was performed. There are

some obstacles like as body part of the colonoscopy

for shape recovery depend on the scene, so that co-

lonoscopy images were cropped for applying the pro-

posed method. Each original colonoscopy image are

shown in Fig.14,18,22, selected regions of blood ves-

sel horizontal plane are shown in Fig.15,19,23, shape

recovery images are shown in Fig.16,20,24 and size

measurement result image are shown in Fig.17,21,25.

Figure 14: Original Image 1. Figure 15: Selected hori-

zontal region for Image 1.

Figure 16: Recovered

Shape for Image 1.

Figure 17: Size Measure-

ment Result in Image 1 af-

ter Extraction.

Figure 18: Original Image 2. Figure 19: Selected hori-

zontal region for Image 2.

Figure 20: Recovered

Shape for Image 2.

Figure 21: Size Measure-

ment Result for Image 2

after Extraction.

Figure 22: Original Image 3. Figure 23: Selected hori-

zontal region for Image 3.

Figure 24: Recovered

Shape for Image 3.

Figure 25: Size Measure-

ment Result for Image 3

after Extraction.

Each C has obtained as 89217, 118153, 23074, re-

spectively. Compared with measured images after ex-

traction and shape recovery result, approximate polyp

shape was reconstructed using blood vessel informa-

tion and obtained parameters.

4 CONCLUSION

This paper proposed a polyp shape recovery met-

hod which mitigated the constraint for applying SFS

to the colonoscopy image based on the vasculature

structure. The proposed approach assumed two light

source endoscope according to the actual environment

for polyp shape retrieval. Parameters for applying

SFS, the camera inner parameters were obtained by

conducted camera calibration, depth Z and reﬂectance

coefﬁcient C were obtained by estimating vascular

horizontal plane and using its border of neighboring

intestinal-inner-walls. From experiments, it is con-

ﬁrmed that the proposed method recovered approx-

imate absolute polyp shape using vascular informa-

tion and obtained parameters from a single endoscope

image. Especially, regardless of generating Lamber-

tian image processing, the proposed method realized

polyp shape recovery from a single endoscope image.

ACKNOWLEDGEMENTS

This research is supported by JSPS Grant-in-Aid for

Scientiﬁc Research (C) (17K00252) and Chubu Uni-

versity Grant.

BIOIMAGING 2019 - 6th International Conference on Bioimaging

110

REFERENCES

Bond, J. H. (1993). Polyp guideline: diagnosis, treatment,

and surveillance for patients with nonfamilial colorec-

tal polyps. Annals of internal medicine, 119(8):836–

843.

Byers, T., Levin, B., Rothenberger, D., Dodd, G. D., Smith,

R. A., Detection, A. C. S., and on Colorectal Cancer),

T. A. G. (1997). American cancer society guidelines

for screening and surveillance for early detection of

colorectal polyps and cancer: update 1997. CA: a can-

cer journal for clinicians, 47(3):154–160.

Carreira, J. and Sminchisescu, C. (2011). Cpmc: Automa-

tic object segmentation using constrained parametric

min-cuts. IEEE Transactions on Pattern Analysis &

Machine Intelligence, (7):1312–1328.

Fischler, M. A. and Bolles, R. C. (1981). A paradigm

for model ﬁtting with applications to image analy-

sis and automated cartography (reprinted in readings

in computer vision, ed. ma ﬁschler,”. Comm. ACM,

24(6):381–395.

Force, U. P. S. T. (1989). Guide to clinical preventive servi-

ces: report of the US Preventive Services Task Force.

DIANE publishing.

Grubbs, F. E. et al. (1950). Sample criteria for testing out-

lying observations. The Annals of Mathematical Sta-

tistics, 21(1):27–58.

Heikkila, J. and Silv

en, O. (1997). A four-step camera ca-

libration procedure with implicit image correction. In

Computer Vision and Pattern Recognition, 1997. Pro-

ceedings., 1997 IEEE Computer Society Conference

on, pages 1106–1112. IEEE.

Horn, B. K. (1989). Obtaining shape from shading infor-

mation. In Shape from shading, pages 123–171. MIT

press.

Iwahori, Y., Tatematsu, K., Nakamura, T., Fukui, S., Wood-

ham, R. J., and Kasugai, K. (2015). 3d shape recovery

from endoscope image based on both photometric and

geometric constraints. In Knowledge-Based Informa-

tion Systems in Practice, pages 65–80. Springer.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:

Convolutional networks for biomedical image seg-

mentation. In International Conference on Medical

image computing and computer-assisted intervention,

pages 234–241. Springer.

Shafer, S. A. (1985). Using color to separate reﬂection com-

ponents. Color Research & Application, 10(4):210–

218.

Tchoulack, S., Langlois, J. P., and Cheriet, F. (2008). A vi-

deo stream processor for real-time detection and cor-

rection of specular reﬂections in endoscopic images.

In Circuits and Systems and TAISA Conference, 2008.

NEWCAS-TAISA 2008. 2008 Joint 6th International

IEEE Northeast Workshop on, pages 49–52. IEEE.

Uijlings, J. R., Van De Sande, K. E., Gevers, T., and Smeul-

ders, A. W. (2013). Selective search for object re-

cognition. International journal of computer vision,

104(2):154–171.

Usami, H., Hanai, Y., Iwahori, Y., and Kasugai, K. (2016).

3d shape recovery of polyp using two light sources

endoscope. In Computer and Information Science

(ICIS), 2016 IEEE/ACIS 15th International Confe-

rence on, pages 1–6. IEEE.

Winawer, S. J., Fletcher, R. H., Miller, L., Godlee, F., Sto-

lar, M., Mulrow, C., Woolf, S., Glick, S., Ganiats, T.,

Bond, J., et al. (1997). Colorectal cancer screening:

clinical guidelines and rationale. Gastroenterology,

112(2):594–642.

Wu, C., Narasimhan, S. G., and Jaramaz, B. (2010). A

multi-image shape-from-shading framework for near-

lighting perspective endoscopes. International Jour-

nal of Computer Vision, 86(2-3):211–228.

Yang, Q., Tang, J., and Ahuja, N. (2015). Efﬁcient and

robust specular highlight removal. IEEE transacti-

ons on pattern analysis and machine intelligence,

37(6):1304–1311.

Yang, Q., Wang, S., and Ahuja, N. (2010). Real-time specu-

lar highlight removal using bilateral ﬁltering. In Eu-

ropean conference on computer vision, pages 87–100.

Springer.

Zhang, Z. (2000). A ﬂexible new technique for camera ca-

libration. IEEE Transactions on pattern analysis and

machine intelligence, 22(11):1330–1334.

Polyp Shape Recovery using Vascular Border from Single Colonoscopy Image

111