Enhanced Waters 2D Muscle Model for Facial Expression Generation

Dinesh Kumar and Dharmendra Sharma

Faculty of Science and Technology, University of Canberra, ACT, Australia

Keywords: Physics-based Model, Muscle Model, Facial Expression, Facial Animation, FACS.

Abstract: In this paper we present an improved Waters facial model used as an avatar for work published in (Kumar

and Vanualailai, 2016), which described a Facial Animation System driven by the Facial Action Coding

System (FACS) in a low-bandwidth video streaming setting. FACS defines 32 single Action Units (AUs)

which are generated by an underlying muscle action that interact in different ways to create facial

expressions. Because FACS AU describes atomic facial distortions using facial muscles, a face model that

can allow AU mappings to be applied directly on the respective muscles is desirable. Hence for this task we

choose the Waters anatomy-based face model due to its simplicity and implementation of pseudo muscles.

However Waters face model is limited in its ability to create realistic expressions mainly the lack of a

function to represent sheet muscles, unrealistic jaw rotation function and improper implementation of

sphincter muscles. Therefore in this work we provide enhancements to the Waters facial model by

improving its UI, adding sheet muscles, providing an alternative implementation to the jaw rotation

function, presenting a new sphincter muscle model that can be used around the eyes and changes to

operation of the sphincter muscle used around the mouth.

1 INTRODUCTION

A widely accepted theoretical foundation for the

control of facial expression generation is the Facial

Action Coding System (FACS). FACS is based on

an anatomical analysis of facial movements and has

been developed by psychologists P. Ekman and W.E

Frieson (Ekman and Frieson, 1977). In 2002, a new

version of FACS was published, with large

contributions by Joseph Hager (Hagar et al., 2002).

It was designed primarily to measure facial

movement relevant to emotion. The aim was to

develop a comprehensive system which could

distinguish all possible identifiable facial

movements. Since every facial movement is the

result of muscular actions on the face, to render

FACS on a computer face model requires a model

on which the FACS Action Units (AUs) can be

easily mapped onto.

In this paper we present an improved Waters

facial model used as an avatar for work published in

(Kumar and Vanualailai, 2016), which describes a

Facial Animation System (FAS) driven by FACS in

a low-bandwidth video streaming setting. The

overall aim is to prepare a facial model on which

FACS AU activations can be directly applied onto

their corresponding facial muscle to generate an

expression or combination of expressions. We note

that the domain of computer facial modelling has

advanced tremendously over the last decade as

described by (Alkawaz et al., 2015) and focus has

shifted more to non-muscle based systems. However

work dedicated to enhancement of muscle based

models in recent years has been few and limited.

Our reasons for selection of Water muscle model

have been due to its simplicity, implementation of

pseudo muscles and the availability of the software

in C++ for the basic model. However Waters face

model comes with limitations in its ability to create

realistic expressions; mainly the lack of a function to

represent sheet muscles, unrealistic jaw rotation

function and improper implementation of sphincter

muscles. Hence in this paper we present a thorough

investigation of the Waters muscle-based model and

provide enhancement to the basic model by:

 adding sheet muscles;

 providing an alternate implementation to the jaw

rotation function;

 presenting a new sphincter muscle equation that

can be used around the eyes;

 changes to operation of the sphincter muscle

used around the mouth; and

262

Kumar, D. and Sharma, D.

Enhanced Waters 2D Muscle Model for Facial Expression Generation.

DOI: 10.5220/0007379302620269

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 262-269

ISBN: 978-989-758-354-4

 improving its UI

Through this work we would also like to highlight

the importance of developing muscle-based models

to represent the anatomy of the human face more

accurately in order to generate realistic expressions.

The rest of the paper is organised as follows: In

section 2 we review related work in the field of

facial modelling. Section 3 describes our Facial

Model component FAS. In section 4, we present the

implementation and test results followed by

conclusion in section 5.

2 RELATED WORK

Initial efforts in 3D facial modelling began with

(Parke, 1972) who developed the first parameterized

facial model. (Waters, 1987) and (Magnenat-

Thalmann et al., 1988) follow soon by developing

pseudo muscle based models. The technique of free

form deformations were also used to create facial

expressions for example in (Kalra, et al., 1992).

(Kahler et al., 2001) utilised geometry based muscle

modelling for facial animation whereas (Ostermann,

1998) used the MPEG-4 standard to animate

synthetic faces.

The state of the art in facial animation has

advanced tremendously over the years. There is

increasing effort by researchers to perfect the facial

model to produce quality and realistic expressions.

As a consequence some new and hybrid methods are

continuously being developed using FACS (Tolba et

al., 2018). For example an interactive region-based

linear 3D face model, developed by (Tena et al.,

2011) effectively divided the facial model into

regions with user-given constraints in the form of

markers placed on the face model. These markers

when activated affected only the region in which

they were placed and produced better effects than

using the same markers on a region less model.

(Lewis et al., 2014) in their paper discuss the

practice and theory of blend shape models. Real time

performance based facial animation that enables the

user to control the facial expression of a digital

avatar in real-time is proposed by (Weise et al.,

2011). (Pauly, 2013) and (Bermano et al., 2013)

proposed similar facial performance based models.

There has also been success in producing facial

animation from video or motion capture data. A

paper by (Sifakis et al., 2005) described an

implementation where muscle activations were

automatically determined from motion capture

marker data. Motion detectors or sensors that are

susceptible to movements can be utilised to detect

facial expressions and then animated on a computer

facial model.

Recent research has shown a renewed interest in

using FACS as the basis for generating and

measuring facial expressions. For example (Alkawaz

et al., 2015) combined blend shape interpolation

(BSI) and FACS to create realistic and expressive

facial animation. They trialled their system on four

basic emotions; anger, happy, sad, and fear defined

in FACS. (Tolba et al., 2018) discussed the

applications and limitations of FACS by comparing

with MPEG-4 facial animation based systems.

Articles such as (Ping et al., 2013; Li et al., 2012;

Sandbach et al., 2012; Ersotelos and Dong, 2008;

Alkawaz et al., 2014) provide a good survey of

techniques developed in the area of facial modelling

in recent times while (Noh and Neumann, 1998)

provides a review on theories and techniques

developed decades ago which are a foundation of

facial modelling techniques of the modern world.

3 FACIAL MODEL IN FAS

In this research we use the Facial Animation System

(FAS) described in (Kumar and Vanualailai, 2016).

The original Waters face geometry is retained and

used in the Facial Model component in FAS. It is

based on facial anatomy which dictates that facial

expressions are created by relaxation and tightening

of facial muscles. These muscles on the face can be

categorized into three types: linear muscles, sheet

muscles and sphincter muscles. Mixtures of these

muscle types coordinate to produce each facial

expression.

Waters modelled two types of muscles: linear

muscles that pull vertices under its region of

influence towards the point of attachment on the

skin; and a sphincter muscle around the mouth that

pulls the vertices under its region of influence

towards the center of an ellipse. The third muscle

type (sheet muscles) was not implemented in the

original Waters model but was described in detail in

(Zhang et al., 2001). The equations we use in this

paper are drawn from (Tanguy, 2001; Edge and

Maddock, 2001) which is based on the original

Waters model publication, but expressed in a

simplified form for understanding. The geometry

comprises of 236 interconnected vertices forming

876 triangular polygons. The reader is directed to

(Waters, 1987) to inspect the original visual

representation of the muscles and the facial model.

In our Facial Model we reduced the number of

linear muscles from 24 to 18. Figure shows the

Enhanced Waters 2D Muscle Model for Facial Expression Generation

263

linear muscles retained in our model. Comparing

this with Waters model one can note that linear

muscles around the mouth have been removed as

they produced unrealistic expressions on the facial

model. They have been replaced a sphincter muscle.

We omit the discussion of the equations of the linear

muscle in this paper as this is about the only change

that was made to this vector muscle. The reader is

directed to (Waters, 1987) for a full description of

linear muscles.

3.1 Enhancements to Waters Model

In the following sub sections we describe the

equations of the sphincter and sheet muscles and

modifications to the original model equations to

bring about enhancements to the Waters face model

to a level that allowed us to use it in FAS. We also

describe the new jaw rotation function and

improvements in the user interface to enable

recordings of expressions defined by AUs.

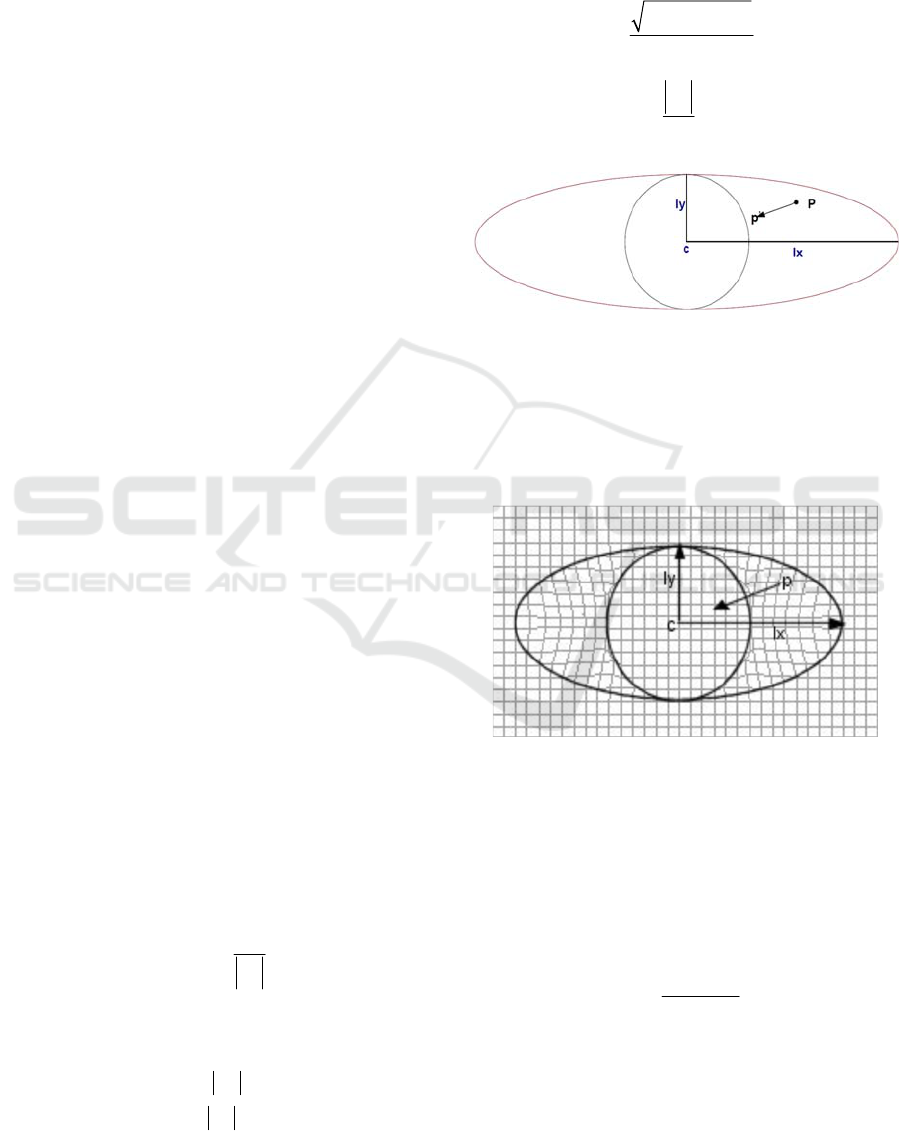
3.1.1 Sphincter Muscles

The sphincter muscle is modeled by Waters as an

elliptical shape and can be simplified to a parametric

ellipsoid. Vertices within the ellipsoid are drawn

towards the center of the ellipsoid (like a drawstring

bag) with maximum movement depended on how far

the vertex position is from the center of the ellipsoid.

Figure 1 and Figure 2 illustrate the sphincter muscle

in the

,xy

plane with the following definitions:

: An arbitrary facial skin point.

: Epicenter of the sphincter muscle influence

area.

: The semi-major axis of the sphincter muscle

influence area.

: The semi-minor axis of the sphincter muscle

influence area.

The following equation therefore can be used to

compute the new position

of the vertices at an

arbitrary point P in the

,xy plane within the

ellipsoid.

pPKD







(1)

where

is the muscle spring constant and

calculated as:

fg for Pc ly

for Pc ly























(2)

where

is the coefficient of the vertex displacement

for the sphincter muscle in the xy plane, and g is

the proportional distance of the vertex position from

the center of the ellipse, i.e.,

22 22

ly P lx P

lxly





(3)







(4)

Figure 1: Sphincter muscle model.

The calculation of

above protects the central

area of the ellipse (bounded by a circle with radius

equal to

) from vertices from piling up on top of

each other towards the center of the ellipse by

muscle contractions.

Figure 2: Vertices contracting towards center of sphincter

muscle. (Edge and Maddock, 2001).

Equations 1-4 simulate the working of the

sphincter model in 2D. In real lips, the skin

protrudes (bulges) towards the center of the lips,

hence displacement in the z axis is needed for 3D

visualisation. This can be achieved by calculating

for



as:

(1 )

Kfg









(5)

where

is a constant greater than 0 and is used to

control the peak of the protrusion. Implementation

of the sphincter muscles around the mouth is shown

in Figure 3. The example expression is created with

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

264

0.3K  and 10Z  . In this paper we modify the

original Waters program to use three sphincter

muscles; one each around the eyes and one covering

the mouth opening area. The sphincter muscle used

around the mouth area is derived from Waters

original sphincter muscle equation where the

vertices converge towards the centre of the muscle.

However the orbicularis oris muscle that surrounds

the eye behaves a bit differently. It does not have the

ability to pull the corners of the eyelids towards the

center of the eye. Instead it is only able to pull the

upper and lower eyelids towards each other. Hence

to use the above sphincter equations for the eyes it

had to be modified so that the vertices converge

towards the semi-major axis of the ellipse defining

the influence area around the eyes. This gives the

model the ability to “squint” eyes.

Figure 3: Application of the sphincter muscle on the area

round the mouth.

Figur illustrates our eye sphincter muscle in the

ݔݕ plane with the same definitions as for the normal

sphincter muscle. We note here that the

displacement is along theݕെܽݔ݅ݏ. The new

equation to compute the new position ݌

ᇱ

of the

vertices at an arbitrary point ܲ in the ݔݕ plane within

the ellipsoid in Figure 5 is:

pPKD







(6)

where

is the muscle spring constant and is

calculated as:

Dfg

(7)

Here,

is the coefficient of the vertex displacement

for the sphincter muscle along the

yaxis

plane

and

is the proportional distance of the vertex

position perpendicular to the

axis , i.e.,

ly P



(8)







(9)

Figure 4: Vertices converging to the semi-major axis.

Figure 5: Sphincter muscle diagram for use around the

eyes.

Figure 6: Using sphincter muscles around the eyes.

0.2K



for left eye (to the reader) and

0.4K 

for the

right eye.

30Z



For displacement in the

axis direction, the

same formula as equation (5) is re-used, where

is a

constant greater than 0. A small value for

causes

the eyelids to bulge out, hence in our

implementation we have set this constant to 30,

which achieves good results. Figure 6 shows a visual

of the application of the new sphincter muscle

activation around the left eye.

3.1.2 Sheet Muscle Model

Unlike the linear and sphincter muscle, sheet

muscles are made up of a series of almost-parallel

fibres spread over a rectangular area. The

displacement of vertices therefore is towards one

end of the rectangle with the other end of the

Enhanced Waters 2D Muscle Model for Facial Expression Generation

265

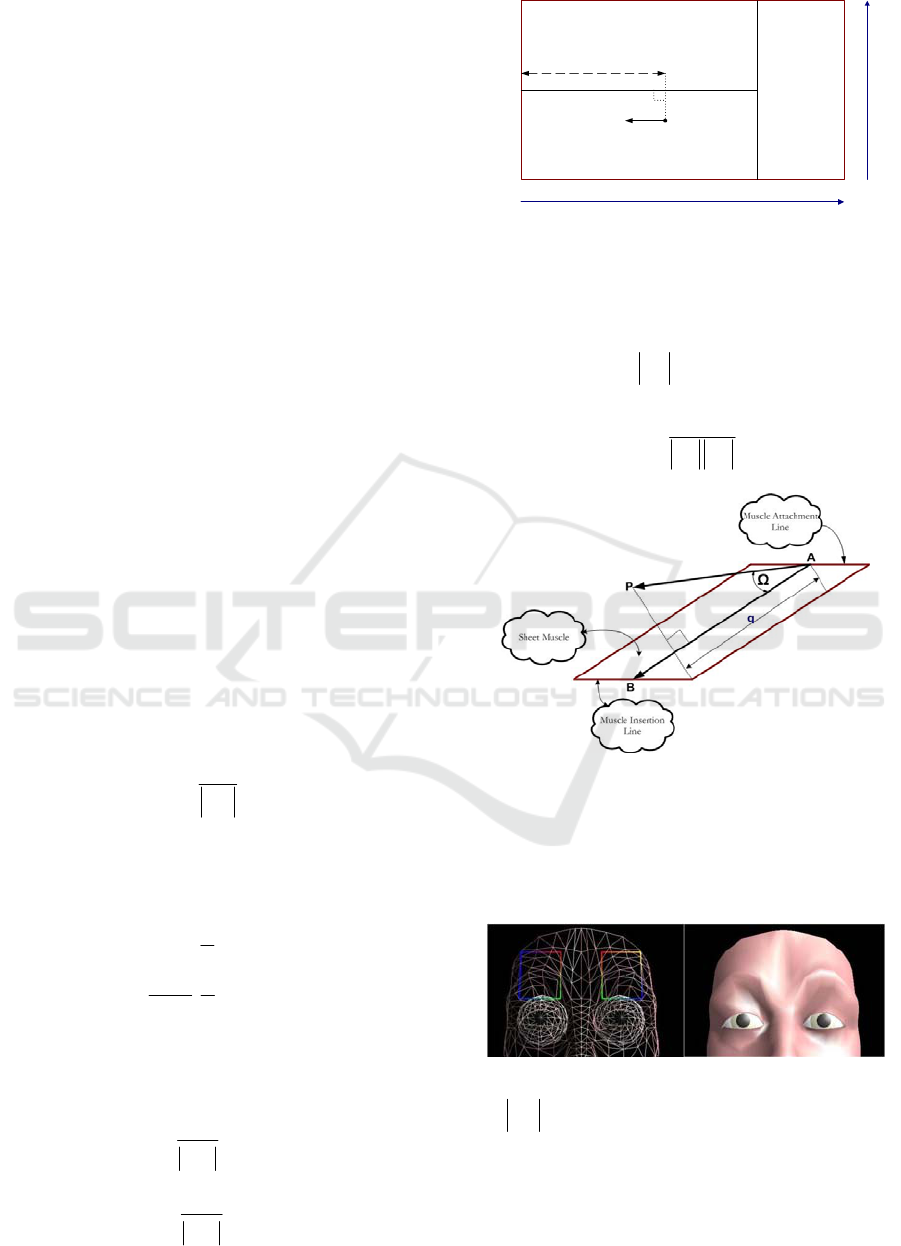
rectangle attached to the bone with maximum

displacement towards the attachment point of the

sheet muscle to the bone. In anatomy, sheet muscles

models muscles such as the frontalis which is

located on the forehead on a human face. Waters in

his face program instead used linear muscles for the

forehead and do not provide a description of sheet

muscles in (Waters, 1987). Hence we use the

description of sheet muscles from (Zhang et al.,

2001). However to achieve the desired effect in our

effort to produce realism in the expressions created

we use Waters linear muscles combined with two

sheet muscles (one on each side of the forehead).

Figure 7 illustrates the sheet muscle with the

following definitions:

: An arbitrary facial skin point.

A : Boundary points defining the attachment line

of sheet muscle to bone.

,ll: Boundary points defining the insertion line of

sheet muscle to skin.

: Middle point of sheet muscle attachment line.

l : Middle point of sheet muscle insertion line.

: Length and width of the rectangle defining

the zone of influence of the sheet muscle

respectively.

l : Distance between arbitrary skin point

and the

attachment line.

The new position



of the vertices at an arbitrary

point

in the ,,

yz plane within the rectangular

zone of influence can be calculated as.

pKD







(10)

where

i indicates the values of the ,,

coordinates of the vertex. Here,

is the muscle

spring constant and

is calculated as:

cos((1 ) 0 1

cos(( ) 1

for

































(11)

where

is the sheet muscle strength factor and set

at 1 in our implementation. Here,



and



are

calculated as:







(12)







(13)

Figure 7: Sheet muscle model.

The relationship between the rectangular sheet

muscle and the arbitrary point

is shown in Figur.

Therefore

q can be calculated using the following:

cosqAP









(14)

arccos 180 /

AP AB

where

AP AB















 



(15)

Figure 8: Relationship between

and the sheet muscle

for calculation of

q .

The placement of sheet muscles on our face

geometry and its effect on raising the forehead is

shown in Figure 9.

Figure 9: Implementation of the sheet muscles.

0.4K



2LAl









3.1.3 Jaw Rotation

In order to create more convincing expressions it is

important for the facial model to allow for jaw

’

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

266

rotations. The human jaw is made up of two parts

namely the upper and lower jaw. The upper jaw

remains fixed while it is the lower jaw that moves.

Waters models the moving lower jaw relative to the

pivot point of the facial model mesh rather than

employing any muscle technique. In his model the

jaw contains vertices of the lower part of the face

which is rotated along the

yaxis

and zaxis



Hence this rotation can be explained using the

following definitions and equations.

: Vertex forming the lower jaw.

: Angle of rotation of the jaw vertex relation to

the root of the facial mesh and is a value between 0

and 4 with 4 indicating the maximum opening.

cos sin

180 180

yy z

pP P

or rotationalong y axis









 

 

 

(16)

sin cos

180 180

zyz

pPP

or rotation along z axis









 

 

 

(17)

This formula is applied on all vertices that form the

jaw. The animator therefore has to specify manually

in advance which vertices would be part of the jaw

of the face. Adjusting the value of

simulates jaw

opening and closing with maximum rotation

produced at the center of the lower lip. This however

creates discontinuity at the corners of the lips as

reported by (Zhang et al., 2001) and illustrated

Figure 10. To keep the cohesion at the corner of the

lips we have given each vertex forming the

moveable part of the lower jaw a weight value in the

range 0.0 to 1.0 depending on its proximity to the

center of the lips. Since the formula above created

maximum rotation at the center of the lip, all

vertices of the lower jaw around the center are

allocated a higher weight value with decreasing

weights towards the corner of the lips. Hence the

corner points of the lips are allocated a weight of 0

meaning no rotation.

Figure 10: Discontinuity at the lip corners. (Parke and

Waters, 1996).

Figure 11: Weights allocated to vertices forming the lower

part of the jaw.

Figure 12: Jaw drop correction.

Figure 11 illustrates the allocation of weights to

vertices forming the lower jaw. After



has been

determined from equations (16) and (17), it is fed

into the following two equations to determine the

final position of vertex

. Here

is the weight at

. Figure 12 shows the improvement in the jaw

rotation function.

(1 )

yy y

ppwP w

or rotationalong y axis











(18)

(1 )

zz z

ppwP w

or rotationalong z axis









(19)

4 IMPLEMENTATION IN FAS

The original Waters face geometry is retained and

used in our project. In addition to the 18 linear

muscles, our model introduces 2 sheet muscles and 3

sphincter muscles. Figure 13 shows all the

implemented muscles in our model. The

manipulation of these muscles to generate facial

expressions is handled via the Expression Editor in

FAS (Kumar and Vanualailai, 2016). Given the

nature of this research the realism of the expression

generated in validated by visual inspection using

FACS as a guide.

Enhanced Waters 2D Muscle Model for Facial Expression Generation

267

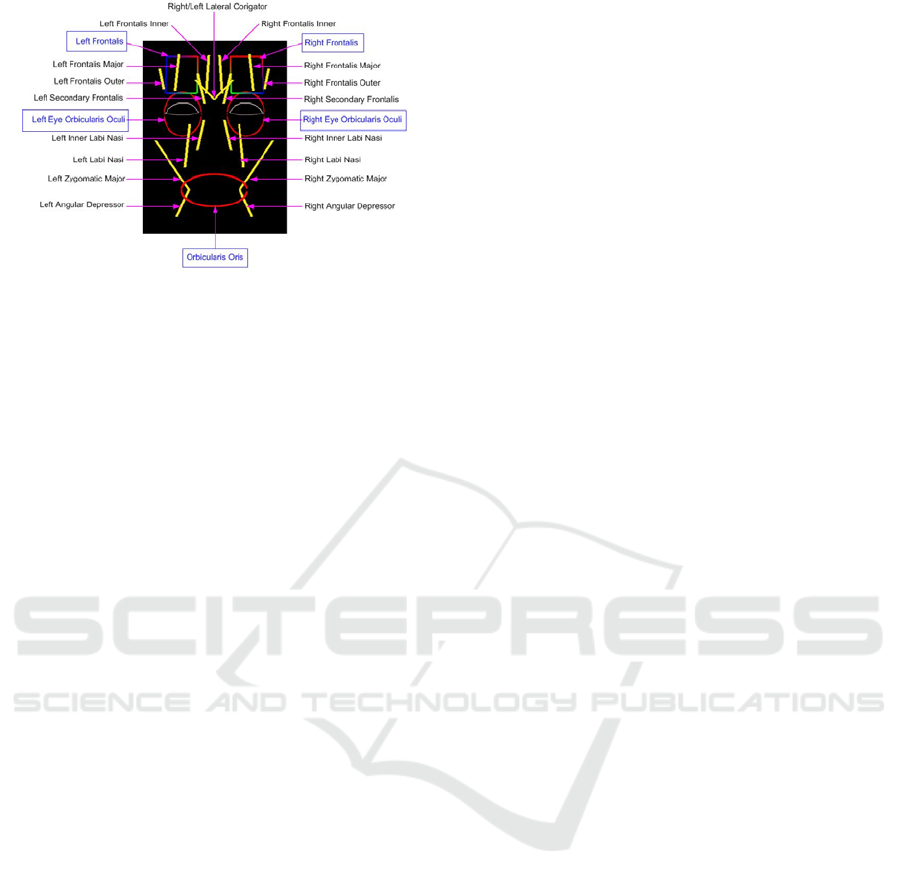
Figure 13: Implemented muscles in our Facial Model.

4.1 Expression Editor

The Expression Editor in FAS gives the user control

over all the muscles (including the jaw) used in our

face model hence allowing a wide range of

expressions to be generated with ease. Since our aim

is to animate facial expression based on FACS AUs,

it gives the flexibility to generate expressions that

can approximate the various AUs defined in FACS.

Using the expression editor the user can manipulate

one or more muscles to match a particular AU

expression. During this activity the calibration is

rendered in the graphics window for the user to note

the deformations on the face model. This allows the

user to fine tune the expression. Once the desired

expression is generated to a satisfactory level it can

then be recorded with the AU number as an

identifier. There is also the possibility to modify an

existing AU expression if desired by the user. A

total of 64 AU expressions can be defined.

A minimum value of 0.0 and maximum value of

2.0 can be chosen as activation values for each

muscle. Beyond activation value of 2.0 gives

unrealistic results as far as facial mesh deformation

is concerned. However the user can use a value from

0.0 to 4.0 (inclusive) for the jaw control.

By the definition of FACS, complex facial

expressions are generated by applying one or more

individual AUs. When these AU expressions are

programmed and stored in our system, it gives us the

possibility to generate many other compound

expressions simply by using combinations of AUs.

4.2 Suitability of Waters Muscle Model

for Facial Animation

Unlike techniques where producing animation

requires direct manipulation of the facial mesh,

Waters muscles are independent of the facial mesh.

This means that the animator has the freedom to

change the facial mesh yet still achieve the same

effect as in using the original mesh. This allows

flexibility in using different character mesh

topologies. It allows for compact representation of

facial geometry where the only information needed

are the muscle parameter values and the skin mesh

data in order to produce expressions. The muscle

functions work on triangulated vertices, which most

graphics hardware are optimized to use, hence

rendering is fast. Further expression parameters can

control groups of muscles at once resulting in

multiple muscle deformation applied to the facial

mesh. The problem areas include the difficulty of

placing muscles on the geometry of the face which

obviously has to be done manually. The muscle

functions basically represent flat architectures hence

they may not be attached to the skin (facial mesh) at

all. Due to this, muscle curvature and volume is also

not taken into account. At times during animation

some mesh vertices can fall prey to influence from

multiple muscle actions, though this problem can be

solved by taking “average” influences of the muscle

on the vertex. Overall given that FACS AUs map

directly to facial muscles, a muscle based model is

desirable.

5 CONCLUSIONS

The Waters muscle model opens a gateway to

excellent research in facial animation controlled by

muscles. They have been used and tested widely by

researchers over the years. Given the aim of our

project to generate facial expressions governed by

FACS, and that FACS basically describes

expressions based on affected muscles on the face,

Waters muscle model becomes the ideal choice for

use since it allowed easy mapping with FACS AUs.

However we do note the advancements in facial

modelling techniques over the years which are not

muscle based but may have potential in mapping

with FACS AUS. The modular design of our FAS

will allow our Facial Model component to be

replaced with a different modeling technique with

ease. Future directions of muscle based model will

be the development of 3D muscles with different

shape, size and volume to mimic natural muscles;

expand and contract with volume displacement

techniques. Using such design we shall be able to

model real facial expression effects.

GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications

268

REFERENCES

Alkawaz, M. H. et al. (2015). Blend Shape Interpolation

and FACS for Realistic Avatar. 3D Research

(Springer Link), 6(6).

Alkawaz, M. H. et al. (2014). Facial Animations: Future

Research Directions and Challenges. 3D Research

(Springer Link), 5(12).

Bermano, A. et al. (2013). Facial Performance

Enhancement Using Dynamic Shape Space Analysis.

ACM Transactions On Graphics (ACM TOG).

Edge, J. D. and Maddock, S. (2001). Expressive Visual

Speech using Geometric Muscle Functions. Proc.

Eurographics UK, pp. 11-18.

Ekman, P. and Frieson, W. (1977). Facial action coding

system. Consulting Psychologists Press.

Ersotelos, N. and Dong, F. (2008). Building Highly

Realistic Facial Animation: A Survey. The Visual

Computer, 24(1), pp. 13-30.

Hagar, J. C. et al. (2002). Facial Action Coding System

investigator's guide, Salt Lake City, UT: A Human

Face.

Kahler, K. et al. (2001). Geometry-based muscle modeling

for facial animation.. In Proc. of Graphics Interface,,

p. 37–46.

Kalra, P. et al. (1992). Simulation of facial muscle actions

based on rational free form deformations.. In Proc. of

Eurographics, pp. 59-69.

Kumar, D. and Vanualailai, J. (2016). Low Bandwidth

Video Streaming using FACS, Facial Expression and

Animation Techniques. Proceedings of the 11th Joint

Conference on Computer Vision, Imaging and

Computer Graphics Theory and Applications

(VISIGRAPP 2016), Volume 1, pp. 226-235.

Lewis, J. P. et al. (2014). Practice and Theory of

Blendshape Facial Models. EUROGRAPHICS State of

the Art Reports 2014.

Li, L. et al. (2012). A Survey of Computer Facial

Animation Techniques. International Conference on

Computer Science and Electronics Engineering.

Magnenat-Thalmann, N. et al. (1988). Abstract muscle

action procedures for human face animation. Visual

Computer, 3(5), pp. 290-297.

Noh, J. and Neumann, U. (1998). A Survey of facial

Modeling and Animation Techniques. Technical

Report, University of Southern California.

Ostermann, J. (1998). Animation of synthetic faces in

MPEG-4. Computer Animation, pp. 49-51.

Parke, F. (1972). Computer generated animation of faces.

ACM Annual Conference.

Parke, F. and Waters, K. (1996). Computer Facial

Animation. s.l.:A K Perters Wellesly.

Pauly, M. (2013). Realtime Performance-Based Facial

Avatars for Immersive Gameplay. Proceedings of the

ACM SIGGRAPH Conference on Motion in Games

2013.

Ping, H. et al. (2013). Computer Facial Animation: A

Review.

nternational Journal of Computer Theory and

Engineering, 5(4).

Sandbach, G. et al. (2012). Static and Dynamic 3D Facial

Expression Recognition: A Comprehensive Survey.

Image Vision Computing, 30(10), pp. 683-697.

Sifakis, E. et al. (2005). Automatic determination of facial

muscle activations from sparse motion capture marker

data. ACM. Trans. on Graphics (SIGGRAPH).

Tanguy, E. (2001). An Abstract Muscle Model for Three

Dimensional Facial Animation. Technical Report,

University of Sheffield, UK.

Tena, J. R. et al. (2011). Interactive Region-Based Linear

3D Face Models. SIGGRAPH.

Tolba, R. M. et al. (2018). Realistic Facial Animation

Review: Based on Facial Action Coding System.

Egyptian Computer Science Journal, 42(1).

Waters, K. (1987). A Muscle Model for animating 3D

facial expressions. Computer Graphics

(SIGGRAPH'87), 21(4), pp. 17-24.

Weise, T. et al. (2011). Realtime Performance-Based

Facial Animation. Transactions on Graphics

(Proceedings SIGGRAPH 2011), 30(4).

Zhang, Y. et al. (2001). Animation of Facial Expressions

by Physical Modelling. EuroGraphics.

Enhanced Waters 2D Muscle Model for Facial Expression Generation

269