A General Framework for Exact Partially Local Alignments

Falco Kirchner

, Nancy Retzlaff

2,1

and Peter F. Stadler

1,2,3,4,5

Bioinformatics Group, Department of Computer Science, Interdisciplinary Center for Bioinformatics,

and Competence Center for Scalable Data Services and Solutions Dresden/Leipzig, Universit

at Leipzig,

artelstraße 16-18, D-04107 Leipzig, Germany

Max Planck Institute for Mathematics in the Sciences, Inselstraße 22, D-04103 Leipzig, Germany

Institute for Theoretical Chemistry, University of Vienna, W

ahringerstraße 17, A-1090 Wien, Austria

Santa Fe Institute, 1399 Hyde Park Road, Santa Fe NM 87501, U.S.A.

Keywords:

Multiple Sequence Alignments, Dynamics Programming.

Abstract:

Multiple sequence alignments are a crucial intermediate step in a plethora of data analysis workﬂows in com-

putational biology. While multiple sequence alignments are usually constructed with the help of heuristic

approximations, exact pairwise alignments are readily computed by dynamic programming algorithms. In

the pairwise case, local, global, and semi-global alignments are distinguished, with key applications in pat-

tern discovery, gene comparison, and homology search, respectively. With increasing computing power, exact

alignments of triples and even quadruples of sequences have become feasible and recent applications e.g. in

the context of breakpoint discovery have shown that mixed local/global multiple alignments can be of practi-

cal interest. vaPLA is the ﬁrst implementation of partially local multiple alignments of a few sequences and

provides convenient access to this family of specialized alignment algorithms.

1 INTRODUCTION

Global multiple alignments are typically constructed

as intermediate data structure to support a compara-

tive or evolutionary analysis homologous sequences.

Alignment problems are naturally treated as optimiza-

tion problems: a scoring function evaluates the sim-

ilarities in an alignment column and/or the pattern

of gaps. Multiple alignments are almost exclusively

treated globally, that is, all parts of the input sequence

is scored. The notion of “local multiple alignments”

appears mostly in the context of phylogenetic foot-

printing (Lukashin and Rosa, 1999; Blanchette et al.,

2002) and related pattern discovery problems (Tabei

and Asai, 2009), where substrings are considered that

appear with a limited number of mismatches in some

or all input sequences.

Local variants of sequence alignment, on the one

hand, play an important role in pairwise alignments.

Local alignments, i.e., maximally similar substrings

within pairs of longer sequences, are a natural way to

identify conserved domains. The semi-global variant

of pairwise alignment, in which one sequence, usu-

ally called “query”, is expected to appear as approxi-

mate substring of a larger “subject”, again is a natural

formalization of homology search, implemented e.g.

in gotohscan (Hertel et al., 2009). Overlap align-

ments (Jones and Pevzner, 2004) allowing free end

gaps on all sequences have applications e.g. in se-

quence assembly (Rausch et al., 2009). Until recently,

the generalization of these variants to more than two

sequences has received very little attention.

Pairwise alignment problems can be solved ex-

actly for a wide range of cost models by means of

dynamic programming. In fact, the algorithms of

Needleman and Wunsch (1970) for global alignments,

Smith and Waterman (1981) for local alignments, and

the extension to afﬁne gap costs by Gotoh (1982) are

among the early, paradigmatic example of dynamic

programming. The basic recursive structure is read-

ily extended to more than two input sequences (Car-

rillo and Lipman, 1988; Lipman et al., 1989); the

time and space complexity, however, grows expo-

nentially with the number of sequences. Exact dy-

namic programming solutions thus have been used in

practice only for 3-way (Gotoh, 1986; Dewey, 2001;

Konagurthu et al., 2004; Kruspe and Stadler, 2007)

or 4-way (Steiner et al., 2011) alignments. Since

multiple sequence alignment problems (for arbitrary

numbers of input sequences X are typically NP-hard

194

Kirchner, F., Retzlaff, N. and Stadler, P.

A General Framework for Exact Partially Local Alignments.

DOI: 10.5220/0007380001940200

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 194-200

ISBN: 978-989-758-353-7

(Kececioglu, 1993; Wang and Jiang, 1994; Bonizzoni

and Della Vedova, 2001; Just, 2001; Manthey, 2003;

Elias, 2006), they are solved by heuristic approxima-

tion algorithms, see Chatzou et al. (2016), Baichoo

and Ouzounis (2017) or Nute et al. (2018) for a recent

reviews.

As the exact 3-way and 4-way alignments have in-

creased in usage, variants of the problem that com-

bine local and global alignments have been proposed

for specialized application scenarios. Al Arab et al.

(2017) considered the fate of sequences in the wake of

mitochondrial genome rearrangements by simultane-

ously comparing the rearranged region to both of its

ancestors. This approach made it possible to distin-

guish tandem duplication random loss (TDRL) from

reversal or transposition events. This specialized 3-

way alignment problem suggested the need to develop

a general theoretical framework for alignments that

consider part of their input local and part global. As

shown by Retzlaff and Stadler (2018) it is possible

– and convenient – to allow the user determine sep-

arately for each input sequence and each of its ends,

whether it is to be treated as global, i.e., deletions of

a preﬁx or a sufﬁx are penalized, or as local, allow-

ing the omission of preﬁxes or sufﬁxes at not cost.

We will brieﬂy outline the theoretical results in the

following section. While the presentation by Retzlaff

and Stadler (2018) is purely theoretical and did not

supply a reference implementation, the present con-

tribution closes this gap.

2 THEORY

The basic idea behind the framework of Retzlaff and

Stadler (2018) boils down to two ingredients: (1)

Each input sequence is either local or global on the

left and either local or global on the right. This is

entirely the user’s choice and provided with the in-

put. (2) In a particular alignment column, a sequence

may be inactive (if up to this column its preﬁx is con-

sidered unaligned), active (if it contributes to the col-

umn either with one of its characters or with a gap

this is scored), or it is dead (if its sufﬁx is consid-

ered unaligned). Consequently a left-local sequence

starts out inactive, while a left-global sequence starts

out active. Correspondingly, a right-global input is

still active at the end of the alignment, while a right-

local sequence must be dead at the end of the align-

ment. The partially local alignment problems can be

solved by dynamic programming just as the classic

pairwise problems mentioned in the introduction. As

usual, a scoring (memoization) table S holds the op-

timal alignments of preﬁxes. The only difference is

{1,2}|{}

{1,2,3}|{}

{1}|{2}

{1,3}|{2}

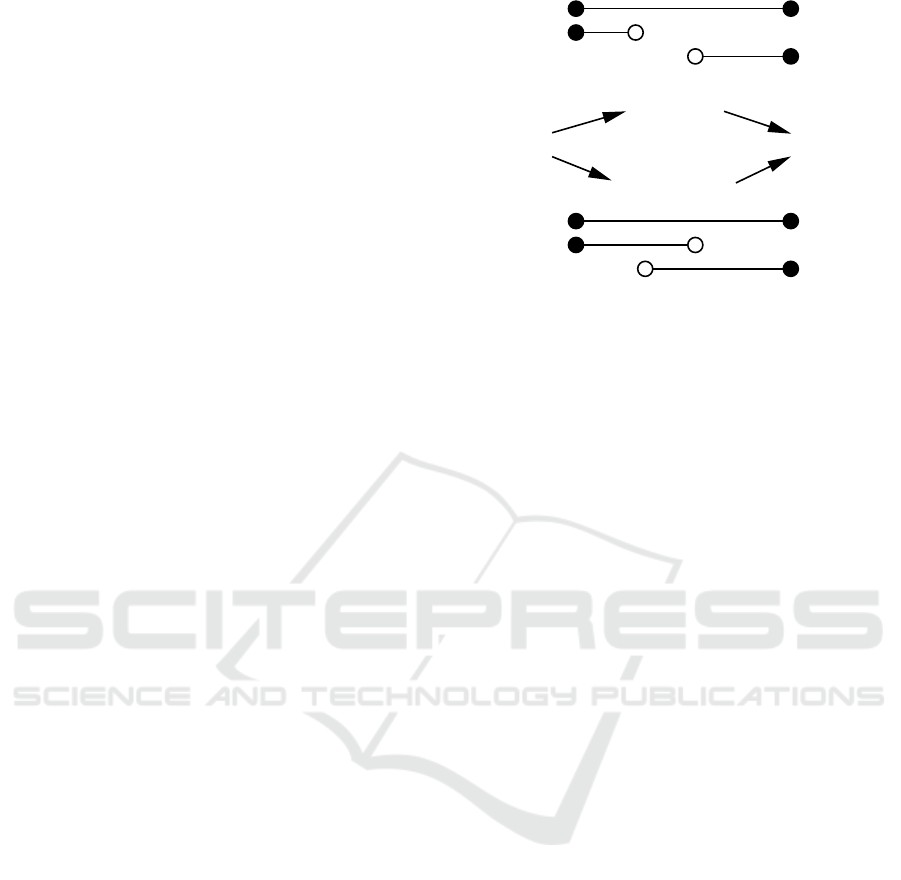
Figure 1: Schematic representation of the breakpoint align-

ment model of (Al Arab et al., 2017), with global reference

sequence 1, right-local preﬁx 2, and left-local sufﬁx 3. The

initial and terminal states of valid alignments are therefore

A|D = {1,2}|{} and {1,3}|{2}, respectively. There are two

distinct path of transitioning between these states with in-

termediates states {1}|{2} (if 2 and 3 do not overlap) and

{1,2,3}|{} (if 2 and 3 overlap in their aligned part). The

black bullets indicate that the correspond end of the se-

quence is present in the alignment, open circles indicate the

preﬁxes of sufﬁxes remain unaligned.

that S now depends not only on the length of preﬁxes

but also on the state (inactive, active, or dead) of each

sequence in a given column of the alignment. It is

sufﬁcient to record the set A of active and D of dead

sequences, since the inactive sequences are given by

X \ {A ∪D}. As the alignment progresses, an inactive

sequence may become active only once, and an active

may transit at most once to the dead state. Consecu-

tive alignment columns thus have state pairs (A

)

and (A,D) that are comparable w.r.t. the partial order

)  (A, D) ⇐⇒

(

∪ D

⊆ A ∪ D

⊆ D

(1)

The state changes can be performed stepwisely. As

shown by Retzlaff and Stadler (2018), (A

) is an

immediate predecessor of (A,D) if either exactly on

one inactive sequence become active or exactly one

active sequence transitions to the dead state. We

denote this relation by ≺≺. The initial condition is

A = A

, where A

is the set of left-global sequences,

and D =

In a quite general form (which uses the heuristic

version of the afﬁne gap cost model for more than two

sequences), the recursion for the optimal alignment

score are of the form

(A,D)

= max











max

(A,D)

I−π

+ s(π)

max

)≺≺(A,D)

(A,D)

+ s

∗

(2)

The variable π (a non-null binary vector) denotes gap

pattern in the last alignment column, the lower multi-

A General Framework for Exact Partially Local Alignments

195

index I describes the lengths of the preﬁxes included

in the alignment including this column. Thus I − π

is the vector of preﬁx lengths in the previous column.

The scoring function s( .) in the most general form

depends on both gap patterns as well as the actual se-

quence entries. The second alternative does not move

in the alignment but changes the state, a step that may

also be associated with a cost s

∗

, which in the most

general case may depend on I, π,A,D,A

. Equa-

tion (2) describes the recursion for additive scores.

The special case that a sequence k that is both left-

and right-local remains completely unaligned is han-

dled by a directed transition from inactive to dead re-

stricted to I

= 0, see Retzlaff and Stadler (2018) for

details.

The notation is illustrated in Fig. 1 for the algo-

rithm introduced by Al Arab et al. (2017). In prin-

ciple, the recursions are easily extended to afﬁne gap

costs. However, this incurs another factor (2

− 1)

in memory for N sequences since the scoring tables

S becomes explicitly dependent on the gap pattern of

the last column. The full recursions for the breakpoint

alignment model with afﬁne gap costs, are given in

the appendix of Retzlaff and Stadler (2018).

The backtracing recursion is a rather straightfor-

ward generalization of the backtracing scheme for the

Smith-Waterman algorithm. The ﬁrst step is to ﬁnd

the optimal score of the partially local alignment. De-

note by (A

∗

) that unique maximal state w.r.t. ,

i.e., A

∗

is the set of all right-global sequences and D

∗

is the set of all right-local sequences. Hence A

∗

∪ D

∗

contains all input sequences. The optimal score is the

maximum over all multi-indices I with constraint that

= n

, the length of the k-th sequence, for all k ∈ A

∗

with the the maximum taken over all indices I

with

k ∈ D

∗

. The maximum value of I

determines the

right boundary of the right-local sequence. The recur-

sion then proceeds, as usual, to ﬁnd the index or state

transition in Eq. (2). The backtracing recursion termi-

nates as soon as all left-global variables k ∈ A

have

reached the left end oft the sequences, i.e., I

= 0 for

all k ∈ A

. The left boundary of a left-local sequences

l /∈ A

equals the index I

at this point.

Equation (2) is the simplest way to explain the re-

cursive structure of the partially local alignment prob-

lem. It has the disadvantage that it provides more than

one way to obtain a particular partial alignment (char-

acterized by I,A,D) since state transition can be per-

formed in arbitrary order. As a consequence, Eq. (2)

cannot be used to compute partition functions over

alignments, and hence to obtain a probabilistic ver-

sion. As described in some detail by Retzlaff and

Stadler (2018), unambiguous recursions can be con-

structed by allowing state transitions from inactive

to active and from active to dead for a sequence k

only in conjunction with appending of a alignment

column for which π

= 1. At the same time, one

needs to consider also all possible state transitions

with (A

) ≺ (A, D). That is,

(A,D)

= max

∗

max

)

I−π

+ s(π) +s

∗

(3)

where max

∗

)

runs over all (A

)  (A,D) such

that k ∈ A \ A

or k ∈ D \ D

implies π

= 1.

3 IMPLEMENTATION

We have implemented the two variants of the align-

ment algorithm for partially local alignments with ad-

ditive gap costs based on Eq. (2) and Eq. (3), respec-

tively. In the practical implementation of Eq. (3) we

omit the formal initial state (A

0) and separately ini-

tialize all left-local sequences k both in the inactive

and the active state for I

= 0. Similarly, we catch the

ﬁnal states at the right end of right-local sequences

without explicitly considering a ﬁnal transition to the

dead state after the last letter has been included into

the alignment. Eq. (3) in general requires the consid-

eration of more state changes in each step than Eq. (2).

While Eq. (2) only considers the Hasse diagram of the

partial order ≺, its transitive closure is required for

Eq. (3). On the other hand, Eq. (3) provides a very

convenient starting point for later extensions e.g. to a

probabilistic version.

vaPLA is written in Java and uses only standard

libraries. The source code is available on GitHub.

In principle, vaPLA is capable of accepting an arbi-

trary number of input sequences (in FASTA format)

together with information on whether each of their

ends is to be treated globally or locally. However,

the resource requirements quickly become prohibitive

with the number of input sequences and in particu-

lar the number of local ends. vaPLA ﬁrst explicitly

constructs the Hasse diagram of the partial order ≺

for Eq. (3) and uses this information to allocated the

memoization tables for the recursions. The partial or-

der can be exported in .dot format and visualized us-

ing a standard graph drawing tools such as graphviz.

For Eq. (2) only the relation ≺≺, i.e., the edges of the

Hasse diagram, is used, while Eq. (3) makes use of

the entire partial order ≺.

The partial order determines the required re-

sources: one

∏

k∈A

O(n

)-size table is required for

each state (A,D). Writing g=|A

∩ A

∗

| for the num-

ber of global sequences, s = |A

\ A

∗

| + |A

∗

\ A

| for

the number sequences that are local and one end and

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

196

global at the other, and ` for the number of local se-

quences, there are

h = 1

(4)

distinct states, because global sequences are always

active, semi-local sequences change either state from

inactive to to active or from active to dead, while local

sequences can pass through all three states. All com-

binations of these states must be considered, since the

relative order (between sequences) of the state transi-

tions is not constrained. With one index variable iter-

ating over each of the N sequences of length O(n), the

memory requirements are O(n

) for each state. The

evaluation of the recursion requires O(2

) score com-

putations for each transition between columns and

states, resulting in an upper bound of O(2

) ef-

fort. The effort is reduced to O(2

hN) by imple-

menting Eq. (2) instead of Eq. (3) as shown in Fig. (3).

Both variants are available in the current implementa-

tion.

Backtracing is implemented in the usual manner:

starting from the position I

∗

and state (A

∗

) of the

optimal score, vaPLA computes the transition that re-

sulted in the optimal score. At present, co-optimal

solutions are not investigated. The ﬁrst solution en-

countered is used. The procedure then continues iter-

atively until a valid start state is reached.

4 BENCHMARK

We use two well known benchmark protein databases

to test and evaluate vaPLA. OXBench (Raghava

et al., 2003) is a completely automatically generated

database whereas BAliBASE (Thompson et al., 2005)

has a manual step for cleaning initial alignments be-

fore the release. Both benchmark sets are intended for

global multiple alignments. We therefore inspected a

subset of the reference alignments and manually in-

spected overhanging ends, which we tagged for local

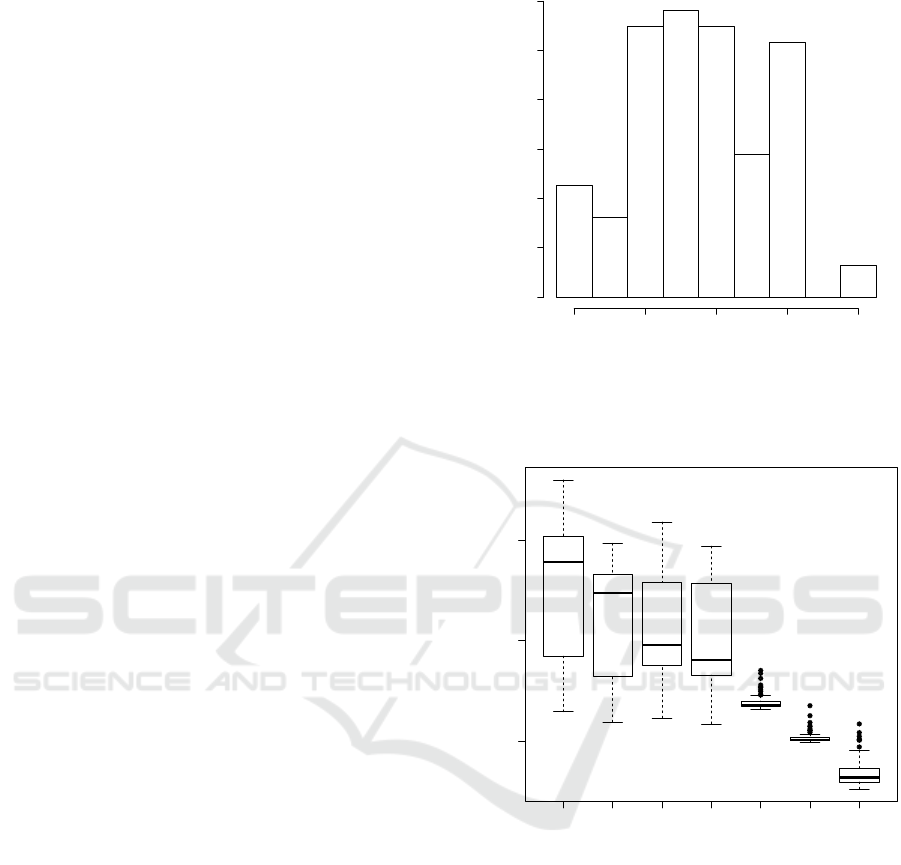
instead of global alignment. Figure 2 summarizes the

distribution of local ends in benchmark set used here.

These sequences are subsequently aligned with

vaPLA as well as three of the most common align-

ment tools: T-Coffee (Notredame et al., 2000; Chang

et al., 2014), MAFFT (Katoh et al., 2005; Nakamura

et al., 2018), and ClustalW (Larkin et al., 2007; Siev-

ers and Higgins, 2018). All three tools are based on

initial pairwise alignments and use essentially pro-

gressive schemes, hence presenting efﬁcient heuris-

tics rather than exact solutions.

Comparing the performance for few and many lo-

cal ends, respectively, we can see in Fig. 3 that the

running time of vaPLA, as expected, strongly depends

#local ends in one alignment

frequency

0 2 4 6 8

0.020.00 0.01 0.03 0.04

0.05

0.06

Figure 2: Frequency distribution of the number of local ends

in the in the data set of benchmark alignments. Only a small

fraction of the alignments is global, while most test align-

ments have 2–6 local ends.

vaPLA>3

vaPLA*>3

vaPLA≤3

vaPLA*≤3

T-Coffee

MAFFT

ClustalW

5 10 15

log(t) [ms]

Figure 3: Running time of vaPLA for alignments with at

most three local ends (e.g. vaPLA≤ 3) and for alignments

with more than three local ends (e.g. vaPLA> 3) com-

pared to heuristic global aligners (T-Coffee, MAFFT, and

ClustalW) that are commonly used in large-scale bioin-

formatics applications. The label vaPLA refers to Eq. (2),

vaPLA* indicated the implementation following Eq. (3).

on how many local ends needs to be handled in one

alignment. Without local ends, i.e., for global align-

ments, the execution time of vaPLA is comparable

with T-Coffee. For partially local alignments we ob-

serve the expected exponential increase with the num-

ber of local ends. Since vaPLA is designed as a refer-

ence implementation of a much more expensive, ex-

act algorithm, it is clear that it cannot be competitive

in terms resource consumption. Figure 3 also com-

A General Framework for Exact Partially Local Alignments

197

vaPLA T−Coffee MAFFT ClustalW

100

Figure 4: Accuracy of vaPLA compared to the heuristic

global alignment tools T-Coffee, MAFFT, and ClustalW.

vaPLA T−Coffee MAFFT ClustalW

PSE

Figure 5: Position shift error of vaPLA compared to the

heuristic global aligners T-Coffee, MAFFT, and ClustalW.

pares the resource consumption for the implementa-

tion of Eqs. (2) and (3), resp. As expected, running

times decrease when Eq. (3) is used since one iterates

only over the immediate predecessors. The effect is

more pronounced for the data set with three or more

local ends, because their Hasse diagrams typically are

larger. Much more interesting than the comparisons

of running times, however, is the question whether

exact multi-way alignments yield an improvement in

accuracy.

The average accuracy, deﬁned as AC = (L − f )/L

where L is the length of the alignment and f is

the number of columns deviating from the reference

alignment, is summarized in Fig. 4. The data show

that vaPLA provides a moderate but noticeable im-

provement relative to all three heuristics, although we

use a simple scoring model and none of the protein-

speciﬁc rules implemented e.g. in ClustalW.

The position shift error PSE as deﬁned by

Raghava et al. (2003) serves as an alternative mea-

sure of alignment accuracy. Consider a pair of

(mis)matched positions i in sequence x and j in se-

quence y in the reference alignment. In the test align-

ment we consider the same position i in x and its

(mis)matched position j

in y and measure the dis-

tance δ = | j − j

|. A similar rule is used to compute

δ if there is an in/del between x and y at position i.

For the details we refer to (Raghava et al., 2003). The

PSE is the average of the contributions δ of all mis-

matched pairs in the reference alignment. Omitted

preﬁxes and sufﬁxes at local ends do not enter the

PSE score. vaPLA exhibits signiﬁcantly smaller po-

sition shift errors than the three heuristics, Fig. 5.

5 DISCUSSION

vaPLA is primarily intended as a reference implemen-

tation against which specialized partially local align-

ments can be tested and benchmarked. We anticipate

at least two use cases. First, vaPLA is useful to to

create test cases and help debugging during the devel-

opment phase of a specialized exact implementation.

More importantly, since vaPLA computed exact solu-

tions for a moderate number of input sequences, it can

be used to generate ground-truth data against which

faster heuristics can be compared. The current version

of vaPLA was not implemented to yield good perfor-

mance while we expect that substantial gains can be

achieved by parallelization with ﬁne grained multi-

threading (Martins et al., 2001). Still it will need to be

tested whether such a solution is realizable in Java.

While biological sequences tend to be rather long

as compared to average word lengths we see a promis-

ing application to alignment of lexical items where

preﬁxing and sufﬁxing seem to play even a bigger role

that in biology. Even though afﬁxes can contain in-

formation, the root of words is most valuable when

doing cross-linguistics comparisons. For conceptual

examples we refer to (Retzlaff and Stadler, 2018).

The computational efforts for exact dynamic pro-

gramming algorithms often can be reduced exclud-

ing subsets of matches using bounds on the achiev-

able scores. Lossless ﬁlters for local pairwise align-

ments have been pioneered by Peterlongo et al. (2008,

2009). Ideas to prune the search space of the DP

problem are discussed e.g. by Schroedl (2005) or

Bilu et al. (2006). Quasi-alignments based on k-mer

matches can be employed as alignment anchors also

in a global context (Nagar and Hahsler, 2013). These

techniques may be used not only to reduce the com-

putational effort of the exact algorithm for input se-

quences of practical interest, but also might serve as

starting points for construcing efﬁcient heuristics for

partially local MSA problems.

The framework of vaPLA lends itself to further ex-

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

198

tensions. First, it is easily possible to derive a prob-

abilistic version. This essentially entails a change in

the scoring from adding score contributions to mul-

tiplying with the corresponding Boltzmann factors.

The corresponding outside algorithm could easily be

constructed along the lines of H

oner zu Siederdissen

et al. (2015). Another extension that could be realized

very easily is to enforce additional constraints on state

transitions. For example, it may be useful in a pattern-

based applications to allow the transition to and from

active only concurrently, i.e., at the same position rel-

ative to remaining input sequences.

Instead of treating state transitions in an acyclic

manner, it is also possible to allow multiple transi-

tions from active back to inactive. This would al-

low certain (context dependent) deletions to occur at

a unit cost. Such “exclusions” have rarely been con-

sidered in sequence alignment but are of some interest

for structured RNAs (Schirmer and Giegerich, 2013).

This idea may be of use in particular when sequences

are provided with structural annotation and deletions

of entire structural elements are to be scored in a spe-

cial way.

Advances in computing technology now make it

feasible to compute exact simultaneous solutions of

alignment problems with more than two sequences.

A combinatorial diversity of distinct alignment prob-

lems arises in this setting just by allowing to distin-

guish local and global ends separately for each input.

We suspect that additional variations on the theme

are of interest, e.g., requiring additional constraints

on pairwise overlaps. The framework and the imple-

mentation presented here is a ﬁrst step towards an sys-

tematic exploration of this largely uncharted universe

of alignments, many of which we suspect will be of

practical use in computational biology.

ACKNOWLEDGMENTS

NR gratefully acknowledges the hospitality of the

Santa Fe Institute, where parts of this work were per-

formed, as well as travel support by the ASU-SFI

Center for Biosocial Complex Systems. The Compe-

tence Center for Scalable Data Services and Solutions

(ScaDS) Dresden/Leipzig is funded by BMBF grant

01IS14014B.

REFERENCES

Al Arab, M., Bernt, M., H

oner zu Siederdissen, C., Tout,

K., and Stadler, P. F. (2017). Partially local three-way

alignments and the sequence signatures of mitochon-

drial genome rearrangements. Alg. Mol. Biol., 12:22.

Baichoo, S. and Ouzounis, C. A. (2017). Computational

complexity of algorithms for sequence comparison,

short-read assembly and genome alignment. Biosys-

tems, 156/157:72–85.

Bilu, Y., Agarwal, P. K., and Kolodny, R. (2006). Faster

algorithms for optimal multiple sequence alignment

based on pairwise comparisons. IEEE/ACM Trans.

Comp. Biol. Bioinf., 3:408–422.

Blanchette, M., Schwikowski, B., and Tompa, M. (2002).

Algorithms for phylogenetic footprinting. J Comput

Biol, 9:211–223.

Bonizzoni, P. and Della Vedova, G. (2001). The complexity

of multiple sequence alignment with SP-score that is

a metric. Theor. Comp. Sci., 259:63–79.

Carrillo, H. and Lipman, D. (1988). The multiple sequence

alignment problem in biology. SIAM J. Appl. Math.,

48:1073–1082.

Chang, J. M., Di Tommaso, P., and Notredame, C. (2014).

TCS: a new multiple sequence alignment reliability

measure to estimate alignment accuracy and improve

phylogenetic tree reconstruction. Mol. Biol. Evol.,

31:1625–1637.

Chatzou, M., Magis, C., Chang, J. M., Kemena, C., Bus-

sotti, G., Erb, I., and Notredame, C. (2016). Multiple

sequence alignment modeling: methods and applica-

tions. Brief Bioinform., 17:1009–1023.

Dewey, T. G. (2001). A sequence alignment algorithm with

an arbitrary gap penalty function. J. Comp. Biol.,

8:177–190.

Elias, I. (2006). Settling the intractability of multiple align-

ment. J. Comp. Biol., 13:1323–1339.

Gotoh, O. (1982). An improved algorithm for matching

biological sequences. J. Mol. Biol., 162:705–708.

Gotoh, O. (1986). Alignment of three biological sequences

with an efﬁcient traceback procedure. J. theor. Biol.,

121:327–337.

Hertel, J., de Jong, D., Marz, M., Rose, D., Tafer, H.,

Tanzer, A., Schierwater, B., and Stadler, P. F. (2009).

Non-coding RNA annotation of the genome of Tri-

choplax adhaerens. Nucleic Acids Res., 37:1602–

1615.

oner zu Siederdissen, C., Prohaska, S. J., and Stadler, P. F.

(2015). Algebraic dynamic programming over general

data structures. BMC Bioinformatics, 16:19:S2.

Jones, N. C. and Pevzner, P. A. (2004). An Introduction to

Bioinformatics. MIT Press, Cambride, MA. Problem

6.22.

Just, W. (2001). Computational complexity of multiple

sequence alignment with SP-score. J. Comp. Biol.,

8:615–623.

Katoh, K., Kuma, K.-i., Toh, H., and Miyata, T. (2005).

MAFFT version 5: improvement in accuracy of mul-

tiple sequence alignment. Nucleic Acids Res., 33:511–

518.

Kececioglu, J. D. (1993). The maximum weight trace prob-

lem in multiple sequence alignment. In Proceedings of

A General Framework for Exact Partially Local Alignments

199

the 4th Symposium on Combinatorial Pattern Match-

ing, volume 684 of Lecture Notes Comp. Sci., pages

106–119, Berlin. Springer.

Konagurthu, A. S., Whisstock, J., and Stuckey, P. J. (2004).

Progressive multiple alignment using sequence triplet

optimization and three-residue exchange costs. J.

Bioinf. and Comp. Biol., 2:719–745.

Kruspe, M. and Stadler, P. F. (2007). Progressive multiple

sequence alignments from triplets. BMC Bioinformat-

ics, 8:254.

Larkin, M. A., Blackshields, G., Brown, N. P., Chenna, R.,

McGettigan, P. A., McWilliam, H., Valentin, F., Wal-

lace, I. M., Wilm, A., Lopez, R., Thompson, J. D.,

Gibson, T. J., and Higgins, D. G. (2007). Clustal W

and Clustal X version 2.0. Bioinformatics, 23:2947–

2948.

Lipman, D. J., Altschul, S. F., and Kececioglu, J. D. (1989).

A tool for multiple sequence alignment. Proc. Natl.

Acad. Sci. USA, 86:4412–4415.

Lukashin, A. V. and Rosa, J. J. (1999). Local multiple se-

quence alignment using dead-end elimination. Bioin-

formatics, 15:947–953.

Manthey, B. (2003). Non-approximability of weighted

multiple sequence alignment. Theor. Comp. Sci.,

296:179–192.

Martins, W. S., Del Cuvillo, J. B., Useche, F. J., and

Theobald, K. B.and Gao, G. R. (2001). A multi-

threaded parallel implementation of a dynamic pro-

gramming algorithm for sequence comparison. In Alt-

man, R. B. A., Dunker, A. K., Hunker, L., Lauderdale,

K., and Klein, T. E., editors, Paciﬁc Symposium on

Biocomputing, volume 6, pages 311–322, Singapore.

World Scientiﬁc.

Nagar, A. and Hahsler, M. (2013). Fast discovery and visu-

alization of conserved regions in DNA sequences us-

ing quasi-alignment. BMC Bioinformatics, 14 (Suppl

11):S2.

Nakamura, T., Yamada, K. D., Tomii, K., and Katoh, K.

(2018). Parallelization of MAFFT for large-scale mul-

tiple sequence alignments. Bioinformatics, 34:2490–

2492.

Needleman, S. B. and Wunsch, C. D. (1970). A general

method applicable to the search for similarities in the

amino acid sequence of two proteins. J Mol Biol,

48:443–453.

Notredame, C., Higgins, D. G., and Heringa, J. (2000). T-

coffee: a novel method for fast and accurate multiple

sequence alignment. Journal of molecular biology,

302:205–217.

Nute, M., Saleh, E., and Warnow, T. (2018). Evaluating

statistical multiple sequence alignment in comparison

to other alignment methods on protein data sets. Syst

Biol.

Peterlongo, P., Pisanti, N., Boyer, F., Pereira do Lago, A.,

and Sagot, M.-F. (2008). Lossless ﬁlter for multiple

repetitions with Hamming distance. J. Discrete Algo-

rithms, 6:497–509.

Peterlongo, P., Sacomoto, G. A. T., Pereira do Lago, A.,

Pisanti, N., and Sagot, M.-F. (2009). Lossless ﬁlter

for multiple repeats with bounded edit distance. Alg.

Mol. Biol., 4:3.

Raghava, G. P. S., Searle, S. M. J., Audley, P. C., Bar-

ber, J. D., and Barton, G. J. (2003). OXBench:

a benchmark for evaluation of protein multiple se-

quence alignment accuracy. BMC Bioinformatics,

4:47.

Rausch, T., Koren, S., Denisov, G., Weese, D., Emde, A.-

K., D

oring, A., and Reinert, K. (2009). A consistency-

based consensus algorithm for de novo and reference-

guided sequence assembly of short reads. Bioinfor-

matics, 25:1118–1124.

Retzlaff, N. and Stadler, P. F. (2018). Partially local multi-

way alignments. Math. Comp. Sci., 12:207–234.

Schirmer, S. and Giegerich, R. (2013). Forest alignment

with afﬁne gaps and anchors, applied in RNA struc-

ture comparison. Theor. Comp. Sci., 483:51–67.

Schroedl, S. (2005). An improved search algorithm for opti-

mal multiple-sequence alignment. J. Artif. Intel. Res.,

23:587–623.

Sievers, F. and Higgins, D. G. (2018). Clustal Omega

for making accurate alignments of many protein se-

quences. Protein Sci., 27:135–145.

Smith, T. F. and Waterman, M. S. (1981). Identiﬁcation

of common molecular subsequences. J Mol Biol,

147:195–197.

Steiner, L., Stadler, P. F., and Cysouw, M. (2011). A

pipeline for computational historical linguistics. Lan-

guage Dynamics & Change, 1:89–127.

Tabei, Y. and Asai, K. (2009). A local multiple alignment

method for detection of non-coding RNA sequences.

Bioinformatics, 25:1498–1505.

Thompson, J. D., Koehl, P., Ripp, R., and Poch, O. (2005).

BAliBASE 3.0: latest developments of the multiple

sequence alignment benchmark. Proteins: Structure,

Function, and Bioinformatics, 61:127–136.

Wang, L. and Jiang, T. (1994). On the complexity of multi-

ple sequence alignment. J Comput Biol, 1:337–348.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

200