A Novel Multispectral Lab-depth based Edge Detector for Color Images

with Occluded Objects

Safa Mefteh

, Mohamed-B

echa Ka

aniche

, Riadh Ksantini

1,2

and Adel Bouhoula

Digital Security Research Lab, Higher School of Communication of Tunis (Sup’Com), University of Carthage, Tunisia

University of Windsor, 401, Sunset Avenue, Windsor, ON, Canada

Keywords:

Multispectral Edge Detection, Lab-D Image, Gradient based Approach, Occlusion Handling.

Abstract:

This paper presents a new method for edge detection based on both Lab color and depth images. The principal

challenge of multispectral edge detection consists of integrating different information into one meaningful

result, without requiring empirical parameters. Our method combines the Lab color channels and depth infor-

mation in a well-posed way using the Jacobian matrix. Unlike classical multi-spectral edge detection methods

using depth information, our method does not use empirical parameters. Thus, it is quite straightforward and

efﬁcient. Experiments have been carried out on Middlebury stereo dataset (Scharstein and Szeliski, 2003;

Scharstein and Pal, 2007; Hirschmuller and Scharstein, 2007) and several selected challenging images (Ro-

senman, 2016; lightﬁeldgroup, 2016). Experimental results show that the proposed method outperforms recent

relevant state-of-the-art methods.

1 INTRODUCTION

Edge detection is one of the most prominent problems

in the ﬁeld of image processing (Zhang et al., 2016;

Saurabh et al., 2014; Silberman et al., 2014). It has

an important role in many computer vision algorithms

and is considered as a fundamental and crucial step

particularly for segmentation, feature extraction and

object recognition. In order to perform a good edge

detection, one should tackle several challenges: vari-

ability of illumination, occlusions, density of edges in

the scene and noises (Nadernejad et al., 2008). Based

on the type of the image, we can identify three cate-

gories of methods for edge detection: grayscale image

edge detection, color image edge detection and Color-

Depth image edge detection (Zhang et al., 2016).

In this paper, we present a novel method for edge

detection by combining both color information and

depth information in well-posed way without using

empirical parameters. First, we apply on color image

the L

gadient algorithm in order to suppress noi-

ses, while preserving important edges (Xu et al.,

2011). Second, we compute the ﬁrst derivative for

each image component (Lab colors and Depth infor-

mation). More precisely, for each pixel of a multis-

pectral image, we form a Jacobian matrix by using

the ﬁrst derivatives. Then, for each pixel, in order to

tease out the pairwise relations of the columns of the

proposed Jacobian matrix, we perform product of this

latter and its transpose. Last, we select the maximal

Eigen value of the resulting matrix as edge informa-

tion. The main advantage of our method is that we do

not use empirical parameters and that is a quite straig-

htforward efﬁcient method. Our proposed approach

has been compared to both Isola et al. (Isola et al.,

2014) and Asif et al. (Asif et al., 2016). These two

methods were chosen because they twin multi chan-

nels into one meaningful result, as the principle of our

method. The approach has been validated on Midd-

lebury stereo dataset (Scharstein and Szeliski, 2003;

Scharstein and Pal, 2007; Hirschmuller and Schar-

stein, 2007) and several selected challenging images

(lightﬁeldgroup, 2016; Rosenman, 2016).

The remaining of this paper is organized as fol-

lows. The next section 2 overviews the state-of-the-

art for edge detectors. Section 3 describes the pro-

posed method in details. Experimental protocol and

results are presented and discussed in section 4. Fi-

nally, section 5 concludes this work by overviewing

the contribution and pointing out issues for future de-

velopment.

272

Mefteh, S., Kaâniche, M., Ksantini, R. and Bouhoula, A.

A Novel Multispectral Lab-depth based Edge Detector for Color Images with Occluded Objects.

DOI: 10.5220/0007380502720279

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 272-279

ISBN: 978-989-758-354-4

2 RELATED WORK

An edge can be described as an acute change in lumi-

nosity. Through the past years, many researchers have

concentrated on implementing algorithms for grays-

cale images in order to detect edges effectively. These

approaches are classiﬁed into two broad categories:

(i) Gradient based edge detection and (ii) Laplacian

based edge detection. In a gradient based edge de-

tection, one looks for the extrema in the ﬁrst order

derivative of the image to ﬁnd edges. Several met-

hods have been developed, such as, the Sobel ope-

rator (Sobel, 1970),Prewitt operator (Prewitt, 1970),

Roberts operator (Roberts, 1963) and Krish operator

(Krish, 1970). These classical operators are characte-

rized by their simplicity. Also, because of the approx-

imation of gradient magnitude, the detection of edges

and their orientations is simple. However, these ope-

rators are sensitive to the noise. In fact, very high

noise will degrade the magnitude of the edges which

will most probably decrease the accuracy of edge de-

tection. Concerning the Laplacian based edge de-

tection, one searches for zero crossings in the second

order derivative of the image to ﬁnd edges. A set of

algorithms have been implemented like Laplacian of

Gaussian (LoG) (Marr and Hildreth, 1980) and Diffe-

rence of Gaussian (DoG) (Davidson and Abramowitz,

1998). Methods of this category are able to ﬁnd the

correct places of edges and their orientations, but they

fail at the corners, curves and where the gray level

pixel intensity varies due to illumination changes.

Since then, some other reﬁned algorithms have

been developed to overcome these limitations, such

as, the Canny edge detector (Canny, 1986) which per-

forms a better detection performance under noisy con-

ditions. Actually, Canny’s algorithm has the advanta-

ges of ﬁnding the best error rate, in order to detect

edges efﬁciently. Although the canny edge detector is

one of the most widely used edge detectors, it suffers

from some drawbacks which include missing edge’s

junctions. With the use of Gaussian kernel in order

to reduce the noise signal, the localization of edges

is harder and inaccurate (Perez and Dennis, 1997).

Canny

s method is also a high time consuming de-

tector. Moreover, it requires setting threshold values

adaptively for each image scene.

To improve the accuracy of edge detection, several

researches have already used color image for complex

situations because it provides more information com-

pared to the grayscale image (monochromatic image).

According to Novack and Shafer (Novack and Shafer,

1987), 90% of edge information in color images can

be found as well as in grayscale images. However,

the remaining 10% may be important in certain com-

puter vision tasks like image segmentation and image

restoration. Thus, authors are convinced that by ana-

lyzing the color information, the efﬁciency and the

performance of edge detectors will be improved. For

instance, Isola et al.(Isola et al., 2014) proposed to de-

tect boundaries through the use of a statistical associ-

ation based on pointwise mutual information (PMI).

By using pixel color and variance information, aut-

hors achieve a good contour detection results. Xin

et al.(Xin et al., 2012) presented a revised version of

Canny algorithm for color images. This approach in-

volves the concept of quaternion weighted average ﬁl-

ter and whole vector analysis. These algorithms have

shown better results than the gray level image proces-

sing method. Using color information, the algorithm

balances between noise elimination and edge preser-

vation. Also, Xu et al. (Chen et al., 2012) introduced

a novel multispectral image edge detection algorithm.

According to authors, a multispectral image can be

well expressed via Clifford algebra which is so suit-

able for processing multidimensional data. The solu-

tion consists of computing a Clifford gradient using

the RGB channels. Then through the Clifford diffe-

rentiation method applied at each point and compa-

ring to its neighbor points, authors determine whether

it is an edge point using a chosen threshold. Although

these methods provided an efﬁcient detection of the

objects in the scene, they usually failed in complex

situations (e.g. stacked or occluded objects). They

were unable to differentiate between occluded objects

having same color. Thus, the boundaries of these ob-

jects will be hardly extracted. Obviously, in this case,

using only color information will be insufﬁcient.

With the development of image acquisition de-

vices, depth information can now be easily extrac-

ted. Depth information is becoming more popular

and more interesting to deal with occluded objects. In

fact, the algorithms of edge detection based on color

information paired with depth information has shown

excellent results of edge detection and differentiation

notably for same occluded objects. Among the most

recent relevant RGB-D edge detection algorithms, we

can mention the work of Asif et al. (Asif et al., 2016),

where the authors have presented a novel object seg-

mentation approach for highly complex indoor sce-

nes. The solution starts with an initial segmentation

step which consists of partitioning the scene into dis-

tinct regions. For this purpose, based on color-depth

image, authors generated a single multi-scale orien-

ted gradient signal. This latter is a linear combination

of oriented gradients determined independently from

six channels: three components of Lab color space,

depth information, surface normal and surface curva-

ture maps of the scene. After that, authors applied a

A Novel Multispectral Lab-depth based Edge Detector for Color Images with Occluded Objects

273

penalization step on this boundary response by ﬁxing

a user-selected threshold to suppress false boundary

responses. The proposed approach improves the per-

formance of the segmentation of stacked and occlu-

ded objects. However, this method integrates empiri-

cal parameters for generating the boundary response

which can be seen as a limitation. Also, the selected

threshold must be adjusted adaptively for each image.

Authors of (Yue et al., 2013) presented a RGB-D ba-

sed edge detection solution that combined both color

data and depth data. First, authors applied Canny edge

detector separately to both color and depth images in

order to extract color-edges image and depth-edges

image. Second, optimized depth-edges also, are re-

trieved by optimizing the depth-edges using the origi-

nal color image, and optimized color-edges are com-

puted from the optimization of color-edges, using the

original depth image. Last, the ﬁnal result is formed

by fusing both optimized depth-edges image and op-

timized color-edges image. This approach can easily

extract the same color occluded objects. However, the

algorithm consists of several time consuming steps.

In order to overcome the aforementioned pro-

blems, a novel algorithm is proposed for edge de-

tection by combining both color information and

depth information in well-principled way. The main

principle of our Lab-D gradient based approach is

to integrate different information into one meaning-

ful combination, without requiring empirical parame-

ters for edge enhancement. That’s why, we mixed

all channels into a Jacobian matrix. Thus, it is quite

straightforward and efﬁcient. Results show that the

proposed method outperforms recent state-of-the-art

methods.

3 PROPOSED METHOD

Based on the work of Drewniok (Drewniok, 1994) for

the multispectral gradient computation, we present an

approach to separate occluded objects using as input

color image and depth image of the scene. Our overall

edge detection approach can be split into two main

steps:

1. Preprocessing step.

2. Performing the gradient-based edge detection in

multi-dimensions.

3.1 Preprocessing Step

According to Cheng et al. (Cheng et al., 2001), se-

lecting the best color model affect the quality of de-

tection process. The RGB color space is suitable for

color display. But due to the high correlation among

the R, G and B components, RGB is considered not

good for color scene segmentation or detection. Thus,

we choose to use the CIE(l*a*b*) color space instead.

Compared to the RGB, CIE(l*a*b*) color space re-

presents color and intensity information more inde-

pendently and simply. Indeed, CIE(l*a*b*) can me-

asure efﬁciently a small color difference as this latter

can be calculated as the Euclidean distance between

two color points. In addition, by modifying simply

the output curves in a and b channels, the CIE(l*a*b*)

can be used to make accurate color balance correcti-

ons, or to adjust the lightness contrast using the L

channel. Authors in (Ganesan P. and Rajkumar, 2010)

review a segmentation method based on CIE(l*a*b*)

color space. The results show that the implementation

based on CIE(l*a*b*) outperform other color spaces

with various types of noises and using various edge

detectors algorithms. So, the CIE(l*a*b*) seems to

be a suitable color model for edge detection.

A Lab-D image is composed of pair of images

Color-D

= (I

Color

, I

Depth

), where I

Color

denotes a tradi-

tional three-channel color image (L channel, a chan-

nel and b channel) and I

Depth

denotes depth image (D

channel). Since all edge detection results are easily

affected by image noise, it is important to ﬁlter out

any noise to avoid false positives. Usually, in order to

smooth I

Color

images, the Gaussian ﬁlter is used. Ho-

wever, when ﬁltering noise using the Gaussian smoo-

thing algorithm, some regions are blurred. Thereby,

the associated edges will not be extracted. Xu et al.

(Xu et al., 2011) presented a novel algorithm that pre-

serves edges after smoothing process. For this rea-

son, authors used L

gradient minimization, which

can remove small-magnitude gradient. The method

suppressed low-amplitude details. Mean-while it glo-

bally optimized the edge detection process. There-

fore, the L

gradient algorithm is utilized in this pa-

per. The gradient operator ∇ applied to a scalar image

function I is deﬁned as follows.

∇I =





∂I

∂x

∂I

∂y





. (1)

The idea is that the gradient’s direction determines the

acute change of intensity, and the gradient’s magni-

tude corresponds to the strength of change. But the

gradient operator acts only on scalar functions. This

is why we compute the ﬁrst order Gaussian derivative

by the convolution of the image I with the Gaussian

function and apply the gradient on them.

∂(I ∗ G)(x, y)

∂x∂y

= I ∗

∂G(x, y)

∂x∂y



I ∗

∂G(x,y)

∂x

, I ∗

∂G(x,y)

∂y



(2)

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

274

where the 2-D Gaussian function G(x,y) is represen-

ted by equation 3:

G(x, y) =

2πσ

exp(−

+ y

2σ

). (3)

In practice, the convolution is done between the con-

sidered image and the convolution masks in both x

and y directions. The pair of convolution masks G

and G

are computed using equations 4 and 5:

−x

2πσ

exp(−

+ y

2σ

). (4)

−y

2πσ

exp(−

+ y

2σ

). (5)

3.2 Performing the Gradient-based

Edge Detection in Multi-dimensions

In order to take into account all information from co-

lor image and depth image, the multi-spectral image

function

−→

S (x, y) forms a vector of m scalars, where m

represents the total of channels derived from I

Color-D

−→

S (x, y) =







(x, y)







. (6)

In our method m = 4 (three-channels of the I

Color

and

one-channel of I

Depth

), So:

−→

S (x, y) =







(x, y)







, (7)

where I

denotes the L channel image, I

denotes the a

channel image, I

denotes the b channel image and I

denotes the depth channel image for each component

−→

S , we compute separately its Gaussian derivative

∇S

, where i ∈ {1...m} by applying the equation 2.

∂S

(x, y)

∂x∂y



∗ G

, S

∗ G





, S



(8)

Then, for each pixel (x,y), we form the Jacobian ma-

trix J with the Gaussian derivatives as shown below:

J =







∂S

(x,y)

∂x∂y

∂S

(x,y)

∂x∂y













(x, y) S

(x, y)

. .

(x, y) S

(x, y)







. (9)

In our work, the Jacobian matrix is represented in

equation 10 as follows:

J =







∂I

(x,y)

∂x∂y

∂I

(x,y)

∂x∂y

∂I

(x,y)

∂x∂y

∂I

(x,y)

∂x∂y













(x, y) I

(x, y)

(x, y) I

(x, y)

(x, y) I

(x, y)

(x, y) I

(x, y)







. (10)

The multi-spectral gradient approach is then the com-

bination between all the image components derivati-

ves, which have been already illustrated in the Jaco-

bian matrix J, in order to get magnitude and direction

of the strongest change at each pixel position. Then,

we compute the J

J matrix to ﬁnd the best compro-

mise between all image gradient components and to

avoid the use of empirical values introduced in (Asif

et al., 2016).

J =





, (11)

where

= S

+ ... + S

= S

+ ... + S

= g

= S

+ ... + S

In our case, we compute g

, g

and g

as fol-

lows:

= I

+ I

= I

+ I

= g

= I

+ I

The magnitude and the direction of the strongest

change of

−→

S corresponds to the greatest eigenvalue

and its associated eigenvector of the matrix J

J, re-

spectively. Actually, according to Drewniok (Drew-

niok, 1994), this extremum can be exploited through

the Rayleigh-quotient of the matrix J

J. In fact,

this is important since the extremum of the Rayleigh-

quotient matrix are found through the eigenvalues of

the matrix. As our multispectral function

−→

S is deﬁ-

ned on two directions x and y, a 2x2 matrix J

J is

found. Then, two eigenvalues λ

and λ

are calcula-

ted for each point (x,y), where λ

max

= max(|λ

|, |λ

|).

Obviously, λ

max

is given by:

max

+ g

)

. (12)

The direction ϕ

max

can be computed with equation 13:

max

∗ arctan

2 ∗ g

− g

. (13)

Finally, at this step an edge image is resulted as

A Novel Multispectral Lab-depth based Edge Detector for Color Images with Occluded Objects

275

shown in equation 14:

edge







max

(1, 1) . . . λ

max

(1, w)

. . .

max

(h, 1) . . . λ

max

(h, w)







(14)

where h denotes the height of the source image and w

denotes the width of the source image.

4 EXPERIMENTAL EVALUATION

AND RESULTS

In this section, in order to tease out the advantage of

using the depth information, we compare our results

with both (Isola et al., 2014; Asif et al., 2016) results.

These comparisons are performed on RGB-D images

and the results are illustrated in Figure 1 and Table 1.

4.1 Experimental Protocol

Our experimental protocol consists of evaluating our

method in terms of edge detection accuracy on stac-

ked and occluded objects. To quantify the perfor-

mance, we use the publicly available Middlebury ste-

reo dataset (Scharstein and Szeliski, 2003; Scharstein

and Pal, 2007; Hirschmuller and Scharstein, 2007). It

contains RGB-D images of different scenes, in which

a large variety of objects (cones, plastic, lampshades

and circles) are stacked and occluded over each ot-

her in several complicated layouts and with someti-

mes same colors. This is a motivating dataset for ob-

ject detection to separate distinct or same occluded

objects. Then, a collection of images with their cor-

respondent depth images (lightﬁeldgroup, 2016; Ro-

senman, 2016) contains a variety of images which are

characterized by different illumination settings, con-

taining several objects with the same color and evi-

dently occluded. The experiments show that our pro-

posed method, using CIE(l*a*b*) color images and

disparity map, is able to effectively handle the occlu-

sion cases in complex scenes with short time consu-

ming. In all experiments, for the L

smoothing algo-

rithm, we selected the values λ = 0.005 and K = 2.0.

All methods are tested using the same system with

an Intel CORE i5 CPU, 8 GByte RAM and Intel(R)

HD Graphics 3000.

4.2 Validation

Here we give details about the conﬁguration that we

have used for the relative works. For the method of

(Asif et al., 2016), in order to get the best gradient

response for each channel (L, a, b or D), three pre-

liminary empirical parameters are setted (ψ1 = 0.95,

ψ2 = 0.5 and ψ3 = 0.5). Also, for the penalization

step, a user selected threshold δb is asked for every

image. In our experiments, when implementing Asif

et al. (Asif et al., 2016) method we kept ﬁxed and set

to δb = 0.14 for all images. For (Isola et al., 2014),

we choose to run experiments for two cases: (i)by

only considering color information(Lab channels) as

the authors suggested (PMI) and (ii)by considering

both color information and depth information too to

see what will be changed by adding depth informa-

tion (PMID).

The Figure 1.(f) illustrates the results of our met-

hod compared to selected works (Isola et al., 2014;

Asif et al., 2016) on several test images. From this ﬁ-

gure, we can clearly notice that the proposed RGB-D

gradient based method outperforms signiﬁcantly the

state-of-the-art methods. Moreover, we can see that

the salient objects in each image are efﬁciently de-

tected. Beside this, we can see that object occlusion is

perfectly handled and edges has been appeared signi-

ﬁcantly. In Figure 1.(c), Figure 1.(d) and Figure 1.(e),

we can notice that some of edges were not preser-

ved, which were preserved by our technique. To vi-

sualize these areas clearly, we have highlighted them

with red circles where edge detection was failed on

the competent methods. We have also measured the

computation time for these approaches. The results

are resumed in the Table 1. We have shown in terms

of time-consuming that our method works faster than

other methods.

4.3 Discussion

In our method, the only parameters used are λ and

K for smoothing with the L

gradient minimization.

After several attempts, we have noticed that λ = 0.005

and K = 2.0 are suitable for most images.

For Asif et al. method (Asif et al., 2016), in or-

der to achieve a good edge detection, we have to

choose a user selected threshold parameter δ

suita-

ble for each image. Also, for Isola et al. method

(Isola et al., 2014), several parameters are selected

beforehand by authors, such as, ρ (free parameter for

optimizing segmentation performance), d (Gaussian

distance) and Z (a normalization constant). Experi-

ments show that these parameters affect dramatically

the edge detection performance in terms of quality

and speed. This is why, we have chosen to propose

and implement an unsupervised method which does

not depend from any parameter and is computatio-

nally adaptive to any type of image. So, for the ex-

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

276

Figure 1: Edge detection results by applying different methods on input images (a) RGB image and (b) depth image. (c) for

RGB information and (d) for both combined color and depth images are the results of Isola et al. (Isola et al., 2014). (e) is the

result of Asif et al. method (Asif et al., 2016). Finally, (f) represents the results of our method.

traction step of the gradient-based edge detection, we

have presented a well-principled edge detection met-

hod without using any empirical parameter by assem-

bling different Lab-D image channels into a Jacobian

matrix. This method is suitable for all images since

we are not supposed to choose any parameter accor-

ding to each image. Moreover, to reduce the noise in

some images (cf. ﬁgure1.(f)), we plan to adapt the

approach proposed by (Yue et al., 2013) as a post-

processing step. The main idea behind this method is

to rely on depth information to remove false-positive

edges.

5 CONCLUSION

A novel method for edge detection has been propo-

sed. Our method consists of acquiring two images

(Lab image and depth image). First of all, we apply

the L

gradient minimization algorithm on the Lab

image in order to suppress noises. Next, we compute

the ﬁrst order gaussian derivative for each channel

separately. Then, we assemble these derivatives on

a Jacobian matrix. After that, in order to obtain the

pairwise relations of the columns of the proposed Ja-

cobian matrix, we perform a product of this latter and

A Novel Multispectral Lab-depth based Edge Detector for Color Images with Occluded Objects

277

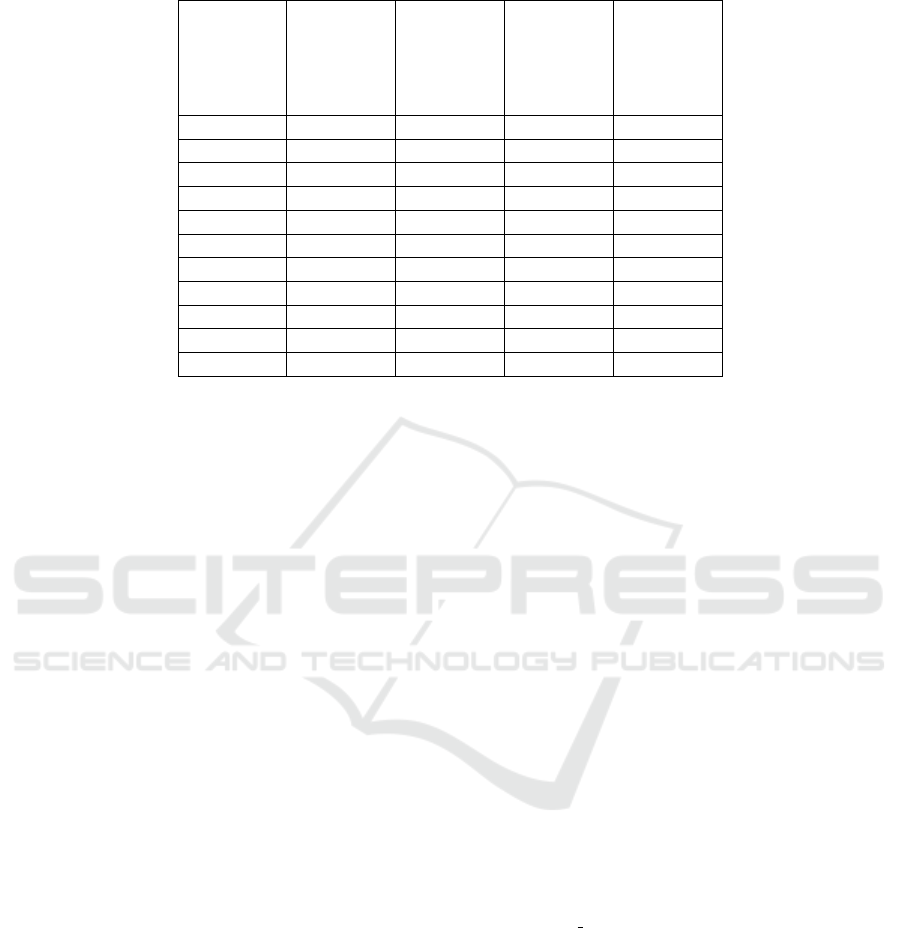
Table 1: Computation time in seconds for different Methods.

Test scene

No.

PMI (sec)

(Isola

et al.,

2014)

PMID

(sec)

(Isola

et al.,

2014)

Asif et al.

method

(sec) (Asif

et al.,

2016)

Our met-

hod (sec)

Image 01 3.15 3.07 0.86 0.539

Image 02 2.13 2.10 0.576 0.349

Image 03 7.68 7.40 1.516 1.127

Image 04 7.35 8.12 1.008 0.883

Image 05 13.80 13.47 1.536 1.305

Image 06 14.70 16.02 1.730 1.692

Image 07 14.69 15.27 1.407 1.253

Image 08 15.36 13.62 2.008 1.271

Image 09 13.44 12.90 1.950 1.129

Image 10 12.99 12.90 1.351 1.251

Image 11 12.61 12.69 1.370 1.136

its transpose. Finally, the maximal Eigen value of the

resulting matrix is selected as edge information.

Our main contribution consists of assembling all

the components of Lab image and depth image (L,a,b

and D) in a well-posed way without requiring any em-

pirical parameters.

Thus, experimental results show an improvement

compared to recent state-of-the-art methods (Isola

et al., 2014; Asif et al., 2016). In fact, our method

distinguishes occluded objects even if they have the

same color. Also, our method takes into account even

the small details in an image.

As future work, we plan to develop a post-

processing step which cleans the resulting image

from non-boundary edges, while preserving details as

much as possible. We will try to do not use any em-

pirical parameter. Then, we will use this method in a

blob detection algorithm.

REFERENCES

Asif, U., Bennamoun, M., and Sohel, F. (2016). Unsupervi-

sed segmentation of unknown objects in complex en-

vironments. Auton. Robots, 40(5):805–829.

Canny, J. (1986). A computational approach to edge de-

tection. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 8(6):679–698.

Chen, X., Hui, L., WenMing, C., and JiQiang, F. (2012).

Multispectral image edge detection via clifford gra-

dient. SCIENCE CHINA Information Sciences,

55(2):260–269.

Cheng, H. D., Jiang, X. H., Sun, Y., and Wang, J. L. (2001).

Color image segmentation: Advances and prospects.

Pattern Recognition, 34:2259–2281.

Davidson, M. W. and Abramowitz, M. (1998). Molecular

expressions microscopy primer: Digital image proces-

sing - difference of gaussians edge enhancement algo-

rithm. Olympus America Inc., and Florida State Uni-

versity.

Drewniok, C. (1994). Multi-spectral edge some experi-

ments on data from landsat-tm. Int. Journal of Remote

Sensing, 15(18):3743–3765.

Ganesan P., V. R. and Rajkumar, R. I. (2010). Segmen-

tation and edge detection of color images using cie-

lab color space and edge detectors. Emerging Trends

in Robotics and Communication Technologies (INTE-

RACT) 2010 International Conference on IEEE, pages

393–397.

Hirschmuller, H. and Scharstein, D. (2007). Evaluation of

cost functions for stereo matching. In IEEE Computer

Society Conference on Computer Vision and Pattern

Recognition (CVPR), pages 1–8.

Isola, P., Zoran, D., Krishnan, D., and Adelson, E. H.

(2014). Crisp boundary detection using pointwise mu-

tual information. In ECCV.

Krish, R. A. (1970). Computer determination of the con-

stituent structure of biological images. Computer and

Biomedical Research, 4(3):315–328.

lightﬁeldgroup (2016). Heidelberg collaboratory for image

processing. http://lightﬁeldgroup.iwr.uni-heidelberg.

de/?page id=713. [Online; accessed 2018-05-16].

Marr, D. and Hildreth, E. (1980). Theory of edge detection.

207:187–217.

Nadernejad, E., Sharifzadeh, S., and Hassanpour, H. (2008).

Edge detection techniques: Evaluations and compa-

risons. Applied Mathematical Sciences, 2(31):1507–

1520.

Novack, C. L. and Shafer, S. A. (1987). Color edge de-

tection. In Proceedings DARPA Image Understanding

Workshop, volume 1, pages 35–37.

Perez, M. M. and Dennis, T. J. (1997). An adaptive im-

plementation of the susan method for image edge and

feature detection. In Proceedings of IEEE Conference

on Image Processing, volume 2, pages 394–397.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

278

Prewitt, J. M. S. (1970). Object enhancement and ex-

traction. Picture Processing and Psychopictorics,

10:15–19.

Roberts, L. G. (1963). Machine perception of three-

dimensional solids. PhD thesis, Massachusetts Insti-

tute of Technology, Dept. of Electrical Engineering.

Rosenman, R. (2016). Depth of ﬁeld generator pro. http:

//www.dofpro.com/. [Online; accessed 2018-05-16].

Saurabh, G., Ross, G., Pablo, A., and Jitendre, M. (2014).

Learning rich features from rgb-d images for object

detection and segmentation. In Lecture Notes in Com-

puter Science, volume 8695, pages 345–360.

Scharstein, D. and Pal, C. (2007). Learning conditional

random ﬁelds for stereo. In IEEE Computer Society

Conference on Computer Vision and Pattern Recogni-

tion (CVPR).

Scharstein, D. and Szeliski, R. (2003). High-accuracy ste-

reo depth maps using structured light. In Proceedings

of the 2003 IEEE Computer Society Conference on

Computer Vision and Pattern Recognition, volume 1

of CVPR’03, pages 195–202.

Silberman, N., Shapira, L., Gal, R., and Kholi, P. (2014).

A counter completion model for augmenting surface

reconstructions. In Proc. ECCV, pages 488–503.

Sobel, I. E. (1970). Camera models and machine percep-

tion. PhD thesis, Stanford University, Calif., USA.

Xin, G., Ke, C., and Xiaoguang, H. (2012). An improved

canny edge detection algorithm for color image. In

IEEE 10th International Conference on Industrial In-

formatics, pages 113–117.

Xu, L., Lu, C., Xu, Y., and Jia, J. (2011). Image smoothing

via l0 gradient minimization. ACM Transactions on

Graphics (SIGGRAPH Asia), 30(6).

Yue, H., Chen, W., Wang, J., and Wu, X. (2013). Combining

color and depth data for edge detection. In Proceeding

of IEEE, 2013 International Conference on Robotics

and Biometrics (ROBIO), pages 928–933.

Zhang, H., Wen, Z., LIU, Y., and Xu, G. (2016). Edge de-

tection from rgb-d image based on structured forests.

Journal of Sensors, 2016. 10 pages.

A Novel Multispectral Lab-depth based Edge Detector for Color Images with Occluded Objects

279