The Impact of the Transversion/Transition Ratio on the Optimal Genetic

Code Graph Partition

Daniyah A. Aloqalaa

, Dariusz R. Kowalski

1,2

, Paweł Bła

zej

, Małgorzata Wnetrzak

Dorota Mackiewicz

and Paweł Mackiewicz

Department of Computer Science University of Liverpool, U.K.

SWPS University of Social Sciences and Humanities, Warsaw, Poland

Faculty of Biotechnology, University of Wrocław, Poland

{dorota, pamac}@smorﬂand.uni.wroc.pl

Keywords:

Code Degeneracy, Graph Theory, Mutation, Set Conductance, Standard Genetic Code, Transition, Transver-

sion.

Abstract:

The standard genetic code (SGC) is a system of rules ascribing 20 amino acids and stop translation signal to 64

codons, i.e triplets of nucleotides. It was proposed that the structure of the SGC evolved to minimize harmful

consequences of mutations and translational errors. To study this problem, we described the SGC structure by

a graph, in which codons are vertices and edges correspond to single nucleotide mutations occurring between

the codons. We also introduced weights (W ) for mutation types to distinguish transversions from transitions.

Using this representation, the SGC is a partition of the set of vertices into 21 disjoint subsets. In this case,

the question about the potential robustness of the genetic code to the mutations can be reformulated into the

optimal graph clustering task. To investigate this problem, we applied an appropriate clustering algorithm,

which searched for the codes characterized by the minimum average calculated from the set W -conductance

of codon groups. Our algorithm found three best codes for various ranges of the applied weights. The average

W -conductance of the SGC was the most similar to that of the best codes in the range of weights corresponding

to the observed transversion/transition ratio in natural mutational pressures. However, it should be noted that

the optimization of the SGC was not as perfect as the best codes. It implies that the evolution of the SGC was

driven not only by the selection for the robustness against mutations or mistranslations but also other factors,

e.g. subsequent addition of amino acids to the code according to the expansion of amino acid metabolic

pathways.

1 INTRODUCTION

The questions about the origin and the structure of

the standard genetic code (SGC) have puzzled biolo-

gists since the ﬁrst codons assignments were discov-

ered (Khorana et al., 1966; Nirenberg et al., 1966).

This nearly universal, with some rare exceptions, set

of coding rules is responsible for transmitting genetic

information stored in DNA molecules into the pro-

tein world. The code uses all possible 64 nucleotide

triplets, i.e. codons, to encode 20 canonical amino

acids and also the signal for stopping the protein syn-

thesis, i.e. the translation. Since the total number of

codons is greater then the number of encoded labels,

the SGC must be degenerate, i.e. there must exist an

amino acid that is encoded by more than one codon.

These redundant codons, called synonymous, are or-

ganized in speciﬁc groups. In most cases, the codons

in such groups differ at the third position, which can

be called a degenerate position. This fact suggested to

Francis Crick that only the ﬁrst two codon positions

were important in a primordial code (Crick, 1968).

The redundancy of the SGC causes other interest-

ing consequences related to the process of single nu-

cleotide mutations. If these changes occur in the de-

generate codon position, then the originally encoded

amino acid will not be changed. These mutations

are called synonymous or silent, whereas those that

change the encoded amino acid or stop translation sig-

nal are named nonsynonymous. It should be noted

that there are two types of nucleotide changes, tran-

sitions and transversions. In the case of transition, a

purine nucleotide, i.e. adenine or guanine, mutates

to another purine (A↔G), or a pyrimidine nucleotide,

Aloqalaa, D., Kowalski, D., Bła

zej, P., Wnetrzak, M., Mackiewicz, D. and Mackiewicz, P.

The Impact of the Transversion/Transition Ratio on the Optimal Genetic Code Graph Partition.

DOI: 10.5220/0007381000550065

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 55-65

ISBN: 978-989-758-353-7

i.e. cytosine or thymine, changes into another pyrim-

idine (C↔T). Transversion are changes in which a

purine mutates to a pyrimidine or vice versa (A↔C,

A↔T, G↔C, G↔T). There are four possible transi-

tions and eight possible transversions. Transitions are

more often observed in sequences than transversions

(Duch

ene et al., 2015; Gojobori et al., 1982; Kumar,

1996; Lynch, 2010; Lyons and Lauring, 2017; Petrov

and Hartl, 1999; Rosenberg et al., 2003; Wakeley,

1996). It may result from a higher mutation rate of

transitions than transversions in nucleic acids due to

physicochemical similarity of the nucleotides. More-

over, transitions are accepted with a greater probabil-

ity because they rarely lead to amino acid substitu-

tions in encoded proteins due to the speciﬁc codon

degeneracy. The transitions are also more frequent

during protein synthesis (Freeland and Hurst, 1998a).

It should be noted, that the synonymous substitu-

tions do not have to be completely neutral mutations,

even though they do not change a coded amino acid.

The speciﬁc codon usage can be associated with co-

translational modiﬁcations of amino acids, efﬁciency

and accuracy of translation as well as co-translational

folding of synthesized proteins (Bulmer, 1991; Her-

shberg and Petrov, 2008; Zhou et al., 2009). The syn-

onymous codon usage can be also modiﬁed as a con-

sequence of selection at the amino acid level (Morton,

2001; Bła

zej et al., 2017b).

The tendency to minimize the number of non-

synonymous substitutions were noticed in the SGC

and this property suggested that the code could have

evolved to minimize harmful consequences of muta-

tions and translational errors (Ardell, 1998; Ardell

and Sella, 2001; Di Giulio, 1989; Di Giulio and

Medugno, 1999; Epstein, 1966; Freeland and Hurst,

1998a; Freeland and Hurst, 1998b; Freeland et al.,

2003; Freeland et al., 2000; Gilis et al., 2001; Gold-

berg and Wittes, 1966; Goodarzi et al., 2005; Haig

and Hurst, 1991; Woese, 1965). The robustness of the

code was usually measured as a difference between

the polarity values of amino acids encoded by codons

before and after a single-point mutation.

Since the genetic code is a set of codons which

are related, e.g. by nucleotide mutations, the general

structure of this code can be well described by the

methodology taken from graph theory (Beineke and

Wilson, 2005; Lee et al., 2014). Similarly to (Tlusty,

2010; Bła

zej et al., 2018a), we assume that the code

encodes 21 items, i.e. 20 amino acids and stop trans-

lation signal, and all 64 codons create the set of ver-

tices of the graph, in which the set of edges corre-

sponds to all possible single nucleotide mutations oc-

curring between the codons. This graph is undirected,

unweighted and regular. Moreover, according to this

representation, each genetic code is a partition of the

set of vertices into 21 disjoint subsets. Therefore, the

question about the potential genetic code optimality

in regard to the mutations can be reformulated into

the optimal graph clustering problem.

In the present study, we investigated the proper-

ties of the SGC using a more general model including

in the graph representation information about tran-

sition to transversion ratio, which was not consid-

ered by (Tlusty, 2010; Bła

zej et al., 2018a). From a

mathematical point of view, we considered a weighted

graph, in which all weights are dependent on the type

of nucleotide substitutions. We also modiﬁed the set

conductance measure, which is widely used in the

graph theory (Lee et al., 2014) and has many prac-

tical interpretations, for example in the theory of ran-

dom walks (Levin et al., 2009) and social networks

(Bollob

as, 1998). In the problem considered here,

the conductance of a codon group is the ratio of the

weights of nonsynonymous mutations to the weights

of all possible single nucleotide mutations, in which

the codons in this group are involved. Therefore, this

parameter can be used as a measure of robustness

against the potential changes in protein-coding se-

quences generated by the single nucleotide mutations.

Basing on the methodology described in (Bła

zej et al.,

2018a), we found some solutions, i.e. the genetic

code structures, of the optimal graph clustering prob-

lem.

2 PRELIMINARIES

2.1 Model Description

To study the general structure of the genetic code we

developed its graph representation. Let G(V, E) be

a graph in which V is the set of vertices represent-

ing all possible 64 codons, whereas E is the set of

edges connecting these vertices. All connections ful-

ﬁl the property that the vertices, i.e. codons u, v ∈ V

are connected by the edge e(u, v) ∈ E (u ∼ v) if and

only if the codon u differs from the codon v in ex-

actly one position. Moreover, we claim that all tran-

sitions are given a weight which equals always to

one, while the transversions are given a weight W ,

where W ∈ [0, ∞). The larger weight indicates that the

transversions are more important than transitions, re-

spectively. The weight can be interpreted as transver-

sion to transition ratio. Hence, the graph G is undi-

rected, weighted and regular with the vertices degree

equal to 9. Moreover, from a biological perspec-

tive, the set of edges represents all possible single nu-

cleotide substitutions, which occur between codons in

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

a DNA sequence. What is more, this model includes

two important types of mutations.

Following the methodology presented in (Bła

zej

et al., 2018a), each potential genetic code C, which

encodes 20 amino acids and stop translation signal is

a partition of the set V into 21 disjoint subsets, i.e.

groups of codons, S. Thus, we obtain the following

representation of the genetic code C:

C = {S

, S

, ··· , S

, S

: S

∩ S

= Ø,S

∪ S

∪ ·· · ∪ S

= V } .

In Figure 1 we showed an example of the parti-

tion of the graph G, which corresponds to the stan-

dard genetic code. From a biological point of view, it

is interesting to study the code structure according to

the types and also the number of connections between

and within the codon groups because these connec-

tions correspond to nonsynonymous and synonymous

substitutions, respectively. It should be noted that

each potential genetic code that minimizes the num-

ber of the nonsynonymous substitutions is regarded

the best in terms of decreasing the biological conse-

quences of mutations. Therefore, the conditions un-

der which the partitions of the graph vertices describe

the best genetic code, are worth ﬁnding.

There are many methods of the optimal graph par-

titioning, which are based on different approaches. In

this work, to investigate the theoretical features of ge-

netic codes in terms of the connections between the

codon groups, we decided to use the set conductance

measure, which plays a central role in the spectral

graph clustering method. The deﬁnition of the set W -

conductance measure including weights for edges is

as follows:

Deﬁnition 2.1. For a given weighted graph G let W

be a weight of transversion connections in G and S be

a subset of V . The W -conductance of S is deﬁned as:

(W ) =

(S, S) + E

trv

(S, S) ·W

|S| · (3 + 6W )

where E

(S, S) is the total number of transition edges

crossing from S to its complement S whereas E

trv

(S, S)

is the total number of transversion edges crossing

from S to its complement

S, and |S| is the number of

vertices belonging to S.

The deﬁnition of the set W -conductance is a good

staring point to describe a quality measure of a given

codon group. Large values of this measure mean that

a substantial fraction of substitutions in which these

codons are involved are nonsynonymous, i.e. they

change one amino acid to another. From the robust-

ness point of view, small values are desirable because

in this case many substitutions are neutral (synony-

mous) and do not change coded amino acids.

What is more, this approach allows us to char-

acterize the properties of the whole genetic code

because following the deﬁnition of the set W -

conductance we deﬁne the average W -conductance of

a genetic code:

Deﬁnition 2.2. The average W -conductance of a

given genetic code C and a given weight W is deﬁned

as:

(W ) =

∑

S∈C

(W ) .

Using the deﬁnition presented above, we are able

to describe the best code in terms of the average W -

conductance, which is deﬁned as follows:

min

(W ) = min

(W ) .

min

(W ) gives us the lower bound of the genetic

code robustness measured in terms of the average

code W -conductance.

2.2 The Clustering Algorithm

In this work we propose a new randomized clustering

algorithm to ﬁnd the optimal genetic code with re-

spect to the minimum average W -conductance. More

formal description of Algorithm 1 provides the struc-

ture of the clustering algorithm. The generic struc-

ture of the clustering algorithm contains inputs, out-

puts (cf. input parameters and output variables in

Table 1), and three functions, namely: AVERAGE-

CONDUCTANCE, PICKFIRSTNODE, and PICKSEC-

ONDNODE. The main function is the AVERAGE-

CONDUCTANCE function, which aims to ﬁnd the op-

timal genetic code with the minimum average W -

conductance. The function includes nested loops of

two levels. The main loop (lines 5-14) counts the

average conductance for each iteration. The second

level loop (lines 7-14) is for picking and merging

nodes from the graph until we have 21 clusters (su-

per nodes). The AVERAGECONDUCTANCE termi-

nates when the graph is clustered to 21 clusters for

each iteration and returns the best genetic code with

the minimum average conductance over all indepen-

dent iterations. The PICKFIRSTNODE (lines 16-30)

and the PICKSECONDNODE (lines 31-47) associate a

probability for each node in the graph and each func-

tion pick a node randomly.

3 RESULTS AND DISCUSSION

The main goal of our work is to ﬁnd the optimal ge-

netic codes in terms of the average W-conductance

min

(W ). Furthermore, we compare the properties of

The Impact of the Transversion/Transition Ratio on the Optimal Genetic Code Graph Partition

AAA

AAT

AAG

AAC

ATA

ATT

ATG

ATC

AGA

AGT

AGG

AGC

ACA

ACT

ACG

ACC

TAA

TAT

TAG

TAC

TTA

TTT

TTG

TTC

TGA

TGT

TGG

TGC

TCA

TCT

TCG

TCC

GAA

GAT

GAG

GTA

GTT

GTG

GTC

GGA

GGT

GGG

GGC

GCA

GCT

GCG

GCC

CAA

CAT

CAG

CAC

CTA

CTT

CTG

CTC

CGA

CGT

CGG

CGC

CCA

CCT

CCG

CCC

GAC

Figure 1: The standard genetic code as an example of the partition of the graph G(V, E). Every group of vertices with the

same colour corresponds to the respective set of codons, which code for the same amino acid or stop translation signal. The

edges represent all possible single nucleotide substitutions. According to (Bła

zej et al., 2018a), modiﬁed.

Table 1: Input parameters and output variables for Algo-

rithm 1.

Input parameters:

1 Adjacent matrix of 64 codons, called A,

where A[i, j] can take:

A[i, j] =











1 if i 6= j and if and only if i differs

from j in exactly one position

0 otherwise

2 Adjacent transition matrix of codons, called B,

where B[i, j] can take 1 only with transition

connections i.e. A↔G, C↔T, otherwise 0

3 W ∈ [0,∞)

4 #iterations ← 20, 000

Output variables:

1 The minimum average conductance

2 The structure of the best genetic code that

gives the minimum average conductance

these codes with the standard genetic code, which is

interesting from the biological point of view.

We run the clustering algorithm (Algorithm 1)

20,000 times independently to ﬁnd the minimum of

the W -average conductance and the structure of the

genetic code that gives the minimum average W -

conductance. We carried out the calculations for the

transversion weight W ∈ [0, 10]. The weights can

be interpreted as a relative ratio between transver-

sions and transitions. Smaller weights mean that tran-

sitions are more frequent than transversions, while

larger weights indicate that the transversions domi-

nate among point mutations.

We found three genetic codes that are best for dif-

ferent ranges of W ∈ [0, ∞]. The genetic code C1 was

best for every W ∈ [0,

], the code C2 for every W ∈

[

, 1] and the code C3 for every W ∈ [1, ∞]. The aver-

age W -conductance for these codes in the function of

weight W is Φ

(W ) =

126W +31

6W +3

, Φ

(W ) =

308W +130

9(2W +1)

, and Φ

(W ) =

94W +52

6W +3

for every W ∈

[0,

], [

, 1], and [1, ∞], respectively. We conjecture

that these codes are optimal in the range of weights

corresponding to the observed transversion/transition

ratio in natural mutational pressures; though, as the

algorithm is randomized (but repeated a large num-

ber of times to reduce the probability of ﬁnding sub-

optimal solutions), the formal proof of their optimal-

ity is still an open question. Figure 2 shows the av-

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

Algorithm 1: The clustering algorithm.

1: function AVERAGECONDUCTANCE(A, B,W, iterations)

2: D = A − B  Create transversion matrix

3: M = B + (W · D)  Create matrix M

4: min-ave-cond ← 2

5: for each iteration do

6: g = [(node, edges) for each node in M]  List g stores each node i in M and its edges

7: while (len(g) > 21 nodes) do  Keep picking and merging nodes until we have 21 clusters

8: u ← PICKFIRSTNODE(g)

9: v ← PICKSECONDNODE(g)

10: Merge nodes u and v

11: conductance = compute conductance for each cluster in g  List conductance stores conductance of 21

clusters using φ

(W ) formula in Deﬁnition 2.1

12: if min-ave-cond>sum(conductance)/len(conductance) then

13: min-ave-cond = sum(conductance)/len(conductance)

14: clusterings-min-ave-cond = g  Stores the structure of the genetic code

15: return min-ave-cond, clusterings-min-ave-cond

16: function PICKFIRSTNODE(g)

17: cond ← [(i,φ

(W )) for each node i in g]  List to store conductance for each node i in g

18: for for each node i in cond do

19: weight[i] ← (i, cond[i]

)  List to store weight for each node i in cond list

20: for for each node i in weight do

21: prob[i] ← (i,

weight[i]

sum(weight)

)  List to store probability of selecting each node i in weight list

22: R ← Generate a random number between 0 and 1

23: j ← 0

24: a ← prob[0]

25: while (R > a) do

26: j ← j + 1

27: a ← a + prob[ j]

28: return j

29: u ← cond[ j]  Select the j

node in the cond list

30: return u

31: function PICKSECONDNODE(g)

32: cond1 ← cond − u  Copy cond list without the selected node u

33: for for each node i in cond1 do

34: edges[i] ← (i, #edges between i and u)

35: for for each node i in cond1 do

36: weight[i] ← (i, (edges[i] + 1)

· cond1[i]

)  List to store weight for each node i in cond1 list

37: for for each node i in weight do

38: prob[i] ← (i,

weight[i]

sum(weight)

)  List to store probability of selecting each node i in weight list

39: R ← Generate a random number between 0 and 1

40: j ← 0

41: a ← prob[0]

42: while (R > a) do

43: j ← j + 1

44: a ← a + prob[ j]

45: return j

46: v ← cond1[ j]  Select the j

node in the cond1 list

47: return v

The Impact of the Transversion/Transition Ratio on the Optimal Genetic Code Graph Partition

erage W -conductance for the best codes and the SGC

depending on the transversion weight.

The average conductance for the codes that are

best for W < 1 increases rapidly with W and then sta-

bilizes for large values. In the case of the code C3,

its conductance decreases at ﬁrst and then also ap-

proaches a certain value. For small W values, the

average conductance is the smallest for the code C1

and the largest for codes C3. In turn, the opposite is

true for large W values. The code C1 is characterized

by the biggest difference between its average conduc-

tance values. The code is very well optimized for the

excess of transitions over transversions but it is very

bad in the opposite case. The average W -conductance

of the SGC shows the general course similar to that of

the C1 and C2 codes.

To compare the properties of the best codes with

the standard genetic code, we computed the func-

tion of the average W -conductance for the SGC,

SGC

(W ) =

10(33W +13)

9(2W +1)

. Then, we subtracted

SGC

(W ) from each of the average W-conductance

function of each best codes (C1,C2,C3) and calcu-

lated the derivative for each produced function as fol-

lows:

1. Deﬁne f 1(W ) = Φ

SGC

− Φ

, then

f 1(W ) =

10(33W + 13)

9(2W + 1)

−

126W + 31

6W + 3

The derivative of f 1(W ) is

f 1

(W ) = −

122

189(2W + 1)

At W = 0, the value of f 1 is equal to 0.2 and

at W =

f 1 is is equal to 0.03. The values of

the conductance function for both codes are the

same at W =

. Below this weight the C1 code

shows a smaller Φ than the SGC and above this

weight, the opposite is true.

2. Deﬁne f 2(W ) = Φ

SGC

− Φ

, then

f 2(W ) =

10(33W + 13)

9(2W + 1)

−

308W + 130

9(2W + 1)

The derivative of f 2(W ) is

f 2

(W ) =

189(2W + 1)

At W = 0, the C2 and the SGC codes have the

same values of Φ, i.e. f 2 = 0. Next, with the

growth of W , f 2 increases, which means that

the average W -conductance of the SGC becomes

larger than that of the C2 code. At W =

, the

value of f 2 is equal to 0.03 and at W = 1 f 2 is

equal to 0.04.

3. Deﬁne f 3(W ) = Φ

SGC

− Φ

, then

f 3(W ) =

10(33W + 13)

9(2W + 1)

−

94W + 52

6W + 3

The derivative of f 3(W ) is

f 3

(W ) =

100

189(2W + 1)

For W <

, Φ

SGC

is smaller than Φ

. Above this

weight, the opposite is true. At W = 1, the value

of f 4 is equal to 0.04 and at W = 3 f 3 is equal to

0.11.

The functions f 1(W ), f 2(W ) and f 3(W ) are dif-

ferences in the average W -conductance between the

SGC and three best codes depending on the transi-

tion weight W . It is evident that the standard genetic

code is optimized for more frequent transitions than

transversions. The SGC can obtain the same average

W -conductance as each of the optimized codes but for

different transversion weights. Nevertheless, the W

is always smaller than 1 in these cases. The mini-

mum distance between the SGC and the best genetic

codes in terms of the average conductance is 0.03

for W =

= 0.53 (Figure 3). Since there are twice

as many possible transversions as transitions, the ex-

pected ratio should be 2, if all nucleotide substitutions

happen with the same probability. Interestingly, the

weights for which Φ

SGC

is close to Φ of the best codes

is in the range of the transversion/transition ratio ob-

served in genomic mutational pressures, i.e. from

1.44 to 0.10 (Kowalczuk et al., 2001; Bła

zej et al.,

2015). However, for each transversion weight, it is

possible to ﬁnd a code better optimized than the SGC

in terms of the average W -conductance, so this code is

not perfectly optimized. Our preliminary analyses of

the alternative genetic codes in this respect showed

that the relationship between their average conduc-

tance depending on the transversion weight has the

course very similar to that of the SGC.

The structure of these best genetic codes is pre-

sented in Table 2. Although the code C1 and C3 are

best for different and extreme W values, they have the

same number of two- and four-codon groups, 10 and

11, respectively. The code C2 has in addition 3 groups

consisting of three codons as well as 8 two-codon

groups and 9 four-codon groups. The SGC is more

diversiﬁed in this respect because it has 2 one-codon

groups, 9 two-codon groups, 2 three-codon groups, 5

four-codon groups and 3 six-codon groups. Thereby,

it is more similar to the code C2.

The code C1 is best for smaller weights of

transversions. Therefore, such mutations are prefer-

ably involved in changes between codon groups of

this code in order to minimize these changes. Con-

sequently, all synonymous substitutions in this code

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

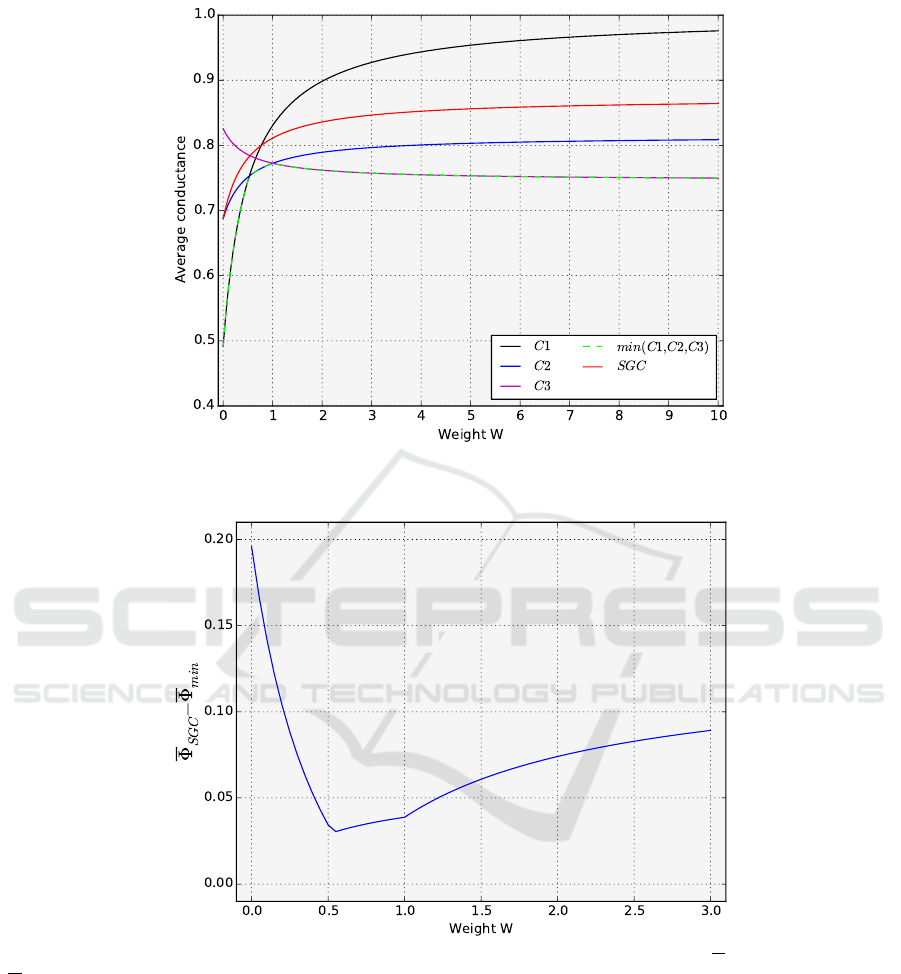
Figure 2: The average conductance for the best codes C1,C2,C3, and min(C1,C2,C3) as well as the standard genetic code

(SGC) for the weights of transversions W ∈ [0, 10].

Figure 3: The difference between the average conductance for the standard genetic code (SGC) (Φ

SGC

) and the best codes

(Φ

min

) for the weights of transversions W ∈ [0, 3].

are transitions. In the case of the code C3, which is

best for larger W , transversions were eliminated from

changes between codon groups as much as possible

to increase the number of transitions. In consequence,

all changes within two-codon groups of this code are

transversions. Since there are only two purines and

two pyrimidines, it is not possible to create four-

codon groups that can change to each other by only

transversions. Therefore, changes within such groups

are both transitions and transversions. The code C2

is a mixture in this respect because the codons in its

two-codon groups can change to each other only by

transitions, while in the other groups by the two types

of mutations. Considering only one point mutations

in the SGC, all changes within two-codon groups are

also transitions and within other groups both tran-

sitions and transversions with exception to the stop

codon group, which also involves only transitions.

Then the SGC is again more similar to the code C2

in this respect.

The Impact of the Transversion/Transition Ratio on the Optimal Genetic Code Graph Partition

Table 2: The structure of the best genetic codes C1,C2, and C3 for W ∈ [0,

], W ∈ [

, 1], and W ∈ [1, ∞], respectively. Each

row describes the codon group for a cluster.

C1 C2 C3

1 {AAA, AAG, AGG, AGA} {AAG, ACG, ATG} {ATA, AAA, AGA, ACA}

2 {AT T, ATC} {AGA, AGG} {AGC, ACC}

3 {TAG, TAA} {AGC, ATC, AAC, ACC} {ACT, TCT }

4 {TAC, TAT, T GT, T GC} {ACA, AAA, ATA} {ACG, AAG,AT G, AGG}

5 {T T T,CT T } {TAA, TAG} {T TA, TAA}

6 {T GA, T GG} {TAC,CAC} {T TC, TAC, TCC, T GC}

7 {TCT,CCT } {T TA,CTA, GTA} {T GG, TAG, TCG, T T G}

8 {TCG, T T G, T TA, TCA} {T T G,CT G} {TCA, T GA}

9 {TCC, T TC,CTC,CCC} {T GA, T GG, T GC, T GT } {GAT, AAT, TAT,CAT }

10 {GTA, ATA, GT G, AT G} {TCA, TCT, TCC, TCG} {GT T, ATT, T T T,CT T }

11 {GTC, GT T } {GAT, AAT, TAT,CAT } {GGA, GCA, GAA, GTA}

12 {GGA, GAA, GAG, GGG} {GAC, GGC, GCC, GTC} {GGT,CGT, AGT, T GT }

13 {GGT, GAT, AGT, AAT } {GT G, GAG, GGG, GCG} {GCG, GAG,GGG, GT G}

14 {GGC, AGC, AAC, GAC} {GGT, AGT} {GCC, GTC, GAC, GGC}

15 {GCG, GCA, ACA, ACG} {GCA, GGA, GAA} {CAA,CTA}

16 {GCC, ACC, GCT, ACT } {GCT, ACT } {CAC, AAC}

17 {CAT,CGT,CGC,CAC} {CAG,CAA} {CT G,CGG,CAG,CCG}

18 {CTA,CT G} {CT T, GT T, AT T, T T T } {CTC, ATC}

19 {CGA,CAA} {CTC, T TC} {CGC,CCC}

20 {CGG,CAG} {CGC,CGG,CGT,CGA} {CCA,CGA}

21 {CCG,CCA} {CCA,CCC,CCT,CCG} {CCT, GCT }

The changes between codons in one group of the

code C3 can occur only in one ﬁxed codon position,

the ﬁrst or the second one. The third codon position

can also be mutated in the code C2. However, the

code C1 contains also the groups in which any two

codon positions can be changed. The SGC contains

many codon groups with synonymous mutations in

the third codon position but there are also three codon

groups involving single changes in two codon posi-

tions.

The comparison of structures of the genetic codes

show that the assignments of amino acids to codons

is not ideally optimized in the SGC. Some similar-

ity of the SGC to the code C2 suggests that the stan-

dard genetic code could evolve under the transver-

sion/transition for which the code C2 is best.

4 CONCLUSIONS

Our results show that the general structure of the

genetic code and the problem of the genetic code

optimality can be successfully reformulated using a

methodology adapted from graph theory in the con-

text of optimal clustering of a speciﬁc graph. To eval-

uate the quality of the genetic code, we calculated

the average code W -conductance including weights

for mutation types. Thereby, we distinguished tran-

sitions and transversions. From the biological point

of view, this measure describes the code robustness

against amino acid and stop translation signal replace-

ments resulting from single nucleotide substitutions

between codons.

We found three best codes with respect to the av-

erage code conductance for various ranges of the ap-

plied weight. The structure of the codes was differ-

ent in comparison to the standard genetic code. The

W -conductance of the SGC was the most similar to

that of the best codes in the range of weights corre-

sponding to the observed small transversion/transition

ratio in the mutational pressure. Other researches

also showed that the SGC performs better for the ex-

cess of transitions over transversions (Freeland and

Hurst, 1998a; Freeland and Hurst, 1998b). It indi-

cates that the SGC is optimized to some extent in

terms of the minimization of amino acid and stop

translation replacements. However, the optimization

was not ideal and for each weight better theoreti-

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

cal codes could be found. In agreement with that,

other investigations also showed that the SGC is not

perfectly robust against point mutations or mistrans-

lations (Bła

zej et al., 2018b; Bła

zej et al., 2016;

Massey, 2008; Novozhilov et al., 2007; Santos and

Monteagudo, 2011; Santos and Monteagudo, 2017;

Wnetrzak et al., 2018).

Most likely, the robustness against mutations was

not the main force that drove the evolution of the ge-

netic code and amino acids were assigned to codons

according to expansion of biosynthetic pathways syn-

thesizing amino acids (Di Giulio, 1999; Di Giulio,

2008; Di Giulio, 2016; Di Giulio, 2017; Wong, 1975;

Wong et al., 2016; Wong, 2007; Di Giulio, 2018). In

this case, the potential minimization of mutation er-

rors could have occurred by the direct optimization of

the mutational pressure around the established genetic

code (Dudkiewicz et al., 2005; Mackiewicz et al.,

2008; Bła

zej et al., 2013; Bła

zej et al., 2017a; Bła

zej

et al., 2015).

The results can have practical consequences in

the context of designing modiﬁed or extended genetic

codes (Xie and Schultz, 2006; Chin, 2014). The aim

of this engineering is to produce peptides or proteins

containing unnatural amino acids and showing an im-

proved activity or completely new functions.

ACKNOWLEDGMENTS

This work was supported by the National Science

Centre, Poland (Narodowe Centrum Nauki, Polska)

under Grants number UMO-2017/27/N/NZ2/00403

and UMO-2017/25/B/ST6/02553.

REFERENCES

Ardell, D. H. (1998). On error minimization in a sequential

origin of the standard genetic code. Journal of Molec-

ular Evolution, 47(1):1–13.

Ardell, D. H. and Sella, G. (2001). On the evolution of

redundancy in genetic codes. Journal of Molecular

Evolution, 53(4-5):269–281.

Beineke, L. W. and Wilson, R. J. (2005). Topics in al-

gebraic graph theory. Cambridge University Press,

Cambridge, UK; New York.

Bła

zej, P., Kowalski, D., Mackiewicz, D., Wnetrzak, M.,

Aloqalaa, D., and Mackiewicz, P. (2018a). The struc-

ture of the genetic code as an optimal graph clustering

problem. bioRxiv.

Bła

zej, P., Mackiewicz, D., Grabinska, M., Wnetrzak, M.,

and Mackiewicz, P. (2017a). Optimization of amino

acid replacement costs by mutational pressure in bac-

terial genomes. Scientiﬁc Reports, 7:1061.

Bła

zej, P., Mackiewicz, D., Wnetrzak, M., and Mackiewicz,

P. (2017b). The impact of selection at the amino acid

level on the usage of synonymous codons. G3-Genes

Genomes Genetics, 7(3):967–981.

Bła

zej, P., Mackiewicz, P., Cebrat, S., and Wa

nczyk, M.

(2013). Using evolutionary algorithms in ﬁnding

of optimized nucleotide substitution matrices. In

Genetic and Evolutionary Computation Conference,

GECCO’13, pages 41–42. Companion ACM.

Bła

zej, P., Miasojedow, B., Grabinska, M., and Mack-

iewicz, P. (2015). Optimization of mutation pressure

in relation to properties of protein-coding sequences

in bacterial genomes. PLoS One, 10:e0130411.

Bła

zej, P., Wnetrzak, M., Mackiewicz, D., and Mackiewicz,

P. (2018b). Optimization of the standard genetic code

according to three codon positions using an evolution-

ary algorithm. PLoS One, 13(8):e0201715.

Bła

zej, P., Wne¸trzak, M., and Mackiewicz, P. (2016). The

role of crossover operator in evolutionary-based ap-

proach to the problem of genetic code optimization.

Biosystems, 150:61–72.

Bollob

as, B. (1998). Modern graph theory, graduate texts

in mathematics vol. 184.

Bulmer, M. (1991). The selection-mutation-drift theory of

synonymous codon usage. Genetics, 129(3):897–907.

Chin, J. W. (2014). Expanding and reprogramming the ge-

netic code of cells and animals. Annual Review of Bio-

chemistry, 83:379–408.

Crick, F. H. (1968). The origin of the genetic code. Journal

of Molecular Biology, 38(3):367–379.

Di Giulio, M. (1989). The extension reached by the mini-

mization of the polarity distances during the evolution

of the genetic code. Journal of Molecular Evolution,

29(4):288–293.

Di Giulio, M. (1999). The coevolution theory of the origin

of the genetic code. Journal of Molecular Evolution,

48(3):253–5.

Di Giulio, M. (2008). An extension of the coevolution the-

ory of the origin of the genetic code. Biology Direct,

Di Giulio, M. (2016). The lack of foundation in the mech-

anism on which are based the physico-chemical theo-

ries for the origin of the genetic code is counterposed

to the credible and natural mechanism suggested by

the coevolution theory. Journal of Theoretical Biol-

ogy, 399:134–40.

Di Giulio, M. (2017). Some pungent arguments against the

physico-chemical theories of the origin of the genetic

code and corroborating the coevolution theory. Jour-

nal of Theoretical Biology, 414:1–4.

Di Giulio, M. (2018). A discriminative test among the dif-

ferent theories proposed to explain the origin of the

genetic code: The coevolution theory ﬁnds additional

support. Biosystems, 169:1–4.

Di Giulio, M. and Medugno, M. (1999). Physicochemical

optimization in the genetic code origin as the number

of codiﬁed amino acids increases. Journal of Molecu-

lar Evolution, 49(1):1–10.

Duch

ene, S., Ho, S. Y., and Holmes, E. C. (2015). Declin-

ing transition/transversion ratios through time reveal

The Impact of the Transversion/Transition Ratio on the Optimal Genetic Code Graph Partition

limitations to the accuracy of nucleotide substitution

models. BMC Evolutionary Biology, 15(1):36.

Dudkiewicz, A., Mackiewicz, P., Nowicka, A., Kowalezuk,

M., Mackiewicz, D., Polak, N., Smolarczyk, K., Ba-

naszak, J., Dudek, M. R., and Cebrat, S. (2005). Cor-

respondence between mutation and selection pressure

and the genetic code degeneracy in the gene evolution.

Future Generation Computer Systems, 21(7):1033–

1039.

Epstein, C. J. (1966). Role of the amino-acid “code” and of

selection for conformation in the evolution of proteins.

Nature, 210(5031):25–28.

Freeland, S. J. and Hurst, L. D. (1998a). The genetic code

is one in a million. Journal of Molecular Evolution,

47(3):238–248.

Freeland, S. J. and Hurst, L. D. (1998b). Load minimiza-

tion of the genetic code: history does not explain the

pattern. Proceedings of the Royal Society of London

B: Biological Sciences, 265(1410):2111–2119.

Freeland, S. J., Knight, R. D., Landweber, L. F., and Hurst,

L. D. (2000). Early ﬁxation of an optimal genetic

code. Molecular Biology and Evolution, 17(4):511–

518.

Freeland, S. J., Wu, T., and Keulmann, N. (2003). The

case for an error minimizing standard genetic code.

Origins of Life and Evolution of the Biosphere, 33(4-

5):457–477.

Gilis, D., Massar, S., Cerf, N. J., and Rooman, M. (2001).

Optimality of the genetic code with respect to protein

stability and amino-acid frequencies. Genome Biol-

ogy, 2(11):research0049–1.

Gojobori, T., Li, W.-H., and Graur, D. (1982). Patterns of

nucleotide substitution in pseudogenes and functional

genes. Journal of Molecular Evolution, 18(5):360–

369.

Goldberg, A. L. and Wittes, R. E. (1966). Genetic code:

aspects of organization. Science, 153(3734):420–424.

Goodarzi, H., Najafabadi, H. S., and Torabi, N. (2005).

Designing a neural network for the constraint opti-

mization of the ﬁtness functions devised based on the

load minimization of the genetic code. Biosystems,

81(2):91–100.

Haig, D. and Hurst, L. D. (1991). A quantitative measure

of error minimization in the genetic code. Journal of

Molecular Evolution, 33(5):412–417.

Hershberg, R. and Petrov, D. A. (2008). Selection on codon

bias. Annual Review of Genetics, 42:287–299.

Khorana, H. G., B

uuchi, H., Ghosh, H., Gupta, N., Jacob,

T., K

ossel, H., Morgan, R., Narang, S., Ohtsuka, E.,

and Wells, R. (1966). Polynucleotide synthesis and

the genetic code. In Cold Spring Harbor Symposia on

Quantitative Biology, volume 31, pages 39–49. Cold

Spring Harbor Laboratory Press.

Kowalczuk, M., Mackiewicz, P., Mackiewicz, D., Nowicka,

A., Dudkiewicz, M., Dudek, M. R., and Cebrat, S.

(2001). High correlation between the turnover of nu-

cleotides under mutational pressure and the dna com-

position. BMC Evolutionary Biology, 1(1):13.

Kumar, S. (1996). Patterns of nucleotide substitution in mi-

tochondrial protein coding genes of vertebrates. Ge-

netics, 143(1):537–548.

Lee, J. R., Gharan, S. O., and Trevisan, L. (2014). Mul-

tiway spectral partitioning and higher-order cheeger

inequalities. Journal of the ACM (JACM), 61(6):37.

Levin, D. A., Peres, Y., and Wilmer, E. L. (2009). Markov

chains and mixing times. American Mathematical So-

ciety, Providence, Rhode Island.

Lynch, M. (2010). Rate, molecular spectrum, and conse-

quences of human mutation. Proceedings of the Na-

tional Academy of Sciences of the United States of

America, 107(3):961–968.

Lyons, D. M. and Lauring, A. S. (2017). Evidence for the

selective basis of transition-to-transversion substitu-

tion bias in two rna viruses. Molecular Biology and

Evolution, 34(12):3205–3215.

Mackiewicz, P., Biecek, P., Mackiewicz, D., Kiraga, J.,

Baczkowski, K., Sobczynski, M., and Cebrat, S.

(2008). Optimisation of asymmetric mutational pres-

sure and selection pressure around the universal ge-

netic code. Computational Science - ICCS 2008,

Proceedings, Lecture Notes in Computer Science,

5103:100–109.

Massey, S. E. (2008). A neutral origin for error minimiza-

tion in the genetic code. Journal of Molecular Evolu-

tion, 67(5):510–516.

Morton, B. R. (2001). Selection at the amino acid level can

inﬂuence synonymous codon usage: Implications for

the study of codon adaptation in plastid genes. Genet-

ics, 159(1):347–358.

Nirenberg, M., Caskey, T., Marshall, R., Brimacombe,

R., Kellogg, D., Doctor, B., Hatﬁeld, D., Levin, J.,

Rottman, F., Pestka, S., et al. (1966). The rna code

and protein synthesis. In Cold Spring Harbor sym-

posia on quantitative biology, volume 31, pages 11–

24. Cold Spring Harbor Laboratory Press.

Novozhilov, A. S., Wolf, Y. I., and Koonin, E. V. (2007).

Evolution of the genetic code: partial optimization of

a random code for robustness to translation error in a

rugged ﬁtness landscape. Biology Direct, 2.

Petrov, D. A. and Hartl, D. L. (1999). Patterns of nucleotide

substitution in drosophila and mammalian genomes.

Proceedings of the National Academy of Sciences of

the United States of America, 96(4):1475–1479.

Rosenberg, M. S., Subramanian, S., and Kumar, S. (2003).

Patterns of transitional mutation biases within and

among mammalian genomes. Molecular biology and

evolution, 20(6):988–993.

Santos, J. and Monteagudo,

A. (2011). Simulated evolution

applied to study the genetic code optimality using a

model of codon reassignments. BMC Bioinformatics,

12.

Santos, J. and Monteagudo,

A. (2017). Inclusion of the ﬁt-

ness sharing technique in an evolutionary algorithm

to analyze the ﬁtness landscape of the genetic code

adaptability. BMC Bioinformatics, 18(1):195.

Tlusty, T. (2010). A colorful origin for the genetic code: In-

formation theory, statistical mechanics and the emer-

gence of molecular codes. Physics of Life Reviews,

7(3):362–376.

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

Wakeley, J. (1996). The excess of transitions among nu-

cleotide substitutions: new methods of estimating

transition bias underscore its signiﬁcance. Trends in

Ecology & Evolution, 11(4):158–162.

Wnetrzak, M., Bła

zej, P., Mackiewicz, D., and Mackiewicz,

P. (2018). The optimality of the standard genetic

code assessed by an eight-objective evolutionary al-

gorithm. BMC Evolutionary Biology, in press, DOI:

10.1186/s12862-018-1304-0.

Woese, C. R. (1965). On the evolution of the genetic code.

Proceedings of the National Academy of Sciences of

the United States of America, 54(6):1546–1552.

Wong, J. T. (1975). A co-evolution theory of the genetic

code. Proceedings of the National Academy of Sci-

ences of the United States of America, 72(5):1909–12.

Wong, J. T., Ng, S. K., Mat, W. K., Hu, T., and Xue, H.

(2016). Coevolution theory of the genetic code at age

forty: Pathway to translation and synthetic life. Life

(Basel), 6(1):E12.

Wong, J. T. F. (2007). Coevolution theory of the genetic

code: A proven theory. Origins of Life and Evolution

of Biospheres, 37(4-5):403–408.

Xie, J. M. and Schultz, P. G. (2006). Innovation: A chemical

toolkit for proteins - an expanded genetic code. Nature

Reviews Molecular Cell Biology, 7(10):775–782.

Zhou, T., Weems, M., and Wilke, C. O. (2009). Translation-

ally optimal codons associate with structurally sensi-

tive sites in proteins. Molecular Biology and Evolu-

tion, 26(7):1571–1580.

The Impact of the Transversion/Transition Ratio on the Optimal Genetic Code Graph Partition