Depth from Small Motion using Rank-1 Initialization

Peter O. Fasogbon

Nokia Technologies, 33100 Tampere, Finland

Keywords:

3D Reconstruction, Depth-map, Factorization, DfSM, Bundle Adjustment, Feature Extraction, Rank-1.

Abstract:

Depth from Small Motion (DfSM) (Ha et al., 2016) is particularly interesting for commercial handheld devices

because it allows the possibility to get depth information with minimal user effort and cooperation. Due

to speed and memory issue on these devices, the self calibration optimization of the method using Bundle

Adjustment (BA) need as little as 10-15 images. Therefore, the optimization tends to take many iterations to

converge or may not converge at all in some cases. This work propose a robust initialization for the bundle

adjustment using the rank-1 factorization method (Tomasi and Kanade, 1992), (Aguiar and Moura, 1999a).

We create a constraint matrix that is rank-1 in a noiseless situation, then use SVD to compute the inverse

depth values and the camera motion. We only need about quarter fraction of the bundle adjustment iteration

to converge. We also propose grided feature extraction technique so that only important and small features are

tracked all over the image frames. This also ensure speedup in the full execution time on the mobile device.

For the experiments, we have documented the execution time with the proposed Rank-1 initialization on two

mobile device platforms using optimized accelerations with CPU-GPU co-processing. The combination of

Rank 1-BA generates more robust depth-map and is signiﬁcantly faster than using BA alone.

1 INTRODUCTION

The use of smartphones is growing continuously no-

wadays and the level of expectation around what these

cameras can do is increasing year by year. Mobile

consumers are starting to expect more technological

capabilities from visual applications on their mobile

devices. These applications include but not limited

to camera refocusing, 3D parallax, augmented reality

and extended depth of ﬁeld (Barron et al., 2015). To

meet these needs, estimating three dimensional infor-

mation is becoming an increasingly important techni-

que, and numerous research efforts have focused on

computing accurate three dimensional information at

a low cost, without the need for additional devices or

camera modiﬁcations. One research direction that has

recently led to renewed interest is the depth estimation

from image sequences acquired from narrow/small

baseline in the range of about 8mm. This is popu-

larly known as Depth from Small Motion (DfSM),

and many research contributions have been made over

the years (Yu and Gallup, 2014), (Joshi and Zitnick,

2014), (Ha et al., 2016), (Corcoran and Javidnia,

2017), (Ham et al., 2017). For hand-held cameras,

small amount of motion is always present, which can

occur accidentally as a result of hand-shaking motion,

tremble, source vibration etc. Depth-map generation

using these small motions can be offered to consu-

mers to accompany their selﬁes, bothie and portraits

camera shots.

1.1 Background

These DfSM methods all have their base on the po-

pular Structure from Motion (SfM) (Sch

anberger and

Frahm, 2016) and Multi-View Stereo (MVS) (Seitz

et al., 2006) techniques. The SfM techniques assume

that a good two-view reconstruction can be obtained

with algebraic methods, which in turn depend on ade-

quate baseline between overlapping views. The base-

line between sequences of frames captured as a sud-

den motion in DfSM is considered so small which re-

stricts the viewing angle of a three-dimensional point

to less than 0.2

◦

(Yu and Gallup, 2014). Due to this

limitation, the popular SfM method fails (Koenderink

and van Doorn, 1991), (Sch

anberger and Frahm,

2016) and the computed depth-map will be highly pe-

nalized. Bundle adjustment (BA) (Hartley and Zisser-

man, 2003), (Triggs et al., 2000) is an indispensable

procedure in the SFM, and use a basic cost function

to evaluate the reprojection error from Undistorted to

Distorted image domain with non-linear least square.

This is used to iteratively reﬁne the camera parame-

ters and three-dimensional points required to gene-

Fasogbon, P.

Depth from Small Motion using Rank-1 Initialization.

DOI: 10.5220/0007381405210528

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 521-528

ISBN: 978-989-758-354-4

521

rate the depth-map. The bundle adjustment used for

SfM methods are not suitable for small motions, the-

refore a modiﬁed bundle adjustment is proposed in

(Ha et al., 2016) under inverse depth representation.

In this case, the reprojection error is estimated from

mapping the points in the Distorted to Undistorted

domain. The sparse three-dimensional points are cre-

ated by random depth initialization (Yu and Gallup,

2014), then plane sweeping based image matching

(Collins, 1996) is employed to create the depth-map.

Finally, Markov Random Field (Komodakis and Pa-

ragios, 2009) approach is employed to regularize the

estimated depth-map effectively.

1.2 Problem Statement

Although DfSM algorithm is specially designed for

small baselines, the estimated camera poses become

unreliable if the motion is unreasonably small. It is

assumed that the required minimum baseline to apply

this approach is reasonable when large number of fra-

mes are acquired, approximately 30 frames (Ha et al.,

2016). As a result of limited memory space on mobile

devices and the execution time issue, we are restricted

to only use 10-15 frames in the depth-map generation

on the mobile devices. The consequence of using this

small number of frame means that the self calibrating

bundle adjustment may not converge fast enough or

not converge at all. In addition, as a result of lack of

features near the image border, the estimated radial

distortion parameters diverge beyond their bound and

may not give meaningful estimation.

Due to these problem, the BA do not always give

correct estimates of the camera parameters and in-

verse depth values. One solution to tackle this issue

might be to use very high number of feature points in

the order of 10,000 and above, or include an additi-

onal photometric bundle adjustment (Alismail et al.,

2017) step if one is restricted to small number of fe-

ature points. In addition, one can bound the camera

parameters during the optimization. However, these

solutions only introduce additional complexity to the

system optimization. Therefore, a good initialization

for the bundle adjustment is vital for the depth-map

accuracy, so we proposed to use factorization techni-

que based on Rank-1 suitable for inverse depth repre-

sentation.

1.3 Summary

In this paper, we describe an uncalibrated Depth

from Small Motion technique using rank-1 initializa-

tion. This approach provides a better initialization

Figure 1: DfSM framework. Our main technical contributi-

ons are in the dashed enclosed boxes.

for the bundle adjustment procedure that takes too

much or doesn’t converge under DfSM. This is par-

ticularly suitable and targeted to speedup processes

for the deployment of the DfSM algorithm on con-

sumer smartphone devices. The Rank-1 factorization

does not only speed up the convergence process but

also allow good initialization for accurate depth-map

generation. Thanks to rank-1 initialization, self cali-

brating Bundle Adjustment (BA) is able to converge

in as little as 10-20 iterations with 10 images. We

also proposed a grided feature extraction to speedup

feature tracking process of the algorithm. Finally,

we optimized various parts of the original algorithm

(Ha et al., 2016) using GPU OpenCL and other CPU

multi-threading techniques. This makes it possible to

produce a detail experiment on a mobile device under

ANDROID platform.

In the next section, we present the uncalibrated

rank-1 factorization for the DfSM problem. Expe-

riments and performance evaluation with the propo-

sed method as compared to optimized CPU only im-

plementations are provided in section 3. Finally, we

made conclusion and future direction in this work.

2 DfSM WITH RANK-1

INITIALIZATION

Fig. 1 illustrates the general overview of the DfSM

algorithm for the depth-map generation in this work.

Some consistent good features over all the video fra-

mes were extracted using grided feature tracking ap-

proach proposed in this work. Then, we initialize the

bundle adjustment procedure using the rank-1 facto-

rization technique, the outcome are the optimized ca-

mera parameters and the inverse depth point values.

Finally, the estimated inverse depth point values and

the camera parameters are used under a dense mat-

ching method to create the depth-map. In the follo-

wing part of the section, we start ﬁrst with coordinate

representation used in this paper, then we explain the

proposed grided-feature extraction, and Rank-1 initi-

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

522

Figure 2: Small motion geometry used in DfSM for uncali-

brated camera using undistorted coordinates (i.e assume no

lens distortion).

alization methods. In the ﬁnal part of the section, we

summarize the DfSM algorithm.

Coordinate Representation. Fig. 2 illustrates the

reference view coordinate origin C

with undistorted

pixel p

0 j

(u, v). The back-projection of p

0 j

(u, v) onto

both the 3D coordinate and i-th view with coordinate

origin C

is denoted as P

and p

i j

. Both i and j sig-

niﬁes j = 1 . . . m points and i = 1 . . . n views. The i-th

camera is related to the reference plane by rotation

matrix R

followed by translation T

. The backpro-

jected 3D point can be parametrized using the inverse

depth ω

as shown in equation (1), where (x

, y

) is

the normalized coordinate of p

0 j

(u, v) derived from

using the inverse of the intrinsic camera matrix K(Ha

et al., 2016) (Hartley and Zisserman, 2003) that em-

beds both the focal length and principal point.

, y

, 1]

(1)

Note that the earlier expressions and explanations

assume no lens distortion whatsoever. Indeed, lenses

are affected by distortion and the most common one

is the radial distortion (Hartley and Zisserman, 2003).

To remove these radial distortion, we need to deduce

a mapping functions F proposed in (Ha et al., 2016)

with radial coefﬁcients k

, k

. This function F helps

to map the distorted points ˜p

0 j

, ˜p

i j

to undistorted ones

0 j

, p

i j

respectively using iterative inverse mapping.

For the simplicity of the rest of this section, we as-

sume the radial lens distortions have been removed.

2.1 Grided Feature Tracking

The feature extraction step is an interest for us here as

a means to speed up the execution time of the whole

algorithm. Our main goal is to reduce as much as pos-

sible the total number of feature points that is tracked

all along the frame sequences. We proposed what is

called a grided feature extraction approach. The full

Figure 3: The setup constraint for the rank-1 problem repre-

sented in normalized image coordinate ¯p from the reference

plane.

resolution image is ﬁrst divided into grids of ﬁxed si-

zes. Then, we proceed by extracting only strongest

harris corners (Harris and Stephens, 1988) in the en-

closed grids. We use Shi-Tomasi score as the mea-

sure of best feature in an enclosed grid (Shi and To-

masi, 1994). The correspondence feature locations to

the other frames are found by Kanade-Lukas-Tomashi

(KLT) method (Lucas and Kanade, 1981).

2.2 Initialization using Rank-1

Without abuse of notation, we denote the normalized

coordinate of both p

0 j

and p

i j

in the reference coor-

dinate as ¯p

0 j

(x, y) and ¯p

i j

(x, y) respectively. Fig. 3

illustrates the coordinate origin that have been cente-

red on the reference plane. In a perfect case depicted

by the ﬁgure, we can see that c

belonging to the re-

ference plane is ﬁxed at origin, and the optical axis

formed by c

is parallel to that of c

We can determine the relative camera rotation R

between keyframe c

and frame c

by (Kneip et al.,

2012). Given these rotations and set of corresponding

features ¯p

0 j

↔ ¯p

i j

, we can estimate an optimal trans-

lation t

between c

and c

using factorization method.

We create a form of ﬂow representation between

the origin c

and c

using the inverse depth point re-

presentation P

as a constraint for the factorization

problem. We formulate the transformation of point

¯p

i j

located on i-th plane onto the reference coordinate

as p

i j

which is computed as follows:

i j

= −R

¯p

i j

(2)

In ﬁg. 3, we have only shown that the position of c

is only approximated (c

≈ −R

). This means that c

and ω

are the most penalized. Therefore, with facto-

rization method one should be able to determine the

Depth from Small Motion using Rank-1 Initialization

523

optimal value for these parameters even under noise

perturbations.

By analysing the inverse depth representation in

equation (1), one can see that (x

, y

) are known from

the position of the features in the reference frame, so

we only need to solve for the inverse depth value ω

The problem to solve is represented in equation (3),

where the Left-Hand-Side matrix M(3n × m) is made

up of ﬂow representation p

i j

to create a signiﬁcantly

over-constrained system of equations. The factori-

zation of M should give the Right-Hand-Side which

consist of the translation matrix C(3n ×1) and inverse

depth matrix D(1 × m).

M = C D







. . . p





















. . . d



(3)

The factorization problem in equation (3) has been

reduced to rank-1 problem, thanks to the inverse depth

representation which means only the inverse depth

is determined. This rank-1 factorization is extensi-

vely studied in computer vision community over the

years (Tomasi and Kanade, 1992), (Joshi and Zit-

nick, 2014), (Aguiar and Moura, 1999a), (Aguiar and

Moura, 1999b),(Tang et al., 2017).

The solution is formulated as a form of non-linear

optimization in equation (4) and solved using SVD

(Golub and Van Loan, 1996). From the equation,

i, j

− c

is a geometric error to be minimized

between the ﬂow representation p

i, j

and the estima-

ted parameters (c

, ω

M − C D

minimize

∑

i=1

∑

j=1

i j

− c

(4)

2.3 Full Algorithm

We summarize the proposed DfSM using rank-1 initi-

alization next in this section. This is a brief summary

that incorporates the approach presented in ths paper

and the DfSM described in (Ha et al., 2016).

Figure 4: Depth-map demo on ”selﬁe” sequence for AN-

DROID mobile device using CPU-GPU optimized co-

processing.

Algorithm 1: DfSM with Rank-1 (iRank1 ).

Input : p

0 j

, p

i j

, where i = 1 . . . n and j = 1 . . . m

Output : K, k

, k

, R

, c

, ω

, depth-map D

Pre-processing :

• Estimate ¯p

i j

, ¯p

0 j

using K. The focal length is

set to the larger value between image width and

height. The principal point is set to the center of

the image.

Bundle Adjustment using Rank-1 initialization :

1. Estimate rotation R

between ¯p

0 j

↔ ¯p

i j

using

(Kneip et al., 2012),

2. Rotate ¯p

i, j

to p

i j

in the reference plane as eqn. (2),

3. Create M matrix using p

i j

, and factorize as eqn.

(4)

4. Reﬁne the camera parameters and depth estimate

using bundle adjustment (Agarwal et al., 2012),

(Huber, 1992).

Dense Matching :

• Apply the dense matching proposed in (Ha et al.,

2016) to determine the depth-map image D.

3 EXPERIMENTS

To demonstrate the efﬁciency and practicality of

the proposed implementation, we developed an inte-

ractive OpenCL ANDROID application that is shown

in ﬁgure 4. The ﬁgure illustrates the reference image

and the corresponding depth-map generated over all

the 10 non-reference images. Experiments were

done with Qualcomm Snapdragon chipset containing

Adreno 540 GPU, with CPU 4GB RAM and 8 cores.

We implemented the proposed algorithm on a smartp-

hone with GPU and CPU optimized co-processing in

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

524

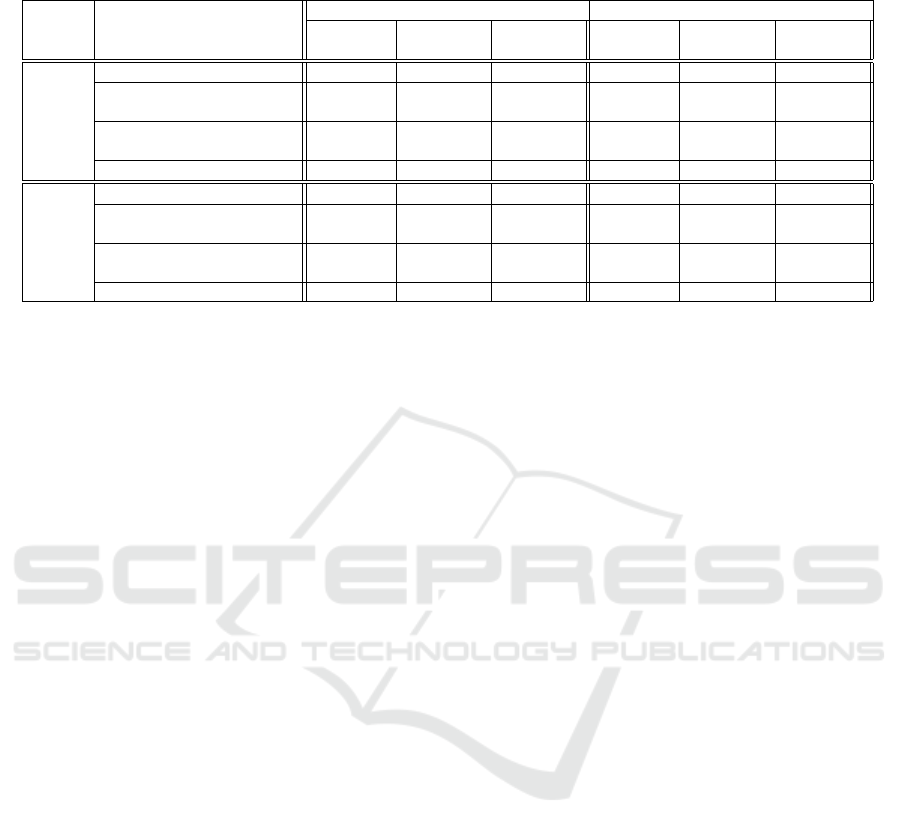
Table 1: Table of total execution time in seconds (s) and convergence result using the Qualcomm snapdragon device on bike

test video samples. NC-100 means no convergence at 100th iteration while C-20 means convergence at 20th iteration.

10 frames 15 frames

CPU-GPU CPU-GPU CPU-GPU CPU-GPU

Device Stages CPU-only iBA iRank1 CPU-only iBA iRank1

Bike1 Read input frame sequence 0.44 0.42 0.45 0.52 0.49 0.50

Feature Extraction 0.885 0.539 0.539 1.375 0.771 0.771

Nb. features 1987 275 275 1941 258 258

Bundle Adjustment 2.05 1.902 0.824 2.303 2.315 0.571

Nb. iteration NC-100 NC-100 C-20 NC-100 C-100 C-15

Dense Matching 28.63 9.43 9.40 30.69 10.14 10.13

Bike2 Read input frame sequence 0.41 0.41 0.42 0.52 0.48 0.50

Feature Extraction 0.812 0.491 0.489 2.011 0.621 0.618

Nb. features 1958 293 293 1923 249 249

Bundle Adjustment 2.13 1.851 0.803 2.40 2.12 0.63

Nb. iteration NC-100 NC-100 C-23 NC-100 C-95 C-10

Dense Matching 28.48 9.14 9.16 30.12 10.29 10.24

order to proper analyze the effectiveness of the pro-

posed method directly on hand-held devices.

3.1 Evaluation on Convergence

We execute the algorithm on two test video clips

”bike1”, and ”bike2”. These test clips are full HD

(1920 × 1080) video using 10 and 15 frames respecti-

vely. The process is initialized using the proposed

grided feature extraction with a ﬁxed grid size of 80

× 80, which provides 275 consistent features that is

tracked all along the non-reference images. Without

the grided feature extraction method, 1987 consistent

features are expected to be tracked. Therefore, the

proposed feature extraction allow approximately 7x

reduction from the original features. The value of the

grid size is optional and can be modiﬁed as seem ﬁt

by the user.

Table 1 provides a summarized execution time of

the algorithms, and also justify the fast convergence

of the proposed method. The CPU-only signiﬁes the

case when the DfSM algorithm is directly transfered

to the mobile platform with some optimizations made

but no grided feature extraction is done here. Howe-

ver, CPU-GPU is an ugraded version to the CPU-

only, with GPU OpenCL acceleration on the dense

matching using 128 depth-plane sweep, and the pro-

posed grided feature extraction. In addition, iRank1

represents the DfSM using rank-1 initialization pro-

posed in this work while iBA represent the one wit-

hout rank-1 initialization.

This table exhibits two important informations;

(1) the time complexity on mobile device measured in

seconds and (2) the convergence information. For the

convergence part, we implore the user to focus on the

Bundle Adjustment row. The iRank1 method con-

verges in approximately 25 iteration for the two bike

examples using 10 images while iBA only partially

converge at 50th iteration when more images were

added to the acquisition. Not only is the rank-1 ini-

tialization vital, it is also fast and converge in about

3 iteration which is approximately 0.009s. In sum-

mary, this approach do not add any time complexity

to the full algorithm and allow fast convergence of the

bundle adjustment in as little as 10 iterations.

We made further test for subjective quality analy-

sis of the proposed method on the earlier bike test se-

quence. Fig. 5 illustrates the test with 10 frames while

ﬁg. 6 illustrates the one with 15 frames. By analyzing

the result in ﬁgure 5, one can see that iRank1 method

is already starting to converge at 10th iteration and ﬁ-

nally converges at 50th iteration with pleasing depth-

map result. However, for this same example, the iBA

only start to converge at the 50th iteration. For the

example in ﬁg. 6 using 15 frames, we can see that

the depth-map provided by iRank1 at 10th iteration

seems to have converged while iBA only shows con-

vergence at 50th iteration. With these experiments,

we have shown the importance of rank-1 initialization

under the DfSM algorithm.

3.2 Evaluation on Self-calibration

As the bundle adjustment proposed in DfSM (Ha

et al., 2016) is designed to self-calibrate the intrinsic

camera parameters, we effect quantitative evaluation

for the camera parameters obtained by the iRank1

proposed in this work. For this experiment, we use

two smartphones that contains Qualcomm snapdra-

gon and Hisilicon Kirin chipsets. These two devi-

ces both have two different lens settings. The initial

focal length is set to the largest value between the

image width and height. We compare the estimated

focal length and radial distortion against the ground

Depth from Small Motion using Rank-1 Initialization

525

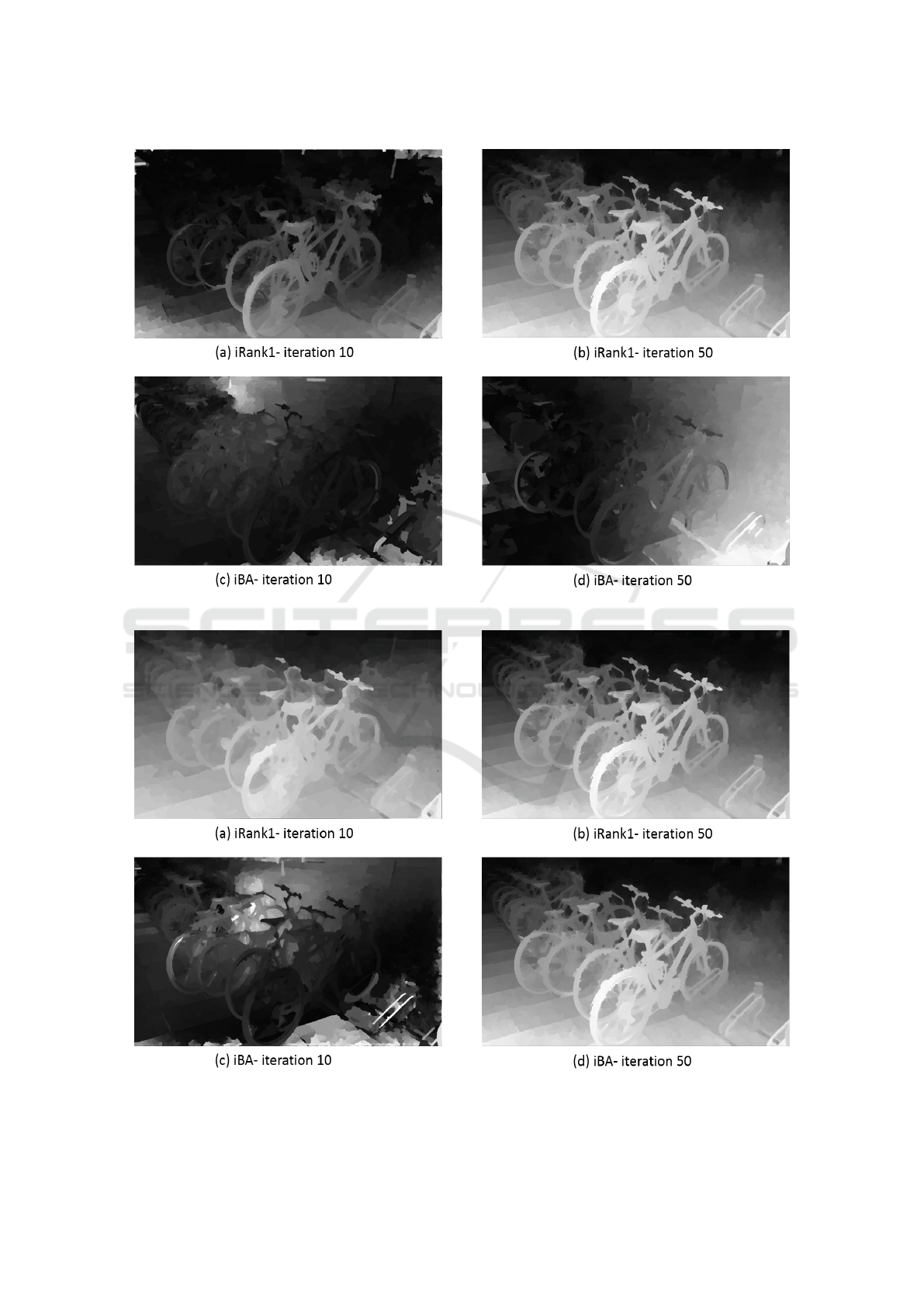
Figure 5: Subjective quality analysis of the depth-map generation between proposed iRank1 and iBA, using 10 frames.

Figure 6: Subjective quality analysis of the depth-map generation between proposed iRank1 and iBA, using 15 frames.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

526

Table 2: Evaluation in pixels unit for the estimated intrinsic camera parameters and radial distortion ones. We have tested 30

video clips in total acquired by two cameras with different lens settings.

Qualcomm Camera Hisilicon Camera

Clip 1(5 videos) Clip 2(10 videos) Clip 3(5 videos) Clip 4(10 videos)

focal length

ground-truth 1360.21 1358.32 1503.71 1505.61

Initial 1280.00 1280.00 1280.00 1280.00

Min 1329.89 1341.84 1478.31 1479.01

Mean 1330.62 1335.16 1519.32 1503.78

Max 1392.06 1371.69 1563.35 1531.32

Distortion

Initial 4.25 4.08 5.72 5.63

Min 0.51 0.39 0.08 0.09

Mean 1.53 1.18 0.63 0.69

Max 2.09 1.34 1.09 1.15

truth. For measuring the distortion error, we generate

a pixel grid and transform their coordinates using the

estimated Distorted-Undistorted image domain radial

distortion function F explained in the original pa-

per (Ha et al., 2016). The transformed coordinates

are again applied with the ground-truth Undistorted-

Distorted image domain model found in the camera

pre-calibration. If the estimated F is reliable, these

sequential transformation should be identity. The dis-

tortion error is measured in pixels using the mean of

absolute distances. The result shows that the estima-

ted parameters are close to the ground truth.

Table 2 shows the experimental result. We captu-

red 15 videos each using camera located on the Qual-

comm and Hisilicon devices. These cameras both

have different lens settings, and the ground-truth ca-

mera parameters are acquired using the camera ca-

libration toolbox (Zhang, 2000). For the qualcomm

test, clip Clip 1(5 videos) and Clip 2(10 videos) make

use of 5 and 10 videos, and each video containing 10

frames. These same procedure is repeated for Hisili-

con device to create the test clips Clip 3(5 videos) and

Clip 4(10 videos) respectively. In total, 30 video clips

are used in this experiment. For the camera parame-

ter, the focal length that is estimated are closer to the

ground-truth. The mean distortion error for the Qual-

comm is around 1.53 pixel while the initial parameter

, k

= 0) gives an error of 4.25 pixel.

4 CONCLUSION

The convergence of the the self-calibrating bundle

adjustment needed to recover the camera parameters

that is required for depth generation in the popular

uncalibrated Depth from Small Motion algorithm (Ha

et al., 2016) has not been well studied. Realistically,

the convergence for the optimization procedure is not

guaranteed even with the use of large number of fra-

mes (i.e approximately 30 images). In this work, we

propose a new method that incorporates the rank-1

factorization as a way to initialize the camera para-

meters and inverse depth points robustly. This appro-

ach allow fast convergence of the bundle adjustment

procedure.

The experimental results on a real mobile platform

is presented. Compared with the state of art, our met-

hod can cope with a very small frame numbers to esti-

mate the parameters required for good depth-map ge-

neration. After several optimizations with OpenCL

GPU and CPU multi-threading procedures, the whole

algorithm on the mobile device take approximately

10s for full HD resolution images. For the future

work, we propose to investigate further the accuracy

of the generated depth-map as compared to the state

of art DfSM methods.

REFERENCES

Agarwal, S., Mierle, K., and Others (2012). Ceres solver.

In http://ceres-solver.org.

Aguiar, P. M. and Moura, J. M. F. (1999a). Factorization

as a rank 1 problem. In Proceedings of IEEE Compu-

ter Society Conference on Computer Vision and Pat-

tern Recognition (Cat. No PR00149), volume 1, pages

178–184.

Aguiar, P. M. Q. and Moura, J. M. F. (1999b). A fast

algorithm for rigid structure from image sequences.

In Proceedings of International Conference on Image

Processing (Cat. 99CH36348), volume 3, pages 125–

129.

Alismail, H., Browning, B., and Lucey, S. (2017). Photo-

metric bundle adjustment for vision-based slam. In

Computer Vision – ACCV 2016, pages 324–341.

Barron, J. T., Adams, A., Shih, Y., and Hernndez, C. (2015).

Fast bilateral-space stereo for synthetic defocus. In

IEEE Conference on Computer Vision and Pattern Re-

cognition (CVPR), pages 4466–4474.

Collins, R. T. (1996). A space-sweep approach to true

multi-image matching. In Proceedings CVPR IEEE

Depth from Small Motion using Rank-1 Initialization

527

Computer Society Conference on Computer Vision

and Pattern Recognition, pages 358–363.

Corcoran, P. and Javidnia, H. (2017). Accurate depth map

estimation from small motions. In IEEE International

Conference on Computer Vision Workshops (ICCVW),

pages 2453–2461.

Golub, G. H. and Van Loan, C. F. (1996). Matrix Com-

putations (3rd Ed.). Johns Hopkins University Press,

Baltimore, MD, USA.

Ha, H., Im, S., Park, J., Jeon, H., and Kweon, I. (2016).

High-quality depth from uncalibrated small motion

clip. In CVPR, pages 5413–5421. IEEE Computer So-

ciety.

Ham, C., Chang, M., Lucey, S., and Singh, S. (2017). Mo-

nocular depth from small motion video accelerated. In

International Conference on 3D Vision (3DV), pages

575–583.

Harris, C. and Stephens, M. (1988). A combined corner and

edge detector. In Proceedings of the 4th Alvey Vision

Conference, pages 147–151.

Hartley, R. and Zisserman, A. (2003). Multiple view geo-

metry in computer vision. New York, NY, USA. Cam-

bridge University Press.

Huber, P. J. (1992). Robust Estimation of a Location Pa-

rameter, pages 492–518. Springer New York, New

York, NY.

Joshi, N. and Zitnick, L. (2014). Micro-baseline stereo.

Technical report.

Kneip, L., Siegwart, R., and Pollefeys, M. (2012). Finding

the exact rotation between two images independently

of the translation. In Computer Vision – ECCV 2012,

pages 696–709, Berlin.

Koenderink, J. J. and van Doorn, A. J. (1991). Afﬁne struc-

ture from motion. J. Opt. Soc. Am. A, 8(2):377–385.

Komodakis, N. and Paragios, N. (2009). Beyond pairwise

energies: Efﬁcient optimization for higher-order mrfs.

In 2009 IEEE Conference on Computer Vision and

Pattern Recognition, pages 2985–2992.

Lucas, B. D. and Kanade, T. (1981). An iterative image re-

gistration technique with an application to stereo vi-

sion. In Proceedings of the 7th International Joint

Conference on Artiﬁcial Intelligence - Volume 2, IJ-

CAI’81, pages 674–679.

Sch

anberger, J. L. and Frahm, J. (2016). Structure-from-

motion revisited. In IEEE Conference on Computer

Vision and Pattern Recognition (CVPR), pages 4104–

4113.

Seitz, S. M., Curless, B., Diebel, J., Scharstein, D., and

Szeliski, R. (2006). A comparison and evaluation

of multi-view stereo reconstruction algorithms. In

IEEE Computer Society Conference on Computer Vi-

sion and Pattern Recognition (CVPR’06), volume 1,

pages 519–528.

Shi, J. and Tomasi (1994). Good features to track. In Pro-

ceedings of IEEE Conference on Computer Vision and

Pattern Recognition, pages 593–600.

Tang, C., Wang, O., and Tan, P. (2017). Globalslam:

Initialization-robust monocular visual SLAM. CoRR,

abs/1708.04814.

Tomasi, C. and Kanade, T. (1992). Shape and motion

from image streams under orthography: a factoriza-

tion method. International Journal of Computer Vi-

sion, 9(2):137–154.

Triggs, B., McLauchlan, P. F., Hartley, R. I., and Fitzgibbon,

A. W. (2000). Bundle adjustment - a modern synthe-

sis. In Proceedings of the International Workshop on

Vision Algorithms: Theory and Practice, ICCV ’99,

pages 298–372, London, UK, UK. Springer-Verlag.

Yu, F. and Gallup, D. (2014). 3d reconstruction from ac-

cidental motion. In IEEE Conference on Computer

Vision and Pattern Recognition, pages 3986–3993.

Zhang, Z. (2000). A ﬂexible new technique for camera

calibration. IEEE Trans. Pattern Anal. Mach. Intell.,

22(11):1330–1334.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

528