On-line Searching in IUPAC Nucleotide Sequences

Petr Proch

azka and Jan Holub

Department of Theoretical Computer Science, Faculty of Information Technology,

Czech Technical University, Th

akurova 2700/9, Prague 6, Czech Republic

Keywords:

Consensus Nucleotide Sequences, Genomic Sequences, Degenerate Pattern Matching, q-gram Inverted Index.

Abstract:

We propose a novel pattern matching algorithm for consensus nucleotide sequences over IUPAC alphabet,

called BADPM (Byte-Aligned Degenerate Pattern Matching). The consensus nucleotide sequences represent

a consensus obtained by sequencing a population of the same species and they are considered as so-called

degenerate strings. BADPM works at the level of single bytes and it achieves sublinear search time on average.

The algorithm is based on tabulating all possible factors of the searched pattern. It needs O (m + mα

logm)-

space data structure and O(mα

) time for preprocessing where m is a length of the pattern and α represents

a maximum number of variants implied from a 4-gram over IUPAC alphabet. The worst-case locate time is

bounded by O(nm

) for BADPM where n is the length of the input text. However, the experiments performed

on real genomic data proved the sublinear search time. BADPM can easily cooperate with the block q-gram

inverted index and so achieve still better locate time. We implemented two other pattern matching algorithms

for IUPAC nucleotide sequences as a baseline: Boyer-Moore-Horspool (BMH) and Parallel Naive Search (PNS).

Especially PNS proves its efﬁciency insensitive to the length of the searched pattern m. BADPM proved its strong

superiority for searching middle and long patterns.

1 INTRODUCTION

DNA sequencing is nowadays the integral part of sev-

eral disciplines like personalized medicine, human

genetics and oncology, forensic biology, microbiol-

ogy and virology. The demand for cheap sequenc-

ing induced the evolution of High-Throughput Se-

quencing (HTS) technologies that can sequence large

stretches of DNA in a massively parallel fashion and

that produce millions of DNA sequences simultane-

ously. The public sources report the necessary time

per one run in the order of hours and the cost per

one million bases lower than 0.012 USD

which is

1121 USD per human genome. Thanks to the general

availability of the sequencing, we face the challenge

of analyzing rapidly increasing number of genomic

sequences, which includes their effective storage in

the form allowing extremely fast searching.

The accessibility of sequencing methods has

also enabled the development of projects focused

on sequencing the population of many individuals

of the same species. These projects include the

1000 Genomes Projects (Consortium, 2011) and the

UK10K project (Consortium, 2015). Each sequenced

https://www.genome.gov/sequencingcostsdata/

population uses its ‘reference genome’, which forms

the basis for studying genetic variations for other in-

dividuals. Pan-genomics (Marschall, 2018) shifts the

reference genome to a representation of all genomic

content in a certain species or a phylogenetic clade.

A consensus sequence drawn from an entire popula-

tion is one of the forms that the reference genome can

take. The consensus sequence can be expressed as a

degenerate string over a degenerate alphabet. We give

a simple example of a consensus sequence expressed

in IUPAC alphabet

in Figure 1. The consensus repre-

sents an alignment of seven different organisms. The

different bases are emphasized with gray color. The

consensus base is given in blue color and it means that

more than one solid bases are valid (e.g. for R both A

or G symbols are valid).

Knuth-Morris-Pratt (KMP) (Knuth et al., 1977)

is one of the most famous pattern matching algo-

rithms and the ﬁrst one ensuring the worst-case time

linear with the length of the text T . Boyer-Moore

(BM) (Boyer and Moore, 1977) family algorithms

represent backward pattern matching approach. BM

algorithm allows skipping of some characters which

leads to lower than linear average time. There exist

https://iupac.org

Procházka, P. and Holub, J.

On-line Searching in IUPAC Nucleotide Sequences.

DOI: 10.5220/0007382900660077

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 66-77

ISBN: 978-989-758-353-7

T C C A G C G C T T A C T C T A T A C C T A A

T C C A G C A C T T A C T C T G T G C C C G C

T C C A G C A C T T A C T C T G T G C C C A C

T C C A G C A C T T A C T C T G T G C C C G C

T C T A G C A C T T A C T C T A T G C C T G C

homo sapiens:

pan paniscus:

chlorocebus sabaeus:

macaca fascicularis:

macaca mulatta:

papio anubis:

callithrix jacchus:

CONSENSUS:

T C Y A G C R C T T A C T C T R T R C C Y R M

Figure 1: Consensus sequence over IUPAC alphabet for dif-

ferent species (chromosome 7: 55 187 593 - 55187 615).

also other variations of this algorithm given by Hor-

spool (Horspool, 1980) or Sunday (Sunday, 1990).

Sufﬁx automaton (often called DAWG – Determin-

istic Acyclic Word Graph) is the essence of another

algorithm achieving sublinear average time BDM

(Backward DAWG Match) (Crochemore and Rytter,

1994). The sufﬁx automaton of the reversed pattern

performs backward searching for the pattern. The

byproduct of the search is always the longest preﬁx

of the pattern occurring at that position in the text

which ensures safe shifting for BDM. Another ap-

proach is to use non-deterministic instead of deter-

ministic automata for searching in the text. So-called

bit-parallelism (D

olki, 1964; Baeza-yates, 1992)

proved to be a very simple way to simulate the non-

deterministic automaton. It exploits the parallelism

provided by bitwise operations in terms of one com-

puter word. It can accelerate the operations up to a

factor w, where w is the number of bits in the com-

puter word. Bit-parallelism is particularly efﬁcient

for the patterns with size lower than the size of the

computer word m ≤ w. Navarro et al. applied the

bit-parallelism to simulate the sufﬁx automaton and

they proposed BNDM algorithm (Navarro and Raf-

ﬁnot, 1998) that achieved 20%-25% improvement in

search time in comparison to its deterministic version

BDM.

The standard pattern matching was naturally ex-

tended to the problem of pattern matching in de-

generate strings, i.e. the strings where each degen-

erate symbol can represent a subset of solid sym-

bols. The very ﬁrst practical algorithm addressing

the pattern matching in degenerate strings was agrep

utility (Wu and Manber, 1992). Next, Navarro et

al. (Navarro and Rafﬁnot, 1998) introduced an exten-

sion of BNDM NR-grep (Navarro and Rafﬁnot, 2002)

allowing classes of characters at each position of the

searched pattern. Holub et al. (Holub et al., 2008)

implemented a version of Boyer-Moore-Sunday algo-

rithm (Sunday, 1990) for degenerate strings and ex-

perimentally proved its superiority over BNDM for

standard pattern lengths. Iliopoulos et al. (Iliopou-

los et al., 2008) presented their algorithm based on

transformation into the ‘restricted pattern matching

problem’. Their implementation runs in O(n) time

where n is a size of the input text for sufﬁciently

small patterns and DNA/RNA alphabet. The algo-

rithm based on Landau and Vishkin’s algorithm was

proposed by Crochemore (Crochemore et al., 2015).

They achieved interesting upper bound O(kn), where

k is maximum number of degenerate positions in the

text and n is the length of the text. However, the

experimentally evaluated implementation of the algo-

rithm was not provided. Finally, the concept of ‘Elas-

tic Degenerate Strings’ was introduced in (Iliopou-

los et al., 2017). Elastic Degenerate Strings provide

another alternative to represent the consensus/pan-

genomic sequences. Later, the practical implementa-

tion of the pattern matching algorithm in Elastic De-

generate Strings was given in (Grossi et al., 2017)

and a version of algorithm allowing errors was pre-

sented in (Bernardini et al., 2017). Recently, Cisłak et

al. (Cisłak et al., 2018) presented SOPanG algorithm

solving elastic degenerate string matching problem in

the same upper bound O(Nd

e), however, achieving

an order of magnitude better time than (Grossi et al.,

2017) in practical experiments.

The nucleotide consensus sequences generated

from vcf (Variant Call Format) ﬁles have the follow-

ing properties. They have very limited number of dis-

tinct symbols in the alphabet (16 symbols of IUPAC

alphabet of which only 4 symbols are solid). At the

same time, the sequences prove a very low rate of de-

generate symbols (between two and three percent for

all chromosomes). The two aforementioned proper-

ties led us to the idea to store the consensus sequences

as a simply encoded strings (over the alphabet of only

solid symbols) together with marking the relatively

rare degenerate positions. Our algorithm BADPM is a

natural extension (for degenerate strings) of the BAPM

algorithm presented in (Proch

azka and Holub, 2017).

It is based on tabulating all possible factors of the

searched pattern. The algorithm performs searching

for all pattern factors in its basic loop. After every

factor occurrence, the occurrence of the whole pattern

must be conﬁrmed.

BADPM works at the level of bytes which ensures

its high speed. This implies that the length of the

tabulated factors is expected to be a multiple of 4.

Our experiments proved that the factor length 8 sym-

bols is ideal trade-off between factor occurrence fre-

quency on one side and memory consumption and the

length of the shift on the other side. However, this ap-

proach ensures sublinear time complexity on average

since frequent shifting in the text can be applied. This

holds especially for longer patterns since the shift is

implied from the pattern length. The space for a sim-

ple data structure (storing the encoded consensus se-

quence) is upper bounded by O(nα + n logn) where n

is a size of the text and α is a maximum possible vari-

ants provided by 4-gram of IUPAC degenerate sym-

On-line Searching in IUPAC Nucleotide Sequences

bols. In practice, the needed space is close to O(n)

since the rate of degenerate symbols in the consensus

sequences is low and the number of possible variants

provided by the occurring 4-grams is low as well. The

ensured worst-case search time is O(nm

) where m

is a size of the searched pattern. However, our ex-

periments proved that the factor hit rate is very low.

Thus, the real time complexity is linear for short pat-

terns (16 ≤ m ≤ 32) and sublinear for longer patterns

(m > 32).

The rest of the paper is organized as follows. We

give deﬁnitions of some basic notions in Section 2.

The Section 3 is dedicated to deﬁnition and detailed

description of BADPM algorithm. We deﬁne PNS (Par-

allel Naive Search) algorithm as a baseline for experi-

mental comparison with BADPM in Section 4. The Sec-

tion 5 summarizes experimental results performed on

real genomic data. We give the conclusion and some

ideas for future work in Section 6.

2 BASIC NOTIONS

Let x = x

..x

be a string composed of single sym-

bols x

of a ﬁnite ordered alphabet Σ. The length of

the string x is n = |x|. The size of the alphabet Σ is

σ = |Σ| = O(1). The start position i and the length

j deﬁne so-called factor (or substring) denoted by

i, j

= x

..x

i+ j−1

. A factor with i = 0 is called preﬁx

and a factor with i + j − 1 = n is called sufﬁx of the

string x. We denote by ε so-called empty string of

length 0. The problem of string pattern matching is

to ﬁnd all occurrences of a pattern P = p

..p

in a

text T = t

..t

where both strings are composed of

symbols from the same alphabet Σ and m  n. Partic-

ularly, we can distinguish two tasks: (i) count when

number of occurrences of P in T is reported and (ii)

locate when exact positions of the occurrences of P

in T are reported.

Pattern substitution method (Manber, 1997) is a

compression method when q-grams of symbols of the

input text T (i.e., Σ

) are substituted with an assigned

byte value b where b ∈ {0,1, ...,255}. The pattern

matching in the compressed (encoded) text means to

ﬁnd all occurrences of the compressed pattern P

the compressed text T

(both deﬁned over the alpha-

bet of byte values b ∈ {0,1,...,255}).

A symbol that represents only a single value is

called solid symbol. For DNA nucleotide sequences,

we consider the following alphabet of solid sym-

bols Σ = {A,C, G,T }. Degenerate symbol is called

a symbol that represents a subset of solid sym-

bols. The number of possible degenerate symbols

is limited by 2

|Σ|

− 1. The degenerate symbol can

be represented as a union of covered solid sym-

bols (e.g. [AC]) or as a speciﬁc single symbol (e.g.

M). For DNA consensus sequences, we consider the

following alphabet of degenerate symbols Σ

IUPAC

{A,C,G,T,R,Y, S,W,K,M, B,D, H,V,N}. The map-

ping IUPAC symbols to the solid symbols is given in

Table 1.

Table 1: Mapping IUPAC degenerate symbols into the sub-

sets of solid symbols.

IUPAC symbol

Subset Bit coding

A {A} h0001i

C {C} h0010i

G {G} h0100i

T {T } h1000i

R {A,G} h0101i

Y {C,T } h1010i

S {C,G} h0110i

W {A,T } h1001i

K {G,T } h1100i

M {A,C} h0011i

B {C,G,T } h1110i

D {A,G, T} h1101i

H {A,C, T} h1011i

V {A,C,G} h0111i

N {A,C,G, T} h1111i

For the degenerate text and the degenerate pattern

we can distinguish the following three pattern match-

ing problems (Iliopoulos et al., 2008). We design our

algorithm to solve the last problem which implies that

it can solve also the previous two problems.

Problem 1. Given a degenerate text T and a pattern

P . The problem is to ﬁnd all the occurrences of P in

T i.e. to ﬁnd all i such that for all j in [1,m], P

∈

i+ j−1

Problem 2. Given a text T and a degenerate pat-

tern P . The problem is to ﬁnd all the occurrences

of P in T i.e. to ﬁnd all i such that for all j in [1,m],

i+ j−1

∈ P

Problem 3. Given a degenerate text T and a degen-

erate pattern P . The problem is to ﬁnd all the occur-

rences of P in T i.e. to ﬁnd all i such that for all j in

[1,m], T

i+ j−1

∩ P

Traditional inverted index consists of two major

components: a vocabulary storing all distinct words

occurring in the text T and a set of posting lists stor-

ing positions of all occurrences of a given word in

the text T . The vocabulary of a q-gram inverted in-

dex (Puglisi et al., 2006) is composed of all possible

q-grams of the alphabet Σ, i.e., Σ

. For the purpose

of block indexing we split the indexed text into single

blocks of a deﬁned ﬁxed size. The posting lists of a

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

block inverted index then store addresses of the blocks

covering the exact positions of occurrences. The exact

positions are determined in the next step when a stan-

dard pattern matching method is performed in terms

of the preselected blocks.

In later description of the algorithm, we use C-

like syntax for bitwise operations. Particularly, we

use | for bitwise-or, & for bitwise-and,  for shift-

left operation and  for shift-right operation.

3 BYTE-ALIGNED DEGENERATE

PATTERN MATCHING

BADPM (Byte-Aligned Degenerate Pattern Matching)

algorithm is focused on searching in consensus nu-

cleotide sequences. It exploits their two basic proper-

ties: (i) very low size of the alphabet, (ii) very low fre-

quency of degenerate symbols in the text. Consider-

ing the alphabet expressing the values of solid bases,

the alphabet has only four symbols. Considering even

the degenerate bases, we still end up with ﬁfteen sym-

bols at most. Furthermore, we experimentally tested

vcf ﬁles from the 1000 Genomes Projects (Consor-

tium, 2011) and we found that the frequency of the

degenerate symbols varies from 2 to 3 percent for dif-

ferent chromosomes.

The idea behind BADPM is to consider the consen-

sus (degenerate) sequence as a solid string and to en-

code it using a simple substitution encoding (Manber,

1997). The encoding method is deﬁned as: f : Σ

7→ B

where B = {0, 1,. .. ,255} and b ∈ B represents a byte

value that is composed as a concatenation of bit cou-

ples given by the single symbols of the 4-gram s ∈ Σ

(A → 00, C → 01, G → 10, T → 11). The degen-

erate symbols in the string are explicitly marked us-

ing variantPos array. Two other auxiliary arrays are

needed to correctly evaluate the degenerate symbols

in the string. Array variantNum stores the number

of byte variants (implied from all degenerate sym-

bols of the byte). Array variants stores the byte vari-

ants/values implied from the degenerate symbols oc-

curring in the given byte. The solid symbols of the

byte are kept as a left and/or right context in terms

of the byte. This approach implies a space waste be-

cause of storing the solid symbols in the byte as the

contexts, however, it accelerates the search since the

byte operation level is kept. The aforementioned aux-

iliary arrays are very easy to serialize. Together with

the base sequence, between 30 and 35 percent of the

original size is used to store the BADPM encoded text.

On the other hand, the encoded IUPAC sequence (us-

ing a simple substitution encoding - 2 IUPAC symbols

encoded with one byte) requires exactly 50 percent of

the original size.

The BADPM encoded text is depicted in Figure 3.

Let α denotes a maximum number of variants implied

from a 4-gram over IUPAC alphabet and n denotes

the length of the input text. The 4-gram over IUPAC

alphabet providing most variants is clearly hNNNNi

that provides α = 4

= 256 variants. We state the fol-

lowing space complexity of the encoded sequence in

bits. Array variantNum storing the number of byte

variants implied from the corresponding degenerate

position clearly requires O(nlog α) space at most. At

most O(nlog n) space is required for variantPos ar-

ray. At most O(nα) space is needed for variants ar-

ray storing all byte variants. The encoded base se-

quence intuitively needs O(n) space. Thus, the total

space complexity is limited by O(nα + n logn). How-

ever, the real space needed for encoded consensus se-

quences ﬁts between 30 and 35 percent of their origi-

nal/unencoded size.

The following algorithms and their complexities

correspond to BADPM variant optimized for Problem 3

if not stated others. BADPM needs a simple prepro-

cessing of the pattern that includes tabulating of all

pattern factors of a given length. The optimal length

of the factors is 8 symbols which means two-byte-

long factors of the encoded pattern. Figure 2 depicts

a simple data structure used to store the tabulated en-

coded factors of the pattern and it demonstrates also

BADPM preprocessing phase when this data structure

is ﬁlled. The dictionary data structure is depicted in

the right part of the ﬁgure and its main part is an ar-

ray (denoted as dictionary) with 65536 entries (corre-

sponding to 65536 different two-byte values). Every

entry can contain a pointer to a list which stores all

occurrences of the factor (corresponding to the entry)

in terms of the pattern. Each element of the list is a

couple (offset, alignment). The offset o represents a

byte position of the factor in the encoded pattern and

it is easy deducible from its starting position i in the

raw/unencoded pattern o = b

i−1

c. The alignment a

represents a position of the factor in terms of the byte

and it can be computed as a = (i − 1) mod 4. We

state the following space complexity of the dictionary

(preprocessed pattern) in bits. The offset o requires

O(log

) bits, however, the alignment a needs only

a constant number of bits O(1). Thus, one element

of the list requires O(logm) space. The space of the

dictionary array is O(α

) and every list can possibly

contains up to m − 7 elements. This implies the total

space complexity O(mα

logm).

In practice, the algorithm uses byte coding for

simpler and faster memory operations. Suppose the

length of the raw pattern m = 128 bases which im-

plies 32 bytes for the encoded pattern P

. Further-

On-line Searching in IUPAC Nucleotide Sequences

... C

00 01 10 11 00 00 11 11 00 00 11...

... 01 11 11 11 00 11 11 11 00 00 01

A C

A T ...

A A C

alignment = 0

alignment = 1

alignment = 2

alignment = 3

6 927

27 708

32 575

50 115

53 185

62 448

64 764

45 296

dictionary

oﬀset

alignment

− 2

A → 00

C → 01

G → 10

T → 11

− 1

− 2

...

Preprocessing process Preprocessed pattern

A T

A C

...

A T

A C

A T ...

A T

A C

A T ...

A T

00 01 10 11 00 00 11 11 00 00 11...

... C

... 01 11 11 11 00 11 11 11 00 00 01

A C

... C

... 01 11 11 11 00 11 11 11 00 00 01

A C

... C

... 01 11 11 11 00 11 11 11 00 00 01

Figure 2: BADPM preprocessing phase for different byte alignments.

more, suppose every 16

symbol is degenerate imply-

ing 3 byte variants on average. BADPM needs to store

128−7+

128

×2 = 137 factors (elements of the lists).

Suppose a simple byte code used to store the offset o

and the alignment a for every factor. Only two bytes

are consumed for every pair (o,a) and still all the in-

formation is encoded at the level of bytes. Thus, for

BADPM the total space is 137 × 2 + 65 536 = 65 810

bytes, plus an overhead needed to implement the lists.

Still, the data structure easily ﬁts into 65 kiB of mem-

ory and it can be kept in a fast level of the computer

memory.

Algorithm 1 describes preprocessing and search-

ing phase of BADPM. The function ENCODE is called

in the preprocessing phase. The function performs

the simple substitution encoding described above. Its

parameters are: the text to be encoded; the starting

index for encoding; and the number of bases/symbols

that need to be encoded. The function returns desired

encoded factor of the text. The function BUILDDIC-

TIONARY is responsible for constituting dictionary D

and storing the shifted versions of the pattern in the

array B. The while cycle (line 4) iterates over all

possible alignments a ∈ {0,1,2,3}. For every align-

ment, the number of bases/symbols that constitute the

longest byte sequence starting at i is computed (line 5)

and the corresponding encoded pattern is obtained

(line 6). The encoded pattern is stored for the given

alignment (line 7) and later is used for direct compar-

ison of bytes (the encoded text with the encoded pat-

tern). Next while cycle (line 9) iterates over all byte

couples of the encoded aligned pattern and all corre-

sponding variants (line 10) and it ensures storing the

couples (offset, alignment) to their corresponding lists

(line 13). E

j,2

represents a variant (composed of en-

coded solid symbols) provided by two-byte substring

of the encoded pattern E starting at position j.

The function BUILDMASK is another part of the

preprocessing. It generates all necessary masks pos-

sibly needed in the last step of the comparison (a pre-

ﬁx and/or a sufﬁx of the encoded pattern with the

corresponding part of the encoded text). Since the

preﬁx and the sufﬁx are smaller than one byte the

masks are necessary to minimize the bitwise opera-

tions and therefore also the needed time. The function

stores the masks in single variables. The variable pref

stores a preﬁx of the encoded pattern (smaller than

one byte) for all possible alignments a ∈ {0, 1,2,3}.

The variable suf stores a sufﬁx of the encoded pattern

(smaller than one byte) for all possible alignments

a ∈ {0, 1,2, 3}. The examples of the stored preﬁxes

and sufﬁxes can be seen in Figure 2 as the symbols

preceding/following the red rectangles. Similarly, the

variables prefMask and sufMask store the masks (used

for bitwise-and operation with the corresponding byte

in the encoded text) needed to compare a preﬁx or the

sufﬁx, respectively of the encoded pattern. The while

cycle (line 23) iterates over only three possible align-

ments. The pref value is stored for the alignments

a ∈ {1, 2,3} (starting from the value 3). The preﬁx for

the alignment a = 0 is an empty string ε and therefore

it is not stored. The pointer to the array of the sufﬁx

values suf is shifted by the value la and it starts from

the position (la + i) mod 4. In every step of the cy-

cle, the algorithm: (i) stores the corresponding preﬁx

value to pref array and the corresponding preﬁx mask

to prefMask array; (ii) stores the corresponding sufﬁx

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

Algorithm 1: BADPM preprocessing and searching phase.

1: function BUILDDICTIONARY(P , m)

2: D ←

0; B ←

3: i ← 0;

4: while i ≤ 3 do

5: b ← b(m − i)/4c×4;

6: E ← ENCODE(P ,i + 1, b);

7: B

← E;

8: j ← 1;

9: while j < b(m − i)/4c do

10: for each variant E

j,2

11: if D

j,2

0 then

12: D

j,2

← create a new list storing offsets and alignments;

13: add a couple of offset and alignment (j −1,i) to the list D

j,2

;

14: j ← j + 1;

15: i ← i + 1;

16: function BUILDMASK(P , m)

17: pref ←

0; prefMask ←

0; prefM ← h0011 1111i;

18: suf ←

0; sufMask ←

0; sufM ← h1111 1100i;

19: prefB ← ENCODE(P ,1, 4)  2;

20: sufB ← ENCODE(P ,m −4,4)  2;

21: la ← m mod 4;

22: i ← 1;

23: while i ≤ 3 do

24: prefMask

4−i

← prefM;

25: sufMask

(la+i) mod 4

← sufM;

26: pref

4−i

← prefB;

27: suf

(la+i) mod 4

← sufB;

28: prefM ← prefM  2; prefB ← prefB  2;

29: sufM ← sufM  2; sufB ← sufB  2;

30: i ← i + 1;

31: function SEARCH(T , n, P , m)

32: BUILDDICTIONARY(P ,m);

33: BUILDMASK(P , m);

34: shift ← bm/4c −2;

35: i ← shift;

36: while i < n do

37: SYNCVARIANTPOINTERS(i);

38: for each variant T

i,2

39: if D

i,2

0 then

40: for each couple of offset and alignment (o,a) ∈ D

41: SYNCVARIANTPOINTERS(i − o);

42: r ← compare sequentially all bytes starting from T

i−o

with B

considering all byte variants;

43: if r = 0 & a 6= 0 then

44: SYNCVARIANTPOINTERS(i −o − 1);

45: r ← compare (T

i−o−1

& prefMask

) with pref

considering all variants T

i−o−1

;

46: if r = 0 & a 6= la then

47: SYNCVARIANTPOINTERS(i −o + shift);

48: r ← compare (T

i−o+shift

& sufMask

) with suf

considering all variants T

i−o+shift

;

49: if r = 0 then

50: report an occurrence at position 4 × (i − o)− a + 1;

51: i ← i + shift;

value to suf array and the corresponding sufﬁx mask

to sufMask array; (iii) shifts auxiliary variables prefM

and prefB two bits right; (iv) shifts auxiliary variables

sufM and sufB two bits left.

The function SEARCH represents the main func-

tion of BADPM. After the preprocessing of the searched

pattern (lines 32 and 33) the algorithm states a safe

shift as the number of whole bytes of the encoded pat-

On-line Searching in IUPAC Nucleotide Sequences

00 01 00 11 00 00 11 11 00 00 11 01

A C

A T

...

4 879

5 903

6 927

dictionary

A → 00

C → 01

G → 10

T → 11

Source sequence

R T

...

i+1

i+2

Encoded sequence

00 01 01 11

00 01 10 11

...

00 00 11 10

00 00 11 11

...

00 10 11 01

00 10 11 10

00 10 11 11

variants

i + 2

variantPos

variantNum

...

j + 1

baseSeq

Preprocessed

pattern

Figure 3: BADPM searching phase. Checking different factors implied from different byte variants.

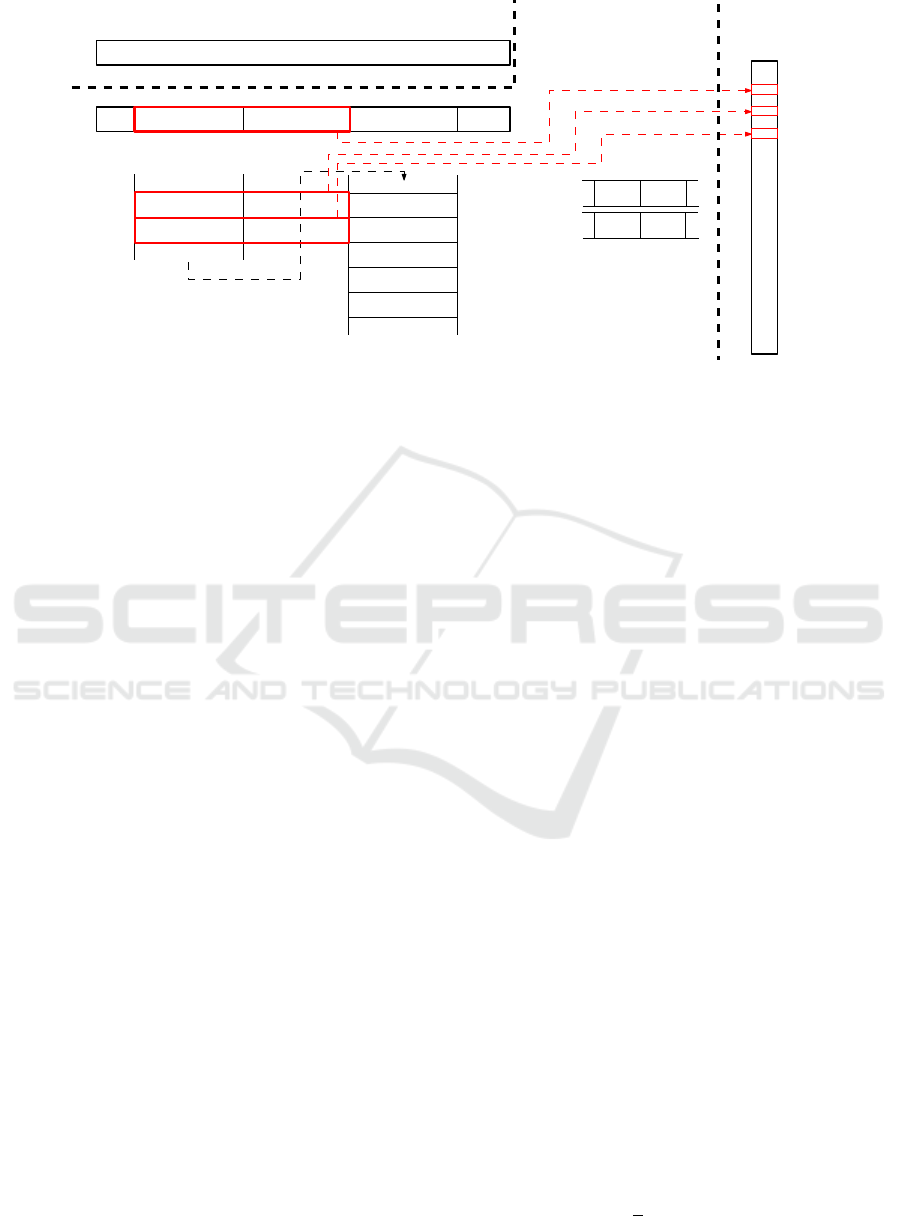
tern minus two (line 34). The while cycle (line 36)

traverses the encoded text T of length n. It always

reads a byte couple value T

i,2

and all its variants and

the corresponding entries in the dictionary D

i,2

are

checked (line 39). The pointers for the array contain-

ing byte variants need to be synchronized for a given

position i − o (line 41). If the dictionary entry D

i,2

empty the algorithm shifts (line 51) and it continues at

the next position. Otherwise, the algorithm has to tra-

verse over all couples (o, a) stored in the correspond-

ing list and perform three-level comparison for every

couple. The ﬁrst level is a comparison of the bytes

in the encoded text (starting at the position given by

the offset o) with the bytes of the encoded pattern B

according to the shift/alignment a (see line 42). The

second level (see line 45) is a comparison of the preﬁx

and it is applied only if the ﬁrst level was successful.

The variant pointers need to be synchronized again

(line 44). The third level (see line 48) is a compari-

son of the sufﬁx and it is applied only if the second

level was successful. If all levels of the comparison

are successful the algorithm reports a new occurrence

at the corresponding position 4 ×(i− o)−a +1 in the

raw text (line 50).

Example 3.1. We state an example to present the way

BADPM processes the degenerate symbols. Suppose

the situation depicted in Figure 3. Current position in

the encoded text is i. The algorithm checks the couple

of bytes B

and B

i+1

. The variant pointers are syn-

chronized (line 37 in Algorithm 1) and the algorithm

checks if B

or/and B

i+1

contain a degenerate symbol.

The check is evaluated according to the next degener-

ate symbol position in variatPos array. The element

variantPos

points to the position i which implies that

byte has more than one variant. The number of

variants is variantNum

= 3. All byte variants are

traversed (line 38 in Algorithm 1 and the red rectan-

gles in Figure 3) and the corresponding entries in the

dictionary are evaluated (lines 39 - 50). The eval-

uation consists of byte-by-byte comparing T

i−o

with

the encoded pattern (with corresponding alignment)

(line 42). The preﬁx and sufﬁx comparison must

be performed as well (line 45 and line 48). All byte

variants are considered in the aforementioned com-

parisons.

4 PARALLEL NAIVE SEARCH

We prepared two simple baseline algorithms for

our experiments: Boyer-Moore-Horspool (BMH) algo-

rithm and Parallel Naive Search (PNS). BMH represents

a version of well-known algorithm (Horspool, 1980)

adapted for degenerate strings. However, PNS (thanks

to its engaging results proved in the experiments) de-

serves a little bit deeper description. The idea of PNS

is based on intrinsic parallelism of computer words

and on a bit representation of the alphabet symbols.

All symbols of IUPAC alphabet are represented using

code words with the size four bits (left or right nibble

of a byte). The bits of a code word represent four solid

symbols of the alphabet Σ

solid

= {A,C, G,T } starting

from the least signiﬁcant bit to the most signiﬁcant

bit. The bits of the code word are set when the rep-

resented symbol includes the given solid symbol (see

the bit coding in Table 1). Both the processed text T

and the searched pattern P need to be encoded in this

fashion.

PNS performs standard forward pattern matching

process. However,

symbols are processed at once

in parallel fashion where w is a size of the computer

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

Algorithm 2: PNS searching phase.

1: function COMPAREWORDS(a, b)

2: sub ← h0001 0000i

w/8

;

3: mask ← h0000 1111i

w/8

;

4: c ← a & b;

5: r

← sub −(c & mask);

6: r

← sub −((c  4) & mask);

7: r ← ((r

& sub)  1) k (r

& sub)

8: function SEARCH(T , n, P , m)

9: pMask ← BUILDPATTERNMASK(P ,m);

10: rMask ← h1100 1111i

w/8

;

11: i ← 1;

12: while i ≤ n −m do

13: j ← 1;

14: r ← h0000 0000i

w/8

;

15: while j ≤ m do

16: r ← r k COMPAREWORDS(T

i+ j,

,pMask

);

17: if (r k rMask) = h11111111i

w/8

then

18: go to shift;

19: j ← j + 1

20: j ← 1;

21: while j ≤ m do

22: r ← r k COMPAREWORDS(T

i+ j,

 4, pMask

);

23: if (r k rMask) = h11111111i

w/8

then

24: go to shift;

25: j ← j + 1

26: report all positions/nibbles corresponding to unset bits in r k rMask;

27: shift:

28: i ← i +

;

word. SEARCH function described in Algorithm 2

represents a basic loop of the algorithm. The param-

eters of the SEARCH function are: an encoded text T ,

a length of the encoded text n, an encoded pattern P ,

a length of the encoded pattern m (the length of the

raw/unencoded pattern is consequently 2m). In the

ﬁrst step (line 9), the searched pattern P is prepro-

cessed into the form of array pMask. The situation

is depicted in the right part of Figure 4. This array

consists of 2m computer words of length w. Every

element of the array contains a mask composed of

code words of the corresponding symbol of pattern

P . The ﬁrst m elements of the array represent the odd

symbols and the last m elements represent the even

symbols of the searched pattern. The variable rMask

represents a register necessary to store the intermedi-

ate results. The register is a computer word composed

bytes. The third and fourth most signiﬁcant bits

of j-th byte rMask

represent the activity of the left

and right nibble of (i + j)-th byte in text T

i+ j

. If the

bit is zero then the corresponding position in the text

is still a candidate for a match. The main loop of

SEARCH function traverses over the encoded text T

(line 12). In every step, a parallel comparison of cor-

responding factor of the text T

i+ j,

is performed. The

odd symbols of the pattern are compared in the ﬁrst

block (lines 15–19). The even symbols of the pattern

are compared in the second block (lines 21–25). This

is a technical optimization implying only one shifting

of the compared text factor T

i+ j,

. Whenever no ac-

tive position remains (no zero bit in rMask, lines 17

and 23), the comparing sequence stops and the text is

shifted (line 28).

The parallel comparison of the text factor T

i+ j,

with pMask

is done in function COMPAREWORDS.

This function is performed in constant time and its

usage is depicted in Figure 4. The bitwise AND

operation between the text factor T

i+ j,

and the

corresponding pMask

is the ﬁrst step (line 4).

Next, the non-empty intersection in terms of single

nibbles need to discovered. The right nibbles are

checked at ﬁrst. The intermediate results of bitwise

AND operation is masked and then subtracted from

sub register where only the fourth most signiﬁcant

bit is set (line 5). If the bit is set even after the

subtraction it means that there is an empty inter-

section (corresponding symbols do not match) and

the corresponding position in the text is excluded

On-line Searching in IUPAC Nucleotide Sequences

A C

...

Source sequence

R T

...

Encoded sequence

0001 0010

...

0111 1000

...

0001 0101

1000 1110

...

2i+15

i+7

Preprocessed pattern

0001 0001 ... 0001 0001

Pattern

A C A T ... A A T C

0010 0010 ... 0010 0010

0001 0001 ... 0001 0001

1000 1000 ... 1000 1000

...

0001 0001 ... 0001 0001

1000 1000 ... 1000 1000

0001 0001 ... 0001 0001

|w|

0001 0000

0001 0001

0000 0000

...

0000 1111 ... 0000 1111

mask

0001 0000 ... 0001 0000

sub

−

0000 0000

0000 0001

0000 0000

...

0001 0000

0000 1111

0001 0000

...

0001 0000

0000 0000

0001 0000

...

0010 0010 ... 0010 0010

...

m + 1

Figure 4: PNS searching phase. The ﬁrst step of comparing the source sequence at position 2i with the preprocessed pattern.

from the potential candidates for a match. The same

operation is performed for the left nibbles (line 6)

and the intermediate results are merge into one

requires O(

m) time at most where w is a size of

the computer word. Very simple preprocessing of the

pattern is required and it takes O(m) time.

Example 4.1. We demonstrate the function COM-

PAREWORDS in the following example (see Figure 4).

Suppose text factor T

2i,16

with a preﬁx “ACVT” and

a sufﬁx “ARTB”. Furthermore, suppose a pattern P

with a preﬁx “ACAT” and a sufﬁx “AATC”. After the

bitwise AND operation between the encoded text fac-

tor and the corresponding mask pMask

only four of

the depicted nibbles have non-empty intersection: the

ﬁrst symbol ‘A’, the third symbol ‘V’, the ﬁrst sym-

bol of the sufﬁx ‘A’ and the second symbol of the suf-

ﬁx ‘R’. The active bits are emphasize with red color.

Next, the comparison of the right nibbles is performed

and the corresponding bitwise AND operation with

the register mask keeps active only the second nibble

of the sufﬁx (symbol ‘R’). Subtraction is performed

and the corresponding bit (fourth most signiﬁcant bit

in the ﬁrst byte of the sufﬁx) stays unset which implies

that the corresponding position 2i + 13 in the text is

still a candidate for a match. The processing of the

left nibbles is skipped to simplify the example.

5 EXPERIMENTS

We present experimental results that give a detailed

comparison of our algorithm BADPM with the afore-

mentioned baseline algorithms. Particularly, we per-

formed the comparison in terms of locate time with

Boyer-Moore-Horspool (BMH) algorithm (Horspool,

1980), with Parallel Naive Search (PNS) algorithm

(see Section 4) and with Backward Nondeterminis-

tic DAWG Matching (BNDM) algorithm (Navarro and

Rafﬁnot, 1998) optimized for IUPAC alphabet. We

planned also a comparison with the algorithm pro-

posed by Iliopoulos in (Iliopoulos et al., 2008). How-

ever, the authors did not provide an implementation

of their algorithm. The essence of BADPM (its byte ori-

entation and its principle of tabulating all factors) pre-

determines this algorithm to search for patterns with

length m ≥ 12 bases. BMH and BNDM shall also proﬁt

from the longer searched patterns, while PNS is prac-

tically independent of the length of the searched pat-

tern m. Theoretically, PNS locate time could worsen

with the growing pattern length thanks to its time

complexity O(

m), however, the experiments did not

prove this trend.

All the tested algorithms were implemented in C

programming language

. We carried out our tests on

Intel



Core

i7-4702MQ 2.20 GHz, 8 GB RAM.

We used compiler gcc version 5.4.0 with compiler

BADPM implementation is available at http://www.

stringology.org/badpm/badpm.zip

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0 200 400 600 800 1000

Locate time [sec]

Pattern length

BADPM SO64 BMH BNDM

Figure 5: Human chromosome 7: Locate time depending

on the length of the searched pattern m.

optimization -O3. The tested patterns were chosen

randomly from the input text and their length m was

ranging from 16 to 1024. All experiments were run in

loop 1 000 times and we report the mean of the run-

ning time in seconds. All reported times represent

measured user time + sys time and they always in-

clude any necessary pattern preprocessing. For eval-

uating the algorithms, we used vcf ﬁles of differ-

ent chromosomes downloaded from 1000 Genomes

Projects (Consortium, 2011)

. The vcf ﬁles were

transformed into the consensus text ﬁles over IUPAC

alphabet using bcftools consensus utility by Sanger

institute with parameter -I denoting the output given

in IUPAC alphabet.

The ﬁrst experiment describes dependency of lo-

cate time on the length of the searched pattern for

single algorithms. BADPM proves strongly improving

locate time when the length of the pattern P grows

up to the value 256 bases. This is expected result

since the shift of BADPM basic loop directly depends

on the length of the pattern. BMH also derives its shift-

ing from the pattern length. However, its improve-

ment is not so strong thanks to small alphabet size

and the degenerate string domain which limits shift-

ing potential of BMH. BNDM should also proﬁt from the

increasing length of the searched pattern, however, it

is limited by the size of the computer word. Since the

length of the pattern exceeds the size of the computer

word BNDM shows no further improvement. BADPM

proved its superiority in locate time for middle-sized

and long patterns. BADPM is almost three-times faster

than BMH for m = 16. PNS and BNDM achieve only a

slightly worse locate time than BADPM for m = 16.

However, BADPM strongly dominates for longer pat-

terns. It substantially improves its locate time until

ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/release/20130

502/

the pattern length m = 256 when the practical lower

bound is achieved.

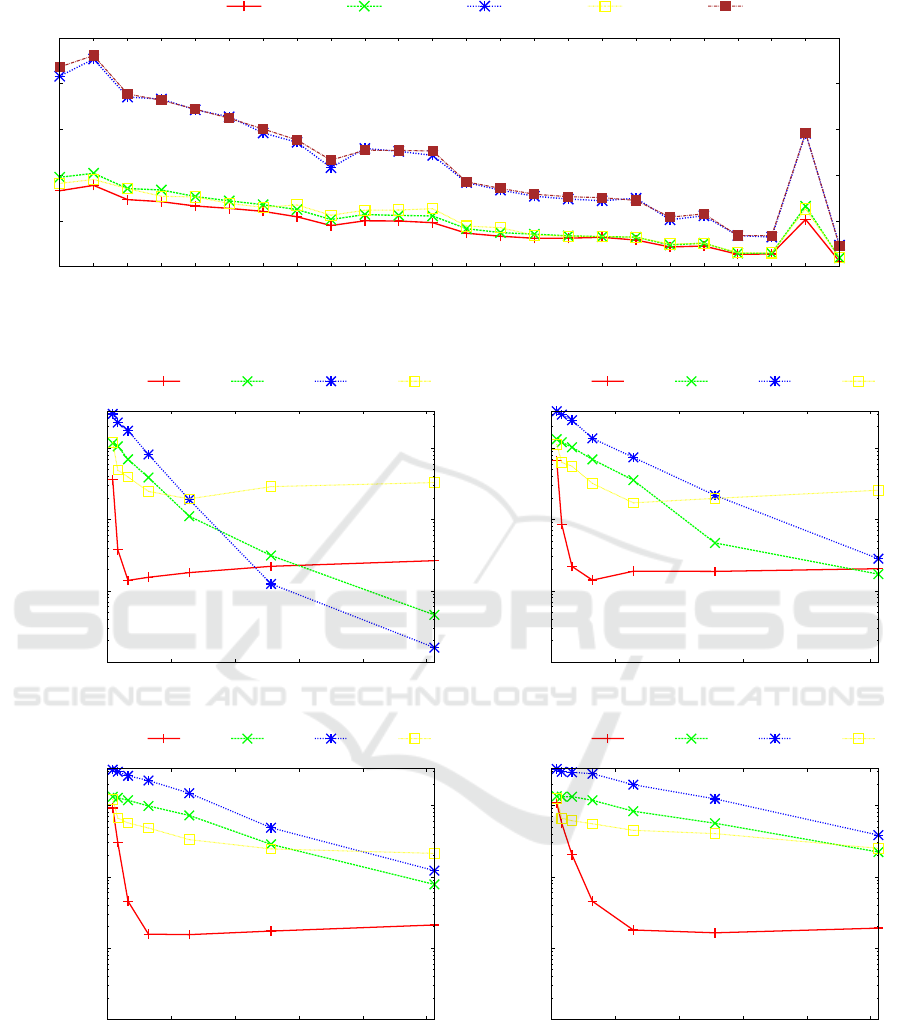
We compared the locate time of single algorithms

on real genomic data obtained from 1000 Genomes

Projects (Consortium, 2011) in our second experi-

ment (see Figure 6). We chose a middle size of the

searched pattern (m = 16) which implies no signiﬁ-

cant shifting beneﬁt for BADPM which dominates es-

pecially for longer patterns. Still, BADPM achieved

the best locate time for all tested chromosomes. PNS

thanks to its parallelism performs a relatively large

shifts corresponding to the computer word size w and

so it achieves also very good locate time over all

tested ﬁles. BNDM proved also very good results since

m = 16 is clearly lower than the size of the computer

word. The second vertical axis in Figure 6 reports the

size of the chromosome ﬁles. The experiment proves

that the locate time of all tested algorithms directly

corresponds to the size of the tested ﬁles.

We combined all tested algorithms with a simple

q-gram block inverted index deﬁned in Section 2 to

achieve locate time that is able to compete with the

times achieved by other index data structures (e.g.

self-indexes). We tested all algorithms for different

block sizes (varying from 12800 to 102 400 bases) of

the q-gram inverted index (see Figure 7). We can ob-

serve that for smaller block sizes (12800 and 25 600

bases, see Figure 7(a) and Figure 7(b)) and for longer

patterns (m ≥ 512 bases) the algorithms with simpler

preprocessing phase (PNS and BMH) dominate. The

reason is that the inverted index performs very efﬁ-

cient ﬁltration of the blocks for longer patterns and

smaller blocks. Thus, the following search algorithm

itself processes only a small portion of the ﬁle and

so the time needed to preprocess the searched pat-

tern dominates over the search time of the algorithm.

The vertical axis in Figure 7 are given in logarithmic

scale to achieve a better overview of the achieved re-

sults. The minimal locate times achieved generally

for the longer patterns are less than one millisecond.

This locate time is two orders of magnitude worse

than the time needed for standard (not degenerate)

pattern matching problem (see Experiments section

in (Proch

azka and Holub, 2017)). However, the time

around one millisecond is still competitive for many

applications.

6 CONCLUSION AND FUTURE

WORK

We proposed the algorithm BADPM optimized for

searching in the degenerate text over an alphabet of

a small size. Practically, BADPM is designed to search

On-line Searching in IUPAC Nucleotide Sequences

0.1

0.2

0.3

0.4

0.5

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 X Y

100

150

200

250

Locate time [sec]

File size [MiB]

Chromosome

BADPM SO64 BMH BNDM File size

Figure 6: Locate time for different human chromosomes for m = 16. The second vertical axis represents the chromosome ﬁle

size.

0.0001

0.001

0.01

0.1

0 200 400 600 800 1000

Locate time [sec]

Pattern length

BADPM SO64 BMH BNDM

(a) Block size = 12 800

0.0001

0.001

0.01

0.1

0 200 400 600 800 1000

Locate time [sec]

Pattern length

BADPM SO64 BMH BNDM

(b) Block size = 25 600

0.0001

0.001

0.01

0.1

0 200 400 600 800 1000

Locate time [sec]

Pattern length

BADPM SO64 BMH BNDM

0.0001

0.001

0.01

0.1

0 200 400 600 800 1000

Locate time [sec]

Pattern length

BADPM SO64 BMH BNDM

(d) Block size = 102 400

Figure 7: Human chromosome 7: Locate time depending on the length of the searched pattern m. The vertical axis is in

logarithmic scale.

very efﬁciently in pangenomic data of a population

of the same species, speciﬁcally vcf ﬁles. BADPM is

based on the idea of BAPM (Proch

azka and Holub,

2017) and it inherits its basic properties: (i) process-

ing at byte level of the input text; (ii) tabulating all

possible factors of the pattern and searching for them

in the ﬁltration step. These two properties ensure

very competitive locate time in the order of millisec-

BIOINFORMATICS 2019 - 10th International Conference on Bioinformatics Models, Methods and Algorithms

onds and sublinear average time complexity. This was

proven on real pangenomic data from 1000 Genomes

Projects (Consortium, 2011).

We plan to design search algorithms for other

forms of pangenomic data in our future work. This

includes the algorithms optimized for so-called Elas-

tic Degenerate Strings which is another form of rep-

resentation genomic data for a population of the same

species.

ACKNOWLEDGEMENTS

The research was partially supported by OP

VVV project Research Center for Informatics no.

CZ.02.1.01/0.0/0.0/16 019/0000765.

REFERENCES

Baeza-yates, R. A. (1992). Text retrieval: Theory and prac-

tice. In In 12th IFIP World Computer Congress, vol-

ume I, pages 465–476. Elsevier Science.

Bernardini, G., Pisanti, N., Pissis, S. P., and Rosone, G.

(2017). Pattern matching on elastic-degenerate text

with errors. In Fici, G., Sciortino, M., and Ven-

turini, R., editors, String Processing and Information

Retrieval, pages 74–90, Cham. Springer International

Publishing.

Boyer, R. S. and Moore, J. S. (1977). A fast string searching

algorithm. Commun. ACM, 20(10):762–772.

Cisłak, A., Grabowski, S., and Holub, J. (2018). Sopang:

online text searching over a pan-genome. Bioinfor-

matics, page bty506.

Consortium, T. . G. P. (2011). A map of human genome

variation from population-scale sequencing. Nature,

473:544 EP –. Corrigendum.

Consortium, T. U. (2015). The uk10k project identiﬁes rare

variants in health and disease. Nature, 526:82 EP –.

Crochemore, M., Iliopoulos, C. S., Kundu, R., Mohamed,

M., and Vayani, F. (2015). Linear algorithm for

conservative degenerate pattern matching. CoRR,

abs/1506.04559.

Crochemore, M. and Rytter, W. (1994). Text Algorithms.

Oxford University Press, Inc., New York, NY, USA.

olki, B. (1964). An algorithm for syntactical analy-

sis. Computational Linguistics, 3:29–46. Hungarian

Academy of Science, Budapest.

Grossi, R., Iliopoulos, C. S., Liu, C., Pisanti, N., Pissis,

S. P., Retha, A., Rosone, G., Vayani, F., and Versari, L.

(2017). On-line pattern matching on similar texts. In

28th Symposium on Combinatorial Pattern Matching,

CPM 2017, July 4-6, 2017, Warsaw, Poland, pages

9:1–9:14.

Holub, J., Smyth, W., and Wang, S. (2008). Fast pattern-

matching on indeterminate strings. Journal of Dis-

crete Algorithms, 6(1):37 – 50. Selected papers from

AWOCA 2005.

Horspool, R. N. (1980). Practical fast searching in strings.

Software: Practice and Experience, 10(6):501–506.

Iliopoulos, C. S., Kundu, R., and Pissis, S. P. (2017). Ef-

ﬁcient pattern matching in elastic-degenerate texts.

In Drewes, F., Mart

ın-Vide, C., and Truthe, B., ed-

itors, Language and Automata Theory and Applica-

tions, pages 131–142, Cham. Springer International

Publishing.

Iliopoulos, C. S., Mouchard, L., and Rahman, M. S. (2008).

A new approach to pattern matching in degenerate

DNA/RNA sequences and distributed pattern match-

ing. Mathematics in Computer Science, 1(4):557–569.

Knuth, D. E., Morris, J. H., and Pratt, V. R. (1977). Fast

Pattern Matching in Strings. SIAM Journal on Com-

puting, 6(2):323–350.

Manber, U. (1997). A text compression scheme that allows

fast searching directly in the compressed ﬁle. ACM

Trans. Inf. Syst., 15(2):124–136.

Marschall, T. (2018). Computational pan-genomics: status,

promises and challenges. Brieﬁngs in Bioinformatics,

19(1):118–135.

Navarro, G. and Rafﬁnot, M. (1998). A bit-parallel ap-

proach to sufﬁx automata: Fast extended string match-

ing. In Proceedings of the 9th Annual Symposium

on Combinatorial Pattern Matching, CPM ’98, pages

14–33, London, UK, UK. Springer-Verlag.

Navarro, G. and Rafﬁnot, M. (2002). Frontmatter, pages

i–iv. Cambridge University Press.

Proch

azka, P. and Holub, J. (2017). Byte-aligned pattern

matching in encoded genomic sequences. In 17th

Int. Workshop on Algorithms in Bioinformatics, WABI

2017, August 21-23, 2017, Boston, MA, USA, pages

20:1–20:13.

Puglisi, S. J., Smyth, W. F., and Turpin, A. (2006). Inverted

Files Versus Sufﬁx Arrays for Locating Patterns in Pri-

mary Memory, pages 122–133. Springer Berlin Hei-

delberg, Berlin, Heidelberg.

Sunday, D. M. (1990). A very fast substring search algo-

rithm. Commun. ACM, 33(8):132–142.

Wu, S. and Manber, U. (1992). Agrep - a fast approximate

pattern-matching tool. In In Proc. of USENIX Techni-

cal Conference, pages 153–162.

On-line Searching in IUPAC Nucleotide Sequences