Calibration of Two 3D Sensors with Perpendicular Scanning

Directions by using a Piece of Paper

Ju-Hwan Lee and Soon-Yong Park

School of Computer Science & Engineering, Kyungpook National University, Daegu, South Korea

Keywords: Calibration, Foot Scanner, Reconstruction, Structured Light Sensor.

Abstract: It is difficult to find the 3D transformation relationship between two 3D sensors when the scanning directions

of the two sensors has very large angle, for example 90 degrees or more. In this paper, we propose a very

simple and efficient calibration method to get 3D transformation between two 3D sensors using a piece of

white-colored paper. A piece of white-colored paper is folded in a quadrangular pyramid shape. The paper

calibration object is placed on the transparent acryl board to get the shape of the object from two 3D sensors

whose scanning direction is about 90 degree. The performance of the proposed calibration method is verified

through 3D model reconstruction experiments. The calibration error between two sensors is less than 0.5 mm.

1 INTRODUCTION

In the shoe industry in the past, customized products

were only offered to people with special needs, such

as medical treatment and athletic players, but many

companies are doing researches to improve customer

satisfaction with the recent trend. An example of

customized products are customized shoes, insole and

so on. To make customized shoes or insole, it is

necessary to know accurate 3D shape information of

customer’s foot.

In the past, the foot measurements were made

using callipers, tape measure and special tools such as

the Foot-Measuring Instrument of Charles F.

Brannock (The Brannock Device Company, 1927).

Alternatively, there is also a measurement method of

foot shape using clay. The above two method is called

contact measurement method. However, contact

measurement results in foot deformity when it is

measured by a person, thus accurate results cannot

always be obtained. In addition, there is a

disadvantage that an accurate measurement is a time-

consuming task.

In order to overcome this problem, many

researches have been done to acquire 3D shape of

human foot using non-contact measurement methods

(Kouchi & Mochimaru, 2001), (Wibowo et al., 2017).

The non-contact method measures the 3D foot shape

through a 3D sensing device composed of laser, white

light or pressure device. It has the advantage of

Figure 1: A circular-type 3D foot scanner using structured

light sensing method.

measuring accurate shape information without

deformation of foot shape and measuring faster than

the contact measurement method.

Several commercial 3D foot scanners are

available already. Examples are LSF-350 foot 3D

scanner of 3DOE solutions (3DOE Solution, 2013),

HP Fitstation’s 3D foot scanner (FitStation, 2018)

and Podia scanner of STT systems (STT Systems,

2018).

In general, the 3D foot scanner is equipped with

two or more 3D sensing devices to acquire shape

information of the entire foot. The sensor of the foot

scanner normally uses structured light for precise

measurement. And the scanning system consists of a

lower 3D sensor which scans the sole of the foot and

162

Lee, J. and Park, S.

Calibration of Two 3D Sensors with Perpendicular Scanning Directions by using a Piece of Paper.

DOI: 10.5220/0007383301620168

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 162-168

ISBN: 978-989-758-354-4

Figure 2: The circular foot scanner consists of an upper 3D

scan sensor and a lower 3D scan sensor.

an upper sensor scans the upper part of the foot. The

two scan results are then combined to obtain the entire

3D shape of the foot.

In a previous paper of this study (Lee et al., 2017),

we developed a three-dimensional circular foot

scanner with upper and lower 3D sensors to obtain the

whole shape of the foot, as shown in Figure 1. For

scanning the whole shape of the foot, the upper sensor

moves along a circular stage and the lower sensor

moves along a linear stage. To obtain the correct

shape of the whole foot, it is necessary to represent

the data acquired from each view point as a single

view point. In order to represent the data obtained

from different viewpoints as a single view point, it is

necessary to know a 3D transformation relation

between the two sensors.

In Figure 2, K

and K

represent the upper and the

lower 3D scanning sensor coordinate systems. The

3D transformation relationship between the two

sensor systems is expressed as T

. T

is represented

by a 3x3 rotation matrix R and a translation vector t.

In general, for two different cameras, the

transformation matrix between two viewpoints can be

obtained by the Zhang algorithm (Zhang, 2000)

which uses a checkerboard. In our previous research,

we also used a checkerboard pattern to find the

transformation relationship between the upper and

lower 3D sensors.

However, the Zhang algorithm is difficult to use

for calibration between two sensors when the angle

between two sensors’s viewing direction is large.

Unfortunately, because most foot scanners use

multiple 3D sensors to obtain soles and foot shapes,

the viewing angles between the sensors are often

more than 90 degrees. In this reason, some researches

have been done to calibrate 3D sensors with large

between large viewing angle by using special

calibration objects.

(Barone et. al., 2013) calibrates two sensors by

placing printed markers on an object. Using markers

has an advantage of being able to know the direction

of the object and clearly identify the feature points for

correction, but placing printed markers on the object

is an inconvenient method. (Mitchelson and Hilton,

2003) use a specially designed LED pattern to

calibrate two sensors. Another calibration method is

using three or more checkerboard pattern attached

perpendicular each other on a cube box. But it is not

easy to make two or more sensors see the three

checkerboard pattern simultaneously.

When a 3D scanning system consists of multiple

3D sensors with large viewing directions, it is

difficult to calibrate the sensor coordinate systems. In

the previous researches, only specially designed

calibration objects and algorithm are used. In

addition, because the 3D scanning systems of the

previous researches have different structure than our

scanning system, it is not easy to employ the previous

methods.

In this paper, we propose a very simple and easy

calibration method for the calibration of two 3D

sensor systems. Especially the proposed method is

applied for the calibration of our 3D foot scanning

system. We evaluate the performance of the proposed

method by obtaining the 3D model of the human foot

using the transformation between the two 3D sensors.

2 CALIBRATION METHOD

USING A PAPER OBJECT

The authors of this paper have reflected on how to

calibrate between two sensors that are more than 90

degree easily and simply. And making of the

calibration object was also focused on using materials

that are readily available from around, so that anyone

can calibrate easily the two sensors. Therefore, the

criteria of the proposed calibration object are as

follows:

1. The material of the calibration object should be

readily available from around.

2. The making of the calibration object should be

easy enough for everyone.

3. Algorithms for calibrating between the two

sensors using a calibration object should also be

simple.

Calibration of Two 3D Sensors with Perpendicular Scanning Directions by using a Piece of Paper

163

2.1 Calibration Object using One Piece

of Paper

As described in the introduction, specially designed

calibration objects can be used for our foot scanner.

However, it is not easy to make a special calibration

object, such an exact square-shape board, attaching

LED patterns, and attaching printed markers on an

object.

In this paper, we try to find a simple and efficient

method for calibration of two 3D sensors which have

orthogonal scanning directions. We propose a very

simple solution by using an easily available piece of

A4 paper. First we make a quadrangular pyramid

object using a piece of A4 paper and use both sensors

to scan the inside and outside shapes of the object.

And then we calibrate between the two sensors by

matching the 3D shapes. The background of making

the calibration object using an A4 paper is as follows:

- The thickness of one piece of A4 paper is less

than 0.1mm.

- After making a quadrangular pyramid object

with a single piece of A4 paper, the inner and the

outer of the object are scanned. Then the two scan

data can be matched with only 0.1 mm error, which is

negligible.

- A piece of A4 paper can be easily obtained from

around.

Figure 3 shows how to scan a calibration object made

with a piece of paper from two 3D sensors. As shown

in the figure, if the scanning of the calibration object

consisting of 3D data from an upper sensor and a

lower sensor, each sensor can acquired 3D surface da-

Figure 3: How to scan a calibration object made from one

paper with two sensors. We can obtain 3D scanning data of

the inner and outer surfaces of calibration objects from two

sensors.

ta of the inside and outside of the calibration object.

The shape of the calibration object does not matter,

while the shape of the calibration object used in this

paper is a pyramid shape that is easy to make, and one

edge of the pyramid is cut out to find the direction of

the object.

Any other shape or material can be used for

calibration object, but it should be very thin. The

thinner the portion corresponding to the side of the

calibration object, the less the calibration error

between the two sensors. In this paper, we make a

calibration object with the shape of a pyramid that is

easiest to make with a piece of paper.

2.2 Calibration Method

In order to represent the data acquired at different

viewpoints as a single coordinate system, we should

find 3D transformation relationship between two

sensors by using the calibration object. The

transformation matrix T

between the two sensors

can be expressed as Eq. 1.





























































(1)

When the calibration object is scanned by the two 3D

sensors, the acquired scan data of the calibration

object is represented by the coordinate system of each

sensor.

If there are 3D surface information of the same

object at different viewpoints, the 3D transformation

matrix between two sensors can be simply found

using the well-known ICP (Iterative Closest Point)

algorithm (Besl and McKay, 1992). Since the scan

resolution of each sensor is different, the 3D

transformation matrix T

between the two sensors

can be obtained using the point-to-plane ICP

algorithm (Low, 2004).

Figure 4 illustrates how to use the point-to-plane

algorithm to find the 3D relationship between two

sensors. In the figure, two 3D surfaces of the scanned

object by sensors K

and K

, are ‘K

surface’ and ‘K

Figure 4: How to use the point-to-plane algorithm to find

the transformation matrix between two points.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

164

surface’, respectively. And the points on the surface

are expressed as p

and q

. Ideally speaking, two 3D

shapes of the calibration object scanned by both

sensors must be the same.

First, the unit normal for all points p

on the ‘K

surface’ is calculated by using neighbour points of p

Then, the 3D point q

on the ‘K

surface’ which is

closest to p

on the ‘K

surface’ is projected onto the

tangent plane of p

. Therefore we can find p’

on the

tangent plane of p

, as the correspondence of q

shown in Eq. 2. By minimizing the error ε, we can

find 3D transformation matrix T

in which the sum

of the distances of p’

and q

is minimized by using

LSM (Least Square Minimization).





















 

(2)

The above point-to-plane ICP can be expressed as

follows pseudocode code.

---------------------------------------------------------------

















While(ε > T

)

// Find the corresponding point q

where the

distance between p

and q

is minimum…











// Find the T matrix that minimizes the error...

































// Convert q

to global coordinate system













---------------------------------------------------------------

Theoretically, when a calibration object made

using a piece of paper is scanned with two sensors,

the 3D transformation relationship between the two

sensors is obtained perfect. However, because the

paper thickness, there is a 0.1mm translation error

between the two sensors. In this paper, we consider

that this small error is negligible in the application of

our 3D foot scanner.

3 EXPERIMENTS

To verify the performance of the proposed method,

we used a circular 3D foot scanner as shown in Fig 5.

As shown in the figure, the upper 3D sensor of the

circular scanner is designed to rotate along the center

axis of the turntable and scans the instep of the foot.

The upper 3D sensor consists of one vision camera

and two line lasers.

The depth of the scanned object surface is calculated

by detecting two line lasers projected on the instep of

the foot from the image of the camera. Therefore, the

rotation sensor scans partial surface of the foot. The

lower 3D sensor of the circular foot scanner consists

of one laser and one camera. The sensor is mounted

on a linear stage, so it scans the bottom part of the

foot. The angle of the upper and lower sensors is

almost 90 degree, but not exactly.

Figure 5: A circular 3D foot scanner for experiments.

To calibrate 3D relationship between the two

sensors, a piece of A4 paper is used. By folding the

paper, we make a pyramid-shaped calibration object

as shown in Figure 6. Any other shape of object can

be use if the object’s outer and inner surface has

enough geometry for ICP matching. The size of the

object is very appropriate for 3D scanning with our

foot scanner. At the one side of the pyramid, there is

a cut-out to distinguish the direction of the object as

shown in the figure.

(a) (b)

Figure 6: Photographs of the calibration object (a) shows

the schematic of the calibration object drawn on a piece of

A4 paper, (b) shows outer surface of the object which is

scanned by the upper sensor, (c) shows inner surface of the

object which is scanned by lower sensors, (d) shows a side

view of the calibration object.

Calibration of Two 3D Sensors with Perpendicular Scanning Directions by using a Piece of Paper

165

Figure 7: A pyramid object placed at a position visible from

both 3D sensors.

As shown in Figure 7, the calibration object is

placed at the center of the circular scanner, and the

calibration object is scanned using both the upper and

lower sensors of the scanner. Figure 8 shows images

of the calibration object captured from the two

cameras. Figure 9 shows the 3D scanning results from

the two sensors. Since the scanned information of the

object is expressed based on the coordinate system of

each sensor, the surface information of the object

scanned by the two sensors in the single coordinate

system can be expressed as shown in Fig 9 (e).

Using the point-to-plane ICP algorithm described

in Section 2.2, we can calculate the three-dimensional

transformation relation between two sensors with the

3D surface information of the calibration object

scanned by each sensor. Figure 10 shows the results

Figure 10: ICP matching result of the two scanned shapes.

Figure 11: Matching error between the two 3D shapes after

ICP transformation.

of the point-to-plane ICP algorithm between the two

sensors. It looks that two shapes are matched exactly

since the color of the two shapes are overlapped.

Therefore, we can confirm that the surface information

of the calibration object expressed in different

coordinate systems is transformed to one coordinate

system.

To analyse the transformation error, the ICP

matching error is shown in Figure 11. From 3D points

on the ‘K

surface’, we find the closest points on the

Figure 8: Images obtained from the upper and lower sensors of the foot scanner.

Figure 9: (a) and (b) shows the scanned 3D points of the calibration object using the left and right lasers of the upper 3D

sensor, (c) shows the scanned 3D points using lower sensor, (d) shows 3D points that combine (a) and (b), (e) shows two

scanned shapes by the upper and lower sensors in the upper sensor’s coordinate system.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

166

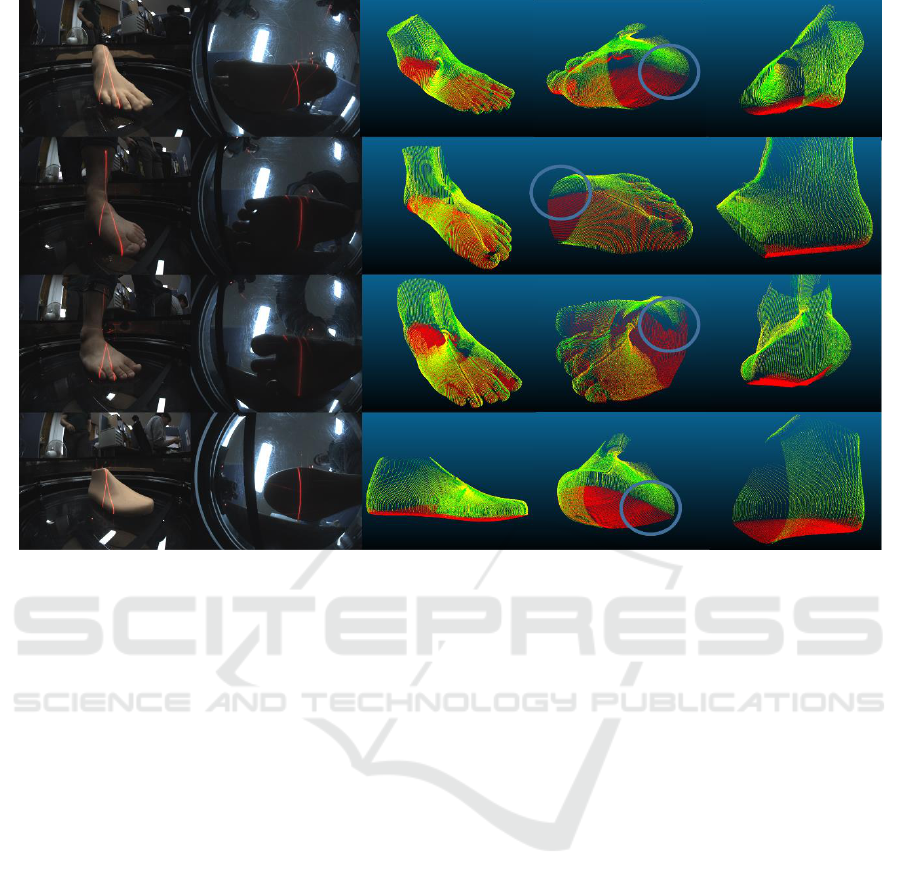
Figure 12: Results of 3D foot models by using the transformation relation between two sensors. From the top, 3D models of

a plastic foot model, human left and right foot, and a plastic raster of shoes.

‘K

surface’. The distance between the closest

matching points is measured and displayed in Figure

11. The overall trans-formation error is less than 0.5

mm on average. Theoretically, the 3D reconstruction

error of the foot scanner is 0.1mm, because it is the

thickness of the paper object. However, in real

experiments, the 3D foot reconstruction error is more

than 0.1 mm. The 3D reconstruction error mainly due

to two reasons. The first is the thickness of the paper

and the second is the reconstruction error of each 3D

sensor.

After the calibration, we know the 3D

transformation between two sensors. Using the

calibration data, the foot scanner can be used to

reconstruction various models after scanning the

object using two sensors. Figure 12 shows results of

modelling after scanning various objects on the foot

scanner. The results show that the 3D model of

human foot obtained from the scanner. The upper and

the lower 3D shapes are matched very exactly. In the

enlarged part of the 3D model, we know that 3D

shapes of two different sensors are aligned very

exactly.

4 CONCLUSIONS

It is difficult to find the 3D transformation

relationship between two sensors when the angle

between the two sensors is perpendicular or 90

degrees or more, such as a foot scanner. Therefore, in

this paper, we propose a simple method to find the 3D

relationship between two sensors with a paper

calibration object. The calibration object proposed in

this paper has advantages that it can be easily made

by anyone and it is easy to obtain an A4 paper. The

transformation relationship between the two sensors

was obtained by using the calibration object, and the

performance of this paper was verified by

reconstructing 3D models of human foot.

ACKNOWLEDGEMENTS

This work was supported by the Industrial Strategic

Technology Development Program (10083642)

funded By the Ministry of Trade, Industry & Energy

(MOTIE, Korea) and This research was supported by

The Leading Human Resource Training Program of

Regional Neo industry through the National Research

Calibration of Two 3D Sensors with Perpendicular Scanning Directions by using a Piece of Paper

167

Foundation of Korea (NRF) funded by the Ministry

of Science, ICT and future Planning (NRF-

2016H1D5A1909829)

REFERENCES

The Brannock Device Company, 1927.

https://brannock.com

Kouchi, M., M. Mochimaru., 2001. Development of a low

cost foot-scanner for a custom shoe making system, 5th

ISB Footwear Biomechanics (2001): 58-59.

Wibowo, D. B., Haryadi, G. D., Widodo, A., Rahayu, S. P.,

2017. Estimation of calcaneal loading during standing

from human footprint depths using 3D scanner. In AIP

Conference Proceedings, volume 1788, pages 030063.

3DOE Solutions, 2013. http://www.3doescanner.com.

FitStation., 2018. https://www.fitstation.com.

STT Systems, 2018. https://www.stt-systems.com.

Lee, M. J., Baek, S. H., Park, S. Y., 2017. 3D foot scanner

based on 360 degree rotating-type laser triangulation

sensor. In Society of Instrument and Control Engineers

of Japan (SICE), 2017 56th Annual Conference, pages.

1065-1070. IEEE.

Zhang, Z., 2000. A flexible new technique for camera

calibration. IEEE Transactions on Pattern Analysis and

Machine Intelligence, volume 22, No.11, pages. 1330-

1334.

Barone, S., Paoli, A., Razionale, A. V., 2013. Multiple

alignments of range maps by active stereo imaging and

global marker framing. Optics and Lasers in

Engineering, 51(2), pages 116-127.

Mitchelson, J., Hilton, A., 2003. Wand-based multiple

camera studio calibration. Center Vision, Speech and

Signal Process.

Besl, P. J., McKay, N. D., 1992. Method for registration of

3-D shapes. In: Sensor Fusion IV: Control Paradigms

and Data Structures. International Society for Optics

and Photonics, pages. 586-607.

Low, K. L., 2004. Linear least-squares optimization for

point-to-plane icp surface registration. Chapel Hill,

University of North Carolina, 4(10).

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

168