
A Content-aware Filtering for RGBD Faces
Leandro Dihl
1
, Leandro Cruz
1
, Nuno Monteiro
2
and Nuno Gonc¸alves
1,3
1
Institute of Systems and Robotics, University of Coimbra, Portugal
2
Institute for Systems and Robotics, University of Lisbon, Portugal
3
Portuguese Mint and Official Printing Office, Portugal
Keywords:
Mesh Geometry Model, Mesh Denoising, Filtering.
Abstract:
3D face models are widely used for several purposes, such as biometric systems, face verification, facial ex-
pression recognition, 3D visualization, and so on. They can be captured by using different kinds of devices,
like plenoptic cameras, structured light cameras, time of flight, among others. Nevertheless, the models gener-
ated by all these consumer devices are quite noisy. In this work, we present a content-aware filtering for 2.5D
meshes of faces that preserves their intrinsic features. This filter consists on an exemplar-based neighborhood
matching where all models are in a frontal position avoiding rotation and perspective. We take advantage of
prior knowledge of the models (faces) to improve the comparison. We first detect facial feature points, create
the point correctors for regions of each feature, and only use the correspondent regions for correcting a point
of the filtered mesh. The model is invariant to depth translation and scale. The proposed method is evaluated
on a public 3D face dataset with different levels of noise. The results show that the method is able to remove
noise without smoothing the sharp features of the face.
1 INTRODUCTION
The current advances of consumer RGBD cameras,
such as light fields cameras (Lytro (Ng et al., 2005)
and Raytrix (GmbH, 2018)), structured light cameras
(Kinect V1 (Microsoft, 2018)), time of flight cameras
(Kinect V2 and Depth Sense (Sony, 2018)) and stereo
cameras (ZED (Stereolabs, 2018)) has allowed the re-
covering of geometric information of a scene. On one
hand, these consumer cameras are cheap and easily
available. On other hand, despite the wide range of
possible applications, the obtained geometry can be
very noisy and contains holes. Our work intends to
improve the geometric model obtained by any RGBD
camera for a specific context, namely faces. This fil-
ter can be used to improve the input model of many
systems based on an RGBD facial model, for exam-
ple: face recognition, facial expression recovery and
pose detection. The goal of this work is: given a tar-
get facial model containing the texture, geometry (a
set of the X, Y, Z points arranged in a grid or a list)
and the respective texture mapping, we want to ob-
tain an RGBD model of the face whose geometry (Z)
is properly filtered.
The proposed filtering method assumes that the
geometric points are regularly arranged. This filter is
based on a statistical prediction process that modifies
each point of the target mesh by comparing its neigh-
borhood with others of the same size from a model
whose geometry is considered appropriate (no noise,
without holes or other spurious artifacts). We denom-
inate this other model by exemplar.
The filtering process assumes that both target and
exemplar are on the same scale and sampling fre-
quency (and then, a set of k × k z-values of target
can be compared to the same size set on exemplar).
However, in general, this is not the case for models
captured by different systems (device + reconstruc-
tion algorithm). Hence, in this work, we will also
present an approach to create an RGBD representa-
tion of the target in the same sampling frequency of
the exemplar.
In this way, the proposed approach begins with
data acquisition, which can be performed using any of
the aforementioned devices, followed by the respec-
tive reconstruction method. A full revision of recon-
struction methods is beyond the scope of this work.
We will keep focus on resampling of a point cloud or
a grid of points containing the geometry XYZ, texture
mapping UV and the texture RGB. After the acquisi-
tion, standardize the target (obtain a regular RGBD
model in the same sampling frequency of the exem-
270
Dihl, L., Cruz, L., Monteiro, N. and Gonçalves, N.
A Content-aware Filtering for RGBD Faces.
DOI: 10.5220/0007384702700277
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 270-277
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
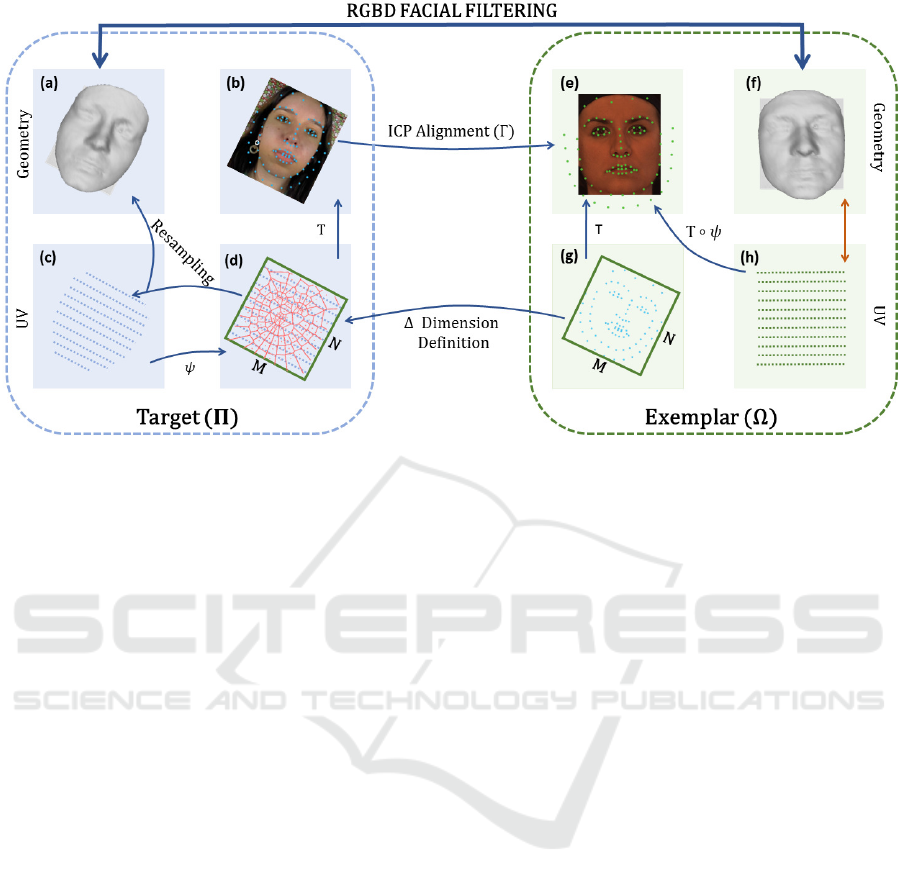
Figure 1: This Figure shows the taxonomy of our method. On the left, it is represented a target Π and its spaces (geometry
(a), texture (b, d) and UV (c)). On the right, it is represented an exemplar Ω, also with its spaces (geometry (f), texture (e, g)
and UV (h)).
plar). It will be explained in Section 3. In Section 4,
we will provide a description of our exemplar-based
filtering method. Finally, in Section 5, we will present
the results and some conclusions.
2 RELATED WORK
In the last years, various filtering approaches have
been proposed to process mesh geometry, denoising
and smoothing meshes aiming the output from 3D
scanners or 3D cameras. The image processing litera-
ture considers that methods of mesh denoising can be
classified in isotropic or anisotropic (Wei et al., 2018).
Isotropic methods are independent of surface ge-
ometry, they normally remove noise and high fre-
quency features together, for example, low-pass fil-
ters were some of the first proposed models to treat
meshes. These filters remove high-frequency noises
but also attenuate sharp features. (Taubin, 1995)
and (Desbrun et al., 1999). Thus, isotropic meth-
ods have difficulty in preserving geometric features.
Anisotropic filters are based on anisotropic geomet-
ric diffusion, which are inspired by scale space and
anisotropic diffusion in image processing (Perona and
Malik, 1990). They are often needed to preserve fea-
tures such as sharp edges and corners.
Yagou et al. (Yagou et al., 2002) modified to the
normal vector of a triangle according to the nor-
mal vectors of its neighbors and then updated the
vertices positions. Liu et al. (Liu et al., 2018)
introduced a new mesh filtering method which is
calculated along the geodesic paths. Intrinsically,
through the integral of property differences along the
geodesic paths, weights calculated between neighbor-
ing faces are much more reliable. Lu and Deng (Lu
et al., 2016) presented a scheme for robust feature-
preserving mesh denoising. Given a noisy mesh input,
their method first estimates an initial mesh, then per-
forms feature detection, identification, and connec-
tion, and finally, iteratively updates vertex positions
based on the constructed feature edges. However, ac-
cording to the authors the approach present problems
in the noisy models with an extreme triangulation or
high levels of noise.
The works proposed by [(Botsch et al.,
2007), (Cho et al., 2014)] also perform mesh
denoising by filtering the face normals, using a
general formulation of the bilateral filter with some
variants. Due to its simplicity and feature-preserving
capability, the bilateral filter has been used in count-
less applications in image processing. Zheng et al.
(Zheng et al., 2011) employed the bilateral filter to
the mesh face normals, then the process of vertex
updated is implemented according to the filtered
normals. The effectiveness of various bilateral filters
mainly relies on the weight of measuring the range
differences.
The aforementioned approaches are based on a lo-
cal geometric neighbor information. If the noise level
is extremely high or if there is not enough informa-
tion due to acquisition problems, the approaches tend
to fail or produce undesired results.
A Content-aware Filtering for RGBD Faces
271

Our main objective is to present a robust filter-
ing model that keeps the information coherent and
reliable even if under the worst situations. This cor-
rection process is similar to that which is solved in
texture-based synthesis techniques (Wei et al., 2009).
Different from texture synthesis, our method has
prior knowledge about face structure. A face has
some particular properties, thus it is important the
filtering keeps them in order to not defeaturing the
model. Although the model and exemplars have dif-
ferent macro-features (for instance, one can be larger
or lengthier than the other), it is possible to ob-
tain a matching of local features because respective
parts still have intrinsic geometric similarities. The
pipeline is illustrated in Figure 4.
3 MODEL STANDARDIZING
Distinct acquisition processes can result in models
with different scales and sampling frequencies. In
this section, we will present how to standardize a face
model.
This work is a content-aware filtering for face
models. It can be adapted for other types of models
whether it has a way to relate a pair of captured mod-
els from different devices. A general relation between
two devices for generic model acquisition is beyond
the scope of this work. However, it may be performed
by calibrating the camera (by using specific patterns,
such as a chess pattern) that allows to relate model
measures, and then, guarantee the same sampling fre-
quency. It is important to highlight that our content-
aware approach does not require any calibration step,
it is performed by Facial Feature Points (FFP) (Wang
et al., 2018) matching.
The standardizing model process consists of
changing of frequency sampling of a given model,
named target Π, according to a base model, named
exemplar Ω. This exemplar is filtering basis. In cases
when we use more than one exemplar to define the
filter, one of them is chosen to be the base, and the
others are also resampled.
The standardizing is performed in two main steps:
(i) the target-exemplar FFP alignment and (ii) the tar-
get resampling. They can be seen in the Figure (Fig-
ure 1). In Section 3.1, we will present the FFP defi-
nition, and the target-exemplar alignment will be pre-
sented in Section 3.2. Following, we can define the
proper model resolution and then perform the resam-
pling. It will be presented in Section 3.3. The correc-
tion of the scale is performed on predictor definition,
that will be explained in Section 4.1.
Figure 2: This Figure shows the initial detected FFPs,
(green points). The new points that are inserted (yellow
points) to split regions that does not satisfy the condition
(3) (forehead and cheeks) or to cover facial part that does
not reached by initial points. Unnecessary points (magenta
points) that are deleted. And, the red points that are inserted
to bound the external FFPs regions.
(a) (b)
(c) (d)
Figure 3: This Figure shows the Facial Feature Points from
exemplar (a) and target (b). (c) shows the FFPs before
alignment and (d) the FFPs after alignment.
3.1 Facial Feature Points (FFPs)
The model standardizing is based on set minutiae
named Facial Feature Points (FFPs). These points
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
272

are also known as facial landmarks, facial fiducial
points and Facial minutiae. They have a semantic
meaning: located around eyes, mouth, nose, chin, and
along face silhouette (Wang et al., 2018). They are
shown in Figure 3 (a) and (b). The generation of these
points is composed of the following steps: (i) detec-
tion, (ii) insertion, and (iii) removal of unnecessary
FFPs. In Section 4.1, we will explain (iv) how to cre-
ate the region of each FFP, based on Voronoi diagram
of these points (Aurenhammer, 1991), and finally ex-
plain (v) how to define the respective points of each
region. It goes without saying that this further steps
are performed on geometry space, hence the FFPs
have to be projected into this space (Figure 1(a)).
For a proper filtering, it is important guarantee a
homogeneity of each FFP region. For this purpose,
the facial covering process shall meet three condi-
tions:
1. All faces must have FFP at correspondent places;
2. The union of regions must cover the whole face;
3. The area of each region must be inversely propor-
tional to the average of expected noise.
These conditions are achieved by an extension
of the set of FFPs proposed by Kazemi and Sulli-
van (Kazemi and Sullivan, 2014). This face detec-
tor uses Histogram of Oriented Gradients (HOG) fea-
ture combined with a linear classifier, a pyramid im-
age, and sliding window detection scheme. After the
points detection, (Green points in the Figure 2), new
points are inserted (i) (Yellow points in the Figure 2)
to split regions that do not satisfy the condition (3).
For example, we added points on the center of the
cheeks and the forehead. These points are generated
between the eyes corners and project them from eye-
brows on the forehead. The cheek points are the cen-
tral points of the two lines created between the mouth
corners and the eyebrows corners, respectively. Fol-
lowing, unnecessary points are removed (ii) (Magenta
points in the Figure 2). It happens in areas where two
neighbor FFPs are often too close, such as the cen-
tral contour of the lips. The red points are inserted to
bound the external FFPs regions.
3.2 Target-exemplar FFP Alignment
Figure 1 shows all elements of these processing. A
model is composed of a list or a grid of points con-
taining the geometry (X,Y,Z)), the texture (an RGB
image) and the UV mapping (a function ψ that asso-
ciates each mesh point to the coordinates of the tex-
ture image).
The alignment of two models starts by defin-
ing the FFP on respective texture. Next, the tar-
get FFPs (Figure 1 (b)) are aligned to the exemplar
FFPs (Figure 1 (e)) by using Iterative Closest Point
(ICP) (Zhang, 1994). This method returns a scale
s ∈ R, a rotation R (2 × 2 matrix), and a translation
c ∈ R
2
that, when applied over the Π FFPs, align
them to Ω FFPs in such a way that minimizes the
difference between the two point sets. It is an affine
transformation that can be represented in homoge-
neous coordinates (adding for each point a third co-
ordinate equals to 1) by the following matrix:
Γ =
sR
c.x
c.y
0 0 1
3×3
(1)
This affine transformation can be visualized in
Figure1. After the alignment, we can perform the tar-
get resampling.
3.3 Target Resampling
The original target is a set Π = {P
1
, ..., P
K
} where we
have P
i
(x
i
, y
i
, z
i
, u
i
, v
i
), that can be a point cloud or a
grid. Without loss of generality, we will assume it
as a point cloud. Additionally, it is provided an im-
age T (which dimension is W × H) that is the tex-
ture of this model. The texture mapping of a point
p
i
is given by a function ψ(p) = (p
i
.u ∗W, p
i
.v ∗ H).
It returns the pixel index of T related to p
i
, i.e. the
color of p
i
is T (ψ(p)). On the other hand, if ( j, i) are
the coordinates of a given point in the texture, then
(u, v) = ψ
−1
( j, i) = (
j
W
,
i
H
). Figure 1(g,h) illustrates
this mapping.
The resampling process consists of creating
a rectangular grid of target points, named ∆ =
{(x
kl
, y
kl
, z
kl
, u
kl
, v
kl
);k = 1..M, l = 1..N}. It is per-
formed by the definition of the coordinates XYZ and
UV of M × N points (∆ dimension) taken regularly
into the target texture space (Figure 1 (g) to (d)). The
resampling is based on a triangulation of points of Π
in UV space.
The definition of M and N (∆ dimension) is based
on the target FFPs transformed into the exemplar
texture space. Each target FFP (into target texture
space) is multiplied on homogeneous coordinates by
Γ. It is created an oriented bounding box around these
transformed points. Finally, M and N are the dimen-
sions of this box.
Once defined these dimensions, we have to cre-
ate the M × N points of ∆. The resampling starts
on texture (samples inside the face bounding box
in target texture space) and for each sample, we
have to define the respective XYZ and UV coor-
dinates. It is also needed to define ( j, i) for each
sample into target texture space, then the respective
A Content-aware Filtering for RGBD Faces
273
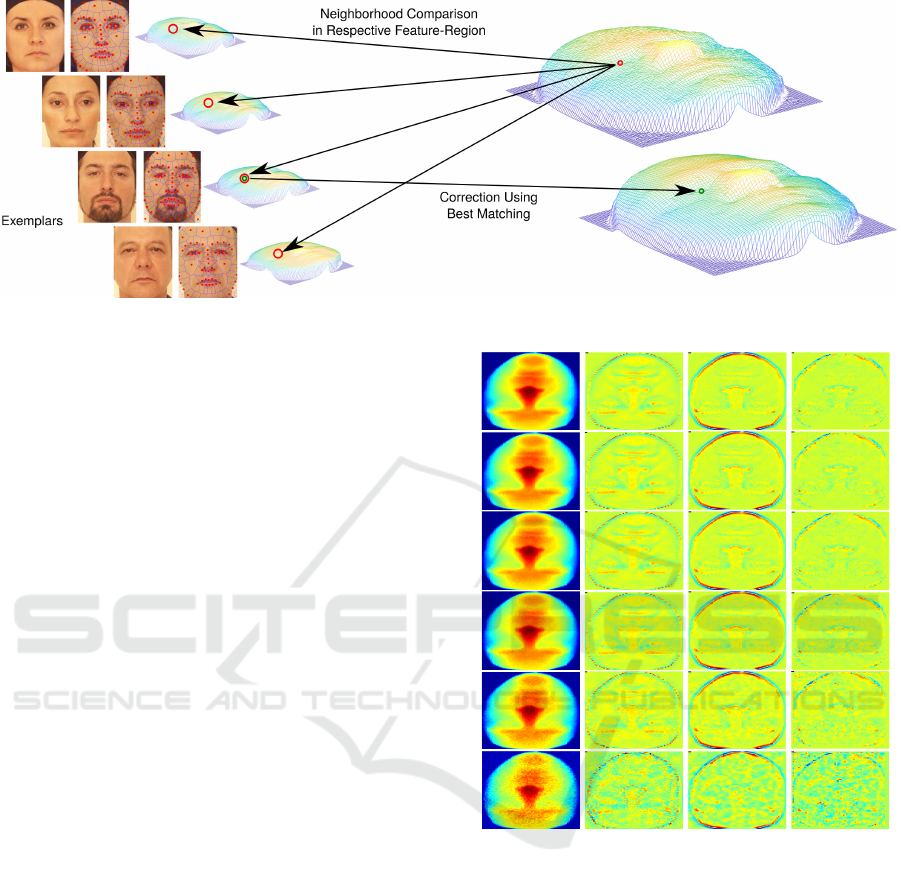
Figure 4: The pipeline of the filtering method.
(u, v) = ψ
−1
( j, i). The coordinates (x, y, z) are ob-
tained based on this (u, v). We create a Delaunay
triangulation (de Berg et al., 2008) of the UV co-
ordinates of all points of Π, and detect the triangle
composed of p
a
, p
b
and p
c
that contains (u, v). It
is noteworthy that p
a
, p
b
, p
c
∈ Π, and then they have
XYZ and UV coordinates. Let λ
a
, λ
b
, λ
c
∈ [0, 1] the
respective barycentric coordinates, then the XYZ co-
ordinates of this point are given by (x
j,i
, y
j,i
, z
j,i
) =
λ
a
(x
a
, y
a
, z
a
) + λ
b
(x
b
, y
b
, z
b
) + λ
c
(x
c
, y
c
, z
c
). There-
fore, it completes all coordinates of ∆ points.
4 FILTERING
The filtering process consists of modifying the Z
value of the target points from a neighbourhood com-
parison of that point with the neighbourhood of equiv-
alent points in the exemplar. In this step, both target
and sample are regular grids at the same sampling fre-
quency.
In Section 4.1, we will present how we define the
predictors of each region associated to an FFP, as
well as the process of neighborhood normalization in
order to guarantee depth scale and translation invari-
ance. Then, in Section 4.2, we will present the cor-
rection process of each point of the target.
4.1 Predictor Definition
The filter is a Nearest Neighbor predictor whose input
is a neighbourhood of a target point containing k × k
Z-values (centered at this point), and the output is the
respective normalized Z-value of the central point of
the closest neighbourhood from exemplars (the nor-
malization will be explained below). We create one
predictor per FFP region, and each one is trained by
using all neighbourhoods in all exemplars that belong
to the respective FFP region.
Figure 5: This image shows the differences between the re-
sults obtained by tested the methods. First column illus-
trates the applied noise, column 2, 3 and 4 show the differ-
ence between the noisy model and the model filtered by the
bilateral, gaussian filters and ours, respectively. The noise
is a random number in the interval [−ασ, ασ], where σ is
the standard deviation of the target model. The alpha values
per row are: 0, 0.5, 0.7, 1.0, 2.0 and 5.0.
The definition of the FFP regions is given by the
Voronoi Diagram. For each exemplar, it is created the
Voronoi Diagram of all FPPs, and for each region, in
turn, all points inside it is used to train the respective
predictor.
Once defined the points per region, it is neces-
sary to achieve a normalization of each neighbour-
hood by subtracting the average and dividing per its
variance. It guarantees that all neighbourhoods can
be compared, since all of them are at the same scale
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
274

Figure 6: This figure shows the results obtained by the
tested filters. Each row shows the noise level applied to the
models which are 0.5, 0.7, 1.0, and 2.0 (respectively) mul-
tiplied by standard deviation. Column one illustrates the
noisy model, column 2, 3 and 4 show filtered models by the
bilateral, gaussian filters, and ours respectively.
and depth translation.
As stated, the predictor performs a nearest neigh-
bor searching which implemented using a Kd-Tree to
accelerate it. In addition, we perform a dimensional-
ity reduction of the neighborhoods of each FFP re-
gion by using PCA (Hertzmann et al., 2001) of the
normalized neighbourhoods.
Our method has only a parameter to adjust, the
k size of the neighbourhood. This value depends on
the correlation length of the facial features on each
region. It is calculated, per each region, according
to the correlation length of all respective neighbour-
hoods (Pierce et al., 2000).
4.2 Correction
The filtering process consists of modifying the ∆
points position according to the predictor. For each
point p ∈ ∆ (i), we determine its respective region
(FFP), (ii) get its neighborhood, normalize it (with
the respective mean and variance), to finally (iii) ap-
ply the projection in the base of the PCA. We use
the normalized and reduced neighborhood in the pre-
diction process. The predictor returns normalized Z-
value of the central point of the best matching neigh-
bourhood. Therefore, we take this value and multiply
it by the variance, and add it up to the average of p ∈ ∆
neighbourhood.
The normalization of the exemplar and target
neighborhood ensures that we can compare them ir-
respective of scale (division by variance) and transla-
tions in depth (subtraction by the mean). In addition,
it is noteworthy that a neighbourhood of the exem-
plar is normalized with its mean and variance, but the
process of unnormalization is performed by using the
mean and variance of the neighborhood of the target
that is being corrected. Thus, we transfer the neigh-
borhood feature of the exemplar to the target, with the
invariance mentioned above. Figure 4 illustrates this
step.
5 RESULTS AND CONCLUSIONS
The initials results were generated using a set of ex-
emplars based on the Bosphorus Database(Savran and
Sankur, 2017). It is intended to research on 3D and
2D human face processing tasks including expression
recognition, facial action unit detection, facial action
unit intensity estimation, face recognition under ad-
verse conditions, etc.
In order to evaluate the results, we performed the
experiments by applying a white noise (Boyat and
Joshi, 2015) to the set of different models. We varied
the noise intensity and compared the results with Bi-
lateral filter (Tomasi and Manduchi, 1998) and Gaus-
sian filter.
Afterwards, we calculated the mean-squared er-
ror (MSE) (Lehmann and Casella, 1998) between the
noisy models and filtered models. Table 1 shows the
quantitative errors on the models used in this experi-
ment. Our method presents the minimum error com-
pared to the others filters, and preserves the details of
the mesh (sharpness). These sharp details can be seen
in Figure 6 (d).
Figure 5 shows the differences between the results
obtained by tested the methods. First column illus-
trates the applied noise, column 2, 3 and 4 show the
difference between the noisy model and the model fil-
tered by the bilateral, gaussian filters and ours, respec-
tively. The noise is a random number in the interval
[−ασ, ασ], where σ is the standard deviation of the
target model. The alpha values per row are: 0, 0.5,
0.7, 1.0, 2.0 and 5.0.
Figure 6 exhibits the results obtained by the tested
A Content-aware Filtering for RGBD Faces
275

Table 1: This table shows the quantitative errors on the
models used in this experiment. The first column is the
noise level. Column 2, 3 and 4 are the results of the mean-
squared error(MSE) (Lehmann and Casella, 1998) between
the noisy models and filtered models.
Noise level Bilateral Gaussian Ours
Filter Filter
0.0 0.6615 1.8459 0.4859
0.5 0.6782 1.8484 0.4991
0.7 0.6970 1.8595 0.5289
1.0 0.7117 1.8819 0.5383
2.0 0.8236 1.9450 0.7218
5.0 2.1309 2.4487 2.1667
filters. Column one illustrates the noisy model (α
equals to 0.5, 0.7, 1.0 and 2.0), column 2, 3 and 4
show filtered models by the bilateral, gaussian filters
and ours respectively.
Figure 7 illustrates the correction of a mesh ob-
tained using DephtSense camera (Sony, 2018). We
first standardized the scale and sampling frequency
regards to the database, and then we corrected using
our filter.
(a) (b)
(c) (d)
Figure 7: This Figure illustrates the correction of a mesh
obtained using DephtSense camera (Sony, 2018). We first
standardized the scale and sampling frequency regards to
the database, and then we corrected using our filter. Figure
(a) shows the acquired noisy mesh, (b) is only the texture,
(c) is the filtered mesh, and (d) is the filtered mesh with
texture.
Figure 8: This Figure shows the results obtained by our fil-
ter on different models. First column illustrates the model
with texture, column 2 shows the ground truth of the mesh
obtained by a 3D scanner, third column is the same mesh
after noise, fourth column shows filtered models by our
method without texture and column 5 shows the textured
filtered models.
Figure 8 demonstrates the results obtained by our
filter on different models. First column illustrates the
model with texture, second column shows the ground
truth of the mesh obtained by a 3D scanner, third col-
umn is the same mesh after noise, and fourth column
shows filtered models by our method without texture.
The use of Bosphorus Database (Savran and
Sankur, 2017) allows us to use these models as a
ground truth. Currently, we are using 20 models as
exemplars randomly chosen. A future work may be
to determine the minimum amount of exemplar that
minimizes filtering error. Reduction of the amount of
neighbourhoods per FFP region (by removing intra-
class redundancy) is left as future work.
Finally, our filtering approach is based on a divi-
GRAPP 2019 - 14th International Conference on Computer Graphics Theory and Applications
276

sion of the model in regions in which all points have
an intrinsic geometric similarity. We presented how to
define these regions for the specific case of faces with
the usage of facial features. Regarding others kinds
of models, it is necessary to use a feature detector that
satisfies the three conditions presented in Section 4.1.
A future work direction is to define general descrip-
tors that can be used for general purpose filtering.
REFERENCES
Aurenhammer, F. (1991). Voronoi diagrams—a sur-
vey of a fundamental geometric data structure. ACM
Comput. Surv., 23(3):345–405.
Botsch, M., Pauly, M., Kobbelt, L., Alliez, P., L
´
evy, B.,
Bischoff, S., and R
¨
ossl, C. (2007). Geometric model-
ing based on polygonal meshes. In ACM SIGGRAPH
2007 Courses, SIGGRAPH ’07, New York, NY, USA.
ACM.
Boyat, A. K. and Joshi, B. K. (2015). A review paper: Noise
models in digital image processing. ArXiv e-prints.
Cho, H., Lee, H., Kang, H., and Lee, S. (2014). Bilateral
texture filtering. ACM Trans. Graph., 33(4):128:1–
128:8.
de Berg, M., Cheong, O., van Kreveld, M., and Overmars,
M. (2008). Computational Geometry: Algorithms and
Applications. Springer.
Desbrun, M., Meyer, M., Schr
¨
oder, P., and Barr, A. H.
(1999). Implicit fairing of irregular meshes using
diffusion and curvature flow. pages 317–324, New
York, NY, USA. ACM Press/Addison-Wesley Pub-
lishing Co.
GmbH, R. (2018). Light field technology.
Hertzmann, A., Jacobs, C. E., Oliver, N., Curless, B., and
Salesin, D. H. (2001). Image analogies. In SIG-
GRAPH.
Kazemi, V. and Sullivan, J. (2014). One millisecond face
alignment with an ensemble of regression trees. In
2014 IEEE Conference on Computer Vision and Pat-
tern Recognition, pages 1867–1874.
Lehmann, E. and Casella, G. (1998). Theory of Point Esti-
mation. Springer Verlag.
Liu, B., Cao, J., Wang, W., Ma, N., Li, B., Liu, L., and Liu,
X. (2018). Propagated mesh normal filtering. Com-
puters & Graphics, 74:119 – 125.
Lu, X., Deng, Z., and Chen, W. (2016). A robust scheme
for feature-preserving mesh denoising. IEEE Trans-
actions on Visualization and Computer Graphics,
22(3):1181–1194.
Microsoft (2018). Kinect for windows.
Ng, R., Levoy, M., Br
´
edif, M., Duval, G., Horowitz, M.,
Hanrahan, P., et al. (2005). Light field photography
with a hand-held plenoptic camera. Computer Science
Technical Report CSTR, 2(11):1–11.
Perona, P. and Malik, J. (1990). Scale-space and edge de-
tection using anisotropic diffusion. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
12(7):629–639.
Pierce, L., Liang, P., Dobson, M. C., and Ulaby, F. (2000).
Texture correlation length: a deconvolution method to
account for speckle in sar images. In IGARSS 2000.,
volume 7, pages 2906–2908 vol.7.
Savran, A. and Sankur, B. (2017). Non-rigid registra-
tion based model-free 3d facial expression recogni-
tion. Comput. Vis. Image Underst., 162(C).
Sony (2018). Sony depthsensing solutions.
Stereolabs (2018). Zed 2k stereo camera.
Taubin, G. (1995). A signal processing approach to fair
surface design. SIGGRAPH ’95, pages 351–358.
Tomasi, C. and Manduchi, R. (1998). Bilateral filter-
ing for gray and color images. In Sixth Interna-
tional Conference on Computer Vision (IEEE Cat.
No.98CH36271), pages 839–846.
Wang, N., Gao, X., Tao, D., Yang, H., and Li, X. (2018). Fa-
cial feature point detection: A comprehensive survey.
Neurocomputing, 275:50 – 65.
Wei, L.-Y., Lefebvre, S., Kwatra, V., and Turk, G. (2009).
State of the art in example-based texture synthesis.
Eurographics STAR.
Wei, M., Huang, J., Xie, X., Liu, L., Wang, J., and Qin, J.
(2018). Mesh denoising guided by patch normal co-
filtering via kernel low-rank recovery. IEEE Transac-
tions on Visualization and Computer Graphics, pages
1–1.
Yagou, H., Ohtake, Y., and Belyaev, A. (2002). Mesh
smoothing via mean and median filtering applied to
face normals. In GMP, pages 124–131.
Zhang, Z. (1994). Iterative point matching for registration
of free-form curves and surfaces. Int. J. Comput. Vi-
sion, 13(2):119–152.
Zheng, Y., Fu, H., Au, O. K., and Tai, C. (2011). Bi-
lateral normal filtering for mesh denoising. IEEE
Transactions on Visualization and Computer Graph-
ics, 17(10):1521–1530.
A Content-aware Filtering for RGBD Faces
277
