Reading Circular Analogue Gauges using Digital Image Processing

Jakob S. Lauridsen

, Julius A. G. Grassmé

, Malte Pedersen

, David Getreuer Jensen

Søren Holm Andersen

and Thomas B. Moeslund

Section of Media Technology, Aalborg University, Denmark

EnviDan, Aalborg, Denmark

Keywords:

Computer Vision, Circular Analogue Gauge, Gauge Reading Principal Component Analysis, Expectation

Maximization, Digital Time Series, Parametric Object Classiﬁcation.

Abstract:

This paper presents an image processing based pipeline for automated recognition and translation of pointer

movement in analogue circular gauges. The proposed method processes an input video frame-wise in a mo-

dule based manner. Noise is minimized in each image using a bilateral ﬁlter before a Gaussian mean adaptive

threshold is applied to segment objects. Subsequently, the objects are described by a set of proposed features

and classiﬁed using probability distributions estimated using Expectation Maximization. The pointer is clas-

siﬁed by the Mahalanobis distance and the angle of the pointer is determined using PCA. The output is a low

pass ﬁltered digital time series based on the temporal estimations of the pointer angle. Seven test videos have

been processed by the algorithm showing promising results. Both source code and video data are publicly

available.

1 INTRODUCTION

Analogue pointer-type dials are widely applied in

both industrial and personal products where informa-

tion such as pressure or speed is displayed. This in-

cludes old waste water pumping stations, which can

have analogue pressure gauges mounted on the pump

as the main instrument to inspect the condition of the

system. Typically a ﬁeld operator is responsible for

reading and recording the data from the gauge to eva-

luate the performance of the pump. This is a time

consuming and expensive process and it is prone to

human errors. An alternative to the manual readings

is to record a video of the gauge and analyze the pres-

sure variations using computer vision techniques.

Figure 1: Illustration of a circular pressure gauge with high-

lighted features and their respective terms.

This paper presents such an approach, that auto-

matically recognizes key parts of analogue circular

gauges and identiﬁes the transient behaviour of the

pointer over the course of the video in order to cre-

ate a digital time series. The terminology that will be

used throughout the paper when describing gauges is

presented in Figure 1.

2 RELATED WORK

One of the early attempts to describe and break down

the problem of digitizing analogue dials was presen-

ted by Sablatnig et al., who proposed a design stra-

tegy for automatically reading dials of various shapes

using pattern recognition techniques (Sablatnig and

Kropatsch, 1994). Some years later Alegria et al. de-

veloped a calibration system capable of reading di-

als using thresholding, image thinning and the Hough

line transform. However, this system was only able

to read dials where the pointer moves in a half circle

(Alegria and Serra, 2000). The Hough line transform

and its variations have since been a popular method

for reading the pointer’s angle yielding feasible re-

sults (Ye et al., 2013) (Jiannan Chi, 2015) (Jiale et al.,

2011). Others have used least squares as an alterna-

tive yielding more accurate results in general (Yang

Lauridsen, J., Grassmé, J., Pedersen, M., Jensen, D., Andersen, S. and Moeslund, T.

Reading Circular Analogue Gauges using Digital Image Processing.

DOI: 10.5220/0007386003730382

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 373-382

ISBN: 978-989-758-354-4

373

et al., 2014) (Wang et al., 2013).

M. Gellaboina uses a rotation of segmented ob-

jects and unwinding of the dial to read round pres-

sure gauges (Gellaboina et al., 2013). The unwin-

ding technique is also used by Zheng et al., who furt-

hermore made the system more robust using colour

correction and perspective transforms (Zheng et al.,

2016). Yi et al. provide an algorithm robust to ax-

ial noise changes by not assuming a perfect circular

shape, ﬁnding the scale marks with the K-means clus-

tering algorithm (Yi et al., 2017).

The aforementioned contributions exclude the as-

sociation of unit related text on the dial to the scale

as a part of the automation. Sun et al. include this in

their contribution by recognizing the numbers in the

dial and associating these to the dial scale (Sun et al.,

2014).

A consistent ﬂaw within the ﬁeld is the lack of

public data, as it has not been possible to locate the

source code, videos, images or other relevant mate-

rial from any of the state-of-the-art methods. Furt-

hermore, several articles lack detailed descriptions of

critical parts of the implementations, leading to a se-

rious inadequacy within the ﬁeld, as it is not possible

to make accurate comparisons and benchmark tests.

3 CONTRIBUTION

Based on the shortcomings of the current state-of-the-

art methods, the following contributions will be pre-

sented in the paper:

• Presentation of a new state-of-the-art method ba-

sed on parametric classiﬁcation of the pointer and

scale marks.

• Application example: obtaining a digital time se-

ries based on a recording of an analogue pressure

gauge.

• Source code and video data are published for ben-

chmarking.

4 APPROACH

We propose a system that takes a video of a circular

analogue gauge as input and translates the signal into

a digital time series.

The overall structure of the module based system

is illustrated in Figure 2 and every part will be descri-

bed in the following sections. It should be noted that

there has not been implemented a module for classi-

fying the dial numbers as there exist excellent open

source solutions capable of handling this.

Preproccesing and

segmentation

Circle ﬁtting

Scale mark and pointer

recognition

Pointer angle

estimation

Time series

Figure 2: Algorithmic structure of automatic pressure rea-

ding system.

4.1 Preprocessing and Segmentation

The need to separate and segment objects with mini-

mal error is a traditional image processing problem.

In the given case, the problem can be boiled down to

handling minor variations in light, contrast, and blur

assuming that the camera is kept relatively steady in

front of a well-lit gauge.

This problem has previously been handled using

local contrast normalization (Gellaboina et al., 2013),

multi-scale retinex to reduce the inﬂuence of different

brightness levels (Zheng et al., 2016), and a laplacian

ﬁlter to enhance the sharpness of the image (Selvathai

et al., 2017).

Our approach to handling irregularities and vari-

ations in the input images is to use a bilateral ﬁlter

followed by an adaptive threshold. An example of an

input image of a standard pressure gauge can be seen

in Figure 3 (a).

The output of running a bilateral ﬁlter on an image

of a gauge can be seen in Figure 3 (b). The bilateral

ﬁlter minimizes noise such as glass transition irregu-

larities and trapped air pockets, which are common in

pressure gauges.

A Gaussian mean adaptive threshold is used to bi-

narize the ﬁltered image as it is robust against variati-

ons in lighting conditions. The thresholded image can

be seen in Figure 3 (c).

After the image has been binarized it is processed

by the grassﬁre algorithm in order to label the objects.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

374

(a) (b) (c)

Figure 3: (a) The input image of a standard pressure gauge.

(b) The bilateral ﬁltered image. (c) The ﬁltered image after

being thresholded.

4.2 Circle Fitting

One of the most common methods to locate the gauge

bezel is to use the Hough circle transform. However,

this method has been found to perform poorly on gau-

ges with chromed bezels, as they are highly reﬂective,

which make the segmentation difﬁcult and may result

in only a part of the bezel being binarized. Therefore,

a more error tolerant method inspired by (Gellaboina

et al., 2013) is used as it has been found to provide

more stable results on segmented circles.

4.2.1 The Circle Fitting Algorithm

In order to determine whether a given object in the

binarized image is circular, the center is ﬁrst determi-

ned by ﬁnding the centroid of the object via the image

Moment of the object contours. Then an overlap va-

lue, V , is introduced as



n 0

C AND rot C

, 10 − n (1)

where C is the original object and C

is a copy of the

object, which is rotated 360 degrees around the center

of C in steps of 10 degrees.

It is assumed that the gauge bezel object is always

circular and among the largest objects, which means

that it will stand out by accumulating the highest va-

lue V .

After having identiﬁed the most likely gauge bezel

object, it is necessary to identify the circle described

by this object as this information is crucial for recog-

nizing the scale marks and the pointer. This is done by

ﬁtting a circle to the object using least squares circle

ﬁtting (Crawford, 1983).

Given a set of N input points x

, y

0 i N

each coordinate x

, y

is translated into another coor-

dinate set (α

, β

) by

◦ ¯x β

◦ ¯y (2)

where the sample mean of the set of coordinates ¯x, ¯y

is given by

¯x



¯y



(3)

The least square center (α

, β

) is found by solving

the system

αα

αβ

ββ

ααα

≡ M

αββ

βββ

≡ M

ααβ

(4)

where M

αα



, M

αβ



and so forth.

The center point can then be transformed back into

the original coordinate system by letting x

, y

, β

≡ ¯x, ¯y and the circle radius can be determi-

ned by

R α

≡ β

≡

αα

≡ M

ββ

(5)

With the gauge circle detected, characteristics of ob-

jects inside of the circle can now be determined.

4.3 Recognition of Scale Marks and

Pointer

The idea of recognizing parts in the gauge dial origi-

nates from (Yi et al., 2017), who recognizes the scale

marks on the dial using features of binary objects and

the clustering technique K-means. This idea can be

expanded by using parametric distributions to recog-

nize both the scale marks and the pointer.

To describe the objects in the dial, ﬁve features

are proposed, which will be outlined in this section

along with sample distribution graphs that illustrate

their capabilities to separate the objects.

The rotated bounding box ratio is a feature me-

ant to capture the oblongness of an object. Each ob-

ject is rotated to be aligned with the horizontal axis

before the bounding box ratio is calculated.

The mass of an object is simply the number of

pixels it contains. To make sure that the mass does

not reach unnecessarily large values, it is transformed

with the natural logarithm.

The compactness is the mass related to the area

of the bounding box.

The distance to gauge center is the Euclidean

distance between the object’s bounding box center

and the center point of the gauge bezel. To ensure

that values are independent to the gauge size in the

frame, the distance is normalized by the gauge radius.

The orientation inaccuracy is given by the Euc-

lidean distance of the orthogonal vector between the

orientation vector of a given object and the gauge cen-

ter. The eigenvector of the largest eigenvalue found

using PCA deﬁnes the orientation vector. The dis-

tance is normalized by the gauge radius.

By describing objects according to these simple

features it becomes possible to differentiate between

them. As illustrated in Figure 4, the pairwise combi-

nations of the proposed features reveal structures that

Reading Circular Analogue Gauges using Digital Image Processing

375

Figure 4: Graphs showing all the feature-pairs and their ability to separate objects. The graphs on the left and right side of the

empty diagonal shows the same feature-pairs but with a different focus. On the left, the red dots illustrate the scale marks and

the blue dots represent noise, which include the pointer objects. On the right, the green dots illustrate the pointer object and

the blue is noise, which include the scale marks.

are capable of separating the objects. All the graphs

are based on manually classiﬁed objects in 49 images

from each of three training videos of pressure gauges

that are presented later.

One example is the feature space spanned by mass

and distance to gauge center, which clearly separa-

tes the pointer object from everything else. Another

example is the distance to gauge center and rotated

bounding box ratio, which separates scale marks and

noise.

The samples give rise to the assumption that ob-

jects in the dial can be classiﬁed using multivariate

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

376

Gaussian distributions. In most of the presented ex-

amples a single Gaussian distribution should be ade-

quate to describe the relevant object, whereas two dis-

tributions seem to be needed in order to cover the

noise.

The Gaussian multivariate distributions are descri-

bed by a mean vector, µ

, and covariance matrix Σ

where the subscript, k, denotes the given distribution.

A mixing coefﬁcient α

is introduced to ensure that

the probability density function integrates to 1 (Bis-

hop and Nasrabadi, 2007). An object can then be des-

cribed by its feature vector, x, and the likelihood of

that object belonging to a class, i, can be expressed

L i x



k i

N x µ

, Σ

(6)

Parameters are ﬁtted using unlabelled samples from

the training videos, which are described later, and the

unsupervised learning technique Expectation Maxi-

mization (EM). The algorithm is run until conver-

gence using initial mean vectors, and diagonal cova-

riance matrices based on the manually classiﬁed ob-

jects. Two feature-pairs are found to be able to dis-

tinguish scale marks, the pointer and noise from each

other.

The feature-pair consisting of the distance to

gauge center and rotated bounding box ratio is used

to classify scale marks. A visualization of the distri-

butions before and after EM can be seen in Figure 5.

The classiﬁcation of new objects is based on the like-

lihood of the objects belonging to a given class.

The mass and distance to gauge center is used to

classify the pointer object and a presentation of the

distribution before and after EM is shown in Figure 5.

When classifying the pointer, only one object needs

to be found. Hence all objects are sorted by their Ma-

halanobis distance to the pointer distribution and the

closest object is assumed to be the pointer.

4.4 Estimation of the Pointer Angle

The angle of the pointer is found using principal com-

ponent analysis (PCA), which is deﬁned as an ortho-

gonal projection of the data set onto a subspace that

maximizes the variance of the projected data.

The binary pixels of the pointer object can be in-

terpreted as a set of two-dimensional points, x, and by

projecting x onto the one-dimensional subspace u

that maximizes the variance of the set, the direction

of the pointer can be determined.

The mean of the projected data can be described

as u

x, where

x is the mean of x. The variance of the

Figure 5: Visualization of distributions before and after es-

timating parameters using the EM algorithm.

projected data can then be found by



n 1

◦ u

x (7)

where N is the amount of points in x and the covari-

ance matrix, S, is given by



n 1

◦

x x

◦

(8)

A practical solution to maximizing the projected

variance, u

, is to set u

equal to the eigenvector

of the largest eigenvalue found in the covariance ma-

trix (Bishop and Nasrabadi, 2007).

However, the orientation of the object needs to be

determined as the vector can point in two directions

seen from the object’s perspective. The pointy end

of the pointer is assumed to always be longer than

the blunt end relative to the center. Therefore, the di-

rection vector formed from the center of the gauge to

the bounding box center of the pointer object is used

to determine the orientation.

With this known, the pointer vector with the lo-

west angle to the direction vector can be determined

using the angle between the vectors. To improve the

direction vector obtained by PCA, the object is crop-

ped with a circle that has the same center as the gauge

and a radius of one ﬁfth of the radius of the gauge

bezel. This is done because the pointer occasionally

passes over the gauge numbers which produces noise

at the tip of the pointer.

The resulting method will extract the angle in each

frame of the video. This angle will have to be related

to a reference location to obtain an absolute angle as

Reading Circular Analogue Gauges using Digital Image Processing

377

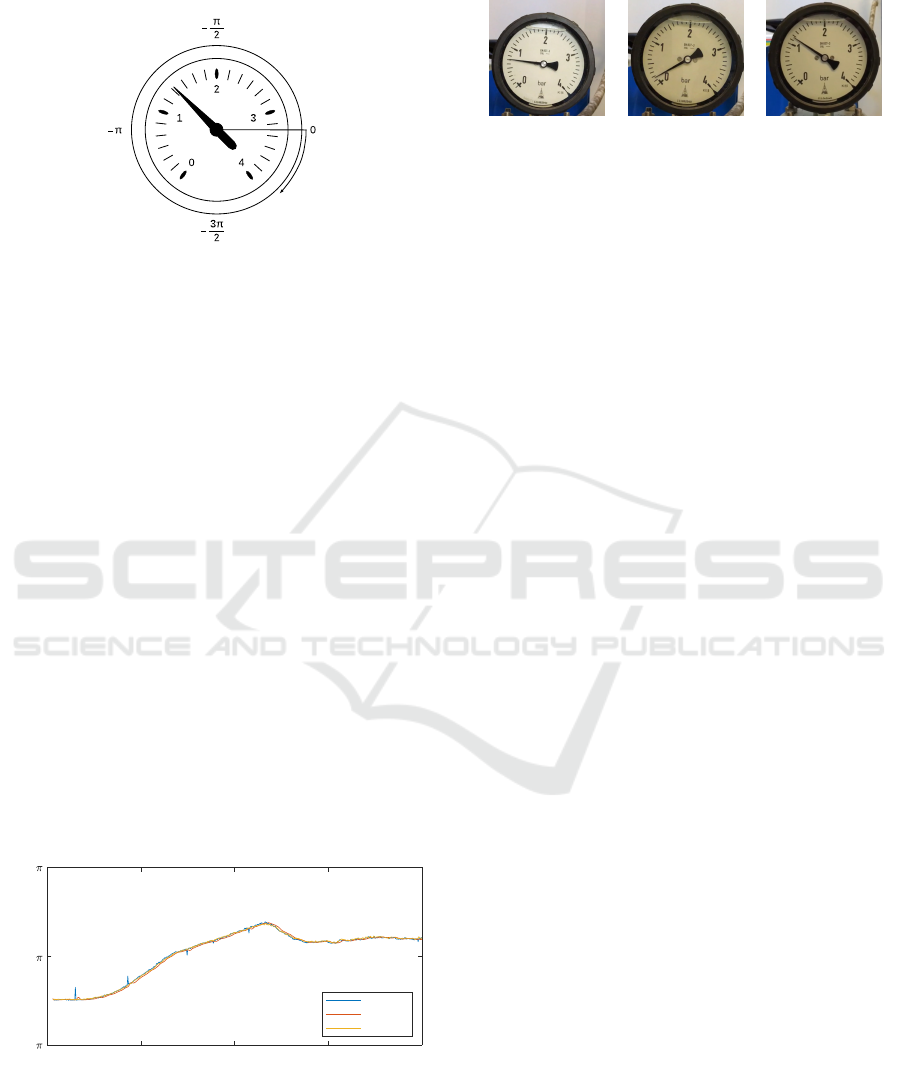
seen in Figure 6, resulting in a time series expressing

the pointer’s angle as a function of time.

Figure 6: Visualization of how the rotation of the pointer is

referenced.

4.5 Data Time Series

As the angle of the pointer can be identiﬁed its tran-

sient behaviour throughout a video can now be consi-

dered. Without any ﬁltering, the pressure time series

becomes noisy as seen in Figure 7. The noise is com-

prised of misinterpreted pointer angles and scenarios

where a direction could not be determined.

Pressure time series recorded manually with digi-

tal pressure sensors from waste water pumping stati-

ons were obtained by consulting [an anonymous en-

gineering company], which specializes in waste water

systems. An FFT of the received time series showed

that the important frequency components were below

1Hz. Therefore, based on the Nyquist–Shannon sam-

pling theorem the frequency resolution should be sa-

tisfactory at a minimum of 2 Hz.

To remove outliers, the 30 Hz recorded signal is

ﬁltered by a tenth-order low pass FIR ﬁlter, which has

a cutoff frequency of 2 Hz. An example of a recorded

time series before and after being ﬁltered is presented

in Figure 7.

0 5 10 15 20

Time [s]

Pointer angle [rad]

Time series

Unfiltered

Filtered

Annotated

Figure 7: Graph illustrating a raw and noisy signal in blue

and its low pass ﬁltered counterpart in red.

5 DATA SET

Figure 8: Images from the train1, train2 and train3 recor-

dings, seen from left to right, respectively.

The data set that has been used consists of 3 training

videos and 7 testing videos of running analog pres-

sure gauges used in the waste water industry. The re-

cordings have been edited to mainly contain the gauge

bezel and scaled to a size of 512 ⊆ 512 pixels. Howe-

ver, the raw videos and additional recorded videos are

also provided in the published data set.

The 3 training videos are recorded under a vari-

ety of conditions to diversify the training set. train1

is stationary with bright lighting, train2 is stationary

with ambient lighting and train3 is hand held with

ambient lighting. Images from the three recordings

can be seen in Figure 8.

The 7 testing videos are edited to match the for-

mat of the training videos and are provided along

with their corresponding annotations. They are na-

med test1, test2, ..., test7 and are all recorded with

a stationary camera under ambient lighting but each

has a unique combination of characteristics, such as

shaking, erratic pointer, angle, water level, bezel re-

ﬂection and light glare that make them relevant to test

against. Images from the seven recordings can be seen

in Figure 9.

6 RESULTS

Figure 12 shows the results of running the algorithm

on test1. The grey dashed lines in the ﬁgure corre-

sponds to a recognized mark in the ﬁrst frame of the

video. The algorithm recognizes scale marks in all

frames, but for visual purposes, only scale marks from

the ﬁrst frame are used. Comparing each measure-

ment of the pointer’s angle to the annotated truth, an

error is assigned.

The histogram plot presented in Figure 10 illustra-

tes the absolute error between the annotated and me-

asured signal in radians. The error is normally distri-

buted with a mean and standard deviation of 0.02 and

0.02 radians, respectively. This low error corresponds

to the pointer being approximately 1 degree offset ac-

cording to the annotated data and in a few cases 2-3

degrees off. The observable negative tail in the nega-

tive area may by caused by periods in test1 where the

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

378

Figure 9: Images from the test1, test2, ..., test7 recordings, seen from left to right, respectively.

Recording: Test1

-0.06 -0.04 -0.02 0 0.02 0.04 0.06

Error [rad]

500

1000

1500

Frequecy [ ]

Figure 10: Histogram of the absolute error between the an-

notated and measured signal of the captured time series of

test1.

pointer is covered or by a periodically present shadow

from the pointer.

In some frames, the implementation of the algo-

rithm fails to produce a meaningful angle of the poin-

ter, at which it gives up and stores NAN as the result.

This is illustrated in Figure 13 that shows the compu-

ted signal from test2 with almost no detected pointer

angles in the last part of the signal.

Figure 14 shows the results of running the propo-

sed algorithm on test3. Here it should be noticed how

the computed angle ﬂuctuates heavily. By inspection

of the annotated data, it can be seen that the pointer

does not change as much as predicted during the given

time periods.

However, as emphasized by Figure 11 a signiﬁ-

cant error occurs at almost exactly ◦π, which is ana-

logue for a half circle rotation. By inspection of the

recorded video it can be seen that the pointer is erratic,

and in some frames the pointy end is nearly invisible

due to heavy motion blur. In those frames the algo-

rithm misjudges the direction of the pointer to be the

blunt end resulting in an error of ◦π radians.

Table 2 shows the number of hits and misses as

well as the mean and standard deviation of the pointer

angle error in radians for the seven test videos. Hits

describe the number of frames where the gauge bezel,

pointer and marks are found such that the angle of the

pointer can be estimated. Misses describe the oppo-

site, where the system is not capable of determining

an angle of the pointer relative to the bezel.

Inspection of test2 and test6 shows that the low hit

rate is due to varying lighting conditions, which is es-

Recording: Test3

-0.3 0 0.3

Error [rad]

200

400

600

800

1000

1200

Frequecy [ ]

Figure 11: Histogram of the absolute error between the an-

notated and measured signal. Notice how there is a signiﬁ-

cant accumulation of erroneous measurements around ◦π.

pecially apparent in the chrome gauge bezels making

them undetectable for the system in large parts of the

recordings.

6.1 Comparison with State-of-the-Art

Over the last couple of decades, many articles have

been published on how to digitise analogue dials

using computer vision and a comparison between the

state-of-the-art methods would, therefore, be appro-

priate. However, even though the meticulousness of

the publications vary, they share the same bad traits

which makes such a comparison difﬁcult to realise.

As presented in the ﬁrst row of Table 1, the data

that have been used for testing the methods generally

consists of images of a single dial, with the excep-

tion of (Jiannan Chi, 2015) and (Yang et al., 2014).

Furthermore, the results are in many cases based on

only a few images taken from the same angle and light

condition (Ye et al., 2013)(Yi et al., 2017)(Sun et al.,

2014)(Jiale et al., 2011)(Wang et al., 2013). This me-

ans that, even though the results may be good, there

is a high possibility that the methods have been over-

ﬁtted to their respective setups. Lastly, none of the

authors has published their source code or test data,

so it is not possible to replicate their ﬁndings.

In order to create a foundation for future bench-

marking tests and comparisons, the entire source code

used for the presented work is published along with

the raw and edited test and training videos.

Reading Circular Analogue Gauges using Digital Image Processing

379

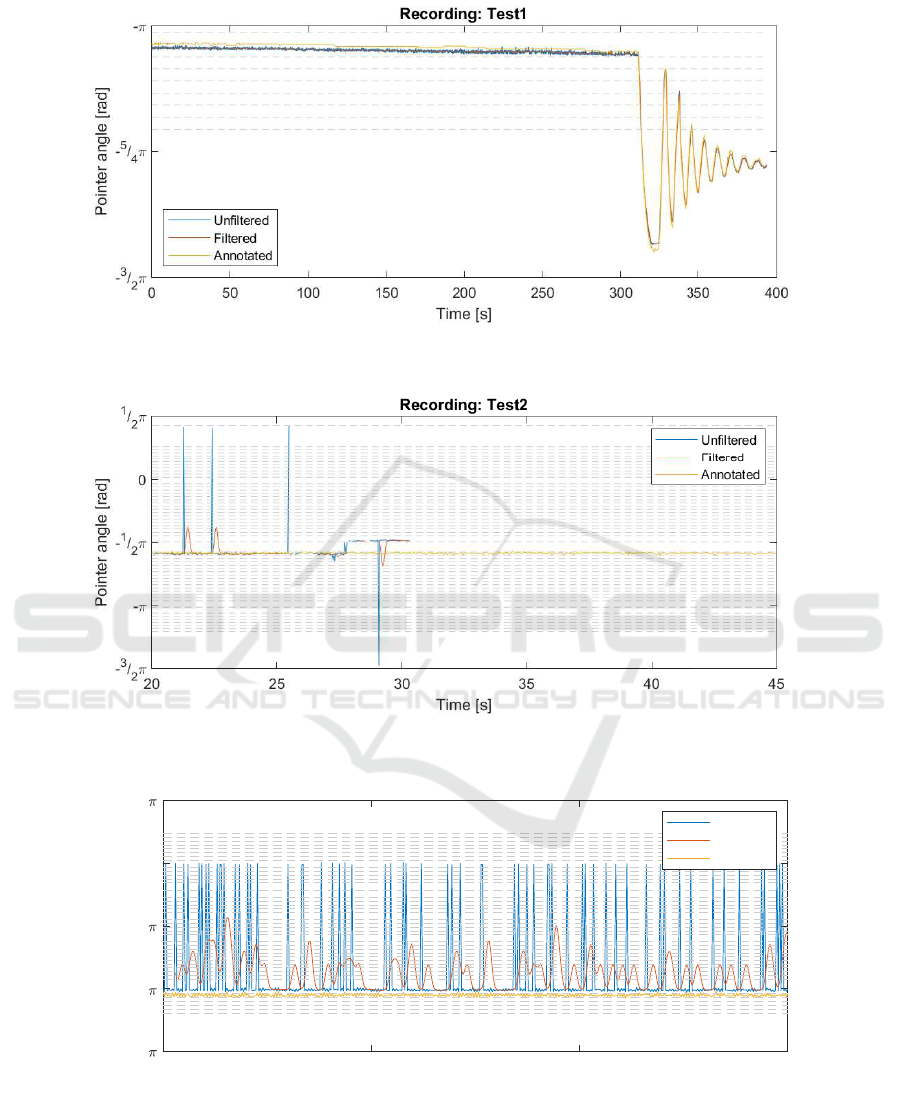
Figure 12: Time series captured by processing test1 using the proposed method. Notice how the measured pointer angle is

closely related to the annotated angle throughout the recording.

Figure 13: Results from performing the algorithm on test2. The system fails to produce any meaningful angle of the pointer

in a signiﬁcant amount of frames.

0 5 10 15

Time [s]

Pointer angle [rad]

Recording: Test3

Unfiltered

Filtered

Annotated

Figure 14: Results from performing the algorithm on test3. The measured signal jumps incorrectly from ◦π to 0 often. This

is due to motion blur of the pointer in test3.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

380

Table 1: Overview of state-of-the-art methods with regards to accessibility and the number of dials involved in the work.

J. Chi X. Ye C. Zheng M. Yi B. Sun H. Jiale B. Yang Q. Wang Proposed

No. of Dials 2 1 1 1 1 1 8 1 10

Open Source No No No No No No No No Yes

Public Data No No No No No No No No Yes

Table 2: Classiﬁcation and error rate of the proposed met-

hod when processing the seven test videos.

Hit Miss µ [rad] σ [rad]

test1 11811 0 0.02 0.02

test2 967 1253 -0.47 1.28

test3 1801 0 -0.42 0.39

test4 1111 0 0.08 0.32

test5 451 0 -0.12 0.39

test6 347 704 -6.07 0.56

test7 571 2 -0.13 0.61

7 CONCLUSION

A method to automatically digitize analog circular

gauges using computer vision is presented with an ap-

plication example of a video recording of a pressure

gauge translated into a digital time series.

The method is based on segmenting objects in

each frame using Gaussian adaptive mean threshol-

ding and subsequently classifying the objects using

probability distributions estimated with the unsuper-

vised learning method Expectation Maximization.

The output of the algorithm is an estimated angle of

the pointer object, which is determined using PCA.

Recordings of seven pressure gauges, mounted on

waste water pumping stations, have been processed

by the algorithm. The mean and standard deviation of

the angle error are calculated for each of the videos

with the best case of µ 0.02 radians and σ 0.02

radians.

However, in three of the recordings, signiﬁcant er-

rors are present. In test2 and test6 the bezel is made

from a reﬂective material, which makes it difﬁcult to

segment objects properly with the proposed method

due to reﬂections. In another case, a problem is iden-

tiﬁed where the angle of the pointer is miscalculated

by ◦π radians due to motion blur.

The shortcomings that have been uncovered in the

tests are related to speciﬁc scenarios, which should be

taken into consideration during the next iteration of

the project. Generally, the results are very promising

and there is a great potential in the proposed parame-

tric classiﬁcation method.

The source code is published at (Lauridsen and

Grassmé, 2018a) and the test and training data is pu-

blished at (Lauridsen and Grassmé, 2018b).

8 FUTURE WORK

The current system only processes a single frame at

a time, neglecting the beneﬁts that might arise from

utilizing data from neighbouring frames. As an ex-

ample, to achieve better estimates for the circle, cen-

ter or for more accurate scale creation the temporal

neighboring data could be utilized. This could also be

used to reduce the errors introduced by motion blur,

where the angle is incorrectly determined by the blunt

end of the pointer.

Exploring other features, higher feature spaces or

other compositions could possibly increase the accu-

racy and make the proposed solution more robust.

The training data could also be more diverse in order

to better generalize to different types of dials. Lastly,

the level of automation can be improved by recogni-

zing the dial numbers and associating those numbers

to the scale marks.

REFERENCES

Alegria, F. C. and Serra, A. C. (2000). Computer vision

applied to the automatic calibration of measuring in-

struments. Measurement, 28(3):185 – 195.

Bishop, C. M. and Nasrabadi, N. M. (2007). Pattern Recog-

nition and Machine Learning. Journal of Electronic

Imaging, 16(4):049901.

Crawford, J. (1983). A non-iterative method for ﬁtting ci-

rcular arcs to measured points. Nuclear Instruments

and Methods in Physics Research, 211(1):223–225.

Gellaboina, M. K., Swaminathan, G., and Venkoparao, V.

(2013). Analog dial gauge reader for handheld devi-

ces. In 2013 IEEE 8th Conference on Industrial Elec-

tronics and Applications (ICIEA). IEEE.

Jiale, H., En, L., Bingjie, T., and Ming, L. (2011). Reading

recognition method of analog measuring instruments

based on improved hough transform. In IEEE 2011

10th International Conference on Electronic Measu-

rement Instruments, volume 3, pages 337–340.

Jiannan Chi, Lei Liu, J. L. Z. J. G. Z. (2015). Machine

vision based automatic detection method of indicating

values of a pointer gauge. In Mathematical Problems

in Engineering, Article ID 283629, volume 2015.

Lauridsen, J. S. and Grassmé, J. G. (2018a). Bit-

bucket pressure gauge reader source code.

https://bitbucket.org/aauvap/pressure-gauge-reader

[Link].

Reading Circular Analogue Gauges using Digital Image Processing

381

Lauridsen, J. S. and Grassmé, J. G. (2018b).

Kaggle pressure gauge reader data set.

http://kaggle.com/juliusgrassme/pressure-gauge-

reader-data [Link].

Sablatnig, R. and Kropatsch, W. G. (1994). Automatic re-

ading of analog display instruments. In Proceedings

of 12th International Conference on Pattern Recogni-

tion, volume 1, pages 794–797 vol.1.

Selvathai, T., S, J. S., Ramesh, S., and KK, R. (2017). Auto-

matic interpretation of analog dials in driver's instru-

mentation panel. In 2017 Third International Confe-

rence on Advances in Electrical, Electronics, Informa-

tion, Communication and Bio-Informatics (AEEICB).

IEEE.

Sun, B., Zhang, C., Liu, Z., Qian, B., and Zhang, H. (2014).

Study of fpga-based visual detection for pointer dial.

In The 26th Chinese Control and Decision Conference

(2014 CCDC), pages 1467–1472.

Wang, Q., Fang, Y., Wang, W., Wu, M., Wang, R., and Fang,

Y. (2013). Research on automatic reading recogni-

tion of index instruments based on computer vision.

In Proceedings of 2013 3rd International Conference

on Computer Science and Network Technology, pages

10–13.

Yang, B., Lin, G., and Zhang, W. (2014). Auto-recognition

method for pointer-type meter based on binocular vi-

sion. JCP, 9(4):787–793.

Ye, X., Xie, D., and Tao, S. (2013). Automatic value iden-

tiﬁcation of pointer-type pressure gauge based on ma-

chine vision. JCP, 8:1309–1314.

Yi, M., Yang, Z., Guo, F., and Liu, J. (2017). A clustering-

based algorithm for automatic detection of automo-

bile dashboard. In IECON 2017 - 43rd Annual Confe-

rence of the IEEE Industrial Electronics Society, pa-

ges 3259–3264.

Zheng, C., Wang, S., Zhang, Y., Zhang, P., and Zhao, Y.

(2016). A robust and automatic recognition system of

analog instruments in power system by using compu-

ter vision. Measurement, 92:413 – 420.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

382