Evaluation of Spatial-Temporal Anomalies in the Analysis of Human

Movement

Rui Varandas

, Duarte Folgado

and Hugo Gamboa

Associac¸

ao Fraunhofer Portugal Research, Rua Alfredo Allen 455/461, Porto, Portugal

Laborat

orio de Instrumentac¸

ao, Engenharia Biom

edica e F

ısica da Radiac¸

ao (LIBPhys-UNL), Departamento de F

ısica,

Faculdade de Ci

encias e Tecnologia, FCT, Universidade Nova de Lisboa, 2829-516 Caparica, Portugal

Keywords:

Time Series, Anomaly Detection, Human Motion, Unsupervised Learning, Industry.

Abstract:

In industrial contexts, the performed tasks consist of sets of predetermined movements that are continuously

repeated. The execution of improper movements and the existence of events that might prejudice the produc-

tive system are regarded as anomalies. In this work, it is proposed a framework capable of detecting anomalies

in generic repetitive time series, adequate to handle human motion from industrial scenarios. The proposed

framework consists of (1) a new unsupervised segmentation algorithm; (2) feature extraction, selection and di-

mensionality reduction; (3) unsupervised classiﬁcation based on Density-Based Spatial Clustering Algorithm

for applications with Noise. The proposed solution was applied in four different datasets. The yielded results

demonstrated that anomaly detection in human motion is possible with an accuracy of 73±19%, speciﬁcity of

74 ± 21% and sensitivity of 74 ± 35%, and also that the developed framework is generic and may be applied

in general repetitive time series with little adaptation effort for different domains.

1 INTRODUCTION

Anomalies consist of events that do not properly con-

form to the expected behaviour of a given dataset.

Anomaly detection has been widely studied and ap-

plied in diverse domains, such as electrocardiogram

(ECG) signals, video from surveillance cameras and

stock markets (Chandola et al., 2009). The impor-

tance of anomaly detection lies in the fact that such

events are usually associated with defective processes

that might cause failures in the future. Taking the ex-

ample of ECG signals, anomalies might be associated

to cardiac arrhythmias, which may be an early or ac-

tual indicative of heart diseases.

The increasing demands of Industry 4.0 require

highly customised products and adaptive manufactur-

ing systems. The detection of unplanned or planned

anomalies in Human movement on industrial produc-

tion lines is a valuable asset for production control

systems. This information is able to deliver intelli-

gence regarding occurrences that might prejudice the

productive process, reducing the overall productivity

and compromising ergonomics and safety at work.

Furthermore, the monitoring of human motion in such

environments allows to detect predetermined move-

ments that the operators are instructed to follow in or-

der to improve production and ergonomic conditions.

Therefore, an anomaly may consist of wrongly per-

formed movements, which may prejudice ergonomic

conditions and improve the risk of appearance of mus-

culoskeletal disorders.

The Human movement in Industrial scenarios can

be monitored using inertial sensors, which provide

tridimensional motion information. For each task as-

sociated with a given workstation on a production

line, there is a well-deﬁned method that must be fol-

lowed to accomplish it. However, since methods

vary according to the workstation, the repetitive iner-

tial data might exhibit different morphologies despite

maintaining the quasi-periodic behaviour.

2 RELATED WORK

Anomaly detection has been the target of extensive

research and various surveys were already published

(Teng, 2010; Chandola et al., 2009).

For instance, HOT SAX is a method based on the

SAX representation, developed in (Thuy et al., 2018),

to ﬁnd discords which are sequences that are the most

dissimilar to its k nearest neighbours. Therefore, this

algorithm, is able to ﬁnd anomalies in time series, but

Varandas, R., Folgado, D. and Gamboa, H.

Evaluation of Spatial-Temporal Anomalies in the Analysis of Human Movement.

DOI: 10.5220/0007386701630170

In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 163-170

ISBN: 978-989-758-353-7

163

it is necessary to know the number of anomalies to be

found a priori.

In (Ren et al., 2017), it was developed the PAPR

representation method coped with the construction of

a Random Walk model with the intent to search for

anomalous patterns in time series. The proposed al-

gorithm was tested in 14 different real world datasets

and compared with the PAA method, achieving higher

results. While PAA method detected 15 anomalies,

PAPR associated with Random Walk (PAPR-RW) al-

gorithm was able to detect 25 anomalies out of 27,

and so, the sensitivity is approximately 92%.

There are numerous other examples of anomaly

detection in time series, such as, network source data

(Chen and Li, 2011), gait analysis (Cola et al., 2015),

streaming data (Ahmad et al., 2017), ECG signals

(Ren et al., 2017), in which arrhythmias may be

viewed as anomalies, and detection of mental stress

(Huysmans et al., 2018), in which case, stress states

may be considered anomalous.

Most mentioned methods, though being adequate

for particular applications, lack the capability of be-

ing applicable in different domains. Furthermore, the

methods that may be applied to various domains, ei-

ther need high numbers of parameters or the required

parameters are difﬁcult to assess, for example the

number of anomalies to detect.

This work comprises the development of a novel

framework for anomaly detection applied to domain-

independent repetitive time series, requiring a low

number of parameters to be selected and in which, the

parameters have physical meaning, facilitating their

estimation. This approach is indicated in our con-

text, because in manufacture environments, different

workstations involve different methods, which results

in different repetitive patterns. Thus, it is able to

cope with different time series domains with mini-

mum adaptation effort. In order to achieve this, our

work presents two major contributions: (1) a new un-

supervised segmentation algorithm for quasi-periodic

time series, which is able to extract repetitive units

from those time series, and (2) an unsupervised learn-

ing approach that relies on an exhaustive set of fea-

tures to provide anomaly detection. The proposed

framework was validated on 4 datasets from different

domains, comprising both synthetic and real data.

3 PROPOSED APPROACH

Anomalies are data points or groups of data points

that do not conform well to the whole dataset. Given

a time series X = {x

, x

, ..., x

}, it is possible to seg-

ment it in M subsequences as

X = {S

, S

, ..., S

} (1)

where each S

, i ∈ {1, 2,..., M} is a subsequence of X

composed of a deﬁned number of data points, that

may vary from segment to segment and each x

,t ∈

{1, 2,..., N} is a measurement at instant t, where N is

the total number of data points. Therefore, the time

series may be represented as

X = {{x

, ..., x

}, ..., {x

M−1

, ..., x

}} (2)

The analysis of each subsequence is usually accom-

plished using a cost function that may indicate dis-

tance or density, for instance. Thus, a subsequence S

is anomalous if

f (S

, S

) > δ ∀ j ∈ [1 : M] (3)

where S

may correspond to all subsequences except

, a model of a normal pattern, or a set of rules that

must obey to be considered a normal segment. The

value of f (S

, S

) is the anomaly score, which can be

considered the anomaly degree of S

and expresses the

amount of dissimilarity to the model. The deﬁnition

of the threshold, δ, controls the sensitivity of each al-

gorithm.

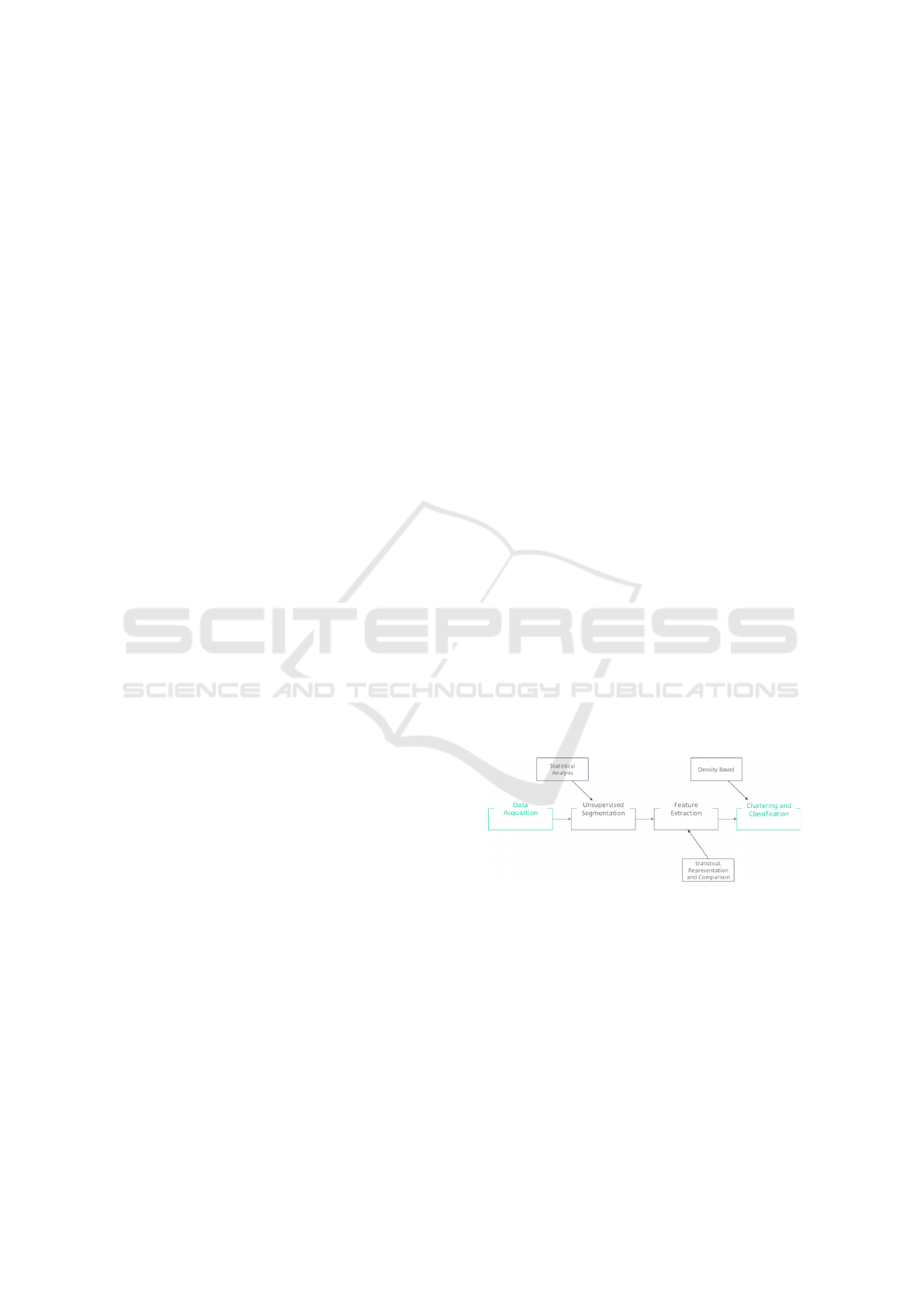
The proposed approach, illustrated in Figure 1,

starts with the application of an unsupervised seg-

mentation algorithm used to extract each cycle from

a repetitive time series. Then, each extracted cycle is

represented by a set of features, followed by a process

of dimensionality reduction using Principal Compo-

nent Analysis. Finally, the transformed feature vector

will be the input for a density based clustering algo-

rithm - DBSCAN.

Figure 1: Diagram of the proposed approach.

3.1 Unsupervised Segmentation

In order to extract cycles from generic repetitive time

series, it was developed a new unsupervised segmen-

tation algorithm, capable of segment time series with-

out prior knowledge about their morphology, period

of repetition or number of cycles, hence, it is consid-

ered dictionary-free.

The developed algorithm is divided into two sep-

arate parts. The ﬁrst part consists of iteratively seg-

menting a given time series in shorter portions, in a

BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing

164

top-down fashion. Starting with k segments, in which

its limits are constrained to be local minima in a spec-

iﬁed range, the progression of the number of itera-

tions results in an increase of the number of segments.

Then, each segment is represented by its mean value,

thus, each iteration is associated with the set of means

of its segments. Each iteration is then represented by

the standard deviation of the set of means.

The main assumption is that in an ideal cyclic sig-

nal, the mean of each cycle is identical to the rest,

therefore, each value in the set of means is equal to

the average value of the set of means, leading to a

standard deviation of 0 (

= ... =

=⇒

= 0, where

, i ∈ {1, ..., M} are the mean values

of each subsequence of a given iteration a,

is the

mean value of the set of means of iteration a and σ

is the standard deviation of the set of means of the

corresponding iteration).

The second part of the developed algorithm is

based on the function of standard deviation vs iter-

ation. The iterations correspondent to local minima

of that function, depicted in the right pane of Figure

2, are selected, as they correspond to the iterations

in which the value of standard deviation decreases,

which means that the segments are more similar.

With those iterations, it is computed the Pearson’s

Correlation Coefﬁcient between each segment and the

rest. Then, each segment is represented by the mean

value of those coefﬁcients and each iteration is repre-

sented by the mean of the representation of its cycles.

Hence, the value that represents each iteration is

restricted to [−1, 1]. The selection of the correct seg-

mentation is based on this value and corresponds to

the iteration with the highest value, meaning that most

segments are highly correlated to all others.

3.2 Feature Extraction and

Dimensionality Reduction

In this work, a comprehensive range of statistical fea-

tures, representation transforms and comparison met-

rics, was used and is summarised in Table 1.

While statistical features and representation trans-

forms are applied for representing each subsequence,

comparison metrics are used to compare each subse-

quence to the total number of subsequences of the

time series. Anomalous subsequences will have a

higher dissimilarity to normal instances, while the

normal subsequences will have a high similarity to

normal instances.

Following feature extraction, the set of features

selected by the user are scaled using a z-score normal-

isation and then transformed by the computation of its

Principal Components, and only the components with

Table 1: Statistical features, representation transforms and

comparison metrics used in this work.

Statistical Features Representation Transforms Comparison Metrics

- Mean Value

- Standard Deviation

- Minimum Value

- Maximum Value

- Inter-Quartile

Range (IQR)

- Number of Peaks

- Median

- Kurtosis

- Skewness

- Duration

Linear Regression

(slope and y-intercept)

- Zero Crossing Rate

- Polarity

- Cumulative Summation

- Histogram

- Fourier Transform

- Wavelet Transform

- Principal Component

Analysis Transform

- Independent Component

Analysis Transform

- PAA in the Amplitude

Domain (AD-PAA)

(Ren et al., 2018)

- PAPR (Ren et al., 2017)

- Subsegment Analysis

- Euclidean Distance

- Dynamic Time

Warping Distance

(DTW)

- Time Alignment

Measurement (TAM)

(Folgado et al., 2018)

- Pearson’s Correlation

Coefﬁcient (PCC)

- Cosine Similarity

variance higher than 0,95 are kept for clustering and

classiﬁcation.

3.3 Clustering and Classiﬁcation

After feature extraction and dimensionality reduction,

the resulting set of features is introduced as the input

for an unsupervised clustering algorithm - DBSCAN

(Ester et al., 1996).

In order to cluster data points, DBSCAN takes two

hyper-parameters, ε and θ. Based in those parameters,

there are three types of data points: core points, which

are the points that have, at least, a number of θ data

points within a range of ε; density-reachable points,

which are points that belong to the neighbourhood of

a core point, that is, are at a distance lower than ε to a

core point, but do not have a number of θ data points

within ε; noise, which are the points that do not have a

number of θ data points within ε and are not density-

reachable points.

DBSCAN is able to cluster data based on its den-

sity, but it does not classify each data point. The

classiﬁcation was performed based on the follow-

ing considerations: given that the input to the algo-

rithm are the features extracted and transformed from

each segment representing the samples, if the num-

ber of segments considered to be anomalous is higher

than the number of segments classiﬁed as normal, the

value of ε increases by 10% and the clustering pro-

cess is performed again. This process is repeated un-

til the number of normal instances is higher than the

number of anomalous instances. Furthermore, noise

points are always regarded as anomalous and, in cases

when there is more than one cluster, only the cluster

with highest number of points is considered normal.

This last consideration is important in cases in which

anomalies may be similar, thus forming clusters of

their own, such as arrhythmias in ECG signals.

Evaluation of Spatial-Temporal Anomalies in the Analysis of Human Movement

165

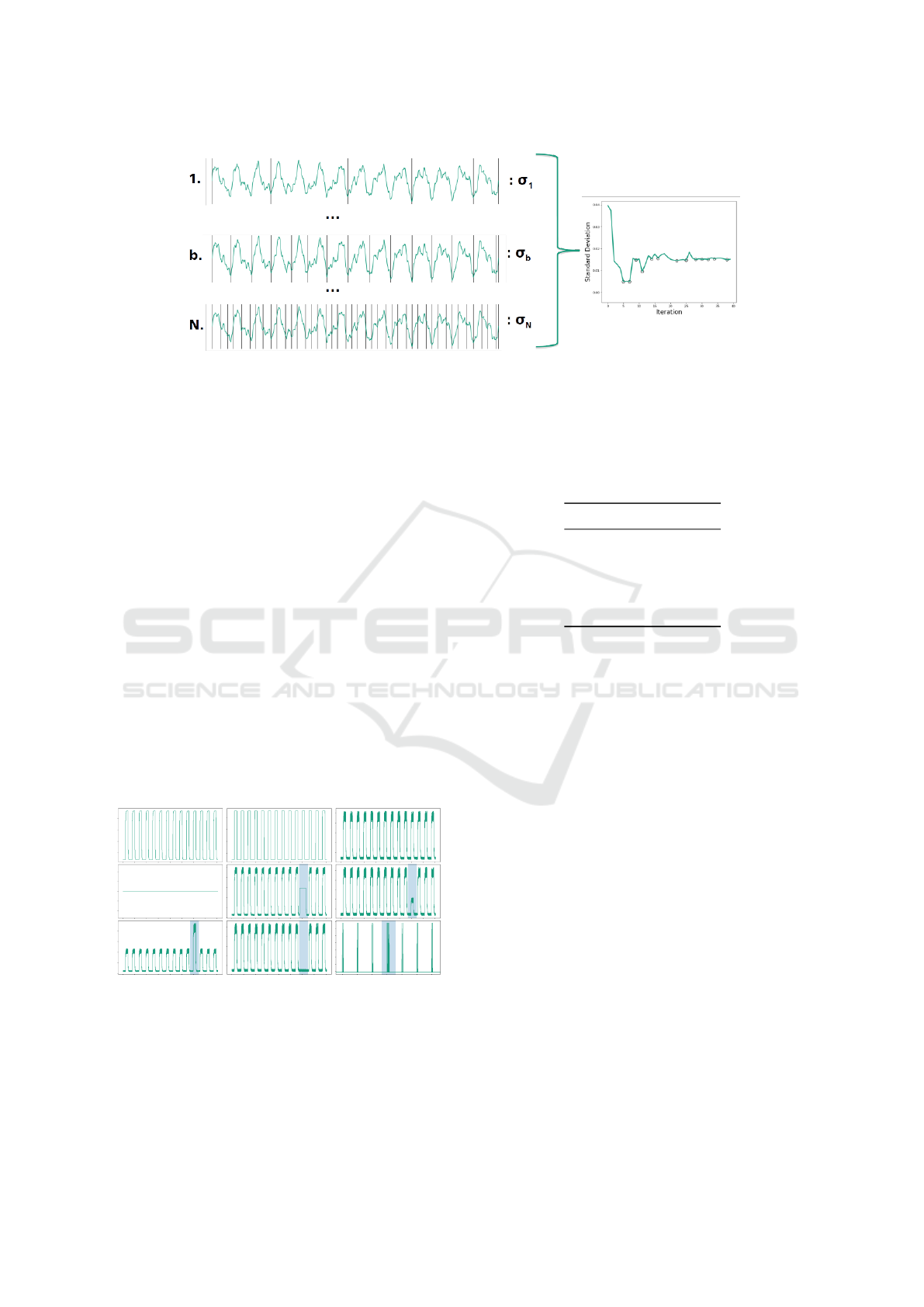
Figure 2: Top-down process of segmentation. Firstly, the time series is segmented in k parts. Then, with each iteration, the

number of segments increases and in each iteration the mean of each segment is computed. Each iteration is represented by

the standard deviation of the set of means of its segments forming a curve such as in the image in right. The negative inﬂexion

points are chosen for the rest of the process. Iteration b corresponds to the correct segmentation and N corresponds to the last

iteration.

4 RESULTS

The validation of the proposed framework was made

with resource to four datasets, two synthetic and two

composed of real-world data in order to demonstrate

the potential of minimum effort application to differ-

ent domains.

4.1 Numenta Anomaly Benchmark

The ﬁrst dataset is composed of 9 artiﬁcial signals

from Numenta Anomaly Benchmark (NAB) (Ahmad

et al., 2017), illustrated in Figure 3, which was created

to test an algorithm developed by Numenta, the Hier-

archical Temporal Memory (HTM). Since the dataset

comprises different types of anomalies, we only se-

lected the ones which fulﬁlled the three assumptions

made by the proposed framework.

Figure 3: Numenta Anomaly Benchmark selected signals.

The four initial signals do not present anomalies and, in the

others, the existing anomalies are identiﬁed by blue shades.

The results obtained for this dataset are shown in

Table 2.

These results were obtained using mean, max-

imum, minimum, median, inter-quartile range and

Table 2: Results of anomaly detection using the Numenta

Anomaly Benchmark.

Metric Value (%)

Accuracy 99, 3

Speciﬁcity 99, 3

Sensitivity 100, 0

Precision 83, 3

F1 score 90, 9

skewness values as the input vector followed by the

procedures described in Section 3. The choice of the

parameters to use in DBSCAN was performed empir-

ically by observing the results and tuning the param-

eters in order to optimise the achieved results. This is

not ideal, because in real life scenarios it is imprac-

ticable to tune the parameters to new signals without

prior knowledge about them. Nevertheless, the pa-

rameters are the same for all signals: θ = 5; ε = 5.

The results show an overﬁtting scenario due to

the optimisation of the parameters that took into ac-

count all signals. Nevertheless, it is important to point

out that the accuracy is not a good metric to assess

the quality of classiﬁcation in an unbalanced dataset,

which contains a considerate higher number of nor-

mal segments than anomalous. For example, in the

considered dataset, there are 147 segments and only

5 of them are anomalous. Thus, classifying all seg-

ments as normal, would give an accuracy of 96,6%,

but the classiﬁer would be useless for anomaly de-

tection. Thus, the most appropriate metrics to study

such scenarios are sensitivity, precision and F1 score.

In this case, all metrics show high results except for

precision, because there was 1 false positive, mean-

ing that 5 positives were correctly classiﬁed among 6

detected positives.

BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing

166

4.2 Pseudo Periodic Synthetic Time

Series

The Pseudo Periodic Synthetic Time Series dataset

was made publicly available by the Center for Ma-

chine Learning and Intelligent Systems of the Bren

School of Information and Computer Science of the

University of California (Dheeru and Karra Taniski-

dou, 2017). It is composed of 10 artiﬁcial signals

composed of 100.000 data points each. These signals

are repetitive, but the cycles are not exactly alike.

These facts make this dataset suitable for testing

the proposed framework, but there is a crucial as-

pect lacking to these signals, which is the presence of

anomalies. Thus, it was generated a set of synthetic

anomalies on amplitude (e.g. noise addition, multipli-

cation by scale vector) and temporal (e.g. nonlinear

temporal distortion) domains. Those anomalies were

randomly introduced in the dataset in a controlled

fashion. This procedure resulted in data augmentation

from 10 to 500 signals, being able to generate a wide

range of different anomaly types in different instants

of the signal.

The results are presented in Table 3. In order

to minimise the inﬂuence of overﬁtting, the hyper-

parameter optimisation was only applied to a small

percentage of data. Therefore, in the validation step,

the majority of data being used was never been sub-

ject to the optimisation procedure. Although this pro-

cedure reduces metric performance, it is more appro-

priate and allows to understand the full extension of

application in real scenarios. The best results were

obtained using the details of the wavelet transform,

in which the mother wavelet was chosen to be of the

family of Daubechies of third order, using θ = 5; ε =

0, 001.

Table 3: Results (mean ± standard deviation) for pseudo-

periodic signals dataset.

Metric Value (%)

Accuracy 91, 6 ±5, 8

Speciﬁcity 91, 9 ± 5, 2

Sensitivity 88 ± 28

Precision 52 ± 19

F1 score 64 ± 23

The results are lower than those obtained for NAB

dataset. This is due to the fact that the anomalies

are not as explicit as the ones in NAB and the fact

that hyper-parameter tuning was performed on a small

percentage of data. Speciﬁcally, the value of pre-

cision of 52% is low due to the fact that anomalies

may be spread across segments, but could not occupy

a whole segment. Thus, given that the classiﬁcation

was made in terms of segments, a segment containing

an anomaly could have normal parts, which would be

wrongly classiﬁed and are considered false positives,

thus reducing the precision.

However, the results are more representative in

terms of generalisation, which is an essential charac-

teristic of machine learning applications.

4.3 MIT BIH Arrhythmia Database

MIT BIH arrhythmia database (Goldberger et al.,

2000) is a dataset composed of real world ECG

recordings acquired in ambulatory. Electrocardiog-

raphy signals represent the measurement of the elec-

trical pulse that propagates through the cardiac mus-

cle in order to stimulate it, resulting on its normal be-

haviour, which enables the entry and exit of blood to

and from the heart. This normal behaviour may be af-

fected by various factors, resulting in the existence of

cardiac arrhythmias.

The referred dataset is composed of both normal

and anomalous heartbeats totalling 110.000 heart-

beats. Each heartbeat was labelled by two specialist

concerning the position of the R peak and its classiﬁ-

cation regarding the classiﬁcation in various types of

arrhythmia.

The R peak annotations were used to segment the

signals in order to guarantee a correct segmentation.

Therefore, a segment consisted of a portion of a signal

from the R peak less 100 data points until the next R

peak minus 100 points.

Moreover, it was applied a Butterworth band-pass

ﬁlter of second order in order to attenuate frequencies

lower than 1 Hz and higher than 20 Hz, enabling to

reduce interference from normal respiratory frequen-

cies, and muscular and digital noise, respectively.

The results are presented in Table 4. The best

features were duration, polarity, linear regression and

maximum value of each heartbeat. Unlike the ﬁrst

two datasets, and because the number of heartbeats

(cycles) per signal is signiﬁcantly higher than in the

previous datasets, it was possible to use the k-Nearest

Neighbour (k-NN) curve to estimate ε, used by the

DBSCAN algorithm, automatically for each signal,

given a ﬁxed θ. Thus, using θ = 5, ε was speciﬁc

for each signal.

The performance metrics reveal that real world

electrophysiological signals have considerably more

complex structures and in which anomalies may oc-

cur in several forms. These results are representa-

tive about the accuracy score, which is high, but F1-

score is low. This means that, the great majority of

the dataset is correctly classiﬁed, but that is because

Evaluation of Spatial-Temporal Anomalies in the Analysis of Human Movement

167

Table 4: Results (mean ± standard deviation) for anomaly

detection for the MIT BIH arrhythmia database.

Metric Value (%)

Accuracy 89 ± 12

Speciﬁcity 92 ± 10

Sensitivity 82 ± 30

Precision 41 ± 33

F1 score 44 ± 33

most normal cycles are considered normal, but several

anomalous cycles are wrongly classiﬁed, which low-

ers the value of sensitivity. However, it is notable the

low adaptation effort needed to apply the developed

generic framework to such a speciﬁc domain such as

ECG signals.

4.4 Human Motion on Industrial

Scenario

Human motion on industrial scenario (HMIS) dataset

was acquired by the authors in a real industrial en-

vironment with resource to a wearable sensor, that

was integrated into bracelets and placed on employ-

ees’ dominant upper member. This placement al-

lowed to monitor the wrist’s movement performed by

each monitored employee, which is relevant once the

tasks performed involve predominantly upper mem-

ber movements.

The sensing device contains an Inertial Measure-

ment Unit (IMU), which measures inertial data with

resource to three sensors: an accelerometer, a gyro-

scope and a magnetometer. The combination of the

three sensors allows a full comprehensive analysis re-

garding the movement of the monitored employee.

Figure 4 shows an example of the measured inertial

data from a single employee. The black vertical lines

indicate the beginning/ending of a work cycle and the

red part is an example of an anomaly in this context,

which corresponds to a signiﬁcant deviation in terms

of morphology in relation to other cycles (the phe-

nomenon is more evident in magnetometer data).

The device was connected via Bluetooth LE to

a smartphone, where the data was stored. Each

recorded acquisition was annotated in real-time at the

beginning of each new cycle and in every occurrence

of anomalies, allowing to build the ground-truth seg-

mentation and labelling.

The acquired data consists of inertial data orig-

inated by the movements performed by 4 different

workers at 3 different workstations where they were

producing different items. All tasks monitored were

repetitive which made them suitable to be tested with

the developed anomaly detection framework. The

sampling frequency of the acquisitions was approx-

imately 100Hz and the total time of the acquisitions

is around 4 hours and 20 minutes.

Moreover, once the number of cycles per signal

varies widely, it was not possible to use the k-NN

curve directly in order to estimate them. The fol-

lowed approach was inspired by the Leave-One-Out

cross validation that is used to test algorithms in the

presence of a low number of instances. Given N sig-

nals, we calculate the parameters for every signal, ex-

cept the signal under evaluation, with resource to the

k-NN curve and then use the mean value of the es-

timated values for the untested signal. This process

was repeated for each signal allowing for an objective

test without inﬂuence from a human observer.

Table 5 summarises the results of anomaly de-

tection using two different methods for time series

segmentation in work cycles: groundtruth annota-

tions and the proposed unsupervised segmentation

algorithm. The results suggest that both methods

have similar performance. The use of the unsuper-

vised segmentation does have signiﬁcant advantages

on real-world deployment as it does not require user

intervention in the overall process.

Table 5: Inﬂuence of unsupervised segmentation on

anomaly detection of human motion inertial data. The re-

sults (mean ± standard deviation) are reported in terms of

percentage (%).

Metrics

Groundtruth

Segmentation

Unsupervised

Segmentation

Accuracy 73 ± 19 71 ± 16

Speciﬁcity 75 ± 22 74 ± 18

Sensitivity 52 ± 45 52 ± 36

Precision 18 ± 23 20 ± 24

F1 score 19 ± 25 20 ± 20

Since previous results suggest that it is feasible

to use the unsupervised segmentation algorithm, the

next step consisted of a comprehensive evaluation

of the features used to describe the detected subse-

quences and thus, able to differentiate between nor-

mal and anomalous instances. Table 6 presents the

results obtained using each feature earlier described

in Table 1. The results show that feature selection in-

ﬂuences the outcome of the clustering algorithm.

The achieved results have overall low perfor-

mance in comparison with previous datasets due

to some factors that will be properly discussed.

Firstly, the process for hyper-parameter optimisation

of DBSCAN algorithm was different from previous

datasets. In the NAB and Pseudo Periodic datasets the

hyper-parameters were speciﬁed and optimised by the

user; in the MIT BIH arrythmia database they were

BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing

168

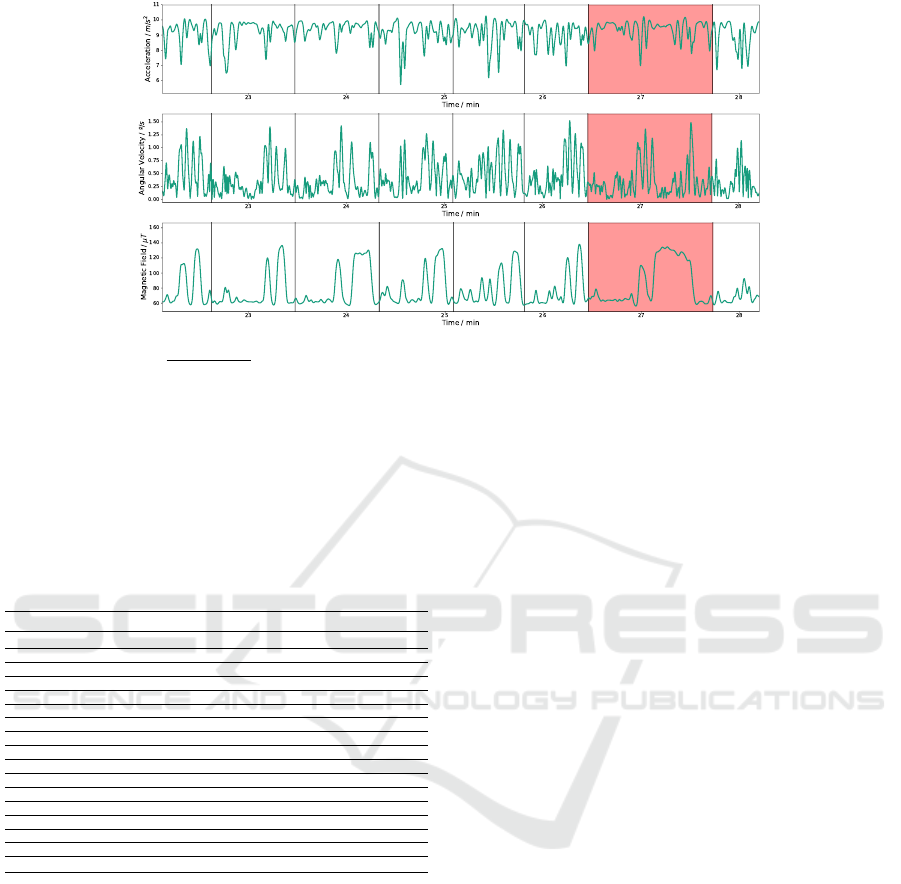
Figure 4: Excerpt of inertial data from a single operator. Each sensor is represented by the magnitude of the three axis x, y

and z (magnitude =

+ y

+ z

). Each plot corresponds to accelerometer, gyroscope and magnetometer data, respectively,

from top to bottom. The black vertical lines indicate the beginning/ending of a work cycle and the red part corresponds to an

anomaly. The anomaly is more evident in magnetometer data.

Table 6: Inﬂuence of feature selection on anomaly detec-

tion of human motion inertial data. The results (mean ±

standard deviation) are reported in terms of percentage (%).

(In the ﬁrst line, the set of features correspond to the mean,

maximum, minimum, IQR, standard deviation, number of

peaks, median, kurtosis, duration, skewness and linear re-

gression).

Features Accuracy Speciﬁcity Sensitivity Precision F1-score

Set of Features 73 ± 19 74±21 74 ± 35 24± 30 30 ± 31

ICA 89 ± 13 96± 11 9 ±28 23 ± 24 6 ± 17

DTW 72 ± 18 77± 21 53 ± 44 15 ± 13 17± 18

TAM 70 ± 19 70± 22 72 ± 41 17 ± 24 23± 28

Fourier Transform 74 ± 16 80 ±19 28 ±34 14 ± 22 13± 17

Polarity 70 ± 17 77 ± 21 38 ± 48 5, 3± 9, 3 8 ± 14

Cumulative Summation 75 ± 20 80 ± 24 28 ± 45 7 ± 12 7 ± 15

Wavelet Approximation 80 ± 23 82 ± 28 40 ±52 20 ± 26 15 ±27

Wavelet Details 65 ± 18 64 ± 22 67 ± 47 14 ± 17 20 ±23

Cosine Similarity 77 ± 21 78 ± 24 53 ± 47 25 ±24 22 ± 28

PCA 75 ± 20 75 ± 25 53 ± 48 20 ±17 19 ± 23

AD-PAA 74 ± 18 75 ± 20 59 ± 47 23 ±29 29 ± 33

Histogram 65 ± 20 65 ± 21 74 ± 32 25 ±30 30 ± 31

Euclidean Distance 73 ± 22 71 ±27 58 ±50 21 ± 17 20 ± 24

Subsegment analysis 67 ± 20 66 ± 21 79 ± 32 18 ±24 25 ± 28

PCC 69 ± 18 76 ± 23 42 ± 47 9 ± 15 6, 6 ±7,3

PAPR 74 ± 18 76 ± 20 64 ± 40 25 ±33 29 ± 33

directly estimated with resource to the k-NN curve.

For the HMIS dataset the parameters were selected by

a Leave-One-Out approach, since the reduced num-

ber of cycles per signal did not allowed to use the k-

NN curve method directly. Secondly, the motion data

was originated from three different workstation which

have different methods and thus, different cyclic be-

haviours and signal morphologies. Therefore, the

mean value of the estimated parameters from different

workstations may not represent the correct value for

neither of them. The most adequate approach would

be to acquire data for a longer period of time in order

to have a dataset composed of longer time series with

a higher number of cycles, which would allow to au-

tomatically estimate the value of parameter ε for each

workstation.

5 CONCLUSIONS

Musculoskeletal disorders are a major concern in

manufacturing environments due to wrongly executed

movements and inadequate postures. Most of the

tasks executed in those environments are repetitive.

Using IMUs to follow human motion, it is possible

to acquire repetitive time series with all the infor-

mation regarding the movements that integrate each

task. Since the method to accomplish each task is

deﬁned with the aim to increase productivity while

preventing the development of musculoskeletal disor-

ders, any signiﬁcant deviation from it may suggest an

occurrence that hinders the productive process. Those

occurrences appear as anomalies on IMU data. This

high-level information is a valuable asset for produc-

tion control systems, being able to constantly iden-

tify opportunities for continuous reﬁnement of the

production processes in lean manufacturing environ-

ments.

In order to accomplish this requirement, the pro-

posed anomaly detection framework was divided into

three stages: (1) unsupervised segmentation; (2) fea-

ture extraction from the extracted subsegments and

(3) unsupervised classiﬁcation using DBSCAN.

The validation stage comprised the performance

evaluation on four datasets from different domains,

which proves the requirements were met with regards

of aspiring to build a framework for unsupervised

anomaly detection on repetitive time series.

The results demonstrated that anomaly detection

in generic repetitive time series in an unsupervised

fashion is feasible, however, at the cost of a reduced

performance when compared to domain-speciﬁc ap-

Evaluation of Spatial-Temporal Anomalies in the Analysis of Human Movement

169

proaches reviewed in the literature. Notwithstand-

ing, a general approach has the value of being eas-

ily adapted in order to be applied in different do-

mains and in repetitive time series with different mor-

phologies, such as the case of different workstations

in manufacture environments. In human motion in-

dustrial scenarios, which are dominated by repeti-

tive movements, it was possible to detect anomalies

in multivariate time series using accelerometer, gyro-

scope and magnetometer data. However, the detec-

tion depends on the correct feature selection in or-

der to be accurate and still it may present low pre-

cision. Another important aspect is the adequate se-

lection of DBSCAN hyper-parameters. This work

demonstrated that a high volume of data and cycles

are required in order to properly automate the hyper-

parameter selection. For challenges with relatively

low volume of data either the hyper-parameter opti-

misation was achieved by user selection (at the cost

of low generalisation properties despite high perfor-

mance values) or by a Leave-One-Out methodology

which resulted in difﬁculties to achieve a set of val-

ues which maintain optimal characteristics for a wide

range of signals.

Future work will consist in validating the frame-

work over a more exhaustive volume of data,

which should facilitate the process of proper hyper-

parameter optimisation. Furthermore, this work was

focused on the development of the described anomaly

detection framework, but it would be important to as-

sess the impact of this system in Industrial production

lines in long-term.

ACKNOWLEDGEMENTS

This work was supported by North Portugal Regional

Operational Programme (NORTE 2020), Portugal

2020 and the European Regional Development Fund

(ERDF) from European Union through the project

Symbiotic technology for societal efﬁciency gains:

Deus ex Machina (DEM) [NORTE-01-0145-FEDER-

000026].

REFERENCES

Ahmad, S., Lavin, A., Purdy, S., and Agha, Z. (2017). Un-

supervised real-time anomaly detection for streaming

data. Neurocomputing, 262:134 – 147. Online Real-

Time Learning Strategies for Data Streams.

Chandola, V., Banerjee, A., and Kumar, V. (2009).

Anomaly Detection: A Survey. ACM Computing Sur-

veys, 41(3):1–58.

Chen, Z. and Li, Y. F. (2011). Anomaly detection based on

enhanced dbscan algorithm. Procedia Engineering,

15:178 – 182. CEIS 2011.

Cola, G., Avvenuti, M., Vecchio, A., Yang, G.-Z., and Lo,

B. P. L. (2015). An on-node processing approach

for anomaly detection in gait. IEEE Sensors Journal,

15:6640–6649.

Dheeru, D. and Karra Taniskidou, E. (2017). UCI machine

learning repository.

Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996).

A density-based algorithm for discovering clusters a

density-based algorithm for discovering clusters in

large spatial databases with noise. In Proceedings of

the Second International Conference on Knowledge

Discovery and Data Mining, KDD’96, pages 226–

231. AAAI Press.

Folgado, D., Barandas, M., Matias, R., Martins, R., Car-

valho, M., and Gamboa, H. (2018). Time Alignment

Measurement for Time Series. Pattern Recognition,

81:268–279.

Goldberger, A. L., Amaral, L. A. N., Glass, L., Hausdorff,

J. M., Ivanov, P. C., Mark, R. G., Mietus, J. E., Moody,

G. B., Peng, C.-K., and Stanley, H. E. (2000). Phys-

iobank, physiotoolkit, and physionet. Circulation,

101(23):e215–e220.

Huysmans, D., Smets, E., Raedt, W. D., Hoof, C. V., Bo-

gaerts, K., Diest, I. V., and Helic, D. (2018). Unsu-

pervised learning for mental stress detection. In Pro-

ceedings of the 11th International Joint Conference

on Biomedical Engineering Systems and Technologies

- Volume 4: BIOSIGNALS, (BIOSTEC 2018), pages

26–35. INSTICC, SciTePress.

Ren, H., Liao, X., Li, Z., and AI-Ahmari, A. (2018).

Anomaly detection using piecewise aggregate approx-

imation in the amplitude domain. Applied Intelli-

gence, 48(5):1097–1110.

Ren, H., Liu, M., Li, Z., and Pedrycz, W. (2017). A Piece-

wise Aggregate Pattern Representation Approach for

Anomaly Detection in Time Series. Knowledge-Based

Systems, 135:29–39.

Teng, M. (2010). Anomaly detection on time series. 2010

IEEE International Conference on Progress in Infor-

matics and Computing, 1:603–608.

Thuy, H. T. T., Anh, D. T., and Chau, V. T. N. (2018).

Comparing three time series segmentation methods

via novel evaluation criteria. In Proceedings - 2017

2nd International Conferences on Information Tech-

nology, Information Systems and Electrical Engineer-

ing, ICITISEE 2017, volume 2018-Janua, pages 171–

176.

BIOSIGNALS 2019 - 12th International Conference on Bio-inspired Systems and Signal Processing

170