
Constrained Multi Camera Calibration for Lane Merge Observation
Kai Cordes and Hellward Broszio
VISCODA GmbH, Hannover, Germany
Keywords:
Multi Camera Calibration, Lane Merge, Multi View, Vehicle Localization.
Abstract:
For the trajectory planning in autonomous driving, the accurate localization of the vehicles is required. Accu-
rate localizations of the ego-vehicle will be provided by the next generation of connected cars using 5G. Until
all cars participate in the network, un-connected cars have to be considered as well. These cars are localized
via static cameras positioned next to the road. To achieve high accuracy in the vehicle localization, the highly
accurate calibration of the cameras is required. Accurately measured landmarks as well as a priori know-
ledge about the camera configuration are used to develop the proposed constrained multi camera calibration
technique. The reprojection error for all cameras is minimized using a differential evolution (DE) optimization
strategy. Evaluations on data recorded on a test track show that the proposed calibration technique provides
adequate calibration accuracy while the accuracies of reference implementations are insufficient.
1 INTRODUCTION
Automated driving is regarded as the most promising
technology for improving road safety and efficiency
in the future (Fallgren et al., 2018). In the early phases
of partially automated driving, the driver is required to
constantly monitor the environment to be able to take
back the control of the vehicles whenever the need
arises. In the future, fully automated driving systems
will allow the driver to remain completely out of the
loop. Vehicles are expected to take over the complete
driving task.
1.1 Automated Driving, Cooperative
Maneuvers
As part of the automated driving tasks, a vehicle
should be able to perform appropriate maneuvers,
such as automatic lane changing whenever needed.
For this, the cooperation with nearby vehicles is cru-
cial. Cooperative maneuvers enhance the safety and
help the vehicles getting through difficult traffic si-
tuations. Vehicle-to-anything (V2X) communication
will ensure the distribution of information using a new
generation of mobile communication technology. A
major need is the accurate localization of the vehi-
cles (Fern
´
andez Barciela et al., 2017). The localiza-
tion of a vehicle is a main part of current research in
projects, such as 5GCAR
1
.
1
http://www.5gcar.eu
In addition to their self-localization capabilities,
vehicles are localized using external sensors, such as
cameras positioned nearby the road. This is crucial
for the integration phase, where only a subset of vehi-
cles is equipped with self-localizing and communica-
ting technology, the connected vehicles. The uncon-
nected vehicles are localized with a multi camera sy-
stem positioned near to the road. One important appli-
cation scenario for the joint localization of connected
and unconnected vehicles is the lane merge (Brahmi
et al., 2018).
1.2 Lane Merge Coordination
In the lane merge, one vehicle merges into a group
of vehicles driving on the motorway as shown in Fi-
gure 1. The goal is the coordination of driving trajec-
tories among a group of vehicles to improve the traffic
safety and efficiency. A subject vehicle is coordina-
ted with remote vehicles driving on the main lane in
order to merge smoothly and safely into the lane wit-
hout collisions and with minimal impact on the traf-
fic flow. The trajectory recommendations are com-
puted based on road user properties such as position,
heading, and speed, continuously transmitted by the
connected cars. It is necessary that the system consi-
ders unconnected, i.e. non-communicating road users
as well. On the one hand, it cannot be assumed that
every road user is connected to the network. On the
other, remotely monitoring incorporates redundant or
even additional information to the system such as hig-
Cordes, K. and Broszio, H.
Constrained Multi Camera Calibration for Lane Merge Observation.
DOI: 10.5220/0007387805290536
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 529-536
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
529

(a) Lane merge sketch (b) Video capture (c) Camera view
Figure 1: Sketch and video capture of the lane merge scenario using a mobile crane. One of the camera views while the lane
merge is performed is shown on the right.
her localization accuracy. This serves the goal of a
smooth lane merge without collisions and with mini-
mal impact on the traffic flow. For coordination and
vehicle feedback of trajectory recommendations and
the lane merge itself, a minimal viewing distance is
required, depending on the speed of the vehicles (Luo
et al., 2016). Thus, for the external observation of
the lane merge, more than one camera is needed. The
observation camera system is positioned next to the
road. The estimated vehicle data is sent to the lane
merge coordination entity via a cellular network. This
entity plans the cooperative maneuver and distribu-
tes corresponding instructions to connected vehicles,
while the behavior of unconnected vehicles is pre-
dicted and considered (Brahmi et al., 2018).
Since the positional accuracy is of key impor-
tance, a highly-accurate calibration is required. The
proposed approach incorporates geometric know-
ledge about the scene and about the installation of the
cameras. The scene knowledge consists of accurately
measured landmarks on the road. For the multi ca-
mera system, the height above the ground and relative
distances between the cameras are measured. This in-
formation in incorporated in a joint optimization of all
cameras.
1.3 Related Work
The accuracy demands for the camera calibration in
tracking applications depends on the tracking sce-
nario. While people trackers focus on the reliable
tracking in the 2D image plane (Milan et al., 2016;
Leal-Taix
´
e et al., 2017), vehicle tracking for coopera-
tive maneuvers requires highly accurate cameras for
two reasons: (1) tracking accuracy in 3D is of special
importance since collisions are to be avoided, and (2)
larger viewing distances are expected which increases
the demand for accurate 2D-3D correspondences.
In vehicle observation, most camera calibration
approaches make use of the road marking and assume
planar roads in the field of view. Tang et al. (Tang
et al., 2018; Tang et al., 2017) use manually selected
lines on road markings for the calibration of the ca-
meras. The UA-DETRAC benchmark (Wen et al.,
2015) neglects camera calibration and focusses on 2D
detections with large variations regarding the vehi-
cle models, the recording conditions (different view-
points and weather conditions), and the vehicle den-
sity.
In contrast to these approaches, we focus on a very
specific setting, the lane merge. Since the goal is the
automated lane merge coordination, we observe one
car merging into the main lane of a multi-lane road
where several other cars are driving. One of the cars
on the main lane opens a gap for the incoming car.
The recorded data is expected to provide valuable in-
formation to learn trajectory recommendations for the
lane merge coordination entity. Since the setup requi-
res large viewing distances, accurate camera parame-
ters are required to fulfill the accuracy demand for the
localization of the vehicles.
We provide the following contributions:
• Practical solution for a suitable multi camera se-
tup dedicated to the lane merge observation sce-
nario
• Incorporation of easily measurable metrics of the
camera setup
• Evaluations with data recorded on a test track
show the accuracy improvements of the proposed
techniques.
In the following Section 2, the data recording se-
tup is briefly described. In Section 3, the propo-
sed multi camera calibration approach is explained
in detail. Section 4 shows experimental results while
Section 5 concludes this paper.
2 LANE MERGE OBSERVATION
The data for the lane merge is recorded on a test track
which provides two lanes of approximately 100m
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
530

(a) CAM
1
(b) CAM
2
(c) CAM
3
(d) CAM
4
Figure 2: Video streams for the three sets (SET
(1)
, SET
(2)
, SET
(3)
from top to bottom). The temporal synchronization for
a set SET
(i)
is done manually. In one row, one point in time is shown for each set. The images demonstrate the lane merge
application. The camera calibration is done using landmarks as shown in Figure 4 using images without vehicles.
length for the main traffic and the acceleration entry
lane for the merging car. The video capturing is done
with four video cameras attached to a mobile crane
(cf. Figure 1). The cameras capture 1920 × 1080
pixels at 50 fps. The temporal synchronization is done
manually in a post processing step using a video edi-
ting tool. For determining the synchronization, a pre-
viously defined signal (headlight flash) is recorded.
Using the manually determined signal in the video
sequences, all the video streams are synchronized as
shown in Figure 2. Four cars drive on the main lanes
while one car on the entry lane merges into the traffic.
3 MULTI CAMERA
CALIBRATION
For the calibration, intrinsic and extrinsic camera pa-
rameters are required. For each camera, the radial dis-
tortion is computed in a preprocessing step using ma-
nually selected lines in the images (Thorm
¨
ahlen et al.,
2003). For the computation of the extrinsic parame-
ters and the focal length (7 parameters), in contrast to
existing approaches in benchmark generation (Tang
et al., 2018; Tang et al., 2017), landmarks on the road
and their GPS positions are used. The GPS positi-
ons are determined using a D-GPS sensor with RTK
precision, which provides a localization accuracy of
approximately 2cm (RTK-DGPS: real time kinema-
tics differential global positioning system). The land-
marks are selected such that (1) they are well distribu-
ted in the region of interest and (2) many of them are
visible in each camera view. Their positions are cho-
sen on edges of the road markings (fifteen positions)
to ease the re-identification in the camera images.
Additional geometrics of the camera setup are col-
lected using a laser scan tool which measures the
height of the camera (distance to the ground plane)
and relative distances between cameras. The camera
setup (example snapshot shown in Figure 3) is tested
for three different positions of the mobile crane with
differently mounted cameras to capture data sets with
different viewpoints.
The proposed calibration procedure leading to
accurate cameras is described in the following secti-
ons. It minimizes the reprojection error as defined in
Section 3.1 uses an evolutionary optimizer shown in
Section 3.2, and is capable of incorporating a priori
known geometric constraints given in Section 3.3.
Figure 3: Panorama snapshot of three out of four cameras
from the observers perspective. The calibration technique
incorporates known distances between cameras. The dis-
tance between the top cameras is 77cm, the distance bet-
ween the top left and the bottom right camera is 127cm.
The basket size is 120 ×60cm, its height is 120cm.
Constrained Multi Camera Calibration for Lane Merge Observation
531

3.1 Cost Function
Using homogeneous coordinates, the 3D-2D corre-
spondence of object point P
j
∈ R
4
and feature point
p
j,k
∈ R
3
is given by the camera projection matrix
A
k
∈ R
3×4
:
p
j,k
= A
k
P
j
(1)
The standard technique for camera calibration is the
resectioning method (Tsai, 1987; Hartley and Zisser-
man, 2003), referred to as single camera optimization.
3.1.1 Single Camera Optimization
For optimizing each camera A
k
independently, the 3D
points P
j
with known 3D coordinates are projected
into the camera planes, resulting in 2D positions p
j
.
The known 2D representations
ˆ
p
j,k
of the landmarks
are manually selected in the images. The squared dis-
tances d(
ˆ
p
j
, A
k
P
j
)
2
determine the reprojection error:
ε
k
=
J
k
∑
j=1
d(
ˆ
p
j,k
, A
k
P
j
)
2
(2)
The minimization of equation (2) with an appropriate
initialization for the camera matrix A
k
gives the cali-
bration result for each camera. A camera matrix is
built using the 7 parameters (C
x
, C
y
, C
z
) (global coor-
dinate position) (pan, tilt, roll)-angles and the focal
length f (Hartley and Zisserman, 2003). The distance
(d(.))
2
is only computed if the 3D point is projected
into the visible region of the camera k resulting in dif-
ferent numbers of points J
k
for each camera.
3.1.2 Multi Camera Optimization
Multi camera calibration enables the joint optimiza-
tion of parameters, such as the knowledge that two ca-
meras have the same focal length. As shown in (Cor-
des et al., 2015), these additional costraints improve
the parameter estimation. The reprojection error is
then determined as:
ε =
K
∑
k=1
J
k
∑
j=1
d(
ˆ
p
j,k
, A
k
P
j
)
2
(3)
In our application, K = 4 cameras and up to
J
k
= 15 points are used, depending on the visibility
of the landmarks in each camera.
3.1.3 Constrained Multi Camera Optimization
Additional constraints for the calibration technique
are given by the camera setup, e.g. measured distan-
ces between two cameras or the height of a camera
above the ground plane. In each of our camera se-
tups, two cameras have nearly the same height above
Figure 4: Visualization of 12 of the 15 landmarks used for
the camera calibration.
the ground plane. Several of these constraints can be
easily exploited using spherical coordinates as shown
in Section 3.3. The global optimization for all para-
meters including special constraints measured in the
test scenario is done using evolutionary computation,
cf. Section 3.2.
3.2 Differential Evolution Optimization
For the minimization of the the cost function (3), the
Differential Evolution (DE) algorithm (Price et al.,
2005) is used. It is known as an efficient global op-
timization method for continuous problem spaces. In
our application 4 cameras with 7 parameters each (po-
sition, orientation, focal length) are employed. The
number of estimated parameters determine the search
space dimension.
DE includes an adaptive range scaling for the ge-
neration of solution candidates. This enables global
search in the case where the solution candidate vec-
tors are spread in the search space and the mean dif-
ference vector is large. In the case of a converging
population the mean difference vector becomes smal-
ler. This enables efficient fine tuning towards the end
of the optimization process (Cordes et al., 2009).
For better convergence, the extended DERSF (DE
with Random Scale Factor) method proposed in (Das
et al., 2005) is used. It leads to a wider distribution
of the candidate vectors and, thus, improves the se-
arch. Since the dimension of the search space is high
(cf. Section 4.1), spreading the population helps in
achieving the global minimum of the cost function.
3.3 Incorporation of Geometric
Constraints
To limit the search space, additional constraints are
included in the optimization. This leads to faster con-
vergence and a higher probability of achieving the
global minimum of the cost function. Therefore, dis-
tances between cameras are provided. The incorpora-
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
532

tion is done using spherical coordinates. The mapping
from Euclidean coordinates to spherical coordinates
(x, y, z)
t
7→ (r, θ, φ)
t
, r ∈ R
+
, θ ∈ [0;π], φ ∈ [0;2π], is:
r
θ
φ
=
√
x
2
+ y
2
+ z
2
arccos(
z
r
)
arctan2(y, x)
(4)
The reverse mapping (r, θ, φ)
t
7→ (x, y, z)
t
is:
x
y
z
=
r · sin(θ) · cos(φ)
r · sin(θ) · sin(φ)
r · cos(θ)
(5)
We parameterize the first camera position C
MAIN
in Euclidean coordinates and determine all other ca-
mera positions C
i
relative to the first one with spheri-
cal coordinates. Then, r in equations (4) and (5) cor-
responds to the camera distance ||C
i
− C
MAIN
||
2
. For
example, the distance between the two top cameras
in Figure 3 is r = 77cm. Incorporating the relative
distances for each of the four cameras decreases the
number of estimated parameters by 3.
From equation (5), it follows that points with the
same height above the ground plane (and positive
orientation) lead to a relative angle θ of θ =
π
2
. Thus,
for the camera CAM
2
, the value θ can be set to θ =
π
2
,
because CAM
1
and CAM
2
are installed at the same
height h (cf. Figure 3). This decreases the number of
estimated parameters by 1.
Both options, the relative camera distance and set-
ting the same height of CAM
1
and CAM
2
, are explored
in Section 4 in experiments X
3
, X
4
, leading to the pro-
posed calibration technique. The incorporation of ge-
ometric constraints in the calibration greatly improves
its accuracy.
4 EXPERIMENTAL RESULTS
For the evaluation, three different camera sets SET
(1)
,
SET
(2)
, SET
(3)
are tested. Each set consists of four
cameras CAM
1
, . . . , CAM
4
attached to the basket of a
mobile crane as visualized in Figure 3. For SET
(1)
,
Figure 5: Example for the reprojection error (here ≈ 12 px
for both reprojected points shown in blue): The image de-
picts a small part of the calibration image of SET
(3)
, CAM
3
.
SET
(2)
the relative camera positions are approxima-
tely the same since only the crane basket height is
changed. The camera orientations were adjusted to
provide an appropriate field of view for each camera.
For SET
(3)
, the mobile crane adopted a new position
and height. All cameras were removed and attached
to new positions at the basket of the crane. Images of
the cameras while the vehicles perform a lane merge
are shown in Figure 2. For the calibration, images
without vehicles are used as shown in Figure 4. The
images have a resolution of 1920 × 1080.
For all cameras, position, orientation, and focal
length are estimated. Since the cameras CAM
1
and
CAM
2
are identical, used with equal zoom factor, the
focal length of these cameras share the same estima-
tion value.
4.1 Setup
For the evaluation, four camera estimation experi-
ments X
i
, i = 1, . . . , 4 are defined, two for single ca-
mera calibration and two for multi camera calibration.
The single camera calibration (X
1
, X
2
) is explained in
Section 3.1.1, the multi camera calibration (X
3
, X
4
) is
explained in Section 3.1.2. A priori known informa-
tion is incorporated as explained in Section 3.3.
X
1
: Estimation of all 7 parameters (position, orien-
tation, focal length) for each camera k indepen-
dently
X
2
: Estimation of 6 parameters - (C
x
, C
y
), orientation,
and focal length - with known ground truth height
C
z
= h
gt
for each camera k independently
X
3
: Estimation of all parameters of the four cameras
using the information that (1) CAM
1
and CAM
2
have the same (unknown) height and (2) CAM
1
and CAM
2
have the same focal length (since these
cameras are identical), leading to 28 − 2 = 26 pa-
rameters
X
4
: Estimation like X
3
, additionally incorporating the
information of the relative distances r
gt
between
CAM
1
and the other cameras, leading to 28 − 2 −
3 = 23 parameters
The relative camera distances r
gt
and the camera
heights h
gt
are measured after installation of the ca-
meras using a laser measure tool.
All approaches receive the same input data which
is the 3D positions of the 15 calibration markers and
their manually selected 2D positions in the images.
The radial distortion coefficients are determined in a
preprocessing step.
The multi camera calibration approaches X
3
, X
4
get a very coarse initialization, such as viewing di-
rection towards the road and a square of 10m × 10m
Constrained Multi Camera Calibration for Lane Merge Observation
533
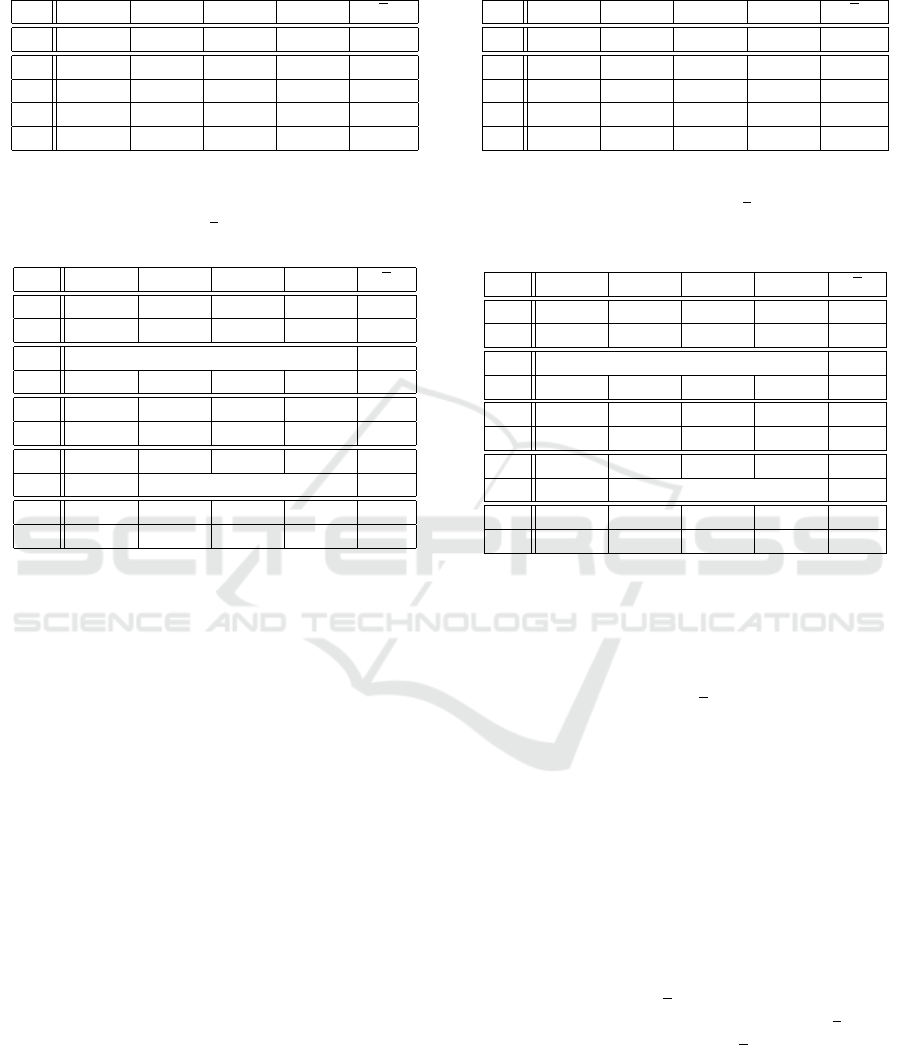
Table 1: Reprojection errors for single and the proposed
multi camera optimization for SET
(1)
. The distances are
measured in pel.
CAM
1
CAM
2
CAM
3
CAM
4
ε
J
k
12 7 12 15
ε
1
5.04 20.22 5.16 9.21 9.91
ε
2
6.59 20.33 7.13 9.22 10.82
ε
3
8.16 19.12 4.43 6.55 9.57
ε
4
8.09 19.20 4.86 6.81 9.74
Table 2: Resulting camera heights h
i
and relative distances
r
i
for single and the proposed multi camera optimization for
SET
(1)
. Their mean error is e. The distances are measured
in m.
CAM
1
CAM
2
CAM
3
CAM
4
e
h
1
8.09 7.85 7.13 7.05 0.30
r
1
0.00 1.81 1.38 1.73 0.44
h
2
set to ground truth h
gt
–
r
2
0.00 1.97 1.02 1.28 0.45
h
3
7.59 7.59 7.12 7.11 0.14
r
3
0.00 0.93 1.26 1.56 0.27
h
4
7.57 7.57 6.94 7.11 0.10
r
4
0.00 set to ground truth r
gt
–
h
gt
7.63 7.63 6.65 7.10 –
r
gt
0.00 0.77 1.62 1.27 –
for the (C
x
, C
y
)-position while the single camera op-
timization techniques X
1
, X
2
, are fairly well initiali-
zed to achieve the best possible minimum of the cost
function. This is done with manual interaction. An
example for reprojected points
ˆ
p
j,k
and their repro-
jection error is given in Figure 5.
Since the DE optimization used for X
3
, X
4
is based
on randomized generation of candidate vectors and a
random initialization (cf. Section 4.3), mean values
of 100 results are reported. The DE optimization em-
ploys common parameters (Price et al., 2005). The
number of particles is set to 300, the number of gene-
rations is 15000. The computation time is about 4 mi-
nutes on our I5 2.5 GHz notebook using unoptimized
code which is still appropriate for the calibration of
all cameras.
4.2 Accuracy Evaluation
The results are given for each of the three sets in-
dependently. We report the reprojection errors for
SET
(1)
, SET
(2)
, and SET
(3)
in Table 1, Table 3, and
Table 5, respectively. The comparisons with ground
truth measurements for the three sets are shown in
the Table 2, Table 4, and Table 6, respectively. The
heights h
gt
of the cameras are determined with a la-
ser measure tool which provides high accuracy (er-
Table 3: Reprojection errors for single and the proposed
multi camera optimization for SET
(2)
. The distances are
measured in pel.
CAM
1
CAM
2
CAM
3
CAM
4
ε
J
k
13 14 13 14
ε
1
4.55 18.59 4.21 8.86 9.05
ε
2
6.66 18.79 6.75 8.86 10.27
ε
3
6.20 13.69 3.61 6.39 7.80
ε
4
6.21 14.03 4.14 6.58 7.74
Table 4: Resulting camera heights h
i
and relative distances
r
i
for SET
(2)
. Their mean error is e. The distances are
measured in m. The relative camera distances r
gt
are equal
to those in SET
(1)
.
CAM
1
CAM
2
CAM
3
CAM
4
e
h
1
5.76 5.27 4.77 4.90 0.21
r
1
0.00 1.12 1.37 1.62 0.32
h
2
set to ground truth h
gt
–
r
2
0.00 0.98 0.96 1.29 0.30
h
3
5.39 5.39 4.77 4.89 0.10
r
3
0.00 1.04 1.03 1.41 0.24
h
4
5.45 5.45 4.65 4.83 0.08
r
4
0.00 set to ground truth r
gt
–
h
gt
5.42 5.42 4.44 4.89 –
r
gt
0.00 0.77 1.62 1.27 –
ror ≈ 1mm), e.g. the height of the reference camera
CAM
1
for SET
(1)
is h
gt
= 7.63m (ground truth), its
height for SET
(2)
is h
gt
= 5.42m.
The experiments X
i
as reported in Section 4.1 lead
to reprojection errors ε
i
(cf. Tables 1, 3, and 5). For
simplicity, the mean errors ε are computed with the
same weight for each camera k, not regarding the
numbers of points J
k
. For the comparison with ground
truth measurements, the estimated camera heights h
i
and the relative camera distances r
i
are shown (cf. Ta-
bles 2, 4, and 6). These values are most demonstra-
tive to show the metrics and errors of the calibra-
tion results. Experiment X
i
lead to results for camera
height h
i
and relative camera distances r
i
. The entries
h
gt
and r
gt
at the bottom of each of the tables depict
the measured ground truth values for camera height
and relative distance.
In all evaluations SET
(1)
, SET
(2)
, and SET
(3)
, the
mean reprojection error ε tends to increase when more
constraints are added to the optimization, i.e. ε for ex-
periment X
2
is always larger than ε for experiment X
1
.
The same holds for experiment X
4
compared to expe-
riment X
3
(for SET
(2)
, the results are comparable).
But, the estimation for the relative distance r
2
in
experiment X
2
tend to better results for all three sets.
It follows that the reprojection error does not provide
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
534

Table 5: Reprojection errors for single and the proposed
multi camera optimization for SET
(3)
. The distances are
measured in pel.
CAM
1
CAM
2
CAM
3
CAM
4
ε
J
k
9 6 4 13
ε
1
8.75 7.06 0.77 10.16 6.69
ε
2
10.19 8.05 5.02 10.71 8.49
ε
3
11.40 9.02 7.26 10.73 9.60
ε
4
14.26 7.79 6.71 10.55 9.83
Table 6: Resulting camera heights h
i
and relative distances
r
i
for single and the proposed multi camera optimization for
SET
(3)
. Their mean error is e. The distances are measured
in m.
CAM
1
CAM
2
CAM
3
CAM
4
e
h
1
4.49 6.69 4.21 4.48 1.12
r
1
0.00 14.18 8.67 3.33 7.98
h
2
set to ground truth h
gt
–
r
2
0.00 7.96 7.44 3.35 5.50
h
3
5.03 5.03 5.26 4.92 0.44
r
3
0.00 1.83 4.34 1.69 1.87
h
4
5.48 5.48 5.70 5.32 0.09
r
4
0.00 set to ground truth r
gt
–
h
gt
5.51 5.51 5.53 5.44 –
r
gt
0.00 0.32 1.40 0.52 –
a good measure for the comparison of the accuracy.
Still, the results for r
2
are far from acceptable with a
mean error of e = 0.45m for SET
(1)
or even e = 5.50m
for SET
(3)
. To subsume, the error for the single ca-
mera calibration regarding camera height and relative
camera distance is surprisingly large. The reason is
the large uncertainty in the direction of the optical
axis of the camera. Variations of the camera posi-
tion in this direction does not affect the reprojection
error much. The small depth in the constellation of
the landmarks in SET
(3)
(side view of the road) make
this set the most challenging among these three.
The experimental setup X
3
improves the accuracy
results (r
3
, h
3
) significantly, leading to e = 0.27m
for the mean relative camera distance for SET
(1)
and
e = 1.87m for SET
(3)
. The results for the estimated
camera height show acceptable values for SET
(1)
and
SET
(2)
(e = 0.14m and 0.10m), but large errors for
SET
(3)
(e = 0.44m). The mean relative camera dis-
tance error of 1.87m in SET
(3)
is still not acceptable.
The best results are achieved in experiment setup
X
4
leading to error distances of 0.10m, 0.08m, and
0.09m for the three camera sets. We can conclude
that X
4
provides the only usable solution for highly
accurate camera calibration.
4.3 Convergence Evaluation
To evaluate the robustness of the optimization, the
most challenging scenario SET
(3)
is examined. in Fi-
gure 6, we show mean and standard deviation of the
camera height for the experiments X
3
and X
4
.
The proposed method X
4
using the relative distan-
ces between the cameras (cf. Section 4.1 for details)
provides a stable and accurate solution while the ex-
periment X
3
comes to uncertain results. The mean
of the camera heights lead to an error of e = 0.44m
(cf. Table 6). The proposed approach using the expe-
rimental setup X
4
has a mean error of e = 0.09m.
5 CONCLUSIONS
For the targeted application of vehicle observation du-
ring a lane merge, a constrained multi camera calibra-
tion technique is designed. For the application, high
localization accuracy is required.
The proposed approach incorporates additional
constraints such as the relative distances between ca-
meras in the optimization. The distance measure-
ments can be done very easily during the camera in-
stallation. This makes the presented approach a very
useful part of the camera installation for the observa-
tion task.
The optimization procedure minimizes the repro-
jection error of known landmark positions on the
road. The global optimization is based on evolutio-
nary computation and provides suitable convergence
behaviour on all test sets. For the accuracy evaluation,
the resulting camera heights are compared. The pro-
posed approach provides a mean error in the camera
height below 10cm for cameras installed at a height
of 5.4-7.6m observing landmarks with a distance of
up to 100m.
ACKNOWLEDGEMENTS
This work has been performed in the framework of
the H2020 5GCAR project co-funded by the EU. The
authors would like to acknowledge the contributions
of their colleagues from 5GCAR.
Constrained Multi Camera Calibration for Lane Merge Observation
535
4
4.5
5
5.5
6
1 2 3 4
height [m]
CAM1
CAM2
CAM3
CAM4
(a) Experiment X
3
: camera heights of SET
(3)
4
4.5
5
5.5
6
1 2 3 4
height [m]
CAM1
CAM2
CAM3
CAM4
(b) Experiment X
4
: camera heights of SET
(3)
Figure 6: Mean and standard deviation for 100 evaluations of the camera height for experiments X
3
(a) and X
4
(b)
(cf. Section 4.1). Here, the most challenging SET
(3)
is shown. For X
4
, much smaller standard deviations are achieved.
REFERENCES
Brahmi, N., Frye, T., Marti
˜
nan, D., Dafonte, P., Abad,
X., S
´
aez, M., Cellarius, B., Gangakhedkar, S., Cao,
H., Sequeira, L., Berger, K., Theillaud, R., Otter-
bach, J., Grudnitsky, A., Villeforceix, B., Allio, S.,
Lefebvre, M., Odinot, J.-M., Tiphene, J., Servel, A.,
Fern
´
andez Barciela, A. E., Broszio, H., Cordes, K.,
and Abbas, T. (2018). 5GCAR Demonstration guide-
lines. https://5gcar.eu/. [Online; accessed 20-October-
2018].
Cordes, K., Hockner, M., Ackermann, H., Rosenhahn, B.,
and Ostermann, J. (2015). WM-SBA: Weighted multi-
body sparse bundle adjustment. In IAPR International
Conference on Machine Vision Applications (MVA),
pages 162–165.
Cordes, K., Mikulastik, P., Vais, A., and Ostermann, J.
(2009). Extrinsic calibration of a stereo camera sy-
stem using a 3D CAD model considering the uncer-
tainties of estimated feature points. In European Con-
ference on Visual Media Production (CVMP) , pages
135–143.
Das, S., Konar, A., and Chakraborty, U. K. (2005). Two im-
proved differential evolution schemes for faster global
search. In Annual Conference on Genetic and Evo-
lutionary Computation, GECCO 05, pages 991–998.
ACM.
Fallgren, M., Dillinger, M., Li, Z., Vivier, G., Abbas, T.,
Alonso-Zarate, J., Mahmoodi, T., Alli, S., Svensson,
T., and Fodor, G. (2018). On selected V2X technology
components and enablers from the 5GCAR project. In
IEEE International Symposium on Broadband Multi-
media Systems and Broadcasting (BMSB), pages 1–5.
Fern
´
andez Barciela, A. E., Servel, A., Tiphene, J., Fallgren,
M., Sun, W., Brahmi, N., Str
¨
om, E., Svensson, T.,
Bernardez, D., Zarate, J. A., Kousaridas, A., Boban,
M., Dillinger, M., Condoluci, M., Mahmoodi, T., Li,
Z., Otterbach, J., Lefebvre, M., Vivier, G., Abbas, T.,
and Wing
˚
ard, P. (2017). 5GCAR scenarios, use ca-
ses, requirements and KPIs. https://5gcar.eu/. [Online;
accessed 20-October-2018].
Hartley, R. I. and Zisserman, A. (2003). Multiple View Ge-
ometry. Cambridge University Press, second edition.
Leal-Taix
´
e, L., Milan, A., Schindler, K., Cremers, D., Reid,
I. D., and Roth, S. (2017). Tracking the trackers:
An analysis of the state of the art in multiple object
tracking. arXiv:1704.02781.
Luo, Y., Xiang, Y., Cao, K., and Li, K. (2016). A dynamic
automated lane change maneuver based on vehicle-
to-vehicle communication. Transportation Research
Part C: Emerging Technologies, 62:87–102.
Milan, A., Leal-Taix
´
e, L., Reid, I. D., Roth, S., and Schind-
ler, K. (2016). MOT16: A benchmark for multi-object
tracking. arXiv:1603.00831.
Price, K. V., Storn, R., and Lampinen, J. A. (2005). Dif-
ferential Evolution - A Practical Approach to Global
Optimization. Natural Computing Series. Springer,
Berlin, Germany.
Tang, Z., Wang, G., Liu, T., Lee, Y., Jahn, A., Liu, X., He,
X., and Hwang, J. (2017). Multiple-kernel based vehi-
cle tracking using 3D deformable model and camera
self-calibration. arXiv:1708.06831.
Tang, Z., Wang, G., Xiao, H., Zheng, A., and Hwang, J.-
N. (2018). Single-camera and inter-camera vehicle
tracking and 3D speed estimation based on fusion of
visual and semantic features. In IEEE Conference on
Computer Vision and Pattern Recognition Workshop
(CVPRw), pages 108–115.
Thorm
¨
ahlen, T., Broszio, H., and Wassermann, I. (2003).
Robust line-based calibration of lens distortion from a
single view. Proceedings of Mirage, pages 105–112.
Tsai, R. (1987). A versatile camera calibration technique
for high-accuracy 3D machine vision metrology using
off-the-shelf tv cameras and lenses. IEEE Journal on
Robotics and Automation, 3(4):323–344.
Wen, L., Du, D., Cai, Z., Lei, Z., Chang, M., Qi, H., Lim,
J., Yang, M., and Lyu, S. (2015). UA-DETRAC:
A new benchmark and protocol for multi-object de-
tection and tracking.
arXiv:1511.04136
.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
536
