Improved Person Detection on Omnidirectional Images with

Non-maxima Supression

Roman Seidel, André Apitzsch and Gangolf Hirtz

Department of Information Technology, Chemnitz University of Technology, Chemnitz, Germany

Keywords:

Ambient Assisted Living, Convolutional Neural Networks, Object Detection, Non-maxima Supression,

Omnidirectional Images.

Abstract:

We propose a person detector on omnidirectional images, an accurate method to generate minimal enclosing

rectangles of persons. The basic idea is to adapt the qualitative detection performance of a convolutional

neural network based method, namely YOLOv2 to ﬁsh-eye images. The design of our approach picks up the

idea of a state-of-the-art object detector and highly overlapping areas of images with their regions of interests.

This overlap reduces the number of false negatives. Based on the raw bounding boxes of the detector we

ﬁne-tuned overlapping bounding boxes by three approaches: the non-maximum suppression, the soft non-

maximum suppression and the soft non-maximum suppression with Gaussian smoothing. The evaluation

was done on the PIROPO database and an own annotated Flat dataset, supplemented with bounding boxes

on omnidirectional images. We achieve an average precision of 64.4 % with YOLOv2 for the class person on

PIROPO and 77.6 % on Flat. For this purpose we ﬁne-tuned the soft non-maximum suppression with Gaussian

smoothing.

1 INTRODUCTION

Convolutional neural networks (CNNs) were treaded

for several tasks in computer vision in the recent ye-

ars. Finding objects in images (i.e. object detection)

belongs to these tasks. A main requirement for the

detection of objects in images for current CNNs are

accurate real-world training data. In this paper we

propose a method to detect objects in ﬁsh-eye images

of indoor scenes using a state-of-the-art object detec-

tor.

The object detection in indoor scenes with a limi-

ted number of image sensors can be reached with ima-

ges from omnidirectional cameras. These cameras are

suited for capturing one room with a single sensor due

to a ﬁeld of view of about 180

◦

. Our goal is to detect

objects in indoor scenes in omnidirectional data with

a detector trained on perspective images.

Beside our application, the ﬁeld of active assis-

ted living, the detection of objects in omnidirectional

image data can be used in mobile robots and in the

ﬁeld of autonomous driving.

The remainder of this paper is structured as fol-

lows: Section 2 presents previous research activities

in object detection. Section 3 illustrates the working

principle of a neural network based object detector.

Section 4 explains how our virtual cameras are ge-

nerated. Section 5 shows the theoretical background

for different variants of non-maximum suppression

(NMS). Section 6 describes our experiments for the

generation of bounding boxes and the evaluation of

our results on common error metrics. Section 7 sum-

marizes the paper’s content, concludes our observa-

tions and gives ideas for future work. The results of

our work, the image data and the evaluation of the re-

sults, can be found at https://gitlab.com/omnidetector/

omnidetector.

2 RELATED WORK

State-of-the-art object detectors predict bounding

boxes on perspective images over several classes. A

region-based, fully connected convolutional network

for accurate and efﬁcient object detection is R-FCN

(Dai et al., 2016). As a standard practice, the results

of the detector based on ResNet-101 architecture (He

et al., 2016) are post-processed with non-maximum

suppression (NMS) using a threshold of 0.3 to the in-

tersection over union (IoU) (Girshick et al., 2013).

The single shot multi-box detector (SSD) by (Liu

et al., 2016) provides an improvement of the net-

474

Seidel, R., Apitzsch, A. and Hirtz, G.

Improved Person Detection on Omnidirectional Images with Non-maxima Supression.

DOI: 10.5220/0007388404740481

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 474-481

ISBN: 978-989-758-354-4

work architecture by adding a backend extra feature

layer on top of VGGNet-16 combined with the idea to

use predictions from multiple feature maps with dif-

ferent resolutions which handles objects with various

sizes. The SSD leads to competitive results on com-

mon object detection benchmark datasets, namely MS

COCO (Lin et al., 2014), ImageNet (Russakovsky

et al., 2015) and PASCAL VOC (Everingham et al.,

2010). The approach we follow is YOLOv2 (Redmon

and Farhadi, 2017). It produces signiﬁcant impro-

vements to increase mean average precision (mAP)

through variable size of models, multi-scale training

and a joint training to predict detections for object

classes without labeled detection data.

Our application is object detection, so we con-

centrate on datasets where labels are minimally en-

closing rectangles (bounding boxes). Common real

world benchmark datasets with labeled objects on

perspective images are presented by (Everingham

et al., 2010), (Krasin et al., 2017), (Li et al., 2017),

(Russakovsky et al., 2015). Omnidirectional images

with multiple sequences in two different indoor rooms

were created in the work of (del Blanco and Carbal-

leira, 2016). A direct approach for detecting objects

in omnidirectional images without CNNs was shown

in the work of (Cinaroglu and Bastanlar, 2014). The

classical HoG features and training a SVM to detect

humans in a transformed INRIA dataset leads to com-

petitive results in recall and precision.

A novel model named Past-Future Memory Net-

work (PFMN) was proposed by (Lee et al., 2018) on

360

◦

videos. One of the main contributions of (Lee

et al., 2018) is to learn the correlation between input

data from the past and future.

In contrast to our work, the authors of Spherical

CNN (Cohen et al., 2018) modify the architecture of

ResNet. Their goal is to build a collection of spherical

layers which are rotation-equivariant and expressive.

3 OBJECT DETECTION

Based on an excellent mAP of 73.4% (10 clas-

ses, VOC2007test) and an average precision (AP) of

81.3% (VOC2007test) for the class person, we use the

You Only Look Once (YOLO) (Redmon et al., 2016)

approach in its second version called YOLOv2 (Red-

mon and Farhadi, 2017). To detect objects in in-

put images YOLOv2 offers a good compromise be-

tween detection accuracy and speed. The model is

trained on ImageNet (Russakovsky et al., 2015) and

the COCO dataset (Lin et al., 2014). The approach

outperforms state-of-the-art methods like Faster R-

CNN (Ren et al., 2015) with ResNet (He et al., 2016)

and SSD (Liu et al., 2016), which still runs signiﬁ-

cantly faster. YOLOv2 predicts the corners of boun-

ding boxes directly with the help of fully connected

layers which are added on top of the convolutional

feature extractor. Additional changes on the network

architecture are the elimination of pooling layers to

obtain a higher resolution output by the convolutional

layers in the network. The input data size of the net-

work is shrinked to operate on 416 ×416 input images

instead of 448 × 448. For the prediction of bounding

boxes in YOLOv2 the fully connected layers are re-

placed by anchor boxes. To counteract the effect to

detect objects with a ﬁxed size, a special feature du-

ring the training is the random selection of input size

of the model, which changes every 10 batches. The

smallest input is 320×320 and the largest 608 × 608.

4 CREATING VIRTUAL VIEWS

FROM AN

OMNIDIRECTIONAL IMAGE

In this chapter we describe the transformation for ge-

nerating virtual perspective views from omnidirectio-

nal image data based on (Findeisen et al., 2013). We

assume, that the omnidirectional camera is calibrated

both intrinsically and extrinsically.

The camera model describes how the coordinates

of a 3D scene point are transformed into the coordi-

nates of a 2D image point. We concentrate on the

central camera model, i.e. all light rays, originating

from the scene points, travel through a single point in

space, called the single effective viewpoint. For the

transformation between the omnidirectional and the

perspective images a mathematical description is ne-

cessary for both camera models.

4.1 Perspective Camera Model

The perspective camera model uses the pinhole

camera model as an approximation. The per-

spective projection of the spatial coordinates given

in the camera coordinate system is stated x

cam

, y

cam

, z

cam

)

and in normalized image coordina-

tes x

norm

= (x

norm

, y

norm

, 1)

. After applying an afﬁne

transformation it is possible to get pixel coordinates

x = (x

img

, y

img

)

. For the linear mapping between the

source and target camera model we use homogeneous

coordinates, denoted as

x = (x, y, 1)

. The relation

between x

norm

and

x is given by

x = K · x

norm

(1)

Improved Person Detection on Omnidirectional Images with Non-maxima Supression

475

where K is the upper-triangular calibration matrix

containing the camera intrinsic:

K =





0 f

0 0 1





. (2)

As shown in (2) the ﬁve intrinsic parameters of a pin-

hole camera are the scale factors in x- and y-direction

( f

, f

), the skewness factor s

and the principle point

of the image (c

, c

In general a scene point is modeled in a world

coordinate system, which is different from the camera

coordinate system (x

cam

). The orientation between

these coordinate systems consists of two parts, na-

mely a rotation R and a translation t (or equivalent

C = −R

−1

· t, where C is the camera center).

The relationship between the scene point in the

world coordinate system

X = (X,Y, Z, 1)

and an

image point in the image coordinate system

x is gi-

ven by

x = P ·

X (3)

where P is a homogeneous 3 × 4 matrix, called the

camera projection matrix (Hartley and Zisserman,

2006). The matrix P contains the parameters of the

extrinsic and intrinsic calibration with

P = K[R|t]. (4)

There are several approaches to extend the camera

model deﬁned above with a description of lens im-

perfections. As long as our target virtual camera is

perfectly perspective and free of lens distortions, we

do not discuss this issue.

4.2 Omnidirectional to Perspective

Image Mapping

Because it is mathematically impossible to transform

the whole omnidirectional image into one perspective

image, we transform a region of 2D image points

from the omnidirectional into the perspective view.

We determine the perspective images through n vir-

tual perspective cameras Cam

, Cam

, . . . , Cam

which are described by their extrinsic parameters R

and t (6 degrees of freedom (DOF)) and intrinsic pa-

rameters K (5 DOF). Instead of determining the pa-

rameters of the perspective camera through a calibra-

tion, we model the virtual camera and determine the

extrinsic (R and t) empirically.

To create the virtual perspective views we change

the extrinsic camera parameter R through the varia-

tion of the angles through the rotation about the axes

x, y and z represented by their Euler angles. To be

more speciﬁc, we rotate about the x-axis and z-axis.

The extrinsic calibration parameters of the omni-

directional camera form the world reference with re-

spect to the virtual perspective cameras. As K con-

tains the scale factors in the horizontal and vertical di-

rections ( f

, f

), K determines the ﬁeld of view (FOV)

of the target images. For perspective images with a re-

solution of 2c

×2c

the horizontal and vertical FOVs

are:

FOV

= 2arctan



2 f



and

FOV

= 2arctan



2 f



, respectively.

(5)

Equation (5) allows us to deﬁne the FOV of the per-

spective camera and to build at least one virtual per-

spective camera, which is able to generate perspective

images, from the omnidirectional camera. Derived

from the horizontal FOV and vertical FOV we deter-

mine the diagonal FOV (FOV

) with:

FOV

= 2arctan



2 f



(6)

where:

c =

+ c

and f =

+ f

(7)

To come to a common FOV of a usual perspective

camera we choose the focal length and the diagonal

image size with respect to the sensor to be equal. This

leads to a simpliﬁcation of (6) with:

FOV

= 2arctan





. (8)

The simpliﬁcation leads to a diagonal FOV of about

53.13

◦

and allows us to choose c and f free, as long

as they are equal.

5 NON-MAXIMUM

SUPPRESSION

Our goal is to ﬁnd the most likely position of the mi-

nimal enclosing rectangle of the object. Therefore we

disable the two ﬁnal steps of YOLOv2 occurring at

the last layers of the network. First, the reduction of

the number of bounding boxes based on their conﬁ-

dence. Second, the union of multiple bounding boxes

of one particular object through soft non-maximum

suppression (Soft-NMS).

In general, the NMS is necessary due to highly

overlapping areas of perspective images after the

transformation to omnidirectional images. To receive

the raw detections of YOLOv2 with conﬁdences bet-

ween 0 and 1, we set the conﬁdence threshold equal

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

476

to zero. To group the resulting bounding boxes, one

suitable measurement is the intersection over union

(IoU). The IoU for two boxes A and B is deﬁned by

the Jaccard index as:

IoU(A, B) =

A ∩ B

A ∪ B

. (9)

Our next step for the reﬁnement of the back-projected

bounding boxes is applying Soft-NMS inspired by

(Bodla et al., 2017). In this approach Soft-NMS is

used to separate bounding boxes to distinguish be-

tween different objects that are close to each other

and to prune multiple detections for one unambiguous

object, back projected from highly overlapped per-

spective views. Bounding boxes which are close to-

gether and fulﬁll the IoU > 0.5 are considered as a uni-

que region of interest (RoI) proposal for each object.

To update the conﬁdences of the bounding boxes, in

the NMS the pruning step can be formulated as a res-

coring function:

(

, IoU(M, b

) < N

0, IoU(M, b

) ≥ N

(10)

Where b

is a bounding box with score s

of the de-

tector and M is the detection box with maximum

score. The parameter N

describes the NMS thres-

hold, which removes boxes from a list of detections

with certain scores, as long as the IoU(M, b

) is gre-

ater than or equal to the NMS threshold. The result

of (10) is a conﬁdence score between zero and one,

which is used to decide what is kept or removed in

the neighborhood of M.

The Soft-NMS approach is able to weight the

score of boxes b

in the neighborhood of M.

(

, IoU(M, b

) < N

s(1 − IoU(M, b

)), IoU(M, b

) ≥ N

(11)

Equation (11) describes the rescoring function for the

Soft-NMS. The goal is to decay the scores above a

threshold N

modeled with a linear function. The sco-

res of the bounding boxes from the detection with a

higher overlap with M have a stronger potential of

being false positives. As a result we get a rating of

the bounding boxes b

with respect to M without chan-

ging the number of boxes. With an increasing overlap

between detection boxes and M the penalty increases.

At a low overlapping area between b

and M the sco-

res will be not affected. To penalize b

stronger if the

IoU becomes close to one, the pruning step can also

be modeled as a Gaussian penalty function:

= s

· e

−

IoU (M,b

)

, ∀b

∈ B \ D, (12)

where B is the set of back-projected raw detections of

YOLOv2 and D is a growing set of ﬁnal detections.

6 EXPERIMENTAL RESULTS

We evaluate our approach on two datasets, that are

single images from an omnidirectional camera of an

indoor scene. To qualitatively evaluate our detection

results we use a labeled image dataset from omnidi-

rectional camera geometry, namely the PIROPO data-

base (People in Indoor ROoms with Perspective and

Omnidirectional cameras). The input images have a

resolution of 600 × 600 pixels, are undistorted and

captured with a ceiling-mounted omnidirectional ca-

mera. The image data contain point labels on the head

of persons. To compare the results of the detection

with respect to the ground truth, we manually cre-

ate bounding box ground truth for the class person in

638 images. The subset of the labeled data of the PI-

ROPO database is available on the website mentioned

in Section 1. Subsequently, we create a new dataset

with multiple persons moving in a room, that we call

Flat. The images of this dataset have a resolution of

1680 × 1680 pixels.

We assume, that our start point is an image from

a virtual perspective camera. The creation of vir-

tual perspective views from omnidirectional images

is described in Section 4.2. We made several expe-

riments to validate the deterministic behavior of YO-

LOv2 by choosing different conﬁdence values for the

detection boxes. While the location of the bounding

box in the image is variable through reproducible at-

tempts, for generating the results we keep the con-

ﬁdence value of the detector (0.8) constant for true

positive detections.

The way, we create the perspective images from

our omnidirectional image data, is described as fol-

lows: We vary both the rotation around the x-axis and

z-axis. The rotation around the z-axis corresponds

to the azimuth of the omnidirectional camera model.

Rotating around the x-axis matches to the elevation

of the omnidirectional camera model. The elevation

is changed from 0.0 to 0.9 with a step size of 0.3. We

choose the four different perspective views to avoid

the black image proportion at the boundaries of the

omnidirectional image, which does not contain ad-

ditional information. The azimuth is changed from

−3.14 to 3.14 with a step size of 0.2, for covering the

whole room with perspective views.

As an additional constraint, we assume in our con-

ﬁguration (camera’s mounting height with respect to

the room size) that the person ﬁts in one perspective

image. After the calculation of the detection results in

the perspective images, we transform these detections

to the omnidirectional source image.

The use of a look-up-table (LUT) for back pro-

jecting the perspective images to the omnidirectional

Improved Person Detection on Omnidirectional Images with Non-maxima Supression

477

image leads to their original position of the source

image in the target image. Additionally, the corners

of the bounding boxes are also transformed with the

help of the LUT. Through the back transformation of

the bounding box corners the new boxes become lar-

ger.

6.1 Bounding Box Reﬁnement

For the grouping of bounding boxes based on their

conﬁdences the YOLOv2 object detector has an in-

cluded NMS, as described in Section 5. If the IoU

is higher than a threshold N

, then multiple boxes of

an object are merged. With the help of a small test

set, we evaluate YOLOv2’s conﬁdence both with the

internal NMS and external NMS, which produces the

same conﬁdence values with equal thresholds. To re-

ﬁne multiple bounding boxes projected from the per-

spective views in the omnidirectional image we use

three variants of NMS.

NMS. First, we apply the classical NMS (see (10))

to reduce bounding boxes with a predeﬁned overlap

threshold N

. We vary the overlap threshold N

from

0.0 to 1.0 with a step size of 0.1.

Soft-NMS. Second, the use of Soft-NMS (see (11)).

The advantage of Soft-NMS is penalizing detection

boxes b

with a higher overlap to M as long as they

are false positives. Based on modeling the overlap

of b

to M as a linear function the threshold N

con-

trols the detection scores. To be more precise, the

detection boxes with high distance to M are not inﬂu-

enced through the function in (11). The boxes that are

close together allocate a high penalty.

Soft-NMS with Gaussian Smoothing. Third, to re-

tort the problem of abrupt changes to the ranked list of

detections, we consider the Gaussian penalty function

as shown in (12). The Gaussian penalty function

is a continuous exponential function, which delivers

no penalty in case of no overlap of the boxes and a

high penalty at highly overlapped boxes. The update

was done iteratively to all scores of the remaining de-

tection boxes. Starting from the detectors raw data,

we vary the conﬁdence threshold C

with the values

0.3, 0.5, 0.7 and 0.8 and the Gaussian smoothing fac-

tor σ with the values 0.1, 0.3, 0.5, 0.7 and 0.9. The

corresponding results in Figure 1 show a single image

from the PIROPO database with the below mentio-

ned variations of thresholds in the rows and columns,

respectively. An effect, which is easily visible is

the changing number of bounding boxes in the ima-

ges. In the top right corner of the matrix (σ = 0.9

and C

= 0.3) the number of boxes for possible can-

didates of true positives is high. The opposite effect,

less number of true positives with a high accuracy is

observable in the bottom left corner of Figure 1 (va-

lues of σ = 0.1 or σ = 0.3 and C

= 0.8). Using σ for

the steering of the smoothness of the merging of the

bounding boxes makes the effects explainable. The

higher we select σ, the closer comes the exponen-

tial function in (12) to 1. Is the exponential function

close to or equal to 1, the number of boxes does not

change. With the knowledge, that the exponential

function cannot become zero, the smaller we set σ,

the smaller is the number of the bounding boxes in

the ﬁnal set D . The Gaussian smoothing function in

the Soft-NMS delivers the best results, compared to

the other variants of NMS.

6.2 Ground Truth Evaluation

A well working example of our approach is shown

in Figure 2. In Figure 2a we show an omnidirectio-

nal input image from our own dataset. The raw de-

tections of YOLOv2 with a high number of possible

true positive candidates without NMS is visualized in

Figure 2b. The ﬁnal detection result after the boun-

ding box reﬁnement is shown in Figure 2c. We apply

Soft-NMS with a Gaussian smoothing function. The

ground truth evaluation is done through manually an-

notated bounding box as shown in Figure 2c.

As scalar evaluation metrics for the detector’s re-

sult we choose precision and recall (Szeliski, 2010),

which leads to precision-recall (PR) curves. Additi-

onally, we determine the AP (Szeliski, 2010). Based

on our application we concentrate on the class person,

that makes the use of mAP obsolete for evaluation.

The precision and recall are based on the three ba-

sic error rates, namely the true positives (TP), the false

positives (FP) and the false negatives (FN). Based on

the number of these values per frame in the dataset

the precision pr and recall re are given by:

pr =

#T P

#T P + #FP

and re =

#T P

#T P + #FN

. (13)

Ideally, the pr and re values in (13) are close to

one, each. The higher the values of the evaluation

metrics, the larger the area under the PR curve, the

better the performance of the detector.

The PR curves in Figure 3 show the evaluation

of our method with manually generated ground truth.

The parameter O

is the overlap threshold for the IoU

from the resulting detection box to the ground truth

box. We consider the PR curves for NMS, Soft-NMS

and Soft-NMS with a Gaussian smoothing function

on omnidirectional images from back-projected per-

spective views and compare them to the results of the

direct application of YOLOv2 to the omnidirectional

images, namely NMS Omni.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

478

= 0.3

(a) σ = 0.1 (b) σ = 0.3 (c) σ = 0.5 (d) σ = 0.7 (e) σ = 0.9

= 0.8

Figure 1: Visualization of results for Soft-NMS with the Gaussian penalty function on an omnidirectional image from the

PIROPO database. The columns are varied over different σ of the Gaussian penalty function. In each row we change the

conﬁdence threshold C

of the Soft-NMS. See text for details.

(a) input data (b) raw detection boxes (c) ground truth (red), detection

(yellow)

Figure 2: Detection result on omnidirectional images for the class person on the Flat dataset.

The steepest curve in Figure 3 is NMS Omni that

reaches a precision of 1 at small recall. The constella-

tion validates our observations, that the YOLOv2 de-

tector localizes the objects in omnidirectional images

accurate with a high number of false negatives.

Table 1: Evaluation on PIROPO and Flat dataset with

average precision for class person.

PIROPO Flat

NMS 56.6 68.3

Soft-NMS Gauss

64.6 77.6

Soft-NMS 57.1 68.1

Omni 41.4 69.6

For further quantitative evaluation we compute the

AP that is the area under the PR curves of Figure 3

and visualized in Table 1. The overlap threshold

= 0.5 follows the PASCAL VOC notation (Eve-

ringham et al., 2010). Additionally, we determine the

weighted mean values of precision for NMS, Soft-

NMS with Gaussian smoothing, Soft-NMS and apply

YOLOv2 to the omnidirectional images directly. The

best (i.e. highest) value of AP is highlighted in bold.

We reach an AP for the class person of 64.6% through

Soft-NMS with a Gaussian smoothing function on PI-

ROPO and 77.6% on the Flat Dataset, respectively.

Salient points of the PR curves in Figure 3 are in-

tersections of the worst performing and the highest

performing approach. Looking at the NMS Omni

graph (blue) and the Soft-NMS Gauss graph (blue)

we observe an intersection at a precision of 0.83 and

recall of 0.35. From this point up to recall of 0.75

the bounding box reﬁnement method with Soft-NMS

Gauss outperforms all other curves without signiﬁ-

cant decrease of precision on PIROPO.

Another people detector on omnidirectional ima-

ges is (Krams and Kiryati, 2017) that use DET curves

on BOMNI database (Demiröz et al., 2012) for evalu-

Improved Person Detection on Omnidirectional Images with Non-maxima Supression

479

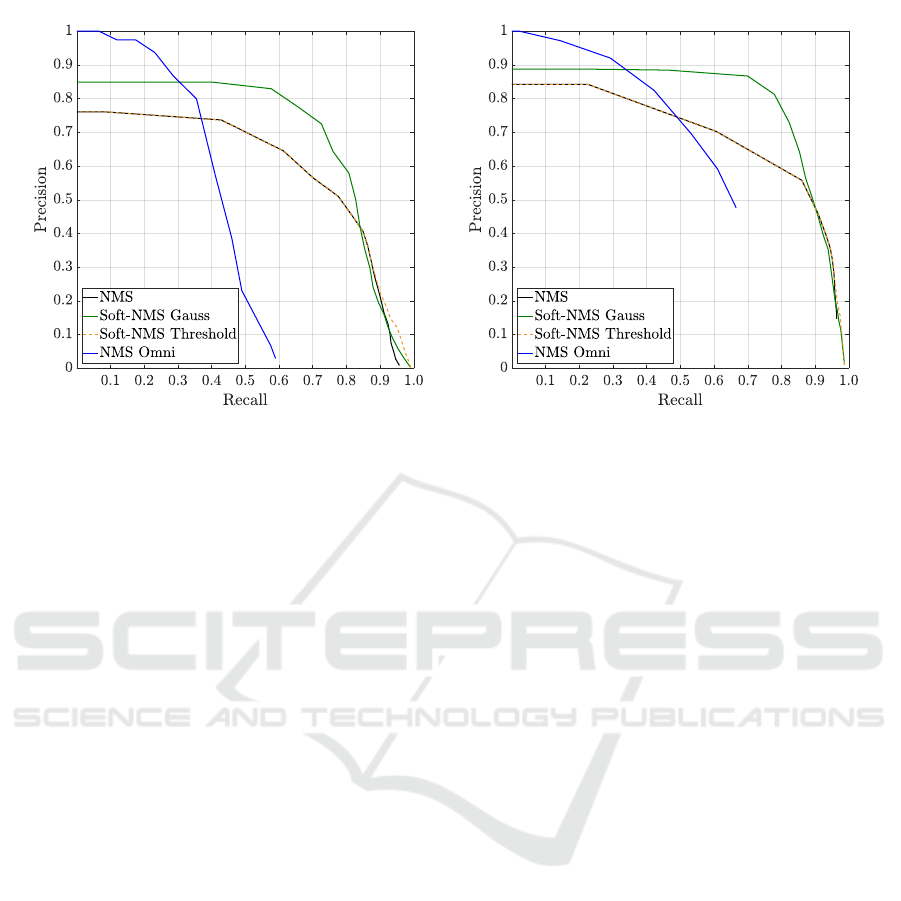
(a) Precision-recall curve on PIROPO (b) Precision-recall curve on our own data (Flat)

Figure 3: The precision-recall curve for NMS, Soft-NMS and Soft-NMS with Gaussian smoothing function on two different

omnidirectional image datasets from back-projected perspective views. The precision-recall curve of NMS Omni show the

direct application of YOLOv2 to the omnidirectional images. O

= 0.5 is the overlap threshold for the IoU from the resulting

detection box to the ground truth box.

ation, therefore we don’t compare our results to this

people detection approach. Due to unavailable public

training datasets with labeled ﬁsh-eye images, we did

not do ﬁne-tuning of YOLOv2 from initial weights

with omnidirectional image data.

We make the following observations. After the

back projection from the perspective to the omnidi-

rectional view bounding boxes are oversized, because

the axis parallelism is not preserved. Through for-

cing parallel box edges with respect to the axis in the

omnidirectional image coordinate system, we do not

receive minimal enclosing rectangles.

For the most of the recall and precision values the

graphs of NMS and Soft-NMS are equal. Only at pre-

cisions smaller than 0.2 we observe different trends as

shown in Figure 3.

7 CONCLUSION

In this work we present a method to detect persons in

omnidirectional images based on CNNs. We apply a

state-of-the-art object detector, namely YOLOv2, to

virtual perspective views and transform the detecti-

ons back to the omnidirectional source images. For

the transformation the step size of the two angles, azi-

muth and elevation was selected in a way, that the

perspective images are highly overlapped. In contrast

to the standard implementation of YOLOv2 we use

the raw detection boxes instead of applying a NMS as

bounding box reﬁnement at the end of the network.

After back projection from perspective to omnidi-

rectional images we apply three different NMS met-

hods for pruning the back-projected bounding boxes

based on conﬁdence and overlap.

We evaluated the bounding box reﬁnement met-

hods, NMS, Soft-NMS with a threshold and Soft-

NMS with Gaussian smoothing on our manually ge-

nerated ground truth on the PIROPO database and the

Flat dataset using PR curves and AP. At O

= 0.5 we

reach an AP for the class person of 64.6% on PIROPO

and 77.6% on Flat through Soft-NMS with Gaussian

smoothing.

Based on the work of transformation from omni-

directional to perspective and vice versa there are a

couple of ideas for future work. One of our central

questions is: how the detection rate of the object de-

tector changes if we consider the lens distortion para-

meters?

To close the gap of missing omnidirectional

ground truth, we will create labeled synthetic and

real-world data. To simplify the data generation we

can use our approach followed by manually reﬁne-

ment of detections to create ground truth on omni-

directional images. To improve the approach at the

point of projecting bounding boxes from perspective

to omnidirectional model it is necessary to minimize

the effect of oversized boxes in omnidirectional ima-

ges.

VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications

480

ACKNOWLEDGEMENTS

This work is funded by the European Regional Deve-

lopment Fund (ERDF) and the Free State of Saxony

under the grant number 100-241-945.

REFERENCES

Bodla, N., Singh, B., Chellappa, R., and Davis, L. S. (2017).

Soft-nms - improving object detection with one line of

code. In IEEE International Conference on Compu-

ter Vision, ICCV 2017, Venice, Italy, October 22-29,

2017, pages 5562–5570.

Cinaroglu, I. and Bastanlar, Y. (2014). A direct approach

for human detection with catadioptric omnidirectio-

nal cameras. In Signal Processing and Communicati-

ons Applications Conference (SIU), 2014 22nd, pages

2275–2279. IEEE.

Cohen, T. S., Geiger, M., Köhler, J., and Welling, M.

(2018). Spherical CNNs. In International Conference

on Learning Representations.

Dai, J., Li, Y., He, K., and Sun, J. (2016). R-FCN: object de-

tection via region-based fully convolutional networks.

In Advances in Neural Information Processing Sys-

tems 29: Annual Conference on Neural Information

Processing Systems 2016, December 5-10, 2016, Bar-

celona, Spain, pages 379–387.

del Blanco, C. R. and Carballeira, P. (2016). The piropo da-

tabase (people in indoor rooms with perspective and

omnidirectional cameras). https://sites.google.com/

site/piropodatabase/, unpublished dataset.

Demiröz, B. E.,

Ismail Ari, Ero

glu, O., Salah, A. A., and

Akarun, L. (2012). Feature-based tracking on a multi-

omnidirectional camera dataset. In 2012 5th Interna-

tional Symposium on Communications, Control and

Signal Processing, pages 1–5.

Everingham, M., Gool, L. J. V., Williams, C. K. I., Winn,

J. M., and Zisserman, A. (2010). The pascal visual

object classes (VOC) challenge. International Journal

of Computer Vision, 88(2):303–338.

Findeisen, M., Meinel, L., Heß, M., Apitzsch, A., and Hirtz,

G. (2013). A fast approach for omnidirectional sur-

veillance with multiple virtual perspective views. In

Proceedings of Eurocon 2013, International Confe-

rence on Computer as a Tool, Zagreb, Croatia, July

1-4, 2013, pages 1578–1585.

Girshick, R. B., Donahue, J., Darrell, T., and Malik, J.

(2013). Rich feature hierarchies for accurate ob-

ject detection and semantic segmentation. CoRR,

abs/1311.2524.

Hartley, R. and Zisserman, A. (2006). Multiple view geome-

try in computer vision (2. ed.). Cambridge University

Press.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep re-

sidual learning for image recognition. In 2016 IEEE

Conference on Computer Vision and Pattern Recog-

nition, CVPR 2016, Las Vegas, NV, USA, June 27-30,

2016, pages 770–778.

Krams, O. and Kiryati, N. (2017). People detection in top-

view ﬁsheye imaging. In 2017 14th IEEE Internatio-

nal Conference on Advanced Video and Signal Based

Surveillance (AVSS), pages 1–6.

Krasin, I., Duerig, T., Alldrin, N., Ferrari, V., Abu-El-

Haija, S., Kuznetsova, A., Rom, H., Uijlings, J., Po-

pov, S., Veit, A., Belongie, S., Gomes, V., Gupta,

A., Sun, C., Chechik, G., Cai, D., Feng, Z., Naray-

anan, D., and Murphy, K. (2017). Openimages: A

public dataset for large-scale multi-label and multi-

class image classiﬁcation. Dataset available from

https://github.com/openimages.

Lee, S., Sung, J., Yu, Y., and Kim, G. (2018). A memory

network approach for story-based temporal summari-

zation of 360

◦

videos. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion, pages 1410–1419.

Li, W., Wang, L., Li, W., Agustsson, E., and Gool, L. V.

(2017). Webvision database: Visual learning and un-

derstanding from web data. CoRR, abs/1708.02862.

Lin, T., Maire, M., Belongie, S. J., Hays, J., Perona, P.,

Ramanan, D., Dollár, P., and Zitnick, C. L. (2014).

Microsoft COCO: common objects in context. In

Computer Vision - ECCV 2014 - 13th European Con-

ference, Zurich, Switzerland, September 6-12, 2014,

Proceedings, Part V, pages 740–755.

Liu, W., Anguelov, D., Erhan, D., Szegedy, C., Reed, S. E.,

Fu, C., and Berg, A. C. (2016). SSD: Single Shot Mul-

tiBox Detector, pages 21–37.

Redmon, J., Divvala, S. K., Girshick, R. B., and Farhadi, A.

(2016). You only look once: Uniﬁed, real-time object

detection. In 2016 IEEE Conference on Computer Vi-

sion and Pattern Recognition, CVPR 2016, Las Vegas,

NV, USA, June 27-30, 2016, pages 779–788.

Redmon, J. and Farhadi, A. (2017). YOLO9000: better, fas-

ter, stronger. In 2017 IEEE Conference on Computer

Vision and Pattern Recognition, CVPR 2017, Hono-

lulu, HI, USA, July 21-26, 2017, pages 6517–6525.

Ren, S., He, K., Girshick, R. B., and Sun, J. (2015). Fas-

ter R-CNN: towards real-time object detection with

region proposal networks. In Cortes, C., Lawrence,

N. D., Lee, D. D., Sugiyama, M., and Garnett, R.,

editors, Advances in Neural Information Processing

Systems 28: Annual Conference on Neural Informa-

tion Processing Systems 2015, December 7-12, 2015,

Montreal, Quebec, Canada, pages 91–99.

Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,

Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bern-

stein, M. S., Berg, A. C., and Li, F. (2015). Imagenet

large scale visual recognition challenge. International

Journal of Computer Vision, 115(3):211–252.

Szeliski, R. (2010). Computer Vision: Algorithms and

Applications. Springer-Verlag New York, Inc., New

York, NY, USA, 1st edition.

Improved Person Detection on Omnidirectional Images with Non-maxima Supression

481