
Circular Fringe Projection Method for
3D Profiling of High Dynamic Range Objects
Jagadeesh Kumar Mandapalli
1
, Sai Siva Gorthi
2
, Ramakrishna Sai Gorthi
1
and Subrahmanyam Gorthi
1
1
Department of Electrical Engineering, Indian Institute of Technology, Tirupati, Andhra Pradesh, 517506, India
2
Department of Instrumentation and Applied Physics, Indian Institute of Science, Bangalore, 560012, India
Keywords:
3D Shape Measurement, Fourier Transform, Fringe Projection, High Dynamic Range.
Abstract:
Fringe projection profilometry is a widely used active optical method for 3D profiling of real-world objects.
Linear fringes with sinusoidal intensity variations along the lateral direction are the most commonly used
structured pattern in fringe projection profilometry. The structured pattern, when projected onto the object of
interest gets deformed in terms of phase modulation by the object height profile. The deformed fringes are
demodulated using methods like Fourier transform profilometry for obtaining the wrapped phase information,
and the unwrapped phase provides the 3D profile of the object. One of the key challenges with the conventional
linear fringe Fourier transform profilometry (LFFTP) is that the dynamic range of the object height that can
be measured with them is very limited.
In this paper we propose a novel circular fringe Fourier transform profilometry (CFFTP) method that uses
circular fringes with sinusoidal intensity variations along the radial direction as the structured pattern. A new
Fourier transform-based algorithm for circular fringes is also proposed for obtaining the height information
from the deformed fringes. We demonstrate that, compared to the conventional LFFTP, the proposed CFFTP
based structure assessment enables 3D profiling even at low carrier frequencies, and at relatively much higher
dynamic ranges. The reasons for increased dynamic range with circular fringes stem from the non-uniform
sampling and narrow band spectrum properties of CFFTP. Simulation results demonstrating the superiority of
CFFTP over LFFTP are also presented.
1 INTRODUCTION
3D shape reconstruction techniques are widely used
in various fields like industrial automation, compu-
ter vision, and medical imaging. Among the availa-
ble methods, fringe projection technique is a com-
monly used active optical method (Gorthi and Ra-
stogi, 2010) for 3D profiling because of its righte-
ous properties like non-contact based non-destructive
operation and its ability to give high resolution. Furt-
hermore, with the fringe projection technique, the 3D
shape of an object can be reconstructed from a single
image, and thus it can be used for real time 3D shape
measurements.
Fig. 1 shows a typical experimental set-up used in
fringe projection technique. A structured pattern, usu-
ally linear fringes with sinusoidal intensity variation
along the lateral direction, is projected onto the object
of interest. The projected pattern gets phase modula-
ted in accordance with the object height profile (or
depth profile), and it is recorded with a camera. The
recorded pattern is phase-demodulated and the result
is unwrapped for obtaining the actual height of the
object at each pixel location.
Several methods have been developed in the lite-
rature for phase demodulation, e.g., Fourier transform
profilometry (Takeda and Mutoh, 1983; Lin and Su,
1995; Su and Chen, 2001), windowed Fourier trans-
form profilometry (Kemao, 2004; Kemao, 2007),
spatial phase detection method (Toyooka and Iwaasa,
1986; Sajan et al., 1998), and wavelet transform met-
hod (Dursun et al., 2004; Zhong and Weng, 2004;
Gdeisat et al., 2006). Since phase demodulation met-
hods result in wrapped phase whose values are map-
ped to the range [−π, π), these are generally followed
by a phase unwrapping procedure. Phase unwrap-
ping is performed using methods like ZπM (Dias and
Leit
˜
ao, 2002), Goldstein’s phase unwrapping (Gold-
stein et al., 1988), branch cut (Gutmann and Weber,
2000), flood fill (Asundi and Wensen, 1998), region
Mandapalli, J., Gorthi, S., Gorthi, R. and Gorthi, S.
Circular Fringe Projection Method for 3D Profiling of High Dynamic Range Objects.
DOI: 10.5220/0007389608490856
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 849-856
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
849
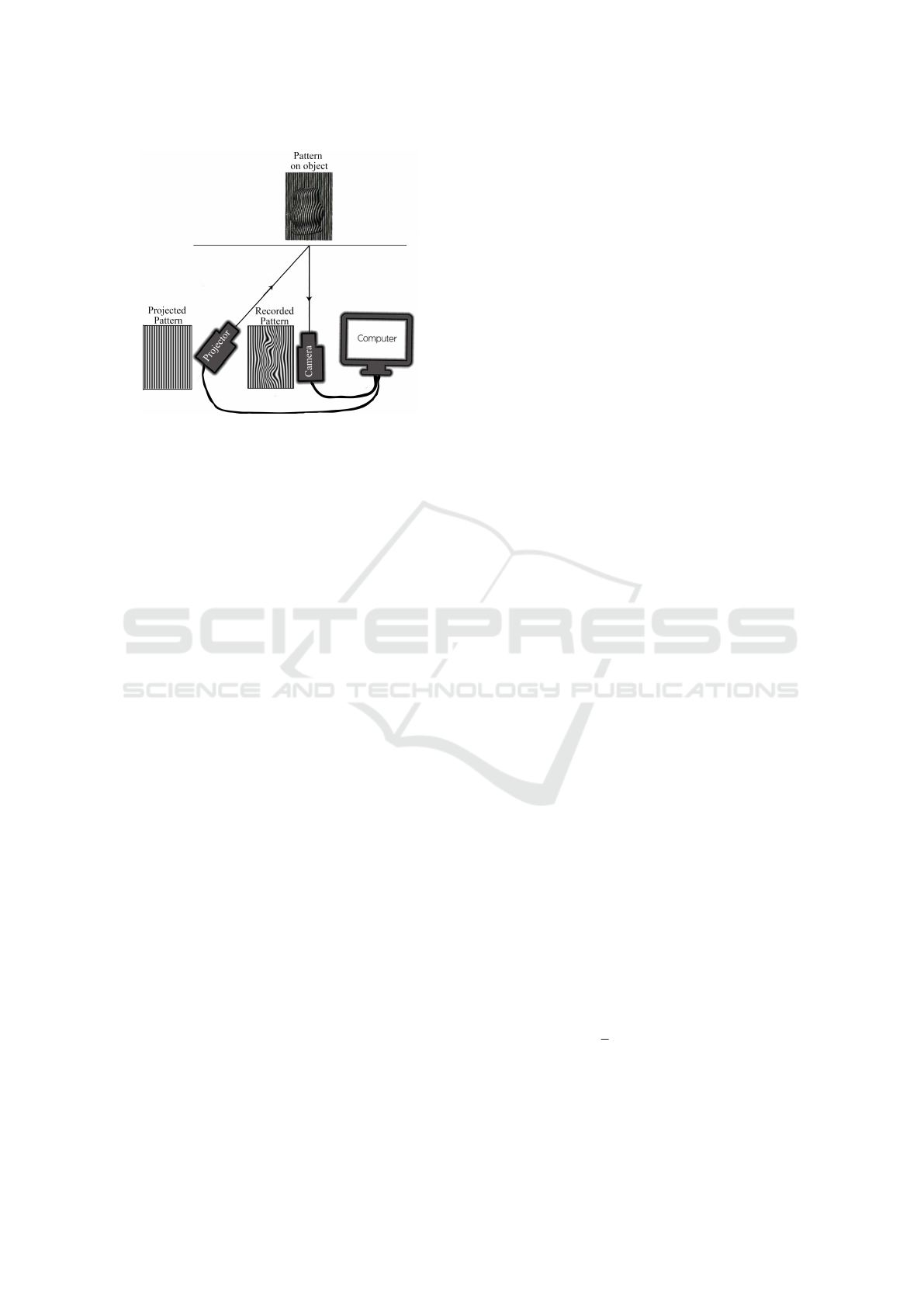
Figure 1: Schematic diagram illustrating the principle of
fringe projection profilometry. Structured pattern generated
in the computer is projected onto the object (lying on refe-
rence plane) through the projector and the phase modulated
pattern is captured through the camera for further analysis.
growing phase unwrapping (Baldi, 2003), regularized
phase tracking (Servin et al., 1999), and multilevel
quality guided phase unwrapping algorithm (Zhang
et al., 2007). It can be noted that the aforementi-
oned phase-demodulation algorithms are applicable
only for linear fringes.
Various types of structured patterns have been pro-
posed in the literature for fringe projection profilome-
try. Typically, the intensity profiles of these structu-
red patterns are repetitive along the lateral direction.
Linear fringes having sinusoidal intensity profile al-
ong the lateral direction are the most commonly used
fringe pattern (Gorthi and Rastogi, 2010). Other
types of patterns include hexagonal grating (Iwata
et al., 2008), linear fringes with triangular intensity
profile (Jia et al., 2008) and sawtooth intensity pro-
file (Chen et al., 2005) along the lateral direction.
In this paper, we propose a novel circular fringe-
based profilometry that employs circular fringes with
sinusoidal intensity variations along the radial di-
rection as the structured pattern. We also propose a
new approach for quantifying the underlying phase
of the radially varying circular fringes. Unlike the
existing linear fringe Fourier transform profilome-
try (LFFTP), the use of circular fringes in the pro-
posed circular fringe Fourier transform profilometry
(CFFTP) have several advantages like relatively more
accurate 3D profiling of the objects at lower carrier
frequencies and even at high dynamic range of the ob-
ject height profile. All these aspects are presented in
detail in the rest of this paper. We note that (Zhao
et al., 2016) have used circular fringes with sinusoi-
dal intensity variations along radial direction. But it is
used for a different purpose of coming up with a new
hardware configuration of camera and projector set-
up, for obtaining a simplified calibration of 3D height
and thus it does not include any algorithms or analysis
for dealing with circular fringe pattern.
The rest of the paper is organized as follows.
Section 2 presents the details of the existing and pro-
posed methods. Section 3 presents a detailed evalua-
tion of the proposed method. Finally, conclusions are
presented in section 4.
2 METHODOLOGY
This section first presents the details of the exis-
ting Linear Fringe Fourier Transform Profilometry
(LFFTP). It is then followed by the details of the pro-
posed Circular Fringe Fourier Transform Profilome-
try (CFFTP).
2.1 Existing Linear Fringe Fourier
Transform Profilometry
The sequence of steps followed for 3D profiling with
LFFTP is depicted with the aid of Fig. 2 along with
illustrative figures at each stage. The intensity profile
of the projected pattern in LFFTP (step 1 of Fig. 2) is
I
p
L
(x, y) = a(x, y) + b(x, y) cos(2π f
c
x + Φ
0
)
where f
c
is the carrier or fringe frequency, (x, y) are
the spatial coordinates, a represents intensity variati-
ons in the background, b represents the non-uniform
reflectivity of the diffusely reflecting object and Φ
0
is
the initial phase (assumed to be zero).
The intensity profile of the recorded phase modu-
lated pattern (step 2 of Fig. 2) is
I
r
L
(x, y) = a(x, y) + b(x, y) cos(2π f
c
x + Φ
L
(x, y)).
(1)
Φ
L
(x, y) in Eq. 1 is the phase term introduced by
the object height profile. In fringe projection techni-
que, generally the underlying phase term in the phase
modulated pattern contains the information about the
shape of the object. Any of the fringe analysis techni-
ques mentioned in the preceding section can be used
on the modulated pattern for quantifying the under-
lying phase term. For ease of analysis, rewriting Eq. 1
in terms of complex exponentials using Euler formula
gives
I
r
L
(x, y) = a(x, y) +
1
2
[c(x, y)e
j2π f
c
x
+ c
∗
(x, y)e
− j2π f
c
x
]
(2)
where c(x , y) = b(x , y) e
jΦ
L
(x,y)
for real b(x,y), and
c
∗
indicates conjugate of c. The desired parameter
Φ
L
(x, y) can be found by retrieving either c(x, y) or
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
850

c
∗
(x, y) from Eq. 2. LFFTP achieves the same by
applying Fourier transform analysis. In LFFTP, the
phase modulated pattern (I
r
L
(x, y)) is first transformed
to Fourier domain (step 3 of Fig. 2). Fourier domain
representation of Eq. 2 is
F {I
r
L
} = A( f
x
, f
y
)+
1
2
[C( f
x
− f
c
, f
y
)+C
∗
( f
x
+ f
c
, f
y
)]
(3)
where F represents Fourier transform. As
a(x, y) represents background intensity variations, the
spectrum of A( f
x
, f
y
) will be in the low frequency
region. The spectral components around carrier fre-
quency ( f
c
) are extracted using a bandpass filter, and
is given by
1
2
C( f
x
− f
c
, f
y
). The filtered spectrum
is then DC shifted (step 4 of Fig. 2), i.e., the re-
sultant spectrum is shifted such that the dominant
spectral component which was previously occurring
at f
c
, occurs now at zero Hertz. The result of DC shift
is
1
2
C( f
x
, f
y
).
The phase function found after the application of
inverse Fourier transform on the DC shifted signal is
wrapped (step 5 of Fig. 2) in the interval [−π, π). On
unwrapping (step 6 of Fig. 2), the result gives the 3D
profile of the object of interest.
Figure 2: Block diagram illustrating the existing linear
fringe Fourier transform profilometry (LFFTP) algorithm.
2.2 Proposed Circular Fringe Fourier
Transform Profilometry
The sequence of steps required for 3D profiling with
CFFTP is depicted with the aid of Fig. 5 along with
illustrative figures at each stage. In CFFTP, the in-
tensity profile of the circular fringe pattern projected
onto the object (step 1 of Fig. 5) is
I
p
C
(x, y) = a(x, y) + b(x, y) cos(2π f
c
p
x
2
+ y
2
). (4)
Let φ
p
(x, y) represent the argument of the cos
function in the above projection equation, i.e., let
φ
p
(x, y) = 2π f
c
p
x
2
+ y
2
. Notice that φ
p
(x, y) has the
shape of a cone for varying values of x and y as shown
in Fig. 3. The minimum value of φ
p
(x, y) is zero, and
it occurs at the origin.
Figure 3: Phase function (φ
p
(x, y)) of the projected pattern.
It has the shape of a cone with a minimum values of zero at
origin.
When the aforementioned circular fringe pattern
is projected onto the object of interest, based on the
height profile of the object at that point, the pattern
accordingly gets shifted in the x direction. Hence, the
intensity profile of the recorded phase modulated pat-
tern in CFFTP (step 2 of Fig. 5) is given by:
I
r
C
(x, y) = a(x, y)+b(x, y) cos(2π f
c
q
(x + δ
y
(x))
2
+ y
2
).
(5)
Let φ
r
(x, y) represent the phase function associa-
ted with the above recorded pattern, and is given by
φ
r
(x, y) = 2π f
c
p
(x + δ
y
(x))
2
+ y
2
. Note that φ
r
(x, y)
differs with φ
p
(x, y) in terms of the modulating term
δ
y
(x). It can be noted that while the vortex of the pro-
jected pattern is at the origin, it is shifted by a value of
δ
0
(0) along the x-axis for the recorded pattern. δ
y
(x)
is introduced due to the object height profile, and thus
it contains the information about the shape of the ob-
ject. δ
y
(x) can be recovered from φ
r
(x, y) if f
c
, x and
y are known. Fringe frequency ( f
c
) is engineering
choice and is known. The parameters x and y present
in φ
p
(x, y) can be used to find δ
y
(x) from φ
r
(x, y). Sol-
ving the phase functions φ
r
(x, y) and φ
p
(x, y) for δ
y
(x)
Circular Fringe Projection Method for 3D Profiling of High Dynamic Range Objects
851

results in the following quadratic equation in δ
y
(x):
δ
2
y
(x) + 2x δ
y
(x) +
(φ
p
(x, y))
2
− (φ
r
(x, y))
2
(2π f
c
)
2
= 0 (6)
The above quadratic equation results in two roots, and
one of them corresponds to the height profile of the
object. The procedure for finding out the actual root
that corresponds to the object height is presented in
the later part of this section.
As stated earlier, all the fringe analysis algorithms
mentioned in section 1 are designed for linear fringes,
and they cannot be directly applied for circular frin-
ges. However, as illustrated in Fig. 4, circular frin-
ges in the rectangular coordinates become linear frin-
ges in the polar coordinates. Hence, any of the linear
fringe analysis methods can be applied after transfor-
ming circular fringes into polar coordinates.
(a) Circular fringes (b) Polar equivalent of
circular fringes
Figure 4: Circular fringes in Cartesian coordinates and their
polar equivalents. Horizontal axis in polar representation is
radius r and vertical axis is angle θ.
The proposed algorithm for retrieving the true
phase of the recorded fringe pattern
Proposed Algorithm for Phase Retrieval
1. As discussed above, in order to be able to ap-
ply any of the existing linear fringe analysis
algorithms, the circular fringe has to be first
transformed into polar coordinates by considering
the centre of the circular fringes as the origin.
To this end, the centre of the recorded circular
fringe is computed, and the coordinate transfor-
mation is applied. The centre of the recorded
circular fringe in our experiments is computed
using ‘imfindcircles’ function in MATLAB. Let
(x
c
, 0) represent the centre of the recorded circular
fringe. Then the equation representing the recor-
ded fringe transformed into the polar coordinates
is given by:
I
r
C
(r
0
, θ) = a(r
0
, θ) + b(r
0
, θ) cos(2π f
c
r
0
), (7)
where
r
0
=
q
(x − x
c
+ δ
y
(x))
2
+ y
2
,
Figure 5: Block diagram illustrating the proposed circular
fringe Fourier transform profilometry (CFFTP) algorithm.
θ = tan
−1
y
(x − x
c
+ δ
y
(x))
.
The result of this polar coordinates transformation
is illustrated in step 3 of Fig. 5.
2. Fourier transform profilometry is applied on the
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
852
fringe pattern represented by Eq. 7. The resulting
frequency domain representation is given by:
F {I
r
C
} = A( f
r
0
, f
θ
) +
1
2
B( f
r
0
− f
c
, f
θ
)+
1
2
B( f
r
0
+ f
c
, f
θ
). (8)
Step 4 of Fig. 5 illustrates the resulting magnitude
spectrum.
3. The spectral components around carrier frequency
are extracted using a bandpass filter. The result of
bandpass filtering is given by
1
2
B( f
r
0
− f
c
, f
θ
), and
it is illustrated in step 5 of Fig. 5.
4. Inverse Fourier transform is applied on the output
of the bandpass filter, and the result is given by:
1
2
b(r
0
, θ) e
j2π f
c
r
0
. As discussed in section 1, the
resultant phase of the above expression is wrap-
ped into the range [−π, π). It is then unwrapped
using any of the phase unwrapping methods, and
is illustrated in step 6 of Fig. 5.
5. The unwrapped phase is transformed back into
Cartesian coordinates to get φ
r
(x, y), and is illus-
trated in step 7 of Fig. 5.
The above mentioned algorithm can extract
φ
p
(x, y), φ
r
(x, y), and the remaining task now is to
compute δ
y
(x) based on Eq. 6.
Solving the quadratic Eq. 6 for each row (y), by
substituting φ
p
and φ
r
, gives two roots for δ
y
(x) as
shown in step 8 of Fig. 5. Two such roots found from
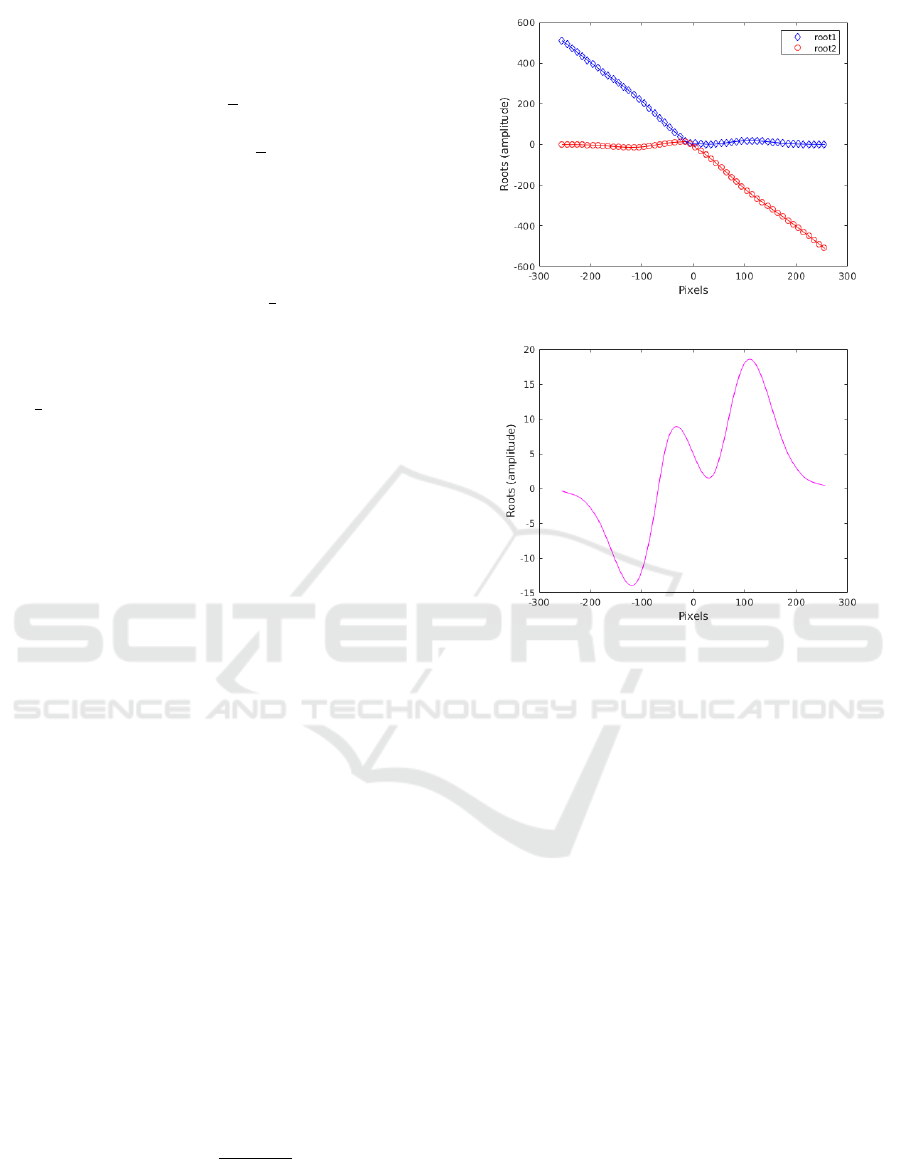
Eq. 6 for one of the rows are shown in Fig. 6(a). The
actual root that corresponds to the height profile of the
object is obtained by imposing the following two con-
straints. Firstly, it is considered that the height profile
is continuous over neighbourhood spatial locations.
Secondly, the difference in the position of vortices of
φ
p
(x, y) and φ
r
(x, y) is relatively nearer to the average
value of the object height profile. Fig. 6(b) shows the
actual root extracted from the two roots displayed in
Fig. 6(a) after imposing the above constraints. Ap-
plying the same procedure for all the rows gives the
actual root corresponding to the shape of the object as
shown in step 9 of Fig. 5.
Finally, after the computation of δ
y
(x), the actual
height profile of the object is obtained using the fol-
lowing calibration equation (Zhang et al., 2002)
H(x, y) =
k δ
y
(x)
d − δ
y
(x)
(9)
where k is the distance between the camera and re-
ference plane, d is the baseline distance between the
camera and projector.
(a) Roots obtained by solving the quadratic Eq. 6.
(b) Actual root extracted form the two roots.
Figure 6: Illustration of the two roots obtained by solving
Eq. 6 for one of the rows, and the extracted actual root that
corresponds to the height profile of the object.
3 RESULTS
In this section, we present a comparison of the results
from the proposed circular fringe projection based
method (CFFTP) with the results from the existing li-
near fringe projection based method (LFFTP). More
specifically, the accuracies of the CFFTP and LFFTP
methods are evaluated for varying dynamic range of
the objects, and also for varying fringe frequencies.
The evaluations are performed on simulated data
with varying shapes and dynamic ranges. Various
shapes are generated through Gaussian Mixture Mo-
dels (GMM) by randomly choosing the locations of
the peaks and valleys with the help of a random num-
ber generator. Fig. 7 shows samples of such randomly
generated object height profiles. While performing
evaluations for varying dynamic range, those rand-
omly generated shapes are scaled accordingly.
Fig. 8 shows the results obtained from LFFTP and
CFFTP when reconstructing the height profile of the
simulated object shown in Fig. 7(a). The fringe fre-
Circular Fringe Projection Method for 3D Profiling of High Dynamic Range Objects
853

(a) (b)
(c) (d)
Figure 7: Sample simulated objects with arbitrary height
profiles.
quency and the dynamic range values used for this
particular evaluation are 20 Hz and ±24 pixels re-
spectively. The left and the right columns of this fi-
gure present the results from the LFFTP and CFFTP
respectively. First row in Fig. 8 shows the projected
patterns. Second row of the same figure shows the
modulated patterns in LFFTP and CFFTP. Fig. 8(e) is
the magnitude spectrum of the deformed linear fringe
pattern, and Fig. 8(f) is the magnitude spectrum of the
deformed circular fringe pattern after transforming
it into polar coordinates. It can be observed from
Fig. 8(e) and Fig. 8(f) that for a given height profile
of the object, the spectral variations in the magnitude
spectrum of LFFTP are relatively more than that of in
CFFTP. Fig. 8(g) and Fig. 8(h) show 3D profiling re-
sults obtained from LFFTP and CFFTP respectively.
In order to quantify the accuracies of the results
from LFFTP and CFFTP, the difference between the
ground truth and the reconstructed output from these
methods are computed at each pixel. These values are
normalized by dividing with the dynamic range (i.e.,
the difference between the maximum and minimum
values of the ground truth). Fig. 8(i) and Fig. 8(j)
show the resulting error plots for LFFTP and CFFTP
respectively. Maximum normalized error values are
found to be 0.37 for LFFTP, and 0.064 for CFFTP.
Thus, the proposed CFFTP resulted in more accurate
3D reconstruction compared to the existing LFFTP.
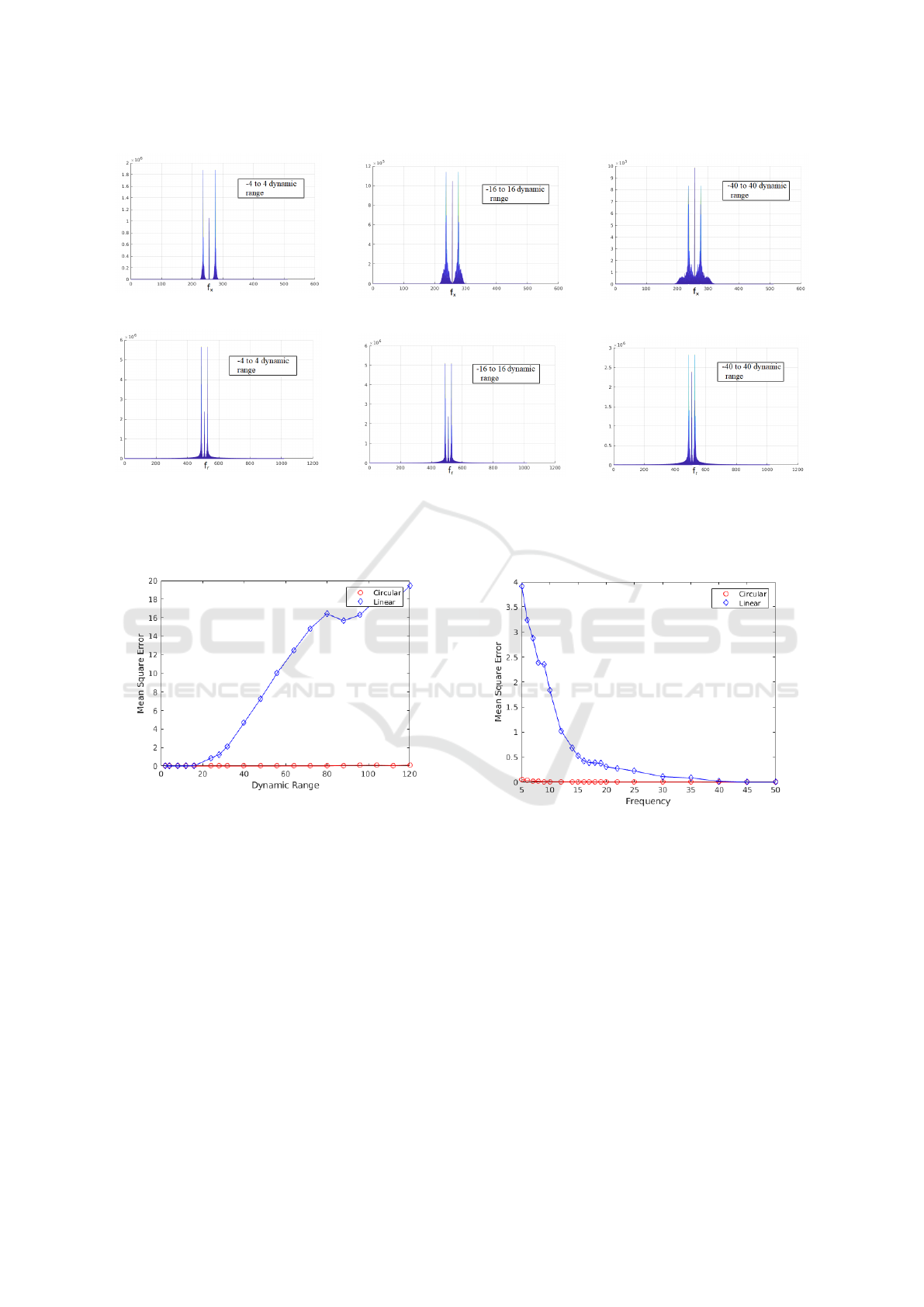
We have also studied the effects of varying the dy-
namic range on the magnitude spectrums of LFFTP
and CFFTP. Fig. 9 presents the magnitude spectrums
of LFFTP and CFFTP for varying dynamic range. It
can be observed from these results that for the propo-
sed CFFTP, aliasing in frequency domain is starting
to occur at relatively high dynamic range values than
(a) (b)
(c) (d)
(e) (f)
(g) (h)
(i) (j)
Figure 8: Simulation results from the existing LFFTP and
the proposed CFFTP are presented in the first and second
columns respectively. Projected fringes, deformed fringes,
magnitude spectrum, reconstructed object height profiles,
and normalized error values are presented in rows 1, 2, 3, 4,
and 5 respectively.
that LFFTP. Because of such narrowband properties
of CFFTP, it is able to more accurately reconstruct the
3D profiles of the objects having high dynamic range
than LFFTP.
Fig. 10 shows the effect of varying the dynamic
range on the 3D reconstruction results of LFFTP and
CFFTP. For this purpose, all the height profiles shown
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
854
(a) LFFTP with a dynamic range of
±4.
(b) CFFTP with a dynamic range of
±4.
(c) LFFTP with a dynamic range of
±16.
(d) CFFTP with a dynamic range of
±16.
(e) LFFTP with a dynamic range of
±40.
(f) CFFTP with a dynamic range of
±40.
Figure 9: Illustration of spectral changes in the magnitude spectrums of the LFFTP and the proposed CFFTP with varying
dynamic range.
Figure 10: Plot of normalized MSE showing the compara-
tive performance of LFFTP and CFFTP for increasing dyna-
mic range of the object height. CFFTP has low normalized
MSE at high dynamic ranges of object height for a fringe
frequency of 20 Hz.
in Fig. 7 are considered, and Mean Square Error
(MSE) values presented in Fig. 10 are the averaged
values computed across all the datasets. Some of the
intermediate MSE values corresponding to this evalu-
ation are presented in Table 1. Notice that if the nor-
malized MSE value is 0.85, it means that the MSE is
85% of the dynamic range of the object height. Thus,
CFFTP is found to result in significantly lower error
values than the existing LFFTP, particularly at high
dynamic range values. Finally, Fig. 11 shows norma-
lized MSE values for varying fringe frequencies, for
a dynamic range of ±24. Similar to the preceding ex-
periment, MSE values are averaged across all the da-
Figure 11: Plot of normalized MSE showing the compa-
rative performance of LFFTP and CFFTP for increasing
fringe frequency. CFFTP has low normalized MSE at low
fringe frequency for a dynamic range of ±24.
tasets. It can be observed that while both LFFTP and
CFFTP perform equally well at high frequencies, the
proposed CFFTP significantly outperforms LFFTP at
low frequencies.
4 CONCLUSIONS
In this paper, we have presented a new circular fringe
Fourier transform profilometry (CFFTP) method for
3D profiling of objects. Unlike the conventional linear
fringes, the proposed method uses circular fringes
Circular Fringe Projection Method for 3D Profiling of High Dynamic Range Objects
855

Table 1: Normalized MSE values in case of LFFTP and
CFFTP for increasing dynamic range of object height.
Dynamic range of Normalized MSE
the object height LFFTP CFFTP
± 4 0.00 0.00
± 8 0.00 0.00
± 16 0.02 0.00
± 24 0.85 0.00
± 40 4.66 0.00
± 56 10.01 0.00
± 80 16.43 0.01
± 120 19.44 0.10
± 160 18.06 5.83
with sinusoidal intensity variations along the radial
direction. A new algorithm is also proposed for retrie-
ving the phase information from the circular fringes.
The proposed CFFTP has been evaluated for varying
dynamic ranges and fringe frequencies. It is found
that the proposed algorithm significantly outperforms
the existing LFFTP, particularly at high dynamic ran-
ges and low fringe frequencies. In the future work,
we plan to evaluate the proposed CFFTP method for
the 3D profiling of the real-world objects.
REFERENCES
Asundi, A. and Wensen, Z. (1998). Fast phase-unwrapping
algorithm based on a gray-scale mask and flood fill.
Applied optics, 37(23):5416–5420.
Baldi, A. (2003). Phase unwrapping by region growing.
Applied optics, 42(14):2498–2505.
Chen, L., Quan, C., Tay, C. J., and Fu, Y. (2005). Shape me-
asurement using one frame projected sawtooth fringe
pattern. Optics communications, 246(4-6):275–284.
Dias, J. M. and Leit
˜
ao, J. M. (2002). The ZπM algorithm:
a method for interferometric image reconstruction in
SAR/SAS. IEEE Transactions on Image processing,
11(4):408–422.
Dursun, A.,
¨
Ozder, S., and Ecevit, F. N. (2004). Conti-
nuous wavelet transform analysis of projected fringe
patterns. Measurement Science and Technology,
15(9):1768.
Gdeisat, M. A., Burton, D. R., and Lalor, M. J. (2006). Spa-
tial carrier fringe pattern demodulation by use of a
two-dimensional continuous wavelet transform. Ap-
plied optics, 45(34):8722–8732.
Goldstein, R. M., Zebker, H. A., and Werner, C. L. (1988).
Satellite radar interferometry: Two-dimensional phase
unwrapping. Radio science, 23(4):713–720.
Gorthi, S. S. and Rastogi, P. (2010). Fringe projection
techniques: whither we are? Optics and lasers in en-
gineering, 48(IMAC-REVIEW-2009-001):133–140.
Gutmann, B. and Weber, H. (2000). Phase unwrapping with
the branch-cut method: role of phase-field direction.
Applied optics, 39(26):4802–4816.
Iwata, K., Kusunoki, F., Moriwaki, K., Fukuda, H., and
Tomii, T. (2008). Three-dimensional profiling using
the fourier transform method with a hexagonal grating
projection. Applied optics, 47(12):2103–2108.
Jia, P., Kofman, J., and English, C. (2008). Error com-
pensation in two-step triangular-pattern phase-shifting
profilometry. Optics and Lasers in Engineering,
46(4):311–320.
Kemao, Q. (2004). Windowed fourier transform for fringe
pattern analysis. Applied Optics, 43(13):2695–2702.
Kemao, Q. (2007). Two-dimensional windowed fourier
transform for fringe pattern analysis: principles, ap-
plications and implementations. Optics and Lasers in
Engineering, 45(2):304–317.
Lin, J.-F. and Su, X. (1995). Two-dimensional fourier trans-
form profilometry for the automatic measurement of
three-dimensional object shapes. Optical Engineer-
ing, 34(11):3297–3303.
Sajan, M., Tay, C., Shang, H., and Asundi, A. (1998). Im-
proved spatial phase detection for profilometry using a
tdi imager. Optics communications, 150(1-6):66–70.
Servin, M., Cuevas, F. J., Malacara, D., Marroquin, J. L.,
and Rodriguez-Vera, R. (1999). Phase unwrapping
through demodulation by use of the regularized phase-
tracking technique. Applied Optics, 38(10):1934–
1941.
Su, X. and Chen, W. (2001). Fourier transform profilo-
metry:: a review. Optics and lasers in Engineering,
35(5):263–284.
Takeda, M. and Mutoh, K. (1983). Fourier transform profi-
lometry for the automatic measurement of 3-d object
shapes. Applied optics, 22(24):3977–3982.
Toyooka, S. and Iwaasa, Y. (1986). Automatic profilome-
try of 3-d diffuse objects by spatial phase detection.
Applied Optics, 25(10):1630–1633.
Zhang, C., Huang, P. S., and Chiang, F.-P. (2002). Mi-
croscopic phase-shifting profilometry based on digi-
tal micromirror device technology. Applied optics,
41(28):5896–5904.
Zhang, S., Li, X., and Yau, S.-T. (2007). Multilevel
quality-guided phase unwrapping algorithm for real-
time three-dimensional shape reconstruction. Applied
optics, 46(1):50–57.
Zhao, H., Zhang, C., Zhou, C., Jiang, K., and Fang, M.
(2016). Circular fringe projection profilometry. Optics
letters, 41(21):4951–4954.
Zhong, J. and Weng, J. (2004). Spatial carrier-fringe pat-
tern analysis by means of wavelet transform: wavelet
transform profilometry. Applied optics, 43(26):4993–
4998.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
856
