Data Multiplexing Through Animated Texture Orientation and Color

Maria-Jesus Lobo and Christophe Hurter

ENAC, Toulouse, France

Keywords:

Information Visualization, Multivariate Visualization, Animated Representations.

Abstract:

Multidimensional data visualization is still a challenge for complex data exploration. Usually, each data

dimension might be mapped to one available visual variable such as position, shape or color. While spatial

and color data mappings have been previously intensively explored, animated encodings have been far less

investigated. However, such techniques are widely used in existing visualizations. In this paper, we propose to

assess the visual assets of direction and orientation of directed animated textures to encode data. We present

a user study that compares three animated textures and a static representation. The results suggest that the

animated techniques can be as effective as the static representation in terms of accuracy and data retrieval

time. Finally, we present some design guidelines to efﬁciently use animated particle visualizations .

1 INTRODUCTION

Minard’s visualization of Napoleon’s march shows

one of the most relevant data representation where

multiple data dimensions are presented at the same

time. Such an astute image is difﬁcult to generalize

and multidimensional data visualization is still today

a challenge. If we consider a 2D surface composed

of two axes (i.e. a screen), it offers two available data

mappings (X and Y coordinate system which can be

mapped to two data dimensions). In addition, other

data dimensions can be mapped with other available

visual variables such as size, color, and shape (Berlin

and Barbut, 1968). These visual variables can also be

animated across time to depict dynamic phenomena,

as in some cartographic applications (DiBiase et al.,

1992; Lobo et al., 2018). However, while spatial and

color data mappings perception have previously been

intensively explored, the perception of animated visu-

alizations have been far less investigated.

This is especially the case with techniques

using directional animated particles (Wegenkittl

et al., 1997; van Wijk, 2002; Scheepens et al.,

2016). These techniques are widely used in

many engaging and pleasing animations to dis-

play ﬂow information. For example, global

wind visualizations (https://earth.nullschool.net/,

https://www.windy.com/ ) show color streams that

represent the strength and direction of the wind.

Other types of visualizations use a color scale

to display temperature data on top of the stream

visualization (https://www.ventusky.com/). The

TV show from the BBC, “Britain from above”

(https://www.bbc.co.uk/programmes/b00d23yx)

shows many instances of animated ﬂows with various

designs. Some examples are depicted in Figure 1.

Figure 1: Example animated particle system to

show ﬂow directions.(https://earth.nullschool.net/,

https://www.windy.com/, https://www.ventusky.com/).

All of these techniques offer the capability to vi-

sually represent two data dimensions. First, the di-

rection of the ﬂow codes one data dimension. Sec-

ond, the color of the ﬂow or the background codes

another data dimension (i.e. stream intensity). While

these techniques are currently used in many applica-

tions and research domains, we still do not know how

efﬁcient at representing these two dimensions simul-

taneously the different representation techniques are.

In this paper, we propose to assess the visual as-

sets of such techniques. We conducted a user study

where we show colored animated particles to visu-

ally map two data dimensions. The results suggest

that techniques based on animated textures can per-

form as well as a static data representation in terms

of accuracy and data retrieval time. Furthermore, we

show that the orientation difference has an inﬂuence

on the color retrieval. Finally, we summarize our ﬁnd-

Lobo, M. and Hurter, C.

Data Multiplexing Through Animated Texture Orientation and Color.

DOI: 10.5220/0007391602890296

In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 289-296

ISBN: 978-989-758-354-4

289

ings with design guidelines to efﬁciently use animated

particle visualizations.

2 RELATED WORK

2.1 Textures for Multivariate

Visualizations

The use of textures for multivariate visualization has

been explored through different techniques such as

brush strokes (Kirby et al., 1999), quantitative tex-

tons (Ware, 2009), contour maps (van Wijk and Telea,

2001) and more recently decal maps (Rocha et al.,

2017). Other techniques, such as the circular dataim-

age (Morphet and Symanzik, 2010) focus speciﬁcally

in displaying angles. These techniques seem to be ef-

fective to depict multiple data attributes for a region,

as textures enable to separate different scalar values.

For example, Ware (2009) compares quantitative tex-

tons to bivariate color maps, and ﬁnd they produce

lower error rates when reading values.

However, all these studies focus on static tech-

niques, and do not explore animated techniques. Fur-

thermore, they compare techniques that are very dif-

ferent from each other, whereas in this study we aim at

comparing only techniques that depict color and ori-

entation

2.2 Textured-based Flow Visualization

The ﬁeld of ﬂow visualization has a long history of

using animated textures to visualize ﬂow character-

istics. Flow visualization techniques are categorized

as direct, texture-based, geometric, and feature-based

(Laramee et al., 2003; McLoughlin et al., 2013). We

review the most relevant existing work to our study

on texture-based ﬂow visualization techniques. For a

more detailed review, we refer the readers to the sur-

veys presented in (Laramee et al., 2003; McLoughlin

et al., 2013).

Laramee et al. (2003) classify texture-based tech-

niques as Spot Noise Techniques, LIC techniques, Tex-

ture advection and GPU-based techniques. LIC tech-

niques apply a convolution to a noise texture that

follows the direction of the vector ﬁeld, resulting in

a dense visualization. Texture advection and GPU-

based techniques distort existing textures along the

direction of the vector ﬁeld using a predeﬁned mesh.

These techniques can be further extended to dis-

play multivariate data through weaving (Urness et al.,

2003), contrast variation (Sanna et al., 2002) or vari-

ations of the initial noise textures (Kiu and Banks,

1996). Several variations and optimizations of these

techniques exist (Stalling and Hege, 1995; Wegenkittl

et al., 1997; Laramee et al., 2003) and it is now possi-

ble to achieve efﬁcient rendering. However, it is still

unclear how these different techniques are perceived

and which one might be more efﬁcient to understand

the characteristics of the depicted ﬂow such as its ori-

entation and direction.

2.3 User Studies

Existing studies (Laidlaw et al., 2005; Moorhead

et al., 2012) comparing static ﬂow visualization tech-

niques suggest that the more visually explicit meth-

ods (showing integral curves, critical points, and ﬂow

directionality) are more effective. Ware et al (2016)

compare animated to static representations to visual-

ize steady ﬂow patterns. The results suggest that an-

imated streamlets are faster and more accurate than

static arrow grids, static streamlets and animated or-

thogonal particles for a pattern detection task. These

studies only consider the ﬂow representation through

animated textures, but do not evaluate the simultane-

ous readability of ﬂow animated direction and color.

Ware et al. (2013) present new designs for a multi-

variate weather display, and evaluate their readability

in a user study. Their results suggest that a map that

combines animated particles, color and texture can be

more readable than the traditional design that uses a

static depiction. Their results suggest that users can

read multiple variables on a weather display, but they

only evaluate one technique of animated particles.

Our study aims at comparing animated texture-

based ﬂow visualization techniques to a static repre-

sentation in both color and direction encoding. As op-

posed to the existing studies, we do not focus specif-

ically on ﬂow data and rather try to evaluate which

technique is better to represent color and orientation

simultaneously.

3 TECHNIQUES

We chose our techniques by reviewing the existing

literature and visualizations used in websites. We

tuned each technique iteratively to achieve the ren-

dering that enabled us to depict the biggest range of

orientation and color values.

3.1 IBFV

Image Based Flow Visualization (van Wijk, 2002) is

a technique for visualizing ﬂows. It is based on im-

age wrapping and blending. For each frame, a white

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

290

noise image is wrapped in the direction of the ﬂow

and then blended with another white noise image, as

depicted in Figure 2. We implemented IBFV as de-

scribed in (van Wijk, 2002). We rendered 60 frames

per second and used a pattern resolution of 128 pixels

with a speed of 110 pixels per second.

t=0s

t=0.2s

t=0.4s

t=0s

t=0.2s

t=0.4s

t=0s

t=0.2s

t=0.4s

Figure 2: Example of IBFV animation depicting 40 de-

grees.

3.2 OLIC

Oriented Line Integral Convolution (Wegenkittl et al.,

1997) encodes both direction and orientation, by dis-

tributing some random droplets and using a ramp-like

convolution kernel, as depicted in Figure 3. This re-

sults in droplets that present a lighter color in the di-

rection of the ﬂow. If animated, each lighter point will

move in the ﬂow direction. This technique is the most

used on existing web visualizations. We implemented

OLIC as described in (Wegenkittl et al., 1997), but

to make it more efﬁcient, we pre-calculate the images

corresponding to a complete phase shift of the kernel.

We use droplets of length 20 pixels and a speed of 40

pixels per second, meaning that each droplet will be

animated twice every second.

t=0s

t=0.2s

t=0.4s

t=0s

t=0.2s

t=0.4s

t=0s

t=0.2s

t=0.4s

Figure 3: Example of OLIC animation depicting 40 de-

grees.

3.3 Drifting Texture

As we would use only linear speeds (to represent

angle and direction) we also added a technique that

scrolls across a static texture, that does not depict nei-

ther orientation nor direction statically, and only uses

dynamics. Figure 4 depicts three frames of a drifting

texture animation. For this technique, we used a speed

of 20 pixels per second and a white noise texture.

t=0s

t=0.2s

t=0.4s

t=0s

t=0.2s

t=0.4s

t=0s

t=0.2s

t=0.4s

Figure 4: Example of DT animation depicting 40 degrees.

3.4 Static Representation

Previous studies suggest that animation might not be

always beneﬁcial (Tversky et al., 2002). Thus we

added a technique that depicts both orientation and di-

rection statically as the baseline. This technique does

not distort colors in any way. We chose to use an ar-

row ﬁeld, as arrows are commonly used to encode di-

rection (Ware et al., 2016), and they are always com-

pletely opaque, so they do not introduce any interfer-

ence with the color we want to represent, as depicted

in Figure 5.

Figure 5: Example of STATIC depicting 40 degrees.

4 USER STUDY

Several studies attempt to understand which color

scale is better for data visualization such as the Color

Brewer tool (Harrower and Brewer, 2003) that helps

mapmakers choose the most suitable color scale to

their data. Our design study is inspired by the more

recent study presented by Liu et al. (2018). In it,

participants were asked to compare color distance,

by choosing the closest color among two options to

a reference color. Their results suggest that multi-

hue color scales perform better than single-hue color

scales and they ﬁnd that the recent color scale Viridis

perform especially well.

Our study uses the same structure, but besides ask-

ing participants to compare colors, we asked them to

compare orientations. In each trial, participants are

asked to choose the closest value among two alterna-

tives to a reference value. We use the same method-

ology to select the reference colors that the one pre-

Data Multiplexing Through Animated Texture Orientation and Color

291

sented by Liu et al. (2018), we consider that the color

scale spans from 0 to 100 and choose 8 equally spaced

color values from 20 to 80. For the angles, we use 36

equally spaced angles between 0 and 360. The two

other values are then selected according to spans as in

(Liu and Heer, 2018). For example, if we use a span

of 20, the closest value will be at a difference of 5

of the reference and the farthest at a difference of 10.

Then, if the reference value is 20, the comparison val-

ues will be either 15 and 30 or 10 and 25. A pretest

with two color spans and three angle spans resulted

in a too long study and as the study presented by (Liu

and Heer, 2018) already studies the color comparison,

we decided to only vary the angle span. Therefore,

we always use a color span of 15 and three different

ANGLE SPAN values: 15, 30, and 45. We chose to

not use smaller ANGLE SPAN values because humans

performance when comparing angles is poor (Cleve-

land and McGill, 1985). Furthermore, following the

suggestions presented by the results of the study, we

chose to use the Viridis color scale, displayed in the

bottom of Figure 7.

As the goal of this techniques is to represent mul-

tiple data dimensions in visualizations that have also

space constraints, such as heat maps, we wanted to

also study the impact of the size of the animated re-

gion on the color and orientation perception for each

technique. So, our user study also considers three val-

ues for the size of the animated patches.

4.1 Hypothesis

We propose a characterization of the techniques

according to the information they encode in their

graphic depiction, if they encode information dynam-

ically and their color density, depicted in Figure 6.

Considering this, we draw two main hypotheses:

• H1: As previous studies suggest that techniques

that present explicitly the attributes of the vector

ﬁeld perform better that techniques than don’t, the

ﬁrst hypothesis is that OLIC and STATIC as they

present both the direction and orientation in the

graphic representation will be more accurate than

the other dynamic techniques for orientation com-

parison. As IBFV and DT require participants

to see the direction of the animation, they should

be particularly inefﬁcient for smaller sizes when

comparing orientations.

• H2: Increasing distance and decreasing

sizes seem to make distinguishing colors

harder(Brychtov

a and C¸

oltekin, 2017). As the

colored area of IBFV and DT is bigger than

the colored area with the other techniques, our

second hypothesis is that these two techniques

Colored Area

No dynamic!

information

Dynamic

orientation +!

direction

No static!

depiction

Static!

orientation +!

direction

OLIC

IBFV

STATIC

Small

Big

Figure 6: Classiﬁcation of the techniques according to the

information encoded dynamically and statically, and the

colored area.

will be more effective to compare colors, but that

the difference will decrease for smaller sizes.

4.2 Participants and Apparatus

Sixteen unpaid volunteers (2 females), daily computer

users, aged 22 to 56-year-old (average 37.3, median

42) participated in the experiment. All had normal

or corrected-to-normal vision and did not suffer from

color blindness. The experiment was implemented

using WebGL in Javascript, and ran on a Laptop Dell

15” Retina (1600x900, 122 dpi) running Windows 10,

equipped with a 2.30 GHz Intel Core CPU, 16 GB

RAM and an NVIDIA GeForce GT 750M graphics.

Participants were asked to seat at approximately 60

cm from the screen. Each participant completed 288

trials and the study lasted about 20 minutes per par-

ticipant.

4.3 Procedure

We followed a 4x3x3 within-subject design with 3

factors: TECHNIQUE, SIZE and ANGLE SPAN. TECH-

NIQUE corresponds to one of the four techniques de-

scribed earlier. To choose the SIZE values, we took as

reference the size of an icon (16 pixels), and we mul-

tiplied it by 2 and 4. The ANGLE SPAN value corre-

sponds to the span between the lower and upper value

of the two comparison values, as mentioned before.

The experiment was organized in technique

blocks, the order of the techniques was counterbal-

anced across participants using a latin square. For the

other factors, we generated a random order for each

participant. For each technique, participants did 36

trials where they compared colors and 36 trials com-

paring orientations. For each technique, we had 3 AN-

GLE SPAN and 3 SIZE. Each SIZE x ANGLE SPAN

combination was used in four trials, where we varied

if the upper or the lower value was the closest angle

or color. For example, for the ANGLE SPAN 30 and a

reference angle of a, if the closest value is the lower

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

292

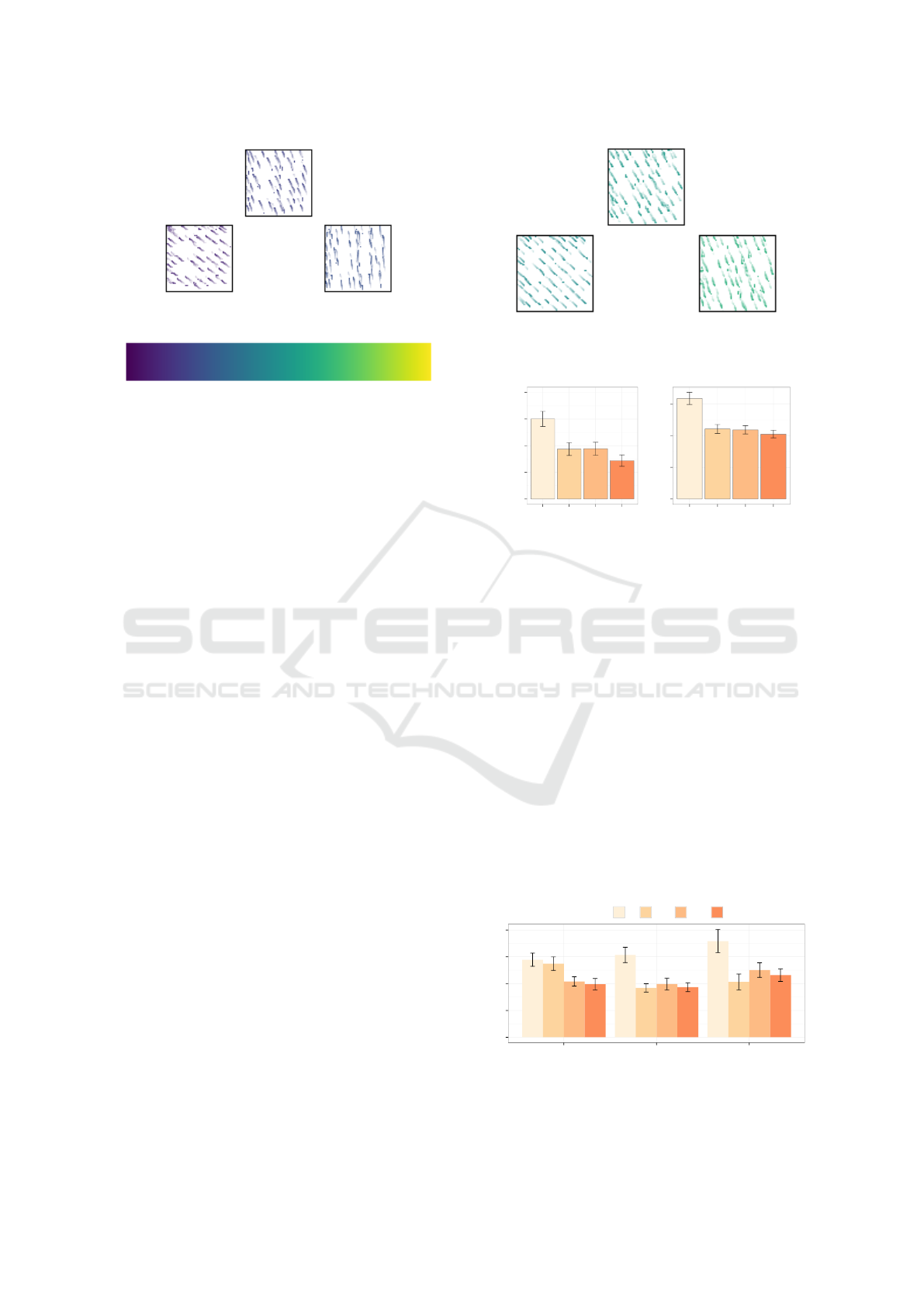
Figure 7: Example of a COLOR trial for OLIC technique.

The participant is asked to chose the closest color to the ref-

erence value (on the top). The Viridis (bottom) color scale

is only visible for these trials.

one, we would display the orientations a-10 and a+20.

This results in 75 trials per block. We generated a

random order of all the combinations of reference an-

gles and colors, and then used the same order for each

participant, as all the other conditions are randomized

between participants.

Participants started each technique block with a

training trial, that used both a color span and an AN-

GLE SPAN that was not used in the experiment. For

each trial, participants ﬁrst read a set of instructions

explaining the study. They then were asked to select

the closest color or angle. Figure 7 depicts a trial of

color comparison and 8 depicts a trial of orientation

comparison. The trials were grouped by comparison

target, and participants either always started by com-

paring colors or orientations in each technique block.

If comparing colors, the trial was complemented by a

depiction of the Viridis color scale.

4.4 Results

4.4.1 Orientations

We used the Aligned Rank Transform (Wobbrock

et al., 2011) procedure for non-parametric data to an-

alyze the ERROR RATE. As Figure 9-(a) illustrates,

TECHNIQUE has a signiﬁcant effect on ERROR RATE

3,525

= 16.17, p < 0.0001). A pairwise post hoc com-

parison revealed a difference between DT and all

other techniques , but no difference between the other

three techniques. ANGLE SPAN has also a signiﬁcant

effect on ERROR RATE(F

2,525

= 35, p < 0.0001), trials

where the angle span was 15 presented a higher error

rate than trials where the angle span was 30 that pre-

sented a higher ERROR RATE than trials where the an-

gle span was 45 (Cohen’s d between 30 and 45: 0.5,

Figure 8: Example of a ORIENTATION trial for OLIC tech-

nique. The participant is asked to chose the closest orienta-

tion to the reference orientation (on the top).

0.0

0.1

0.2

0.3

0.4

DT IBFV OLIC STATIC

Technique

Error Rate

DT IBFV OLIC STATIC

Technique

Time (s)

(a) (b)

Figure 9: (a)Average ERROR RATE per TECHNIQUE for

ORIENTATION. (b)Average TIME per TECHNIQUE for ORI-

ENTATION. Error bars represent the 95% conﬁdence inter-

vals.

between 15 and 45: 0.85). Finally, SIZE does also

have an effect on the error rate F

2,525

= 4.8, p < 0.0001.

Both smaller sizes present signiﬁcantly a bigger er-

ror rate than the SIZE = 64. There are no effects due

to the interaction between the factors (TECHNIQUE x

SIZE: F

6,525

= 0.56, p = 0.5, TECHNIQUE x ANGLE

SPAN: F

6,525

= 1.86, p = 0.08, SIZE x ANGLE SPAN:

4,525

= 0.92, p = 0.45, TECHNIQUE xSIZE x ANGLE

SPAN: F

12,525

= 0.88, p = 0.56).

TECHNIQUE has also a signiﬁcant effect on TIME

3,45

= 6.95, p < 0.0001, η

= 0.14) as depicted in

Figure 9-(b). DT is signiﬁcantly slower than all the

other techniques, that present no signiﬁcant differ-

ence in between them. The SIZE also has an effect on

TIME (F

2,30

= 5.62, p < 0.0001, η

= 0.02). SIZE=16

16 32 64

Size

Time (s)

Technique

DT IBFV OLIC STATIC

Figure 10: Average TIME per SIZE and TECHNIQUE for

ORIENTATION. Error bars represent the 95% conﬁdence in-

tervals.

Data Multiplexing Through Animated Texture Orientation and Color

293

0.0

0.1

0.2

0.3

0.4

DT IBFV OLIC STATIC

Technique

Error rate

DT IBFV OLIC STATIC

Technique

Time (s)

(a) (b)

Figure 11: (a) Average ERROR RATE per TECHNIQUE for

COLOR. (b) Average TIME per TECHNIQUE for COLOR. Er-

ror bars represent the 95% conﬁdence intervals.

16 32 64

Size

Time (s)

Technique

DT IBFV OLIC STATIC

Figure 12: Average TIME per SIZE per TECHNIQUE for

COLOR. Error bars represent the 95% conﬁdence intervals.

takes longer than SIZE = 32, and SIZE = 64 takes

longer than SIZE = 32. The ANOVA reveals a signiﬁ-

cant TECHNIQUE x SIZE interaction effect (F

6,90

= 3.9,

p < 0.0001, η

= 0.02) on TIME, ad depicted in Figure

10. For the SIZE = 16, IBFV and DT are signiﬁcantly

slower than OLIC and STATIC, but for SIZE = 32

and SIZE = 64, there is no signiﬁcant difference for

IBFV, OLIC and STATIC, and all of them are faster

than DT.

4.4.2 Colors

As for ORIENTATION we used the Aligned Rank

Transform procedure for non-parametric data to an-

alyze the ERROR RATE. TECHNIQUE also has a sig-

niﬁcant effect here on ERROR RATE (F

3,525

= 46.7,

p < 0.0001), as depicted in Figure 11-(a). A pairwise

post hoc comparison reveals that OLIC is the more

error-prone technique, followed by STATIC. DT and

IBFV present the lowest error rates and present no

signiﬁcant difference between them. The ANOVA

also reveals an effect of SIZE(F

2,525

= 11.6, p < 0.0001).

The condition were SIZE = 64 was less error-prone,

than SIZE = 16 and SIZE = 32. There is also an ef-

fect of the interaction SIZExTECHNIQUE(F

6,525

= 2.9,

p < 0.0001), as depicted in Figure 13. When SIZE

= 16, there is only a signiﬁcant difference between

OLIC and IBFV. But when SIZE = 32 and SIZE = 64,

DT and IBFV are no different but are different from

OLIC and STATIC, the last one being signiﬁcantly

less error-prone than OLIC. The ANOVA also reveals

an effect of ANGLE SPAN on ERROR RATE(F

2,525

4.58, p = 0.01). The results suggest that the AN-

GLE SPAN = 15 is less error-prone than the other

two conditions. There is also an effect of the inter-

actions ANGLE SPANxTECHNIQUE(F

6,525

= 2.89, p <

0.0001), SIZE x ANGLE SPAN(F

6,525

= 2.89, p = 0.02),

and TECHNIQUE x SIZE x ANGLE SPAN(F

12,525

= 2.56,

p < 0.0001). Looking at each TECHNIQUE and SIZE

individually, we found no effect for the different val-

ues of ANGLE SPAN. Looking at each SIZE per TECH-

NIQUE, we only ﬁnd an effect for OLIC for the SIZE

= 16, where the ANGLE SPAN = 15 presents less errors

than the ANGLE SPAN=30.

TECHNIQUE (F

3,45

= 5.39, p < 0.0001, η

= 0.067)

and TECHNIQUE x SIZE (F

6,90

= 2.68, p = 0.02, η

0.044) also have an effect on TIME for COLOR tri-

als as depicted in Figure 11-(a). DT and STATIC

are signiﬁcantly faster than IBFV that is faster than

OLIC. As depicted in Figure 12, for all SIZE values,

DT is the fastest technique. It is signiﬁcantly faster

than IBFV and OLIC for SIZE = 16, but not from

STATIC. For SIZE = 32, DT is signiﬁcantly faster

than all the other three, IBFV and STATIC are signif-

icantly faster than OLIC. For SIZE = 64, DT is only

different from OLIC, that is the slowest no matter the

size.

5 DISCUSSION

The graphic depiction of both direction and orienta-

tion does not seem to offer an advantage for OLIC

in comparison to IBFV and STATIC overall for ORI-

ENTATION comparisons, H1 is rejected. Also, con-

trary to what we expected, the SIZE does not seem

to have an effect on the ORIENTATION perception ac-

curacy. However, it does impact the time measure.

For the smaller SIZE, OLIC and STATIC are faster.

This could mean that the depiction of both orienta-

tion and direction that these techniques present is es-

pecially useful in smaller sizes, when is more difﬁcult

to see the direction and orientation of the animation.

However, the dynamic aspect of OLIC does not seem

to be useful enough to make it faster than STATIC.

IBFV and DT are the most accurate technique for

COLOR comparison, and thus H2 is supported; hav-

ing a more dense representation of the color seems to

make a difference for an accurate color comparison.

In fact, the results achieved with these techniques are

similar to the ones presented in the recent study of

Liu et al. (2018). OLIC is the worst technique for

comparing colors. This difference depends also on

the size; for the smallest size, STATIC is no differ-

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

294

0.0

0.1

0.2

0.3

16 32 64

Size

Error rate

Technique

DT IBFV OLIC STATIC

Figure 13: Average ERROR RATE per TECHNIQUE for

COLOR. Error bars represent the 95% conﬁdence intervals.

ent from IBFV and DT. As the size decreases, the

difference of sizes between the techniques decreases

as well, and thus the results agree with the relation-

ship between size and color comparison (Brychtov

and C¸

oltekin, 2017). We can hypothesize that OLIC

does not perform well for the smallest size because

contrary to STATIC it distorts the color by varying

its luminosity across the particle. Regarding time,

DT is the fastest technique. As DT uses a translat-

ing texture, it does not transform the color in any way,

contrary to IBFV that blends the color with the noise

texture at each iteration. This could explain why the

color comparison with DT is fastest.

Surprisingly, we found an effect of ANGLE SPAN

in the accuracy of COLOR trials, that suggest that

when the animations present a smaller ANGLE SPAN,

participants are more accurate comparing colors.

The difference is signiﬁcant when ANGLE SPAN=15,

where the animations’ orientations are at a distance

of 5 and 10 degrees of the reference animation.

We could hypothesize that the orientation difference

might affect the color comparison, making easier to

compare color when the angles are closer. However,

further studies are needed to test this hypothesis.

6 SUMMARY AND FUTURE

WORK

The results of our study suggest that the dynamic

component of IBFV enables users to compare ORI-

ENTATION as accurately as a static technique and

COLOR as accurately as presenting the color with-

out distortion. We recommend thus the usage of this

technique when depicting those two visual variables

together. However, the results might depend on the

size of the depicted area. If the area to display is too

little, perceiving the orientation with IBFV becomes

difﬁcult, and an alternative technique might be better,

such as STATIC.

Our study presents multiple limitations. First, we

tunned the different techniques in a way we thought

they better depicted both the color and the orienta-

tion. But this design choices might have hampered

some techniques. For example, we chose to apply the

color to OLIC particles, instead of applying it to the

background. Several examples on the web instead use

white semi-transparent particles on top of a colored

background. We chose this design to avoid introduc-

ing a third color to the technique, and to keep the

particles visible. However, to keep the OLIC parti-

cles distinguishable, they cannot be very dense, mak-

ing the color comparison more difﬁcult than with the

other techniques.

Second, to keep the design space manageable, we

did not control for the speciﬁc angles or color values.

Some participants mentioned that comparing orienta-

tions with light colors such as yellow was more difﬁ-

cult than with darker colors, especially for the IBFV

technique. Also, some angles or quadrant compar-

isons might be easier than others. Further studies

could be designed in order to test these hypotheses.

Furthermore, we could reproduce the study using an

iso-luminant color scale (Gregory, 1977), to avoid the

effects of lightness variations.

Dynamic techniques also offer the possibility of

mapping data dimensions to the parameters of the an-

imation. In this study, we focused on ORIENTATION

and COLOR because they present a higher granular-

ity. However, some animation variables such as fre-

quency and speed have already been used successfully

in the case of animated textures in graph edges (Ro-

mat et al., 2018), and using them in animated textures

is an interesting line of future work.

ACKNOWLEDGEMENTS

This research was partly supported by SESAR H2020

project ENVISION grant agreement No 783270.

REFERENCES

Berlin, J. and Barbut, M. (1968). Semiologie graphique:

Les diagrammes, les r

eseaux, les cartes. Paris

Gauthier-Villars.

Brychtov

a, A. and C¸

oltekin, A. (2017). The effect of

spatial distance on the discriminability of colors in

maps. Cartography and Geographic Information Sci-

ence, 44(3):229–245.

Cleveland, W. S. and McGill, R. (1985). Graphical per-

ception and graphical methods for analyzing scientiﬁc

data. Science, 229(4716):828–833.

DiBiase, D., MacEachren, A. M., Krygier, J. B., and

Reeves, C. (1992). Animation and the role of map de-

Data Multiplexing Through Animated Texture Orientation and Color

295

ographic Information Systems, 19(4):201–214.

Gregory, R. L. (1977). Vision with isoluminant colour con-

trast: 1. a projection technique and observations. Per-

ception, 6(1):113–119. PMID: 840617.

Harrower, M. and Brewer, C. A. (2003). Colorbrewer.org:

An online tool for selecting colour schemes for maps.

The Cartographic Journal, 40(1):27–37.

Kirby, R. M., Marmanis, H., and Laidlaw, D. H. (1999).

Visualizing multivalued data from 2d incompressible

ﬂows using concepts from painting. In Proceedings of

the Conference on Visualization ’99: Celebrating Ten

Years, VIS ’99, pages 333–340, Los Alamitos, CA,

USA. IEEE Computer Society Press.

Kiu, M.-H. and Banks, D. C. (1996). Multi-frequency noise

for lic. In Proceedings of Seventh Annual IEEE Visu-

alization ’96, pages 121–126.

Laidlaw, D. H., Kirby, R. M., Jackson, C. D., Davidson,

J. S., Miller, T. S., da Silva, M., Warren, W. H., and

Tarr, M. J. (2005). Comparing 2d vector ﬁeld visual-

ization methods: a user study. IEEE Transactions on

Visualization and Computer Graphics, 11(1):59–70.

Laramee, R. S., Jobard, B., and Hauser, H. (2003). Im-

age space based visualization of unsteady ﬂow on sur-

faces. In Proceedings of the 14th IEEE Visualization

2003 (VIS’03), page 18. IEEE Computer Society.

Liu, Y. and Heer, J. (2018). Somewhere over the rainbow:

An empirical assessment of quantitative colormaps. In

Proceedings of the 2018 CHI Conference on Human

Factors in Computing Systems, CHI ’18, pages 598:1–

598:12, New York, NY, USA. ACM.

Lobo, M., Appert, C., and Pietriga, E. (2018). Anima-

tion plans for before-and-after satellite images. IEEE

Transactions on Visualization and Computer Graph-

ics, pages 1–1.

McLoughlin, T., Laramee, R. S., Peikert, R., Post, F. H., and

Chen, M. (2013). Over two decades of integration-

based, geometric ﬂow visualization. Computer

Graphics Forum, 29(6):1807–1829.

Moorhead, R. J., Swan, J. E., Cai, S., Liu, Z., Martin, J. P.,

and Jankun-Kelly, T. J. (2012). A 2d ﬂow visualiza-

tion user study using explicit ﬂow synthesis and im-

plicit task design. IEEE Transactions on Visualization

and Computer Graphics, 18:783–796.

Morphet, W. J. and Symanzik, J. (2010). The circular

dataimage, a graph for high-resolution circular-spatial

data. International Journal of Digital Earth, 3(1):47–

71.

Rocha, A., Alim, U., Silva, J. D., and Sousa, M. C. (2017).

Decal-maps: Real-time layering of decals on surfaces

for multivariate visualization. IEEE Transactions

on Visualization and Computer Graphics, 23(1):821–

830.

Romat, H., Appert, C., Bach, B., Henry-Riche, N., and

Pietriga, E. (2018). Animated edge textures in node-

link diagrams: A design space and initial evaluation.

In Proceedings of the 2018 CHI Conference on Hu-

man Factors in Computing Systems, CHI ’18, pages

187:1–187:13, New York, NY, USA. ACM.

Sanna, A., Zunino, C., Montrucchio, B., and Montuschi,

P. (2002). Adding a scalar value to texture-based

vector ﬁeld representations by local contrast analysis.

In Proceedings of the Symposium on Data Visualisa-

tion 2002, VISSYM ’02, pages 35–41, Aire-la-Ville,

Switzerland, Switzerland. Eurographics Association.

Scheepens, R., Hurter, C., Wetering, H. V. D., and Wijk, J.

J. V. (2016). Visualization, selection, and analysis of

trafﬁc ﬂows. IEEE Transactions on Visualization and

Computer Graphics, 22(1):379–388.

Stalling, D. and Hege, H.-C. (1995). Fast and resolution

independent line integral convolution. In Proceedings

of the 22nd annual conference on Computer graphics

and interactive techniques, pages 249–256. ACM.

Tversky, B., Morrison, J. B., and Betrancourt, M. (2002).

Animation: can it facilitate? International journal of

human-computer studies, 57(4):247–262.

Urness, T., Interrante, V., Marusic, I., Longmire, E., and

Ganapathisubramani, B. (2003). Effectively visual-

izing multi-valued ﬂow data using color and texture.

In Proceedings of the 14th IEEE Visualization 2003

(VIS’03), VIS ’03, pages 16–, Washington, DC, USA.

IEEE Computer Society.

van Wijk, J. J. (2002). Image based ﬂow visualization. ACM

Trans. Graph., 21(3):745–754.

van Wijk, J. J. and Telea, A. (2001). Enridged contour maps.

In Proceedings of the conference on Visualization’01,

pages 69–74. IEEE Computer Society.

Ware, C. (2009). Quantitative texton sequences for legible

bivariate maps. IEEE Transactions on Visualization

and Computer Graphics, 15(6):1523–1530.

Ware, C., Bolan, D., Miller, R., Rogers, D. H., and Ahrens,

J. P. (2016). Animated versus static views of steady

ﬂow patterns. In Proceedings of the ACM Symposium

on Applied Perception, SAP ’16, pages 77–84, New

York, NY, USA. ACM.

Wegenkittl, R., Groller, E., and Purgathofer, W. (1997). An-

imating ﬂow ﬁelds: Rendering of oriented line integral

convolution. In Proceedings of the Computer Anima-

tion, CA ’97, pages 15–, Washington, DC, USA. IEEE

Computer Society.

Wobbrock, J. O., Findlater, L., Gergle, D., and Higgins,

J. J. (2011). The aligned rank transform for nonpara-

metric factorial analyses using only anova procedures.

In Proceedings of the SIGCHI Conference on Human

Factors in Computing Systems, CHI ’11, pages 143–

146, New York, NY, USA. ACM.

IVAPP 2019 - 10th International Conference on Information Visualization Theory and Applications

296