
GPU Accelerated Sparse Representation of Light Fields
Gabriel Baravdish, Ehsan Miandji and Jonas Unger
Department of Science and Technology, Linköping University, Bredgatan 33, Norrköping, Sweden
Keywords:
Light Field Compression, Gpgpu Computation, Sparse Representation.
Abstract:
We present a method for GPU accelerated compression of light fields. The approach is by using a dictionary
learning framework for compression of light field images. The large amount of data storage by capturing light
fields is a challenge to compress and we seek to accelerate the encoding routine by GPGPU computations.
We compress the data by projecting each data point onto a set of trained multi-dimensional dictionaries and
seek the most sparse representation with the least error. This is done by a parallelization of the tensor-matrix
product computed on the GPU. An optimized greedy algorithm to suit computations on the GPU is also
presented. The encoding of the data is done segmentally in parallel for a faster computation speed while
maintaining the quality. The results shows an order of magnitude faster encoding time compared to the results
in the same research field. We conclude that there are further improvements to increase the speed, and thus it
is not too far from an interactive compression speed.
1 INTRODUCTION
Light field imaging has been an active research topic
for more than a decade. Several new techniques have
been proposed focusing on light field capture (Liang
et al., 2008; Babacan et al., 2012), super-resolution
(Wanner and Goldluecke, 2013; Choudhury et al.,
2017), depth estimation (Vaish et al., 2006; Williem
and Park, 2016), refocusing (Ng, 2005), geometry
estimation (Levoy, 2001), and display (Jones et al.,
2016; Wetzstein et al., 2012). A light field repre-
sents a subset of the Plenoptic function (Adelson and
Bergen, 1991), where we store the outgoing radiance
at several spatial locations (r
i
,t
j
), and along multi-
ple directions (u
α
,v
β
), as well as as the spectral data
λ
γ
. Note that here we consider a discrete function
l(r
i
,t
j
,u
α
,v
β
,λ
γ
) containing the light field of a scene.
The ongoing advances in sensor design, as well as
computational power, have enabled imaging systems
capable of capturing high resolution light fields along
angular and spatial domains. A key challenge in such
imaging systems is the extremely large amount of data
produced. Difficulties arise in terms of bandwidth du-
ring the capturing phase and the storage phase. Fast
and high quality compression is essential for existing
imaging systems, as well as future designs due to the
rapid increase in the amount of data produced.
In (Miandji et al., 2013) and (Miandji et al., 2015),
a learning based method for compression of light
fields and surface light fields is proposed. After di-
viding a collection of light fields into small two di-
mensional (2D) patches (i.e. matrices), a training
algorithm computes a collection of orthogonal basis
functions. These orthogonal basis functions are in
essence code words that enable sparse representation
(Elad, 2010) of light fields. We refer to these basis
functions as dictionaries, a commonly used term in
sparse representation literature (Aharon et al., 2006).
The training process is performed once on a collection
of light fields. Once the dictionaries are trained, the
next step is to project the patches from a light field we
would like to compress onto the dictionaries. The re-
sult is a set of sparse coefficients, which significantly
reduces the storage cost. While the method produces
a representation with a small storage cost and high
reconstruction quality, the projection step is computa-
tionally expensive. This makes the utility of the algo-
rithm for capturing light fields impractical.
In this paper we propose a GPU accelerated algo-
rithm that enables the sparse representation of light
field data sets for compression. This algorithm repla-
ces the projection step discussed in (Miandji et al.,
2013) and (Miandji et al., 2015), given a set of pre-
computed 2D dictionaries. Moreover, we show that
our algorithm can be extended to higher dimensions,
i.e. instead of using 2D patches, we use 5D patches
for light fields. The higher dimensional method is
shown to be favorable in terms of performance. While
we focus on light fields, we believe our method can
be used for variety of other large scale data sets in
Baravdish, G., Miandji, E. and Unger, J.
GPU Accelerated Sparse Representation of Light Fields.
DOI: 10.5220/0007393101770182
In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2019), pages 177-182
ISBN: 978-989-758-354-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
177

graphics, e.g. measured BTF and BRDF data sets.
2 TWO DIMENSIONAL
COMPRESSION
Let {T
(i)
}
N
i=1
∈ R
m
1
×m
2
be a collection of patches ex-
tracted from a light field or light field video. The
training method described in (Miandji et al., 2013)
computes a set of K two dimensional dictionaries
{U
(k)
,V
(k)
}
K
k=1
, where U
(k)
∈ R
m
1
×m
1
and V
(k)
∈
R
m
2
×m
2
. Using a constraint of sparsity during trai-
ning, this model enables sparse representation of
a light field patch in one dictionary, i.e. T
(i)
=
U
(k)
S
(i)
(V
(k)
)
T
, where S
(i)
is a sparse matrix.
We assume that a collection of dictionaries
{U
(k)
,V
(k)
}
K
k=1
is trained using the method descri-
bed in (Miandji et al., 2013) or (Miandji et al.,
2015). With a slight abuse of notation, let {T
(i)
}
N
i=1
∈
R
m
1
×m
2
be a set of patches from a light field we would
like to compress. Note that the training set and the
data set we would like to compress are distinct. For
compression, i.e. computing sparse coefficients for
each patch, we proceed as follows: Each patch is pro-
jected onto all dictionaries as S
(i,k)
= V
(k)
T
(i)
(U
(k)
)
T
.
Then we set a maximum of m
1
m
2
− τ elements of
S
(i,k)
with the smallest absolute value to zero, where τ
is a user defined sparsity parameter. The nullification
is also controlled with a threshold parameter on the
representation error, denoted ε. The coefficient ma-
trix among the set {S
(i,k)
}
K
k=1
that is the sparsest with
least error is stored. Since each patch uses one dictio-
nary among K dictionaries, we also store the index of
the dictionary used for each patch, which is called a
membership index.
We compute the product S
(p,k)
= V
(k)
T
(p)
(U
(k)
)
T
for p patches in parallel on the GPU. This is done by
launching equal amount of threads as the total num-
ber of elements among all patches. Then, we let each
thread extract a row of a patch T
(i)
and copy it to the
on-chip cached memory, also called shared memory.
Each thread computes the inner product between the
row of the patch and the column of the given dicti-
onary. The data is stored as one long vector on the
memory, and to find the corresponding row of a patch
i and a thread j, we use the expression in Equation 2.
3 MULTIDIMENSIONAL
COMPRESSION
For multidimensional compression, we seek the
most sparse representation of an n-dimensional patch
T
(i)
∈ R
m
1
×m
2
×...×m
n
under a given set of K multidi-
mensional dictionaries
U
(1,k)
,...,U
(n,k)
K
k=1
. Algo-
rithm 1 is an extension of the greedy method presen-
ted in (Miandji et al., 2015) that achieves this goal.
The algorithm computes a dictionary membership in-
dex a ∈ [1,...,K], where K is the number of dictio-
naries, and sparse coefficients S
(i)
using a threshold
for sparsity τ and a threshold for error ε. Note that
Algorithm 1 is repeated for all the patches {T
(i)
}
N
i=1
.
There are several steps in the algorithm that are com-
putationally expensive and need to be implemented in
such a way that utilize the highly parallel architecture
of modern GPUs. In particular, step 3 of the algo-
rithm perfoms multiple n-mode products between a
tensor and a matrix. Similarly, in step 6 we have a
similar operation, as well as an expensive norm com-
putation. In what follows, we will present algebraic
manipulations of the computationally expensive steps
of the algorithm, as well as GPU-friendly implemen-
tation techniques.
Linear algebra computations are often memory
bounded. Therefore, to minimize the memory tran-
sactions between the CPU and GPU we compute and
store all
ˆ
N ≤ N number of data points in parallel on
the GPU, where
ˆ
N is the maximum number of data
points that can fit in the GPU memory and N is the
total number of data points. Moreover, we describe
the procedure to parallelize and compute the tensor-
matrix product on the GPU in section 3.1.
Algorithm 1: Compute coefficients and the membership in-
dex.
Require: A patch T
i
, error threshold ε, sparsity τ, and
dictionaries
U
(1,k)
,..., U
(n,k)
K
k=1
Ensure: The membership index a and the coefficient ten-
sor S
1: e ∈ R
K
← ∞ and z ∈ R
K
← 1
2: for k = 1 ... K do
3: X
(k)
← T
(k)
×
1
U
(1,k)
T
·· · ×
n
U
(n,k)
T
4: while z
k
≤ τ and e
k
> ε do
5: Y ← Nullify (
∏
n
j=1
m
j
) − z
k
smallest element
of X
(k)
6: e
k
←
T
(i)
− Y ×
1
U
(1,k)
·· · ×
n
U
(n,k)
2
F
7: z
k
= z
k
+ 1
8: end while
9: X
(k)
← Y
10: end for
11: a ← index of min(z)
12: if z
a
= τ then
13: a ← index of min(e)
14: end if
15: S
(i)
← X
(a)
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
178
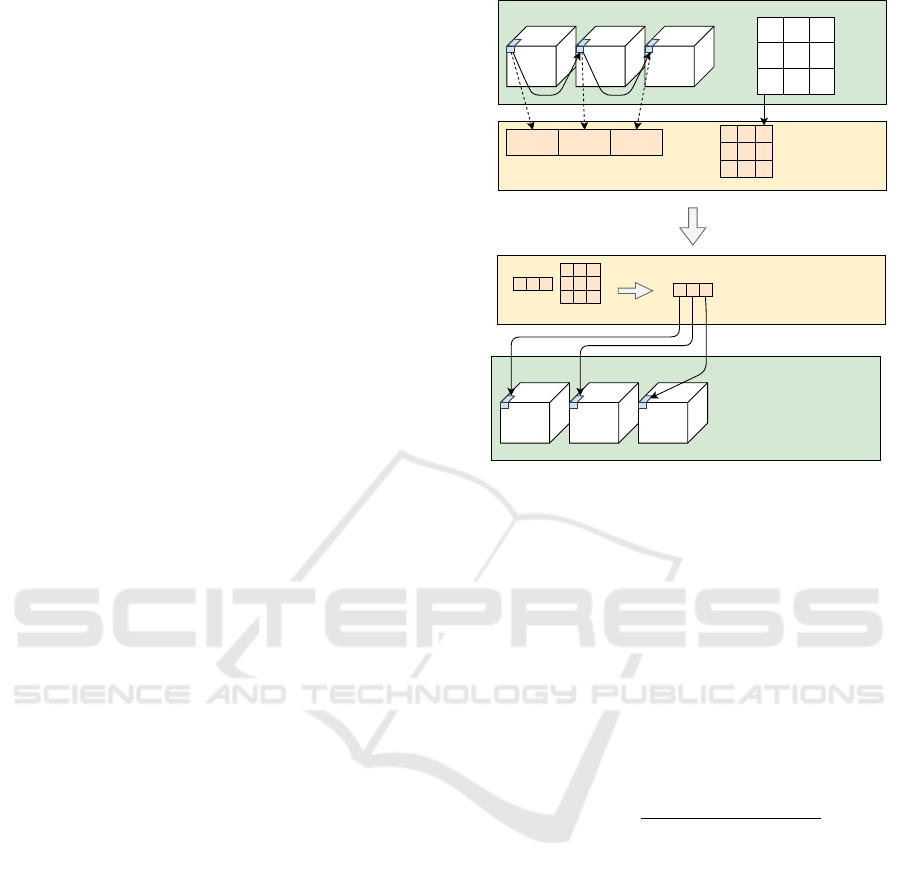
3.1 Computing the n-mode Product on
the GPU
A tensor is an n-dimensional array of order n, or n
modes. A fiber is specified by fixing every index
but one of a tensor. We use the same tensor notation
and colon notation as (Kolda and Bader, 2009), where
X (i
1
,:,i
3
) represents a fiber with all elements along
2-mode of a third-order tensor.
The definition of the tensor-matrix product, as
with the more common matrix-vector product, is an
inner product between every fiber in the tensor along
the n-th dimension and every column in the corre-
sponding matrix. Thus, the task is to extract each fiber
of the tensor and perform an inner product.
In order to efficiently extract a fiber along the n-
mode we unfold a tensor X ∈ R
I
1
×...×I
N
to a matrix.
Let
I =
∏
n=1
I
n
and
ˆ
I
n
= I/I
n
, n ∈ {1, . . . , N}
(1)
represent the total amount of elements in a tensor X .
We unfold X to a I ×
ˆ
I
n
matrix and map each element
with the subscripts (i
1
,i
2
,...,i
n
) to the matrix index
(i
n
, j), see Equation 2. By unfolding the tensor we
ensure that the n-th order fibers are rearranged to be
the columns of the resulting matrix. By the same ap-
proach the matrix can be unfolded to a single column
vector. This vectorization allows us to take advantage
of the linear memory structure and efficient memory
accesses on the GPU. Memory linearization is impor-
tant for minimal cost of memory transaction from and
to the global memory.
A tensor element x
i
1
,i
2
,...,i
N
is mapped to the entry
(i
n
, j) of X
(n)
by
j =
N
∑
k=0
k6=n
i
k
J
k
, where J
k
=
k−1
∏
m=1
m6=n
I
m
.
(2)
For tensor sizes that are small enough, it is more
convenient to let each thread compute the inner pro-
duct of a fiber and all the columns in a dictionary ma-
trix. This is due to the computational overhead of
thread collaborations. When traversing along the n-
th dimension, the group of threads in a block stores
m
n
tensor fiber elements and m
2
n
dictionary elements
from the global memory to the shared memory, see
Figure 1. The inner product between a fiber and all
the columns in a dictionary is then computed on the
shared memory. The resulting fiber is stored at the
same location on the global memory due to the dicti-
onary being squared matrices.
Global memory
T(1,1,1,1) T(1,1,1,2) T(1,1,1,3)
Shared memory
U
(n)
Shared memoryU
(n)
T(1,1,1,:)
Global memory
X(1,1,1,:)
X(1,1,1,:)
T(1,1,1,:)
Figure 1: The n-mode product on the GPU. Here T is a
4D-tensor and the first thread is traversing along the fourth
dimension. Observe that this is just an illustration of the
concept, the data points are not explicitly stored as tensors
on the global memory.
3.2 Computing Sparse Coefficient
Tensors
In this section we will cover how to transform the
norm of the n-mode product of a sparse tensor into
almost a single instruction, see line 10 in Algorithm
1.
The Frobenius norm of a tensor X is the square
root of the sum of the squares of all its elements
k
X
k
F
=
v
u
u
t
I
1
∑
i
1
=1
I
2
∑
i
2
=1
···
I
N
∑
i
N
=1
x
2
i
1
i
2
...i
N
. (3)
Let the norm of a tensor be defined as Equation 3.
Let
T = X ×
1
U
(1,k)
··· ×
n
U
(n,k)
X = T ×
1
(U
(1,k)
)
T
··· ×
n
(U
(n,k)
)
T
(4)
and
˜
T = Y ×
1
U
(1,k)
··· ×
n
U
(n,k)
V = X − Y
< Y,V > = 0,
(5)
such that Y is a sparse version of X ,
U
(1,k)
...U
(n,k)
N
n=1
form orthonormal basis and
V is the complementary dense version of X with
respect to Y.
GPU Accelerated Sparse Representation of Light Fields
179

We will use the orthogonal invariance property
from
U
(1,k)
...U
(n,k)
N
n=1
, which preserves the norm, i.e
kX k
2
= < X ,X >
= < X ,T ×
1
(U
(1,k)
)
T
··· ×
n
(U
(n,k)
)
T
>
= < X ×
1
U
(1,k)
··· ×
n
U
(n,k)
,T >
= < T ,T >
= kT k
2
(6)
By using Equation 4 and Equation 5 we can now de-
fine the problem as
kT −
˜
T k
2
= kT k
2
− 2 < T ,
˜
T > + k
˜
T k
2
,
(7)
and for the inner product we have that
< T ,
˜
T > = < T ,Y ×
1
U
(n,k)
··· ×
n
U
(1,k)
>
= < T ×
1
(U
(1,k)
)
T
··· ×
n
(U
(n,k)
)
T
,Y >
= < X , Y >
= < V + Y, Y >
= < V,Y > + < Y, Y >
= 0 + < Y, Y >
= kYk
2
.
(8)
With the property of orthogonality in Equation 6 and
Equation 8 we can rewrite Equation 7 to
kT −
˜
T k
2
= kT k
2
− 2kYk
2
+ kYk
2
= kT k
2
− kYk
2
(9)
We can now take advantage of the result in Equa-
tion 9 in our iterative routine. Since Y is sparse and
we iteratively include one element at a time from X ,
we can break this down to an element-wise update.
We have from Equation 3, together with a linear in-
dex j of P as the total number of elements, that
kT k
2
F
=
I
1
∑
i
1
=1
I
2
∑
i
2
=1
···
I
N
∑
i
N
=1
t
2
i
1
i
2
...i
N
=
P
∑
j=1
t
2
j
.
(10)
By putting Equation 9 and Equation 10 together we
have
kT k
2
F
− kYk
2
F
=
P
∑
j=1
t
2
j
−
P
∑
l=1
y
2
j
.
(11)
We exploit the sparse structure of Y and iteratively
add one element at a time from X . Let 0 < M < τ,
where M is the number of nonzero coefficients in the
sparse tensor Y at a specific iteration and τ is the spar-
sity paremeter. Then, from Equation 9 and the formu-
lation of Equation 11 together with the index l as the
location to the nonzero coefficients, we finally have
kT k
2
F
− kYk
2
F
=
N
∑
j=1
t
2
j
−
M
∑
l=1
y
2
l
.
(12)
4 RESULTS
The results for the GPU implementation were
achieved with Nvidia GeForce GTX Titan Xp and
Intel Xeon CPU W3670 at 3.2 GHz. Since the
computations were performed on the GPU only one
CPU core was used.
The timings for the CPU version were obtained
by a machine with four Xeon E7-4870, a total of 40
cores at 2.4 GHz. The data sets we used to evalute
our method were acquired by Stanford University
(Computer Graphics Laboratory, 2018). For the
training of the dictionaries we used the following
light fields: Lego Truck, Chess, Eucalyptus Flowers,
Jelly Beans, Amethyst, Bunny, Treasure Chest and
Lego Bulldozer. In order to create 5D data points we
used the central 8x8 views of the light fields. The
data points of each data set have the dimensions m
1
=
5, m
2
= 5, m
3
= 3, m
4
= 8 and m
5
= 8.
For the testing set we used Lego Knights (1024x1024
image resolution), Tarot Cards and Crystal Ball
(1024x1024 image resolution) and Bracelet
(1024x680 image resolution), see Figure 2. We
used sparsity parameter τ = 300, τ = 390, τ = 412,
respectively for the three data sets. We set the
threshold parameter ε = 5 × 10
−5
, ε = 5 × 10
−5
and
ε = 7 × 10
−5
, respectively.
We show the encoding time of the presented met-
hod, see Table 1, where we compare CPU time and
GPU time. We evaluated our method with K = 64
number of dictionaries. The total encoding time for
the CPU for the three data sets are 124 seconds, 122
seconds and 83 seconds, respectively. Comparing this
to our GPU implementation we get 8.5 seconds, 8.3
seconds and 5.2 seconds. Normalizing these results
to K = 1, we get the following timings per dictionary:
133.2 ms for Lego Knights, 129.8 ms for Tarot Cards
and Crystal Ball and 81.6 ms for Bracelet. Compa-
red to the CPU timings: 1937 ms, 1906 ms and 1296
ms, respectively. As seen in Table 1, we get a sig-
nificant computation speedup by processing the data
points segmentally in parallel on the GPU.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
180

Figure 2: Reference views of the Lego Knights, Tarot Cards and Crystal Ball and Bracelet data sets.
Table 1: The measured time for the Lego Knights data set with K = 64 dictionaries, sparsity τ = 300 and threshold ε =
5 × 10
−5
. Further we have K = 64, τ = 390 and ε = 7 × 10
−5
for the Tarot Cards. Lastly, we have K = 64, τ = 412 and
ε = 5 × 10
−5
for the Bracelet data set.
Data set GPU Time (s) CPU Time (s) Speedup
Lego Knights 8.5 124 x14.54
Tarot Cards 8.3 122 x14.70
Bracelet 5.2 83 x15.90
5 CONCLUSIONS
We have presented a GPU accelerated light field com-
pression method. The implemented method scales
in both memory and speed for higher dimensions -
which leads to faster computations, not only by faster
GPUs, but also by GPUs with larger memory. With
an order of magnitude faster computation speed, we
are able to produce a high quality compression that is
equivalent to the results of similar work in the rese-
arch field.
We also show that computations on a single GPU
outperforms even massively parallel CPUs. For even
faster performance, multiple GPUs can be used simul-
taneously.
With very few changes we can use same imple-
mentation for the training phase on the GPU. This
would accelerate the creation of the dictionaries more.
REFERENCES
Adelson, E. H. and Bergen, J. R. (1991). The plenoptic
function and the elements of early vision. In Com-
putational Models of Visual Processing, pages 3–20.
MIT Press.
Aharon, M., Elad, M., and Bruckstein, A. (2006). k -svd:
An algorithm for designing overcomplete dictionaries
for sparse representation. Signal Processing, IEEE
Transactions on, 54(11):4311–4322.
Babacan, S., Ansorge, R., Luessi, M., Mataran, P. R., Mo-
lina, R., and Katsaggelos, A. K. (2012). Compressive
light field sensing. IEEE Trans. on Image Processing,
21(12):4746–4757.
Choudhury, B., Swanson, R., Heide, F., Wetzstein, G., and
Heidrich, W. (2017). Consensus convolutional sparse
coding. In 2017 IEEE International Conference on
Computer Vision (ICCV), pages 4290–4298.
Computer Graphics Laboratory, S. U. (2018). Stanford uni-
versity - the (new) stanford light field archive. http:
//lightfield.stanford.edu/. Accessed: 2018-07-23.
Elad, M. (2010). Sparse and Redundant Representations:
GPU Accelerated Sparse Representation of Light Fields
181

From Theory to Applications in Signal and Image Pro-
cessing. Springer Publishing Company, Incorporated,
1st edition.
Jones, A., Nagano, K., Busch, J., Yu, X., Peng, H. Y., Bar-
reto, J., Alexander, O., Bolas, M., Debevec, P., and
Unger, J. (2016). Time-offset conversations on a life-
sized automultiscopic projector array. In 2016 IEEE
Conference on Computer Vision and Pattern Recogni-
tion Workshops (CVPRW), pages 927–935.
Kolda, T. G. and Bader, B. W. (2009). Tensor decompositi-
ons and applications. SIAM Review, 51(3):455–500.
Levoy, M. A. (2001). The digital michelangelo project.
Computer Graphics Forum, 18(3):xiii–xvi.
Liang, C.-K., Lin, T.-H., Wong, B.-Y., Liu, C., and Chen,
H. H. (2008). Programmable aperture photography:
multiplexed light field acquisition. In Proc. of ACM
SIGGRAPH, volume 27, pages 1–10.
Miandji, E., Kronander, J., and Unger, J. (2013). Lear-
ning based compression of surface light fields for real-
time rendering of global illumination scenes. In SIG-
GRAPH Asia 2013 Technical Briefs, SA ’13, pages
24:1–24:4, New York, NY, USA. ACM.
Miandji, E., Kronander, J., and Unger, J. (2015). Compres-
sive image reconstruction in reduced union of subspa-
ces. Comput. Graph. Forum, 34(2):33–44.
Ng, R. (2005). Light field photography with a hand-held
plenoptic camera. Computer Science Technical Report
CSTR 2, 11:1–11.
Vaish, V., Levoy, M., Szeliski, R., Zitnick, C. L., and Kang,
S. B. (2006). Reconstructing occluded surfaces using
synthetic apertures: Stereo, focus and robust measu-
res. In 2006 IEEE Computer Society Conference on
Computer Vision and Pattern Recognition (CVPR’06),
volume 2, pages 2331–2338.
Wanner, S. and Goldluecke, B. (2013). Variational light
field analysis for disparity estimation and super-
resolution. IEEE Transactions of Pattern analysis and
machine intelligence, 36(3).
Wetzstein, G., Lanman, D., Hirsch, M., and Raskar, R.
(2012). Tensor displays: Compressive light field synt-
hesis using multilayer displays with directional back-
lighting. ACM Trans. Graph., 31(4):80:1–80:11.
Williem, W. and Park, I. K. (2016). Robust light field depth
estimation for noisy scene with occlusion. In 2016
IEEE Conference on Computer Vision and Pattern Re-
cognition (CVPR), pages 4396–4404.
VISAPP 2019 - 14th International Conference on Computer Vision Theory and Applications
182
